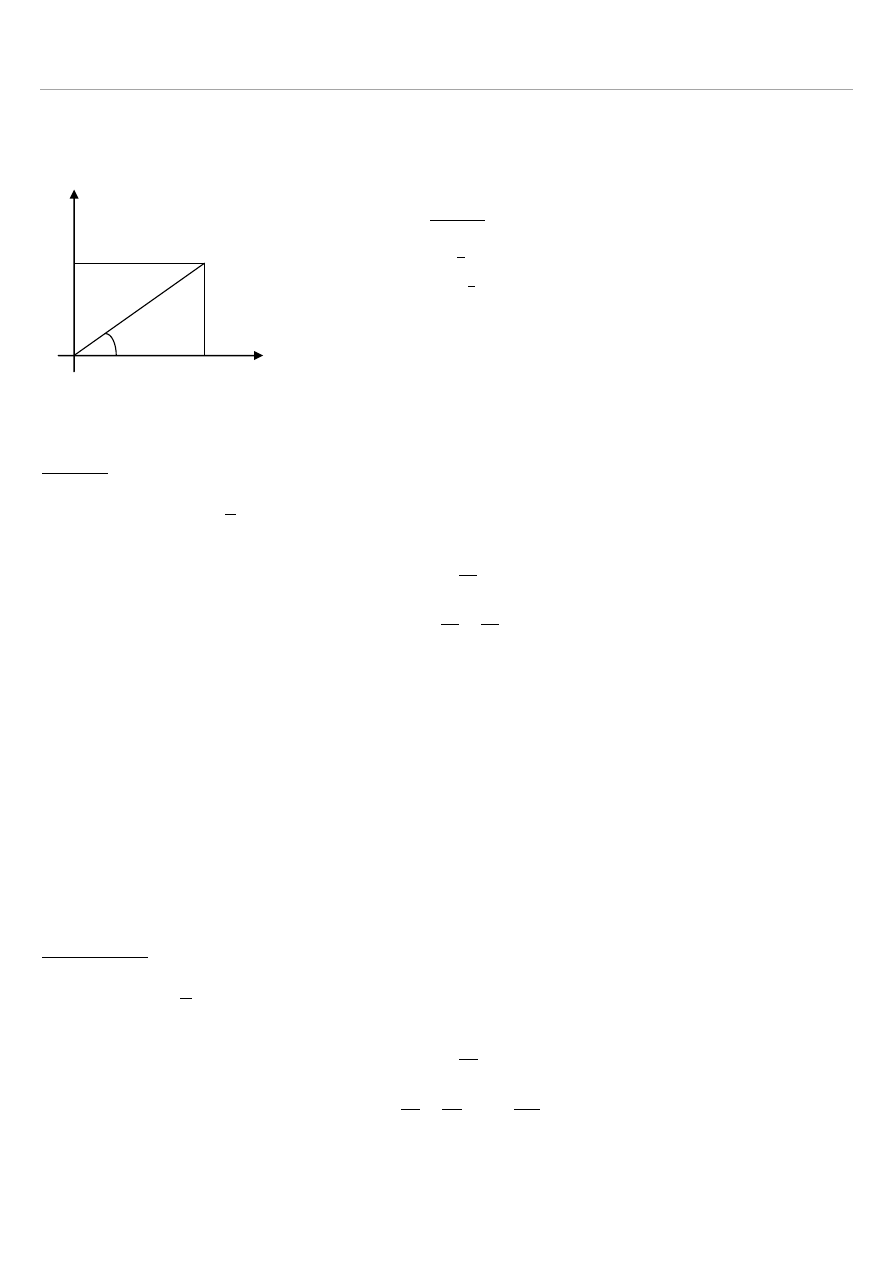
Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

1

Zad. 1 (1 pkt)
Podać relacje wiążące współrzędne kartezjańskie (x, y) i biegunowe (ρ, φ) punktu na płaszczyźnie.

y

x

P = (x,y) = (ρ,φ)

ρ

y

φ

x

Zad. 2 (1 pkt)
Prędkość: prędkość średnia, prędkość chwilowa, szybkość, jednostki.

Prędkość jest wektorem i jest definiowana jako zmiana wektora położenia w czasie. Prędkość chwilowa jest
pochodną wektora położenia po czasie. Szybkość jest skalarem i jest wartością wektora prędkości. Jednostką
prędkości i szybkości jest

.

— prędkość średnia

— prędkość chwilowa

— prędkość
— szybkość
— zmiana wektora położenia
— czas, w którym nastąpiło przemieszczenie

Zad. 3 (2 pkt)
Przyspieszenie: definicja i jednostki, przyspieszenie styczne i normalne, związek tych składowych z
szybkością i krzywizną toru.

Przyspieszenie jest wektorem i jest definiowane jako zmiana wektora prędkości w czasie. Przyspieszenie
chwilowe jest pochodną wektora prędkości po czasie i drugą pochodną wektora położenia po czasie. Jednostką
przyspieszenia jest

.

— przyspieszenie średnie

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

2

— przyspieszenie chwilowe

— zmiana wektora prędkości
— czas, w którym nastąpiła zmiana prędkości

— przyspieszenie styczne

— przyspieszenie normalne

— prędkość
— promień krzywizny toru

Zad. 4 (2 pkt)
Dla ruchu ze stałym przyspieszeniem a

0

, dane są warunki początkowe r(0) = r

0

i v(0)=v

0

. Korzystając

z definicji prędkości i przyśpieszenia, obliczyć zależność r(t).

Zad. 5 (2 pkt)
Podać (lub wyprowadzić) wyrażenia na składowe radialne i transwersalne wektorów położenia,
prędkości i przyspieszenia cząstki w ruchu płaskim, opisanym w biegunowym układzie współrzędnych.

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

3

Zad. 6 (1 pkt)
Sformułować I i II zasadę dynamiki Newtona dla pojedynczej cząstki oraz III zasadę dynamiki
Newtona dla pary cząstek.

I zasada dynamiki:
W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało
pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

II zasada dynamiki:
Jeśli siły działające na ciało nie równoważą się (czyli siła wypadkowa jest różna od zera), to ciało porusza się z
przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała.

III zasada dynamiki:

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

4

Oddziaływania ciał są zawsze wzajemne. Siły wzajemnego oddziaływania dwóch ciał mają takie same wartości,
taki sam kierunek, przeciwne zwroty i różne punkty przyłożenia (każda działa na inne ciało).

— siła wypadkowa

— prędkość
— przyspieszenie
— masa ciała

— siła z jaką działa ciało 1 na ciało 2

— siła z jaką działa ciało 2 na ciało 1

Zad. 7 (1 pkt)
Korzystając z definicji momentu pędu i momentu siły

, wyprowadzić relację łączącą te dwie

wielkości (dla pojedynczej cząstki).

Zad. 8 (2 pkt)
Podać definicję energii potencjalnej oraz sformułować i udowodnić zasadę zachowania energii
mechanicznej dla pojedynczej cząstki.

Energia potencjalna – energia jaką ma układ ciał umieszczony w polu sił zachowawczych, wynikająca z
rozmieszczenia tych ciał. Równa jest pracy, jaką trzeba wykonać, aby uzyskać daną konfigurację ciał, wychodząc
od innego rozmieszczenia, dla którego umownie przyjmuje się jej wartość równą zero. Jest funkcją skalarną, której
gradient ze znakiem ( ) jest równy sile opisującej pole.

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

5

Q.E.D.

— energia potencjalna w punkcie a

— energia potencjalna w punkcie b

— energia kinetyczna w punkcie a

— energia kinetyczna w punkcie b

— zmiana energii potencjalnej

— praca

Zad. 9 (2 pkt)
Dany jest układ N cząstek oddziałujących ze sobą siłami newtonowskimi, tj. takimi, że

=

, dla

każdej pary cząstek i, j; na układ ten nie działa żadna siła zewnętrzna. Udowodnić, że w układzie takim
pęd całkowity jest stały w czasie (zasada zachowania pędu).

— całkowity pęd układu cząstek

— pęd cząstki i

— siła wypadkowa działająca na cząstkę i

— siła oddziaływania cząstki i na cząstkę j

— siła oddziaływania cząstki j na cząstkę i

— siła zewnętrzna działająca na cząstkę i

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

6

— całkowita siła zewnętrzna działająca na układ cząstek

Zad. 10 (1 pkt)
Sformułować zasadę zachowania momentu pędu w układzie izolowanym N cząstek.

Suma momentów pędu poszczególnych cząstek w układzie izolowanym jest stała w czasie.

— moment pędu cząstki i

Zad. 11 (1 pkt)
Podać definicję środka masy w układzie N cząstek. Jak dla izolowanego układu N cząstek, w
dowolnym układzie inercjalnym zmienia się położenie środka masy?

Środek masy układu cząstek jest punktem, w którym skupiona jest cała masa w opisie układu jako masy
punktowej.

— położenie środka masy

— położenie cząstki i

— masa cząstki i

Środek masy układu izolowanego w dowolnym układzie inercjalnym pozostaje w spoczynku lub porusza się
ruchem jednostajnym.

Zad. 12 (2 pkt)
Co to jest siła harmoniczna, jaką ma postać równanie Newtona dla oscylatora harmonicznego i jakie
jest rozwiązanie tego równania? Podać, jakie warunki początkowe w pełni określają ruch takiego
oscylatora. Ile wynosi okres drgań takiego oscylatora?

Siła harmoniczna – siła proporcjonalna do wychylenia ciała z punktu równowagi skierowana do
początku układu.

Równanie Newtona:

Rozwiązanie równania:

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

7

— siła
— stała sprężystości
— odchylenie od położenia równowagi
— masa ciała drgającego w oscylatorze
— amplituda drgań oscylatora
— faza początkowa drgań oscylatora

— częstość kołowa drgań oscylatora

— okres drgań oscylatora
— częstotliwość drgań oscylatora

Warunki początkowe określające ruch oscylatora: ,

Zad. 13 (2 pkt)
Jaką ma postać równanie Newtona dla drgań tłumionych z siłą oporu proporcjonalną do prędkości i
jakie jest rozwiązanie tego równania dla przypadku słabego tłumienia? Podać charakterystyczne cechy
drgań tłumionych w porównaniu z drganiami bez tłumienia.

Równanie Newtona:

Rozwiązanie równania:

— siła
— stała sprężystości
— odchylenie od położenia równowagi
— masa ciała drgającego w oscylatorze

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

8

— amplituda drgań oscylatora
— współczynnik tłumienia

— częstość kołowa drgań oscylatora

— czas relaksacji

W drganiach tłumionych amplituda zmniejsza się, a okres drgań wydłuża, natomiast w drganiach bez tłumienia
pozostają one stałe.

Zad. 14 (3 pkt)
Podać postać równania Newtona dla oscylatora harmonicznego z niezerowym tłumieniem oraz
harmoniczną siłą zewnętrzną. Jaka jest postać rozwiązania tego równania ważna, gdy warunki
początkowe przestają mieć znaczenie? Jak amplituda takiego rozwiązania zależy od częstości siły
wymuszającej oraz co to są rezonans i częstość rezonansowa.

Równanie Newtona:

Rozwiązanie równania:

Rezonans – zjawisko wzmocnienia drgań poprzez zwiększenie ich amplitudy do pewnej wartości maksymalnej,
którą osiąga dla częstości rezonansowej.

Częstość rezonansowa – częstość wymuszeń, dla której zachodzi zjawisko rezonansu (zwiększenie amplitudy).

— amplituda

— siła wymuszająca

— częstość siły wymuszającej

— częstość rezonansowa

Zad. 15 (1 pkt)
Sformułować prawo powszechnej grawitacji Newtona; jaka jest wartość stałej grawitacji G i jak
brzmi zasada superpozycji dla sił grawitacji?

Prawo powszechnej grawitacji:

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

9

Między dowolną parą ciał posiadających masy pojawia się siła przyciągająca, która działa na linii łączącej ich
środki, a jej wartość rośnie z iloczynem ich mas i maleje z kwadratem odległości.

— siła grawitacji
— stała grawitacji

— masa ciała 1

— masa ciała 2

— odległość między środkami ciał
— wersor r

Zasada superpozycji dla sił grawitacji:
Siła pochodząca od kilku źródeł jest wektorową sumą sił, jakie wytwarza każde z tych źródeł.

Zad. 16 (1 pkt)
Jak natężenie pola grawitacyjnego zależy od odległości od środka cienkiej powłoki kulistej o
promieniu R i masie M?

— natężenie pola grawitacyjnego
— stała grawitacji
— masa ciała
— odległość od środka ciała
— wersor r

Dla :

Dla :

Zad. 17 (1 pkt)
Sformułować I prawo Keplera w formie dokładnej i przybliżonej.

I prawo Keplera (w. dokładna):
Masa zredukowana obiega środek masy po krzywej stożkowej, a środek masy znajduje się w ognisku
krzywej stożkowej.

I prawo Keplera (w. przybliżona):
Każda planeta Układu Słonecznego porusza się wokół Słońca po elipsie, w której w jednym z ognisk jest Słońce.

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

10

Zad. 18 (2 pkt)
Korzystając z zasady zachowania momentu pędu, udowodnić II prawo Keplera.

II prawo Keplera:

Dowód:

— prędkość polowa (wektor prostopadły do płaszczyzny orbity)

— wektor powierzchni o wartości pola zakreślanego w czasie dt przez promień wodzący o początku w ognisku
orbity
— odległość od ogniska orbity (promień wodzący)
— nieskończenie mały wektor przemieszczenia w ruchu po orbicie
— moment pędu planety
— pęd planety
— masa planety
— prędkość liniowa planety na orbicie

Zad. 19 (2 pkt)
Korzystając z I i II prawa Keplera, udowodnić III prawo Keplera dla ruchu planet po orbitach
eliptycznych. Uwaga! W I prawie Keplera, parametr p elipsy dany jest wzorem:

.

Q.E.D.

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

11

— wektor pola ograniczonego orbitą planety
— wersor S
— półoś wielka elipsy
— półoś mała elipsy
— wersor b
— okres obiegu planety
— moment pędu planety
— parametr elipsy
— stała grawitacji

— masa ciała 1

— masa ciała 2

Zad. 20 (1 pkt)
Bryła sztywna: określić pojęcie oraz podać dwa podstawowe równania dynamiki.

Bryła sztywna – układ N cząstek o stałej odległości od siebie i oddziałujących między sobą siłami centralnymi.

— pęd bryły sztywnej

— siła zewnętrzna działająca na bryłę sztywną

— moment pędu bryły sztywnej

— moment siły działający na bryłę sztywną

Zad. 21 (1 pkt)
Co to jest wektor prędkości kątowej w ruchu obrotowym bryły sztywnej?

W ruchu obrotowym bryły sztywnej istnieje jednoznacznie zdefiniowany wektor

o takiej własności, że dla

każdego punktu bryły sztywnej wyznaczonego przez wektor wodzący jego prędkość jest dana wzorem:

Zad. 22 (2 pkt)
Jak energia kinetyczna bryły sztywnej E

k

wyraża się przez wektor prędkości kątowej

i składowe

tensora momentu bezwładności

? Co to są i jakimi są dane wyrażeniami składowe tegoż tensora

momentu bezwładności?

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

12

Gdy osie układu odniesienia pokrywają się z głównymi osiami układu współrzędnych następuje uproszczenie:

Składowe tensora momentu bezwładności to 9 liczb opisujących rozkład masy w bryle sztywnej.

Zad. 23 (3 pkt)
Podać równania Eulera i ich rozwiązanie dla symetrycznego bąka w nieobecności sił zewnętrznych;
opisać ruch tego bąka: co to są precesja, stożek polhodii i stożek herpolhodii.

3 równania Eulera:

Dla bąka symetrycznego:

Rozwiązania:

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

13

Precesja – zjawisko zmiany kierunku osi obrotu obracającego się ciała. Oś obraca się wtedy zakreślając
powierzchnię stożkową.

Stożek polhodii – stożek który jest zakreślany przez wektor prędkości kątowej.

Stożek herpolhodii – stożek który jest zakreślany przez wektor momentu pędu.

Zad. 24 (1 pkt)
Sformułować twierdzenie o osiach równoległych (twierdzenie Steinera).

Twierdzenie Steinera:
Moment bezwładności bryły sztywnej względem dowolnej osi jest równy sumie momentu bezwładności względem
osi równoległej do danej i przechodzącej przez środek masy bryły oraz iloczynu masy bryły i kwadratu odległości
między tymi dwiema osiami.

— moment bezwładności względem osi przechodzącej przez środek masy

— moment bezwładności względem osi równoległej do pierwszej osi
— masa bryły sztywnej
— odległość miedzy osiami

Zad. 25 (1 pkt)
Sformułować prawo Hooke’a dla odkształceń normalnych; co to jest moduł Younga E ?

Prawo Hooke’a:
Odkształcenie ciała pod wpływem działającej na niego siły jest wprost proporcjonalne do tej siły.

— siła rozciągająca (ściskająca)
— pole przekroju poprzecznego
— zmiana długości
— długość początkowa
— moduł Younga

Moduł Younga – wielkość określająca sprężystość materiału. Wyraża ona, charakterystyczną dla danego materiału,
zależność względnego odkształcenia liniowego materiału od naprężenia, jakie w nim występuje w zakresie
odkształceń sprężystych.

Zad. 26 (1 pkt)
Jak zmieniają się wymiary poprzeczne przy rozciąganiu (ściskaniu) i co to jest współczynnik
Poissona ?

Podstawy Fizyki – Mechanika MS

Przykładowe pytania egzaminacyjne

14

— zmiana szerokości
— szerokość początkowa
— zmiana wysokości
— wysokość początkowa
∆l — zmiana długości
l — długość początkowa
— współczynnik Poissona

Współczynnik Poissona - stosunek odkształcenia poprzecznego do odkształcenia podłużnego przy osiowym stanie
naprężenia. Współczynnik Poissona jest wielkością bezwymiarową i nie określa sprężystości materiału, a jedynie
sposób w jaki się on odkształca.