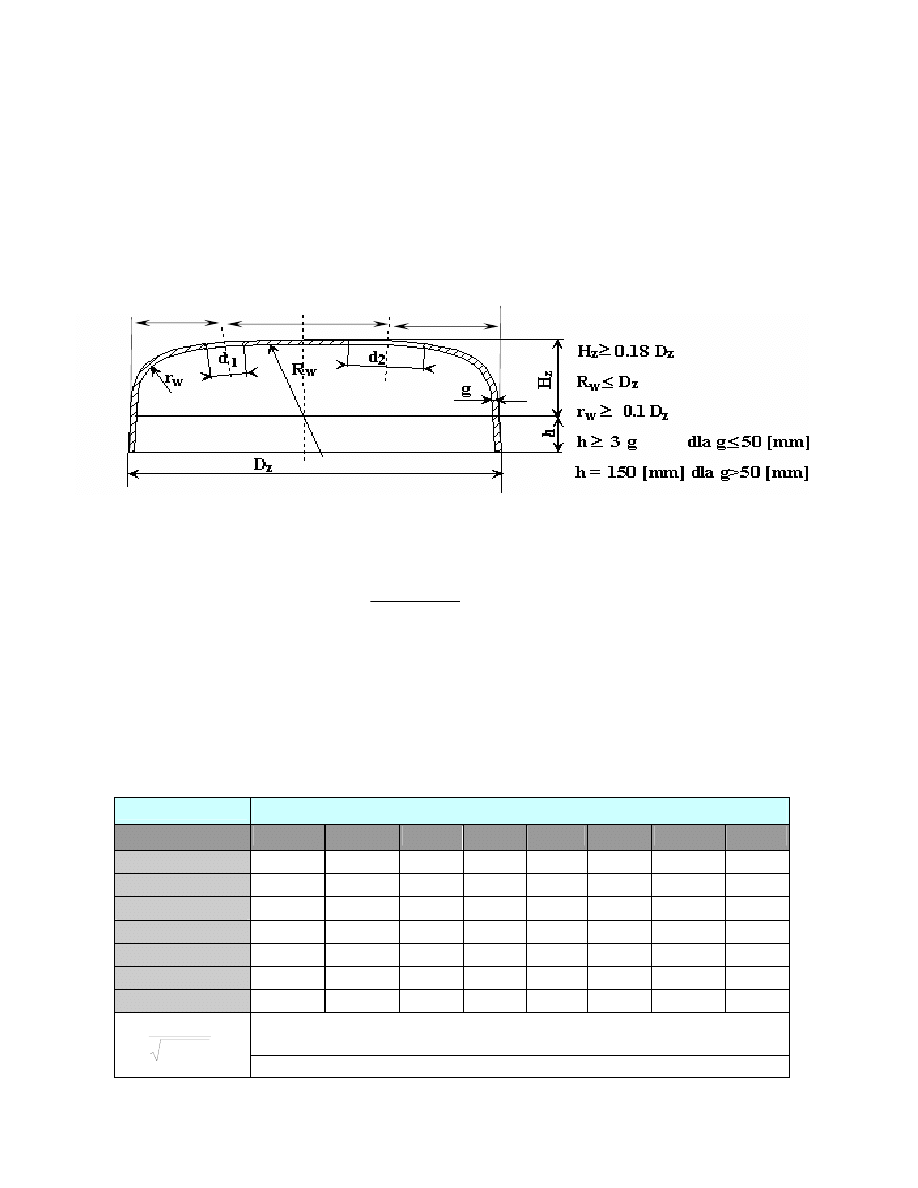
5.a. Obliczanie grubości ścianek dennic sferoidalnych (elipsoidalnych)
Średnice
Średnice dennic, podobnie jak i zbiorników, są znormalizowane i zgodnie z normą BN-64/2201-01 wynoszą:
D
z
= 0.219, 0.273, 0.324, 0.356, 0.406, 0.457 lub 0.508 [m], dla średnic zewnętrznych lub D
w
= 0.6, 0.7, 0.8, (0.9),
1.0, (1.1), 1.2, (1.3), 1.4, (1.5), 1.6, (1.7), 1.8, (1.9), 2.0, 2.2, 2.4, 2.6, 2.8, 3.0, 3.2, 3.4, 3.6, 4.0 dla zbiorników oraz
dodatkowo dla kolumn 4.5, 5.0, 6.3, 8.0 i 10.0 [m]. Wartości w nawiasach dotyczą średnic płaszczy grzejnych.
Profile den elipsoidalnych i koszykowych oraz znajdujące się w dnie otwory, o ile są, powinny spełniać
podane poniżej warunki na: H
z
, D
z
, R
w
, r
w
, l
0
, l
z1
i l
zi
.
l
0
l
z2
l
z1
l
0
> d
1
l
zi
> 0.1 D
z
Grubość ścianki
W dennicy sferycznej grubość ścianki wyznacza się z zależności:
3
2
1
0
4
c
c
c
k
y
D
p
g
r
w
z
rz
+
+
+
⋅
⋅
⋅
=
[m]
gdzie:
p
o
[MN/m
2
] jest ciśnieniem obliczeniowym,
D
z
[m] jest średnicą zewnętrzną dennicy,
k
r
[MN/m
2
] jest wartością naprężeń dopuszczalnych na rozciąganie,
y
w
[ - ] jest współczynnikiem wytrzymałościowym powłoki (Tablica) [8], zależnym od kształtu dennicy H
z
/D
z
i
wielkości największego z otworów w dnie, opisanym funkcją
ω, przy czym dla den bez otworów lub z otworami
wzmocnionymi pierścieniami
ω = 0.
yw
Hz /Dz 0.18
0.2
0.25
0.3
0.35
0.4
0.45
0.5
ω = 0.0
3.37 2.9 2 1.53
1.3
1.18 1.12 1.1
ω = 0.5
3.37 2.9 2 1.65
1.42
1.3 1.23 1.2
ω = 1.0
3.37 2.9 2.3 2 1.81
1.7 1.63 1.6
ω = 2.0
3.92 3.68 3.21
2.92
2.69 2.5 2.33 2.2
ω = 3.0
4.87 4.61 4.1 3.77
3.52
3.32 3.15 3
ω = 4.0
5.78 5.53 4.99
4.58
4.28
4.04 3.86 3.7
ω = 5.0
6.77 6.5 5.9
5.41
5.03
4.76 4.52 4.35
Dla wartości pośrednich stosować interpolację, przyjmować wartości
zaokrąglone do drugiego miejsca po przecinku.
rz
z
g
D
d
=
ω
Za (d) przyjmować średnicę największego otworu.
13
c
1
, c
2
i c
3
[m] są naddatkami na: korozję, tolerancję wyrobów walcowanych i inne nieprzewidziane w obliczeniach
oddziaływania np. wahania temperatury, zmęczenie materiału (Tablica) [8]:
Naddatek na korozję zależny od stopnia
odporności materiału
c
1
c
1
= s. τ
s [m/rok] wyznacza się z tablic stopni
odporności dla różnych materiałów
τ -czas eksploatacji zbiornika [lata]
Naddatek na tolerancję grubości blach
walcowanych (ujemna odchyłka tolerancji)
c
2
c
2
= 0.0005 [m] dla blach o grubości g <5 [mm],
c
2
= 0.0006 [m] dla blach 6 < g < 7 [mm],
c
2
= 0.0008 [m] dla blach 8 <g < 20 [mm],
c
2
= 0.001 [m] dla blach g > 20 [mm].
Naddatek na inne naprężenia (np.termiczne)
c
3
ustala projektant, zwyczajowo 0.001 [m]
Przykład obliczania grubości ścianek dennicy sferycznej
Przykład I Tematem projektu jest cylindryczny, pionowy i bezciśnieniowy zbiornik przeznaczony do
magazynowania 2 ton oleju opałowego. Zbiornik ma być umieszczony 2.5 [m] nad poziomem gruntu, na zewnątrz i
ma być eksploatowany przez
τ = 5 [lat]. Z dotychczasowych obliczeń otrzymano: V
nom
= 3.2 [m
3
], D
w
=1.6 [m],
p
o
= 0.1 [MPa], t
o
= 50 [
o
C], k
r
= 145.8 [MPa] dla den wypukłych i stali St3S i średnica króćca d
z
= 0.133 [m].
Dane/Założenia:
Obliczenia:
Wyniki:
5. Grubość dennicy
5.1. Obliczenie naddatków
τ = 5 [lat],
Zał.: g>0.01 [m],
8 <g < 20 [mm]
czyli c
2
= 0.0008
[m],
c
3
= 0.001 [m].
Dobrana w poprzednim punkcie, jako materiał konstrukcyjny zbiornika,
stal St3S w oddziaływaniu z olejem opałowym ma I stopień odporności
korozyjnej, któremu odpowiada szybkość korozji s = 0.0001 [m/rok] stąd:
c
1
=
τ s = 0.0005 [m], a następnie:
c = c
1
+ c
2
+ c
3
= 0.0005+0.0008+0.001 = 0.0023 [m]
c = 0.0023 [m]
5.2. Obliczenia wstępne, g
rz,I
grubość dennicy - I przybliżenie
D
w
=1.6 [m],
p
o
= 0.1[MPa],
k
r
= 145.8 [MPa]
c = 0.0023 [m]
Założenie wstępne: D
z
≈ D
w
, y
w
= 1.
0026
.
0
0023
.
0
8
.
145
4
1
6
.
1
1
.
0
4
3
2
1
0
1
,
=
+
⋅
⋅
⋅
=
+
+
+
=
c
c
c
k
y
D
p
g
r
w
z
rz
[m]
Dla znormalizowanej dennicy stalowej, tłoczonej o małej wypukłości
(PN-69/M-35413) (Mat.Pom.[5.1]) najmniejsza grubość ścianki dennicy
wynosi g
d
= 0.006 [m] a h
w
= 0.207 [m].
g
rz,1
= 0.003 [m]
h
w
= 0.207 [m]
g
d
= 0.006 [m]
5.3. Skorygowanie naddatku na korozję
c
1
= 0.0005 [m],
6 < g
d
< 7 [mm],
czyli c
2
= 0.0006
c
3
= 0.001 [m].
Ponieważ zmieniła się grubość blachy dennicy, w stosunku do założonej
(g > 0.01 [m]), więc trzeba skorygować wartość c
2
i c:
c = c
1
+ c
2
+ c
3
= 0.0005 + 0.0006 + 0.001 = 0.0021 [m]
c = 0.0021 [m]
14
5.4 Wyznaczenie H
z
/D
z
i
ω dla dna z otworami ω ≠ 0
g
rz
=g
d
=0.006 [m]
H
z
=h
w
=0.207[m]
d = 0.14 [m].
Wersja I. Zał., że w dennicy jest otwór o średnicy d = 0.14 [m], w który
wspawany jest króciec o średnicy d
z
= 0.133 [m], a otwór nie ma pierścienia
wzmacniającego:
D
z
= D
w
+ 2g
rz
= 1.6 + 2
.
0.006 = 1.612 [m]
H
z
/D
z
= 0.207/1.612 = 0.1284
Wartość H
z
/D
z
< 0.18, czyli, gdyby liczony zbiornik był zbiornikiem
ciśnieniowym, to zgodnie z przepisami UDT [8] należałoby wybrać inną
dennicę. Ponieważ jednak zbiornik jest bezciśnieniowy można pozostać przy
tej dennicy przyjmując, że H
z
/D
z
= 0.18.
423
.
1
006
.
0
612
.
1
14
.
0
=
⋅
=
=
rz
z
g
D
d
ω
Wartość
ω = 1.423 zawarta jest w Tablicy pomiędzy ω = 1.0 i = 2.0 więc
obliczenia y
w
dla H
z
/D
z
= 0.18 należy przeprowadzić poprzez interpolację
pomiędzy skrajnymi wartościami
ω.
D
z
= 1.612 [m]
H
z
/D
z
= 0.1284
ω = 1.423
5.5. Obliczeniowa y
w
dla H
z
/D
z
= 0.18
ω = 1.423
y
w(
ω =1.0)
= 3.37
y
w(
ω =2.0)
= 3.92
Z proporcji:
0
.
1
0
.
2
37
.
3
92
.
3
0
.
1
423
.
1
37
.
3
−
−
=
−
−
w
y
wynika, że: y
w
= 3.603
y
w
= 3.603
5.6. Grubość dennicy g
rz,2
- II przybliżenie
D
z
=1.612 [m],
p
o
= 0.1[MPa],
k
r
= 145.8 [MPa]
y
w
= 3.603
c = 0.0021 [m]
0031
.
0
0021
.
0
8
.
145
4
603
.
3
612
.
1
1
.
0
4
0
2
,
=
+
⋅
⋅
⋅
=
+
=
c
k
y
D
p
g
r
w
z
rz
[m],
Obliczona grubość ścianki dennicy nie przekracza przyjętej w pierwszym
przybliżenia wartości, więc w tym miejscu obliczenia można zakończyć
przyjmując najbliższą znormalizowaną dla tej średnicy dennicy wartość: g
rz
= 0.006 [m],
g
rz
= 0.006 [m]
5.7. Obliczanie y
w
dla
ω = 0
ω = 0
H
z
/D
z
= 0.18
Wersja II. Zał. W dennicy nie ma otworu, a jeżeli jest to z prawidłowo
obliczonym i wspawanym pierścieniem wzmacniającym.
Wartościom
ω = 0 i H
z
/D
z
= 0.18 odpowiada w Tablicy y
w
= 3.37
y
w
= 3.37
5.8. Grubość dennicy bez otworów g
rz,1
(I przybliżenie)
D
z
=1.612 [m],
p
o
= 0.1 [MPa],
k
r
= 145.8 [MPa]
y
w
= 3.37,
c = 0.0021 [m]
003
.
0
0021
.
0
8
.
145
4
37
.
3
612
.
1
1
.
0
4
0
1
,
=
+
⋅
⋅
⋅
=
+
=
c
k
y
D
p
g
r
w
z
rz
[m],
Dalsze obliczenia nie są już konieczne i można je skończyć na I
przybliżeniu, przyjmując najmniejszą dla tej średnicy dennicy wartość
grubości jej ścianek: g
rz
= 0.006 [m].
g
rz
= 0.006 [m]
3.9
y
w
2
y
w
3.37
1.0
1.423
ω
2.0
15
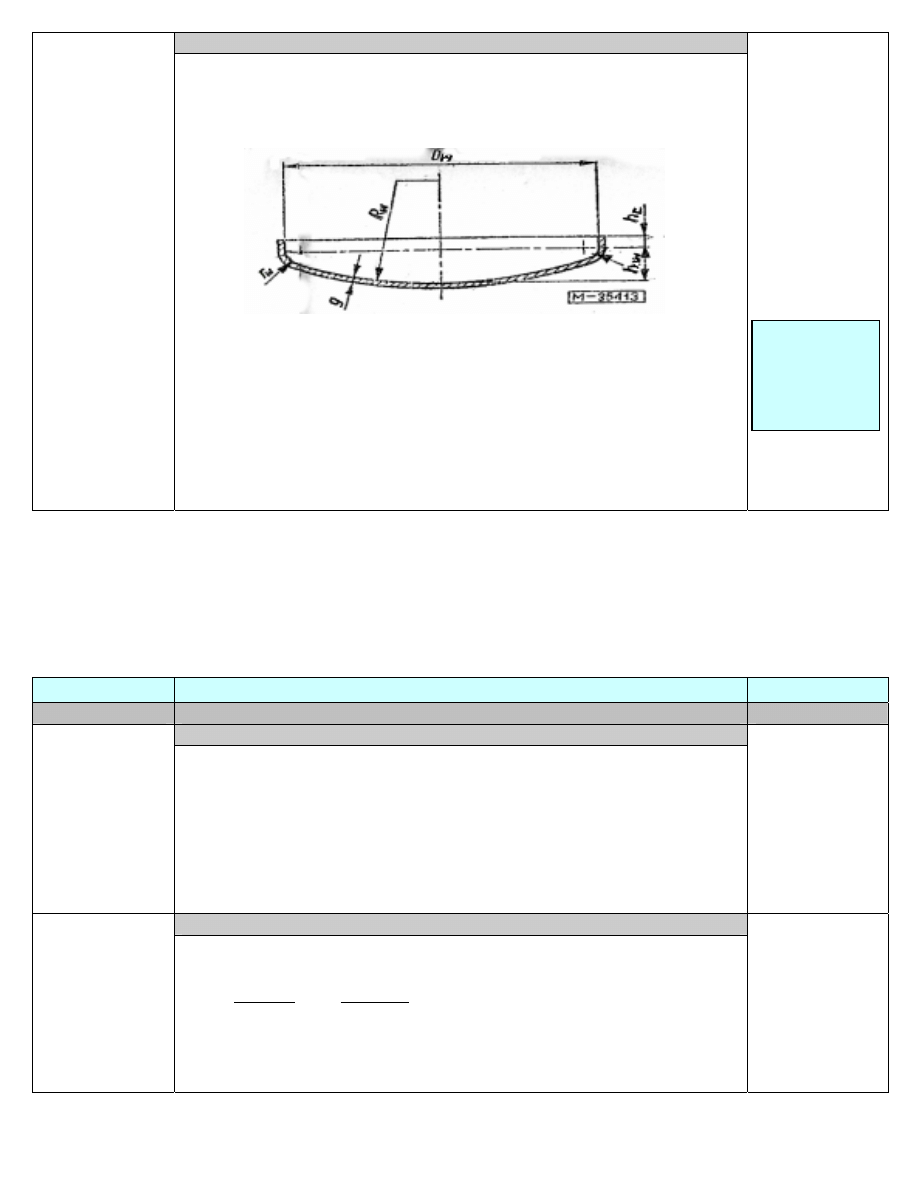
5.9 Wyznaczenie pozostałych parametrów dennicy
Zgodnie z normą PN-69/M-35413 (Mat.Pom.[5.1]), dla zadanej średnicy,
najmniejszą możliwą grubość dennicy stalowej ze stali St3S, tłoczonej o
małej wypukłości jest grubości g
rz
= 0.006 [m]. Pozostałe dane i wymiary tej
dennicy są następujące:
V = 0.249 [m
3
] (objętość dotyczy tylko elipsoidalnej części dna – do
wysokości h
w
), h
w
= 0.207 [m], h
c
= 0.040 [m], R
w
= 2 [m], r
w
= 0.06 [m] i
masa G = 122.5 [kg]
Przeprowadzone obliczenia wskazują jednak, że dobrana dennica jest
przewymiarowana, gdyż dla podanego w zadaniu ciśnienia i średnicy
grubość ścianki dennicy mogłaby być dwa razy cieńsza i to bez względu na
to, czy znajduje się w niej otwór na króciec, czy jest bez otworu.
Taką dennicę pod numerem katalogowym PFB3 oferuje f-ma
ITALINOX-Polska (Mat.Pom.[5.10])
g
rz
= 0.006 [m]
V = 0.249 [m
3
]
h
w
= 0.207 [m]
h
c
= 0.040 [m]
G = 122.5 [kg]
Przykład II. Tematem projektu jest cylindryczny, poziomy zbiornik o pojemności V = 4.5 [m
3
], ciśnieniu p = 15
[at] i temperaturze t = 15 - 50 [
o
C] przeznaczony do magazynowania amoniaku. Zbiornik ma być umieszczony w
pomieszczeniu piwnicznym o wysokości 3 [m], skąd przetłaczany jest amoniak na wysokość 4 [m] do hali
sprężarek. Zbiornik ma byś eksploatowany przez
τ = 5 [lat]. Z dotychczasowych obliczeń otrzymano: V
nom
= 5.0
[m
3
], D
w
=1.6 [m], p
o
= 1.6 [MPa], t
o
= 50 [
o
C], k
r
=147.8 [MPa] (dla den wypukłych) i stali 1H18N9T.
16
Dane/Założenia:
Obliczenia:
Wyniki:
5. Grubość dennicy z króćcami bez pierścieni wzmacniających
5.1. Obliczenie naddatków grubości c
τ = 5 [lat],
Zał.:
g > 0.02 [m],
czyli:
c
2
= 0.001[m],
c
3
= 0.001 [m].
Dobrana w poprzednim punkcie, jako materiał konstrukcyjny zbiornika,
stal stopowa 1H18N9T w oddziaływaniu z amoniakiem ma I stopień
odporności korozyjnej, któremu odpowiada szybkość korozji s = 0.0001
[m/rok] stąd:
c
1
=
τ s = 0.0005 [m], a następnie:
c = c
1
+ c
2
+ c
3
= 0.0005+0.001+0.001 = 0.0025 [m]
c = 0.0025 [m]
5.2. Obliczenia wstępne, grubość dennicy g
rz,1
– I przybliżenie
D
w
=1.6 [m],
p
o
= 1.6[MPa],
k
r
= 147.8 [MPa]
c = 0.0025 [m]
Założenie wstępne: D
z
≈ D
w
, y
w
= 1.
00683
.
0
0025
.
0
8
.
147
4
1
6
.
1
6
.
1
4
0
1
,
=
+
⋅
⋅
⋅
=
+
=
c
k
y
D
p
g
r
w
z
rz
[m]
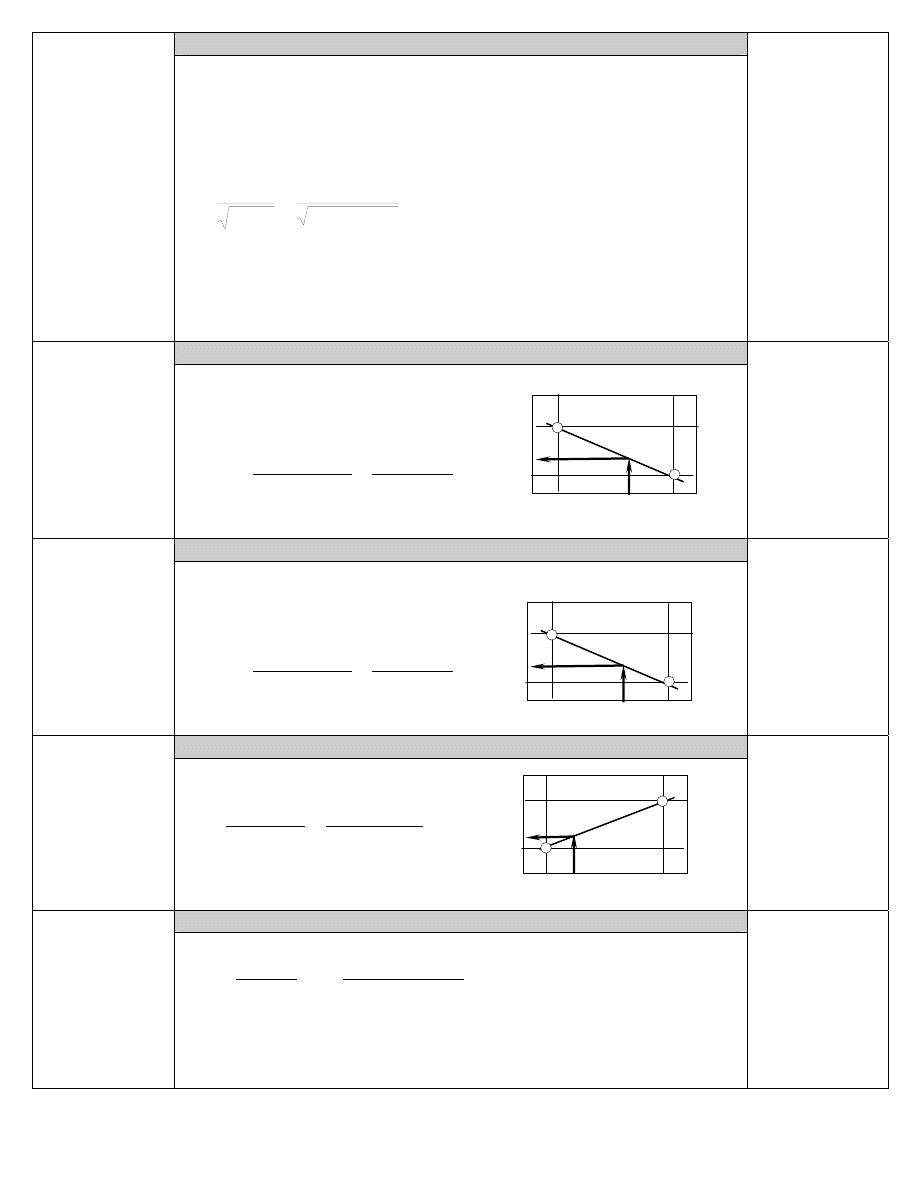
najbliższa znormalizowana grubość ścianki dennicy (PN-75/M-35412 a
także Mat.Pom.[5.3]) wynosi g
rz,1
= 0.007 [m]. Dla tej dennicy h
w
= 0.4 [m]
g
rz,1
= 0.007 [m]
h
w
= 0.4 [m]
5.3 Wyznaczenie H
z
/D
z
i
ω dla dna z otworami ω ≠ 0
D
w
=1.6 [m],
g = 0.007 [m]
H
z
= h
w
=0.4 [m]
d = 0.14 [m]
Wersja I. Założenie, że w dennicy znajdują się otwory na króćce, z
których największy ma średnicę d = 0.14 [m].
D
z
= D
w
+ 2g
w
= 1.6 + 2
.
0.007 = 1.614 [m]
H
z
/D
z
= 0.4/1.614 = 0.2478
317
.
1
007
.
0
614
.
1
14
.
0
=
⋅
=
=
rz
z
g
D
d
ω
Ponieważ obliczona wartość
ω zawarta jest pomiędzy ω = 1 i ω = 2,
należy zastosować podwójną aproksymację, polegającą na obliczeniu y
w
dla
H
z
/D
z
= 0.2478 przy
ω = 1 i ω = 2, a następnie wyniki ponownie
aproksymując dla
ω = 1.231.
D
z
= 1.614 [m]
H
z
/D
z
= 0.2478
ω = 1.317
5.4. Obliczanie y
w
dla
ω = 1.0
H
z
/D
z
= 0.2478
Obliczenie y
w
dla zadanej wartości
ω = 1.0 i dla H
z
/D
z
= 0.2475 zawartej
pomiędzy 2.5 i 3.0
dla:
20
.
0
25
.
0
3
.
2
9
.
2
20
.
0
2478
.
0
9
.
2
−
−
=
−
−
w
y
stąd: y
w(1.0)
= 2.326
y
w(1.0)
= 2.326
5.5. Obliczanie y
w
dla
ω = 2.0
H
z
/D
z
= 0.2478
Obliczenie y
w
dla zadanej wartości
ω = 2.0 i dla H
z
/D
z
=0.284 zawartej
pomiędzy 2.5 i 3.0
dla:
20
.
0
25
.
0
21
.
3
68
.
3
20
.
0
2478
.
0
68
.
3
−
−
=
−
−
w
y
stąd: y
w(2.0)
= 3.231
y
w(2.0)
= 3.231
5.6. Obliczeniowa y
w
dla
ω = 1.56
ω = 1.317,
y
w(1.0)
= 2.326,
y
w(2.0)
= 3.231
Z proporcji:
0
.
1
0
.
2
326
.
2
231
.
3
0
.
1
317
.
1
326
.
2
−
−
=
−
−
w
y
wynika, że: y
w
= 2.622
y
w
= 2.622
5.7. Grubość dennicy g
rz,2
(II przybliżenie) i zweryfikowanie D
z
D
z
= 1.614 [m]
p
o
= 1.6[MPa],
k
r
= 147.8 [MPa]
y
w
= 2.622
c = 0.0025 [m]
0139
.
0
0025
.
0
8
.
147
4
622
.
2
614
.
1
6
.
1
4
0
2
,
=
+
⋅
⋅
⋅
=
+
=
c
k
y
D
p
g
r
w
z
rz
[m],
Obliczona wartość przekracza przyjętą w I przybliżeniu grubość o 100 %,
więc konieczne są dalsze obliczenia, przeprowadzone tym razem dla:
D
z
= D
w
+ 2g
rz,2
= 1.6 + 0.028 = 1.626 [m]
g
rz,2
= 0.014 [m]
D
z
= 1.628 [m]
y
w
0.20
H
0.25
2.9
2.3
y
w
0.2478
z
/D
z
3.68
3.21
y
w
0.20
H
0.25
y
w
0.2478
z
/D
z
3.231
y
w
2.326
y
w
1.0
2.0
1.317
ω
17
5.8. Skorygowanie naddatku grubości c
c
1
= 0.0005 [m]
dla: 8 < g
rz,2
< 20
[mm] c
2
= 0.0008
[m],
c
3
= 0.001 [m].
Ponieważ zmieniła się grubość blachy dennicy, w stosunku do założonej
(g > 0.02 [m]), więc trzeba skorygować wartość c
2
i c:
c = c
1
+ c
2
+ c
3
= 0.0005 + 0.0008 + 0.001 = 0.0023 [m]
c = 0.0023 [m]
5.9. Ponowne obliczenie: H
z
/D
z
,
ω i y
w
D
z
= 1.628 [m]
H
z
= h
w
=0.4 [m]
d = 0.14 [m]
H
z
/D
z
= 0.4/1.628 = 0.246
927
.
0
014
.
0
628
.
1
14
.
0
=
⋅
=
⋅
=
rz
z
g
D
d
ω
Dalsze obliczenia można przeprowadzić tak jak powyżej, przez podwójną
aproksymację, ale tym razem wybrano drugą (przybliżoną metodę) a
mianowicie, założono że:
H
z
/D
z
= 0.246 ≈ 0.25,
ω = 0.927 ≈ 1.0,
którym to wartościom odpowiada (Tablica [8]) współczynnik osłabienia y
w
=
2.3
y
w
= 2.3
5.10 Wyznaczenie obliczeniowej grubości dennicy g
rz,3
(III przybliżenie)
D
z
= 1.628 [m]
p
o
= 1.6[MPa],
k
r
= 147,8 [MPa]
y
w
= 2.3,
c = 0.0023 [m]
0124
.
0
0023
.
0
8
.
147
4
3
.
2
628
.
1
6
.
1
4
0
3
,
=
+
⋅
⋅
⋅
=
+
=
c
k
y
D
p
g
r
w
z
rz
[m]
Otrzymane grubości dennicy w II i III przybliżeniu różnią się tylko o 7 %
i są mniejsze niż przyjęty naddatek c, więc obliczenia grubości ścianki
dennicy można już zakończyć.
g
rz
= 0.014 [m]
5.11. Obliczanie y
w
dla
ω = 0
ω = 0
H
z
/D
z
= 0.2478
Wersja II. Zał. W dennicy albo nie ma otworów, albo, jeżeli są, to z
prawidłowo obliczonym i wspawanym pierścieniem wzmacniającym.
Dla
ω = 0 i H
z
/D
z
= 0.2478, zawartej pomiędzy 2.5 i 3.0, y
w
można
obliczyć poprzez dwukrotną aproksymację, jak to zrobiono wyżej, lub
prościej przyjmując założenie, że: H
z
/D
z
= 0.2478 ≈ 0.25, dla której to
wartości y
w
= 2.0 (patrz Tablica [8])
y
w
= 2.0
5.12. Grubość dennicy bez otworów g
rz,1
(I przybliżenie)
D
z
= 1.628 [m]
p
o
= 1.6[MPa],
k
r
= 147,8 [MPa]
y
w
= 2.0,
c = 0.0023 [m]
0111
.
0
0023
.
0
8
.
147
4
0
.
2
628
.
1
6
.
1
4
0
1
,
=
+
⋅
⋅
⋅
=
+
=
c
k
y
D
p
g
r
w
z
rz
stąd: D
z
= D
w
+ 2g
w
= 1.6 + 2
x
0.012 = 1.624 [m]
H
z
/D
z
= 0.4/1.622 = 0.2466 ≈ 0.25
Dla
ω = 0 i H
z
/D
z
= 0.25 y
w
= 2.0 pozostaje bez zmian
g
rz,1
= 0.012 [m]
D
z
= 1.624 [m]
H
z
/D
z
= 0.25
18
5.13. Grubość dennicy bez otworów g
rz,1
(II przybliżenie)
D
z
= 1.624 [m]
p
o
= 1.6[MPa],
k
r
= 147,8 [MPa]
y
w
= 2.0,
c = 0.0023 [m]
0111
.
0
0023
.
0
8
.
147
4
0
.
2
624
.
1
6
.
1
4
0
2
,
=
+
⋅
⋅
⋅
=
+
=
c
k
y
D
p
g
r
w
z
rz
Ponieważ wartość grubości ustaliła się, więc dalsze obliczenia nie są
konieczne.
g
rz,2
= 0.012 [m]
5.14 Wyznaczenie rzeczywistej grubości dennicy g
rz
Najbliższa znormalizowana grubość dennicy, zgodnie z normą PN-75/M-
35412 (Mat.Pom.[5.3]) wynosi g
rz
= 0.014 [m] dla den z otworami i g
rz
=
0.012 [m] bez otworów. Pozostałe parametry tej dennicy, według oznaczeń
na rysunku, są następujące:
V = 536 [dm
3
] = 0.536 [m
3
] (objętość dotyczy tylko elipsoidalnej części dna
– do wysokości h
w
)
h
w
= 0.4 m, h
c
= 0.060 [m] lub 0.040 [m] (g
rz
= 0.012 [m]) i masa G = 347
[kg] lub G = 286 [kg]
g
rz
= 0.014 [m]
V = 0.536 [m
3
]
h
w
= 0.4 [m]
h
c
= 0.060 [m]
G = 347 [kg]
Literatura (zamieścić na końcu części pisemnej projektu)
[8] Urząd Dozoru Technicznego, Warunki techniczne dozoru technicznego, Urządzenia ciśnieniowe, Obliczenia
wytrzymałościowe, DT-UC-90/WO-O, Wydawnictwo Poligraficzne Bydgoszcz 1991.
19
Document Outline