6.5. Analiza postoptymalizacyjna

Po wyznaczeniu rozwiązania optymalnego zadania PL przeprowadza się analizy

dotyczące wrażliwości otrzymanego rozwiązania na zmiany parametrów zadania.
W szczególności interesuje nas odpowiedź na pytania:

a)

Dla jakich zmian parametru

j

c

(współczynnika funkcji celu ) nie ulegnie zmianie

optymalne rozwiązanie(wartości zmiennych pozostaną takie same) zadania?

b)

Jak może się zmienić wartość ograniczenia

i

b , aby rozwiązanie optymalne było

wyznaczone przez tą samą bazę (te same zmienne bazowe)?

Rozważmy najpierw przypadek a)

Załóżmy, że zmieniamy wartość współczynnika

k

c przy zmiennej decyzyjnej

k

x o

k

c

∆

.

I. Jeśli zmienna

k

x nie jest zmienną bazową dla rozwiązania optymalnego, to w

wierszu wskaźnikowym zmieni się tylko

k

∆

(ponieważ nie zmieniają wartości

B

j

B

j

z

′

′

=

α

c

o

oraz pozostałe współczynniki funkcji celu dla

k

j

≠

). Nowa wartość

wskaźnika dla zmiennej

k

x

będzie równa:

k

k

k

k

k

k

k

k

k

c

c

c

z

c

c

z

∆

−

∆

=

∆

−

−

=

∆

+

−

=

∆

)

(

)

(

~

.

Jeśli rozwiązywane zadanie było zadaniem na maksimum to wyznaczone poprzednio

rozwiązanie optymalne nie ulegnie zmianie, gdy:

k

k

k

k

k

c

c

∆

≤

∆

⇒

≥

∆

−

∆

⇒

≥

∆

0

0

~

.

Stąd przyjęcie zamiast wartości współczynnika przy niewiadomej

k

x dowolnej liczby

z przedziału

>

∆

+

−∞

k

k

c

,

(

nie zmieni rozwiązania optymalnego ani wartości funkcji

celu.

Jeśli rozwiązywane zadanie było zadaniem na minimum to wyznaczone poprzednio

rozwiązanie optymalne nie ulegnie zmianie, gdy:

k

k

k

k

k

c

c

∆

≥

∆

⇒

≤

∆

−

∆

⇒

≤

∆

0

0

~

.

Zatem przyjęcie zamiast wartości współczynnika przy niewiadomej

k

x dowolnej liczby

z przedziału

)

,

∞

+

∆

+

<

k

k

c

nie zmieni rozwiązania optymalnego ani wartości funkcji

celu.

II. Jeśli zmienna

k

x jest zmienną bazową dla rozwiązania optymalnego, to w wierszu

wskaźnikowym zmienią się wszystkie

j

∆

dla zmiennych niebazowych (ponieważ

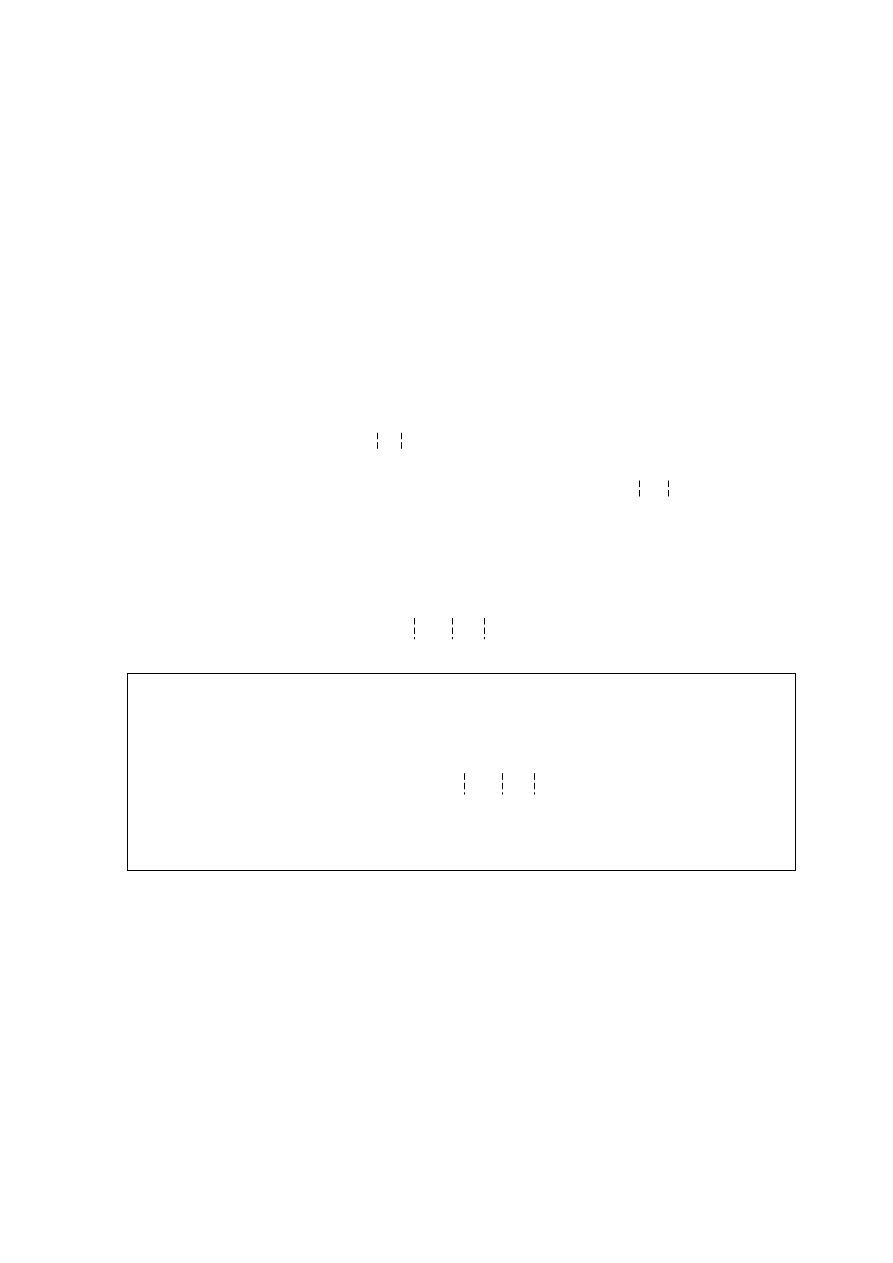
zmieniają wartości

B

j

B

j

z

′

′

=

α

c

o

). Nowe wartości wskaźników optymalności dla

zmiennych niebazowych

j

x

będą równe:

j

k

j

c

z

−

=

∆

~

~

.

Jeśli rozwiązywane zadanie było zadaniem na maksimum to wyznaczone poprzednio

rozwiązanie optymalne nie ulegnie zmianie, gdy dla wszystkich zmiennych niebazowych
nowe wartości wskaźników optymalności będą nieujemne (dla zadania na minimum
wszystkie muszą być niedodatnie) Rozwiązanie odpowiedniego układu nierówności
z jedną niewiadomą wyznacza przedział dla dopuszczalnych zmian współczynnika

k

c .

W tym przypadku zmienia się wartość funkcji celu o

k

k

c

f

∆

⋅

Θ

=

∆

.

Rozważmy teraz przypadek b)

Nim rozpatrzymy odpowiedź na postawione w tym punkcie pytanie przypomnijmy

pewne wiadomości z algebry liniowej dotyczącej własności operacji elementarnych
wykonywanych na wierszach macierzy, mianowicie:

Jeśli macierz blokową

[

]

b

I

A

(gdzie macierz

A jest macierzą nieosobliwą;

macierz

I jest macierzą jednostkową oraz b jest wektorem) przy pomocy operacji

elementarnych na wierszach przekształcimy do macierzy postaci

[

]

x

B

I

, to

1

−

=

A

B

oraz

b

B

x

⋅

=

.

Jeśli wektory (

n

p

p

p

,

,

,

2

1

K

) tworzą bazę B przestrzeni

n

R i w tej bazie wyznaczone

są współrzędne liniowo niezależnych wektorów:

B
n

n

B

B

α

a

α

a

α

a

=

=

=

,

,

,

2

2

1

1

K

oraz

wektor

B

β

b

=

, to po zmianie bazy B w tej przestrzeni na bazę B’ wektor b będzie miał

nowe współrzędne dane wzorem:

[

]

B

B
n

B

B

β

α

α

α

⋅

−

1

2

1

L

.

Z powyższego wynika, że:

Wartości zmiennych bazowych

B

x w rozwiązaniu optymalnym (zmienne niebazowe

przyjmują wartości zerowe) można wyznaczyć jako iloczyn macierzy B i wektora
ograniczeń b, czyli

b

B

x

⋅

=

B

op

.

Macierz

B

jest zbudowana z wektorów

[

]

B
m

B

B

b

b

b

L

2

1

, których współrzędne

są wyznaczone w bazie rozwiązania optymalnego i które odpowiadają kolejnym

wektorom bazowym dla startowej tablicy simpleks.

Wektor

T

m

i

b

b

b

]

[

1

L

L

=

b

jest wektorem ograniczeń.

W rozwiązaniu optymalnym wszystkie zmienne decyzyjne i zmienne swobodne, zgodnie
z warunkami brzegowymi, muszą być nieujemne (wszystkie zmienne sztuczne muszą przyjąć
wartości zerowe, aby rozwiązanie było dopuszczalne), zatem

0

x

≥

B

op

.

Stąd otrzymujemy układ nierówności

0

b

B

≥

⋅

,

którego rozwiązanie określa dopuszczalne zmiany wartości parametru

i

b , przy których nie

zmienia się baza wyznaczająca rozwiązanie optymalne.
Ilustracje dotyczącej analizy postoptymalizacyjnej zawierają przykłady AP-1 i AP-2.

Problemy analizy postoptymalizacyjnej są także omówione np. w pozycji [3] s.53-66.