Grupowanie metod ¾

a k-´srednich

Jacek Kluska

Politechnika Rzeszowska

2010

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

1 / 14

Na czym polega metoda grupowania k-´srednich?

Algorytm grupowania k-´srednich opracowa÷J. MacQueen (1967) a
nast ¾

epnie J. A. Hartigan i M. A. Wong (1975).

Algorytm grupowania k-´srednich s÷

u·

zy do klasy…kacji, tzn.

grupowania obiektów na podstawie atrybutów do k grup.
Grupowanie polega na minimalizacji sumy kwadratów odleg÷

o´sci

mi ¾

edzy danymi i odpowiednimi centrami grup (klastrów).

Celem grupowania k-´srednich jest sklasy…kowanie danych.

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

2 / 14

Przyk÷

ad

Dane s ¾

a 4 obiekty b ¾

ed ¾

ace danymi ucz ¾

acymi; ka·

zdy obiekt ma 2 atrybuty.

Obiekt

x

y

Klasa

Lekarstwo A

1

1

?

Lekarstwo B

2

1

?

Lekarstwo C

4

3

?

Lekarstwo D

5

4

?

M

=

x

A

x

B

x

C

x

D

=

1 2 4 5
1 1 3 4

Celem jest zgrupowanie tych obiektów do k

=

2 grup lekarstw.

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

3 / 14

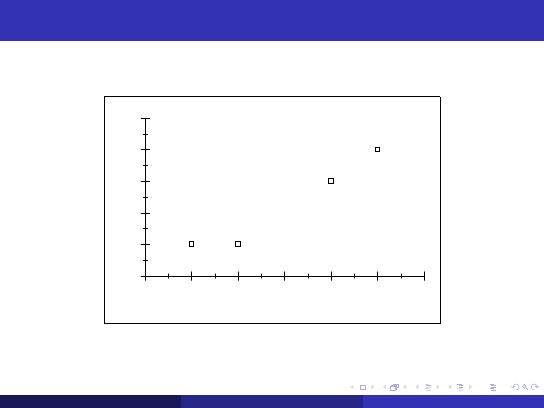
Przyk÷

ad - c.d.

0

1

2

3

4

5

6

0

1

2

3

4

5

x

y

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

4 / 14

Algorytm grupowania k-´srednich

Najpierw

okre´slamy liczb ¾

e grup (klastrów) k,

zak÷

adamy punkt centralny dla ka·

zdej grupy.

Jako pocz ¾

atkowe punkty centralne mo·

zemy wybra´c k losowo wybranych

obiektów lub k pierwszych obiektów.

Wykonaj kroki a·

z do osi ¾

agni ¾

ecia stanu stabilnego, tzn. gdy ·

zaden

obiekt nie mo·

ze opu´sci´c grupy:

1

Wyznacz wspó÷

rz ¾

edne punktów centralnych.

2

Wyznacz odleg÷

o´s´c mi ¾

edzy ka·

zdym obiektem i ka·

zdym punktem

centralnym.

3

Zgrupuj obiekty na podstawie minimalnej odleg÷

o´sci (znajd´z

najbli·

zszy punkt centalny).

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

5 / 14

Przyk÷

ad - c.d.: pocz ¾

atkowe punkty centralne

Za÷

o·

zenie. Pocz ¾

atkowe punkty centralne: lekarstwo A, lekarstwo B:

c

1

= [

1, 1

]

,

c

2

= [

2, 1

]

0

1

2

3

4

5

6

0

1

2

3

4

5

x

y

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

6 / 14

Przyk÷

ad - c.d.: odleg÷

o´sci mi ¾

edzy obiektami a punktami

centralnymi

Dla x

A

= [

1, 1

]

, x

B

= [

2, 1

]

, x

C

= [

4, 3

]

, x

D

= [

5, 4

]

, przyjmuj ¾

ac

odleg÷

o´s´c Euklidesow ¾

a, w iteracji “0” otrzymujemy macierz odleg÷

o´sci:

D

0

= f

d

i ,j

g

2,4

= fk

c

i

x

j

kg

2,4

, j

2 f

A, B, C , D

g

D

0

=

k

c

1

x

A

k k

c

1

x

B

k k

c

1

x

C

k k

c

1

x

D

k

k

c

2

x

A

k k

c

2

x

B

k k

c

2

x

C

k k

c

2

x

D

k

D

0

=

0.00 1.00 3.61 5.00
1.00 0.00 2.83 4.24

grupa 1,

(

i

=

1

)

grupa 2,

(

i

=

2

)

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

7 / 14

Przyk÷

ad - c.d.: grupowanie obiektów

Dla

D

0

=

0.00 1.00 3.61 5.00
1.00 0.00 2.83 4.24

grupa 1
grupa 2

wyznaczamy macierz grup (wskazanie minimalnego elementu w kolumnie)

G

0

= f

g

i ,j

g

2,4

, g

i ,j

=

1

,

d

i ,j

=

min

c

=

1,2

f

d

c ,j

g

0

oth.

G

0

=

1 0 0 0
0 1 1 1

grupa 1
grupa 2

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

8 / 14

Przyk÷

ad - c.d. - iteracja 1: wyznaczenie punktów

centralnych

Wyznaczenie nowego punktu centralnego dla ka·

zdej grupy na podstawie

aktualnych przynale·

zno´sci

M

= f

m

i ,j

g

2,4

=

1 2 4 5
1 1 3 4

,

G

0

=

1 0 0 0
0 1 1 1

grupa 1
grupa 2

c

new

1

=

g

1,1

x

A

+

g

1,2

x

B

+

g

1,3

x

C

+

g

1,4

x

D

g

1,1

+

g

1,2

+

g

1,3

+

g

1,4

=

1x

A

+

0x

B

+

0x

C

+

0x

D

1

+

0

+

0

+

0

=

1 1

c

new

2

=

g

2,1

x

A

+

g

2,2

x

B

+

g

2,3

x

C

+

g

2,4

x

D

g

2,1

+

g

2,2

+

g

2,3

+

g

2,4

=

0x

A

+

1x

B

+

1x

C

+

1x

D

0

+

1

+

1

+

1

=

11

3

8
3

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

9 / 14

Przyk÷

ad - c.d. - iteracja 1: wyznaczenie macierzy

odleg÷

o´sci i macierzy grup

Dla c

1

= [

1, 1

]

, c

2

=

11

3

8
3

, macierz odleg÷

o´sci

D

1

= f

d

i ,j

g

2,4

=

k

c

1

x

A

k k

c

1

x

B

k k

c

1

x

C

k k

c

1

x

D

k

k

c

2

x

A

k k

c

2

x

B

k k

c

2

x

C

k k

c

2

x

D

k

=

0

1.0

3.6056

5.0

3.1447 2.357 0.4714 1.885 6

grupa 1
grupa 2

macierz grup

G

1

=

1 1 0 0
0 0 1 1

grupa 1
grupa 2

G

1

6=

G

0

)

kontynuuj iteracj ¾

e.

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

10 / 14

Przyk÷

ad - c.d. - iteracja 2: wyznaczenie punktów

centralnych

Wyznaczenie nowego punktu centralnego dla ka·

zdej grupy na podstawie

aktualnych przynale·

zno´sci

M

= f

m

i ,j

g

2,4

=

1 2 4 5
1 1 3 4

,

G

1

=

1 1 0 0
0 0 1 1

grupa 1
grupa 2

c

new

1

=

g

1,1

x

A

+

g

1,2

x

B

+

g

1,3

x

C

+

g

1,4

x

D

g

1,1

+

g

1,2

+

g

1,3

+

g

1,4

=

1x

A

+

1x

B

+

0x

C

+

0x

D

1

+

1

+

0

+

0

=

3
2

1

c

new

2

=

g

2,1

x

A

+

g

2,2

x

B

+

g

2,3

x

C

+

g

2,4

x

D

g

2,1

+

g

2,2

+

g

2,3

+

g

2,4

=

0x

A

+

0x

B

+

1x

C

+

1x

D

0

+

0

+

1

+

1

=

9
2

7
2

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

11 / 14

Przyk÷

ad - c.d. - iteracja 2: wyznaczenie macierzy

odleg÷

o´sci i macierzy grup

Dla c

1

=

3
2

1

, c

2

=

9
2

7
2

, macierz odleg÷

o´sci

D

2

= f

d

i ,j

g

2,4

=

k

c

1

x

A

k k

c

1

x

B

k k

c

1

x

C

k k

c

1

x

D

k

k

c

2

x

A

k k

c

2

x

B

k k

c

2

x

C

k k

c

2

x

D

k

=

0.5

0.5

3.2016

4.6098

4.3012 3.5355 0.70711 0.70711

grupa 1
grupa 2

macierz grup

G

2

=

1 1 0 0
0 0 1 1

grupa 1
grupa 2

G

2

=

G

1

)

STOP.

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

12 / 14

Przyk÷

ad - c.d.: rezultat

Macierz grup

G

2

=

1 1 0 0
0 0 1 1

grupa 1
grupa 2

pokazuje, ·

ze

Obiekt

x

y

Klasa

Lekarstwo A

1

1

1

Lekarstwo B

2

1

1

Lekarstwo C

4

3

2

Lekarstwo D

5

4

2

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

13 / 14

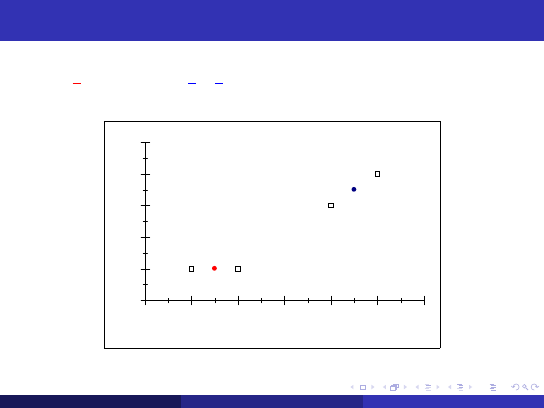
Przyk÷

ad - c.d.: interpretacja wyniku

c

1

=

3
2

1

,

c

2

=

9
2

7
2

0

1

2

3

4

5

6

0

1

2

3

4

5

x

y

Jacek Kluska (Politechnika Rzeszowska)

(k-means clustering)

2010

14 / 14