1

ELEMENTY SYMETRII

Element symetrii

obiekt geometryczny taki jak linia, płaszczyzna lub punkt,
względem którego dokonuje się operacji symetrii.

Operacja symetrii

przekształcenie ciała, po dokonaniu którego każdy punkt ciała
pokrywa się z równoważnym punktem (w szczególności z
samym sobą) przed wykonaniem transformacji.

• oś symetrii C

n

ELEMENTY SYMETRII

• płaszczyzna symetrii

σ

• środek symetrii i

• oś niewłaściwa (inwersyjna) S

n

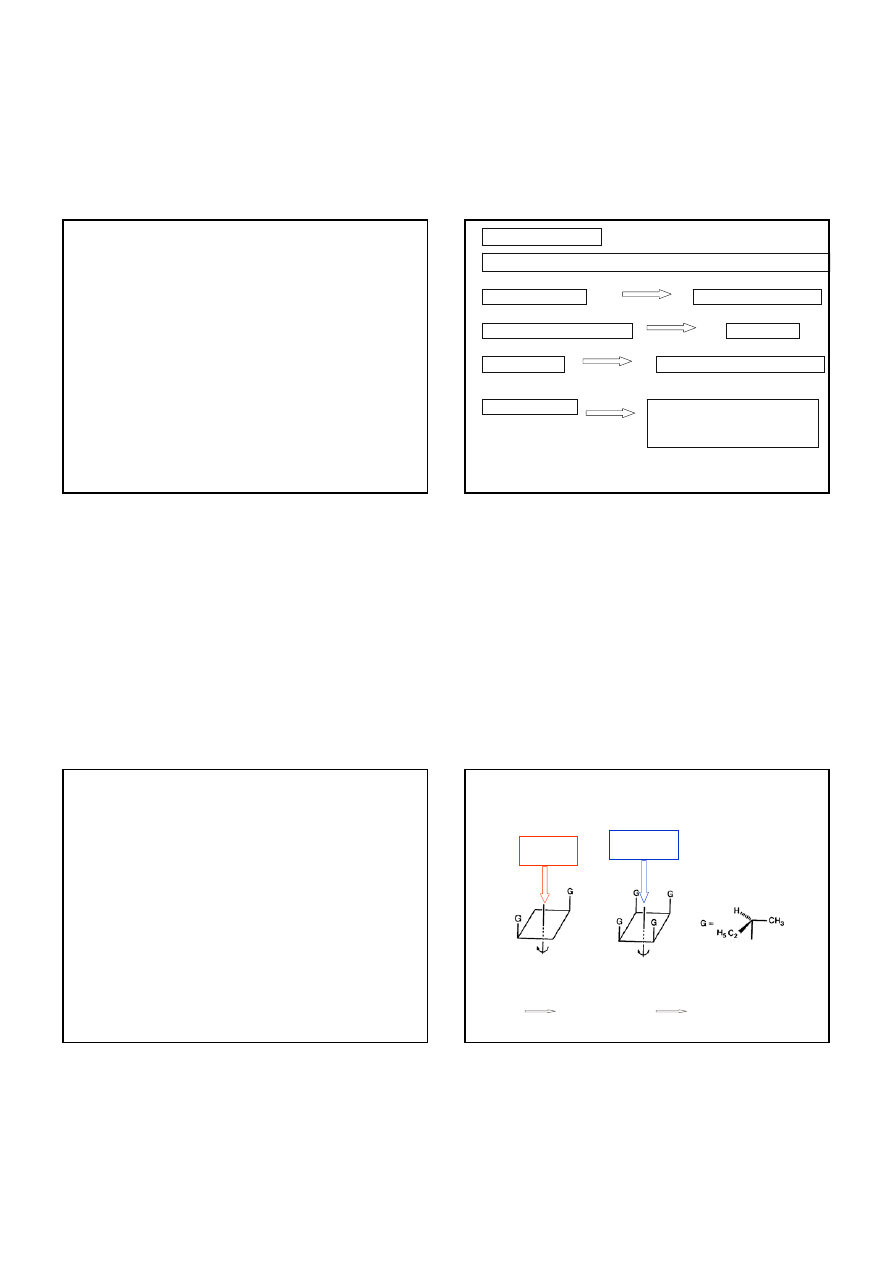
ELEMENTY SYMETRII

OŚ WŁAŚCIWA

Elementy symetrii

Operacje symetrii

PŁASZCZYZNA

odbicie w płaszczyźnie

ŚRODEK SYMETRII (INWERSJI)

inwersja

jeden lub kilka obrotów wokół tej osi

OŚ NIEWŁAŚCIWA

jedna lub więcej następujących

operacji złożonych: obrót, a po nim

odbicie w płaszczyźnie prostopadłej

do osi obrotu

ELEMENTY SYMETRII – oś właściwa

C

n

n

– krotność osi; największa wartość n, dla której obrót o kąt 2

π/n

prowadzi do konfiguracji równoważnej

cis

-(2R,2’R)-di-sec-butylocyklobutan

r

-1,c-2,c-3,c-4-(2R,2’R,2’’R,2’’’R)-tetra-sec-

butylocyklobutan

oś czterokrotna

C

4

– czwartego

rzędu

oś dwukrotna

C

2

– drugiego

rzędu

oś C

1

uniwersalny element

symetrii

operacja identyczności

(E

lub

I

)

2

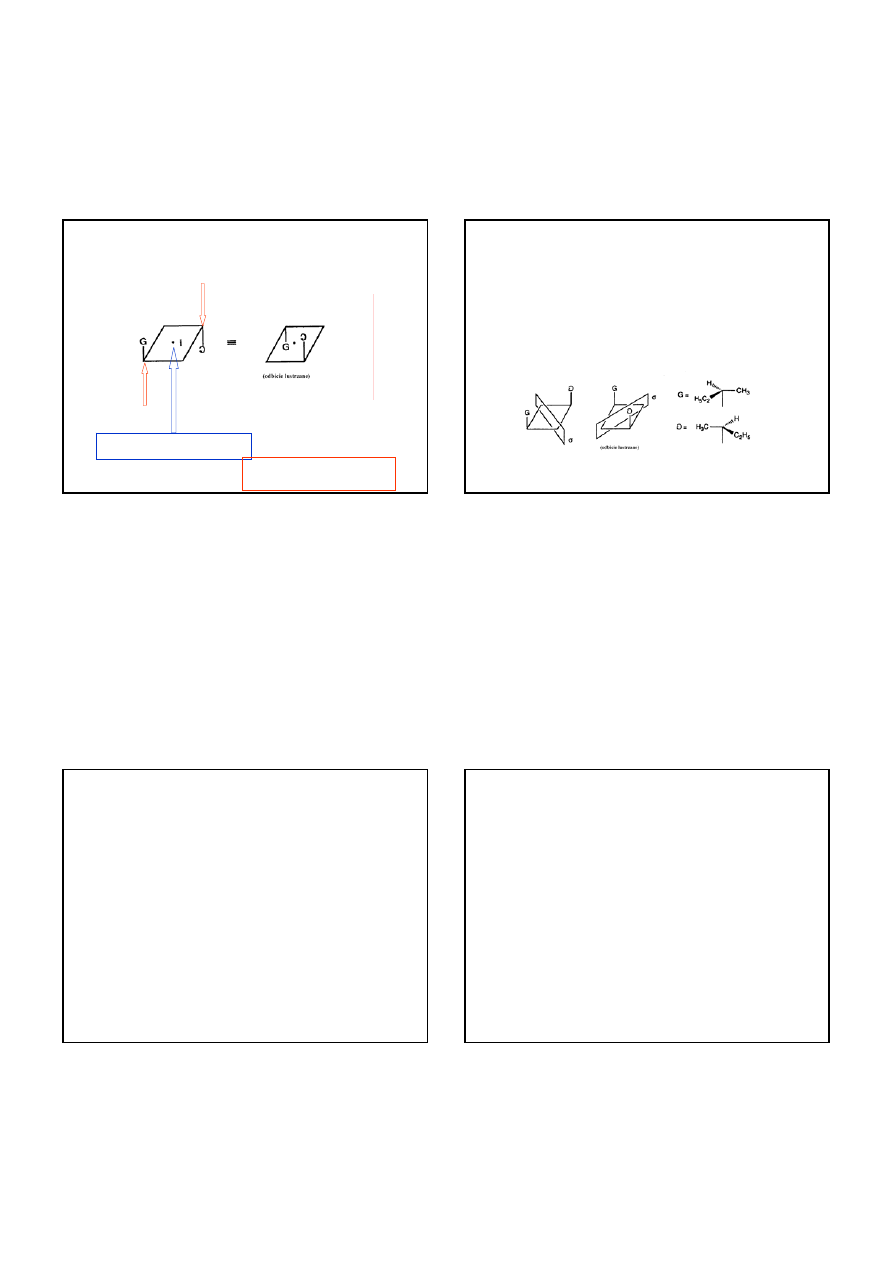
ELEMENTY SYMETRII – środek symetrii

i

trans

-(2R,2’S)-di-sec-butylocyklobutan

punkt, w którym znajduje się początek układu kartezjańskiego;
zamiana współrzędnych (x,y,z) każdego atomu na współrzędne
(-x,-y,-z) prowadzi do konfiguracji równoważnej atomów cząsteczki

jedyny atom cząsteczki, który nie zmieniłby

swojego położenia w wyniku operacji symetrii tzn.

inwersji

Inne atomy muszą występujępować w cząsteczce

parami; każdy z nich musi mieć swój

odpowiednik, z którym zamienia się miejscem

podczas inwersji

ELEMENTY SYMETRII – środek symetrii

i

n

-krotne wykonywanie operacji inwersji i

n

n

parzyste

i

n

=E

n

nieparzyste

i

n

=i

cząsteczki mające środek symetrii:

9

cząsteczki typu AB

6

o strukturze

ośmiościanu,

9

płaskie cząsteczki AB

4

,

9

płaskie cząsteczki AB

2

C

2

typu trans,

9

cząsteczki liniowe typu ABA,

9

eten, benzen

środek symetrii nie występuje w cząsteczkach, w których występuje
więcej niż jeden rodzaj nieparzystych atomów

cząsteczki o wysokiej symetrii nie mające środka symetrii:

C

5

H

5

-

(płaski pięciobok)

cząsteczki typu AB

4

o strukturze czworościanu

ELEMENTY SYMETRII – płaszczyzna symetrii

σ

•przechodzi przez ciało,

cis

-(2R,2’S)-di-sec-butylocyklobutan

•atomy leżące na płaszczyźnie zajmują szczególne położenie – operacja odbicia względem
płaszczyzny nie zmienia ich położenia,

•każda cząsteczka płaska musi mieć jedną płaszczyznę wyznaczoną przez atomy tworzące
cząsteczkę,

•liczba atomów danego rodzaju nie leżących na płaszczyźnie symetrii musi być parzysta,

•jeżeli w cząsteczce mającej płaszczyznę symetrii jest tylko jeden atom danego rodzaju, to musi
on znajdować się na każdej płaszczyźnie symetrii cząsteczki

ELEMENTY SYMETRII – płaszczyzna symetrii

σ

n

-krotne wykonywanie operacji inwersji

σ

n

n

parzyste

σ

n

= E

n

nieparzyste

σ

n

=

σ

cząsteczki mające płaszczyzny symetrii:

9

cząsteczki liniowe o nieskończonej liczbie płaszczyzn symetrii

9

cząsteczki typu NH

3

, CHCl

3

o trzech płaszczyznach symetrii

9

kompleksy o strukturze płaskiej, np. [PtCl

4

]

-2

o pięciu płaszczyznach symetrii

9

cząsteczki o strukturze czworościanu foremnego mają sześć płaszczyzn symetrii

9

cząsteczki o strukturze ośmiościanu foremnego mają dziewięć płaszczyzn symetrii

3

ELEMENTY SYMETRII – oś niewłaściwa (inwersyjna)

S

n

• złożenie dwóch operacji symetrii: obrotu właściwego oraz następującego po nim
odbicia w płaszczyźnie prostopadłej do osi obrotu; obrót niewłaściwy o kąt 2

π/n

oznacza się symbolem S

n

• jeżeli cząsteczka ma oś C

n

i prostopadłą do niej płaszczyznę symetrii,

to ma także i oś inwersji S

n

• cząsteczka może mieć oś S

n

wtedy, gdy nie ma, ani osi C

n

, ani prostopadłej do

niej płaszczyzny symetrii

σ

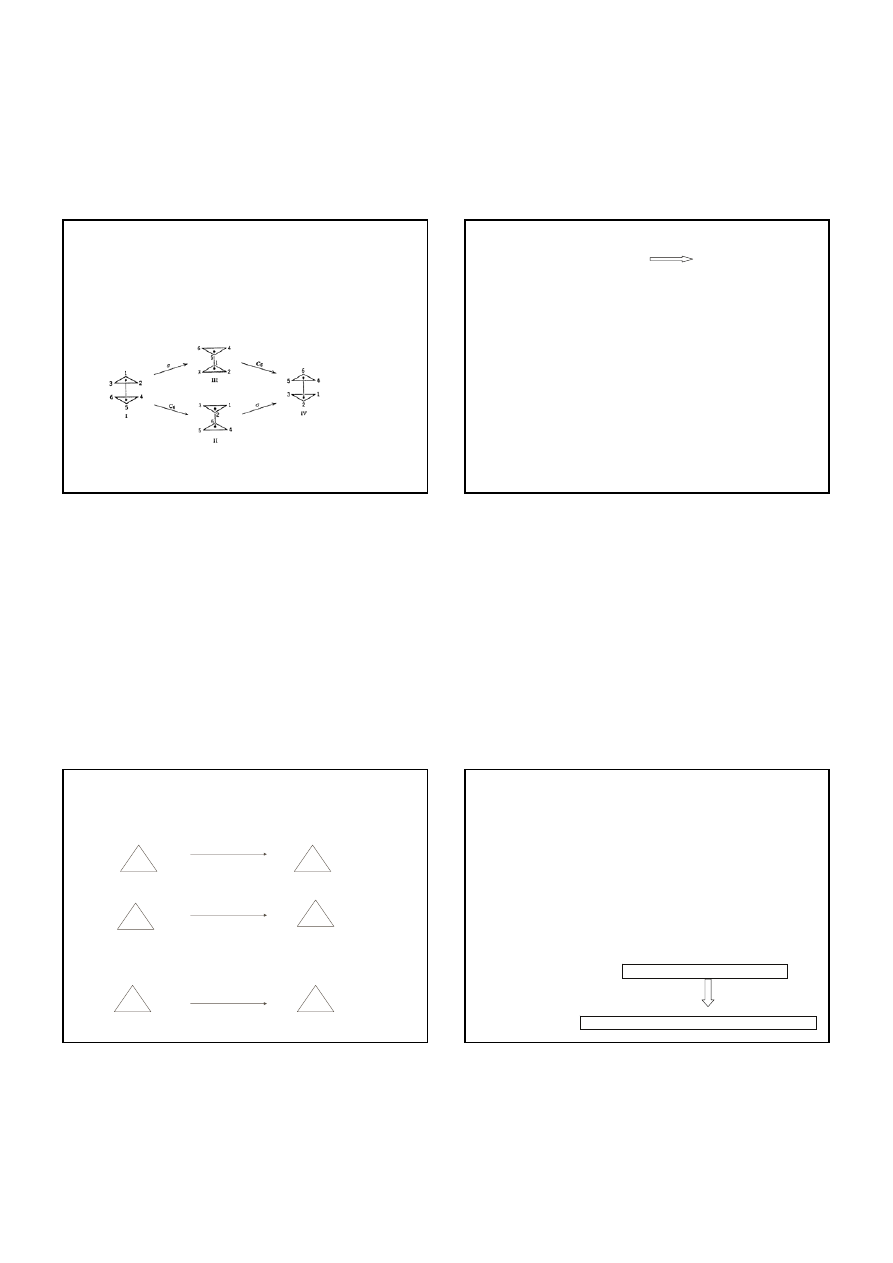
konformacja II = konformacja III

oraz

konformacja I = konformacja IV

ALE

konformacja II

≠ konformacja I

oś właściwa C

6

i płaszczyzna symetrii

σ nie są

elementami symetrii cząsteczki etanu

ALE

złożenie tych dwóch elementów symetrii jest
elementem symetrii cząsteczki – osią niewłaściwą S

6

prosta C–C jest osią trzeciego rzędu C

3

cząsteczki etanu

1

2

3

obrót o kąt 2

π/3

3

1

2

1

2

3

1

2

3

obrót o kąt 2

× 2π/3

obrót o kąt 3

× 2π/3

2

3

1

1

2

3

A

B

A

C

A

D = A

ELEMENTY SYMETRII – oś niewłaściwa (inwersyjna)

S

n

element symetrii oś inwersyjna S

n

operacje S

n

, S

2

n

, S

3

n

, ...

dla n – parzystego

operacje S

n

, S

2

n

, S

3

n

, ... S

n

n

S

n

n

wykonywane są operacje C

n

,

σ, C

n

,

σ, ...n – razy

n

– parzyste, to wykonanie n razy odbicia daje jedność

czyli

S

n

n

= C

n

n

C

n

n

= E

tym samym

S

n

n

= E

Zbiór operacji S

6

, S

2

6

, S

3

6

, S

4

6

, S

5

6

, S

6

6

można, np. zapisać

S

6

,

S

2

6

= C

2

6

= C

3

,

S

3

6

= S

2

= i,

S

4

6

= C

2

3

,

S

5

6

,

S

6

6

= E

czyli S

6

, C

3

, i, C

2

3

, S

5

6

, E

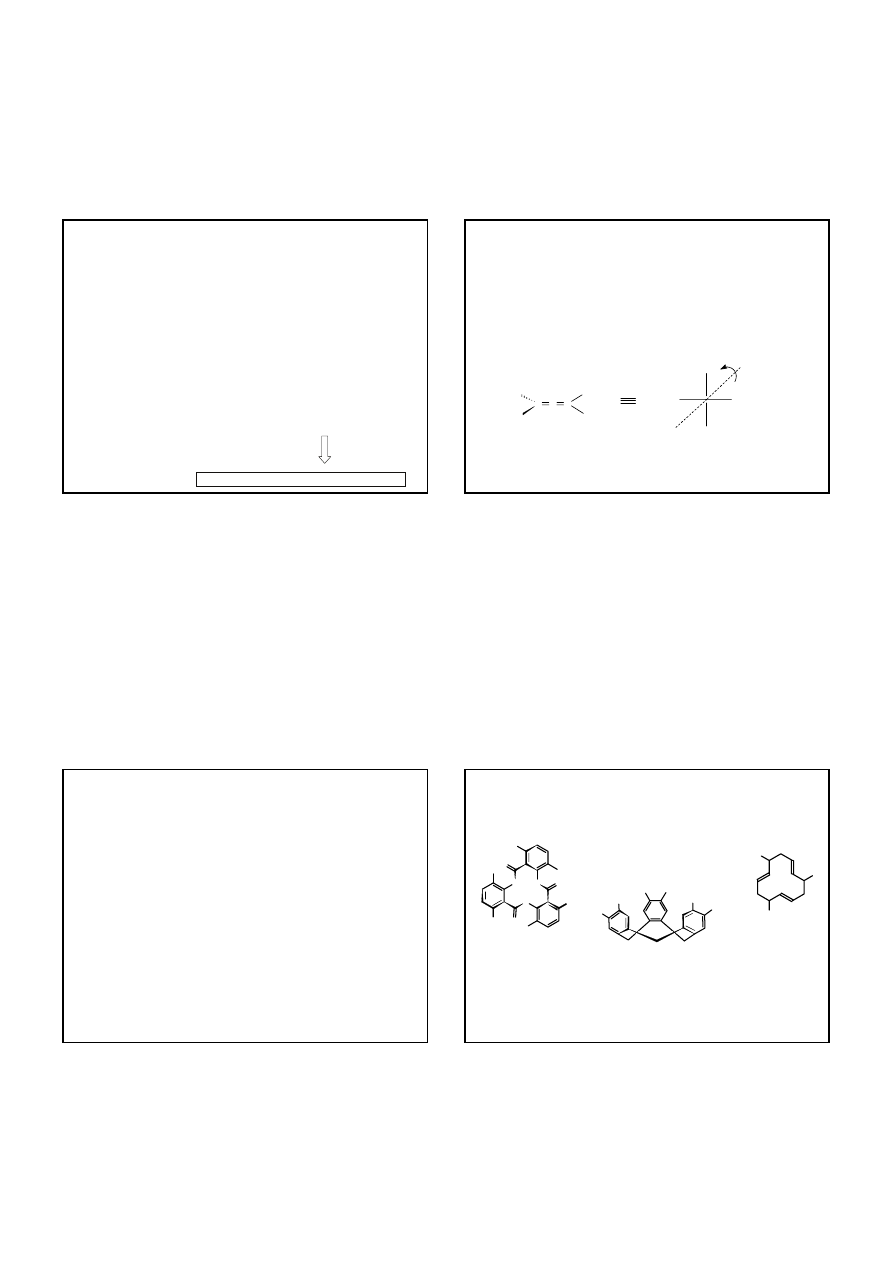
ELEMENTY SYMETRII – oś niewłaściwa (inwersyjna)

S

n

Operacje C

3

, C

2

3

, E są generowane przez oś C

3

Z istnienia osi S

6

wynika istnienie osi C

3

z istnienia osi S

n

parzystego rzędu wynika istnienie osi C

n/2

4

ELEMENTY SYMETRII – oś niewłaściwa (inwersyjna)

S

n

Zbiór operacji S

5

, S

2

5

, S

3

5

, S

4

5

, ... można, np. zapisać

S

5

= C

5

, a następnie

σ,

S

2

5

= C

2

5

,

S

3

5

= C

3

5

, a następnie

σ,

S

4

5

= C

4

5

,

S

5

5

=

σ

S

6

5

= C

5

,

S

7

5

= C

2

5

, a następnie

σ,

S

8

5

= C

3

5

,

S

9

5

= C

4

5

, a następnie

σ,

S

10

5

= E

S

11

5

=C

5

, a następnie

σ,

od operacji S

2n+1

n

ciąg operacji zaczyna powtarzać się

element S

n

dla n nieparzystego generuje 2n operacji

Grupy punktowe zawierające cząsteczki chiralne

Grupa punktowa C

1

9

charakteryzują się najniższym stopniem symetrii;

cząsteczki typu Cabcd, np. CHFClBr

9

jedyny element symetrii – identyczność równoważna z osią

symetrii C

1

.

Zbiór niepowtarzających się operacji symetrii danej cząsteczki tworzy grupę;
różne grupy odpowiadają różnym rzeczywistym cząsteczkom

Grupy punktowe zawierające cząsteczki chiralne

Grupy punktowe C

n

jeden element symetrii – oś właściwa C

n

grupa punktowa C

2

np.

( –)- i (+)-kwas winowy,
chiralne bifenyle,
1,3-dipodstawione alleny

C C C

H

Cl

Cl

H

C

2

Cl

H

H

Cl

1,3-dichloroallen

Grupy punktowe zawierające cząsteczki chiralne

Grupy punktowe C

n

jeden element symetrii – oś właściwa C

n

grupa punktowa C

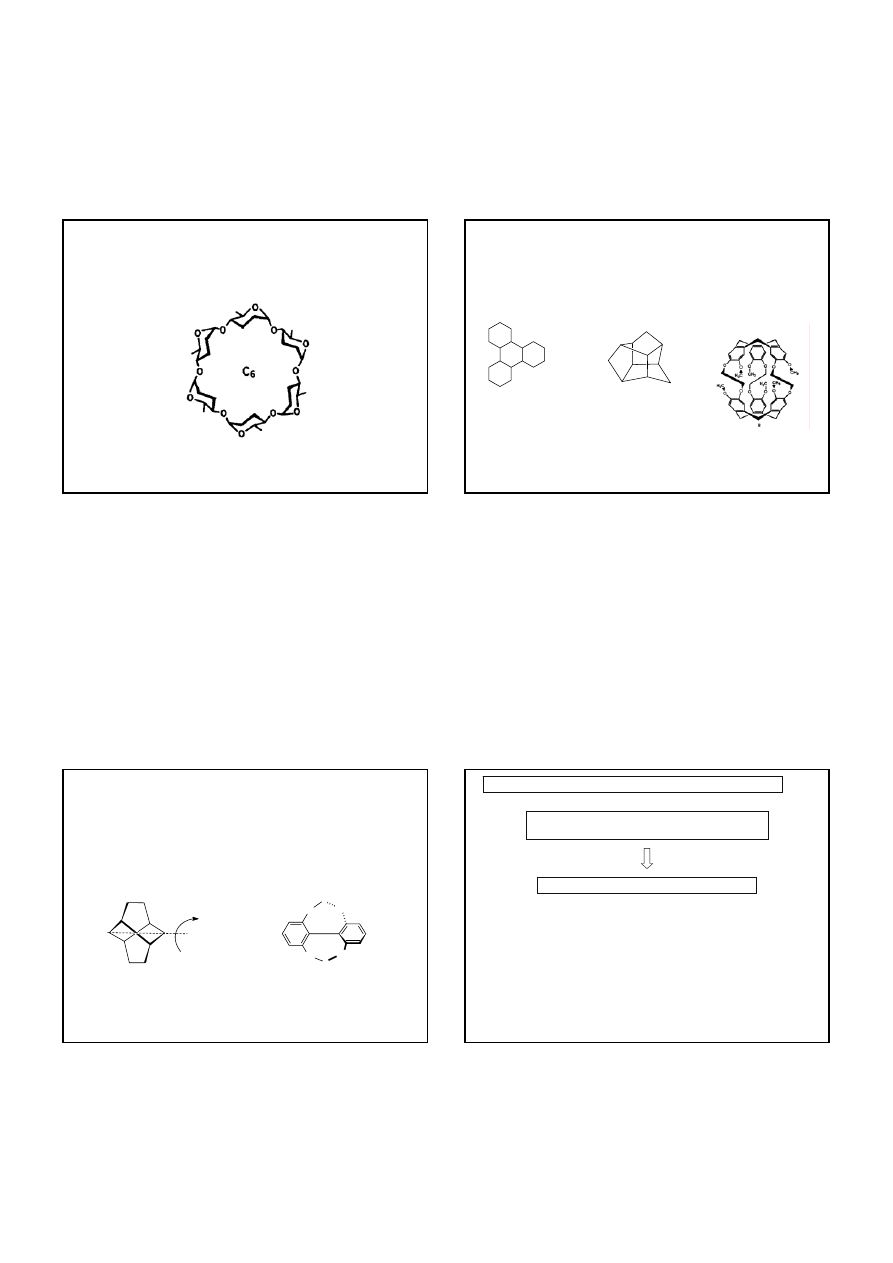
3

tri-o-tymotyd cztery konformacje,
z których dwie mają symetrię C

3

a

dwie C

1

; energia racemizacji ok.

22 kcal/mol

H

3

C

CH

3

CH

3

Pochodne cyklotriweratrylenu są stosunkowo optycznie
trwałe (energia aktywacji dla racemizacji wynosi ok. 26.5
kcal/mol)

trans,trans,trans

-3,7,11-trimetylo-

1,5,9-dodekatrien C otrzymano
poprzez trimeryzację (typu
głowa-do-głowy) 1,3-pentadienu.

O

O

O

O

O

O

Me

i

Pr

Me

i

Pr

Me

i

Pr

X

Y

X

Y

Y

X

X = OCH

3

Y = OH, OCH

3

5

Grupy punktowe zawierające cząsteczki chiralne

Grupy punktowe C

n

jeden element symetrii – oś właściwa C

n

grupa C

6

cykloheksaamyloza, tzw.

α-cyklodekstryna

Grupy punktowe zawierające cząsteczki chiralne

Grupy punktowe D

n

n

osi symetrii C

2

⊥ głównej osi właściwej C

n

grupa punktowa D

2

np.

twistan, zmostkowane bifenyle,

C2

CH

2

CH

2

X

CH

2

CH

2

X

X = O, S, C=O

Grupy punktowe zawierające cząsteczki chiralne

Grupy punktowe D

n

n

osi symetrii C

2

⊥głównej osi właściwej C

n

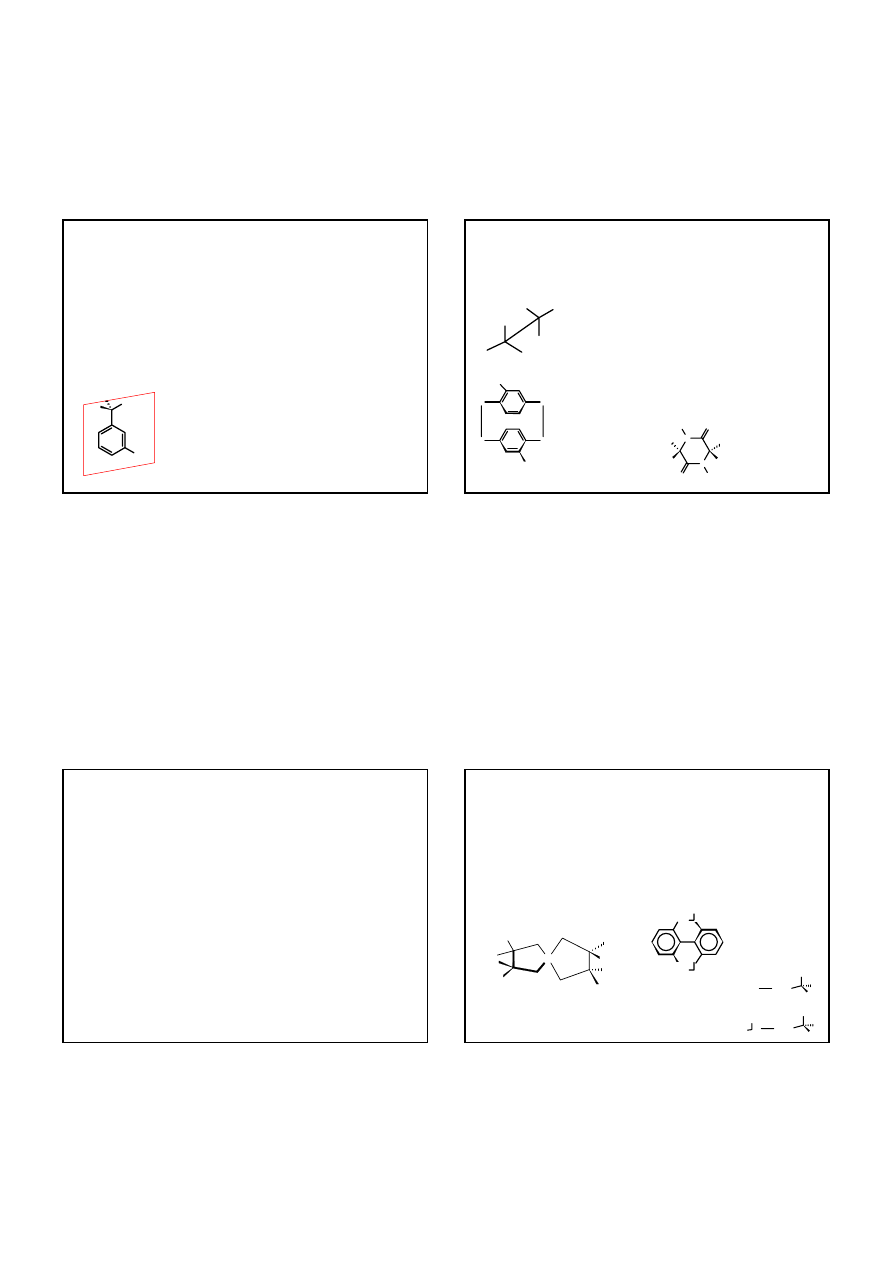
grupa punktowa D

3

.

.

.

trans- transoid-trans-transoid-
trans-

perhydrotrifenylen –

pierwszy związek z grupy D

3

otrzymany w optycznie czynnej
formie

trishomokuban

dimer cyklotriweratrylenu

Grupy punktowe zawierające tylko cząsteczki achiralne

Grupy punktowe inne niż C

n

i D

n

posiadają

płaszczyzny, środki symetrii czy osie.

cząsteczki należące do nich są achiralne

6

Grupa punktowa C

s

(lub C

1h

)

Grupy punktowe zawierające tylko cząsteczki achiralne

operacje symetrii dla cząsteczek należących do tej grupy:

E

i

σ

elementy symetrii – płaszczyzna symetrii

σ

przykłady cząsteczek należących do tej grupy:

¾

cząsteczki typu CH

2

XY i CR

2

XY,

¾

aldehydy (RHC=O)

¾

chloroeten CH

2

=CHCl

¾ m

-bromochlorobenzen

H

H

H

Br

Grupy punktowe zawierające tylko cząsteczki achiralne

n

= 4m+2 gdzie

m

= 0, 1, 2, ...

występuje także środek inwersji

Grupy punktowe S

n

elementy symetrii – n-krotna inwersyjna oś symetrii S

n

n

– parzyste brak

płaszczyzn symetrii

niezbędna oś symetrii C

n/2

towarzysząca osi S

n

n

= 4m

gdzie m = 0, 1, 2, ...
brak środka inwersji

n

– nieparzyste

S

n

towarzyszy zawsze oś C

n

pozioma płaszczyzna

σ

h

(grupy nazywają się C

nh

)

Grupy punktowe zawierające tylko cząsteczki achiralne

Grupy punktowe S

n

elementy symetrii – n-krotna inwersyjna oś symetrii S

n

Grupa punktowa S

2

(lub C

i

)

operacje symetrii dla cząsteczek należących do tej grupy:

E

i i

elementy symetrii – oś inwersyjna S

2

(i)

przykłady cząsteczek należących do tej grupy:

¾

mezo-2,3-dibromobutan w konformacji

antiperiplanarnej

¾

dichloro[2.2]paracyklofan

¾

trans-diketopiperazyna (powstała z L- oraz D-Ala)

Br

Br

H

CH

3

H

3

C

H

N

N

H

O

H

O

H

3

C

H

H

CH

3

CH

2

C

CH

2

C

Cl

Cl

H

2

H

2

R

S

Grupy punktowe zawierające tylko cząsteczki achiralne

Grupy punktowe S

n

elementy symetrii – n-krotna inwersyjna oś symetrii S

n

Grupa S

4

przykładem cząsteczki należącej do tej grupy jest np.
związek typu spiro czy pochodna bifenylu

operacje symetrii dla cząsteczek należących do tej grupy:

E

, S

1

6

, C

2

i S

3

4

N

H

3

C

H

3

C

CH

3

CH

3

L

L

CH

3

CONH

Ph

H

S

L:

R

H

CONH

Ph

CH

3

:

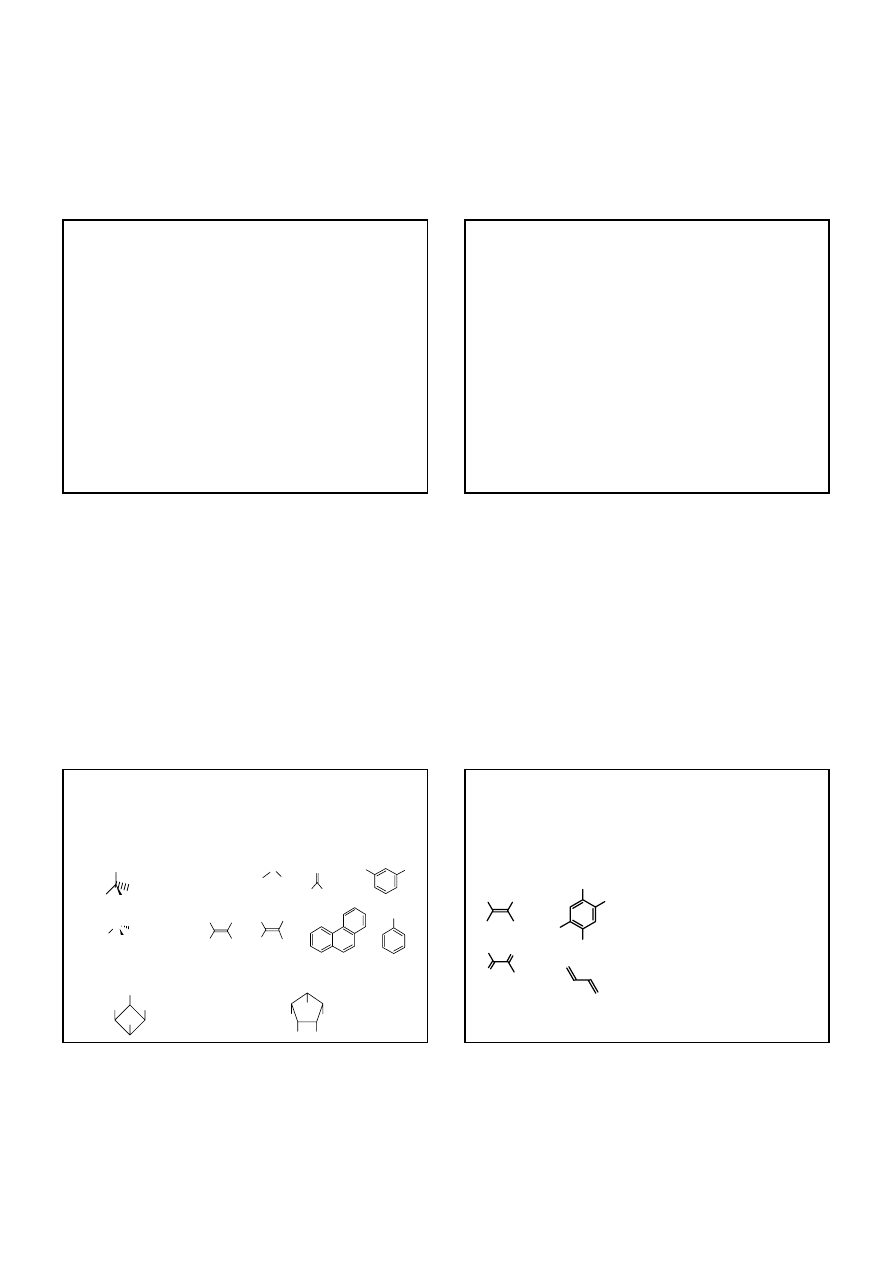
7

Grupy punktowe zawierające tylko cząsteczki achiralne

Kombinacje tych płaszczyzn z osiami symetrii generują
większość grup punktowych symetrii C

n

lub D

n

płaszczyzny symetrii –

wertykalna

σ

v

zawiera główną oś symetrii

diagonalna

σ

d

zawiera główną oś symetrii

horyzontalna

σ

h

prostopadła do głównej osi symetrii

Grupy punktowe zawierające tylko cząsteczki achiralne

grupy punktowe C

nv

jedna oś symetrii C

n

n

wertykalnych (pionowych) płaszczyzn symetrii

σ

v

,

które zawierają oś symetrii C

n

oraz przecinają się

na niej

Br

Br

F

F

H

F

H

Cl

Cl

H

H

O

H

H

O

H

H

C

2v

Cl

Cl

Cl

Cl

Cl

Br

Br

Br

Br

'

dla planarnych pierscieni

C

5v

C

4v

N

H

H

H

H

Cl

Cl

Cl

C

3v

Grupy punktowe zawierające tylko cząsteczki achiralne

grupa punktowa C

∝

v

oś symetrii C

∝

– obrót o nieskończenie mały kąt

oś symetrii C

∝

,

w której przecinają się płaszczyzny symetrii,

ale brak innych elementów symetrii

przykłady cząsteczek należących do tej grupy
(tzw. symetria stożkowa):

¾

chlorowodór

¾

tlenek węgla

¾

chloroetyn

Grupy punktowe zawierające tylko cząsteczki achiralne

grupy punktowe C

nh

oś symetrii C

n

płaszczyzna symetrii

σ

h

, która jest prostopadła do

osi symetrii C

n

operacje symetrii E, C

2

, i,

σ

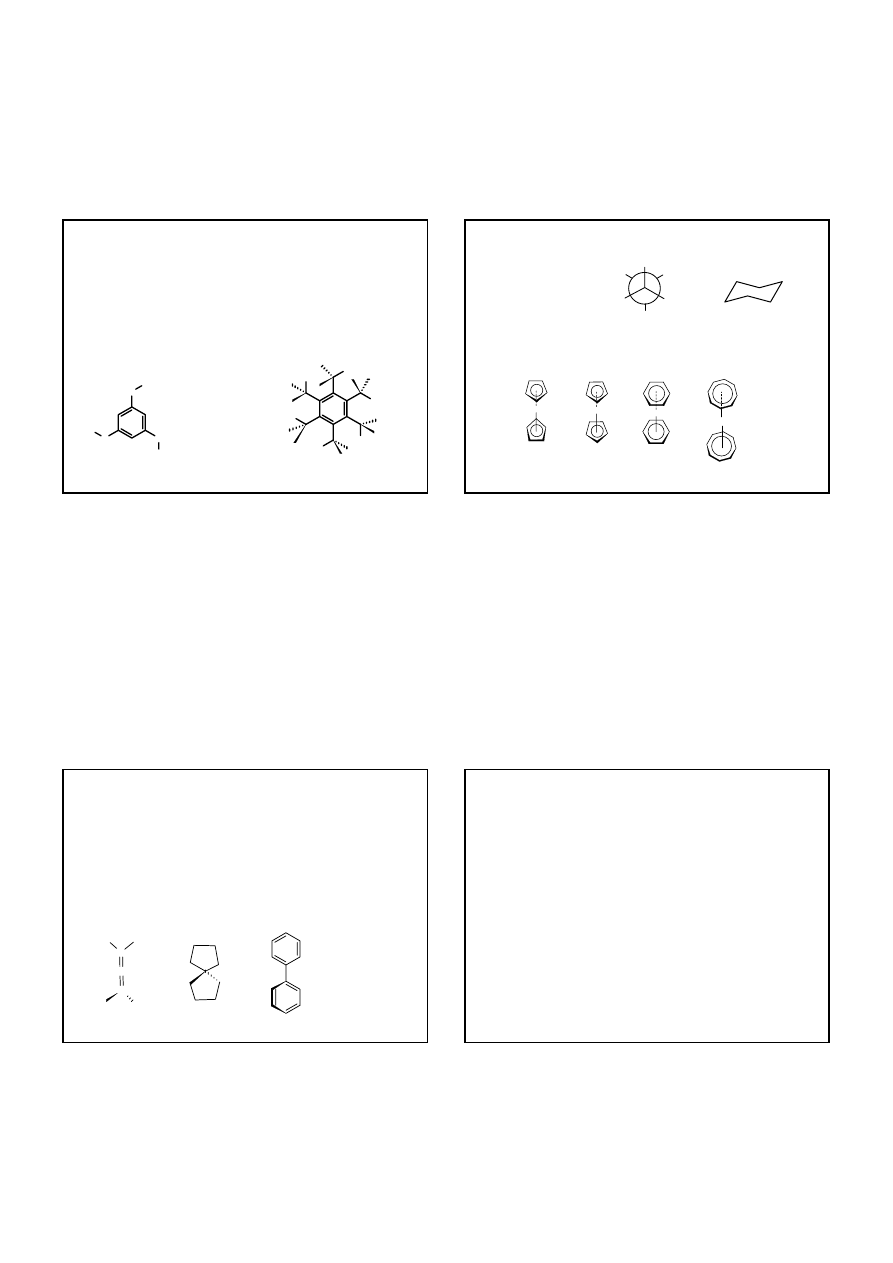
przykłady cząsteczek należących do tej grupy:

¾ trans-

dibromoeten

¾ s-trans-

1,3-butadien

¾

1,4-dibromo-2,5-dichlorobenzen

grupy punktowe C

2h

Br

H

H

Br

O

H

H

O

Cl

Br

Cl

Br

8

Grupy punktowe zawierające tylko cząsteczki achiralne

grupy punktowe C

nh

wyższe grupy punktowe C

nh

–

należą do nich cząsteczki występujące w
określonych konformacjach

O

H

O

H

O

H

grupa punktowe C

6h

H

H

H

H

H

H

grupa punktowe C

3h

Grupy punktowe zawierające tylko cząsteczki achiralne

grupy punktowe D

nd

jedna oś symetrii C

n

n

prostopadłych do niej osi symetrii C

2

n

płaszczyzn symetrii

σ

d

(diagonalne, przekątne)

które przecinają się na osi głównej symetrii C

n

operacje symetrii E, C

2

, 2C’

2

, 2

σ

d

, S

1

4

, S

3

4

grupy punktowe D

2d

C

C

C

H

H

H

H

D

2d

przykłady cząsteczek należących do tej grupy:

¾

alleny

¾

spirany

¾

bifenyle

Grupy punktowe zawierające tylko cząsteczki achiralne

grupy punktowe D

nd

wyższe grupy punktowe D

nd

–

cząsteczki występują w takich grupach
raczej rzadko

grupa punktowe D

3d

H

H

H

H

H

H

Fe

Fe

Cr

U

D

5d

D

5h

D

6h

D

8h

Grupy punktowe zawierające tylko cząsteczki achiralne

grupy punktowe D

nh

jedna oś symetrii C

n

n

prostopadłych do niej osi symetrii C

2

płaszczyznę symetrii

σ

h

operacje symetrii E, C

2

, 2C’

2

, 2

σ

v

,

σ

h

, i

grupa punktowa D

2h

przykłady cząsteczek należących do tej grupy:

¾

eten

¾

1,4-dichlorobenzen

¾

naftalen, antracen

9

D

3h

D

6h

Grupy punktowe zawierające tylko cząsteczki achiralne

grupy punktowe D

nh

jedna oś symetrii C

n

n

prostopadłych do niej osi symetrii C

2

płaszczyznę symetrii

σ

h

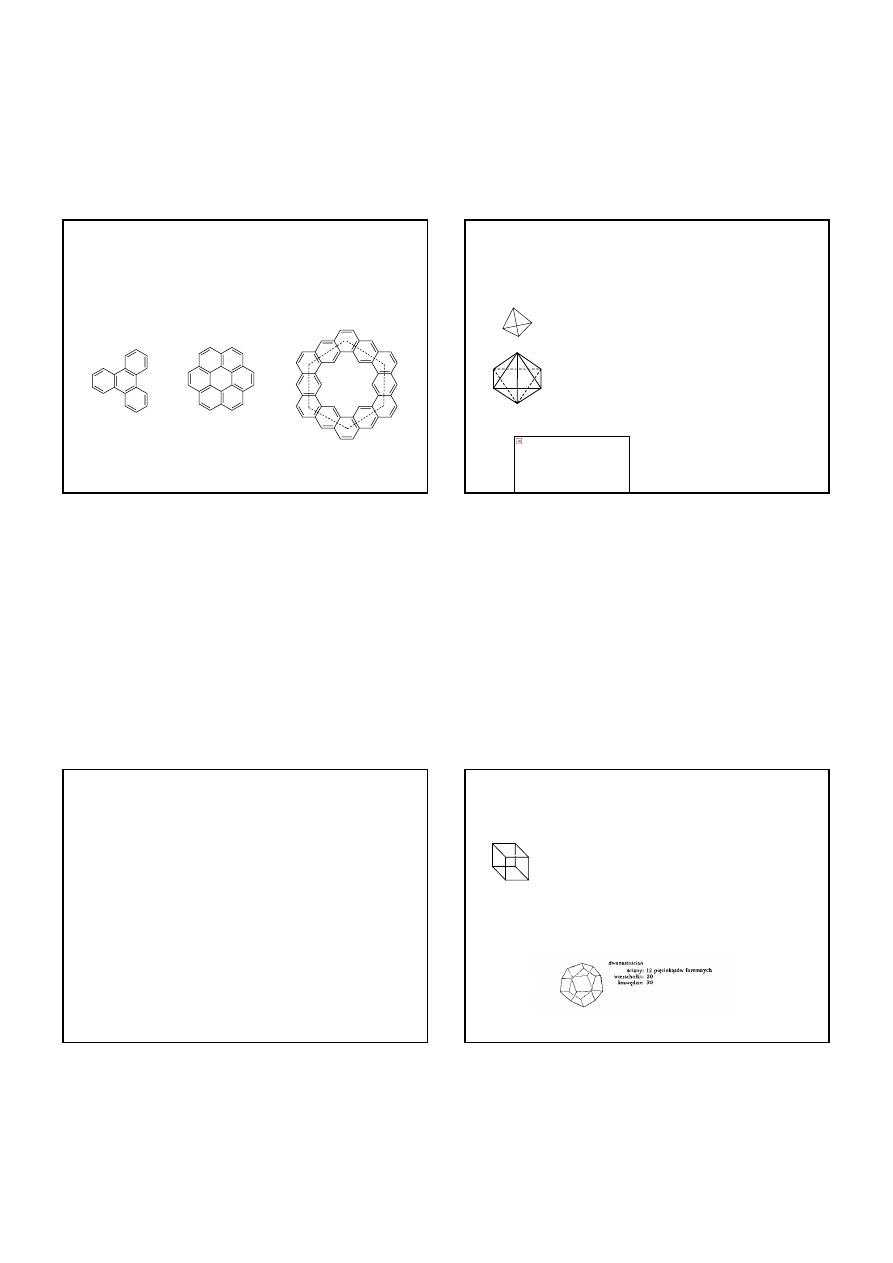
trifenylen

koronen

kekulen

Grupy punktowe zawierające tylko cząsteczki achiralne

grupa punktowa D

∝

h

oś symetrii C

∝

,

w której przecinają się płaszczyzny symetrii

przykłady cząsteczek należących do tej grupy
(tzw. symetria cylindryczna):

¾

wodór cząsteczkowy

¾

ditlenek węgla

¾

etyn

∝

osi symetrii C

2

prostopadłych do osi głównej symetrii C

∝

płaszczyzna symetrii prostopadła do osi głównej symetrii C

∝

Grupy punktowe odpowiadające bryłom platońskim

Aby zbudować wielościan foremny należy w jednym punkcie połączyć
co najmniej trzy ściany.
Dla trójkątów równobocznych:

•

trzy trójkąty o wspólnym wierzchołku (czworościan)

•

cztery trójkąty o wspólnym wierzchołku (ośmiościan)

•

pięć trójkąty o wspólnym wierzchołku (dwudziestościan)

ściany: 8

trójkątów równobocznych

wierzchołki: 6

krawędzie: 12

ściany:

4 trójkąty równoboczne

wierzchołki: 4

krawędzie: 6

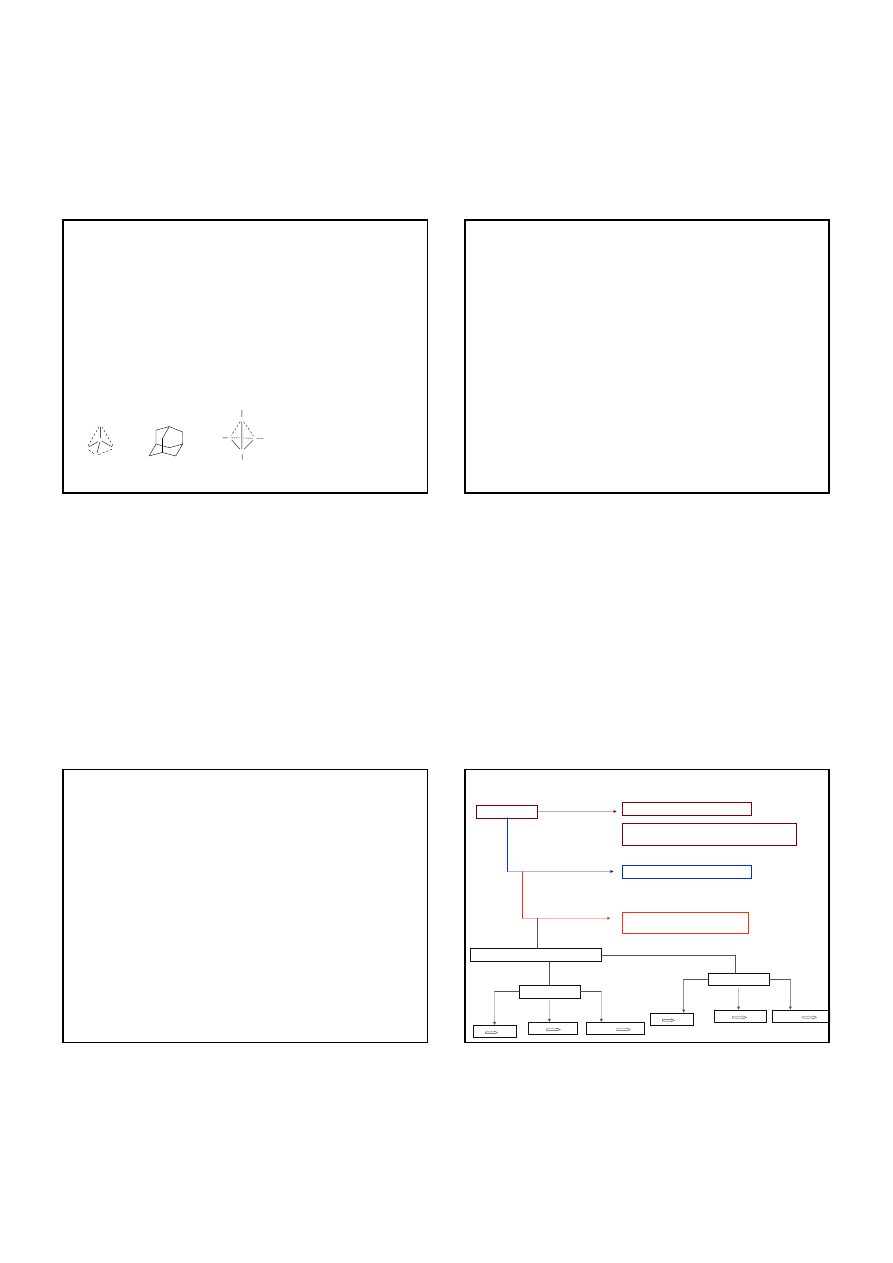
Grupy punktowe odpowiadające bryłom platońskim

Dla kwadratów:

trzy kwadraty o wspólnym wierzchołku – sześcian

Dla pięciokątów foremnych:

trzy pięciokąty o wspólnym wierzchołku

–

dwunastościan (3 x108

° = 324°< 360°)

ściany:

3 kwdraty wierzchołki: 8
krawędzie: 12

10

Tetraedr (czworościan) ma następujące elementy i operacje symetrii:

¾

trzy osie S

4

, które pokrywają się z osiami x, y, z

(generowane operacje S

4

, S

2

4

=C

2

, S

3

4

)

¾

trzy osie C

2

, które pokrywają się z osiami x, y, z

(każda generuje operację C

2

)

¾

cztery osie C

3

, z których każda przechodzi przez

jeden wierzchołek i środek czworościanu (każda
generuje operację C

3

i C

2

3

razem osiem)

¾

sześć płaszczyzn symetrii

Przykłady cząsteczek:

metan
adamantan
cząsteczka hipotetyczna

grupa punktowa T

d

C

H

H

H

H

C

C

C

C

R

R

R

R

A

B

C, R = H

T

d

Grupy punktowe odpowiadające bryłom platońskim

Grupy punktowe odpowiadające bryłom platońskim

Oktaedr (ośmiościan) ma następujące elementy i operacje symetrii:

trzy osie S

4

, które przechodzą przez przeciwległe wierzchołki (każda generuje

operacje S

4

, S

2

4

=C

2

, S

3

4

)

trzy osie C

2

, które pokrywają się z osiami S

4

(każda generuje operację C

2

)

trzy osie C

4

, które pokrywają się z osiami S

4

i C

2

(każda generuje operacje C

4

, C

3

4

i C

2

,

ale tylko C

4

, C

3

4

nie zostały jeszcze wymienione)

sześć osi C’

2

, które przechodzą przez środki przeciwległych krawędzi (każda

generuje operację C’

2

)

cztery osie S

6

, które przechodzą przez środki przeciwległych ścian trójkątnych (każda

generuje operacje S

6

, S

3

6

=C

3

, i, C

2

3

, S

5

6

)

cztery osie C

3

, które pokrywają się z osiami S

6

(każda generuje operacje C

3

, C

2

3

,

generowane również przez S

6

)

środek inwersji (wymieniony w pcie 5)

trzy płaszczyzny symetrii, które przechodzą przez cztery spośród sześciu
wierzchołków ośmiościanu (operacje

σ

h

)

sześć płaszczyzny symetrii, które przechodzą przez dwa wierzchołki i dzielą na
połowy przeciwległe krawędzie nie zawierające tych wierzchołków(operacje

σ

d

)

grupa punktowa O

h

Grupy punktowe odpowiadające bryłom platońskim

Dodekaedr (dwunastościan) oraz zikosaedr (dwudziestościan) mają
taka samą symetrię; Należą do grupy punktowej I

h

, która

charakteryzuje się 120 operacjami (E, 12C

5

, 12C

2

5

, 20C

3

, 15C

2

, i,

12S

10

, 12 S

3

10

, 20S

6

, 15

σ)

grupa punktowa I

h

OKREŚLANIE SYMETRII CZĄSTECZEK

CZĄSTECZKA

ETAP I

™

CZĄSTECZKI LINIOWE: C

∝v

, D

∝h

™

GRUPY O KILKU OSIACH WYŻSZEGO RZĘDU:

T, T

h

, T

d

, O, O

h

, I, I

h

,

ETAP II

BRAK OSI OBROTÓW – C

1

, C

s

, C

i

ETAP III

OŚ NIEWŁAŚCIWA – S

4

, S

6

, S

8

.....

n

– parzyste

oś C

n

nie będąca konsekwencją S

2n

BRAK C

2

⊥ C

n

n C

2

⊥ C

n

n

σ

v

C

nv

σ

h

D

nh

σ

h

C

nh

n

σ

d

D

nd

BRAK

σ

D

n

BRAK

σ

C

n

ETAP IV

ETAP V