1

Mechanika ogólna

Wykład nr 1

Wprowadzenie

Podstawowe pojęcia

Rachunek wektorowy

Wypadkowa układu sił

Równowaga

2

Przedmiot



Mechanika ogólna, techniczna,

teoretyczna.



Dział fizyki, zajmujący się badaniem

ruchu ciał materialnych, ustalaniem

ogólnych praw ruchu ciał materialnych

oraz zastosowaniem tych praw do

pewnych wyidealizowanych ciał

rzeczywistych, jakimi są punkt

materialny oraz ciało doskonale sztywne

(ramy, kraty).

3

Program zajęć



Podstawowe pojęcia.



Podstawy rachunku wektorowego.



Układy sił i stan równowagi.



Reakcje więzów w układach płaskich.



Siły wewnętrzne

–

w ustrojach kratowych;

–

w belkach;

–

w ustrojach ramowych.



Charakterystyki geometryczne figur

płaskich.

4

Literatura



[1] J. Leyko:

Mechanika ogólna



[2] J. Leyko:

Mechanika ogólna w zadaniach



[3] Z. Cywiński:

Mechanika budowli w

zadaniach

(Tom 1)



[4] J. Naleszkiewicz:

Mechanika techniczna



[5] A. Chudzikiewicz:

Statyka budowli

(Tom 1)



[6] P. Jastrzębski, J. Mutermilch,

W. Orłowski:

Wytrzymałość materiałów

(Tom 1)

5

Zaliczenie



Ćwiczenia:

– obecności;
– ćwiczenie projektowe;
– kolokwia.



Egzamin:

– część pisemna;
– część ustna.

6

Działy mechaniki



Statyka – bada przypadki, kiedy siły działające na

ciało nie wywołują sił bezwładności, tj. są

przykładane w nieskończenie długim czasie oraz

równoważą się wzajemnie.



Kinematyka – zajmuje się badaniem ruchu ciał

niezależnie od czynników wywołujących ten ruch.

Przedmiotem badań są: droga, prędkość,

przyspieszenie itd.



Dynamika – rozpatruje ruch ciał w zależności od sił

działających na nie, bada zależności między takimi

wielkościami jak: prędkość, przyśpieszenie, pęd, siła,

energia itd.

7

Zasady dynamiki Newtona

(1)



Prawo I
Punkt materialny, na który nie działa

żadna siła lub działające siły

równoważą się, pozostaje w spoczynku

lub porusza się ruchem jednostajnym

po linii prostej.

8

Zasady dynamiki Newtona

(2)



Prawo II
Przyspieszenie punktu materialnego jest

wprost proporcjonalne do siły działającej na

ten punkt, a odwrotnie proporcjonalne do

masy punktu materialnego. Przyjmuje ono

zwrot i kierunek zgodny ze zwrotem i

kierunkiem wektora siły.

P = m a

P

a

m

9

Zasady dynamiki Newtona

(3)



Prawo III
Dwa punkty materialne działają na

siebie dwoma siłami równymi co do

wartości, tym samym kierunku, ale o

przeciwnym zwrocie.

P

1

P

2

2

1

P

P



2

1

P

P





10

Idealizacje (1)



Punkt materialny – ciało o nieskończenie

małych wymiarach, ale posiadający swoją

masę. Punkt materialny modeluje ciała o

bardzo małych wymiarach w porównaniu z

wymiarami obszaru, w którym ciało się

porusza. Wymiary te powinny być na tyle

małe, aby można było pominąć zmiany

ułożenia tego ciała względem układu

odniesienia, wywołane przez obrót.

11

Idealizacje (2)



Ciało doskonale sztywne – ciało, w

którym odległości między jego punktami

nie zmieniają się. Ciało takie nie podlega

odkształceniom pod wpływem sił,

działających na to ciało. Ciało doskonale

sztywne może być modelem ciała

rzeczywistego, gdy odkształcenia tego

ciała są pomijalnie małe w stosunku do

wymiarów tego ciała.

12

Idealizacje (3)



Zasada zesztywnienia
Warunki równowagi sił działających na

ciało odkształcalne nie zostanie

naruszona przez zesztywnienie tego

ciała. Punkt przyłożenia siły nie ulega

przesunięciu mimo odkształcenia

konstrukcji.

13

Zasada superpozycji



Działania poszczególnych obciążeń są

od siebie niezależne.



Efekt działania (odkształcenie, siła

wewnętrzna) dwóch lub więcej

wpływów (obciążeń) może zostać

wyznaczony jako suma efektów

wywołanych działaniem tych wpływów

oddzielnie.

14

Skalar i wektor



Skalar – wielkość, do opisania której niezbędne jest

podanie jednej wartości w odniesieniu do

określonego punktu w przestrzeni.



Wektor – wielkość, do opisania której poza

wartością miary (modułu, długości wektora),

niezbędne jest także podanie kierunku (ułożenia linii

działania), zwrotu (uporządkowanie punktów od

początku do końca wektora), punktu zaczepienia.
Wektor może zostać przedstawiony jako

uporządkowana para punktów, z których jeden jest

początkiem wektora, a drugi jego końcem.

15

Przykłady



Skalary:

– gęstość, masa;



Wektory

– przemieszczenie, prędkość,

przyspieszenie, siła.

16

Podstawowe jednostki



Masa: g (gram); kg = 1000 g (kilogram)



Długość: mm = 0.001 m (milimetr);

m (metr); km = 1000 m (kilometr)



Czas: s (sekunda); min = 60 s (minuta);

h = 60 min = 3600 s (godzina)



Siła: N = kg m/s

2

(niuton);

kN = 1000N (kiloniuton)



Moment siły: Nm (Niutonometr)

17

Rodzaje wektorów



Wektory zaczepione – związane z

punktem przyłożenia;



Wektory ślizgające się – mogące

poruszać się wzdłuż linii działania (np.

wektory sił w mechanice);



Wektory swobodne – mogą zostać

przyłożone w dowolnym punkcie (np.

wektory momentów sił).

18

Działania na wektorach



Suma wektorów;



Różnica wektorów;



Mnożenie wektora przez skalar;



Iloczyn wektorów:

– skalarny;
– wektorowy;
– mieszany;
– inne wielokrotne iloczyny wektorów.

19

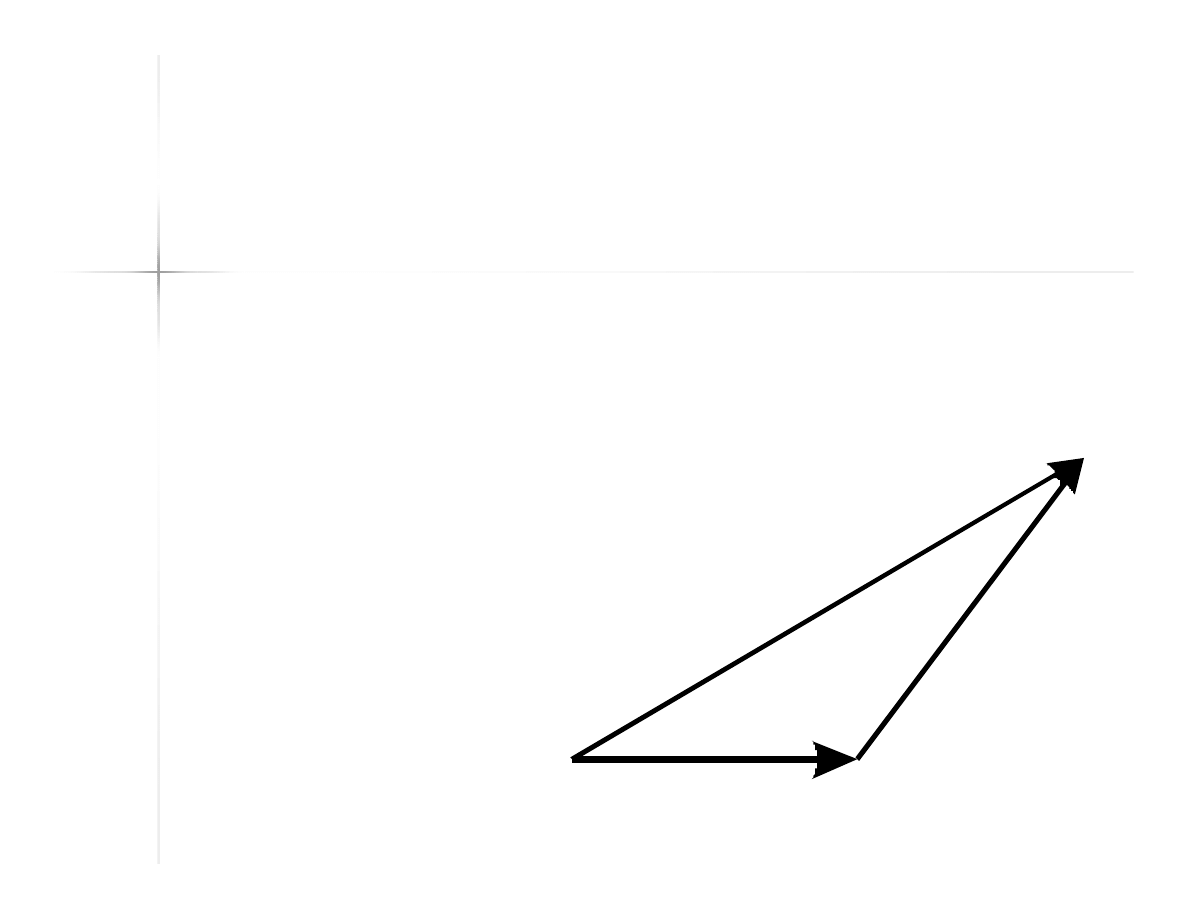
Dodawanie wektorów

]

,

,

[

z

y

x

a

a

a



a

]

,

,

[

z

y

x

b

b

b



b

]

,

,

[

z

z

y

y

x

x

b

a

b

a

b

a









c

a

b

b

a

c











Suma wektorowa wektorów a i b:

a

b

c

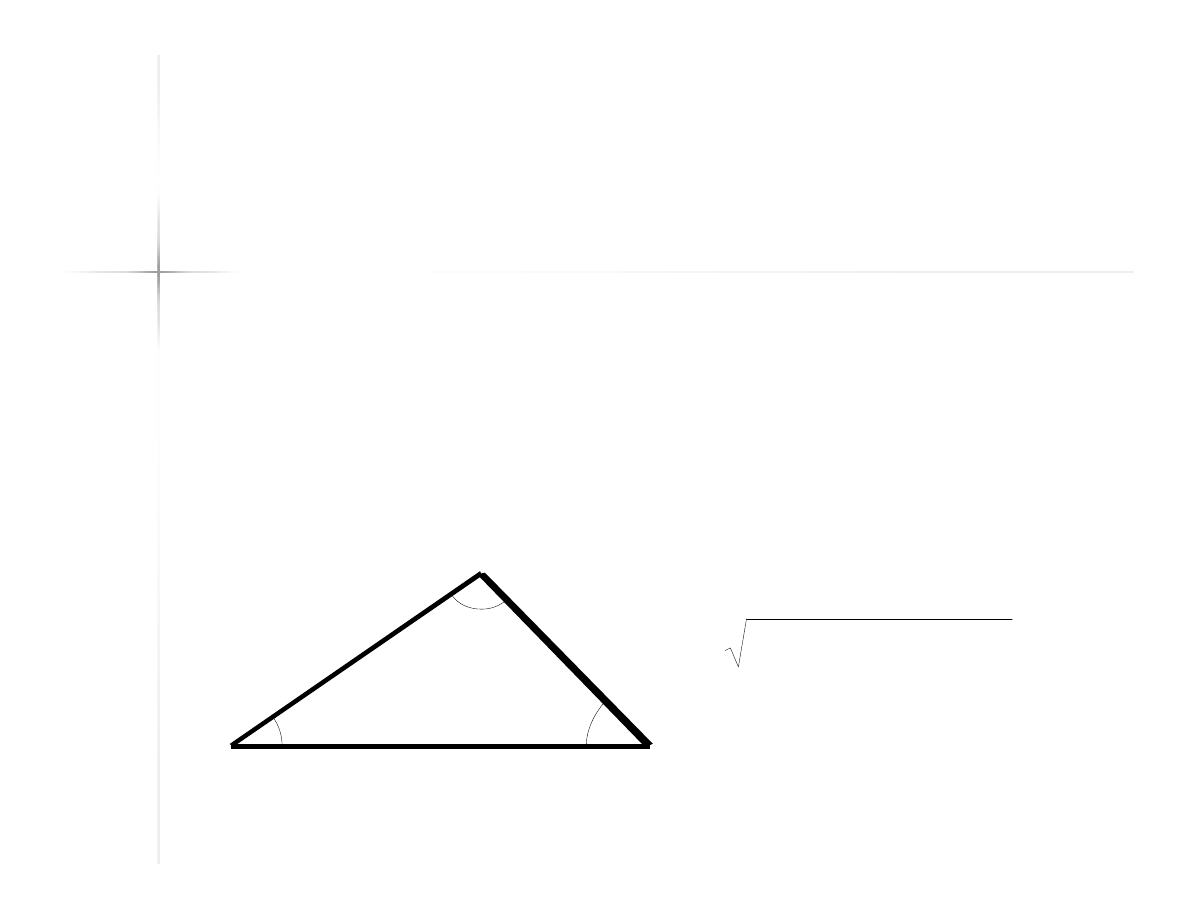
20

Twierdzenie cosinusów



Kwadrat długości boku trójkąta leżącego

naprzeciw kąta



jest równy sumie

kwadratów długości boków leżących przy

tym kącie oraz podwojonego iloczynu tych

długości boków i cosinusa tego kąta



.



cos

2

2

2

ab

b

a

c







a

c

b







21

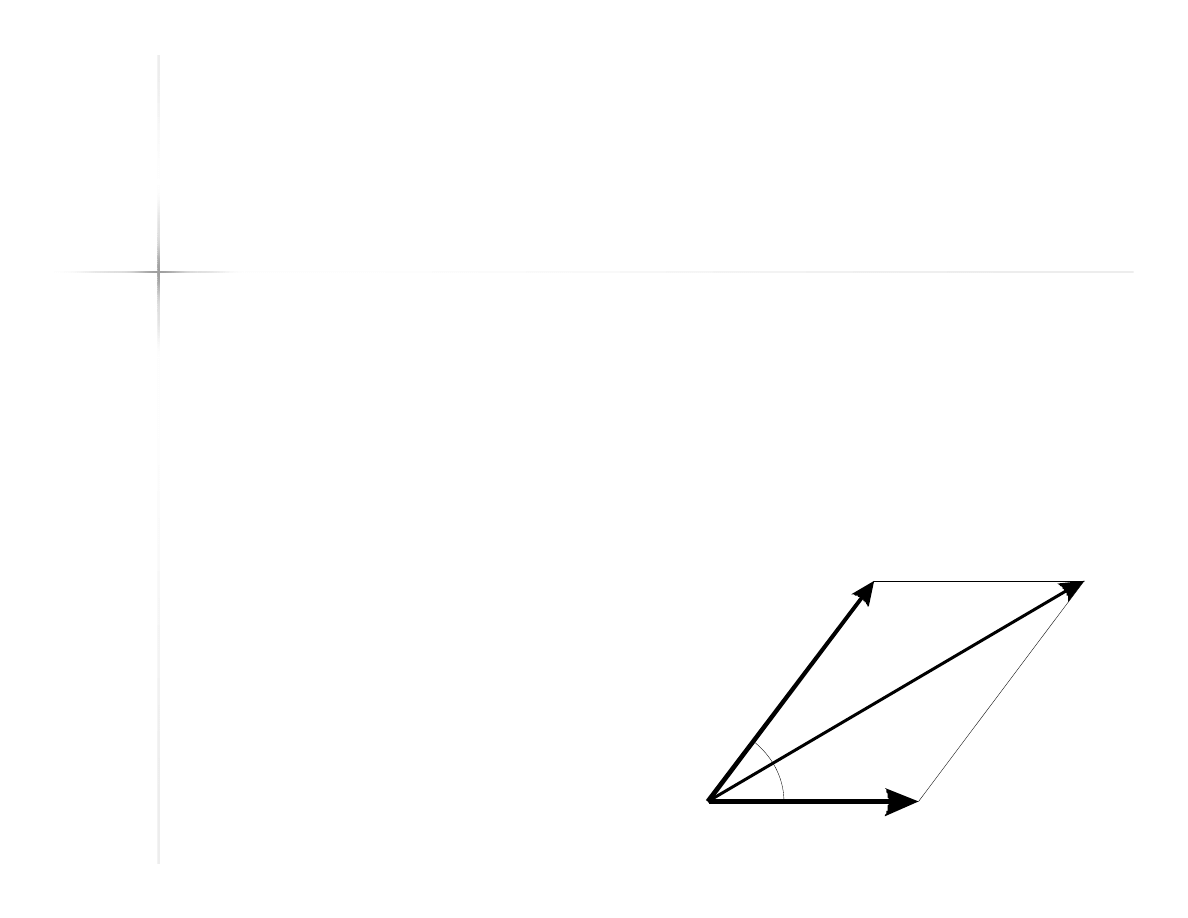
Zasada równoległoboku



Suma dwóch wektorów może zostać

przedstawiona jako przekątna

równoległoboku zbudowanego na

bazie sumowanych wektorów

przecinająca kąt między tymi

wektorami.

a

b



c

22

Odejmowanie wektorów

(1)



Różnica wektorów a i b jest równa

sumie wektora a i wektora

przeciwnego do b:

]

,

,

[

z

y

x

b

b

b









 b

]

,

,

[

z

z

y

y

x

x

b

a

b

a

b

a













b

a

c

]

,

,

[

z

y

x

a

a

a



a

]

,

,

[

z

y

x

b

b

b



b



Różnica wektorów b i a jest równa sumie

wektora b i wektora przeciwnego do a:

]

,

,

[

z

y

x

a

a

a

a











]

,

,

[

z

z

y

y

x

x

a

b

a

b

a

b













a

b

d

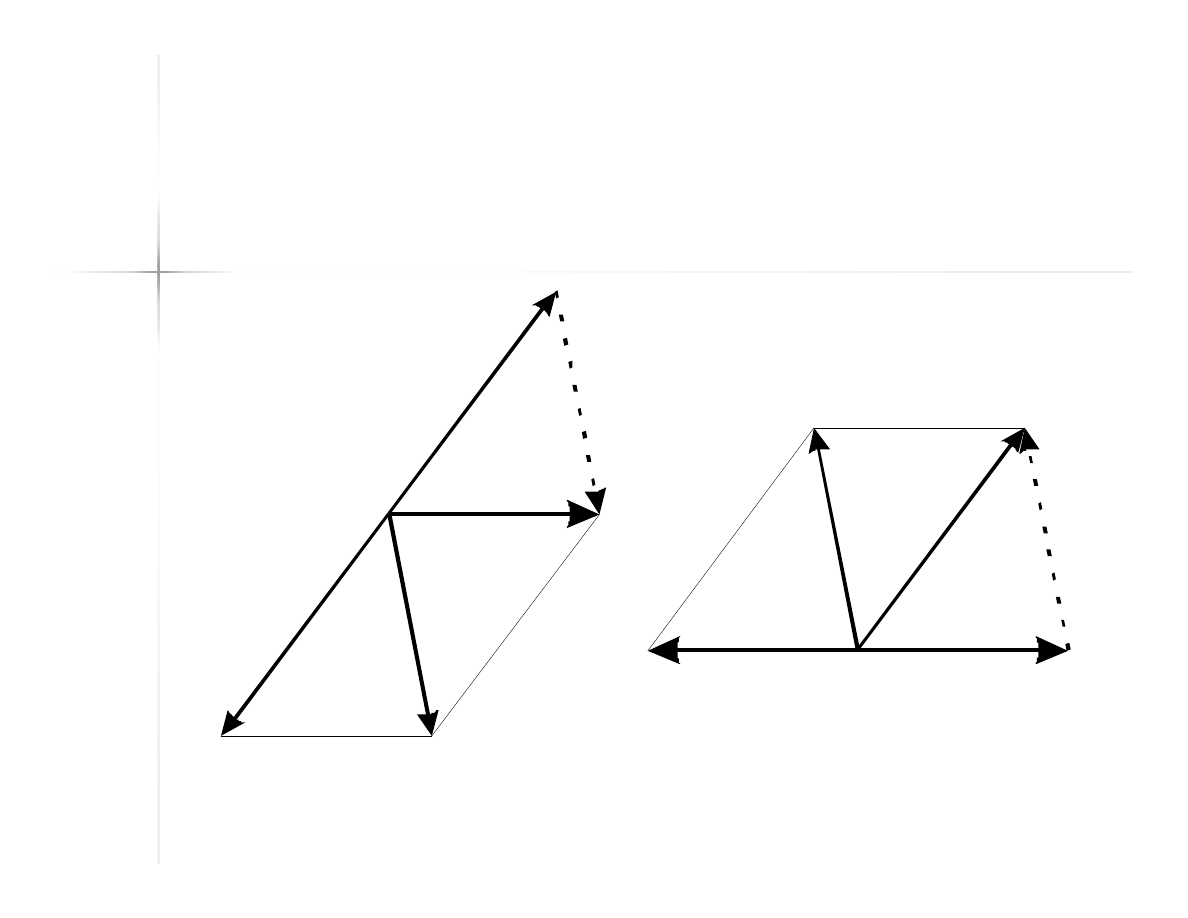
23

Odejmowanie wektorów

(2)

a

-b

c

b

a

-a

d

b

 

b

a

b

a

c











 

a

b

a

b

d











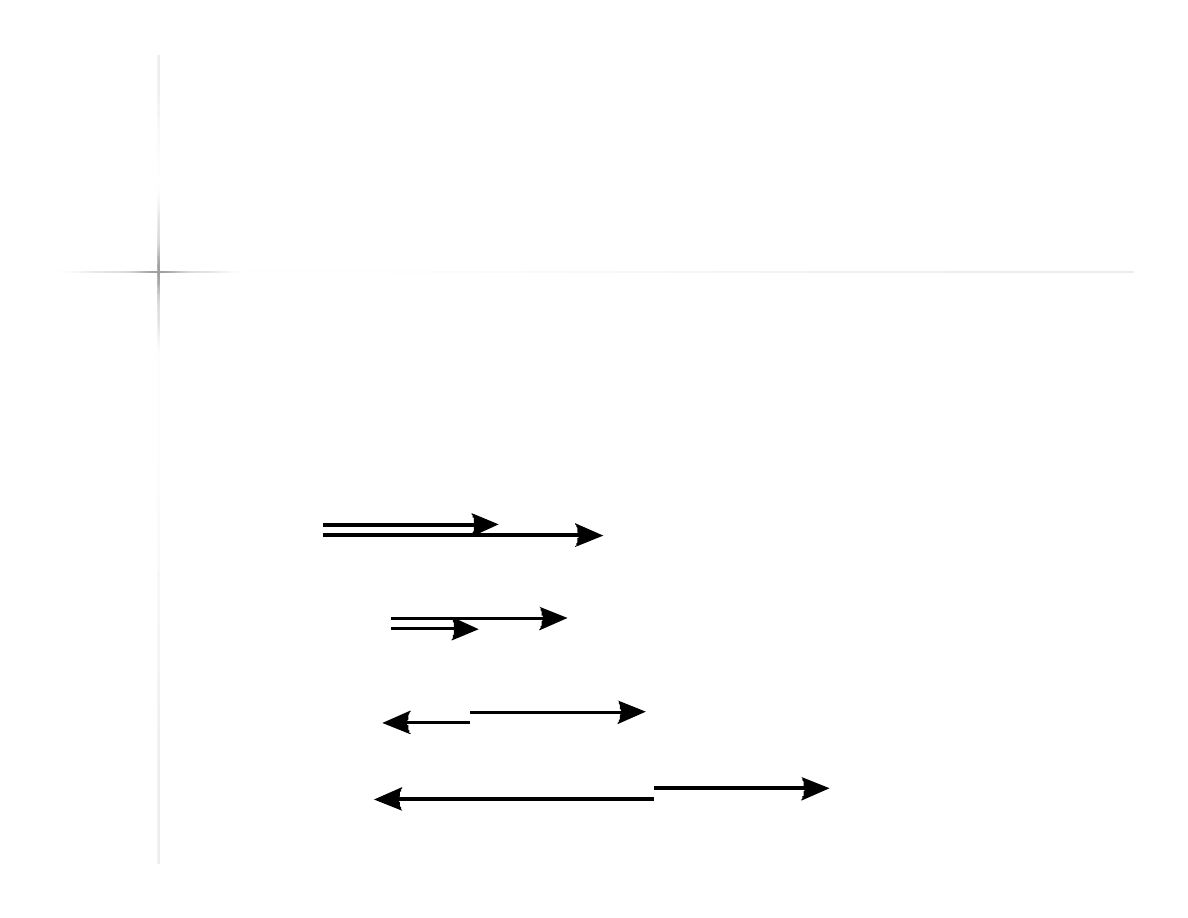
24

Skalowanie wektora



Mnożenie wektora przez skalar (n) w wyniku czego

otrzymuje się wektor o takim samym kierunku, mierze
n razy większej (przy |n|>1) lub 1/n razy mniejszej

(przy |n|<1) i takim samym zwrocie, jeżeli n>0, zaś

przeciwnym, jeżeli n<0.



n>1



0<n<1



-1<n<0



n<-1

a

n

a

·

a

n

a

·

a

n

a

·

a

n

a

·

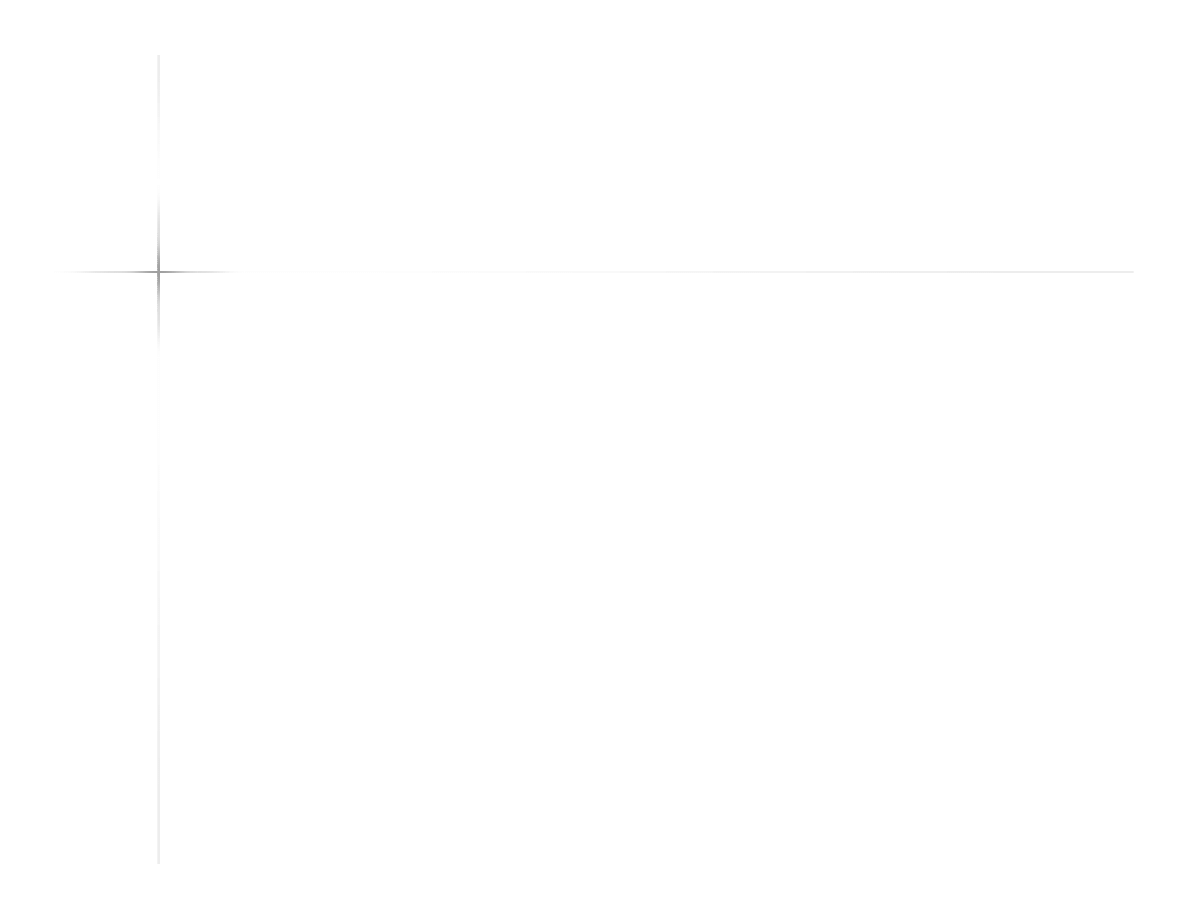
25

Iloczyn skalarny

(1)



Wielkość skalarna równa iloczynowi

modułów mnożonych wektorów i

cosinusa kąta zawartego między nimi

(iloczyn miary jednego wektora przez

rzut prostokątny drugiego na kierunek

pierwszego).

26

Iloczyn skalarny

(2)

]

,

,

[

z

y

x

a

a

a



a

]

,

,

[

z

y

x

b

b

b



b

z

z

y

y

x

x

b

a

b

a

b

a

b

a

s

















)

,

(

cos

b

a

b

a



a

b



b

cos



a

co

s

27

Iloczyn wektorowy

(1)



Wektor o kierunku prostopadłym do

płaszczyzny wyznaczonej przez mnożone

wektory, zwrocie określonym zgodnie z

regułą śruby prawoskrętnej i mierze

równej iloczynowi miar mnożonych

wektorów i sinusa kąta między nimi

(pole powierzchni równoległoboku

zbudowanego na mnożonych

wektorach).

28

Iloczyn wektorowy

(2)

]

,

,

[

z

y

x

a

a

a



a

]

,

,

[

z

y

x

b

b

b



b

b

a

c





a

b

d





c

d

















2

2

2

)

,

(

sin

x

y

y

x

z

x

x

z

y

z

z

y

b

a

b

a

b

a

b

a

b

a

b

a

b

a

d

c

























b

a

c

i

j

k

 a

a

a

b

b

b

x

y

z

x

y

z

z

y

x

z

y

x

a

a

a

b

b

b

k

j

i

d



a

b

c



a

b

d



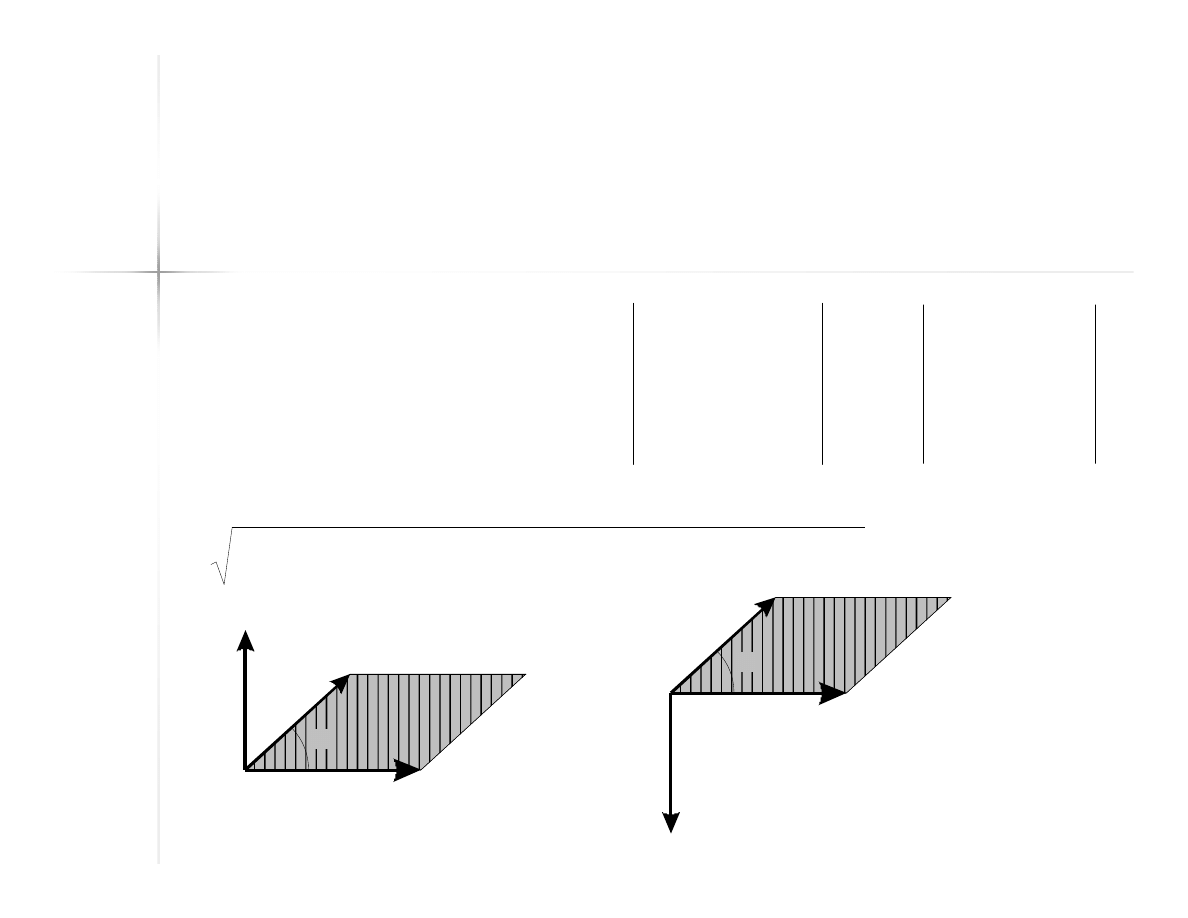
29

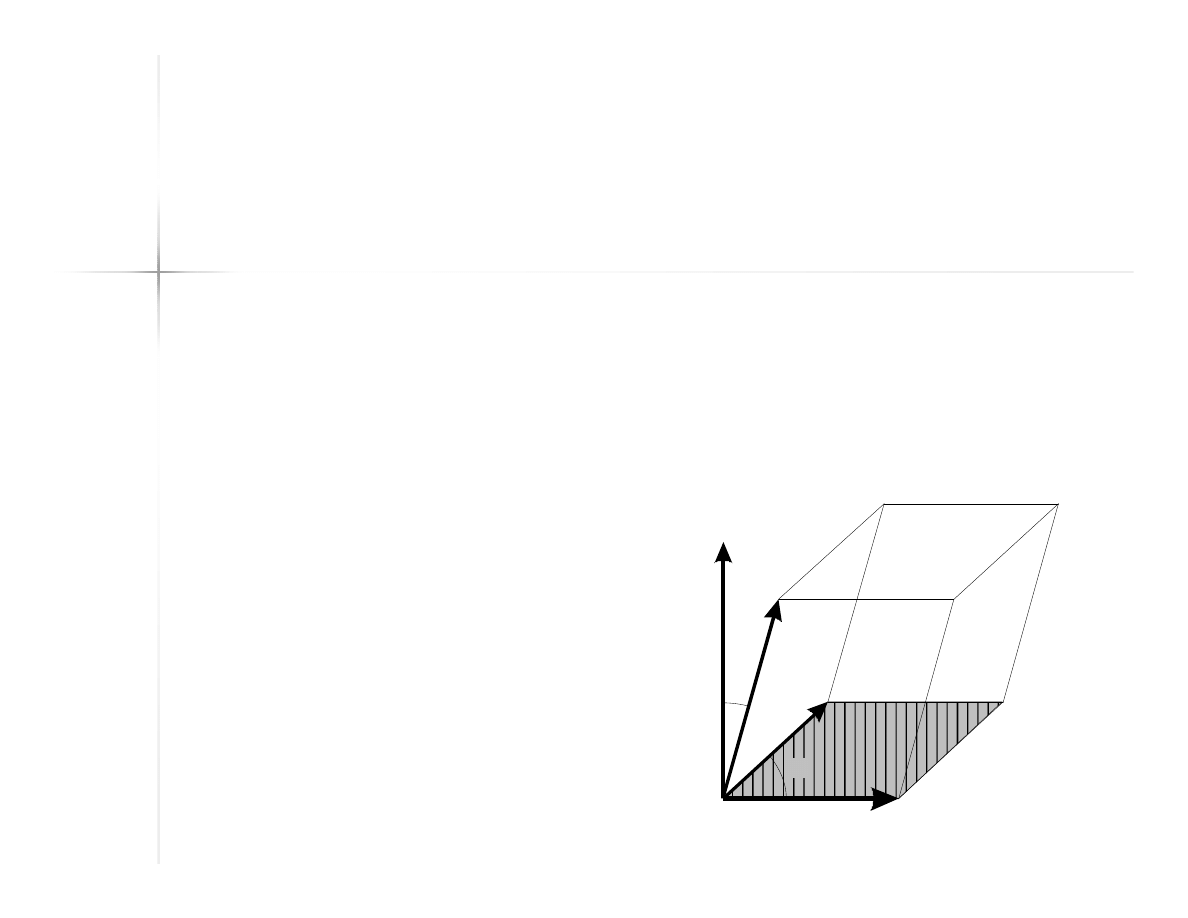
Iloczyn mieszany



Wielkość skalarna – objętość

równoległościanu zbudowanego na

mnożonych wektorach jako na

krawędziach.

c

b

a



)

(





V

a

b

c

d







sin

ab

d







cos

sin

c

ab

V







cos

c

d

V







c

d



30

Przemienność działań



Suma wektorów i iloczyn skalarny są

działaniami przemiennymi, natomiast

różnica wektorów i iloczyn wektorowy

nie są przemienne.

a – b = c

b – a = d =>

d = -c

a

× b = c

b

× a = d => d = -c

31

Pojęcie siły



Siła – wzajemne oddziaływanie ciał,

które przejawia się w wyprowadzeniu

ciała ze stanu spoczynku, bądź przez

zmianę ruchu już poruszającego się

ciała. Aby scharakteryzować siłę

należy podać wektor, opisujący tą siłę,

oraz punkt przyłożenia siły.

32

Układy sił



Układ sił – dowolna grupa oddziaływań ciał

zewnętrznych na analizowane ciało, czyli zbiór

sił, których punkty przyłożenia, znajdują się w

analizowanym obszarze.



Równoważne układy sił
Dwa układy sił są równoważne wtedy, gdy

zastąpienie jednego układu, działającego na

ciało sztywne, przez drugi układ sił nie wywoła

zmiany stanu ruchu czyli nie spowoduje

zmiany kierunku ruchu, prędkości,

przyśpieszenia, itd.

33

Wypadkowa



Siła wypadkowa – wektor, który jest

sumą wszystkich wektorów sił z

układu, przyłożonego do punktu

materialnego i stanowi układ

równoważny, pod warunkiem, że siła

wypadkowa jest przyłożona do tego

samego punktu.

34

Płaski i przestrzenny

układ sił



Układ sił nazywamy płaskim jeżeli

kierunki wszystkich sił tego układu

położone są w jednej płaszczyźnie, w

innym przypadku układ nazywamy

przestrzennym.

35

Układ sił zbieżnych



Układ sił zbieżnych – linie działania

wszystkich sił przecinają się w jednym

punkcie, tzw. punkcie zbieżności.



Określanie wypadkowej układu sił:

– działających wzdłuż jednej prostej;
– zbieżnych



metoda graficzna;



metoda analityczna.

36

Siły działające wzdłuż

jednej prostej



Wypadkowa układu sił działających wzdłuż

jednej prostej jest wektorem o także

działającym wzdłuż tej prostej, zwrocie

zgodnym z większą ze składanych sił i mierze

równej sumie, gdy miary wektorów

składowych są zgodne, lub różnicy miar

wektorów składowych, gdy zwroty

składowych są przeciwne.

P

1

P

2

W

P

1

P

2

W

2

1

P

P

W





2

1

P

P

W





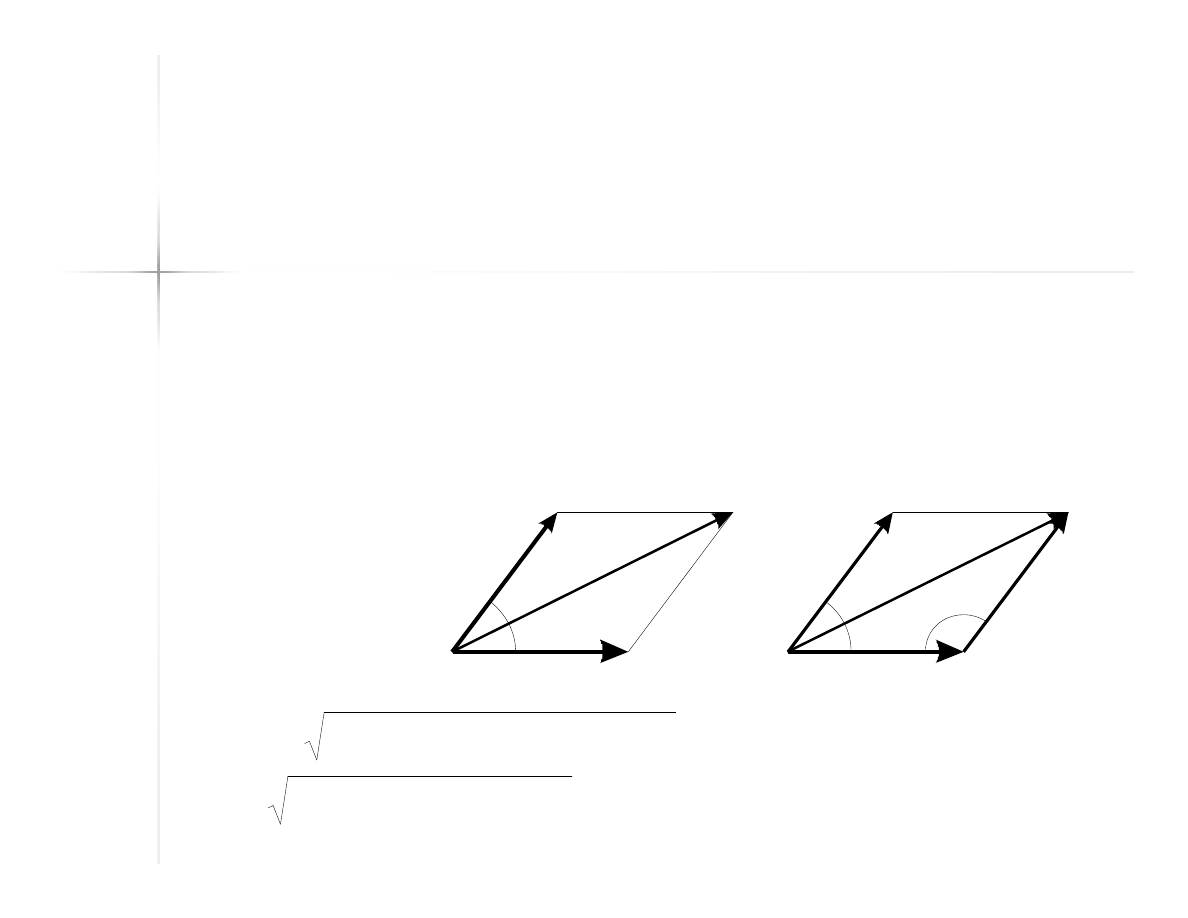
37

Wypadkowa

- metoda graficzna



Wypadkowa układu dwóch sił może zostać

wyznaczona jako przekątna równoległoboku

zbudowanego w oparciu o wektory

składowe przecinająca kąt między tymi

wektorami.

P

1

P

2



P

1

P

2





P

2

W

W







cos

2

)

cos(

2

2

1

2

2

2

1

2

1

2

2

2

1

P

P

P

P

P

P

P

P

W

















38

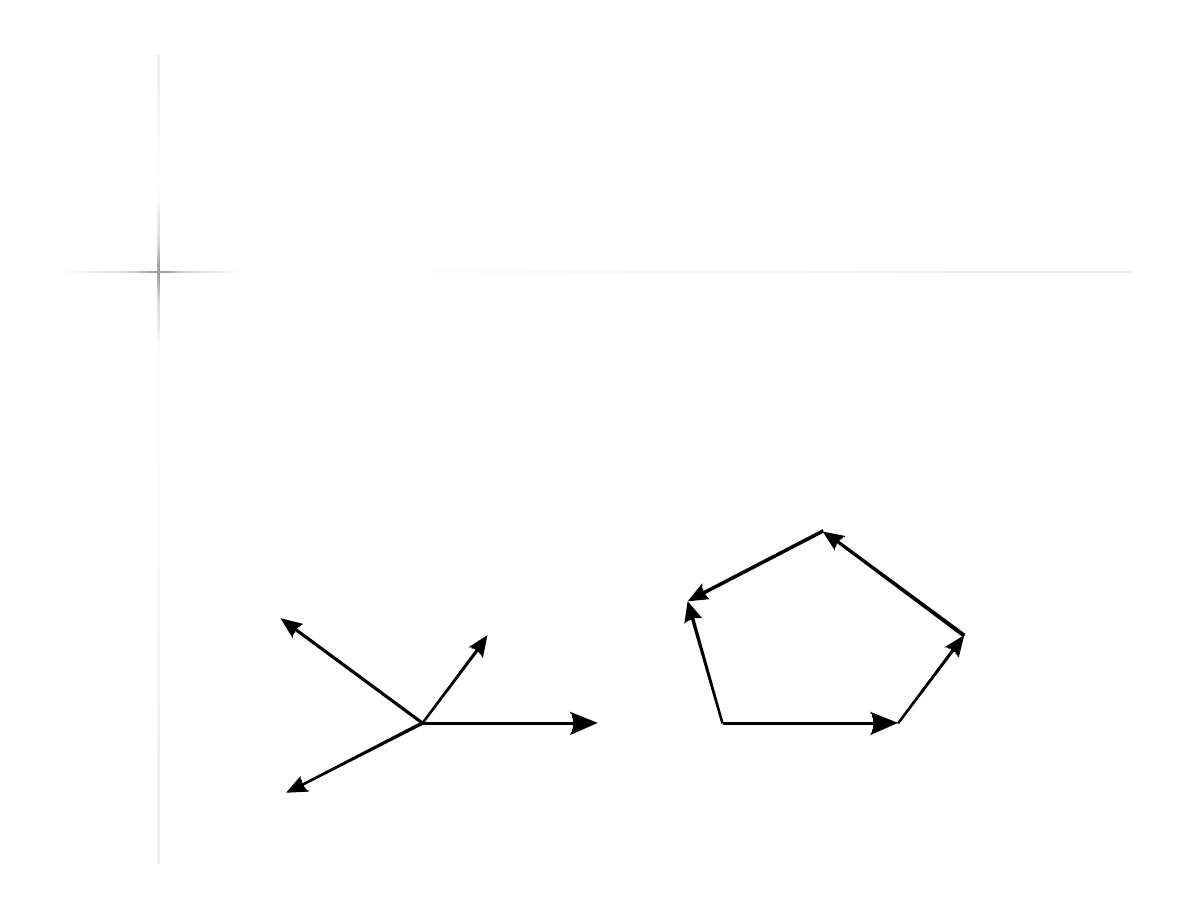
Wielobok sznurowy



Do końca pierwszej siły przykłada się

początek siły następnej itd. Początek

pierwszej siły połączony z końcem

ostatniej określa wypadkową.

P

1

P

2

W

P

3

P

4

P

1

P

2

P

3

P

4

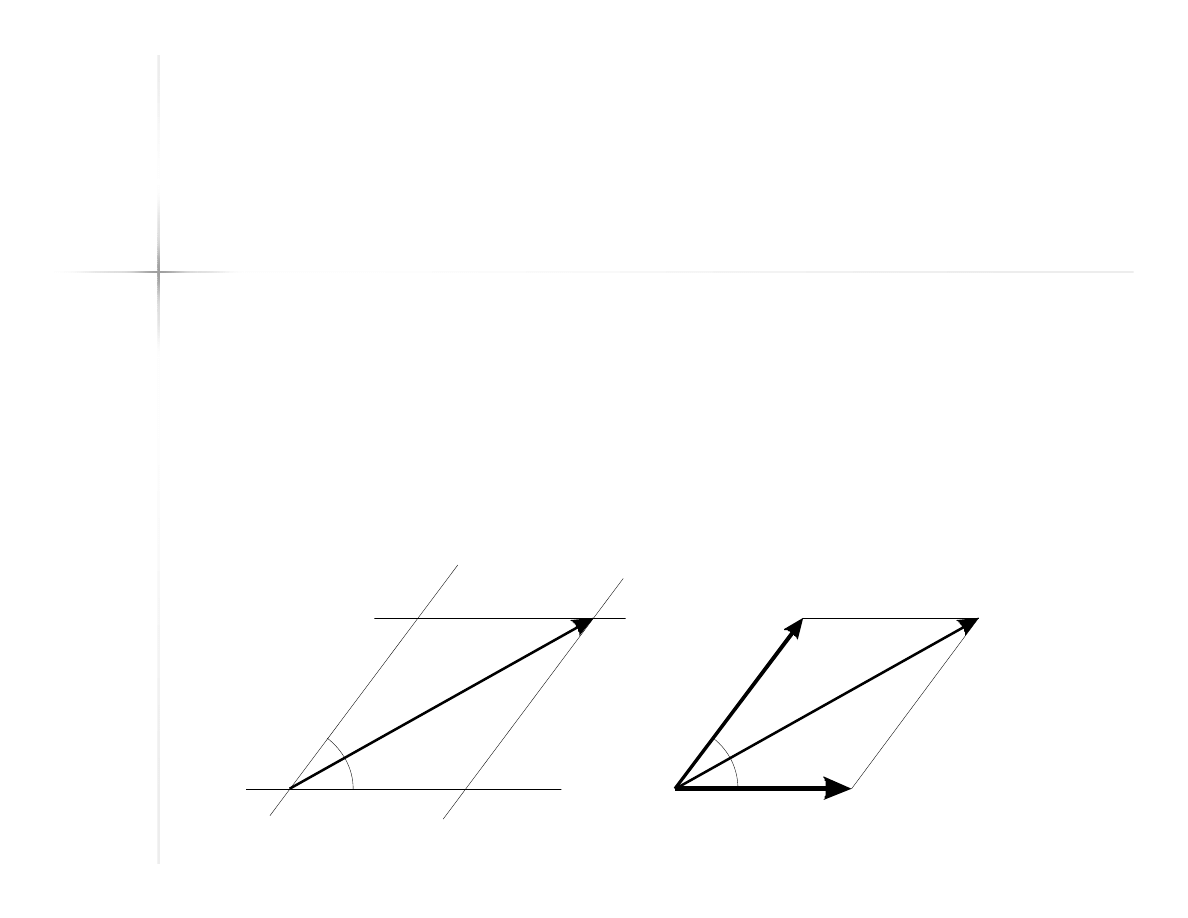
39

Rozkładanie siły na

składowe



Przez początek i koniec danej siły

przeprowadza się kierunki, na które siła

ma zostać rozłożona. Siły składowe

mogą zostać wyznaczone jako boki tak

zbudowanego równoległoboku.



P



P

1

P

2

P

1

2





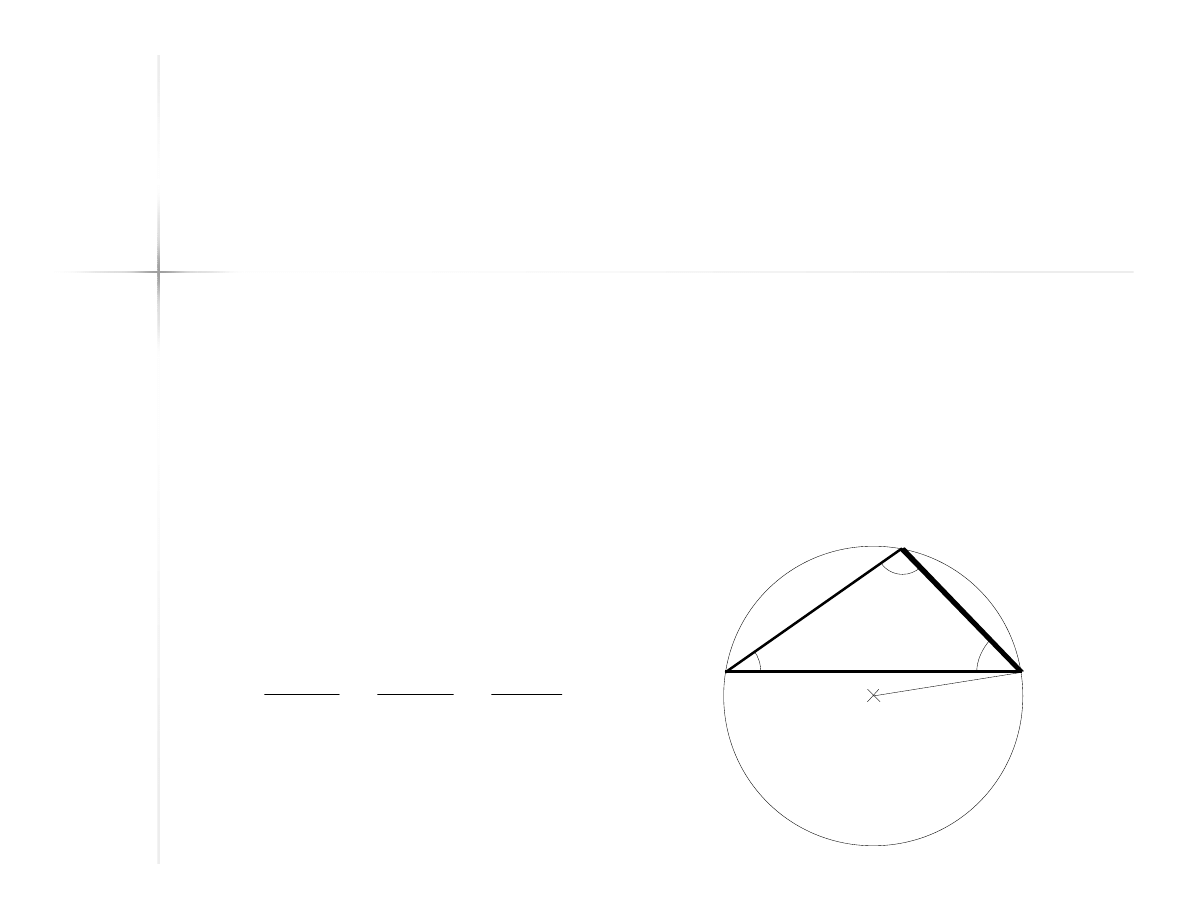
40

Twierdzenie sinusów



W dowolnym trójkącie stosunek

długości boku do sinusa

przeciwległego kąta jest stały i równa

się długości średnicy okręgu opisanego

na trójkącie.

R

a

c

b







R

c

b

a

2

sin

sin

sin













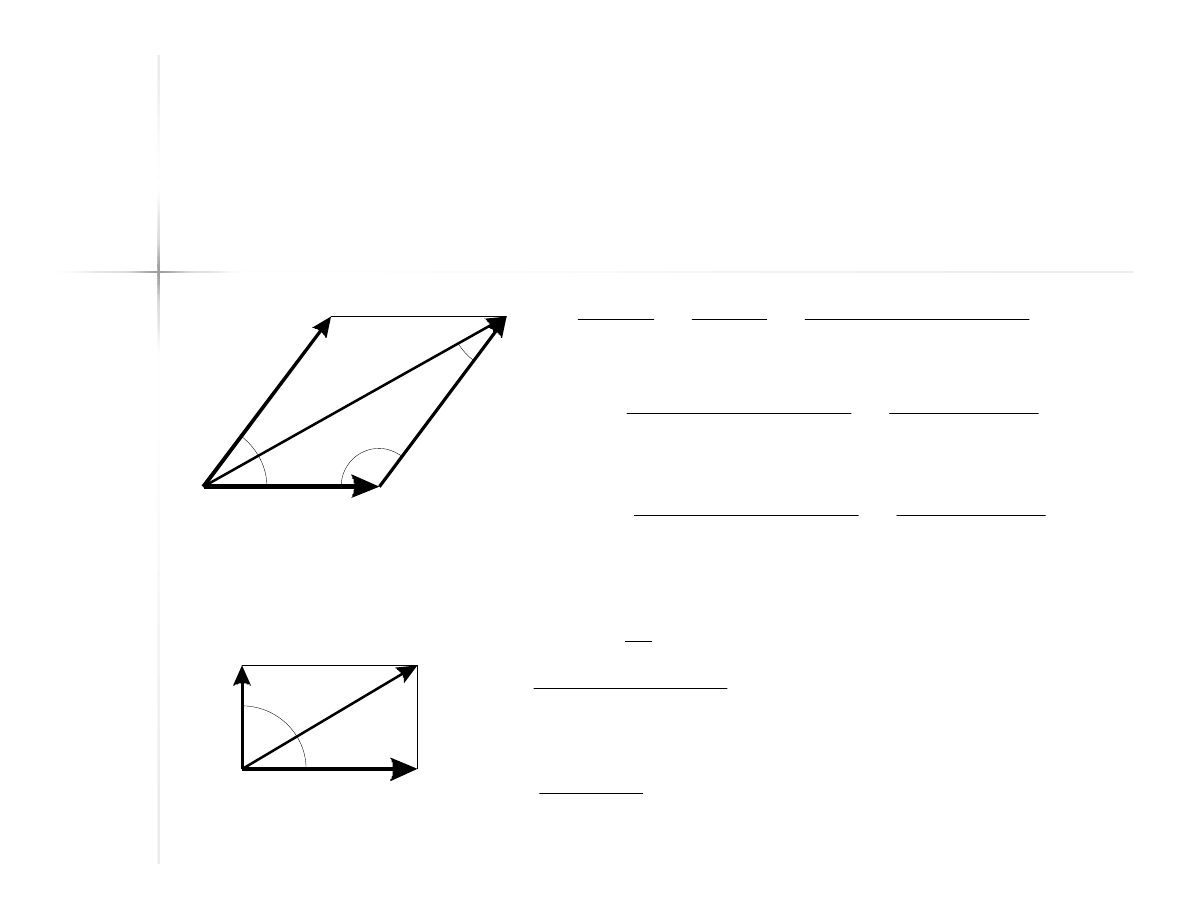
41

Miary wektorów

składowych



























sin

sin

sin

2

1

P

P

P





































sin

sin

sin

sin

1

P

P

P





































sin

sin

sin

sin

2

P

P

P



















cos

sin

2

sin

P

P

P

x













 









sin

sin

sin

P

P

P

y





P

1

P

2



P





P

2



P

x

P

y

P





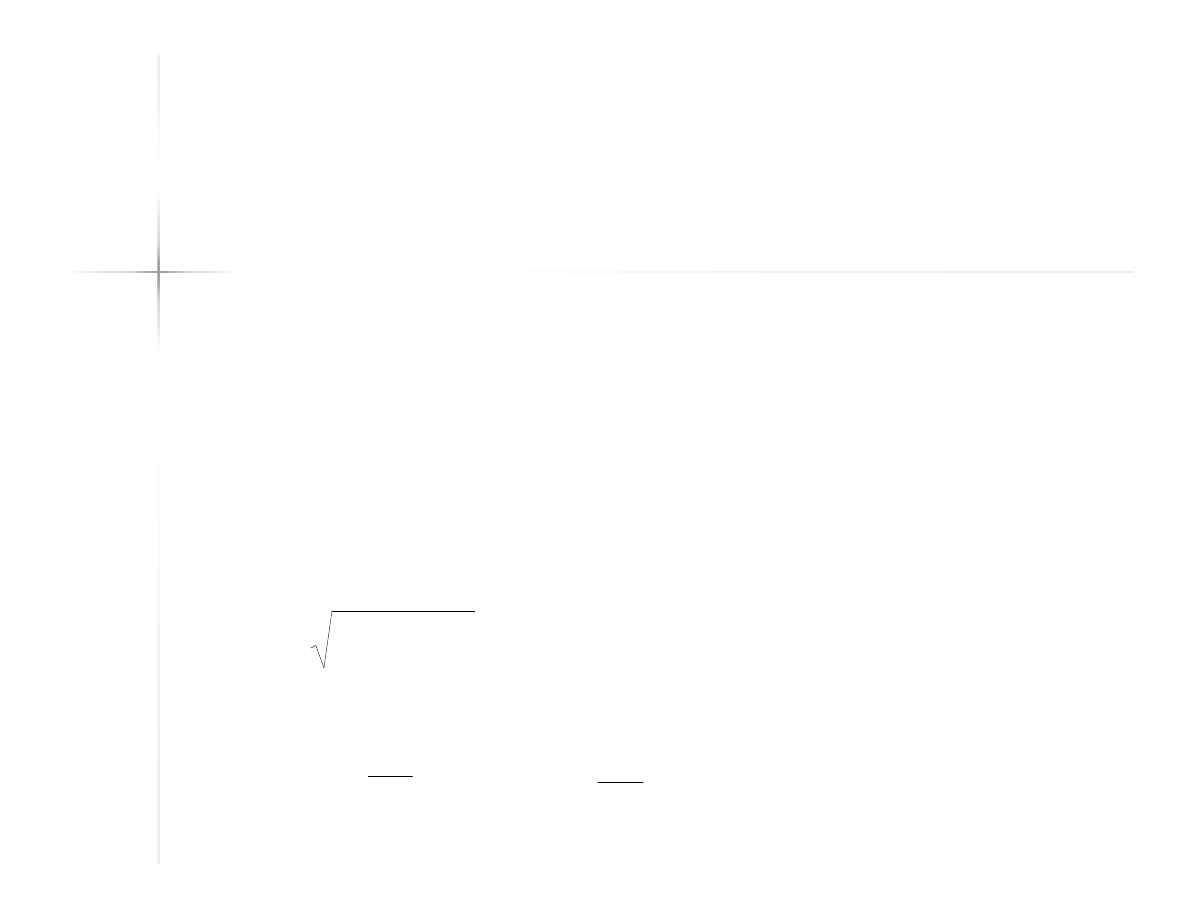
42

Wypadkowa

- metoda analityczna



Składowe sił układu:



Składowe wypadkowej:



Siła wypadkowa:



Kierunek wypadkowej:

i

i

ix

P

P



cos



i

i

iy

P

P



sin



nx

x

x

x

P

P

P

W









...

2

1

ny

y

y

y

P

P

P

W









...

2

1

2

2

y

x

W

W

W





W

W

x





cos

W

W

y





sin

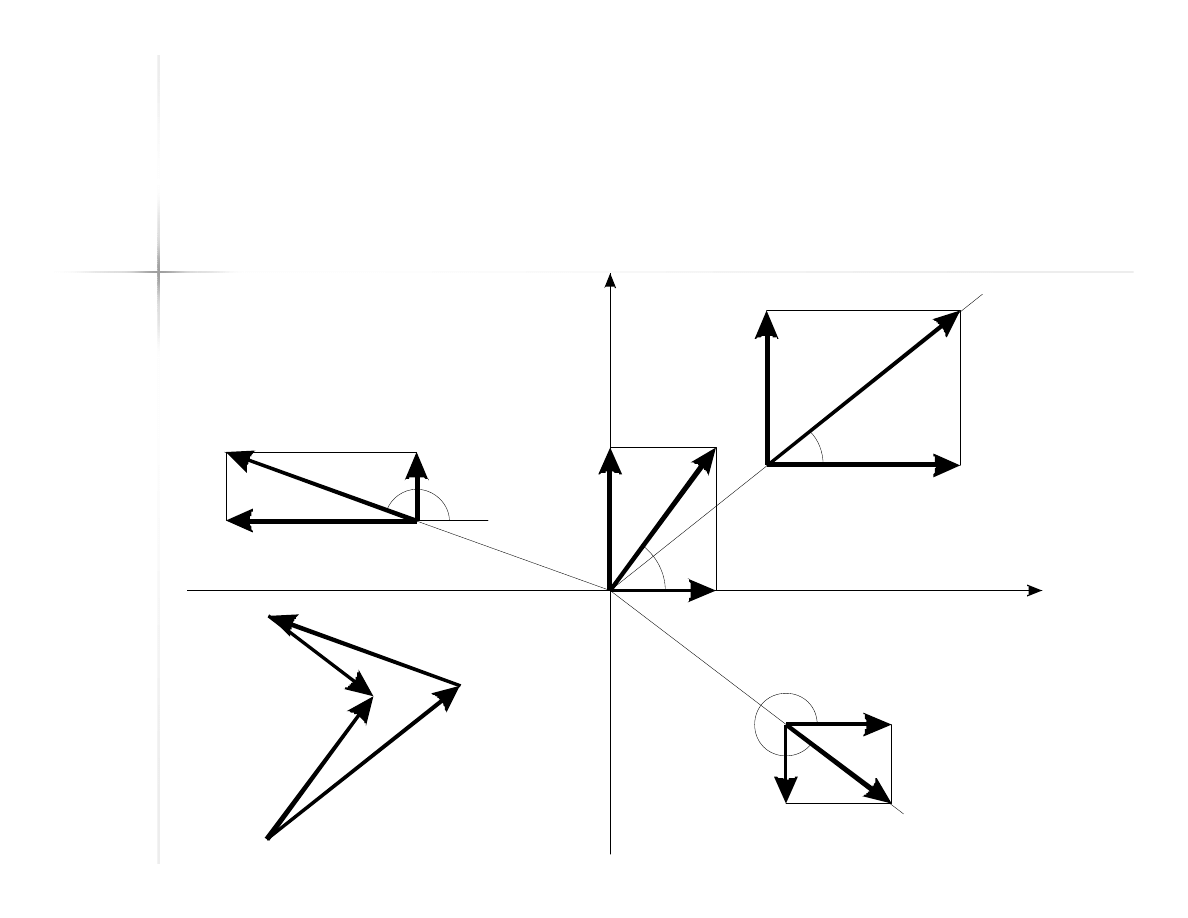
43

Przykład

x

y

P

1x

P

1y

P

1

P

2x

P

2

P

2y

P

3x

P

3y

P

3

P

1

P

2

P

3

W

W

W

x

W

y















44

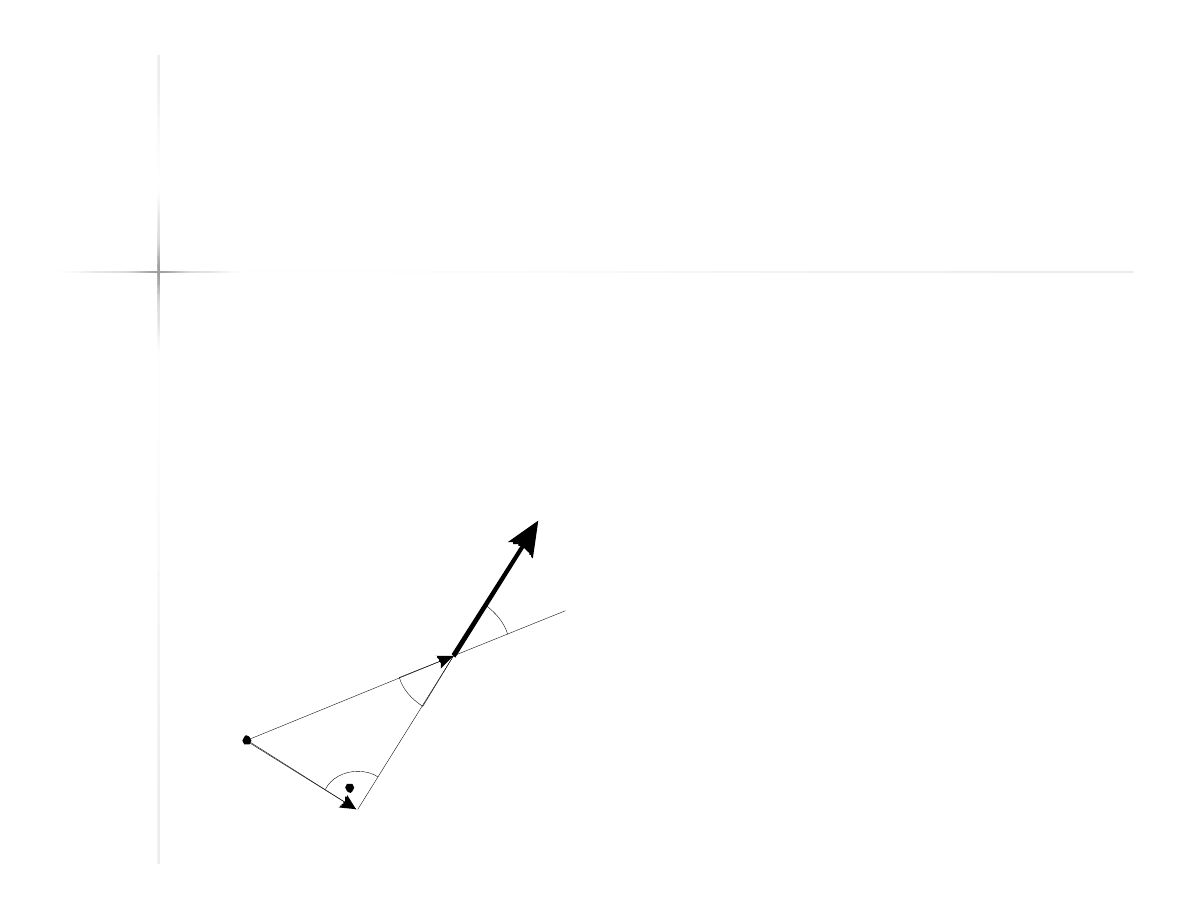
Moment siły

(1)



Moment siły względem punktu – iloczyn

wektorowy promienia wodzącego, czyli

wektora łączącego omawiany punkt i punkt

przyłożenia siły, oraz wektora siły:

O

P

r

r

┴





P

r

M





P

O



sin

P

r

M

P

O







sin







r

r

P

r

M

P

O







45

Moment siły

(2)



Moment siły względem prostej -

Momentem względem prostej

nazywamy iloczyn wektorowy

promienia wodzącego, czyli wektora

łączącego punkt prostej najbliższy

kierunkowi siły i punkt przyłożenia siły,

i wektora siły:

M

l

=r

× P

46

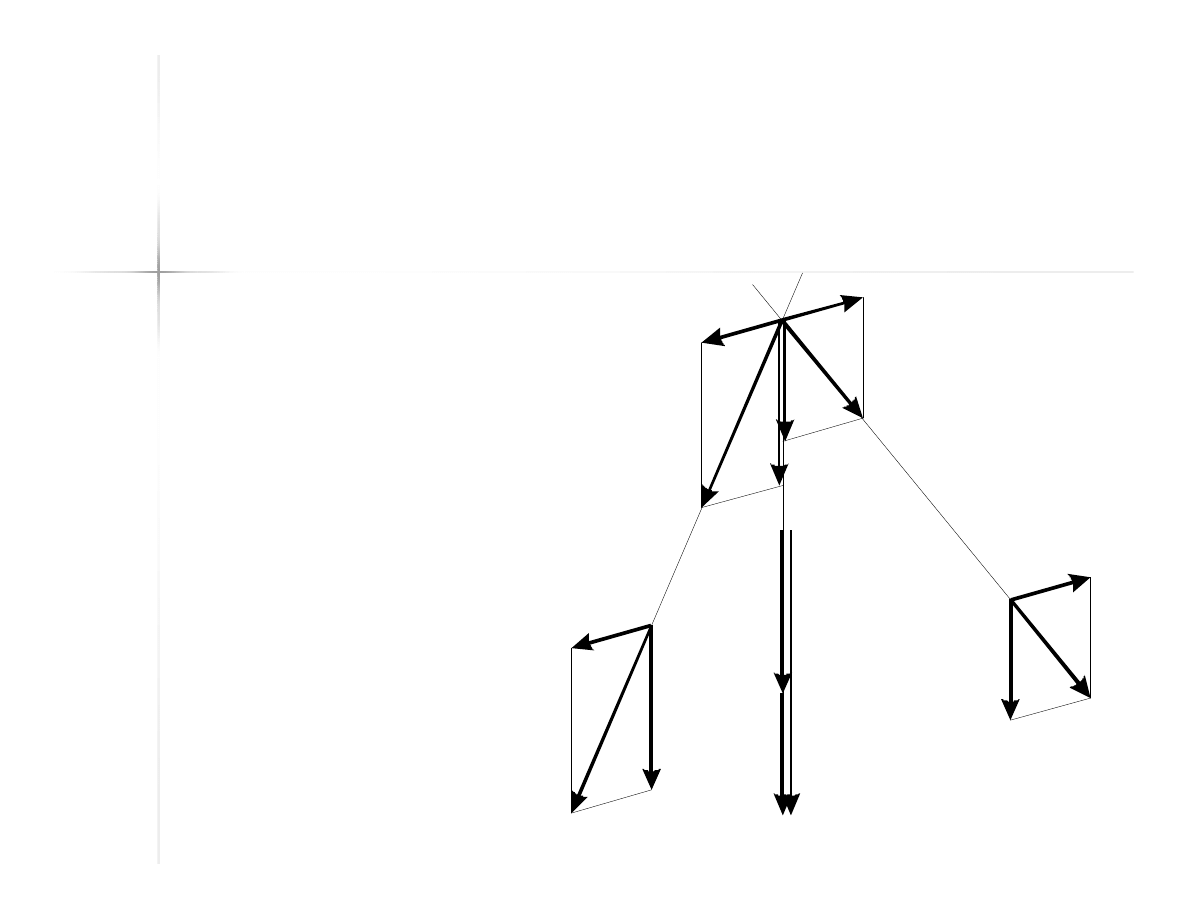
Wypadkowa układu sił

równoległych



Przyłożenie układu

zerowego (układ sił

równoważących się,

np. dwie siły o

takiej samej mierze,

linii działania i

przeciwnych

zwrotach) nie

wpływa na stan

równowagi ciała.

W

P

1

P

2

Z

Z

Z

Z

W

2

W

1

W

1

W

2

P

2

P

1

P

1

P

2

47

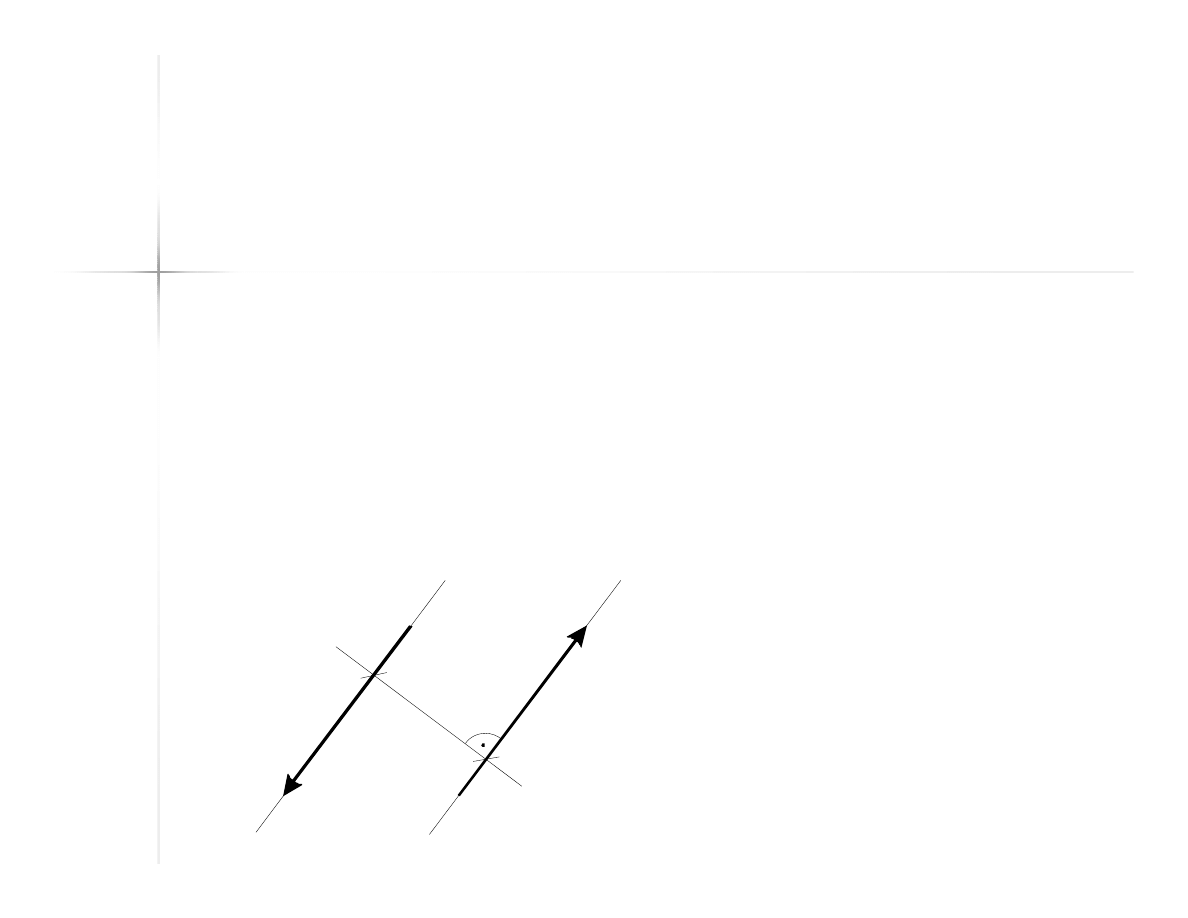
Para sił



Parę sił stanowią dwie siły o równoległych

liniach działania, o przeciwnych zwrotach,

zaś o tych samych miarach.



Ramię pary sił – odległość pomiędzy

kierunkami sił nosi nazwę ramienia pary sił.

P

P

P





2

1

Pa

M



P

1

P

2

a

48

Dowolny płaski układ sił

(1)



Redukcja do siły wypadkowej przyłożonej w biegunie

redukcji i wypadkowego momentu względem tego

bieguna (pary sił).



Siły składowe mogą zostać przeniesione do bieguna

redukcji, pod warunkiem przyłożenie momentu od

tych sił względem bieguna redukcji.



Wypadkową siłę wyznacza się dla układu zbieżnego

przyłożonego w biegunie redukcji.



Wypadkowy moment jest równy sumie momentów od

sił składowych.

W

P

M

r P

M



















i

i

n

o

i

i

i

n

io

i

n

x

1

1

1

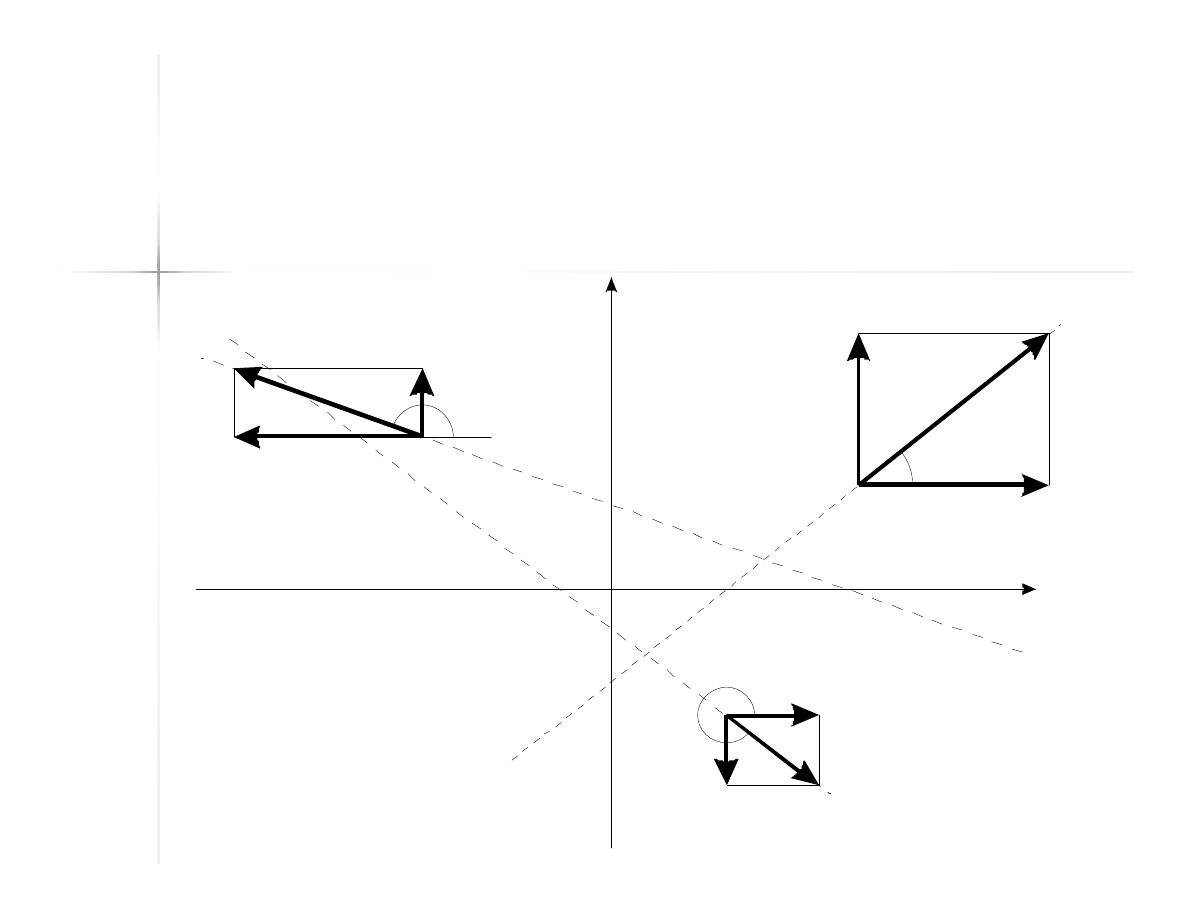
49

Przykład

(1)

x

y

P

2x

P

2

P

2y

P

3x

P

3y

P

3









P

1x

P

1y

P

1





(x ,y )

1

1

(x ,y )

3

3

(x ,y )

2

2

0

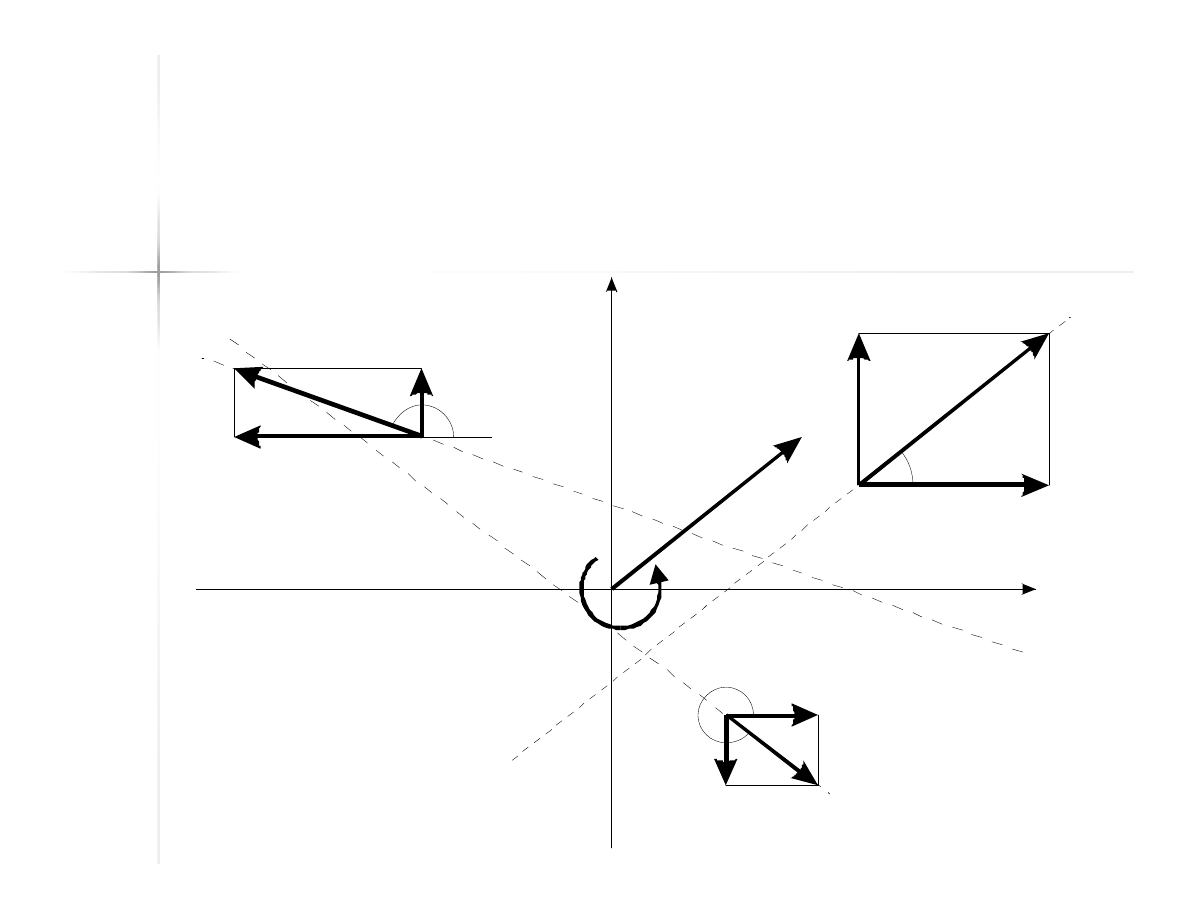
50

Przykład

(2)

x

y

P

1x

P

1y

P

1

P

2x

P

2

P

2y

P

3x

P

3y

P

3













P

1

M

P1

0

0

1

1

1

1

1

0

x

P

y

P

M

y

x

P







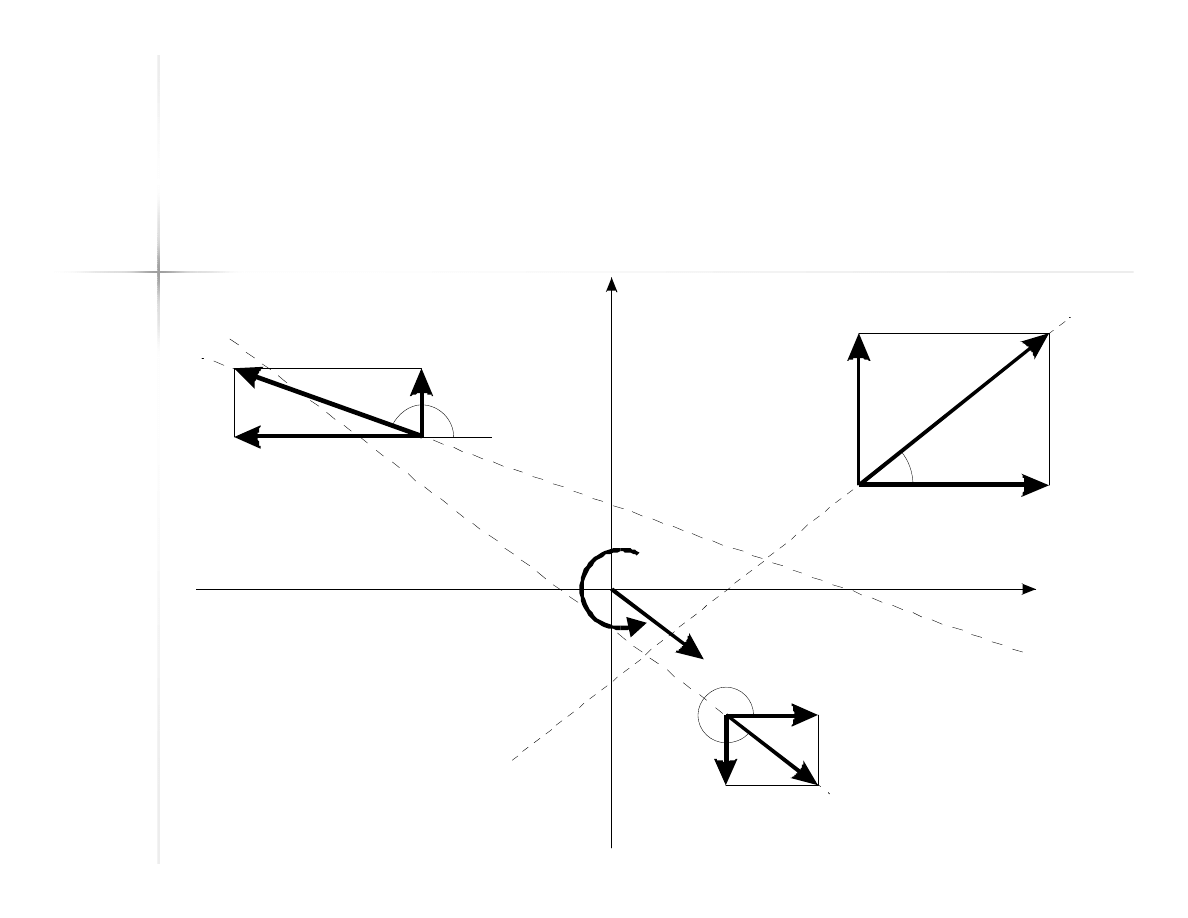
51

Przykład

(3)

x

y

P

1x

P

1y

P

1

P

2x

P

2

P

2y

P

3x

P

3y

P

3













M

P2

0

0

P

2

2

2

2

2

2

0

x

P

y

P

M

y

x

P







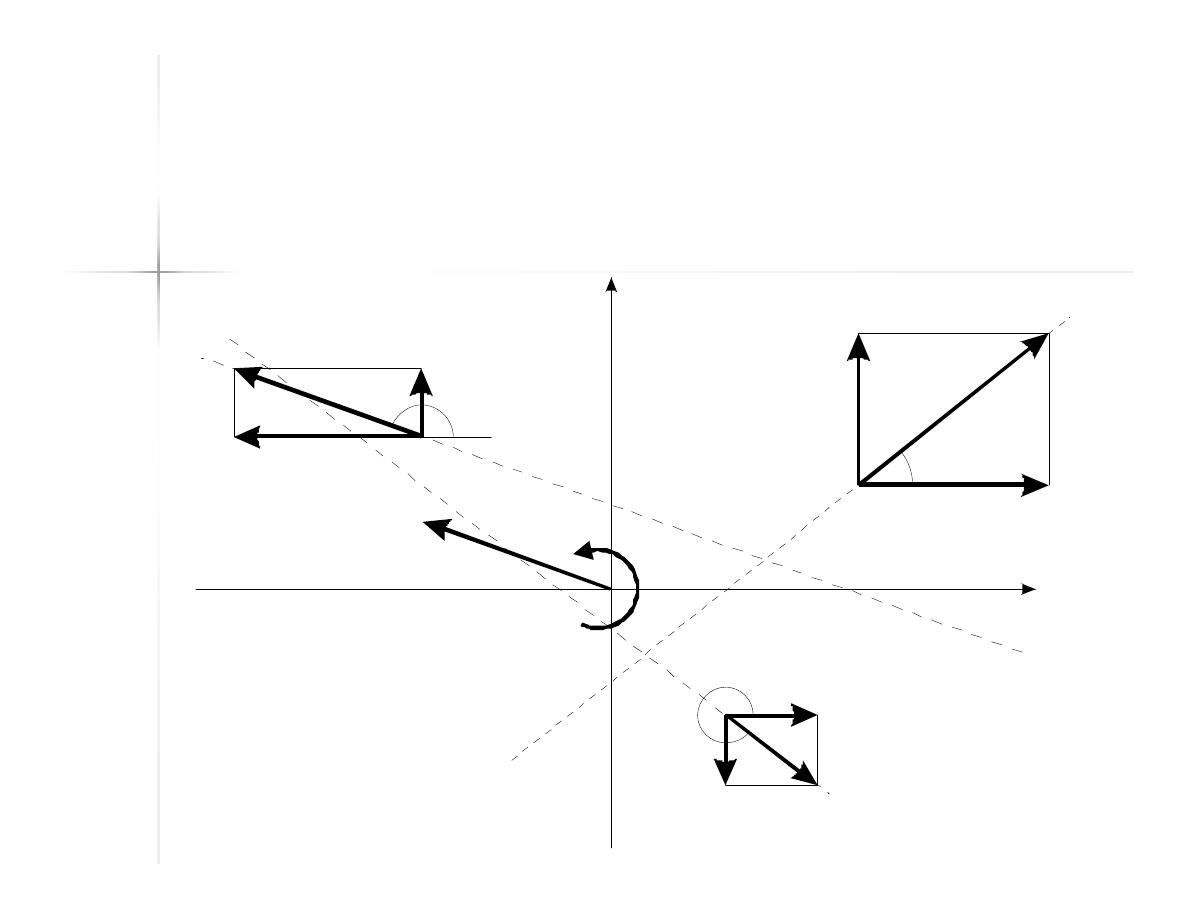
52

Przykład

(4)

x

y

P

1x

P

1y

P

1

P

2x

P

2

P

2y

P

3x

P

3y

P

3













M

P3

0

0

P

3

3

3

3

3

3

0

x

P

y

P

M

y

x

P







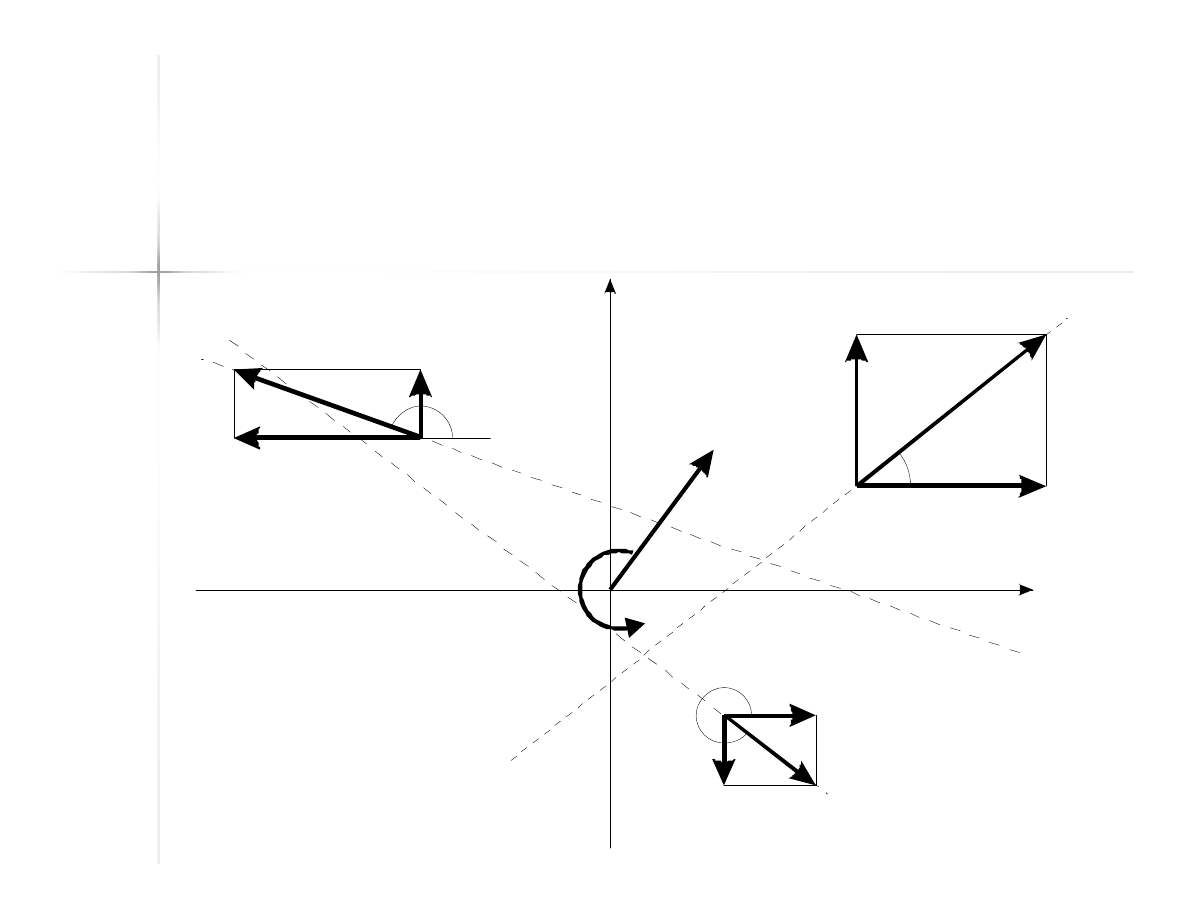
53

Przykład

(5)

x

y

P

1x

P

1y

P

1

P

2x

P

2

P

2y

P

3x

P

3y

P

3













M

0

0

W

3

0

2

0

1

0

0

P

P

P

M

M

M

M







54

Dowolny płaski układ sił

(2)



Wypadkowy moment może zostać

przedstawiony jako:

– wektor momentu;
– para sił;
– moment od siły wypadkowej przyłożonej

nie w biegunie redukcji, a na linii

działania wyznaczonej tak, że moment od

siły wypadkowej równy jest momentowi

od sił składowych.

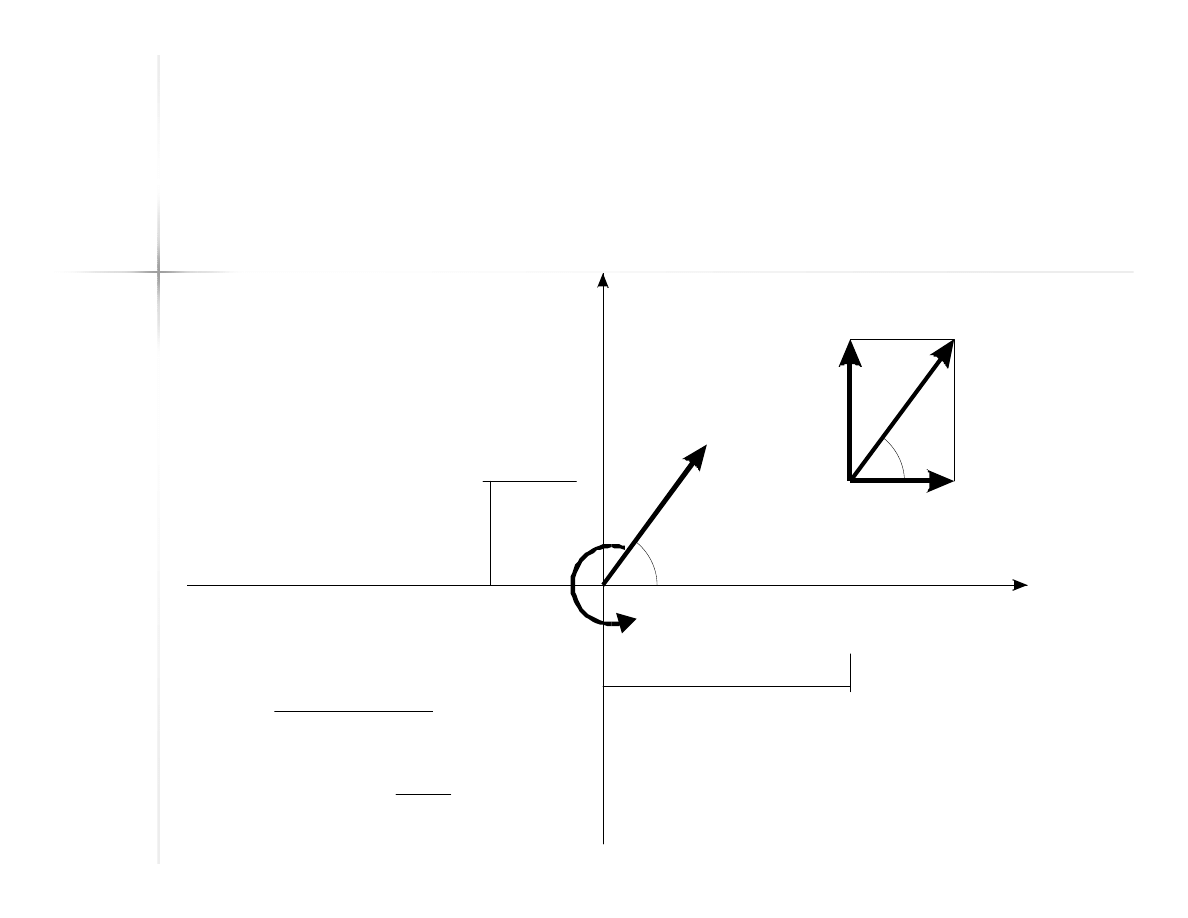
55

Moment od wypadkowej

x

y

W

y

M

0

0

W



W

W

x

x

0

y

0

0

0

0

x

W

y

W

M

y

x







x

y

W

M

x

W

y

0

0

0





x

W

M

x

y

0

0

0

tg







56

Uogólnienie w przestrzeni



Układ sił zbieżnych – redukcja do siły

wypadkowej przyłożonej w punkcie

zbieżności.



Dowolny przestrzenny układ sił –

redukcja do wypadkowej siły i

wypadkowego momentu.

57

Stan równowagi



Równowaga statyczna
Punkt materialny (ciało sztywne) znajduje

się w stanie równowagi, jeżeli pod wpływem

działającego na ten punkt (ciało) układu sił,

punkt (ciało) nie porusza się lub porusza się

ruchem jednostajnym po linii prostej. Układ

sił, wywołujący opisane stany ruchu punktu

materialnego (ciała sztywnego), nazywa się

układem zrównoważonym lub

równoważnym zeru.

58

Oswobodzenie z więzów



Ciało nieswobodne można myślowo

oswobodzić z więzów, zastępując ich

działanie reakcjami.



Ciało oswobodzone z więzów można

traktować jako swobodne pod

działaniem sił czynnych (obciążeń) i

biernych (reakcji).

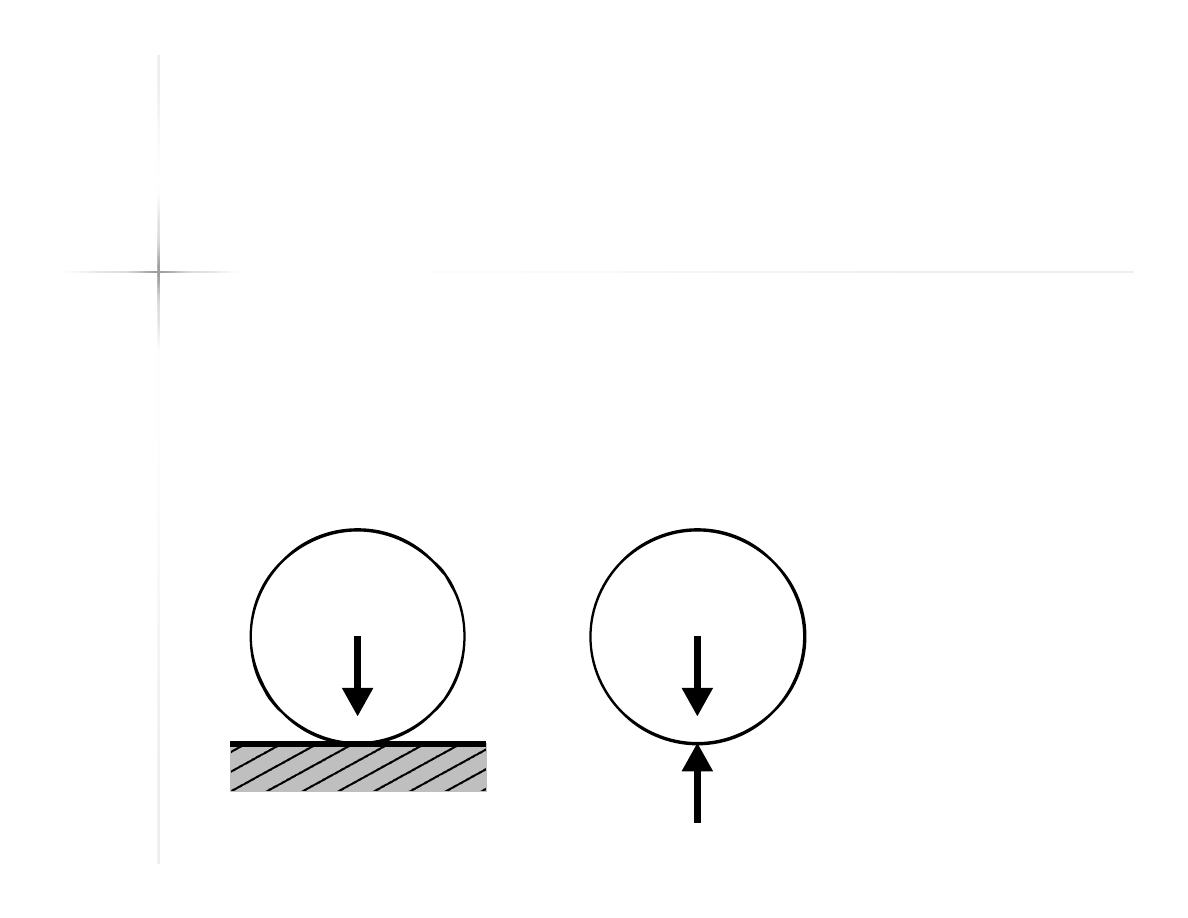
59

Równowaga dwóch sił



Układ dwóch sił pozostaje w

równowadze, jeżeli siły te leżą na

jednej prostej, mają przeciwne zwroty

i takie same miary.

G

R



G

R





G

G

R

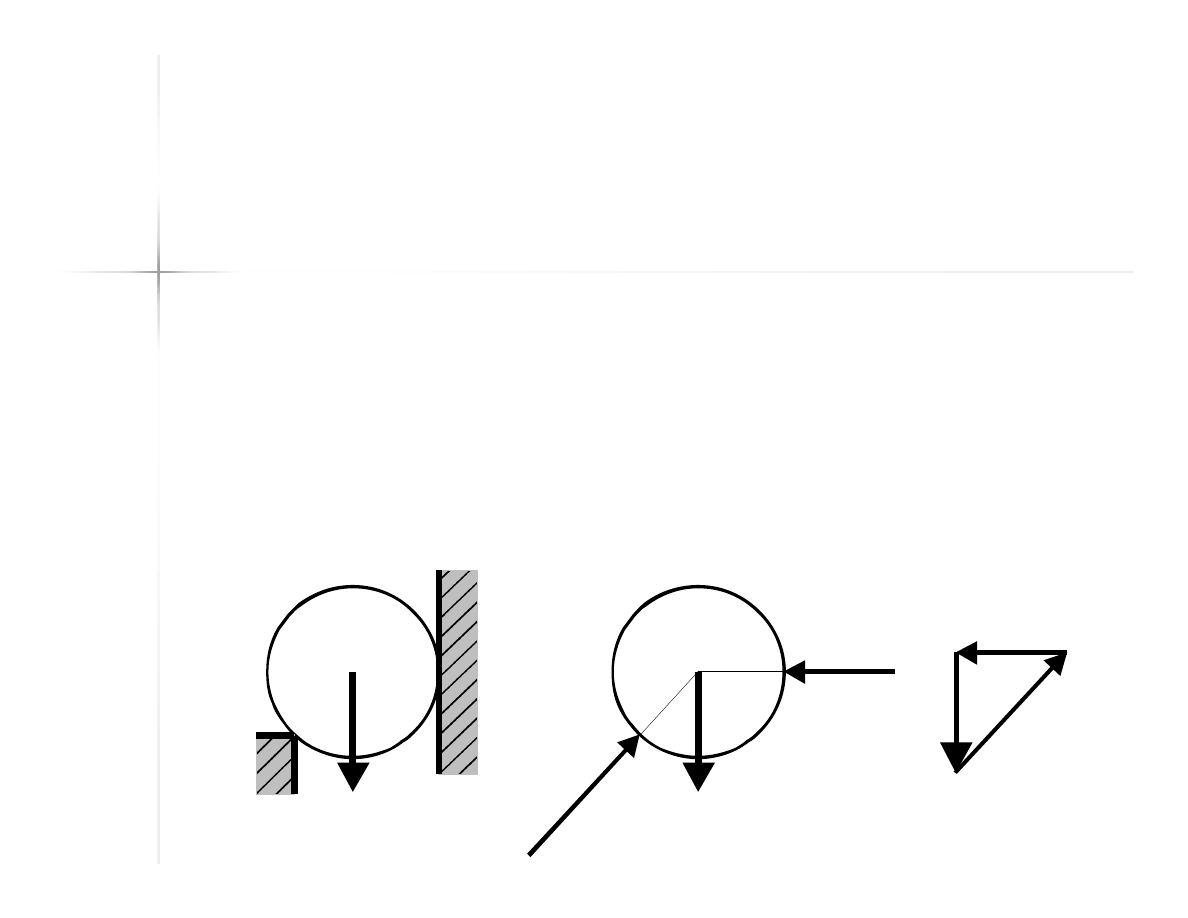
60

Równowaga trzech sił



Układ trzech sił jest zrównoważony,

jeżeli siły te tworzą płaski układ sił,

przecinają się w jednym punkcie, zaś

wielobok sznurowy zbudowany z tych

sił jest zamknięty.

G

A

B

R

B

G

R

A

R

B

R

A

G

61

Równowaga par sił



Aby układ par sił, działających w

jednej płaszczyźnie na ciało sztywne,

znajdował się w równowadze, suma

momentów tych par musi być równa

zero.

M

i

i

n







1

0

62

Warunki równowagi

układu zbieżnego

Wypadkowa układu sił musi być równa 0, tj.

zamyka się wielobok sznurowy sił

(graficznie), a sumy rzutów sił układu na

osie układu współrzędnych muszą być

równe zeru (analitycznie).



Płaski układ sił



Przestrzenny układ sił

P

P

P

ix

i

n

iy

i

n

iz

i

n



















1

1

1

0

0

0

;

;

P

P

ix

i

n

iy

i

n













1

1

0

0

;

;

63

Warunki równowagi

dowolnego układu sił

(1)



Płaski układ sił

lub

lub

l

C

B

A

n

i

iC

n

i

iB

n

i

iA





















,

,

0

;

0

;

0

1

1

1

M

M

M

x

AB

n

i

iB

n

i

iA

n

i

ix























0

;

0

;

0

1

1

1

M

M

P

0

;

0

;

0

1

1

1



















n

i

iO

n

i

iy

n

i

ix

P

P

M

64

Warunki równowagi

dowolnego układu sił

(2)



Przestrzenny układ sił

0

;

0

;

0

0

;

0

;

0

1

1

1

1

1

1





































n

i

iz

n

i

iy

n

i

ix

n

i

iz

n

i

iy

n

i

ix

P

P

P

M

M

M