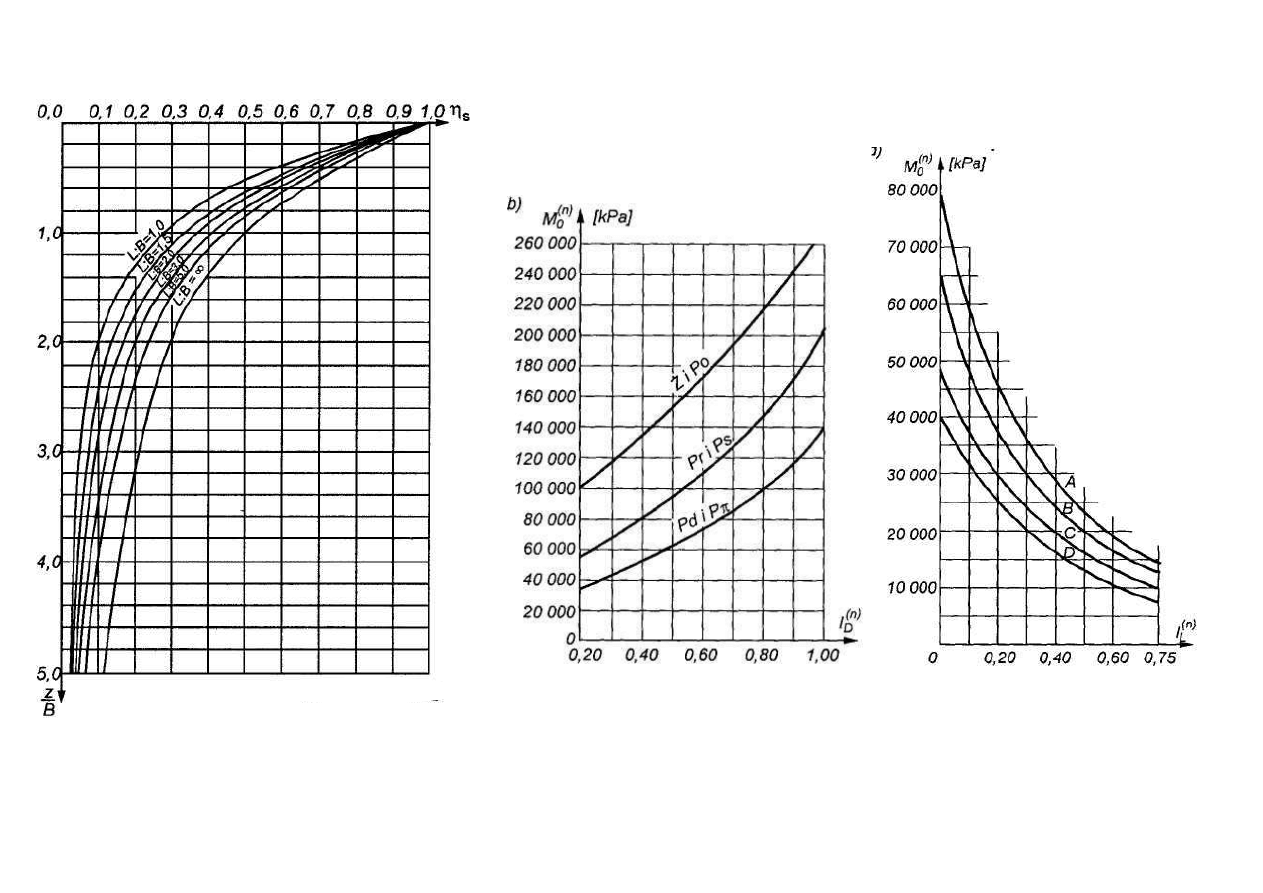
Rys. 1. Nomogram do określania wartości

współczynnika

η

s

Rys. 2. Zależności korelacyjne modułu M

0

od I

D

lub I

L

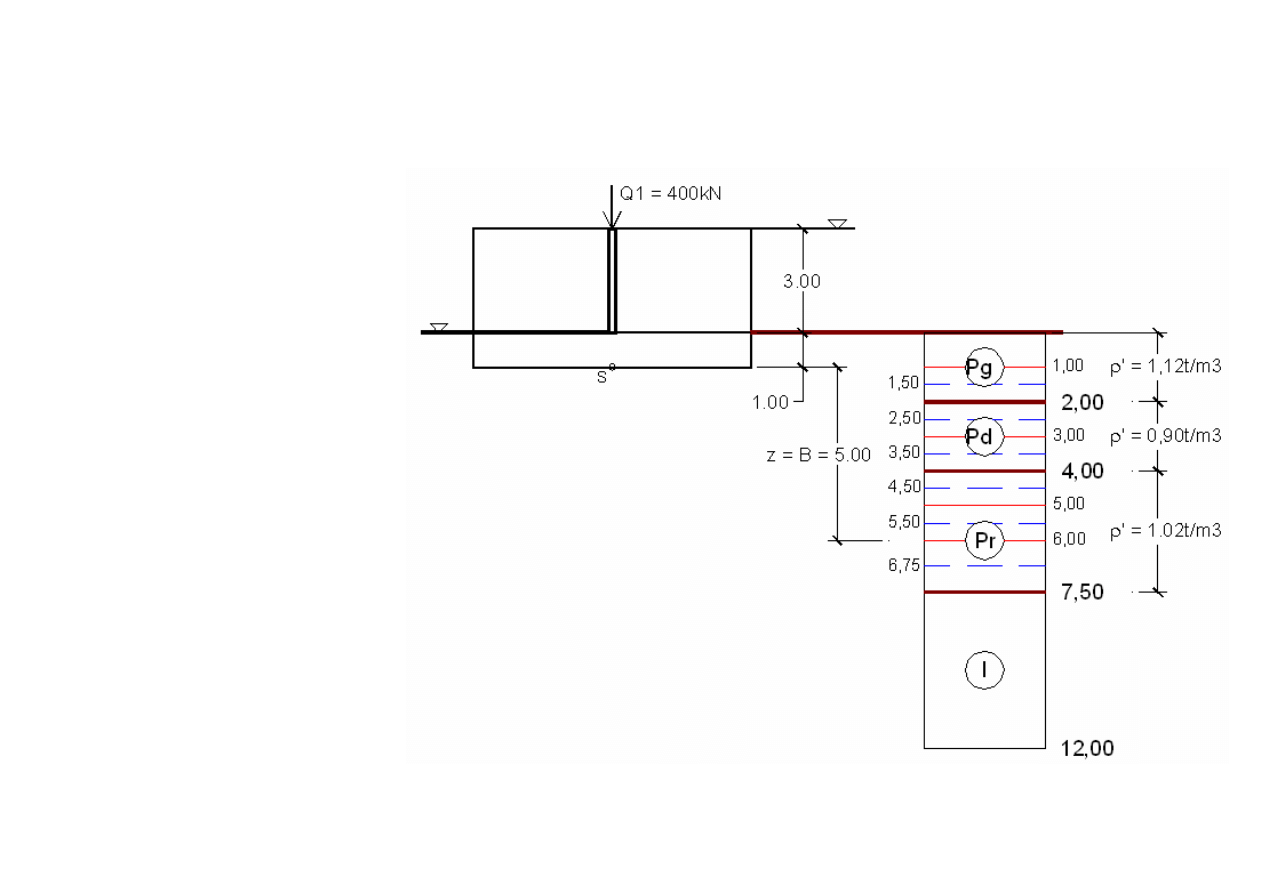
Obliczenia naprężeń pierwotnych, wtórnych, dodatkowych i całkowitych

1.

W obliczeniach naprężeń i osiadań
wartość efektów oddziaływań określa
się przy założeniu charakterystycznych
wartości oddziaływań i właściwości
gruntu

γ

F

,

γ

M

= 1,0;

2.

Naprężenia pierwotne liczymy na
granicach, a wtórne i dodatkowe w
środkach wydzielonych warstewek
obliczeniowych, do głębokości na
której spełniony jest warunek -

ρ

σ

σ

z

zd

⋅

≤

3

,

0

lub do spągu warstwy

ściśliwej, jeżeli powyższy warunek
spełnia się w tej warstwie, nie płycej
jednak niż:

m

B

z

0

,

5

=

=

;

3.

Naprężenia całkowite liczymy na
granicach warstw geotechnicznych;

4.

Warstewki obliczeniowe o miąższości
do 1,0 m;

Schemat obliczeniowy. Podział na

warstewki obliczeniowe.

Obliczenia naprężeń pierwotnych, wtórnych, dodatkowych i całkowitych

Naprężenia pierwotne

∑

⋅

⋅

=

g

h

z

ρ

σ

ρ

[kPa]

gdzie:

h - wysokość wydzielonej warstewki gruntu w [m],

ρ

- gęstość objętościowa wydzielonej warstewki gruntu w [t/m

3

],

g - przyspieszenie ziemskie, g = 9,81 [m/s

2

].

Naprężenia wtórne

s

os

zs

η

σ

σ

⋅

=

[kPa]

gdzie:

L – długość sekcji płyty fundamentowej jazu w m,
B – szerokość sekcji płyty fundamentowej jazu w m,,
h - głębokość zalegania środka warstewki mierzona od poziomu terenu w m,
z - głębokość zalegania środka warstewki mierzona od poziomu posadowienia w m,

Naprężenia dodatkowe

(

)

ρ

σ

η

σ

o

rs

s

zd

q

−

=

[kPa]

Naprężenia całkowite

zd

z

zt

σ

σ

σ

ρ

+

=

[kPa]

Tabela 3. Zestawienie obliczeń naprężeń w podłożu pod fundamentem sekcji jazu przed i po wykonaniu wykopu oraz obciążeniu jego
konstrukcją

M

ią

żs

zo

ść

w

a

rs

tw

y

g

ru

n

tu

G

ę

st

o

ść

o

b

ję

to

śc

io

w

a

M

ią

żs

zo

ść

w

a

rs

te

w

e

k

P

o

zi

o

m

o

b

li

cz

e

n

io

w

y

N

a

p

rę

że

n

ia

p

ie

rw

o

tn

e

P

o

zi

o

m

o

b

li

cz

e

n

io

w

y

G

łę

b

o

k

o

ść

m

ie

rz

o

n

a

o

d

p

o

zi

o

m

u

p

o

sa

d

o

w

ie

n

ia

d

o

ś

ro

d

k

a

w

a

rs

te

w

k

i

B

z

W

sp

ó

łc

zy

n

n

ik

z

a

n

ik

u

n

a

p

rę

że

ń

η

N

a

p

rę

że

n

ia

w

tó

rn

e

N

a

p

rę

że

n

ia

d

o

d

a

tk

o

w

e

N

a

p

rę

że

n

ia

c

a

łk

o

w

it

e

[m]

R

o

d

za

j

g

ru

n

tu

ρ

r

[t/m

3

]

h [m]

[m]

σσσσ

z

ρρρρ

[kPa]

[m]

z [m]

-

-

σσσσ

zs

[kPa]

σσσσ

zd

[kPa]

σσσσ

zt

[kPa]

1

2

3

4

5

6

7

8

9

10

11

12

13

2,0

P

g

1,12

0

1,0

1,0

2,0

11,0

22,0

1,0

1,5

2,0

0

0,5

1,0

0

0,10

0,20

1,00

0,90

0,81

11,0

9,9

8,9

58,8

52,9

47,6

69,8

69,6

2,0

P

d

0,90

1,0

3,0

4,0

30,8

39,7

2,5

3,5

4,0

1,5

2,5

3,0

0,30

0,50

0,60

0,73

0,58

0,52

8,0

6,4

5,7

42,9

34,1

30,6

70,3

3,5

P

r

1,02

1,0

1,0

1,5

5,0

6,0

7,5

49,7

59,7

74,7

4,5

5,5

6,7

7,5

3,5

4,5

5,75

6,50

0,70

0,90

1,15

1,30

0,47

0,38

0,30

0,26

5,2

4,2

3,3

2,9

27,6

22,3

17,6

15,3

90,0

Obliczenia spodziewanych osiadań.

Osiadania liczymy dla każdej z wydzielonych wyżej warstewek gruntu, do głębokości ustalonej według warunku:

ρ

σ

σ

z

zd

⋅

≤

3

,

0

Osiadanie wydzielonej warstewki gruntu:

M

h

s

M

h

s

s

s

s

zs

zd

⋅

=

⋅

=

+

=

σ

λ

σ

//

0

/

//

/

[cm]

s’ i s’’ - osiadanie pierwotne i wtórne warstwy w cm,

σ

zs

- naprężenie wtórne w środku warstwy w kPa,

σ

zd

- naprężenie dodatkowe w środku warstwy kPa,

h - grubość warstwy w cm,
M

0

- moduł ściśliwości pierwotnej w kPa,

M - moduł ściśliwości wtórnej w kPa,

λ

- współczynnik przyjmujący wartości 0 i 1 w zależności od stopnia odprężenia się podłoża

podczas wykonywania robót fundamentowych:

λ

= 0 - gdy czas wznoszenia budowli (od wykonania wykopów fundamentowych do

zakończenia stanu surowego) nie trwa dłużej niż 1 rok,

λ

= 1 - gdy czas wznoszenia budowli jest dłuższy niż 1 rok,

Moduł ściśliwości wtórnej należy oznaczyć przekształcając równanie na wskaźnik skonsolidowania gruntu:

M

M

E

E

0

0

=

=

β

stąd

β

0

M

M

=

gdzie:

M – moduł ściśliwości wtórnej w kPa,
M

0

– moduł ściśliwości pierwotnej w kPa,

E – moduł pierwotnego odkształcenia gruntu w kPa,
E

0

– moduł wtórnego odkształcenia gruntu w kPa,

β

– współczynnik określany na podstawie tabeli.

7. Obliczenie spodziewanych osiadań.

Sprawdzenie warunku stanu granicznego użytkowania.

Tabela 3. Wartości parametrów zależnych od rodzaju gruntu [PN-B-03020:1981]

Grunty sposte

Grunty spoiste

Parametr

Ż, Po

P

r

, P

S

P

d

, P

Π

A

B

C

D

ν

0,2

0,25

0,3

0,25

0,29

0,32

0,37

δ

0,9

0,83

0,74

0,83

0,76

0,7

0,565

β

1,0

0,9

0,8

0,9

0,75

0,6

0,8

ν

– współczynnik Poissona

(

) (

)

(

)

ν

ν

ν

δ

−

⋅

−

⋅

+

=

=

=

1

2

1

1

0

0

M

E

M

E

M

M

E

E

0

0

=

=

β

Tabela 4. Zestawienie obliczeń spodziewanych osiadań do głębokości h = 7,5 m,

M

ią

żs

zo

ść

w

a

rs

tw

y

Z

a

g

łę

b

ie

n

ie

śr

o

d

k

a

w

a

rs

tw

y

N

a

p

rę

że

n

ia

d

o

d

a

tk

o

w

e

M

o

d

u

ł

śc

iś

li

w

o

śc

i

p

ie

rw

o

tn

e

j

O

si

a

d

a

n

ia

p

ie

rw

o

tn

e

N

a

p

rę

że

n

ia

w

tó

rn

e

M

o

d

u

ł

śc

iś

li

w

o

śc

i

w

tó

rn

e

j

O

si

a

d

a

n

ia

w

tó

rn

e

C

a

łk

o

w

it

e

o

si

a

d

a

n

ia

Lp

Rodzaj gruntu

h [cm]

[m]

σ

zd

[kPa] M

0

[kPa]

s’ [cm]

σ

zs

[kPa]

M

[kPa]

s’’[cm]

s [cm]

1

P

g

, I

L

= 0,35

100

1,5

52,9

20550

0,257

9,9

34260

0,029

0,286

2

100

2,5

42,9

0,095

8,0

0,014

0,109

3

P

d

, I

D

= 0,30

100

3,5

34,1

45080

0,076

6,4

56350

0,011

0,087

4

100

4,5

27,6

0,033

5,2

0,006

0,039

5

100

5,5

22,3

0,026

4,2

0,004

0,030

6

P

r

, I

D

= 0,40

150

6,75

17,6

84340

0,031

3,3

93710

0,005

0,036

SUMA

0,518

0,069

0,587