Teoria sprężystości

Wykład 3

Materialny ośrodek ciągły;

naprężenia

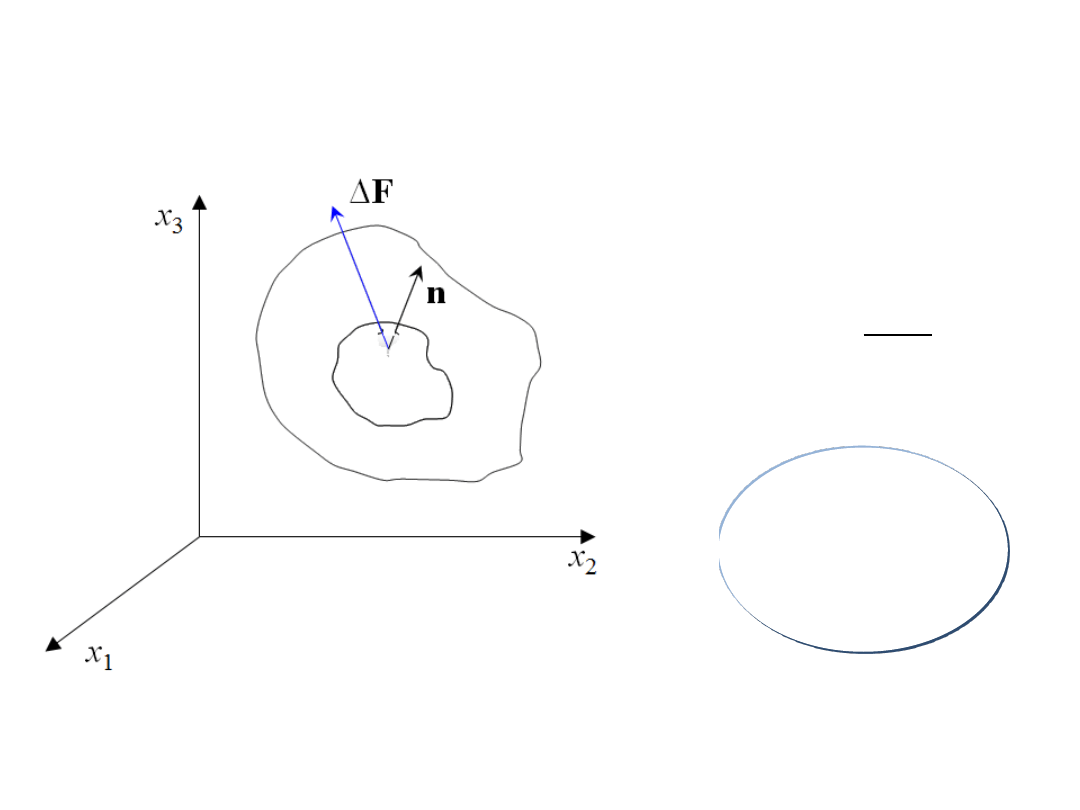
Wektor naprężenia

s

d

d F

T

n



2



s

Zakłada się brak
obciążeń
momentowych!

Wektor naprężenia

k

S



3

3

2

2

1

1

,

,

k

k

k

k

k

k

T

T

T













ij



3

Rozważmy element powierzchniowy równoległy do jednej z płaszczyzn układu
współrzędnych

Pierwszy wskaźnik określa
orientację elementu
powierzchniowego

Drugi wskaźnik numeruje
współrzędną wektora
naprężenia

Tensor naprężenia

Bilans pędu, bilans krętu

M

K

R

P









,











V

V

dV

dS

X

T

R

n















V

V

dV

dS

X

r

T

r

M

n











V

V

dV

dV





v

r

K

v

P

,

4

Prawa Eulera (obowiązujące dla bryły sztywnej)

Siły

powierzchniowe

Siły

objętościowe

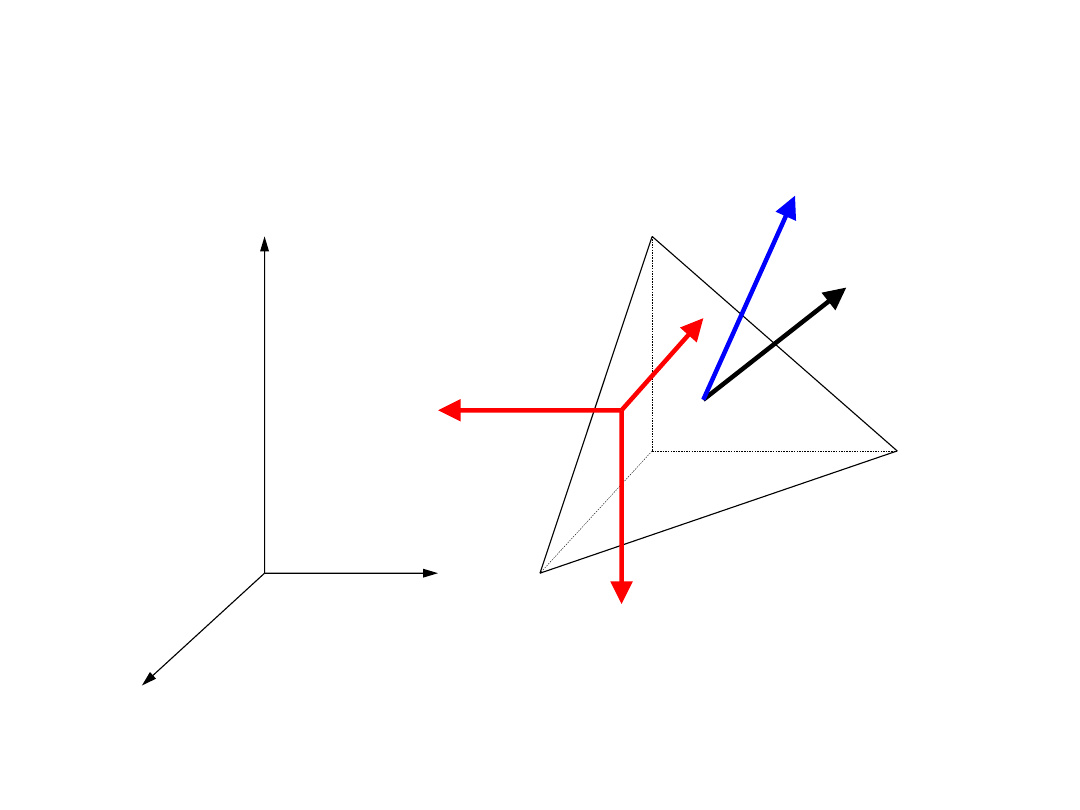
Wzór Cauchy’ego

5

n

T

21



22



x

1

x

2

x

3

n

23



P

Wzór Cauchy’ego

















dS

h

v

dS

h

X

dS

T

dS

n

dS

n

dS

n

3

1

3

1

'

1

1

1

3

3

31

2

2

21

1

1

11



































 





















n

31

3

21

2

11

1

1







n

n

n

T







n

ji

j

i

n

T





n

6

Naprężenia główne

j

ij

i

n

T







n





0





j

ji

ji

n











0

det





ji

ji







7

Zakładamy, że tensor naprężenia jest symetryczny.
Stawiamy pytanie: W jakim kierunku wektor naprężenia jest prostopadły do
elementu powierzchniowego, na który działa?

?

j

n

Układ równań liniowych

jednorodnych

Sytuacja w pełni analogiczna do rozważanej w przypadku tensora odkształcenia

Naprężenia główne

0

3

2

2

1

3









I

I

I







33

22

11

1













I

33

31

13

11

33

32

23

22

22

21

12

11

2































I

33

32

31

23

22

21

13

12

11

3





















I

8

3

2

1

3

3

1

3

2

2

1

2

3

2

1

1







































I

I

I

Naprężenia główne

n

n

T

n

T

n

n

n

n











 









,

i

j

ji

i

i

j

ji

i

n

n

n

T

n

T





9

Inne sformułowanie zagadnienia

Normalna

składowa

wektora naprężenia

Zagadnienie własne dla tensora naprężenia można interpretować jako
poszukiwanie takich kierunków, dla których składowa ta osiąga wartość
ekstremalną!

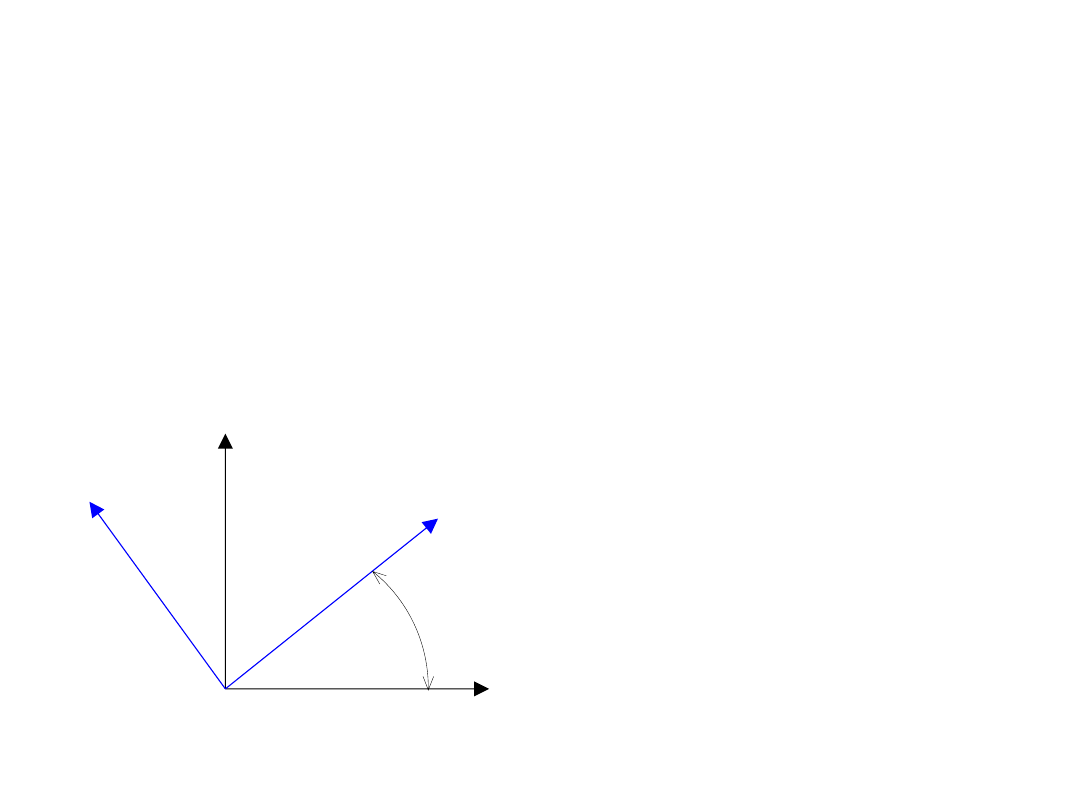
Płaski stan naprężenia

0

31

32

33













 

 

 

 

























1

0

0

0

cos

sin

0

sin

cos









Q

10

Stan naprężeń, w którym

nazywa

się płaskim stanem naprężenia w płaszczyźnie

x

1

x

2



x

y

x’

y’

Płaski stan naprężenia

xy

y

x























21

12

22

11

,

,

























cos

sin

2

sin

cos

2

2

1

1

'

11

'

xy

y

x

jk

k

j

x





















































2

2

'

2

2

'

sin

cos

cos

sin

cos

sin

2

cos

sin

















xy

y

x

xy

xy

y

x

y

11

Oznaczamy

Podobnie

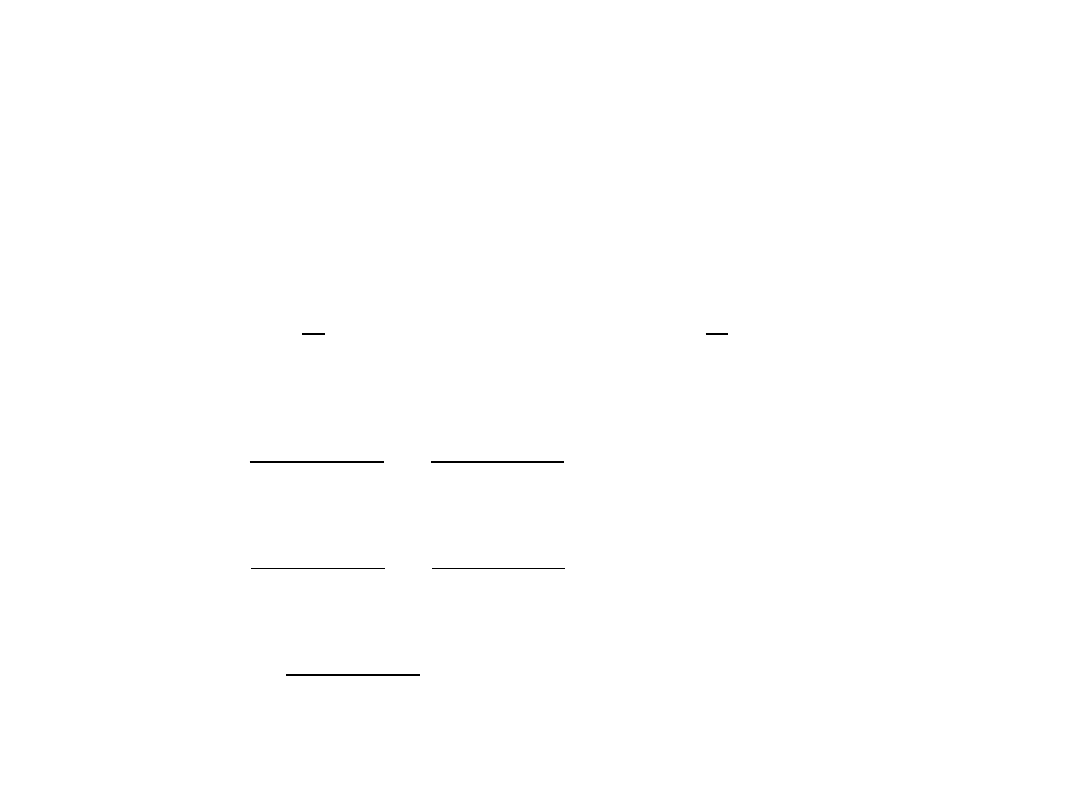
Płaski stan naprężenia























2

cos

1

2

1

cos

,

2

cos

1

2

1

sin

1

cos

2

sin

2

1

2

cos

2

2

2

2





























































2

cos

2

sin

2

2

sin

2

cos

2

2

2

sin

2

cos

2

2

'

'

'

xy

y

x

xy

xy

y

x

y

x

y

xy

y

x

y

x

x





























12

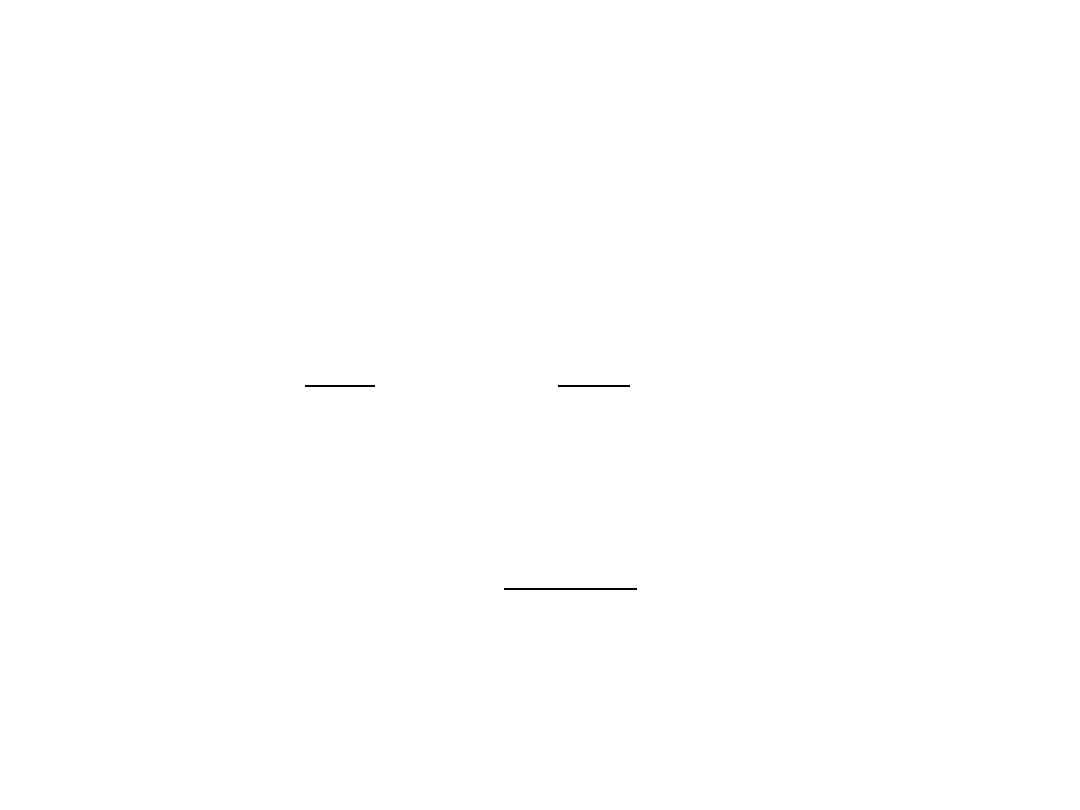
Płaski stan naprężenia

'

'

'

'

'

'

2

,

2

xy

y

xy

x

y

x

y

x









































0

2

2

tg

2

tg

'











xy

y

x

xy

g













13

Zauważmy, że

przy czym

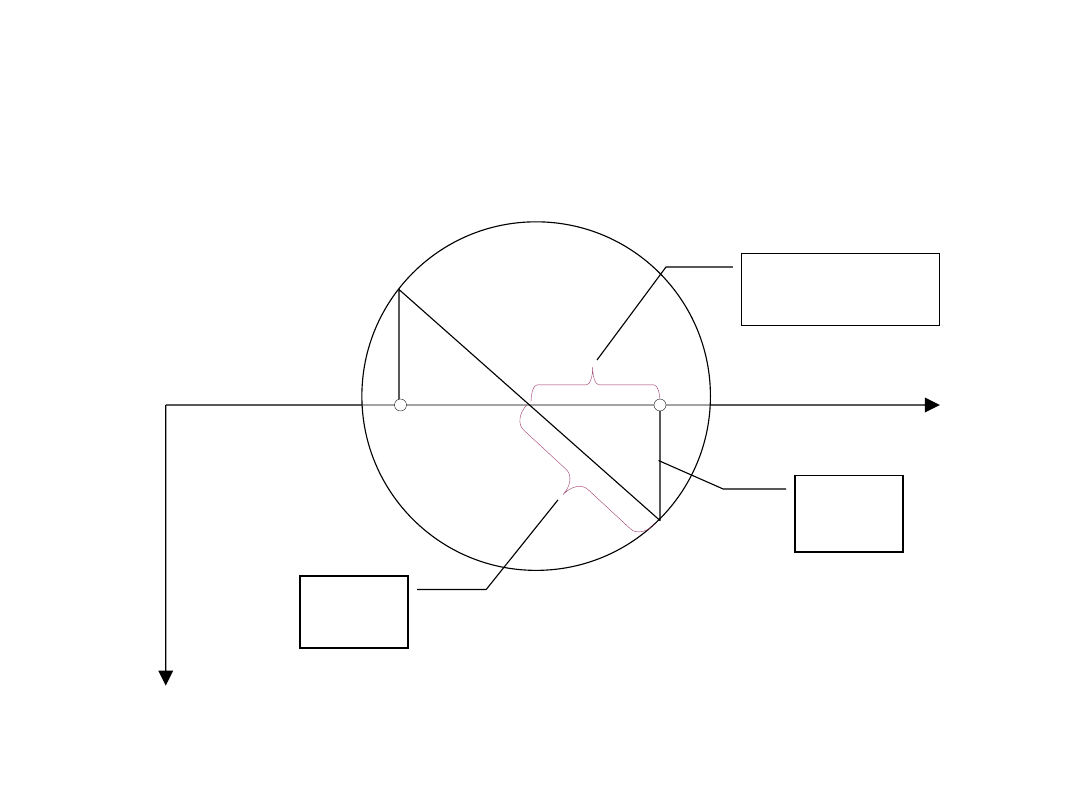
Koło Mohra

14







xy

½ (



x

-



y

)

?



x



y

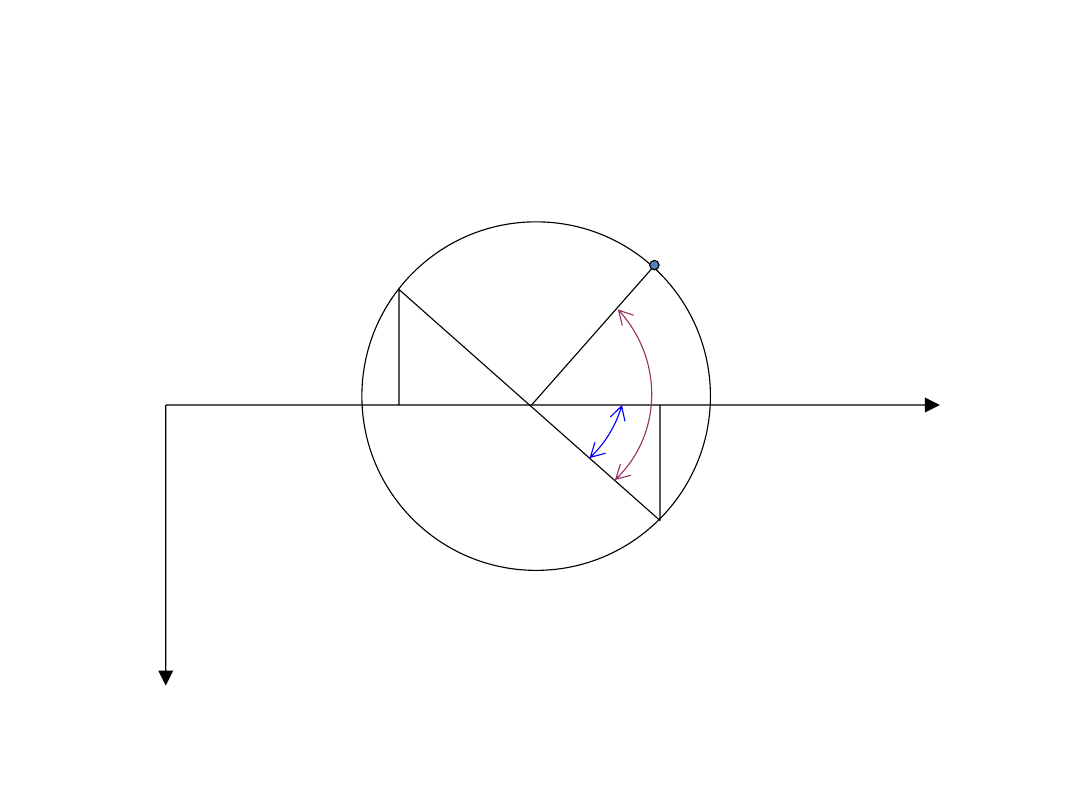
Koło Mohra





'

'

,

xy

x





15





2





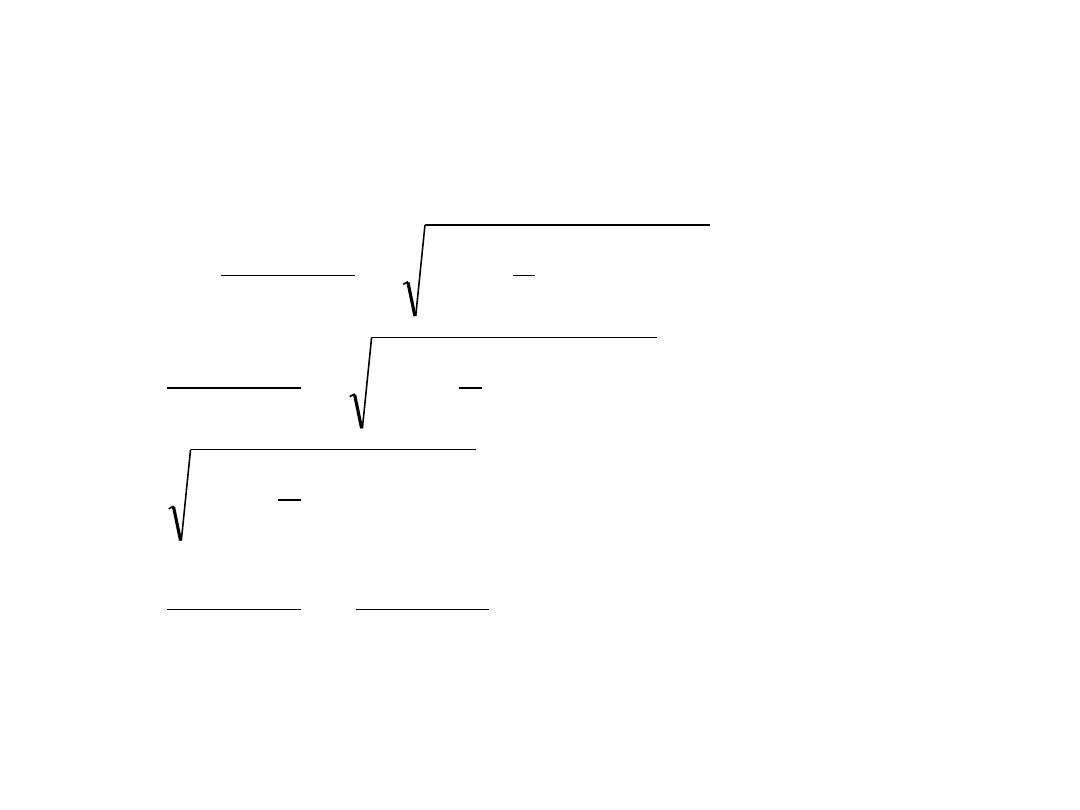
Koło Mohra







































































2

sin

2

cos

2

2

sin

2

sin

4

1

cos

2

cos

4

1

2

2

cos

4

1

2

2

2

2

2

2

2

'

xy

y

x

y

x

y

x

xy

y

x

xy

y

x

y

x

xy

y

x

x













































16

(…)

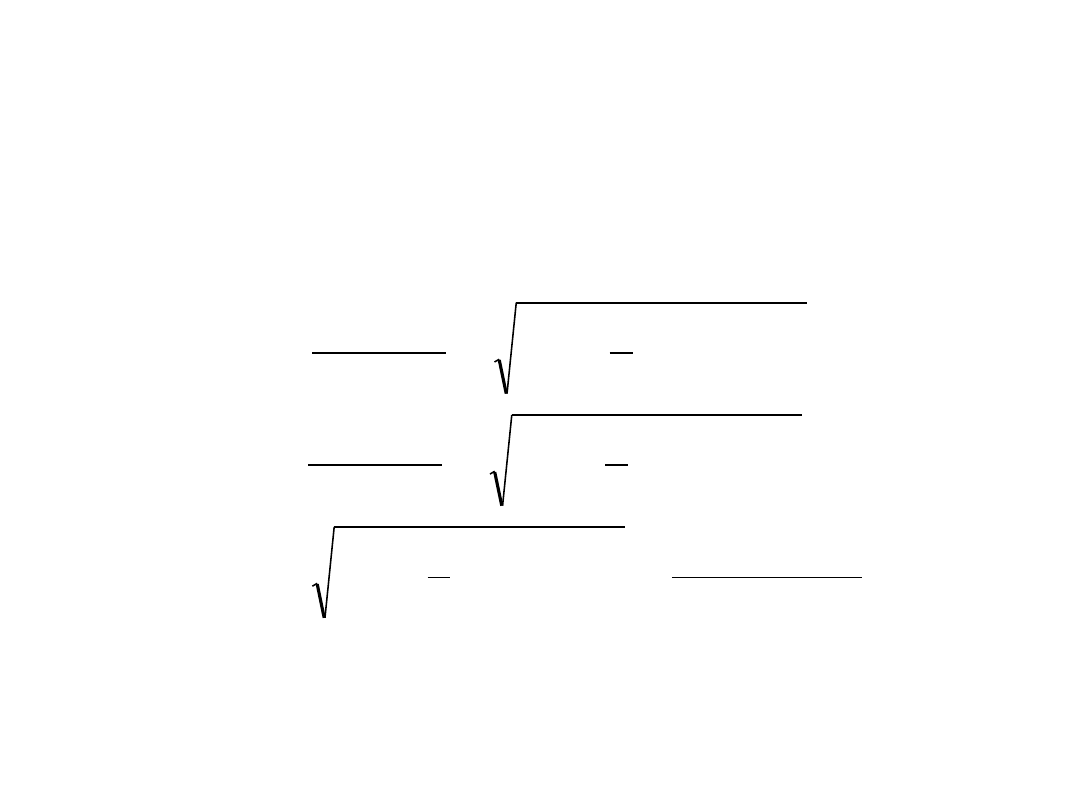
Koło Mohra













2

4

1

4

1

2

4

1

2

min

max

2

2

max

2

2

min

2

2

max



































































y

x

xy

y

x

xy

y

x

y

x

xy

y

x

17

Ekstremalne wartości naprężeń normalnych – naprężenia główne