1

Ćwiczenie 4

Badanie przepływu cieczy - prawo Bernoulli'ego i zwężka Venturi'ego

I. Celem ćwiczenia jest wyznaczenie pola przekroju (średnicy) kanału w zwężce

Venturi’ego na dowolnej jego długości, przy wykorzystaniu prawa Bernoulli’ego.

II. Wprowadzenie

Prawo

Bernoulli’ego

jest

podstawowym

prawem

hydrodynamiki,

sformułowanym w 1738 roku przez szwajcarskiego matematyka Daniela Bernoulli’ego.

Dotyczy ono prawidłowości rządzącej przepływem ustalonym wyidealizowanej cieczy

(nielepkiej, nieściśliwej). Przez przepływ ustalony rozumiemy taki, podczas którego w

każdym miejscu w cieczy prędkość ruchu pozostaje stała.

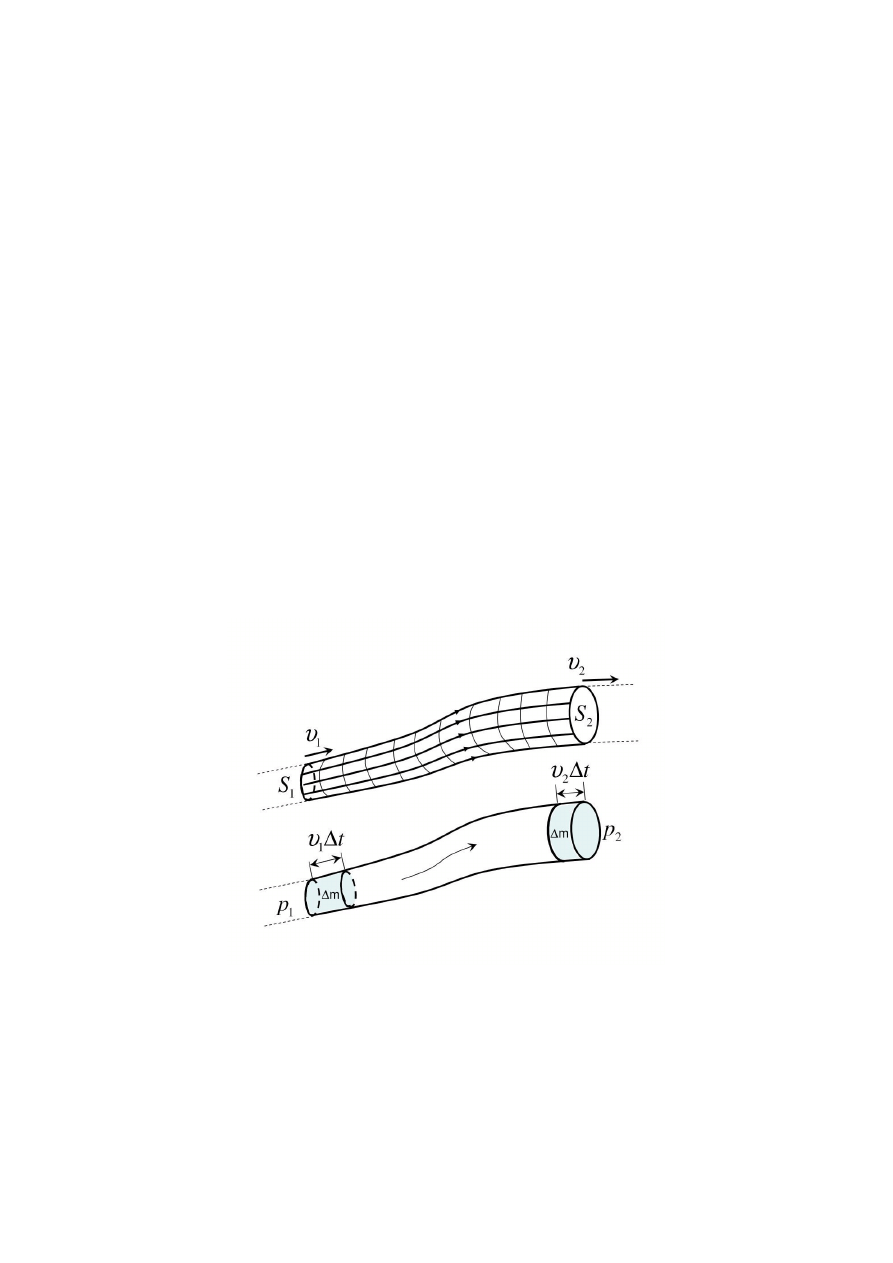
Rozważamy przepływ w rurce o zmiennej średnicy (rys.4.1). Zakładamy iż, tyle

cieczy ile wpływa na jednym końcu rurki musi wypłynąć na drugim.

Rys.4.1. Przepływ w rurce o zmiennej średnicy

Masa cieczy przepływająca przez przekrój S

1

w czasie Δt wynosi:









 



1 1 1

2 2 2

m

S v t

S v t

(4.1)

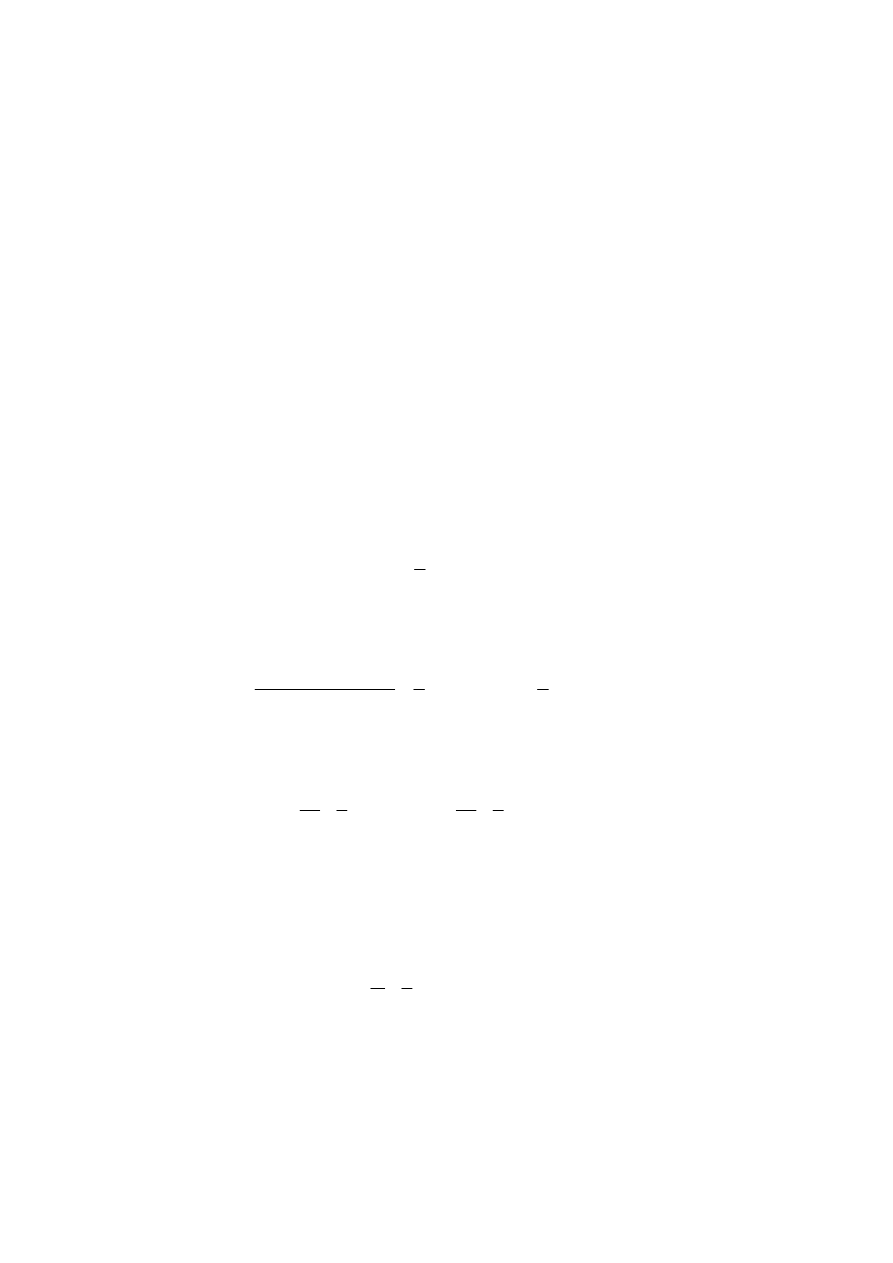
2

a zatem:

1 1 1

2

2 2

S v

S v







(4.2)

Praca wykonana przez ciśnienie w cieczy:

1 1 1

2

2 2

W

p S v t

p S v

t





 



(4.3)

Zmiana energii masy Δm przy przejściu od powierzchni S

1

do powierzchni S

2

:





1 1 1

2

2 2

2

1

p S v t

p S v

t

m E

E

 

  



(4.4)

gdzie: E

1

, E

2

– energia przypadająca na jedn. masy, odpowiednio na powierzchni S

1

i S

2

.

Całkowitą energię na jednostkę masy cieczy można przedstawić w postaci sumy energii

kinetycznej, potencjalnej E

p

i pewnej energii wewnętrznej cieczy U:

2

1

2

p

E

v

E

U







(4.5)

Porównując równania (4.4) i (4.5) otrzymujemy:

2

2

1 1 1

2

2 2

2

2

2

1

1

1

1

1

2

2

p

p

p S v t

p S v

t

v

E

U

v

E

U

m

 

















(4.6)

Pamiętając zależność (4.1) równanie (4.6) możemy zapisać w postaci:



















2

2

1

2

1

1

1

2

2

2

1

2

1

1

2

2

p

p

p

p

v

E

U

v

E

U

(4.7)

Dla cieczy nieściśliwej i bez lepkości wyraz z energią wewnętrzną jest taki sam po obu

stronach równania i wzdłuż rurki mamy:









2

1
2

p

p

v

E

const

(4.8)

Równanie (4.8) jest jedną z postaci prawa Bernoulli’ego.

3

Zwężka Venturi’ego służy do pomiaru natężenia przepływu cieczy lub gazu.

Zasada jej działania oparta jest na równaniu Bernoulli’ego w postaci:











2

2

ot

v

gh

p

const

(4.9)

Z równania tego wynika, iż suma ciśnień: statycznego, dynamicznego i otoczenia jest

stała w dowolnym przekroju rurociągu. Możemy zatem zapisać, że:





s

gh p

(4.10)















2

2

1

2

1

2

2

2

s

ot

s

ot

v

v

p

p

p

p

(4.11)













2

2

1

2

2

1

2

s

s

p

p

v

v

(4.12)

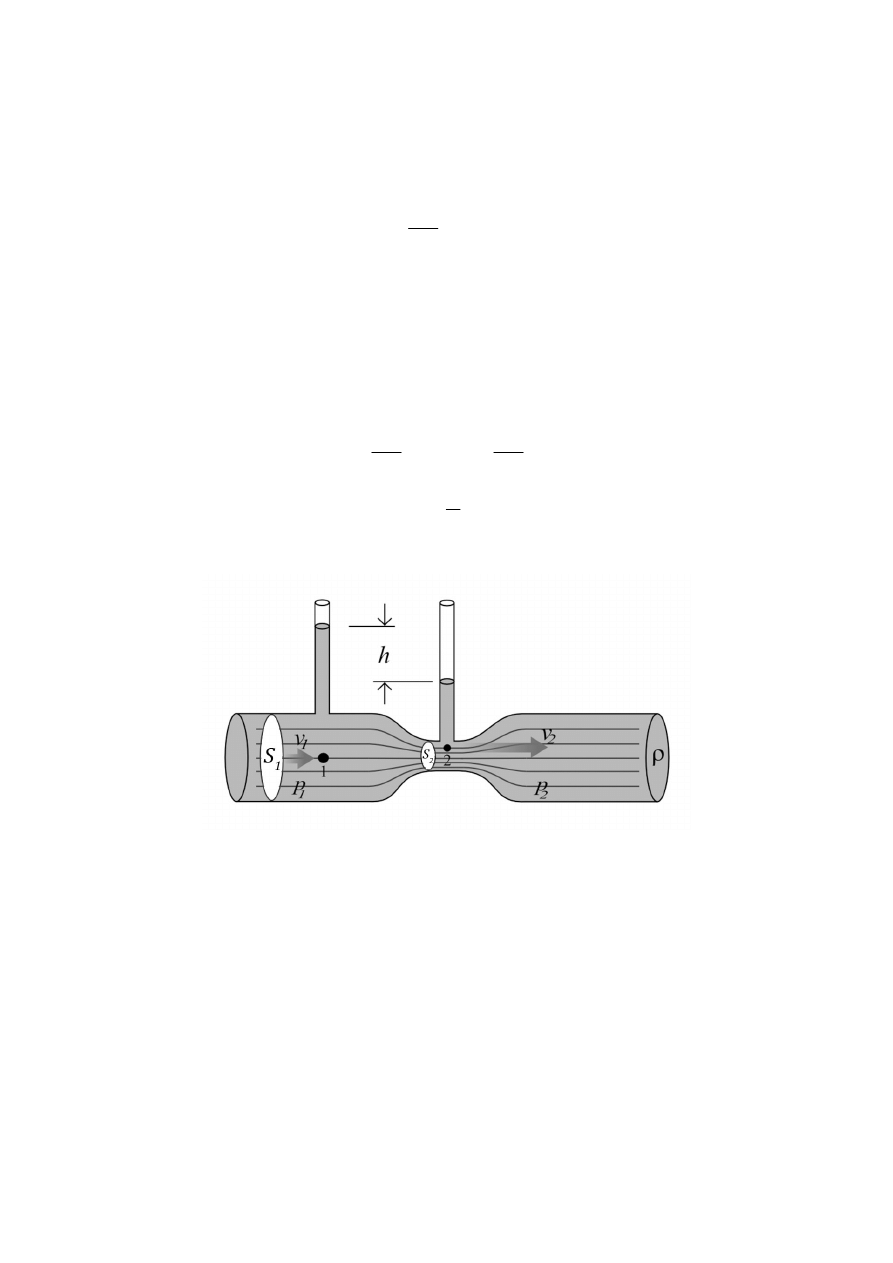
Rys.4.2. Zasada działania zwężki Venturi’ego

Ciśnienie statyczne mierzone w punkcie 1 jest wyższe od ciśnienia mierzonego w

punkcie 2. Pole przekroju, które przechodzi przez punkt 1 jest większe od pola

przekroju przechodzącego przez punkt 2. Jak wynika z równania ciągłości strugi:















1 1

2 2

m

vS

v S

v S

(4.13)

prędkość płynu w punkcie 1 jest niższa niż w punkcie 2.

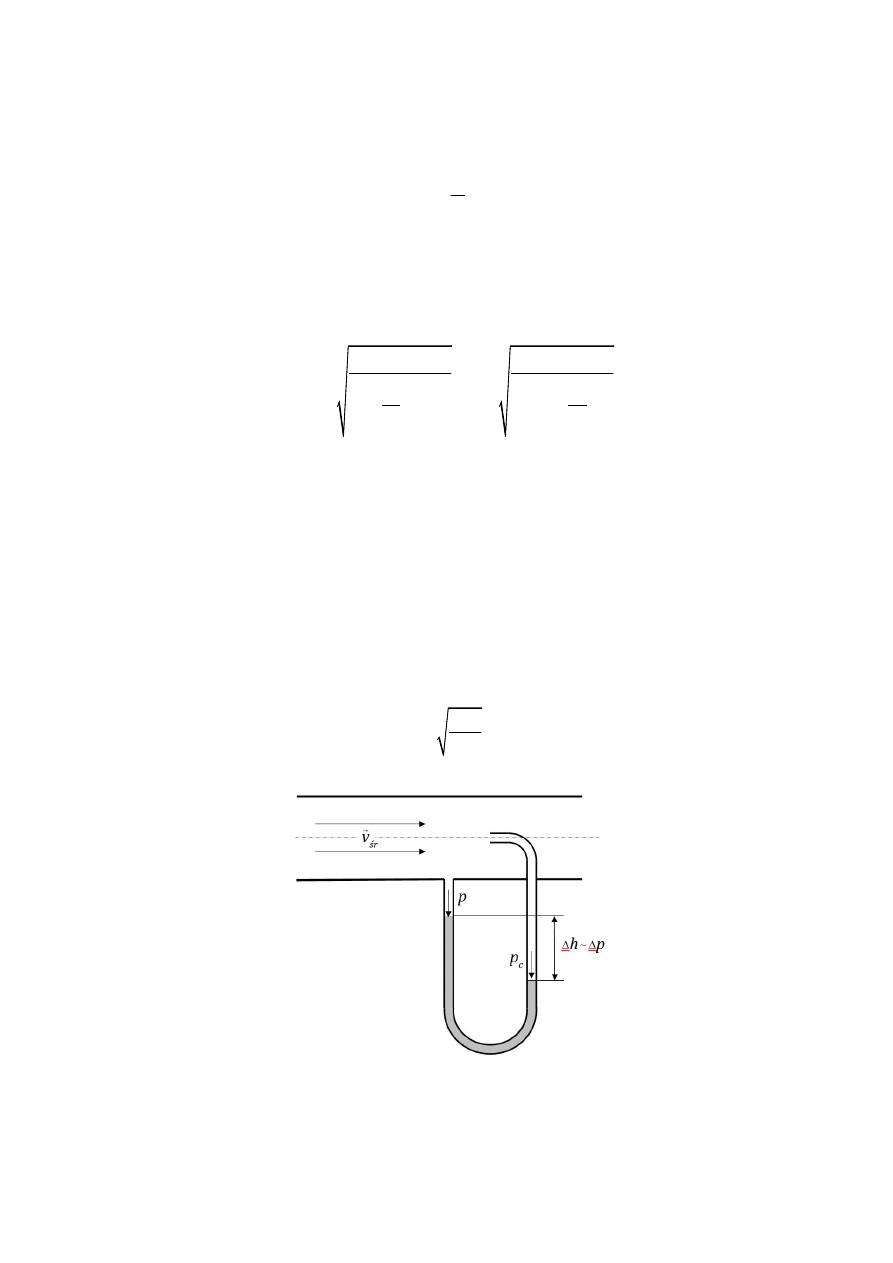
Łącząc ze sobą równanie Bernoulli’ego oraz równanie ciągłości strugi:

4
































 

2

2

1

2

2

1

1 1

2 2

2

s

s

p

p

v

v

m

vS

v S

v S

(4.14)

Otrzymamy następujący wzór na strumień masowy:























































































1

2

1

2

1

2

2

2

1

2

2

1

2

2

1

1

s

s

s

s

p

p

p

p

m

S

S

S

S

S

S

(4.15)

Za pomocą powyższej zależności możemy wyznaczyć masowy strumień płynu bez

znajomości prędkości w przekroju 1 i 2.

Najprostszym urządzeniem do pomiaru prędkości płynu jest rurka Pitota, która

służy do pomiaru różnicy ciśnienia spiętrzania (ciśnienie całkowite) i ciśnienia

statycznego. Mierzona różnica ciśnień jest proporcjonalna do kwadratu prędkości płynu.

2 p

v







(4.16)

Rys.4.3. Schemat działania rurki Pitota umieszczonej w osi kanału przepływowego

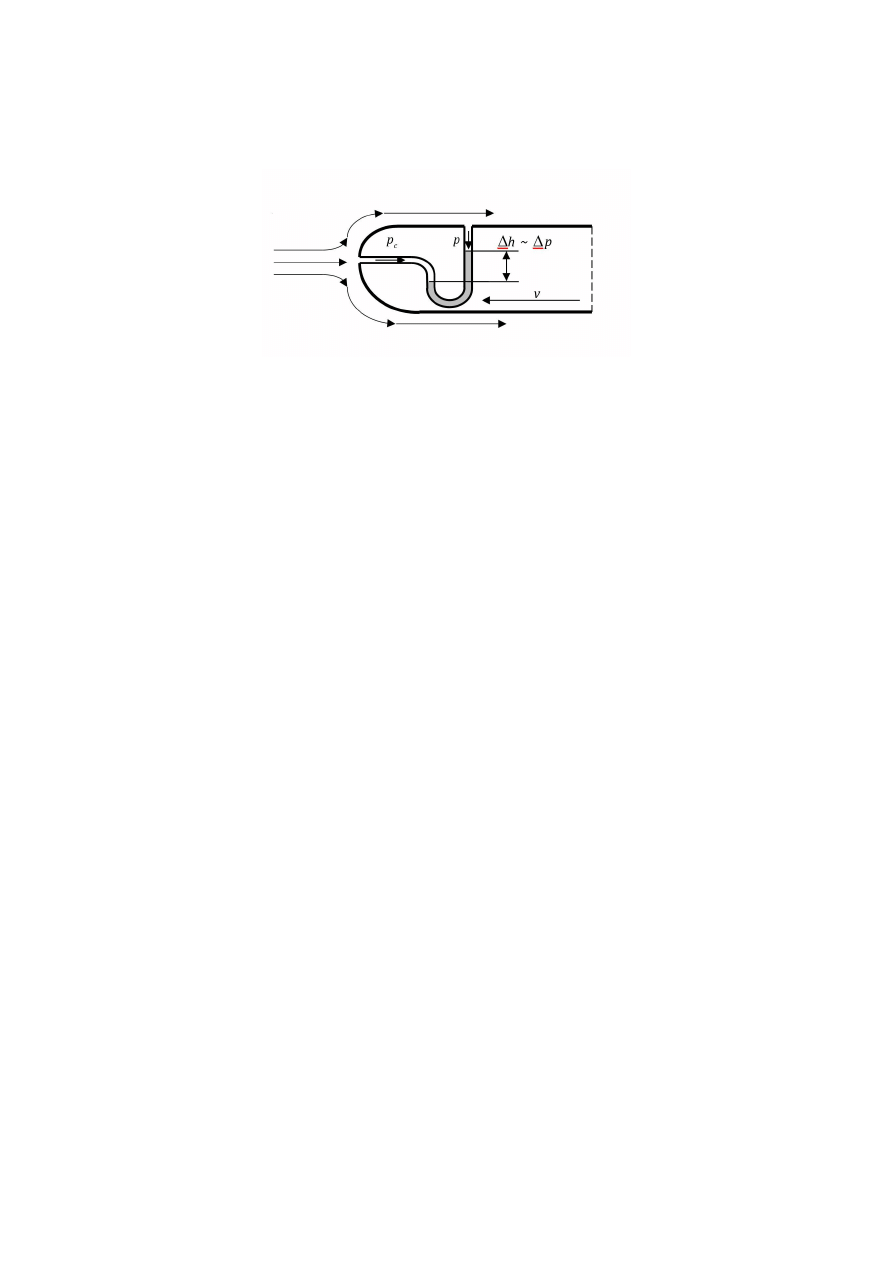
5

Ponieważ prędkość jest względna, to prędkość ruchu ścianki względem płynu można

określić mierząc ciśnienie płynu na czole (przód) ścianki.

Rys.4.4. Czoło (przód) ścianki rurki Pitota

Z równania Bernoulli’ego i równaniem ciągłości strugi związany jest paradoks

hydrauliczny, który polega na tym, że zmniejszenie przekroju kanału przepływowego

zwiększa prędkość przepływu płynu (v

1

> v

2

⇒ S

1

< S

2

), co z kolei zmniejsza jego

ciśnienie (v

1

> v

2

⇒ p

1

< p

2

) i odwrotnie zwiększenie przekroju kanału przepływowego

zmniejsza prędkość przepływu płynu i zwiększa jego ciśnienie (S ↑ ⇒ p ↑ ∩ v ↓). W

potocznym mniemaniu zmniejszenie przekroju kanału przepływowego zwiększa

prędkości przepływu płynu i jednocześnie zwiększa jego ciśnienie, co nie jest zgodne z

rzeczywistością.

6

III. Przebieg ćwiczenia

Stanowisko do demonstracji twierdzenia Bernoulli’ego (rys.4.5) składa się z

następujących elementów: zbiornika na wodę wyposażonego w pompę wodną (8),

rotametru (3) do pomiaru natężenia przepływu wody, kanału zbieżno–rozbieżnego (10)

stanowiącego zwężkę Venturi’ego, rurki Pitota (7) umieszczonej w osi kanału (10),

panelu z rurkami manometrycznymi (6) do pomiaru ciśnienia statycznego w różnych

punktach kanału (10) oraz zaworów: zaworu (4) odpowietrzającego rurki

manometryczne, zaworu zwrotnego (5), zaworu regulacyjnego zbiornika wodnego (1) i

zaworu regulacyjnego przepływu wody (2) przez kanał zbieżno-rozbieżny (10).

Rys.4.5. Zdjęcie stanowiska do demonstracji twierdzenia Bernoulli’ego

7

Przygotowanie stanowiska pomiarowego

Procedura przygotowania stanowiska pomiarowego ma zapewnić prawidłowe

wypełnienie wodą rurek manometrycznych w panelu (6) i przebiega według

następującego schematu:

1. Zamknąć zawór regulacyjny zbiornika wodnego (1) oraz zawór regulacyjny

przepływu wody (2).

2. Włączyć pompę wodną i otworzyć całkowicie zawór regulacyjny przepływu wody

(2).

3. Otworzyć powoli zawór regulacyjny zbiornika wodnego (1) aż do osiągnięcia

maksymalnego przepływu. Gdy wszystkie rurki manometryczne całkowicie wypełnią

się wodą i nie będzie w nich pęcherzyków powietrza, zamknąć zawór regulacyjny

przepływu wody (2) oraz zawór zbiornika wodnego (1). Ważne jest, aby zachować tę

kolejność zamykania.

4. Odłączyć zawór zwrotny (5) i otworzyć zawór odpowietrzający (4).

5. Otworzyć powoli zawór regulacyjny przepływu wody (2). Można zaobserwować, jak

rurki manometryczne zaczynają wypełniać się powietrzem.

6. Gdy poziom wody we wszystkich rurkach manometrycznych opadnie do pożądanej

wysokości (70-80 mm) zamknąć zawór regulacyjny przepływu wody (2), podłączyć

zawór zwrotny (5) lub zamknąć zawór odpowietrzający (4).

7. Po wykonaniu czynności opisanych w punktach 1-6, we wszystkich rurkach

manometrycznych poziom wody powinien mieć ten sam poziom.

Sposób wykonania ćwiczenia

1. Wypełnić wszystkie rurki manometryczne, jak opisano w powyższym podrozdziale.

2. Otworzyć zawór regulacyjny zbiornika wodnego (1) i zawór regulacyjny przepływu

wody (2).

3. Ustalić natężenie przepływu wody i odczytać jego wartość z rotametru (3).

4. Umieścić czoło rurki Pitota (7) w pierwszym położeniu (minimalne ciśnienie).

Poczekać do chwili, gdy ustabilizuje się poziom wody w rurce manometrycznej

podłączonej do rurki Pitota (7). Proces ten może trwać kilka minut.

8

5. Gdy wysokości poziomu wody w obu rurkach manometrycznych ustabilizuje się,

określić różnicę wysokości pomiędzy nimi (h

Tp

– h

i

). Różnica ta odpowiada ciśnieniu

kinetycznemu określonemu przez wzór:

 

2

v

p

2g

;

6. Określić pole przekroju kanału za pomocą następującej zależności:



Q

S

v

;

gdzie: Q – objętościowe natężenie przepływu,

v – prędkość przepływu wody określona w punkcie 5.

7. Powtórzyć kroki opisane w punktach 4-6 dla innych ustawień położenia czoła rurki

Pitota (7).

8. Powtórzyć wszystkie powyższe czynności dla różnych natężeń przepływu wody. Dla

każdego natężenia przepływu, pola przekroju kanału muszą być mniej więcej takie

same.

9. Zalecane natężenia przepływu wody dla tego doświadczenia to: 5 [l/min], 10 [l/min]

i 15 [l/min]

9

IV. Bibliografia

[1] Błażejewski, R., 1991, 100 prostych ćwiczeń z wodą i powietrzem, Wyd. Nauk.-

Techn., Warszawa

[2] Lewandowski, J. B., 2006, Mechanika płynów, Wyd. AR w Poznaniu,

[3] Orzechowski, Z., Prywer, J., Zarzycki, R., 2001, Mechanika płynów w inżynierii

środowiska , WNT, Warszawa,

[4] Sobota, J., 1994, Hydraulika, T. I i II, AR Wrocław,

[5] Troskolański, A. T., 1969, Hydromechanika, WNT, Warszawa,

10

Karta pomiaru pola przekroju kanału w zwężce Venturi’ego

Imię i nazwisko studenta: 1 ………………………………………………………………………….…………….

2 ………………………………………………………………………….…………….

3 ………………………………………………………………….…………………….

4 ……………………………….……………………………………………………….

Rok studiów: ………………………………………

Grupa: ……………..…………………………………

Data: …………………………………………………..

Godzina: …………………………………………….

Temperatura otoczenia: ……………………...

Ciśnienie otoczenia: ……………………………

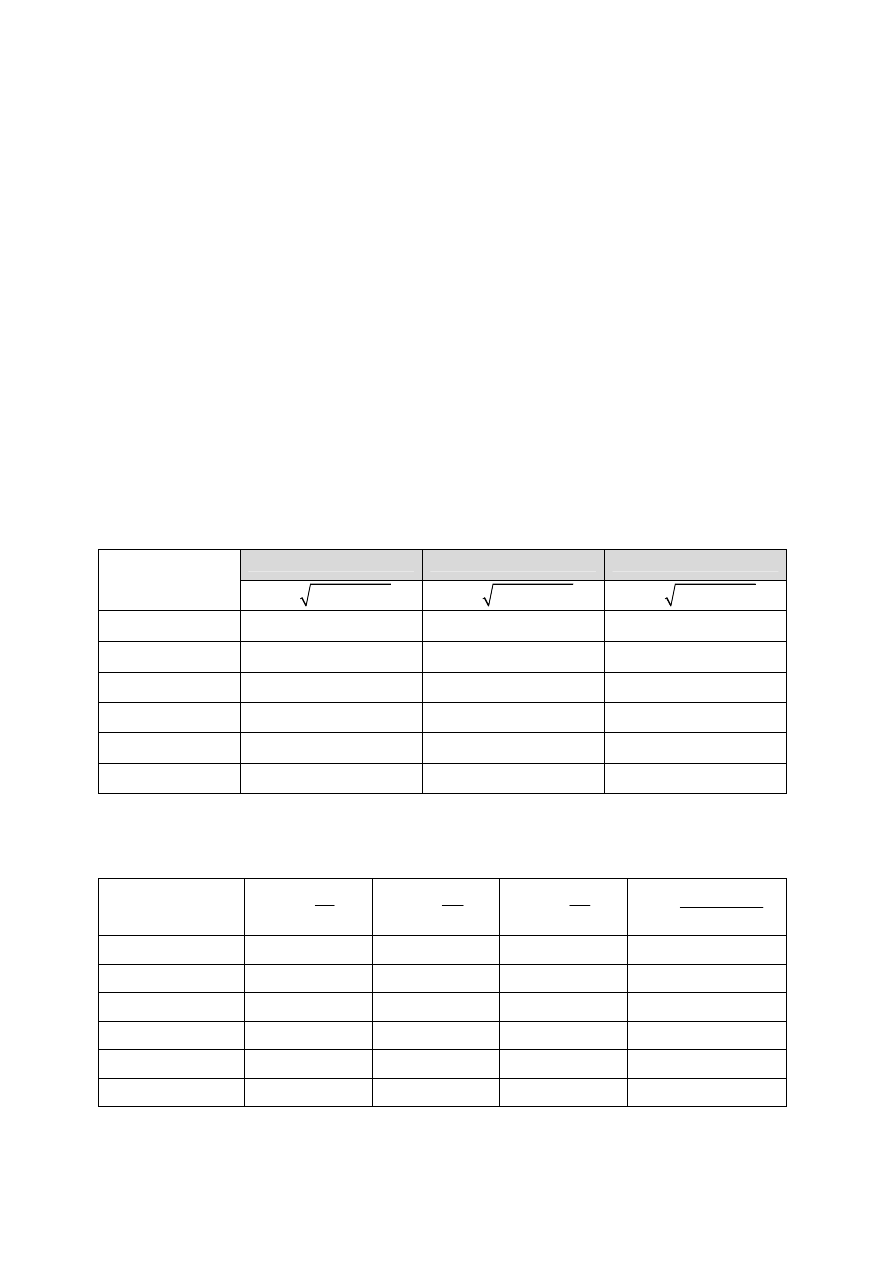
Tab.4.1. Zestawienie wyników pomiaru

Q

1

= [l/min] Q

2

= [l/min] Q

3

= [l/min]

1

2 (

)

TP

i

v

g h

h





2

2 (

)

TP

i

v

g h

h





3

2 (

)

TP

i

v

g h

h





h

TP

– h

1

h

TP

– h

2

h

TP

– h

3

h

TP

– h

4

h

TP

– h

5

h

TP

– h

6

Tab.4.2. Zestawienie wyników pomiaru

1

1

1

Q

S

v



2

2

2

Q

S

v



3

3

3

Q

S

v



1

2

3

3

S

S

S

S





  

h

TP

– h

1

h

TP

– h

2

h

TP

– h

3

h

TP

– h

4

h

TP

– h

5

h

TP

– h

6