Drgania swobodne 

 

 

 

Drgania swobodne normalne jednowymiarowego układu jednakowych mas 

Drgania swobodne (drgania własne) są to 

drgania

 ciała wywołane wychyleniem z położenia 

równowagi trwałej, kiedy na ciało nie działają żadne siły, poza siłami określającymi 
położenie równowagi i siłami dążącymi do jej przywrócenia. 

Amplituda

 drgań zależy od 

wielkości początkowego wychylenia (energii potencjalnej) lub od prędkości początkowej 
(energii kinetycznej) nadanej ciału. 

Częstotliwość drgań własnych  

Ciała mogą mieć wiele 

częstotliwości

 drgań własnych. W szczególności częstotliwości te 

mogą być wielokrotnością częstotliwości najmniejszej (

wyższe harmoniczne

). Częstotliwość 

wzbudzania poszczególnych drgań własnych zależy od sposobu wzbudzania i ilości 
dostarczonej energii. Na przykład dzwon po uderzeniu wykonuje drgania, które powodują 
drgania 

powietrza

 słyszane przez nas jako 

dźwięk

. Uderzając dzwon w różnych miejscach, z 

różną siłą, różnymi przedmiotami - spowodujemy, że będziemy słyszeli różnie brzmiące 
dźwięki - o różnej barwie. Oznacza to, że za każdym razem dzwon wykonuje nieco inne 
drgania. Drgania te będą różniły się 

składem widmowym

, czyli będą wzbudzane drgania 

własne o różnych częstotliwościach i natężeniach. 

Drgania pod wpływem sił sprężystości 

Częstotliwość drgań własnych zależy tylko od własności fizycznych i kształtu ciała, 
lub układu drgającego, jeżeli drgania wykonywane są pod wpływem wewnętrznych 

sił 

sprężystości

 ciała. Na przykład drgania własne 

struny

 zależą od materiału, z którego 

wykonana jest struna (dokładniej 

modułu Younga

), grubości struny i stopnia jej 

naprężenia

.Innym przykładem może być ciało o masie m wykonujące poziome drgania 

spowodowane oddziaływaniem 

sprężyny

 o 

współczynniku sprężystości

 k. 

Częstotliwość drgań własnych tego układu wyraża wzór 

 

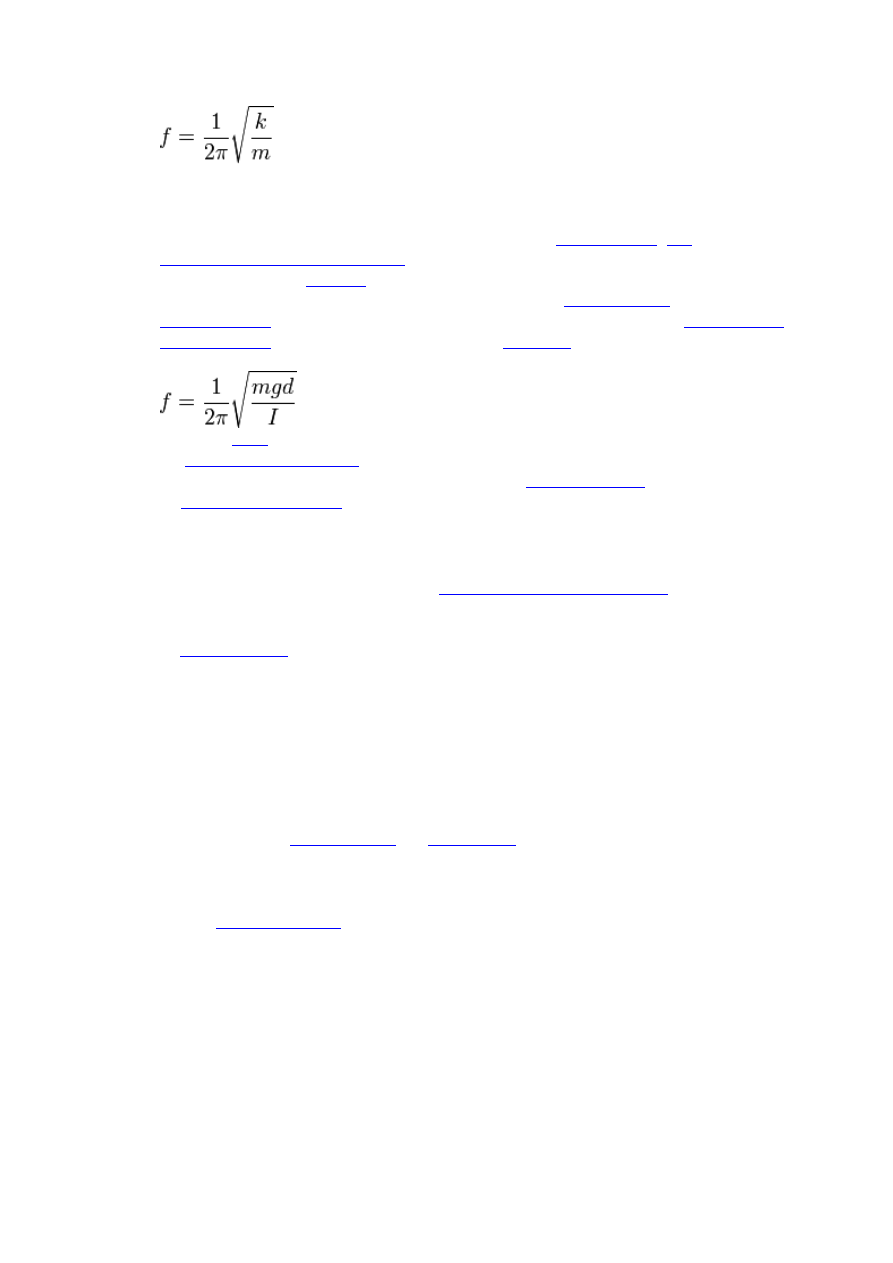
Drgania swobodne pod wpływem sił zewnętrznych 

Siłami będącymi przyczyną drgań własnych może być 

siła grawitacji

, 

siła 

oddziaływania elektrostatycznego

 i inne. Przykładem drgań własnych wywoływanych 

zewnętrzną siłą jest 

wahadło

. Częstotliwość drgań wahadła zależy nie tylko od jego 

kształtu i punktu zawieszenia, lecz również od wartości 

przyspieszenia 

grawitacyjnego

. Dlatego częstotliwość ta będzie nieco różna na różnych 

szerokościach 

geograficznych

 i zdecydowanie inna na innych 

planetach

. W przypadku wahadła 

fizycznego wzór na częstotliwość drgań własnych ma postać 

 

gdzie m - 

masa

 wahadła; 

g - 

przyspieszenie ziemskie

; 

d - odległość punktu zawieszenia wahadła od jego 

środka ciężkości

; 

I - 

moment bezwładności

 wahadła. 

Drgania harmoniczne  

Szczególnym rodzajem drgań swobodnych są 

drgania harmoniczne swobodne

 zachodzące 

gdy siła przywracająca równowagę jest proporcjonalna do wychylenia. Drgania takie 
wykonują ciała sprężyste, jeżeli amplituda drgań nie jest zbyt duża. Dla małych drgań jest 
spełnione 

prawo Hooke'a

, mówiące o proporcjonalności siły do wielkości odkształcenia. Ruch 

wahadła jest przybliżeniem ruchu harmonicznego. Im mniejszy jest kąt maksymalnego 
wychylenia wahadła od kierunku pionowego, tym bardziej ruch ten jest zbliżony do ruchu 
harmonicznego. 

Ortogonalne drgania własne  

Dla ciał mogących wykonywać drgania własne o różnej częstotliwości, kierunkach lub 
układach można określić zestaw takich drgań, że każde drganie jest sumą drgań własnych. 
Drgania takie nazywamy 

ortogonalnymi

 lub 

normalnymi

. Drgania takie zachodzą niezależnie 

od siebie. Każde drganie ciała, przedstawiające dowolnie skomplikowane drganie, może być 
jednoznacznie określone jako suma drgań normalnych. 

Przykładem są 

krzywe Lissajous

 wyznaczane przez wahadło wykonujące drgania w dwóch 

prostopadłych płaszczyznach.