2010-02-12

1

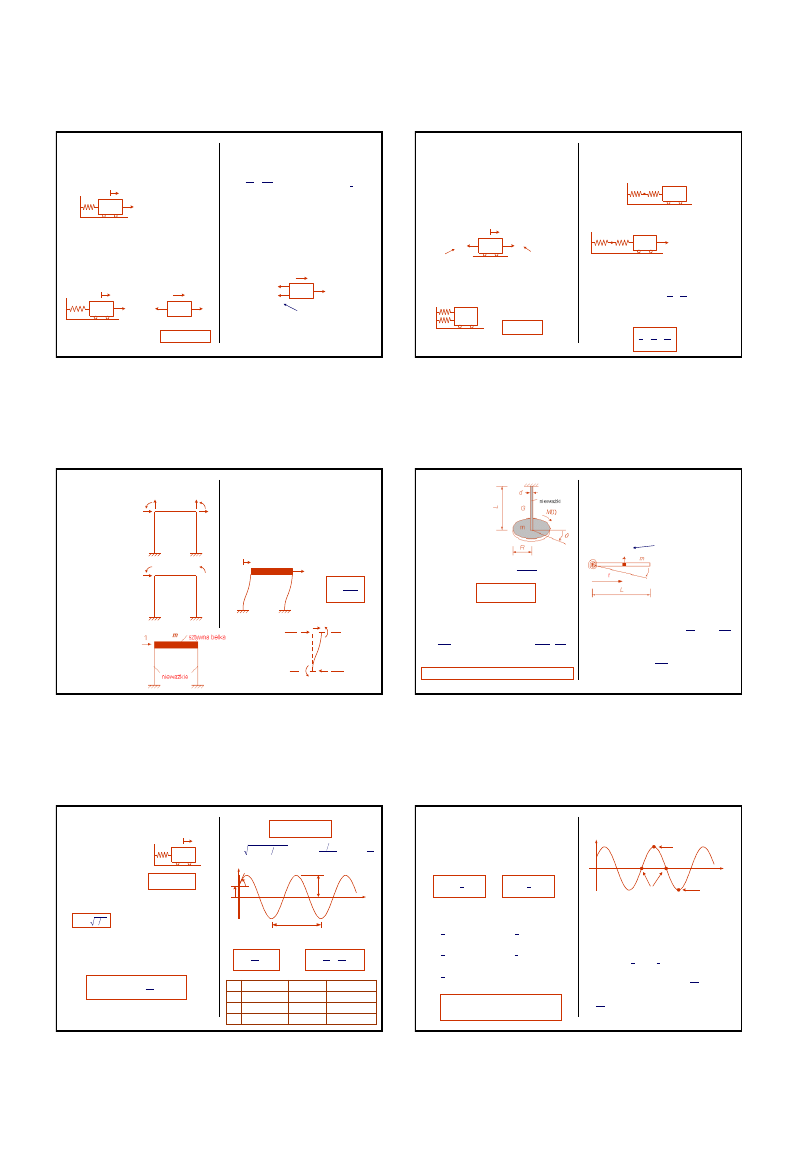
Rozważamy układ o jednym stopniu swobody (1SS)
złożony z masy m połączonej z ostoją za pomocą
więzi sprężystej o sztywności k.

Dynamika konstrukcji 1.1

1SS - Wprowadzenie

W położeniu równowagi statycznej u = 0

k (N/m)

Druga zasada dynamiki Newtona

)

t

(

p

u

k

u

m

)

t

(

u

k

)

t

(

p

F(t)

)

t

(

u

m

















Zasada

D’Alemberta

0

)

t

(

u

m

)

t

(

u

k

)

t

(

p











fikcyjna siła bezwładności

Równowaga dynamiczna

Równanie ruchu można wyprowadzić dwojako.

Układ

jest

w

równowadze

dynamicznej.

Wprowadzając siłę bezwładności o zwrocie
przeciwnym do zwrotu

przyśpieszenia, równą

iloczynowi

masy

i

przyśpieszenia

można

układać równania równowagi statycznej.

Siły działające na oswobodzoną masę

k

m

)

(t

u

)

(t

p

k

m

0

>

)

(t

u

)

(t

p

)

(t

p

)

(t

ku

)

(t

u



)

(t

p

)

(t

ku

)

(t

u



)

(t

u

m 



)

t

(

F

u

E

u

L

s













Całkowitą siłę działającą na punkt materialny z
więzami można zapisać także jako:

2

u

k

(t)

)

t

(

2

1





s

E

u

p

L

gdzie

Sztywność k

Definicja

sztywności k jest taka sama jak w

metodzie

przemieszczeń:

Sztywność k jest równa reakcji (sile
zewnętrznej) potrzebnej do utrzymania
układu w równowadze pod działaniem
przemieszczenia u = 1.

Dynamika konstrukcji 1.2

Połączenie równoległe dwóch sprężyn

Sztywność układu:

2

1

k

k

k





Połączenie szeregowe dwóch sprężyn

k

m

1

=

u

.1

k

1

k

m

2

k

1

k

m

2

k

1

F

d ,

1

m

1

=

u

k

2

2

F

d ,

Sztywność układu:

2

2

2

d

k

F

d

k

F





1

1

1

k

F

F





2

1

:

statyka

1

1

2

1

2

1











k

k

k

k

d

d

2

1

1

1

1

k

k

k





więź sprężysta

siła zewnętrzna

Przykład

3

24

L

EI

k



Rama

może mieć 1SS

jeśli

składa

się

z

ciężkiego dachu opartego
na lekkich kolumnach.

Dynamika konstrukcji 1.3

1

2

6

5

4

3

1

2

3

1

=

u

k

1

3

12

L

EI

2

6

L

EI

3

12

L

EI

2

6

L

EI

Niektóre konstrukcje można liczyć jako 1SS

W zadaniu statyki, ta
rama ma 6 stopni
swobody.

Pomijając odkształcalność
podłużną odrzucamy 3
stopnie swobody.

Masą m układu 1SS jest masa dachu.

Sztywność można określić tradycyjnie:

Ruch obrotowy

)

(

:

t

M

C

J

dynamice

w



























V

R

R

h

h

R

m

dr

r

d

h

dV

r

mR

J













2

0

4

2

0

3

2

2

2

2















L

V

mL

dr

A

AL

m

r

dV

r

0

2

2

2

3

d

































m

r

r

J

m

Dynamika konstrukcji 1.4

Układ o 1SS może
znajdować się w ruchu
obrotowym.

L

G

d

π

C

C

M

:

statyce

w

32

4







J







Przykład:
Obliczenie J

dla obracającego się pręta

J

– moment bezwładności tarczy kołowej

względem osi pręta d:

moment wynikający z bezwładności obrotowej

elementarna siła
bezwładności

dm

r







3

2

mL

J



1SS

– Drgania swobodne

Drgania własne

)

sin(

B

)

cos(

A

)

(

t

t

t

u

n

n









m

k

n





n

t

t

u

u

u

u

u

u



B

A

o

o

o

o























0

0

)

sin(

C

)

(









t

t

u

n

(s)

T

n

n







2

(Hz)

T

f

n

n

n







2

1



(rad/s)

A i B

określa się z warunków początkowych

co można zapisać w postaci:

częstość kołowa

Dynamika konstrukcji 1.5

Układ drga wokół
położenia równowagi
statycznej bez siły
wymuszającej.

Równanie ruchu:

0





u

k

u

m 



Rozwiązanie:

)

sin(

)

cos(

)

(

o

o

t

u

t

u

t

u

n

n

n













k

m

)

(t

u

C

sin

C

cos

)

(

C

o

o

o

o

u

u

u

u

n

n





















2

2

okres drgań

częstość fizyczna

o

u

o

u

n

T

u

t

C

ω=2π/T [rad/s]

f=1/T [Hz]

n=60/T [c/min]

ω=

1

6,283

0,1047

f=

0,1592

1

0,0167

n=

9,549

60

1

Energia w drganiach własnych

W

każdej chwili czasowej energia całkowita

E jest

sumą energii kinetycznej E

k

oraz

energii

odkształcenia sprężystego E

s

.

2

2

1

)

(

)

(

t

u

m

t

E

k





2

2

1

)

(

)

(

t

u

k

t

E

s











)

(

C

)

(

sin

C

)

(

cos

C

)

sin(

C

)

cos(

C

)

(

)

(

)

(

m

k

k

t

k

t

m

t

k

t

m

t

E

t

E

t

E

n

n

n

n

n

n

n

s

k

2

2

2

2

2

2

2

2

2

2

1

2

1

2

1

2

1

2

1















































E(t)

jest stała, czyli układ wykonuje

drgania zachowawcze.

Uwaga :

zasadę zachowania energii można

zapisać za pomocą równania różniczkowego.

2

2

2

1

2

1

u

k

u

m

t

E







)

(

0

d

d





t

E

0

0













ku

u

m

u

ku

u

u

m

t

E













d

d

Dynamika konstrukcji 1.6

u

t

max

=

0

=

k

E

s

E

0

=

=

k

E

s

E

max

0

=

=

k

E

s

E

max

Układ zachowawczy

2010-02-12

2

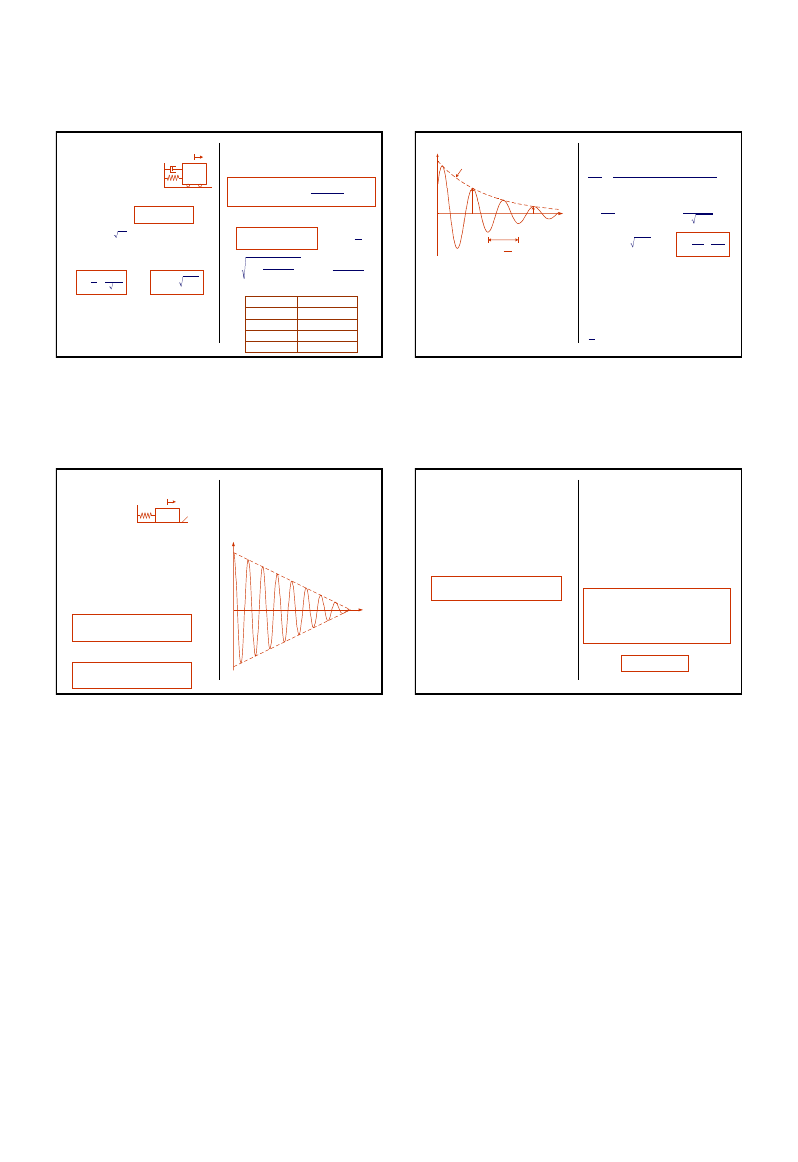
DRGANIA SWOBODNE TŁUMIONE

0







u

k

u

c

u

m







km

c

c

gdy

r

2









)

sin(

B

)

cos(

A

)

(

t

t

t

u

D

D

t

n















e

km

c

c

c

r

2







2

1









n

D

ω









)

cos(

B

)

sin(

A

)

sin(

B

)

cos(

A

)

(

t

t

t

t

t

u

D

D

D

D

D

D

t

t

n

n

n









































e

e



D

n

t

t

u

u

u

u

u

u

ω

ξω

B

A

A

o

o

0

o

o

0















































)

sin(

)

cos(

)

(

o

o

o

t

u

u

t

u

t

u

D

D

D

n

t

n

















e

)

sin(

C

)

(















t

t

u

D

t

n

e

D

u

u

n

ω

ξω

θ

C

cos

o

o







Opory ruchu

w

układzie

można

przedstawić

w

postaci liniowej

więzi lepkiej

(wiskotycznej), w

której siła

oporu jest proporcjonalna
do

prędkości ruchu:

)

(t

u

c

f

D







A i B

określa się z warunków początkowych

Rozwiązanie można zapisać także w postaci:

Dynamika konstrukcji 1.7

Równanie ruchu:

współczynnik tłumienia

częstość drgań

2

2



















D

u

u

u

n

ω

ξω

o

o

o

C



C

sin

o

u



θ

k

m

)

(t

u

c

to rozwiązaniem jest:

Konstrukcje

γ=2ξ

Stalowe

0,010-0,025

Drewniane

0,030-0.050

Murowe

0,040-0,080

Żelbetowe

0,050-0,100

Współczynniki tłumienia

Zanikanie ruchu

D

pT

t

t

n

p

n







D

D

D

D

D

pT

n

)

pT

(t

n

t

p

n

n

n

n

n

n

n

)

)

pT

(t

(

)

t

(

u

u

ξω

ξω

ξω

e

θ

ω

e

θ

ω

e



















sin

C

sin

C

2

n

n

n

p

n

n

1

p

T

p

u

u

D























2

ln

p

n

n

u

u

p

















ln

2

1

.







1

1

1

0

2

p

Dynamika konstrukcji 1.8

Pomiar

drgań swobodnych może dostarczyć

informację o częstości drgań i współczynniku
tłumienia konstrukcji

D

D

T





2



t

e

n





C

n

t

p

n

t

+

n

u

p

n

u

+

u

t

odstęp czasu między dwoma
maksymalnymi wychyleniami

p

n

n

u

i

u



Energia całkowita w trakcie drgań tłumionych jest
zużywana na pokonywanie oporów ruchu, kosztem
energii kinetycznej









0

E

E

dt

d

2

s

k

















u

c

u

u

m

ku

u

u

m

u

ku

















Liczbę ξ dla p=1, tj. przy dwóch kolejnych
maksymalnych wychyleniach nazywamy
logarytmicznym dekrementem tłumienia

Dynamika konstrukcji 1.9

Drgania swobodne z tłumieniem COULOMBA

k

m

)

(t

u

dry friction

Tłumienie Coulomba
wynika z tarcia między
dwoma suchymi
powierzchniami.

Siła oporu tarcia F =



N, gdzie



oznacza

współczynnik tarcia kinetycznego, a N jest siła
normalną między powierzchniami kontaktu.

Zakładamy, że F nie zależy od prędkości
ruchu a jej zwrot jest przeciwny do kierunku
wychylenia.

Równanie ruchu z lewej do prawej strony:

F

u

k

u

m











k

F

t

t

t

u

n

n

/

)

sin(

B

)

cos(

A

)

(











1

1

Równanie ruchu z prawej do lewej strony:

F

u

k

u

m









k

F

t

t

t

u

n

n

/

)

sin(

B

)

cos(

A

)

(











2

2

Stałe A

1

, B

1

, A

2

, B

2

zależą od warunków

początkowych ruchu w kolejnych półokresach.

Typowy wykres ruchu:

u

t

Dynamika konstrukcji 1.10

UKŁAD O SKOŃCZONEJ LICZBIE

STOPNI SWOBODY - WSS

 

 

 

 

 

   

)

t

(

)

t

(

p

u

k

u

c

u

m

1

p

q

k

q

c

q

m

WSS

SS

























 
 
 

m

c

k

Macierze mas i

sztywności można otrzymać

np. na podstawie dyskretyzacji konstrukcji
(elementami

skończonymi).

Macierz

tłumienia musi być określona w inny

sposób.

TŁUMIENIE

Występują różne modele tłumienia, jednak
najczęściej stosuje się liniowy model tłumienia
wiskotycznego z

dwóch powodów:

• równania ruchu są proste
• wyniki otrzymane na podstawie tego

modelu

są dość zgodne z wynikami

eksperymentu

Jednak wtedy

współczynnik tłumienia



można określić jedynie doświadczalnie.

macierz sztywności

macierz tłumienia

macierz mas (bezwładności)

P

q

K

q

C

q

B











