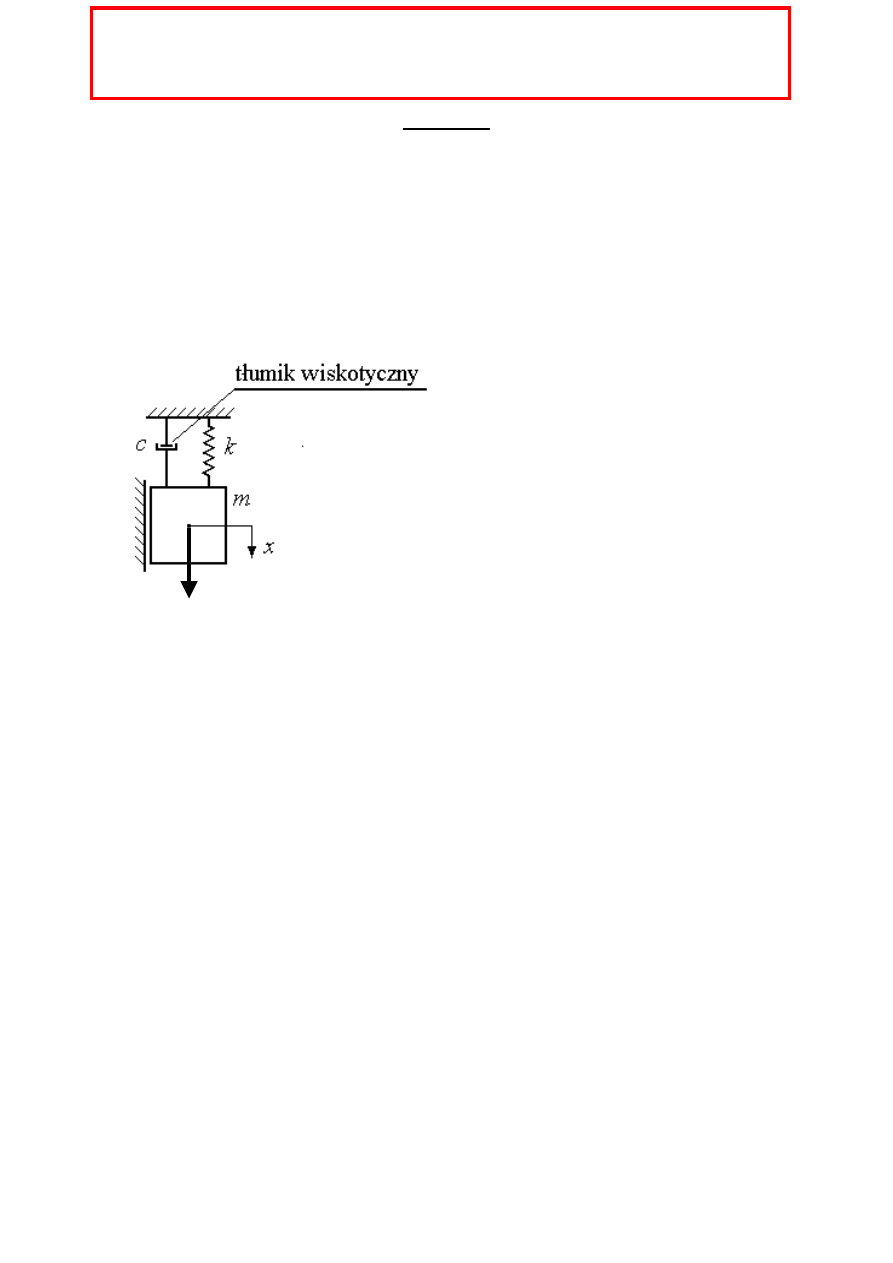
Wykład 2
Drgania swobodne tłumione
W rzeczywistych układach drgających mamy do czynienia ze zjawiskiem
rozpraszania energii. Nie jest spełniona zasada zachowania energii
mechanicznej.
Drganie układów liniowych z uwzględnieniem rozproszenia energii możemy
opisać równaniem:
- siła tłumienia drgań, która
wprowadzona została w celu
uwzględnienia efektu
rozproszenia energii.
F(t) - siła wymuszająca, którą na razie
(drgania swobodne)
przyjmujemy równą zero.
W rzeczywistych konstrukcjach mechanicznych przyjmujemy założenie że
siła
tłumienia
jest
proporcjonalna do prędkości drgań
.
c – stały współczynnik tłumienia
Model tłumienia opisany tym równaniem nosi nazwę tłumienie wiskotyczne
(płynne).
Korzyści wynikające z zastosowania modelu wiskotycznego
1. zachowanie liniowości równania różniczkowego drgań
2. model ten jest właściwym opisem rzeczywistego rozpraszania energii drgań
mechanicznych.
Rozwiązanie równania różniczkowego drgań (rozwiązanie ogólne) możemy
przedstawić w postaci:
A, B
są stałymi całkowania, wynikającymi z podanych warunków
początkowych
)
(t
F
kx
F
x
m
d
=
+
+
&&
d
F
x
c
F
d
&
=
0
=
+
+
kx
x
c
x
m
&
&&
t
s
t
s
Be
Ae
x
2
1
+
=
F(t)
Uwaga: przypadki podawania
błędnych
adresów e–mail
W celu otrzymania kopii materiałów, należy wysłać pocztę na adres:
kkalinsk@sunrise.pg.gda.pl
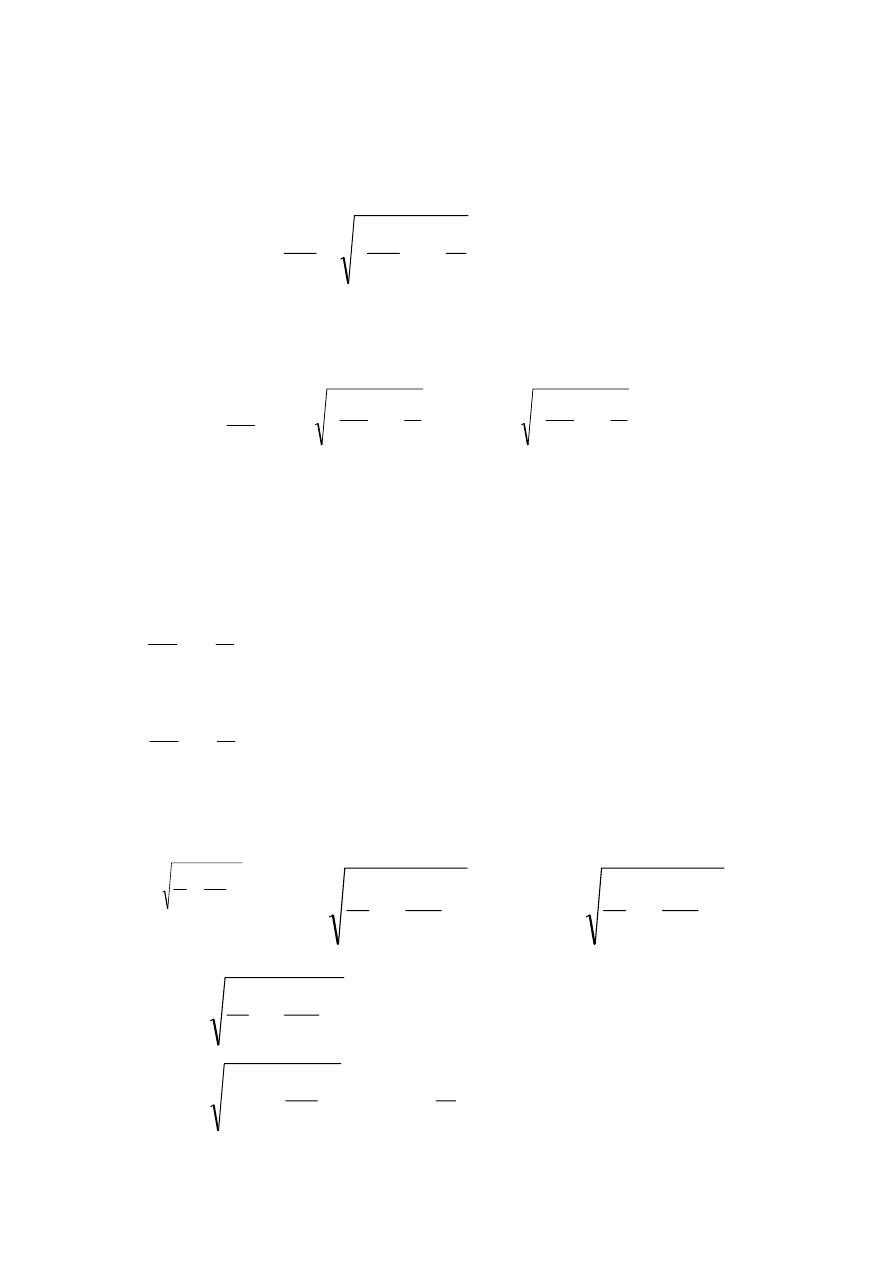
są pierwiastkami równania charakterystycznego, wyznaczanymi
według wzoru:
Uwzględniając te pierwiastki, rozwiązanie równania różniczkowego przyjmie
postać:
Funkcja przemieszczenia x zależy od wyrażenia występującego pod
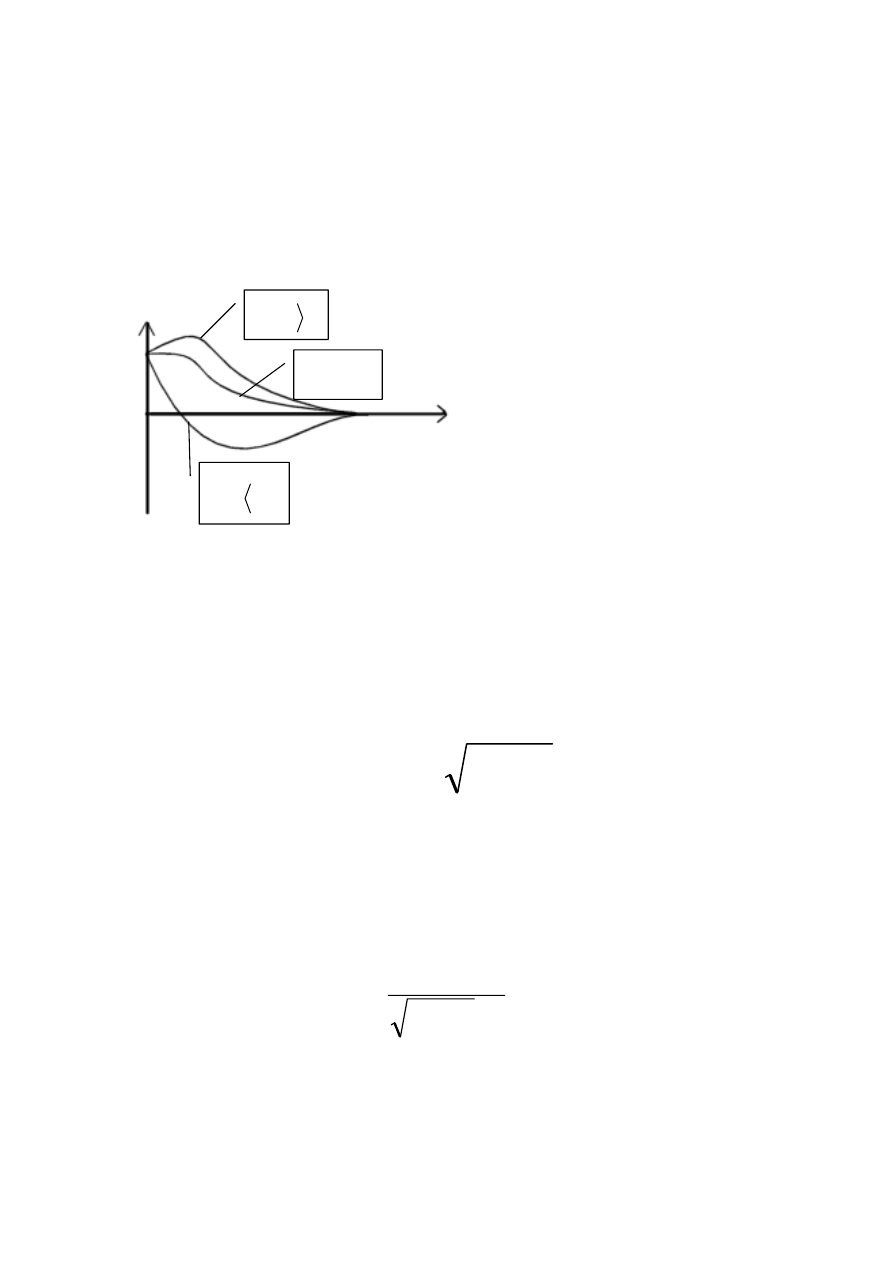
pierwiastkiem i rozróżniamy przypadki:
1.
W takim przypadku wykładniki mają wartości
dodatnie, zaś rozwiązanie x jest sumą funkcji
wykładniczych (nieokresowych), czyli nie ma drgań.
2.
W takim przypadku funkcja wykładnicza przyjmuje
następującą postać
i funkcję tę możemy zapisać
Częstość drgań swobodnych tłumionych
2
1
, s
s
0
2
2
1
2
2
/
1
>
−
±
−
=
s
m
k
m
c
m
c
s
+
=
⋅
−
−
⋅
−
−
t
m
k
m
c
t
m
k
m
c
m
c
Be
Ae
e
x
2
2
2
2
2
0
2
2
>
−
m
k
m
c
0
2
2
<
−
m
k
m
c
⋅
−
±
⋅
−
=
⋅
−
t
m
c
m
k
j
t
m
c
m
k
e
t
m
c
m
k
j
2
2
2
2
sin
2
cos
2
t
m
c
m
k
ω
=
−
2
2
2
2
2
2
n
t
n
m
k
m
c
ω
ω
ω
=
=
−
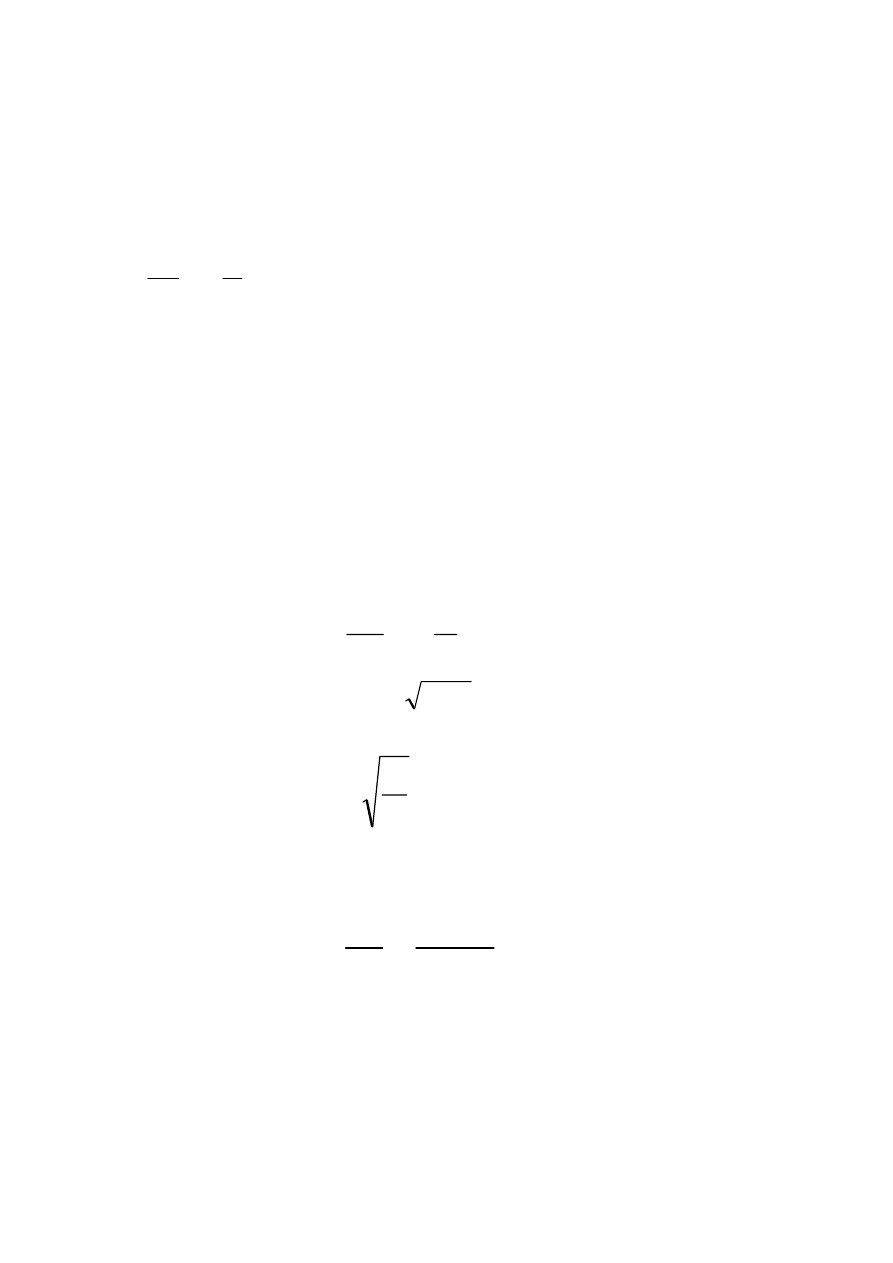
Układ fizyczny, w którym obserwujemy rozproszenie energii, wykonuje drgania
tłumione o częstości kołowej
ω
t
, opisanej podanym wzorem. Z zależności tej
wynika, że
częstość
ω
t
jest mniejsza od częstości
ω
n
.
W rzeczywistych układach drgających różnica między tymi częstościami jest
nieznaczna, dochodząca do 2–3%
3.
Przypadek ten określa stan graniczny pomiędzy
ruchem drgającym, czyli okresowym, a ruchem
nieokresowym.
Jest to warunek, przy którym zanikają drgania
mechaniczne.
Zwiększenie współczynnika tłumienia c od 0 aż do wartości spełniających
warunek 3 spowoduje zanik drgań.
Tłumienie spełniające ten warunek nosi nazwę: tłumienie krytyczne.
Jeżeli:
Bezwymiarowy współczynnik tłumienia
(dzeta)
w takim stanie są drgania mechaniczne
stan graniczny określony tłumieniem krytycznym
nie ma drgań w tym stanie
0
2
2
=
−
m
k
m
c
m
k
c
m
k
m
c
kr
kr
⋅
=
=
−
2
0
2
2
n
kr
n
m
c
m
k
ω
ω
2
=
=
n
kr
m
c
c
c
ω
ζ
2
=
=
1
1
1
>
=
<
ζ
ζ
ζ
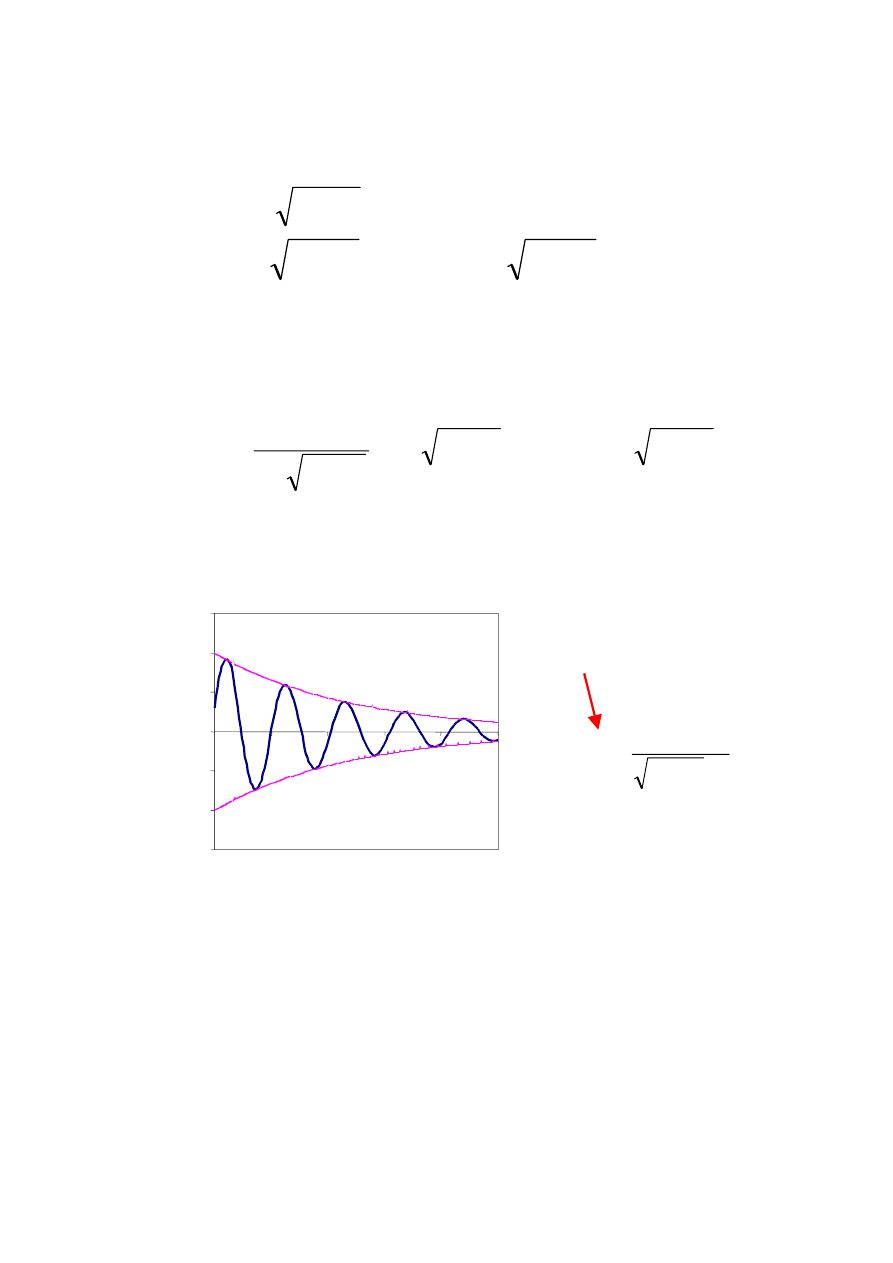
W przypadku ruchu oscylacyjnego, dla którego
ζ
< 1 rozwiązanie równania
różniczkowego możemy zapisać w postaci
(
)
=
+
⋅
−
=
−
ϕ
ω
ζ
ζω
t
Xe
x
n
t
n
2
1
sin
(
)
(
)
[
]
t
c
t
c
e
n
n
t
n
ω
ζ
ω
ζ
ζω
2
2
2
1
1
cos
1
sin
−
+
−
=
−
Po uwzględnieniu warunków początkowych, podobnie jak przy drganiach
nietłumionych, otrzymamy rozwiązanie w postaci:
Aby zaistniały drgania swobodne tłumione, przynajmniej jeden z warunków
początkowych musi być
≠0
Sinusoida gasnąca ograniczona jest obwiednią będącą funkcją wykładniczą.
(
)
(
)
−
+
−
⋅
−
+
=
−
t
x
t
x
x
e
x
n
n
n
n
t
n
ω
ζ
ω
ζ
ζ
ω
ζω
ζω
2
0
2
2
0
0
1
cos
1
sin
1
&
Wykres przedstawia sinusoidę
gasnącą, której okres drgań
(tłumionych) podany jest
wzorem i jest dłuższy od
okresu drgań nietłumionych.
n
T
ω
ζ
π
2
1
2
−
=
Efekt rozpraszania energii
„wydłuża” sinusoidę.
-0,15
-0,1
-0,05
0
0,05
0,1
0,15
0
2
4
6
8
10
t
n
Xe
ςω
−
−
t
n
Xe
ςω
−
ϕ
sin
0
X
x =
t
Ruch przy tłumieniu krytycznym
W takim przypadku rozwiązanie równania różniczkowego przy uwzględnieniu
warunków początkowych przyjmuje postać
Niezależnie od rodzajów ekstremów lokalnych (min. lub max.) obserwujemy
asymptotyczną (nieokresową) zbieżność przy t dążącym do
∞.
Logarytmiczny dekrement tłumienia
Rozważmy funkcję opisującą drgania tłumione
Rozważmy dwie wartości tej funkcji
gdzie:
Otrzymujemy wówczas
(
)
[
]
0
0
0
x
t
x
x
e
x
n
t
n
+
+
=
−
ω
ω
&
x
t
0
0
x&
0
0
=
x&
0
0
x&
Przebieg funkcji zależy od
warunku początkowego
narzuconego na prędkość
przy założeniu, że x
0
>0
0
x&
(
)
ϕ
ω
ζ
ζω
+
−
=
−
t
Xe
x
n
t
n
2
1
sin
( )
(
)
τ
+
=
=
t
x
x
t
x
x
2
1
n
ω
ζ
π
τ
2
1
2
−
=
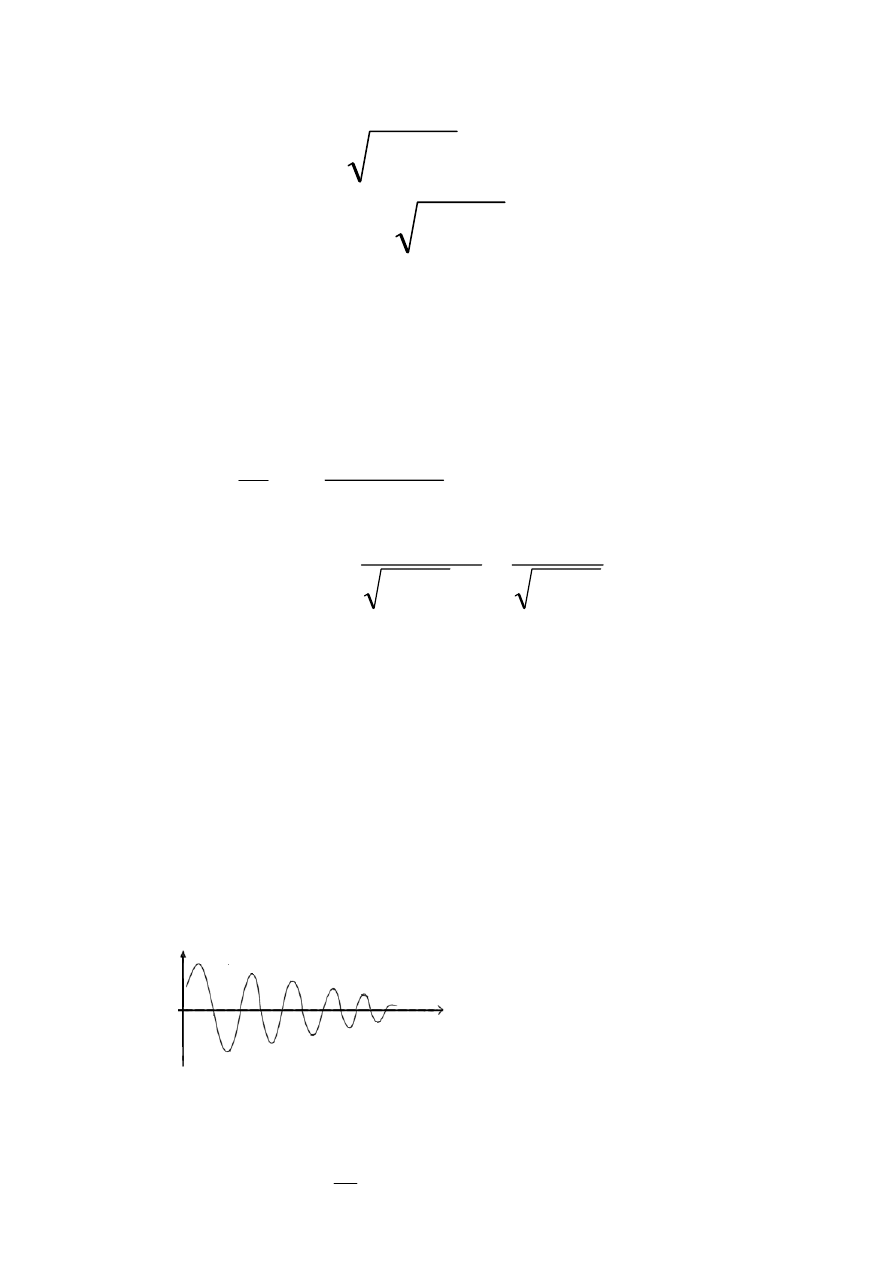
W szczególnym przypadku, czas t
1
określony dla pierwszego maksimum
krzywej gaśnięcia. Stanowi temu odpowiada przemieszczenie x
1
. Wówczas czas
odpowiadający drugiemu maximum wynosi t
1
+
τ
, zaś odpowiednia amplituda
wynosi x
2
. Obliczamy następujące wyrażenie
Dla małych
ζ
⇒
δ
≅ 2
π
ζ
Współczynnik
δ
(delta) oznacza logarytmiczny dekrement tłumienia i mierzy
szybkość zanikania drgań swobodnych tłumionych. W przypadku niewielkich
tłumień jest on proporcjonalny do bezwymiarowego współczynnika
ζ
. Celowość
wprowadzenia współczynnika
δ
uzasadnia łatwy sposób jego wyznaczenia na
podstawie obserwacji sinusoidy gasnącej. Znając współczynnik
δ
możemy
wyznaczyć współczynnik
ζ
, który określa rozproszenie energii w układzie.
Identyfikacja współczynnika tłumienia w układzie drgającym realizowana w
następujących etapach:
I. Wzbudzenie drgań tłumionych i obserwacja krzywej gaśnięcia
II. Wyznaczenie amplitud w maksimach lokalnych x
1
, x
2
III. Obliczenie współczynnika
(
)
(
)
[
]
ϕ
τ
ω
ζ
ϕ
ω
ζ
τ
ζω
ζω
+
+
−
=
+
−
=
+
−
−
1
2
)
(
2
1
2
1
1
sin
1
sin
1
1
t
Xe
x
t
Xe
x
n
t
n
t
n
n
(
)
2
2
2
1
1
2
1
2
ln
ln
ln
1
1
ζ
πζ
ω
ζ
π
ζω
τ
ζω
δ
τ
ζω
τ
ζω
ζω
−
=
−
=
=
=
=
=
+
−
−
n
n
n
t
t
n
n
n
e
Xe
Xe
x
x
2
1
ln
x
x
=
δ
0
=
∂
∂
+
∂
∂
+
∂
∂
−
∂
∂
x
U
x
D
x
T
x
T
dt
d
&
&
IV. Określenie współczynnika
V. Wyznaczenie współczynnika tłumienia
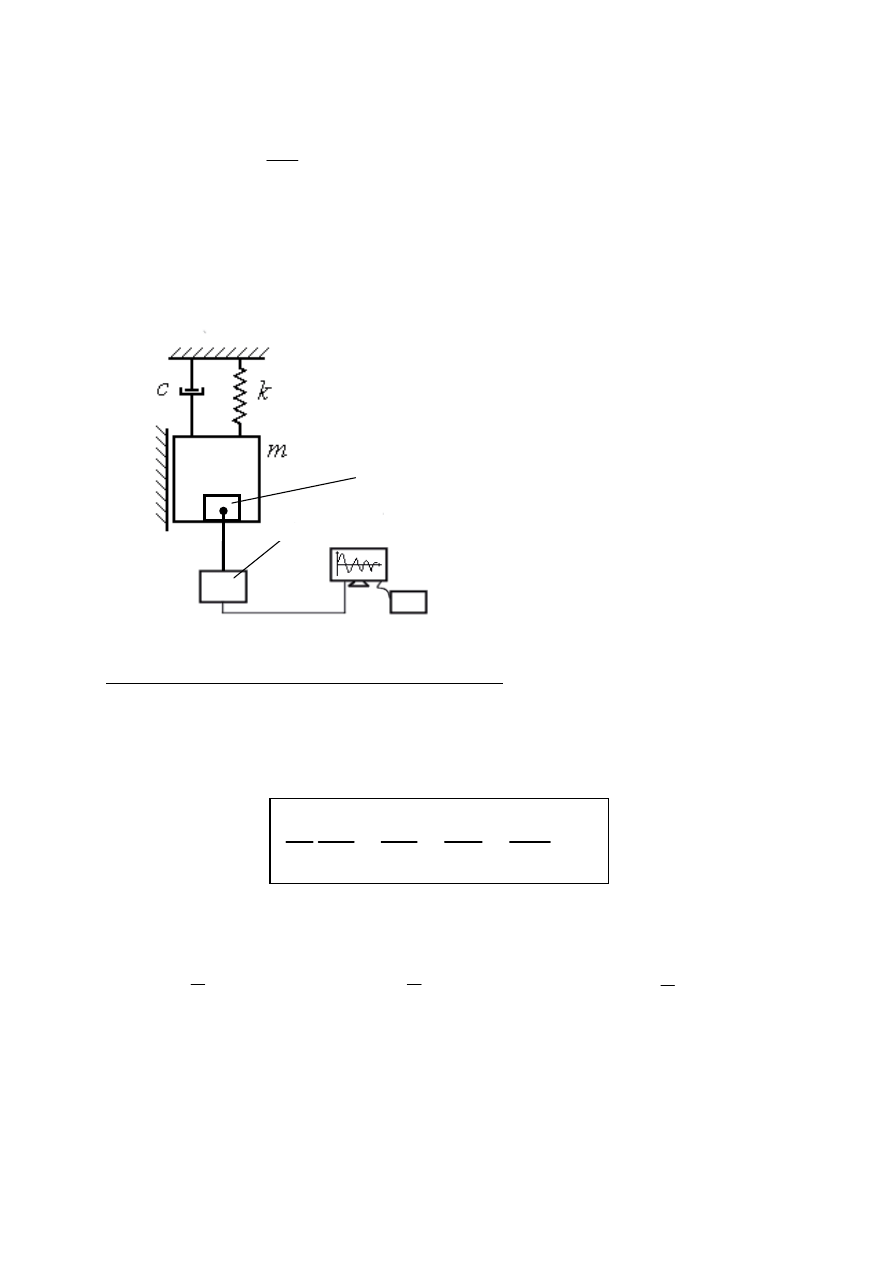
Realizacja eksperymentalna identyfikacji tłumienia w układzie
Drgania swobodne tłumione w ruchu zależnym
• Nie jest spełniona zasada zachowania energii mechanicznej
• Dla ruchu drgającego wzdłuż współrzędnej uogólnionej x stosujemy
równanie Lagrange’a II rodzaju:
Energia kinetyczna:
Funkcja rozproszenia Energia
potencjalna:
energii
(dyssypacji):
2
2
1
x
m
T
&
=
2
2
1
x
c
D
&
=
2
2
1
kx
U
=
W rezultacie, otrzymujemy równanie dynamiki układu zredukowanego:
π
δ
ζ
2
=
n
kr
m
c
c
ω
ζ
ζ
2
=
⋅
=
,
0
=
+
+
kx
x
c
x
m
&
&&
( )
( )
=
=
0
0
0
0
x
x
x
x
&
&
WARUNKI
POCZĄTKOWE
c
k
m
Komputer z kartą pomiarową
Czujnik bezwładnościowy – piezoelektryczny
(mierzy przyśpieszenia masy drgającej) do 20 kHz
Idea:
- uderzenie młotkiem testowym (zadany
warunek początkowy)
- obserwacja drgań na ekranie komputera
W rezultacie:
δ
i
różne dla i =1,…,k
Wzmacniacz ładunku
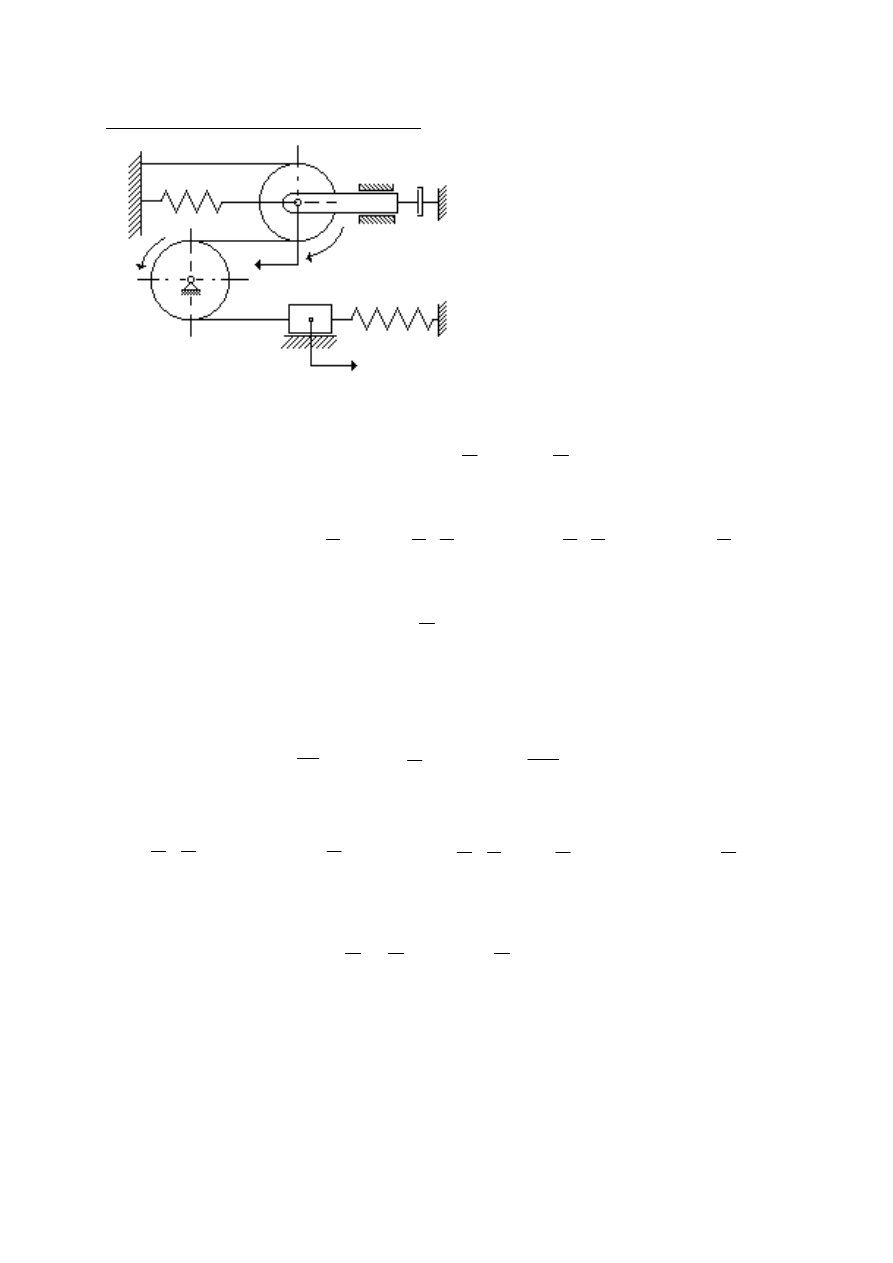
Układ drgający o 1 stopniu swobody:
Dane:
m
1
=2 kg
r
1
=0.05 m
m
2
=1.5 kg
r
2
=0.1 m
m
3
=3 kg
k
1
=1
×10
4
N/m
k
2
=2
×10
4
N/m
c
1
=100 Ns/m
Energia potencjalna:
2
2
2
1
1
2
1
2
1
x
k
x
k
U
+
=
Energia kinetyczna:
2
3
2
2
2
2
2
2
1
2
1
1
2
1
1
2
1
2
1
2
1
2
1
2
1
2
1
x
m
r
m
r
m
x
m
T
&
&
&
&
+
⋅
⋅
+
⋅
⋅
+
=
ϕ
ϕ
Funkcja rozproszenia energii:
2
1
1
2
1
x
c
D
&
=
x – współrzędna uogólniona
Równania więzów:
2
2
r
x
=
ϕ
2
1
x
x
=
1
1
2r
x
=
ϕ
2
2
2
1
2
1
4
1
2
1
kx
x
k
k
k
U
=
+
=
43
42
1
2
2
3
2
1
2
1
2
1
8
3
2
1
x
m
x
m
m
m
m
T
&
&
4
4
4
3
4
4
4
2
1
=
+
+
=
2
2
1
2
1
4
1
2
1
x
c
x
c
c
D
&
&
3
2
1
=
⋅
=
( )
( )
m/s
1
0
m
1
.
0
0
=
=
x
x
&
m
1
, r
1
m
2
, r
2
m
3
k
1
k
2
ϕ
1
ϕ
2
c
1
x
1
x
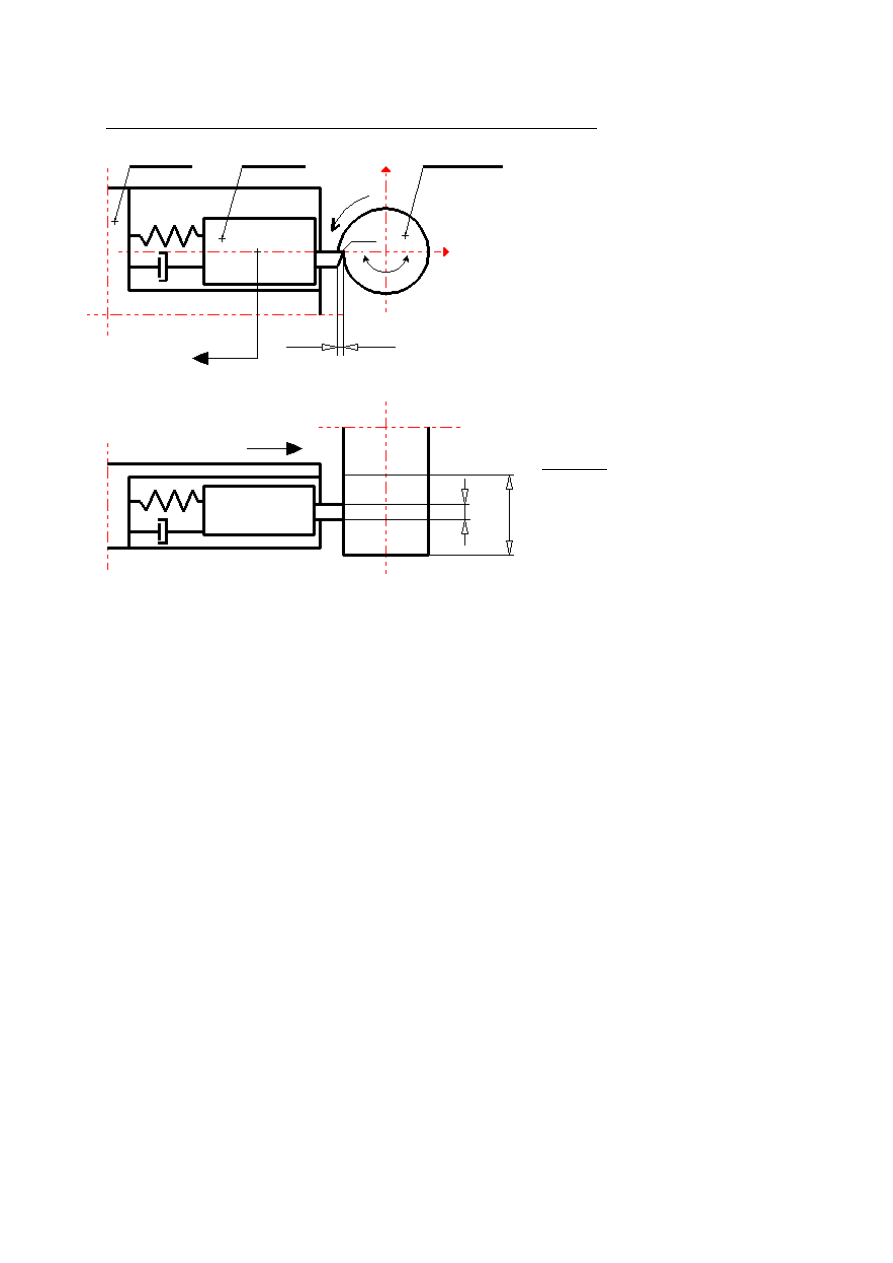
Drgania imaka nożowego podczas toczenia ortogonalnego
Masa imaka: m=24 kg
Sztywność zamocowania
imaka:
k
1
=1.5
×10
7
N/m
Tłumienie zamocowania
imaka:
c=1500 Ns/m
Opór
właściwy
skrawania:
k
s
=4
×10
8
N/m
2
Szerokość
skrawania:
b=2.8 mm
Zadana
grubość warstwy
skrawanej:
h
D
=0.2 mm
Uwaga:
k
2
=b k
s
jest
dodatkową sztywnością
w
układzie
Na imak oddziałuje zmienna w czasie siła skrawania:
(
)
x
h
b
k
F
D
s
s
−
=
Równanie dynamiki przyjmie postać:
s
F
x
k
x
c
x
m
=
+
+
1
&
&&
,
a po przekształceniu oraz pominięciu po prawej stronie stałej składowej:
D
s
s
bh
k
F
=
– postać:
{
0
2
1
=
+
+
+
x
k
k
bk
k
x
c
x
m
s
43
42
1
&
&&
Jest to równanie drgań swobodnych tłumionych układu o jednym stopniu
swobody.
x
c
ϕ
k
s
h
D
≡ f
b
f
l
d
k
1
n
0
m
Podstawa
imaka
Imak
nożowy
Przedmiot
obrabiany
x
2
x
1