1
I. KINEMATYKA
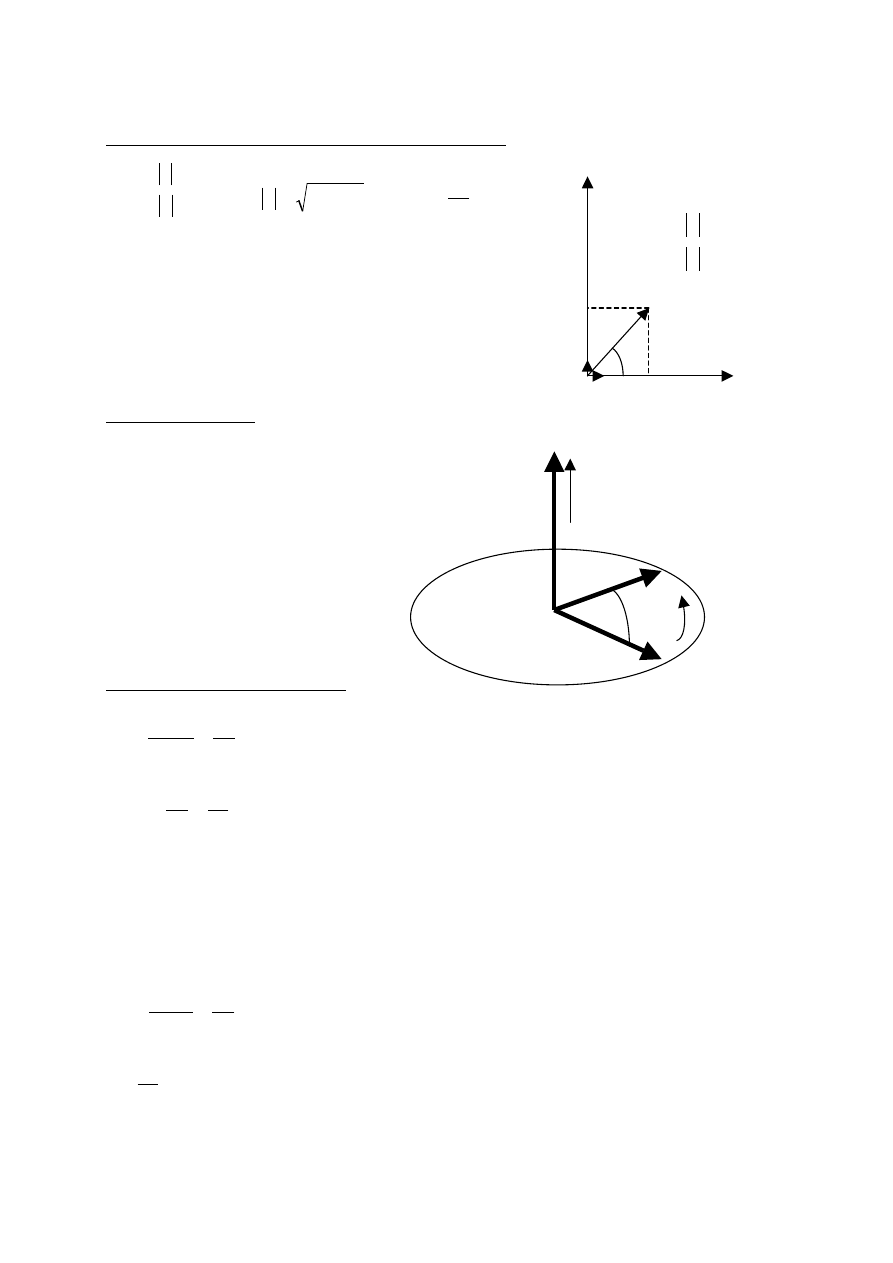
Składanie i rozkładanie wektorów. Metoda analityczna.
Mnożenie wektorów
Iloczyn k·a jest nowym wektorem,
Iloczyn skalarny
Iloczyn wektorowy
ϕ
sin
b
a
b
a
c
⋅
=
×
=
r
r
r
a
b
b
a
r
r
r
r
×
−
=
×
Kinematyka punktu materialnego
Prędkość średnia v
śr
t
x
t
t
x
x
v
sr
∆
∆
=
−
−
=
0
0
Prędkość chwilowa
dt
dx
t
x
v
t
=
∆
∆
=
→
∆
0
lim
Droga jako funkcja czasu
vt
x
x
t
gdy
t
t
v
x
x
wtedy
dt
v
dx
vdt
dx
x
x
t
t
+
=
=
−
=
−
=
=
∫
∫
0
0
0
0
0
)
(
0
0
Ruchu zmienny –
przyspieszenie średnie
t
v
t
t
v
v
a
sr
∆
∆
=
−
−
=
0
0
Znając przyspieszenie
a = a(t), można znaleźć prędkość tego ruchu ze związku:
at
v
v
wtedy
t
gdy
t
t
a
v
v
adt
v
dt
dv
a
+
=
=
−
=
−
=
⇒
=
0
0
0
0
0
)
(
,
ϕ
ϕ
sin
cos
a
a
a
a
y
x
r
r
=
=
x
ϕ
y
a
r
ϕ
ϕ
sin
cos
a
a
a
a
y
x
r
r
=
=
j
r
i
r
x
a
y
a
(
)
y
x
y
x
b
j
b
i
b
a
j
a
i
a
r
r
r
r
r
r
+
=
+
=
y
y
y
x
x
x
b
a
c
b
a
c
b
a
c
+
=
+
=
+
=
,
r
r
r
'
a
k
a
a
k
r
r
r
=
=
y
y
x
x
b
a
b
a
ab
b
a
+
=
=
⋅
ϕ
cos
r
r
ϕ
kierunek
palców
kierunek
kciuka
b
r
a
r
c
r
x
y
y
x
a
a
tg
a
a
a
=
+
=
ϕ
,
2
2
r
2
Prędkość w ruchu jednostajnie zmiennym jest liniowo zależna od czasu
Droga w ruchu jednostajnie przyspieszonym
2
2
)
(
2
0
0
2
0
0
0
0
0
0
0
0
at
t
v
x
x
czyli
at
t
v
x
x
dt
at
dt
v
dx
dt
at
v
dx
at
v
v
i
vdt
dx
t
t
x
x
+
+
=
+
=
−
+
=
⇒
+
=
+
=
=
∫
∫
∫
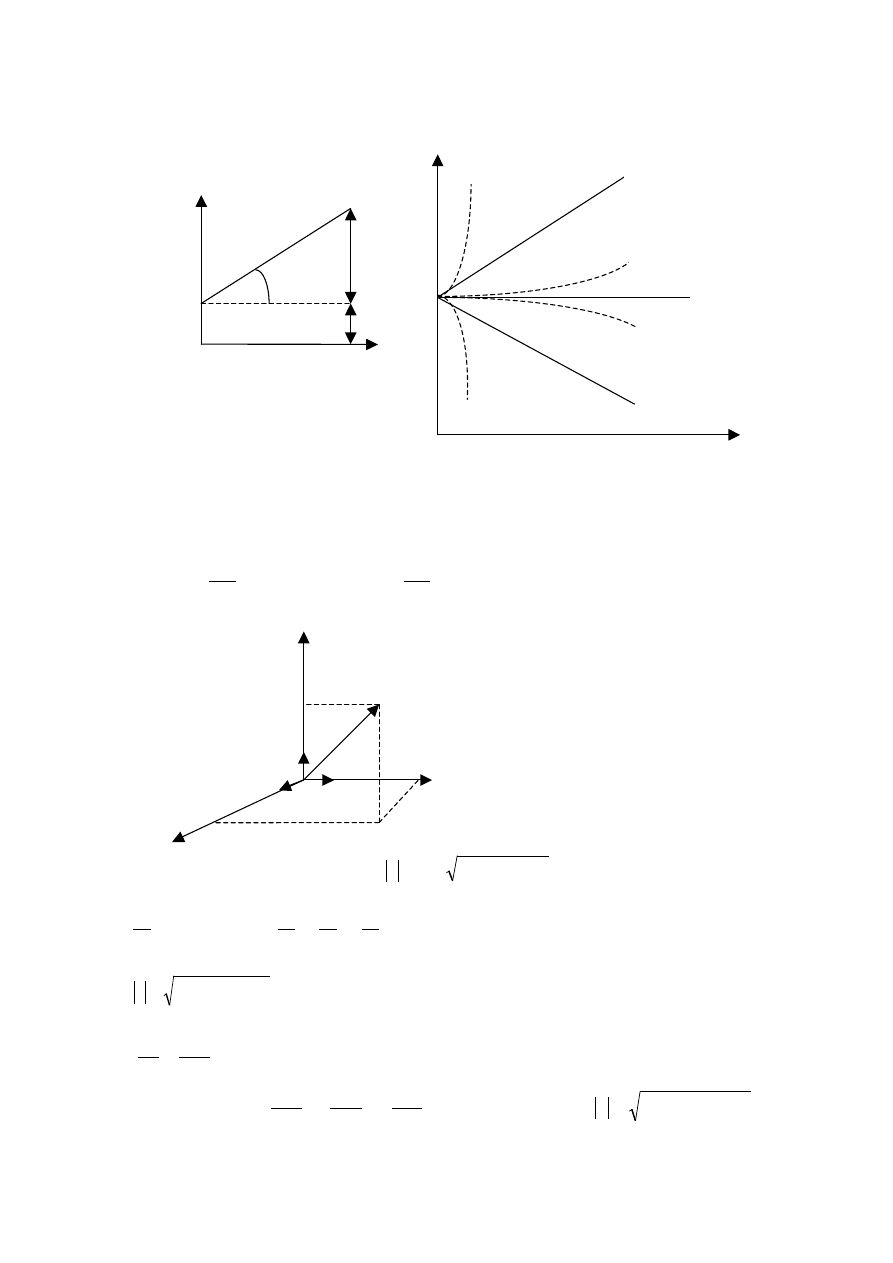
Układ trójwymiarowy – wektor wodzący
r punktu przestrzeni
2
2
2
z
y
x
r
r
czym
przy
k
z
j
y
i
x
r
+
+
=
=
+
+
=
r
r
r
r
r
1. Prędkość poruszającego się punktu jest wtedy zdefiniowana wzorem:
k
dt
dz
j
dt
dy
i
dt
dx
k
v
j
v
i
v
dt
r
d
v
z
y
x
r
r
r
r
r
r
r
r
+
+
=
+
+
=
=
a
bezwzględna wartość prędkości wynosi
2
2
2
z
y
x
v
v
v
v
v
+
+
=
=
r
2. Przyspieszenie poruszającego się punktu jest definiowane wzorem:
2
2
2
2
2
2
2
2
2
2
2
log
z
y
x
z
y
x
a
a
a
a
a
icznie
ana
k
dt
z
d
j
dt
y
d
i
dt
x
d
k
a
j
a
i
a
a
dt
r
d
dt
v
d
a
+
+
=
=
+
+
=
+
+
=
=
=
r
r
r
r
r
r
r
r
r
r
r
3. W ruchu prostoliniowym – prędkość i przyspieszenie:
v
α
v
t
at
v
0
v
0
ruch jednostajny
ruch jednostajnie opóź.
a=const
ruch opóź. |a| rośnie
ruch przysp. |a| maleje
ruch przysp. |a| rośnie
ruch jednostajnie przysp.
a=const
ruch opóż. |a| maleje
tg
α
= a
t
z
r
x
y
k
i
j
gdzie
i,j,k – są wektorami
jednostkowymi
(wersorami)
odpowiednich osi
współrzędnych.

3
2
2
,
dt
s
d
dt
dv
a
dt
ds
v
=
=
=
gdzie s - oznacza odcinek przebytej drogi
a) ruch prostoliniowy jednostajny
,
0
0
=
=
+
=
=
⇒
=
⇒
=
=
∫
dt
dv
a
i
s
vt
vdt
s
vdt
s
dt
ds
v
const
v
gdzie s
0
– jest odcinkiem drogi przebytym do chwili początkowej t=0
b) ruch prostoliniowy jednostajnie przyspieszony (a>0) i opóźniony (a<0) –
charakteryzuje się stałym przyspieszeniem, mamy więc
∫
∫
∫
+
+
=
+
=
=
+
=
=
=
0
0
2
0
0
2
1
)
(
s
t
v
at
dt
v
at
vdt
s
v
at
adt
v
const
a
gdzie v
0
– oznacza tzw. prędkość początkową tj. wartość prędkości w chwili początkowej t=0
Szczególne przypadki ruchu jednostajnie przyspieszonego:
1. SPADEK SWOBODNY
2
0
2
1
0
gt
s
gt
v
v
g
a
=
=
=
=
2. RZUT PIONOWY W DÓŁ
2
0
0
0
2
1
0
gt
t
v
s
gt
v
v
v
g
a
+
=
+
=
≠
=
3. RZUT PIONOWY W GÓRĘ
2
0
0
0
2
1
0
gt
t
v
s
gt
v
v
v
g
a
−
=
−
=
≠
−
=
4. RZUT POZIOMY
g
h
v
x
h
y
gdy
g
y
v
x
gt
y
t
v
x
2
2
2
1
0
0
2
0
=
=
=
⇒
=
=
5. RZUT UKOŚNY
g
v
x
y
gdy
gt
t
v
y
t
v
x
v
gt
v
gt
dt
dy
v
v
v
dt
dx
v
g
dt
dv
a
dt
dv
a
y
y
ox
x
y
y
x
x
α
α
α
α
α
2
sin
0
2
1
sin
cos
sin
cos
0
2
0
2
0
0
0
0
0
=
=
−
=
=
+
−
=
+
−
=
=
=
=
=
−
=
=
=
=
v
0
x
α
y
parabola
α
cos
0
v
v
ox
=
oy
v
v
=
α
sin
0
4
II. DYNAMIKA
Zasady dynamiki Newtona
I zasada - PRAWO BEZWŁADNOŚCI
II zasada
III zasada – PRAWO AKCJI I REAKCJI
Masa ciała
Pęd
II zasada dynamiki
:
a
m
dt
dm
v
dt
v
d
m
dt
dm
v
v
m
dt
d
F
const
m
gdy
a
m
dt
v
d
m
v
m
dt
d
dt
p
d
F
const
m
gdy
dt
p
d
F
r
r
r
r
r
v
r
v
r
r
r
r
r
+
=
+
=
=
≠
=
=
=
=
=
=
)
(
)
(
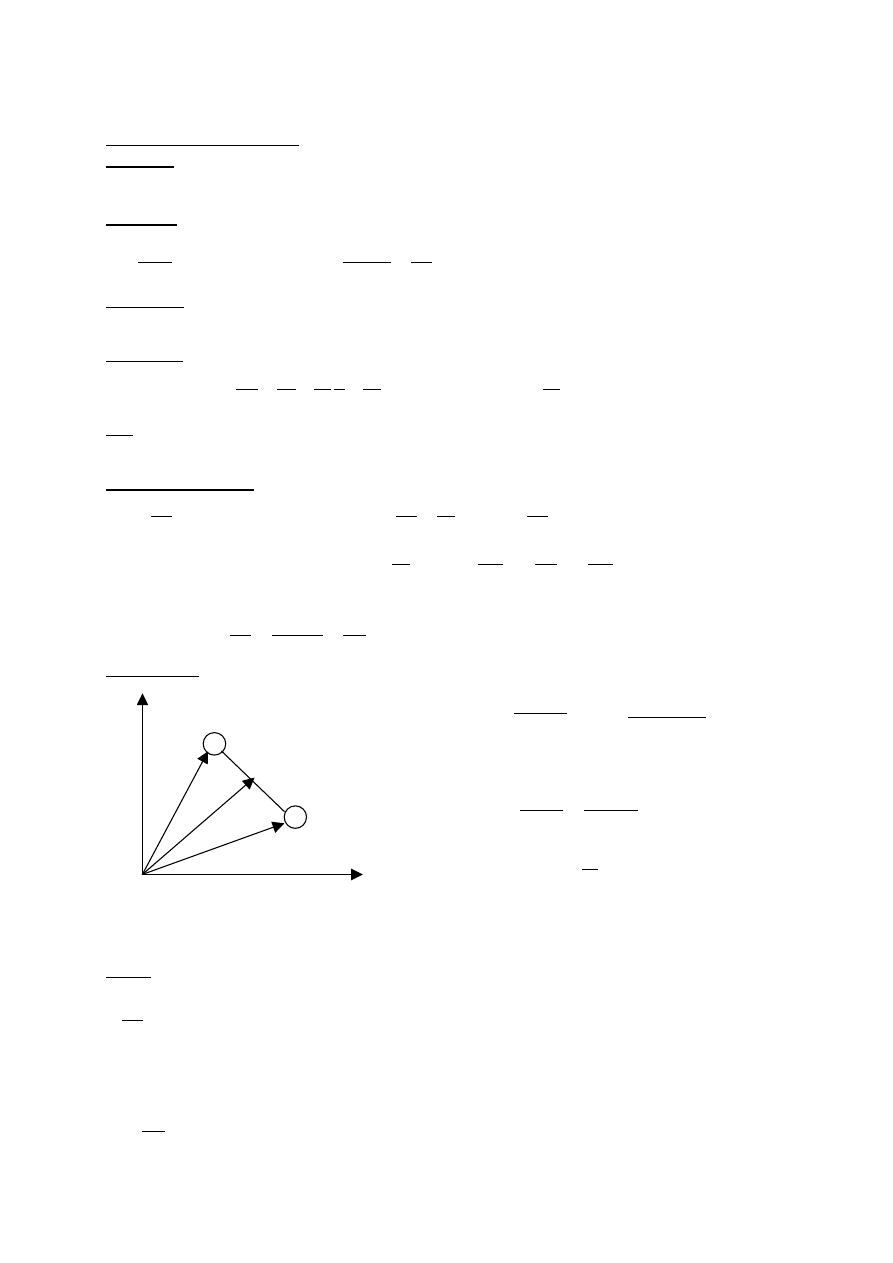
Zasada zachowania pędu
Ś
rodek masy
Prawo ruchu środka masy
Popęd
Prawo pędu i popędu
∑
∑
∑
=
=
=
=
i
i
i
i
v
m
p
P
f
F
gdy
dt
P
d
F
r
r
r
r
r
r
r
,
m
2
m
1
r
2
r
1
R
x
y
∑
∑
=
i
i
i
i
i
m
r
m
R
r
r
dV
dm
m
V
gdzie
dV
dV
r
dm
dm
r
R
ρ
ρ
ρ
ρ
=
⇒
=
=
=
∫
∫
∫
∫
r
r
r
0
0
=
=
wyp
F
gdy
a
r
r
v
v
m
m
const
v
v
v
t
t
v
a
a
m
m
a
m
ma
0
0
0
0
0
0
0
0
=
⇒
=
=
=
=
⇒
=
v
m
p
r
r
=
∑
=
=
=
=
=
=
m
i
i
wyp
wyp
wyp
F
F
gdzie
dt
p
d
dt
v
m
d
a
m
F
czyli
m
F
a
1
)
(
r
r
r
r
r
r
r
r
B
A
F
F
r
r
−
=
2
1
2
2
1
1
m
m
r
m
r
m
R
+
+
=
zew
i
i
i
ś
rm
F
a
m
a
M
r
r
r
=
=
∑
const
P
wtedy
dt
P
d
dt
v
M
d
dt
v
d
M
a
M
F
zew
=
=
=
=
=
=
r
r
r
r
r
r
0
)
(
)
0
(
2
1
2
1
1
2
→
∆
=
Π
=
=
=
−
=
∆
∫
∫
t
const
F
dla
dt
F
p
d
p
p
p
t
t
p
p
r
r
r
r
r
r
t
F
p
∆
=
∆
=
Π
r
r
r
dt
F
p
d
F
dt
p
d
r
r
r
r
=
⇒
=
t
F
p
t
const
F
dla
dt
F
p
d
p
p
p
t
t
p
p
∆
=
∆
=
Π
→
∆
=
Π
=
=
=
−
=
∆
∫
∫
r
r
r
r
r
r
r
r
r
)
0
(
2
1
2
1
1
2
5
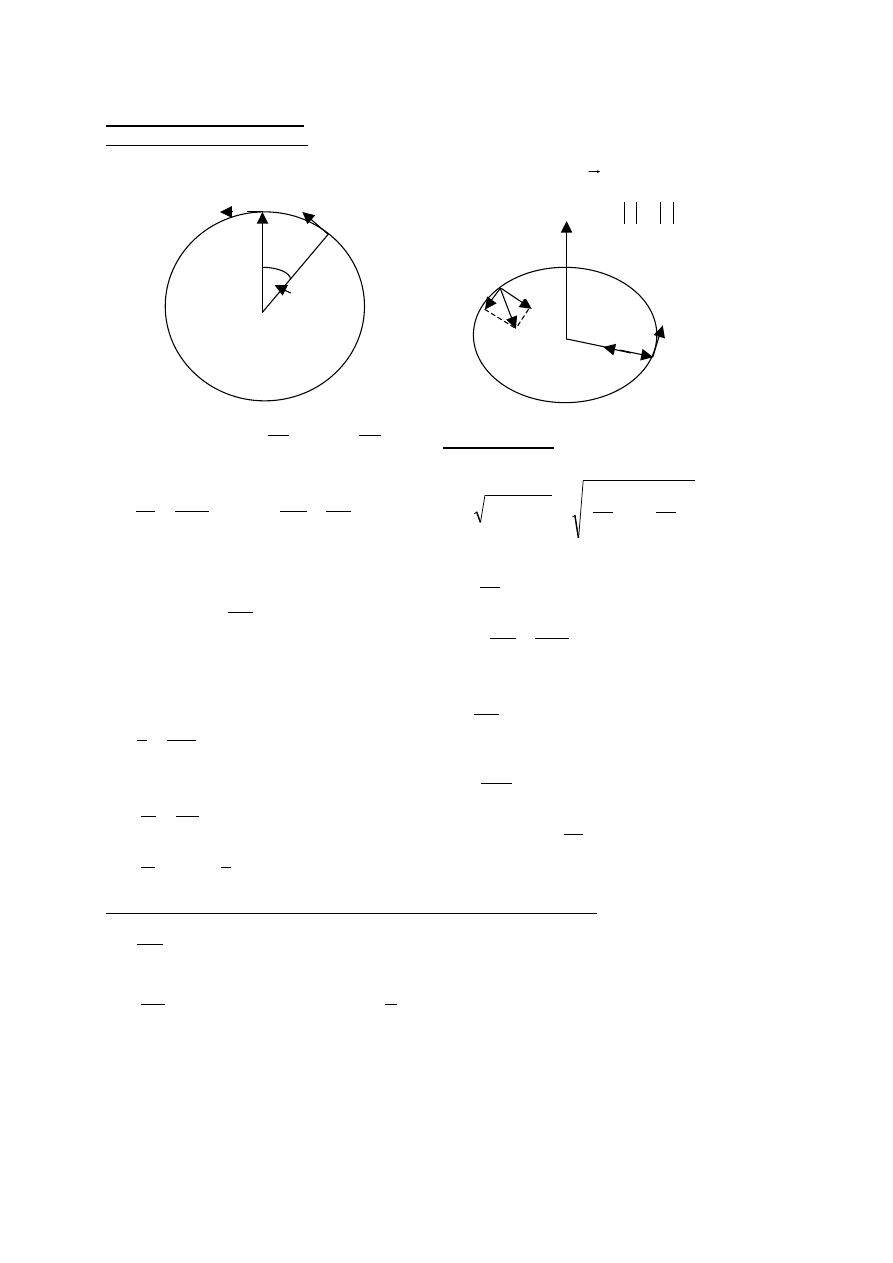
III. RUCH OBROTOWY
Ruch jednostajny po okręgu
wektorowej
notacji
w
r
v
r
v
dt
d
t
i
t
r
dt
ds
v
r
s
r
s
r
s
r
s
r
r
r
×
=
=
=
∆
∆
=
∆
∆
=
=
∆
=
∆
⇒
∆
=
∆
⇒
∆
=
∆
=
∆
ω
ω
α
α
ω
α
α
α
α
α
sin
∫
+
=
=
=
⇒
=
=
0
α
ω
ω
α
ω
α
α
ω
ω
t
dt
dt
d
dt
d
const
Ruch po okręgu -
ruch okresowy
=
=
=
=
=
=
=
=
=
=
s
Hz
T
f
bo
n
T
t
oraz
r
v
r
s
bo
T
r
t
s
v
1
1
2
2
2
2
2
π
α
π
π
α
ω
ω
π
π
Ruch jednostajnie przyspieszony (
ε
>0) i opóźnionym (
ε
<0),
ε
=const
(
)
∫
∫
∫
+
+
=
+
=
=
⇒
=
+
=
=
=
⇒
=
0
0
2
0
0
2
1
α
ω
ε
ω
ε
ω
α
α
ω
ω
ε
ε
ω
ε
ω
ω
ε
t
t
dt
t
dt
dt
d
t
dt
dt
d
dt
d
r
∆α
∆
s
v
v
const
v
const
v
≠
=
r
a
t
ω
ω
ω
ω
r
v
a
d
a
d
a
const
v
i
r
bo
const
=
=
r
r
ω
Przyspieszenie
d
t
a
a
a
r
r
r
+
=
2
2
2
2
2
+
=
+
=
r
v
dt
dv
a
a
a
d
t
Przyspieszenie styczne
dt
d
gdzie
r
dt
d
dt
d
r
a
r
v
ale
dt
dv
a
t
t
ω
ε
ε
α
ω
ω
=
=
=
=
=
=
2
2
Przyspieszenie dośrodkowe
r
v
v
r
a
dt
d
a
d
d
2
2
2
2
=
=
=
=
ω
ω
α
6
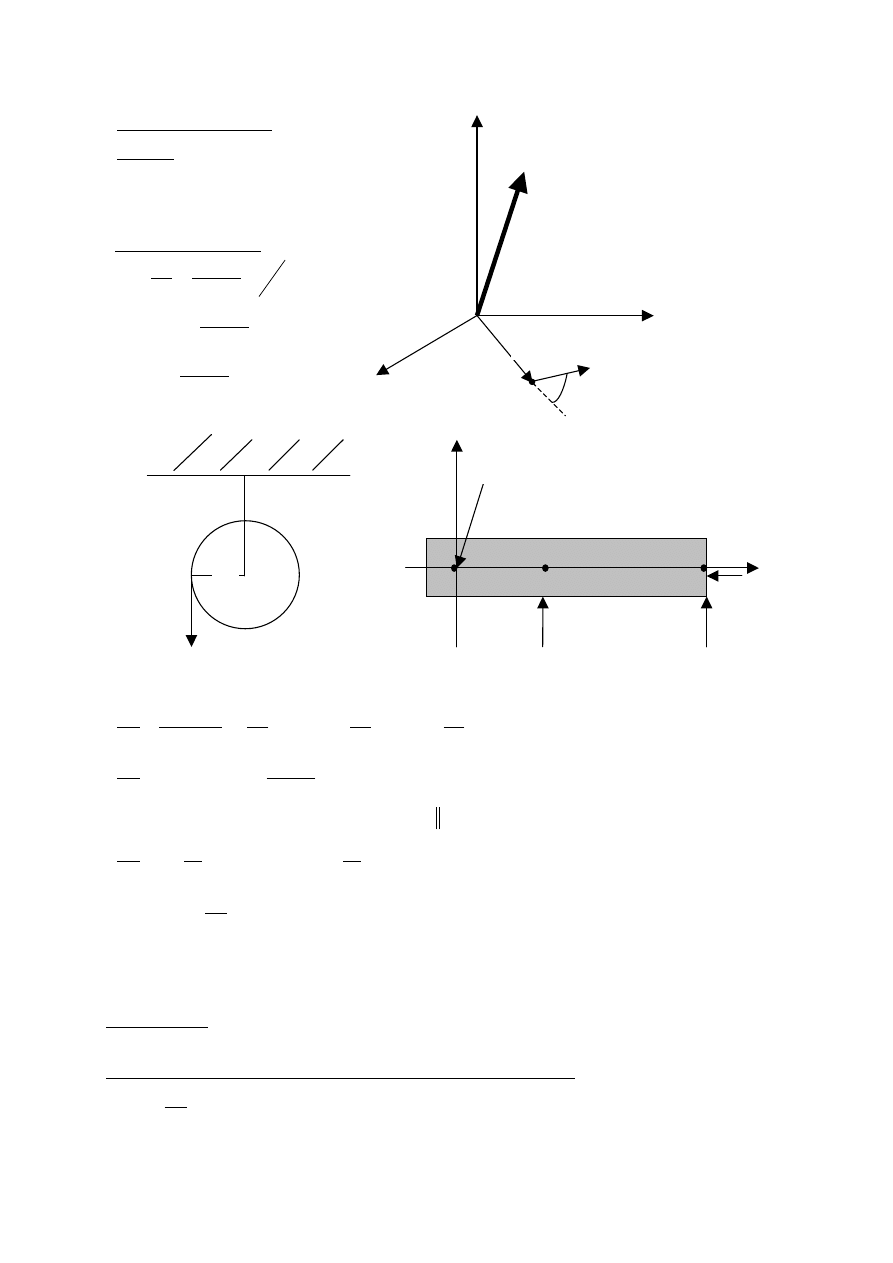
Ciało sztywne - ruch środka masy
a
M
F
zew
r
r
=
Równanie ruchu - II zasada dynamiki dla ruchu obrotowego ciała
dt
L
d
M
zew
r
r
=
F
1
F
r
A
0
B
F
2
oś obrotu
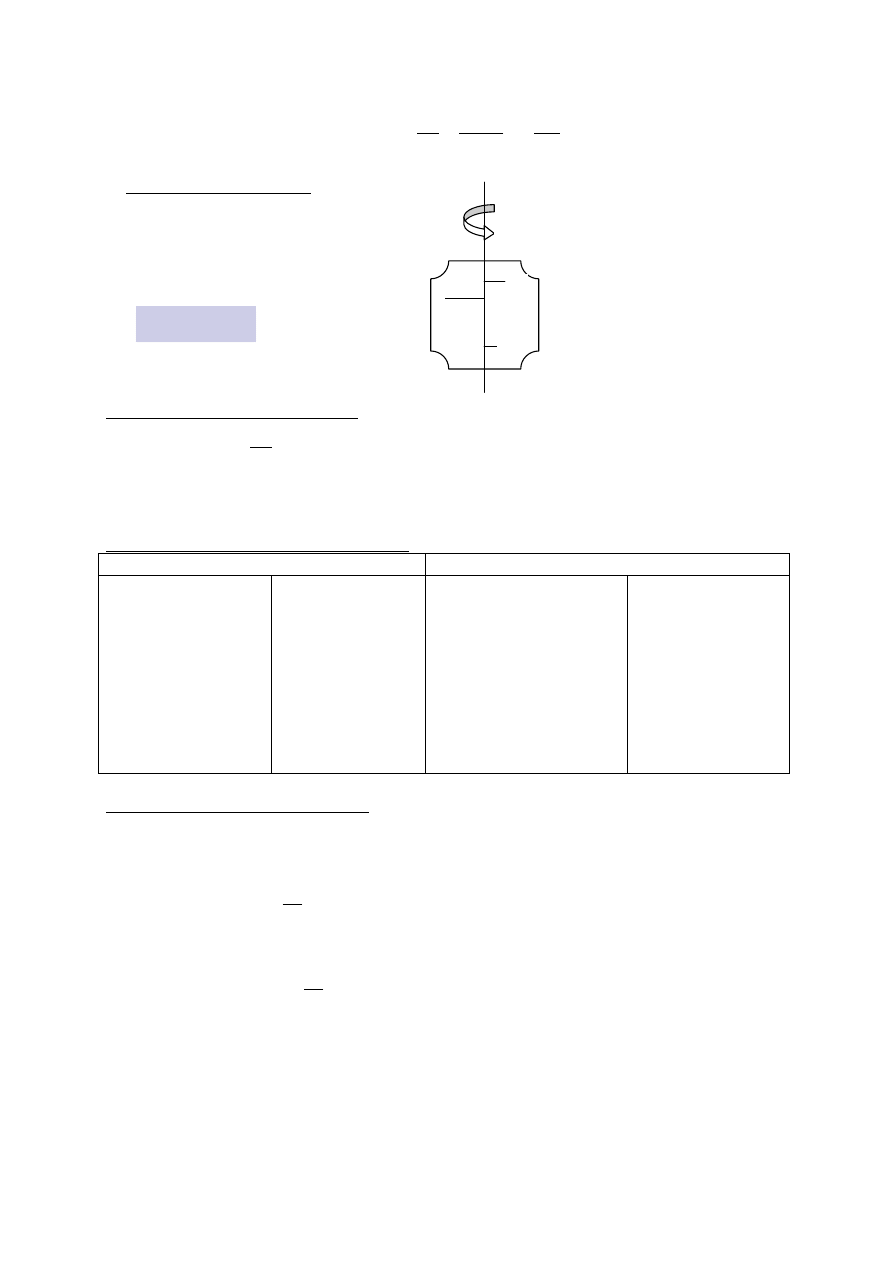
z
0
θ
m
r
p
x
y
L
Moment pędu cząstki
ω
r
r
I
L
=
θ
sin
,
rp
L
p
r
L
=
×
=
r
r
r
Różniczkując po dt równanie na moment pędu
p
r
L
r
r
r
×
=
dt
L
d
M
czyli
v
m
dt
d
r
M
i
v
m
dt
d
r
dt
L
d
v
v
v
v
v
v
bo
v
m
v
dt
v
m
d
r
v
m
v
dt
L
d
v
dt
r
d
ale
dt
p
d
r
p
dt
r
d
dt
p
r
d
dt
L
d
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
=
×
=
×
=
=
⋅
⋅
=
×
=
×
×
+
×
=
=
×
+
×
=
×
=
),
(
)
(
,
0
0
sin
,
0
)
(
)
)
(
(
)
(
),
(
)
(
)
(
0
F
r
M
r
r
r
×
=
θ
sin
rF
M
=
Moment siły cząstki
F
r
dt
v
m
d
r
M
dt
v
m
d
r
F
r
r
dt
v
m
d
dt
p
d
F
r
r
r
r
r
r
r
r
r
r
r
r
r
×
=
×
=
×
=
×
×
=
=
)
(
,
)
(
,
)
(
7
ε
r
r
I
M
=
( )
ε
ω
ω
ε
r
r
r
r
r
r
r
I
dt
d
I
dt
I
d
dt
L
d
M
I
M
=
=
=
=
=
lub
Zasada zachowania momentu pędu
const
L
i
dt
L
d
wtedy
M
zew
=
=
=
r
r
r
0
0
Całkowity moment pędu układu izolowanego
const
v
m
r
p
r
L
i
i
i
i
i
i
=
×
=
×
=
∑
∑
r
r
r
r
r
Ruch prostoliniowy i obrotowy – analogie
RUCH PROSTOLINIOWY
RUCH OBROTOWY
Przemieszczenie
Prędkość
Przyspieszenie
Masa
Siła
Praca
Energia kinetyczna
Moc
Pęd
x
v = dx/dt
a = dv/dt
m
F = ma
W = ∫F dx
E
k
= ½mv
2
P = Fv
p = mv
Przemieszczenie kątowe
Predkość kątowa
Przyspieszenie kątowe
Moment bezwładności
Moment siły
Praca
Energia kinetyczna
Moc
Moment pędu
α
ω
= d
α
/dt
ε
= d
ω
/dt
I
M = I
ε
W = ∫M d
θ
E
k
= ½I
ω
2
P = M
ω
L = I
ω
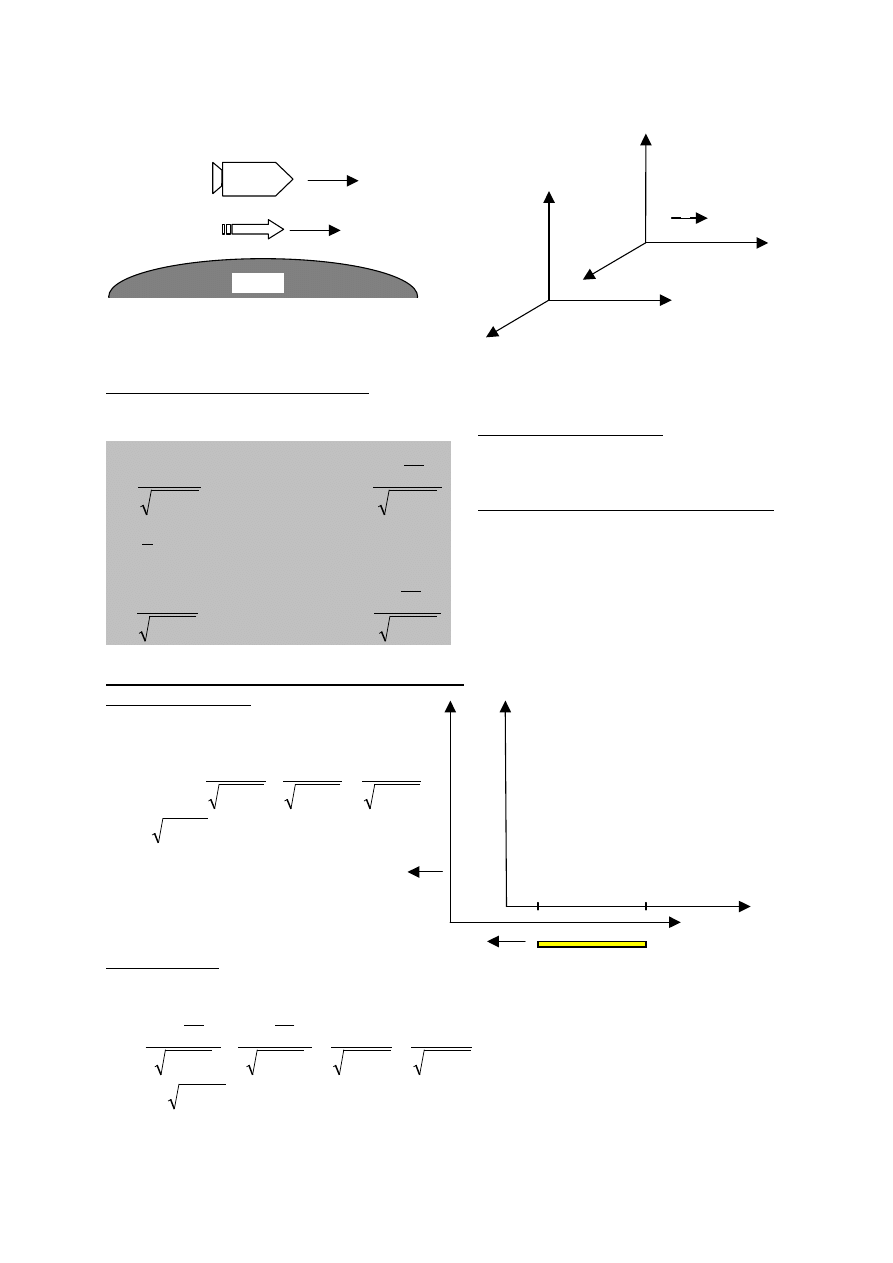
Siły bezwładności (lub siły pozorne) - układ nieinercjalny
m
a = F + F
B
F* = - ma*
F* = F
od
+
F
c
gdzie F
od
= mω
2
r = mv
2
/r
F
c
= 2m
ω
v
bo
F
c
prostopadła do
v i
ω
ω
ω
ω
przy czym
F
od
– siła odśrodkowa
F
c
– siła Coriolisa
ω
r
i
r
i
m
i
I – moment bezwładności
I =
ΣΣΣΣ
m
i
r
i
2
,
I = ∫∫∫∫r
2
dm = ∫∫∫∫
ρρρρ
r
2
dV, dm=
ρ
dV,
Twierdzenie Steinera
2
0
md
I
I
+
=
)
(
2
2
2
2
2
2
v
m
F
r
v
m
r
m
v
m
F
c
c
r
r
r
×
=
=
=
=
ω
ω
ω
r
v
bo
r
m
v
m
F
r
v
m
r
m
v
m
F
od
od
r
r
r
r
r
r
r
r
r
×
=
×
×
=
×
=
=
=
=
ω
ω
ω
ω
ω
ω
)]
(
[
)
(
2
2
8
IV. KINEMATYKA I DYNAMIKA RELATYWISTYCZNA
Transformacja Galileusza i Lorentza
t
t
z
z
y
y
vt
x
x
=
=
=
+
=
'
,
'
,
'
,
'
Transformacja Galileusza
1
,
1
)
(
'
,
'
,
'
,
1
'
2
2
2
<
=
−
+
=
=
=
−
+
=
c
v
x
c
v
t
t
z
z
y
y
vt
x
x
β
β
β
Transformacja Lorentza czasoprzestrzeni
,
1
'
)
(
'
,
'
,
'
,
1
'
2
2
2
β
β
−
−
=
=
=
−
−
=
x
c
v
t
t
z
z
y
y
vt
x
x
Konsekwencje transformacji czasoprzestrzeni:
Kontrakcja długości (skrócenie Lorentza)
2
0
'
0
2
'
0
2
'
1
2
'
2
1
2
0
1
2
0
1
1
1
1
,
β
β
β
β
−
=
−
=
−
+
−
−
+
=
−
=
−
=
l
l
l
vt
x
vt
x
x
x
l
x
x
l
l
0
’
– długość poruszającego się pręta,
l
0
– długość pręta w spoczynku
Dylatacja czasu (wydłużenie)
2
'
2
2
1
2
2
2
1
2
2
2
'
1
'
2
1
2
1
1
1
1
)
(
1
)
(
'
'
,
β
β
β
β
β
−
∆
=
∆
−
∆
=
−
−
=
−
+
−
−
+
=
∆
−
=
∆
−
=
∆
t
t
t
t
t
x
c
v
t
x
c
v
t
t
t
t
t
t
t
t
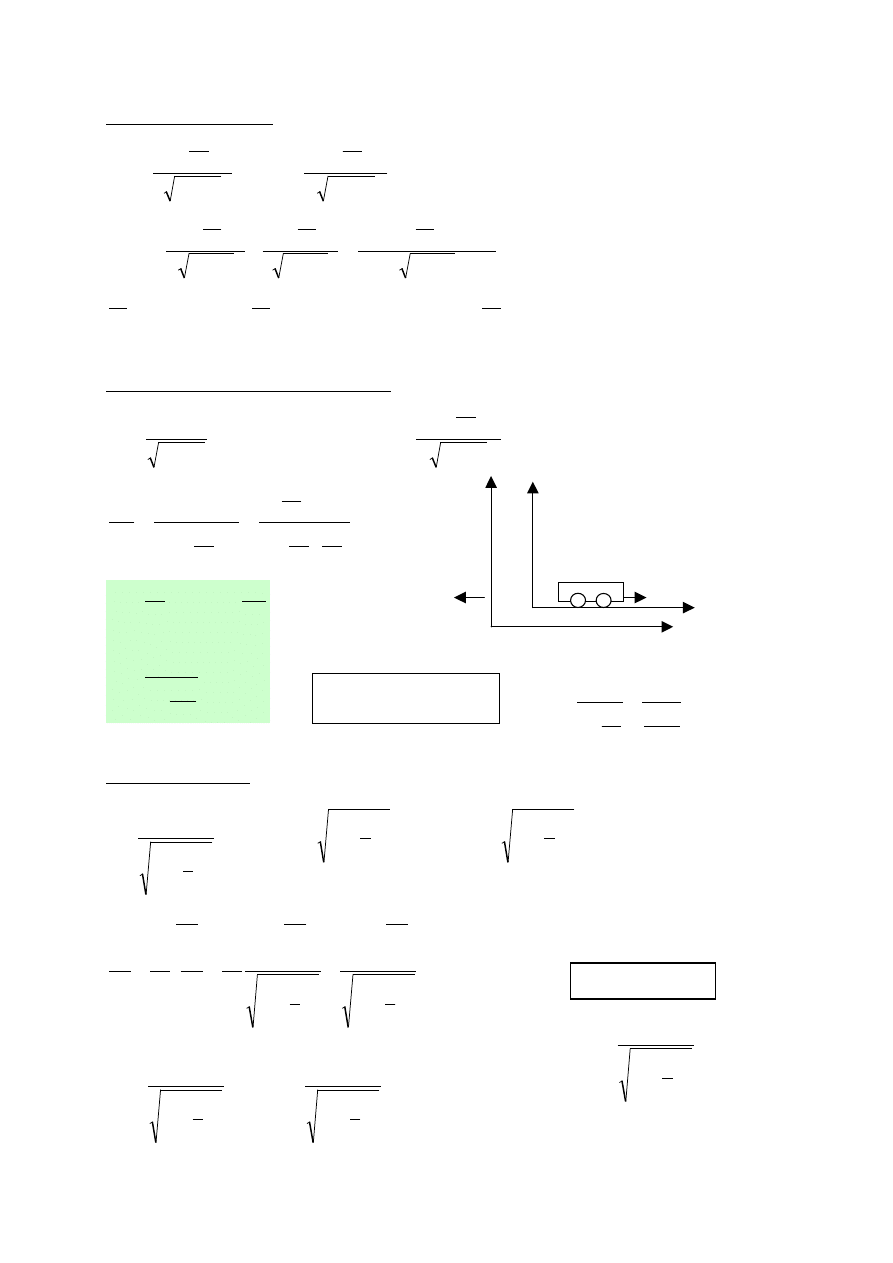
Pan Prim
Pan X
z’
y
z
x
x’
v
y’
pan
X widziany przez pana Prima
x
1
’
x
2
’
y’
y
v
x
2
x
1
Pan X
x
x’
A
Ziemia
v
imp
v
B
Pojazd kosmiczny
B
Impuls światła
9
Jednoczesność zdarzeń
2
2
2
2
'
2
2
1
2
1
1
1
)
(
1
)
(
'
β
β
−
+
=
−
+
=
∆
x
c
v
t
t
i
x
c
v
t
t
0
)
(
0
0
)
(
0
1
)
(
1
)
(
1
)
(
'
'
2
1
2
2
1
2
1
2
2
2
1
2
2
1
2
2
1
2
1
2
2
2
2
1
2
≠
−
≠
>
=
−
=
−
−
+
−
=
−
+
−
−
+
=
−
x
x
c
v
czyli
x
x
oraz
c
v
x
x
c
v
czyli
x
x
c
v
t
t
x
c
v
t
x
c
v
t
t
t
β
β
β
czyli t
1
=t
2
, ale t
1
’≠t
2
’
Dodawanie prędkości według Einsteina
,
1
)
(
'
,
'
,
'
,
1
'
2
2
2
β
β
−
+
=
=
=
−
+
=
dx
c
v
dt
dt
dz
dz
dy
dy
vdt
dx
dx
2
'
'
'
'
1
c
vu
v
u
u
dt
dx
u
i
dt
dx
u
x
x
x
x
x
+
+
=
=
=
Pęd relatywistyczny
Czas własny:
τ
τ
τ
τ
τ
τ
d
dz
m
p
d
dy
m
p
d
dx
m
p
c
v
dt
d
c
v
t
c
v
t
z
y
x
0
0
0
2
2
2
,
1
1
1
=
=
=
−
=
⇒
−
=
⇒
−
=
,....
1
,
1
1
1
1
2
0
2
0
2
2
−
=
−
=
−
=
−
=
⋅
=
c
v
v
m
p
c
v
v
m
p
zatem
c
v
v
c
v
dt
dx
d
dt
dt
dx
d
dx
y
y
x
x
x
τ
τ
2
0
1
−
=
c
v
v
m
p
r
v
y
u
x
x
v
x’
y‘
Wzór Einsteina na
dodawanie prędkości
,
)
)(
(
1
)
(
2
2
'
'
dt
dx
c
v
v
dt
dx
dx
c
v
dt
vdt
dx
dt
dx
+
+
=
+
+
=
Ogólnie pęd
Dla
u
x
= c
c
c
v
c
v
c
c
vc
v
c
u
x
=
+
+
=
+
+
=
2
'
1
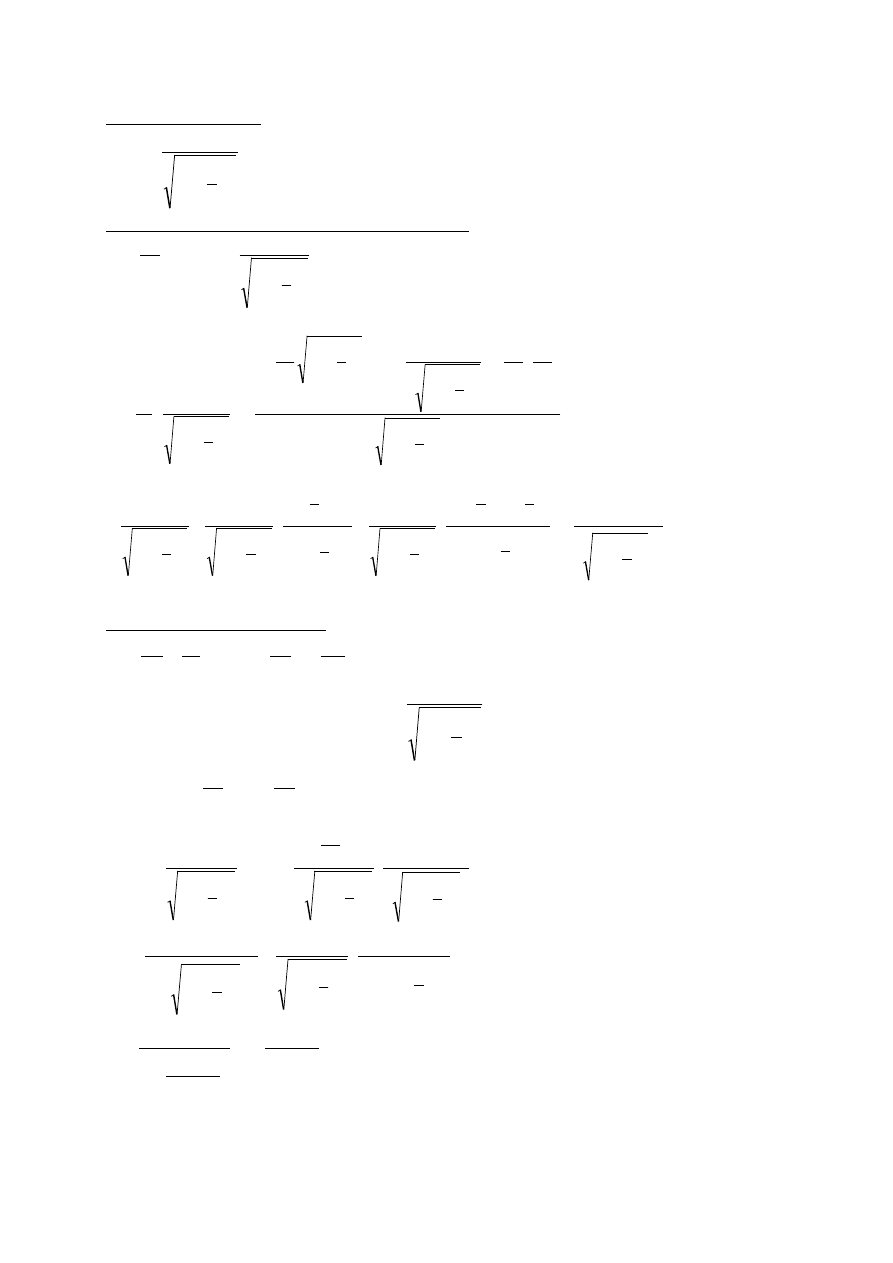
10
Masa relatywistyczna
2
0
1
)
(
−
=
c
v
m
v
m
gdzie m
0
– masa spoczynkowa
Druga zasada dynamiki w postaci relatywistycznej
2
0
1
−
=
=
c
v
v
m
p
dt
p
d
F
r
r
r
r
3
2
0
2
2
2
2
0
2
2
2
0
2
0
2
2
2
0
2
0
2
0
1
1
1
1
1
1
1
1
2
1
2
1
1
1
−
=
−
+
−
−
=
−
⋅
−
+
−
=
=
−
⋅
−
−
−
−
=
−
=
c
v
a
m
c
v
c
v
c
v
c
v
a
m
c
v
c
v
c
v
a
m
c
v
a
m
c
v
dt
v
d
c
v
c
v
v
m
c
v
dt
v
d
m
c
v
v
m
dt
d
F
r
r
r
r
r
r
r
r
r
r
Dla v<<c
→
v/c
→
0
F = ma
Równoważność masy i energii
( )
dt
dm
v
dt
v
d
m
v
m
dt
d
dt
p
d
F
r
r
r
r
r
+
=
=
=
m = m(t),
m = m(v)
i
2
0
1
−
=
c
v
m
m
dm
v
v
d
v
m
v
dm
v
v
v
d
m
dt
s
d
dm
v
dt
s
d
v
md
s
d
F
⋅
+
⋅
=
⋅
⋅
+
⋅
⋅
=
+
=
⋅
2
r
r
r
r
r
r
r
r
r
r
r
r
=
−
⋅
−
−
−
=
−
=
2
2
2
0
2
0
1
1
1
2
2
1
c
v
c
v
v
d
c
v
m
c
v
m
d
dm
r
r
=
−
⋅
⋅
−
=
−
⋅
=
2
2
2
0
3
2
2
0
1
1
1
c
v
c
v
d
v
c
v
m
c
v
c
v
d
v
m
r
r
r
r
2
2
2
2
2
2
v
c
v
d
v
m
c
v
c
c
v
d
v
m
−
⋅
=
−
⋅
=
r
r
r
r
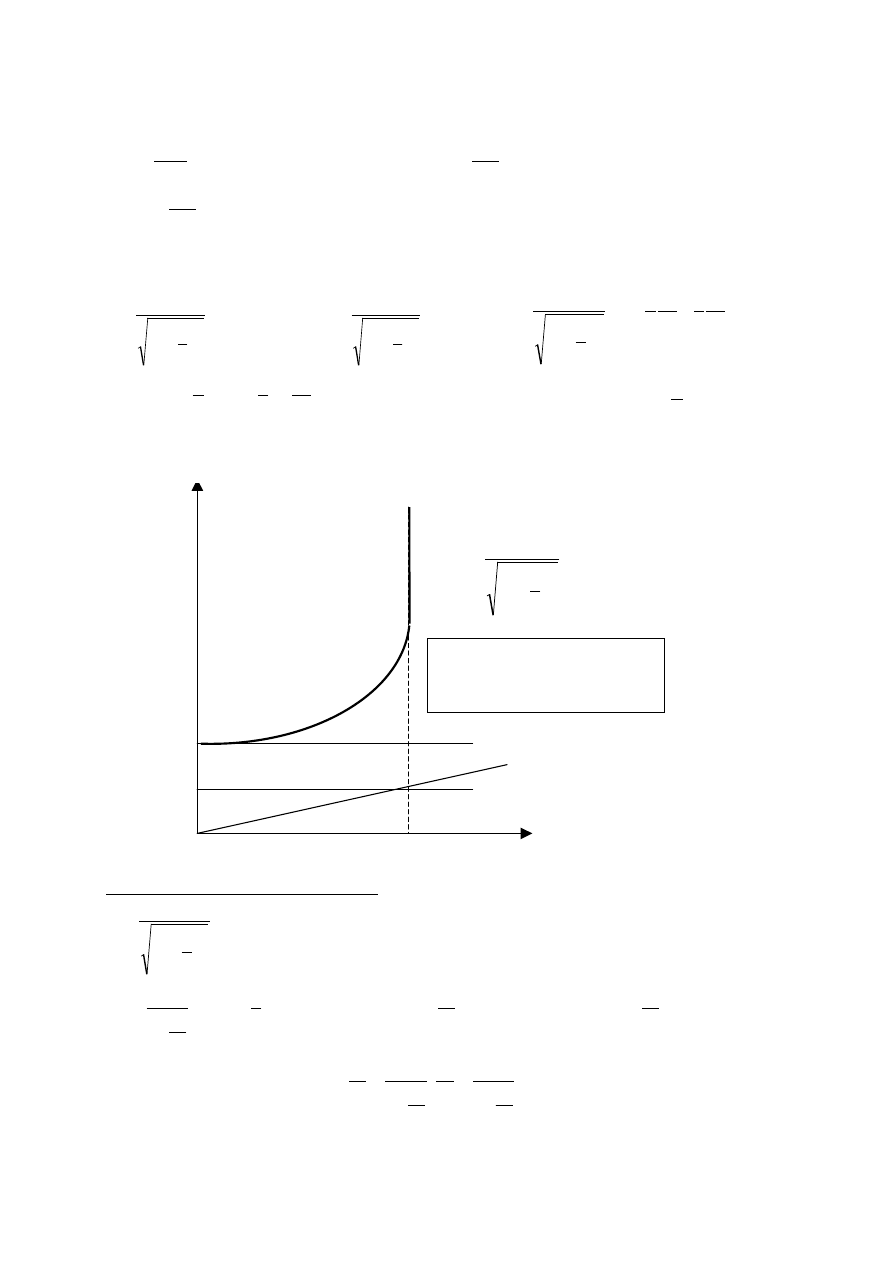
(
)
dm
v
c
v
d
v
m
2
2
−
=
⋅
r
r
11
( )
2
2
2
2
2
)
(
mc
d
dm
c
dm
v
dm
v
c
s
d
F
=
=
+
−
=
r
r
ds
dE
F
p
−
=
E
p
= U,
ds
dU
F
−
=
0
)
(
)
(
)
(
2
2
2
=
+
=
−
=
−
=
dU
mc
d
i
mc
d
dU
mc
d
ds
ds
dU
Fds
const
U
mc
E
=
+
=
2
v
≠
0
R
E
c
v
c
m
gdzie
const
U
c
v
c
m
E
=
−
=
+
−
=
2
2
0
2
2
0
1
1
....
8
3
2
1
1
1
1
4
4
2
2
2
+
+
+
=
−
c
v
c
v
c
v
const
U
c
v
m
v
m
c
m
E
=
+
+
+
+
=
..
8
3
2
1
2
4
0
2
0
2
0
Energia i pęd cząstki relatywistycznej
2
2
2
2
2
2
2
0
2
2
2
2
4
2
0
2
2
2
2
2
4
2
0
2
2
2
2
4
2
0
2
4
2
0
2
2
2
2
4
2
0
2
2
2
2
4
2
0
2
2
2
0
1
1
1
1
1
c
p
c
c
v
v
m
c
v
c
v
c
m
c
v
E
bo
c
p
c
m
E
c
v
E
c
m
E
c
m
c
v
E
E
c
m
E
c
v
c
v
c
m
E
c
v
c
m
E
=
⋅
−
=
⋅
−
=
+
=
+
=
⇒
=
−
⇒
=
−
⇒
−
=
−
=
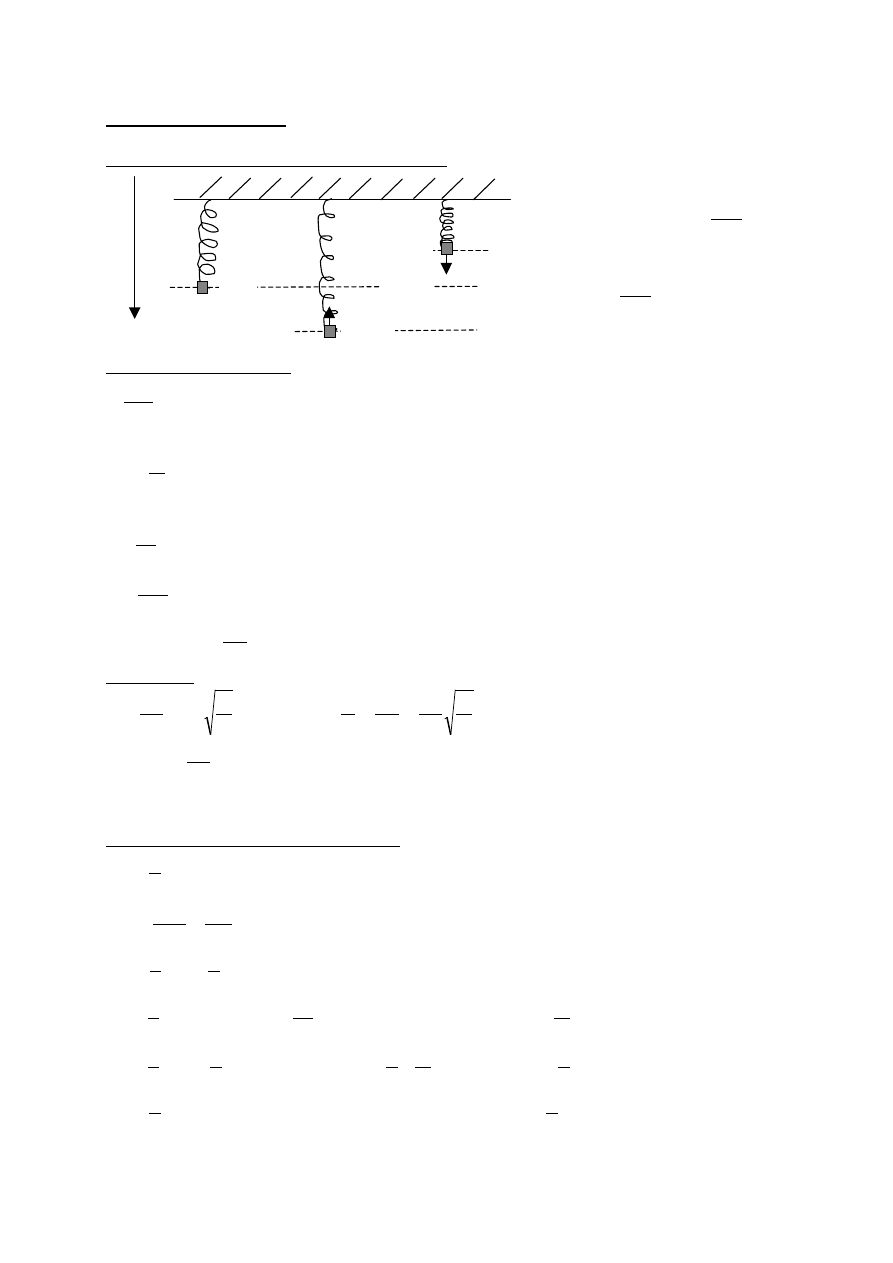
m
0
c
2
½ m
0
c
2
E
k
= ½mv
2
v/c
1,0
E
2
2
0
1
−
=
c
v
c
m
E
R
E
R
– opisuje relatywistyczną
postać energii całkowitej bez
pola sił potencjalnych (U=0).
U
c
m
E
+
=
2
0
gdy v=0
E = mc
2
gdy v
≠
0 oraz U=0
gdy v<<c
U
v
m
c
m
E
+
+
=
2
0
2
0
2
1
12
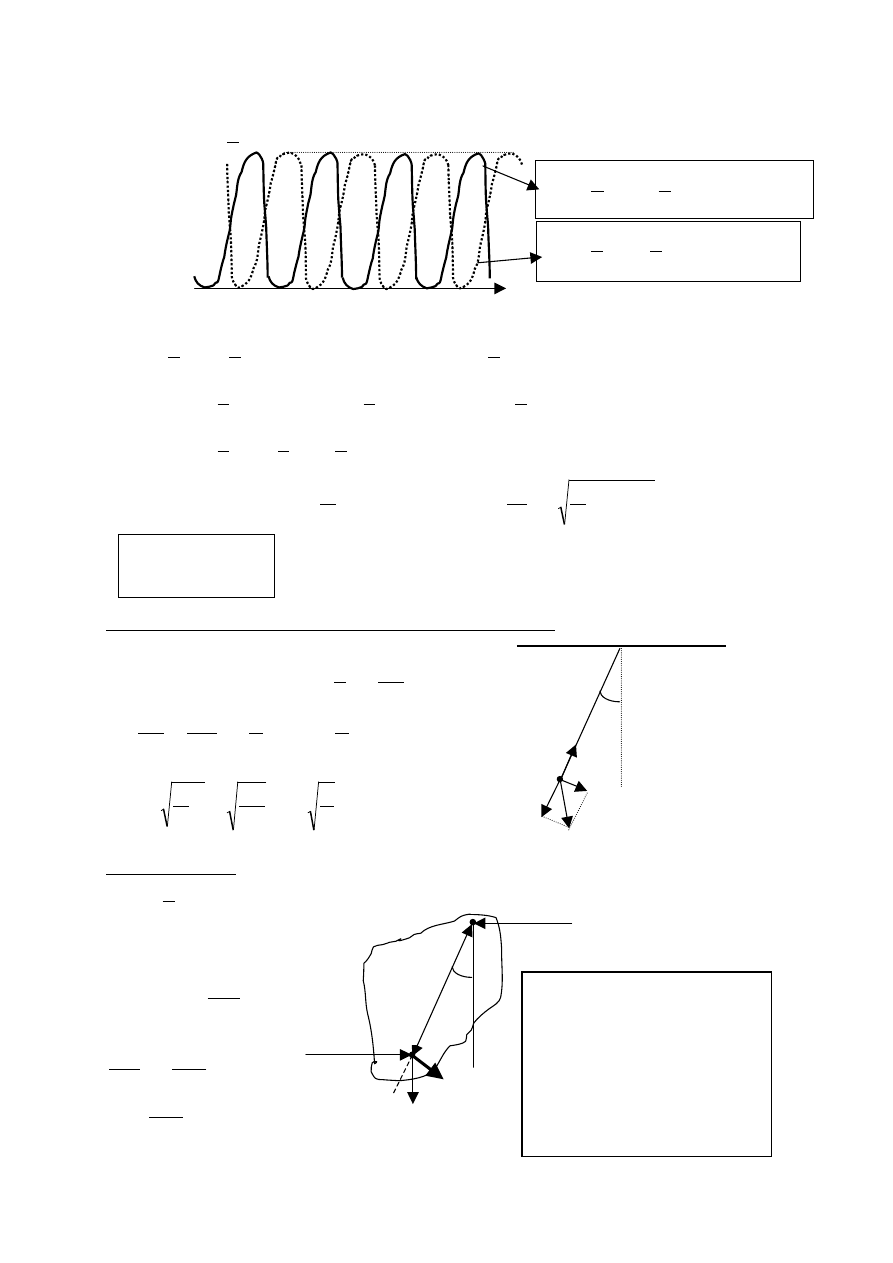
V. RUCH DRGAJĄCY
Prosty oscylator harmoniczny - równanie ruchu
Ruch harmoniczny prosty
0
2
2
=
+
kx
dt
x
d
m
równanie
)
cos(
δ
ω
+
=
t
A
x
rozwiązanie
m
k
=
2
ω
)
cos(
)
sin(
)
cos(
2
2
2
δ
ω
ω
δ
ω
ω
δ
ω
+
−
=
=
+
−
=
=
+
=
t
A
dt
x
d
a
t
A
dt
dx
v
t
A
x
)
cos(
]
2
cos[
]
)
2
(
cos[
δ
ω
δ
π
ω
δ
ω
π
ω
+
=
+
+
=
+
+
=
t
A
t
A
t
A
x
Okres ruchu
m
k
T
f
i
k
m
T
π
π
ω
π
ω
π
2
1
2
1
2
2
=
=
=
=
=
T
f
π
π
ω
2
2
=
=
,
ω
– częstość kołowa – jednostka [rad/s], f – częstością drgań oscylatora,
A - amplituda ruchu, (
ω
t +
δ
) - faza ruchu,
δ
– stała fazowa (faza początkowa).
Energia w prostym ruchu harmonicznym
kx
dx
dU
dx
dE
F
t
A
x
i
kx
E
p
p
−
=
=
−
=
+
=
=
)
cos(
2
1
2
δ
ω
)
(
cos
2
1
2
1
2
2
2
δ
ω
+
=
=
t
kA
kx
E
p
)
(
sin
2
1
)
(
sin
2
1
)
(
sin
2
1
2
1
),
sin(
2
1
2
2
2
2
2
2
2
2
2
2
δ
ω
δ
ω
δ
ω
ω
ω
δ
ω
+
=
+
=
+
=
=
=
+
−
=
=
=
t
kA
t
A
m
k
m
t
A
m
mv
E
wtedy
m
k
gdzie
t
A
dt
dx
v
i
mv
E
k
k
)
(
cos
2
1
)
cos(
2
1
2
2
2
δ
ω
δ
ω
+
=
+
=
=
t
kA
E
czyli
t
A
x
ale
kx
E
p
p
m
F = 0
F = -kx
F = -kx
x = 0
x
F = ma i F = -kx,
0
lub
2
2
2
2
=
+
=
=
−
kx
dt
x
d
m
dt
x
d
m
ma
kx
13
Maksymalna wartość
2
2
2
max
2
1
2
1
A
m
kA
E
k
ω
=
=
2
max
2
1
kA
E
p
=
2
2
2
2
2
2
1
)
(
cos
2
1
)
(
sin
2
1
kA
t
kA
t
kA
E
E
E
p
k
=
+
+
+
=
+
=
δ
ω
δ
ω
)
(
)
(
)
(
2
1
2
1
2
1
2
2
2
2
2
2
2
2
2
2
2
x
A
m
k
dt
dx
v
i
x
A
m
k
v
x
A
k
mv
czyli
kA
kx
mv
E
E
E
p
k
−
±
=
=
−
=
⇒
−
=
=
+
=
+
=
Wahadło matematyczne – jako przykład ruchu harmonicznego
α
sin
mg
F
−
=
sinα ~
α
i
F~
αααα
.
l
g
x
l
g
dt
x
d
l
mg
k
ma
kx
x
l
mg
l
x
mg
mg
mg
F
=
−
=
=
=
−
=
−
=
−
=
−
≈
−
=
2
2
2
,
,
sin
ω
α
α
Okres drgań w ruchu harmonicznym
g
l
mg
ml
k
m
T
π
π
π
2
2
2
=
=
=
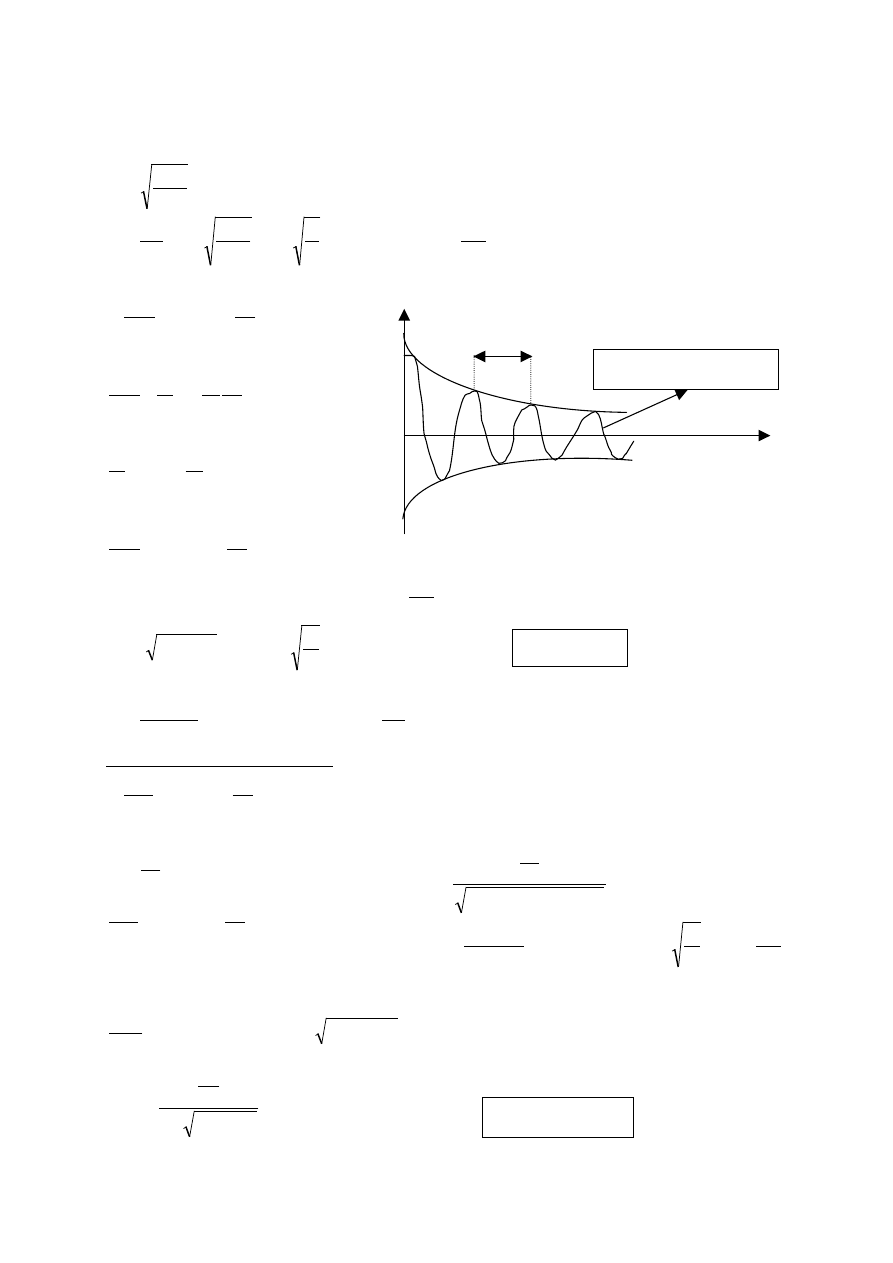
Wahadło fizyczne
r
mg
r
G
M
a
x
a
x
⋅
=
⋅
=
=
⇒
=
ϕ
ϕ
sin
sin
M = - mgasinφ i M = Iε
2
2
sin
dt
d
I
mga
ϕ
ϕ
=
sinφ~φ
I
mga
I
mga
dt
d
=
−
=
2
2
2
ω
ϕ
ϕ
mgcosα
α
mgsinα
mg
x = lα
l
l
m
R
α
v
max
→
x = 0
v = 0
→
x = A
)
(
sin
2
1
2
1
2
2
2
δ
ω
+
=
=
t
kA
mv
E
k
)
(
cos
2
1
2
1
2
2
2
δ
ω
+
=
=
t
kA
kx
E
p
t
2
2
1
kA
E
E
E
p
k
=
+
=
0
φ
G = mg
a
O
O’
ϕ
Ś
rodek
masy
Punkt
obrotu
m – masa wahadła
a – odległość masy od osi obrotu
I – moment bezwładności wahadła
względem osi obrotu
ϕ
– kąt wychylenia z położenia
równowagi
ω
– częstość kołowa
ϕ
0
– amplituda
α
– stała fazowa
l
r
– długość zredukowana
14
I
mga
gdzie
t
=
+
=
ω
α
ω
ϕ
ϕ
)
cos(
0
ma
I
l
gdzie
g
l
mga
I
T
r
r
=
=
=
=
π
π
ω
π
2
2
2
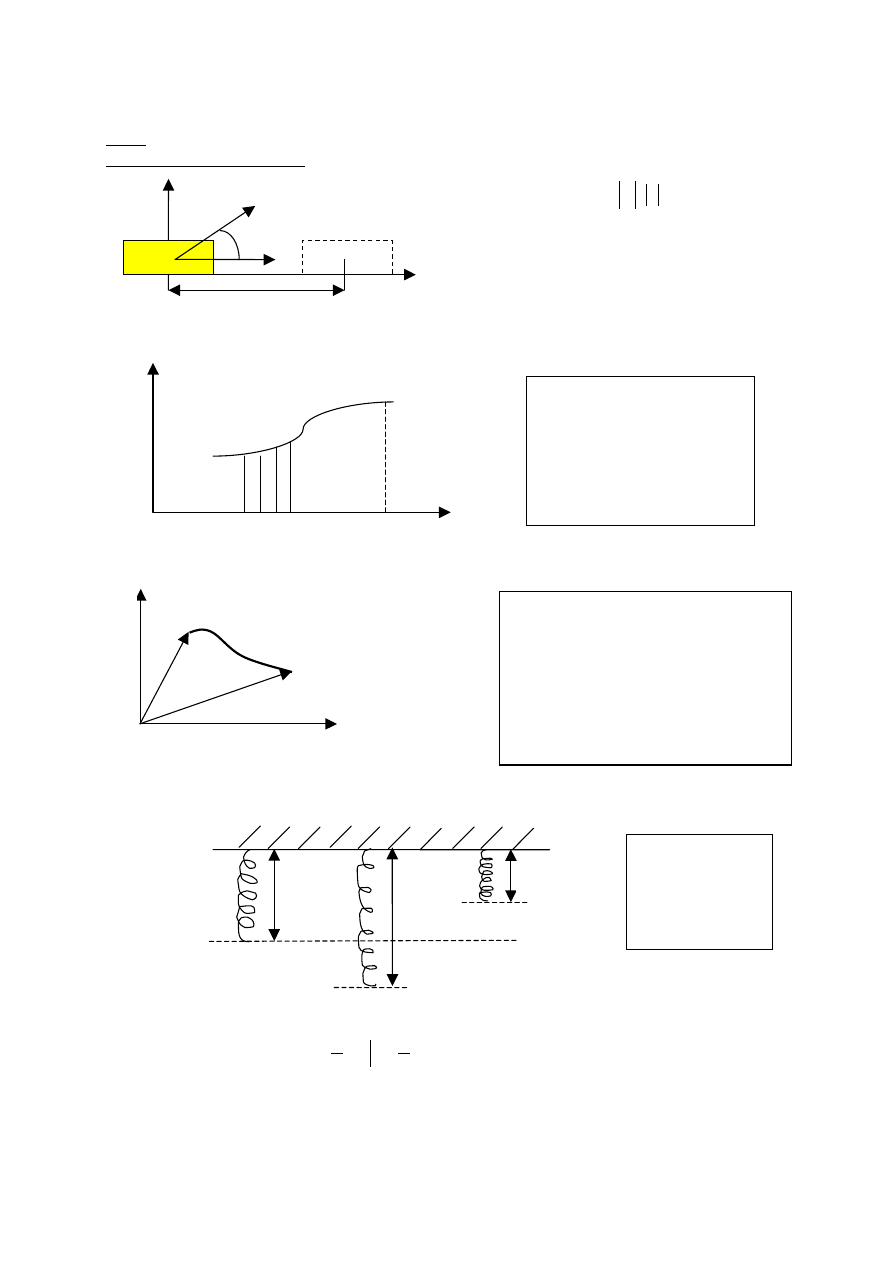
Ruch harmoniczny tłumiony (k
1
- współczynnik oporu ośrodka)
0
2
2
,
0
0
2
2
1
0
1
2
2
1
2
2
=
+
+
=
=
=
+
+
−
−
=
dt
dx
x
dt
x
d
wtedy
m
k
m
k
i
dt
dx
m
k
x
m
k
dt
x
d
czyli
dt
dx
k
kx
dt
x
d
m
β
ω
β
ω
m
k
m
k
gdzie
t
e
x
x
t
=
−
=
=
+
=
−
0
2
2
0
1
1
1
0
2
)
cos(
ω
β
ω
ω
β
α
ω
β
Tłumienie
λλλλ
(T – okres ruchu harmonicznego tłumionego,
δ
– dekrement tłumienia)
T
i
T
gdzie
e
T
t
x
t
x
T
β
λ
δ
ω
π
λ
β
=
=
=
=
+
=
ln
2
)
(
)
(
Ruch harmoniczny wymuszony
t
B
dt
dx
x
dt
x
d
wtedy
m
F
B
dodatkowo
oznaczymy
i
t
F
dt
dx
k
kx
dt
x
d
m
2
2
0
2
2
0
2
0
1
2
2
sin
2
sin
ω
β
ω
ω
=
+
+
=
+
−
−
=
x = x
0
sin(
ω
2
t – φ)
x
0
, φ – wielkości stałe
2
2
0
0
0
2
2
0
2
2
2
0
2
,
2
0
β
ω
β
β
ω
ω
ω
ω
−
=
−
=
=
⇒
=
m
F
x
d
dx
rez
rez
t
x
)
cos(
0
α
ω
β
+
=
−
t
e
x
x
t
T
(
ω
0
2
>
β
2
)
2
2
2
2
0
2
β
ω
ω
+
=
rez
m
k
m
k
gdzie
tg
m
F
x
2
,
2
4
)
(
1
0
2
2
2
0
2
2
2
2
2
2
2
0
0
0
=
=
−
=
+
−
=
β
ω
ω
ω
β
ω
ϕ
ω
β
ω
ω
15
VI. PRACA I ENERGIA
Praca
- wykonana przez stałą siłę.
- wykonana przez siłę zmienną
Ogólnie – pracę siły na pewnym odcinku drogi definiujemy
W szczególnym przypadku
W = F · r
F = const, r - droga – linia prosta mająca kierunek siły
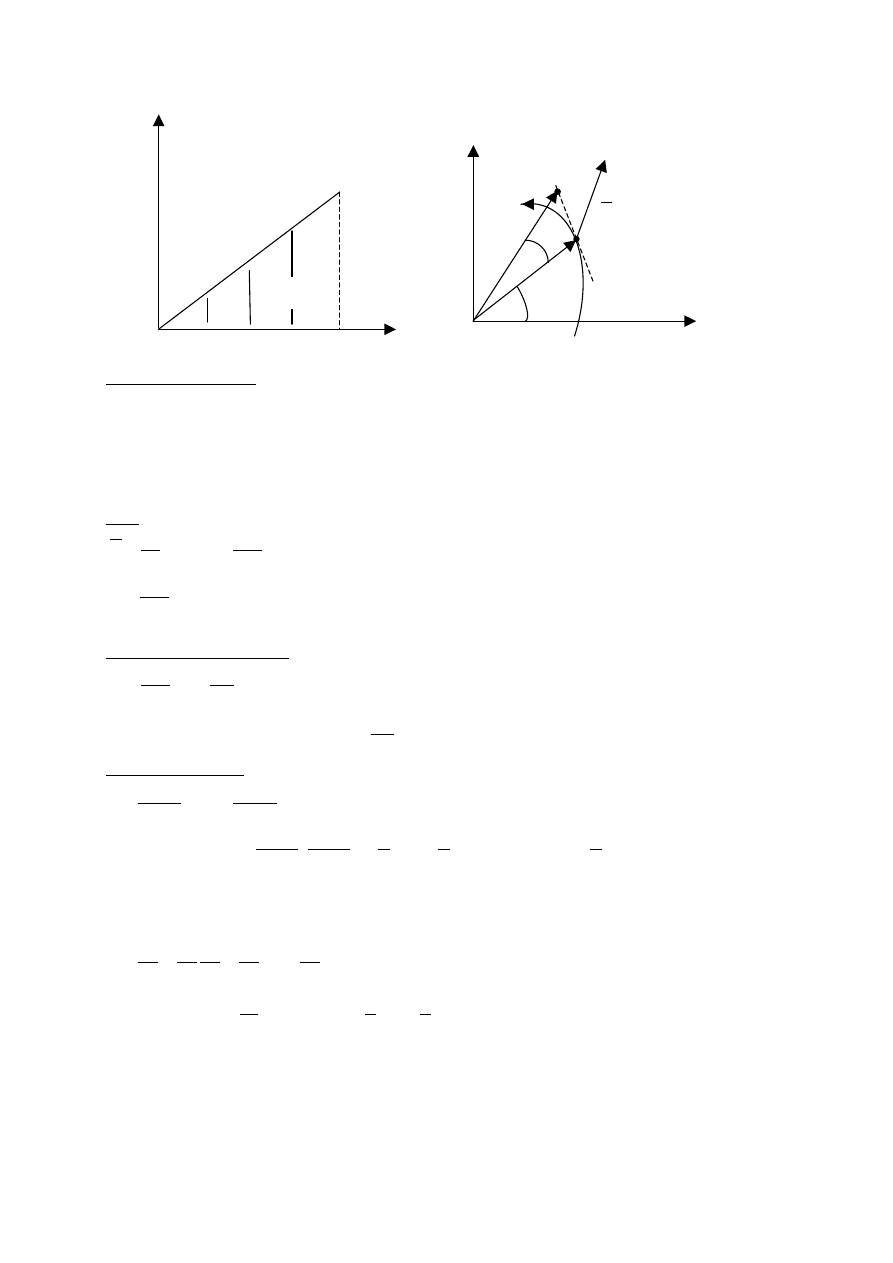
Przykład - sprężyna przymocowana do ściany.
F’(x) – siła przeciwnie skierowana do siły sprężystości F(x) dla x
1
= 0 i x
2
= x,
W
12
=½kx
2
r
2
r
1
F
x
y
x
0
x
x
α
Fcos
α
d
F
x
2
F(x)
∆
x
x
1
x
∆
W = F
∆
x
∑
∆
=
2
1
12
x
x
x
F
W
r
r
∫
∑
=
∆
=
→
∆
2
1
2
1
0
12
lim
x
x
x
x
x
Fdx
x
F
W
∫
⋅
=
2
1
r
r
r
d
F
W
r
r
r
1
– wektor wodzący w
początkowym punkcie drogi
r
2
– wektor wodzący w końcowym
punkcie drogi, po której porusza się
punkt.
F = -k(x-x
0
)
Prawo
Hooke’a,
F = -kx
α
α
cos
cos
Fs
W
s
F
s
F
W
=
⋅
⋅
=
•
=
r
r
v
r
W = F·s dla F
||
s;
αααα
= 0
0
W = F·s = 0 dla F
⊥
s;
αααα
= 90
0
∫
∫
=
=
=
=
x
x
x
kx
kx
kxdx
dx
x
F
W
0
0
2
0
2
2
1
2
1
)
(
'
16
W ruchu obrotowym
ds = rd
θ
, Fcos
ϕ
– składowa siły F w kierunku ds
ϕ
θ
θ
ϕ
ϕ
cos
cos
cos
Fr
M
bo
d
M
dW
d
Fr
ds
F
s
d
F
dW
=
=
=
=
=
r
r
M – wartość chwilowego momentu siły działającego na ciało sztywne względem osi 0.
Moc
t
W
P
=
dt
dW
P
=
jednostka [J/s] = [W]
dt
dW
P
=
jeśli W ~ t
wtedy
P =W/t
Moc w ruchu obrotowym
dt
d
a
Md
dW
bo
M
P
M
dt
d
M
dt
dW
P
θ
ω
θ
ω
ω
θ
=
=
=
=
=
=
,
Energia kinetyczna
t
v
v
x
t
v
v
a
2
,
0
0
+
=
−
=
2
0
2
0
0
2
1
2
1
2
max
mv
mv
t
v
v
t
v
v
m
x
F
W
−
=
+
⋅
−
=
=
=
i
2
2
1
mv
E
k
=
dx
dv
v
v
dx
dv
dt
dx
dx
dv
dt
dv
a
=
=
=
=
k
k
k
E
E
E
W
∆
=
−
=
0
Twierdzenie o pracy i energii
0
,
=
∆
=
=
k
E
W
const
v
v, v
0
– prędkość punktu materialnego na końcu i początku drogi
F
x
kx
F’= kx
½ kx
2
x
ϕ
d
θ
r(t+dt)
θ
P
F
ds
P(t+dt)
r(t)
O
y
x
v
0
– prędkość cząstki w chwili t=0
v – prędkość w chwili t
∫
∫
=
=
x
x
Fdx
s
d
F
W
0
r
r
2
0
2
2
1
2
1
0
0
0
mv
mv
dv
mv
dx
dx
dv
mv
Fdx
W
v
v
x
x
x
x
−
=
=
=
=
∫
∫
∫

17
W ruchu obrotowym
E
k
= ½I
ω
ω
ω
ω
2
gdy M – moment siły = const
,
ϕ
- obrót o pewinien kąt
W = M
ϕϕϕϕ
=
∆∆∆∆
E
k
= Fs
E
k
= ½mv
2
+ ½I
ω
ω
ω
ω
2
ωα
ω
ω
ω
ω
I
dt
d
I
dt
d
I
I
dt
d
dt
dW
=
=
=
=
2
2
2
1
)
2
1
(
α
ωα
ω
I
M
I
M
=
=
II zasada dynamiki dla ruchu obrotowego ciała sztywnego
Energia potencjalna
k
x
x
E
mv
mv
Fdx
W
∆
=
−
=
=
∫
2
0
2
2
1
2
1
0
∆
E
k
= -
∆
E
p
dx
x
F
x
E
x
E
zatem
dx
x
F
E
czyli
Fdx
E
x
x
p
p
x
x
p
x
x
k
)
(
)
(
)
(
)
(
0
0
0
0
∫
∫
∫
=
−
−
=
∆
=
∆
const
mv
x
E
mv
x
E
E
mv
mv
Fdx
x
E
x
E
p
p
k
x
x
p
p
=
+
=
+
∆
−
=
−
=
=
−
∫
2
0
0
2
2
2
0
0
2
1
)
(
2
1
)
(
lub
2
1
2
1
)
(
)
(
0
Prawo zachowania energii kinetycznej i potencjalnej.
2
2
1
)
(
mv
x
E
E
E
E
p
k
p
+
=
+
=
∫
∆
=
−
−
=
p
p
E
dx
x
f
bo
x
E
dx
d
x
F
)
(
)
(
)
(
Zasada zachowania energii mechanicznej
const
mv
mgh
=
+
2
2
1
h – wysokość punktu materialnego od powierzchni Ziemi
P
R
v
0
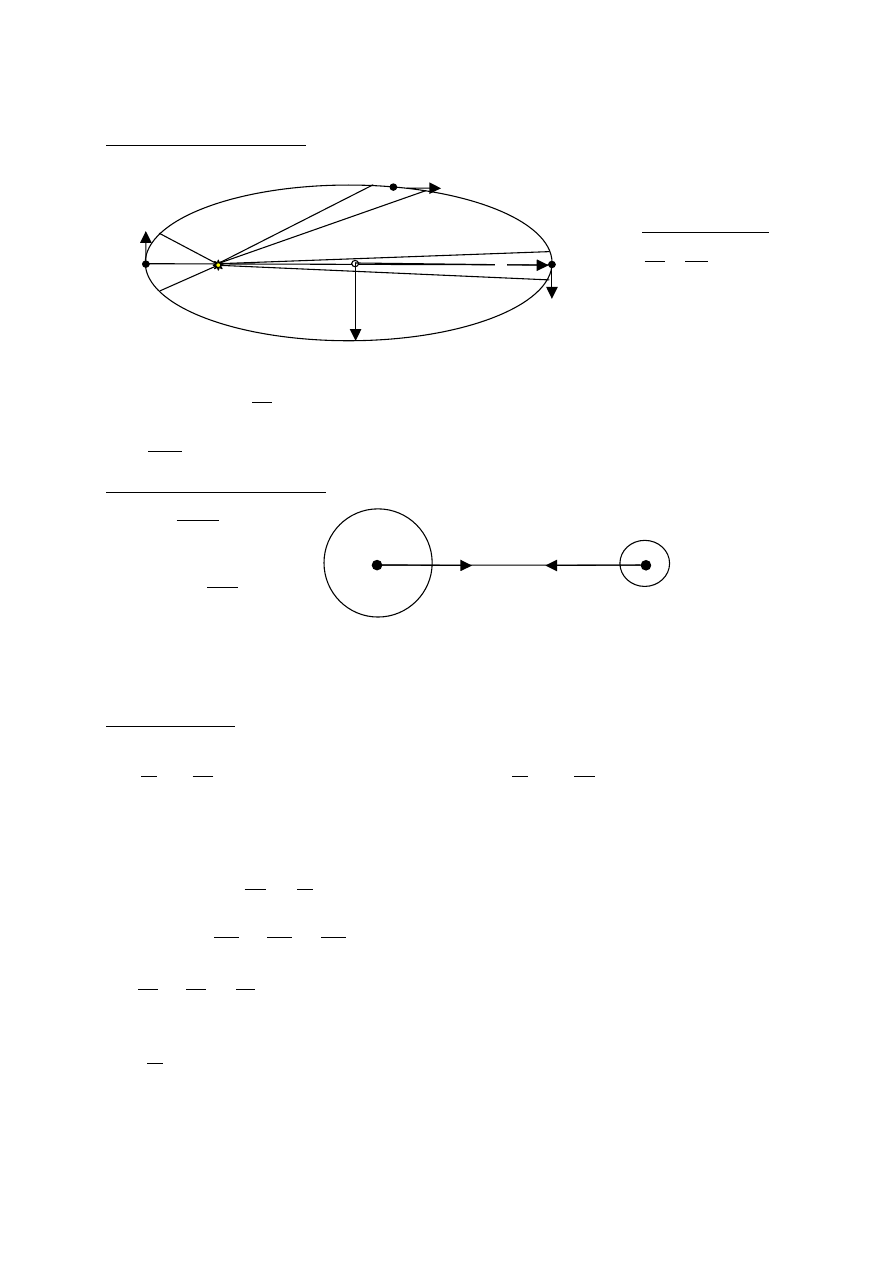
Ruch postępowo-obrotowy ciała sztywnego
2
2
1
ω
p
k
I
E
=
i
I
p
= I
0
+ MR
2
I
p
– moment bezwładności wzgl. osi przechodzącej przez
pkt. P,
I
0
– moment bezwładności wzgl. osi równoległej do osi
przechodzącej przez środek ciężkości, czyli
0
2
0
2
0
2
2
2
0
,
2
1
2
1
2
1
2
1
v
R
bo
Mv
I
MR
I
E
k
=
+
=
+
=
ω
ω
ω
ω
v
0
= R
ω
– jest prędkością liniową środka masy cylindra
względem nieruchomego pkt. P
18
VII. GRAWITACJA
Prawa Keplera ruchu planet
Siła dośrodkowa
r
v
a
a
m
F
d
d
d
2
=
=
r
r
a
d
– jest przyspieszeniem dośrodkowym
r
v
m
F
d
2
r
r
=
r – odległość planety od Słońca.
Prawo powszechnego ciążenia
12
3
2
1
12
r
r
m
m
G
F
r
r
−
=
r - odległość punktów materialnych
G – stała grawitacji (wyznaczona przez Cavendisha)
r
12
– wektor wodzący punktu materialnego m, |r
12
| = r
Pole grawitacyjne
Natężenie pola grawitacyjnego
2
r
M
G
m
E
E
=
=
jedn. [N/kg]=[m/s
2
]
r
r
M
G
m
F
E
r
r
r
3
−
=
=
r – wektor wodzący punktu, w którym wyznaczamy natężenie pola grawitacyjnego
wytworzonego przez punkt M,
V - potencjał
NABLA
OPERATOR
k
z
j
y
i
x
k
z
V
j
y
V
i
x
V
V
E
m
F
r
r
M
G
gradV
E
r
r
r
r
r
r
r
r
r
r
r
r
∂
∂
+
∂
∂
+
∂
∂
=
∇
∂
∂
+
∂
∂
+
∂
∂
−
=
∇
−
=
=
−
=
−
=
)
(
3
Przyspieszenie grawitacyjne
m
F
a
g
r
r
=
tzn., że
E
a
g
v
r
=
S
v
B
B
A
v
A
P
v
b
a
2
r
Mm
G
F
=
r = |
r
12
|
M
F
g
F
g
m
III prawo Keplera
2
2
2
1
3
2
3
1
T
T
a
a
=
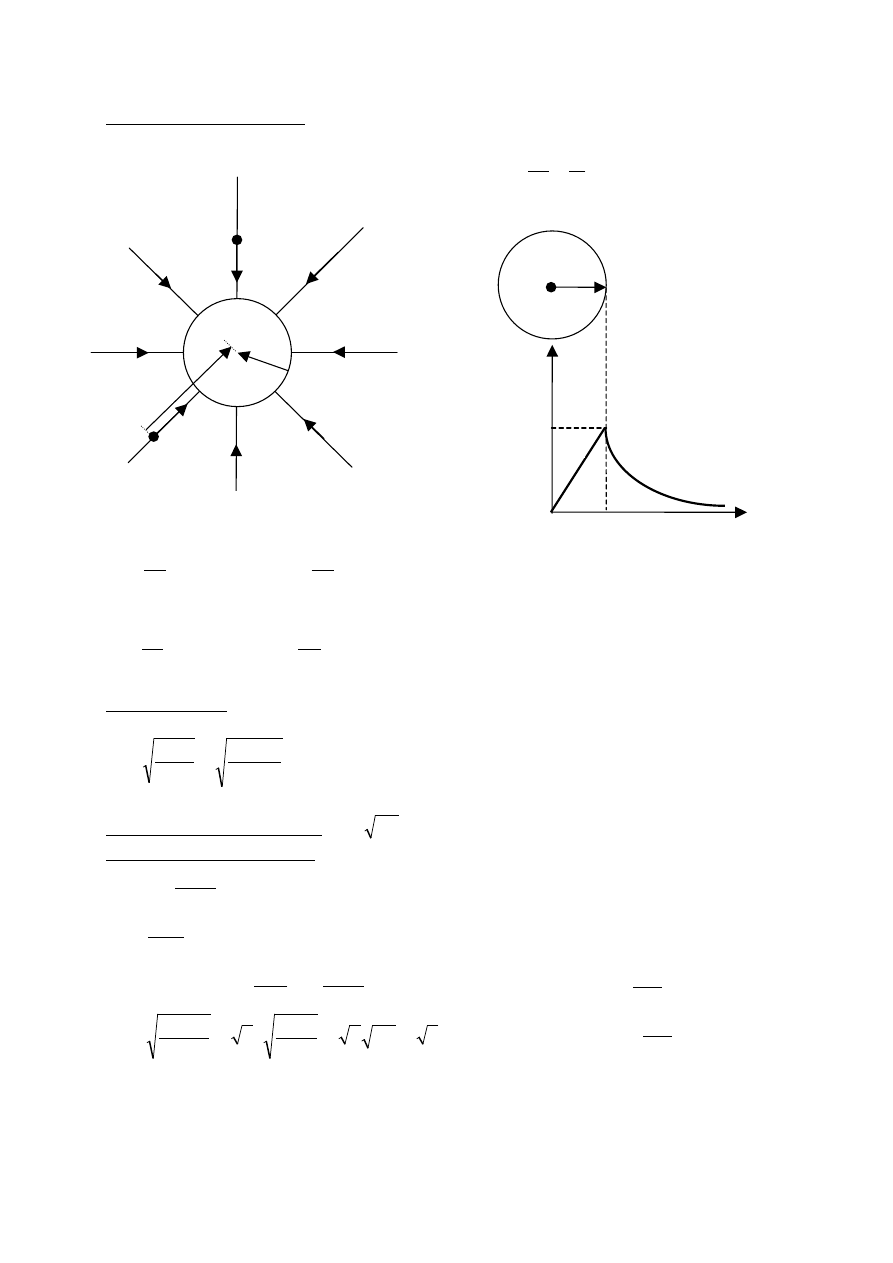
19
Pole grawitacyjne centralne
Linie sił pola centralnego
Natężenie pola centralnego
m
F
r
M
G
E
=
=
2
Sztuczne satelity
Prędkość satelity (M
Z
– masa i R – promień) na wysokości h
)
(
h
R
GM
r
GM
v
z
z
s
+
=
=
Okres obiegu T = 2
π
r/v
s
Pierwsza prędkość kosmiczna
gR
v
I
=
Drugą prędkością kosmiczną
R
m
M
G
E
z
p
−
=
gdzie R – promień Ziemi, M
z
– masa Ziemi.
2
2
II
k
mv
E
=
.
I
Z
Z
II
Z
II
p
k
v
gR
R
GM
R
GM
v
R
m
M
G
mv
E
E
⋅
=
=
⋅
=
=
=
=
∆
+
∆
2
2
2
2
2
,
0
2
R
M
G
gR
R
M
G
g
Z
Z
=
=
2
V
F
g
M
R
r
m
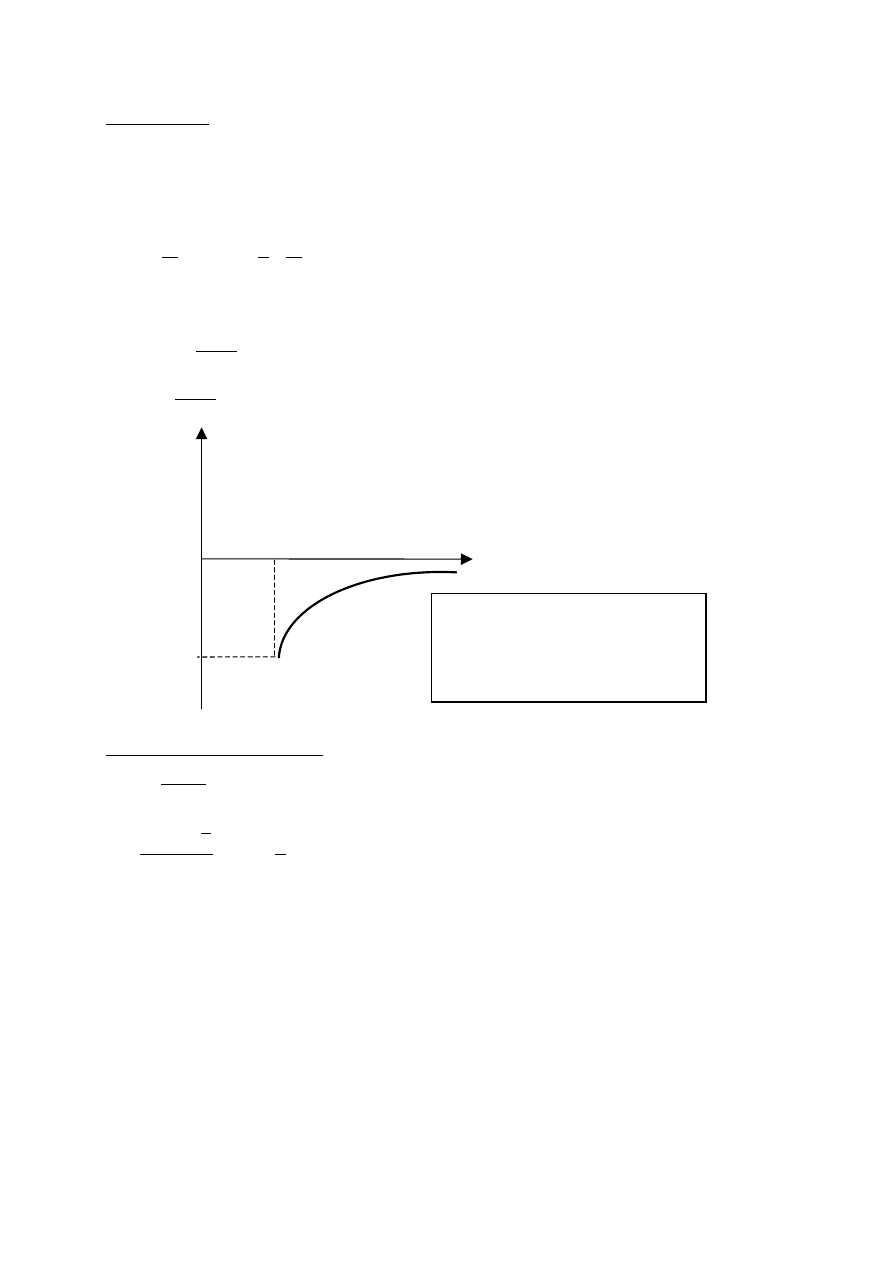
M
E
max
E~r
E~1/r
2
r
2
2
R
M
G
E
r
M
G
E
R
r
=
→
=
=
- wewnątrz kuli - rośnie
~ r
2
3
R
M
G
E
r
R
M
G
E
R
r
=
→
=
=
- na zewnątrz kuli - maleje
~ r
2
20
Potencjał pola
∆
E
p
= W
F = F
g
= mg
W = Fh = mgh
∆∆∆∆
E
p
=W=mgh-mgh
0
,
dla h
0
=0
wtedy
E
p
= mgh
)
1
1
(
0
r
r
GmM
r
F
E
p
−
−
=
−
=
r – odległość punktu, w którym wyznaczamy energię potencjalną punktu materialnego m, od
punktu materialnego M, r
0
– odległość punktu odniesienia do punktu materialnego M
r
m
M
G
r
E
z
p
−
=
)
(
r
0
= ∞,
R
m
M
G
E
z
p
−
=
,
r=R
Potencjał pola grawitacyjnego
r
GM
m
r
GmM
V
m
r
E
r
V
p
1
1
)
(
)
(
−
=
−
=
=
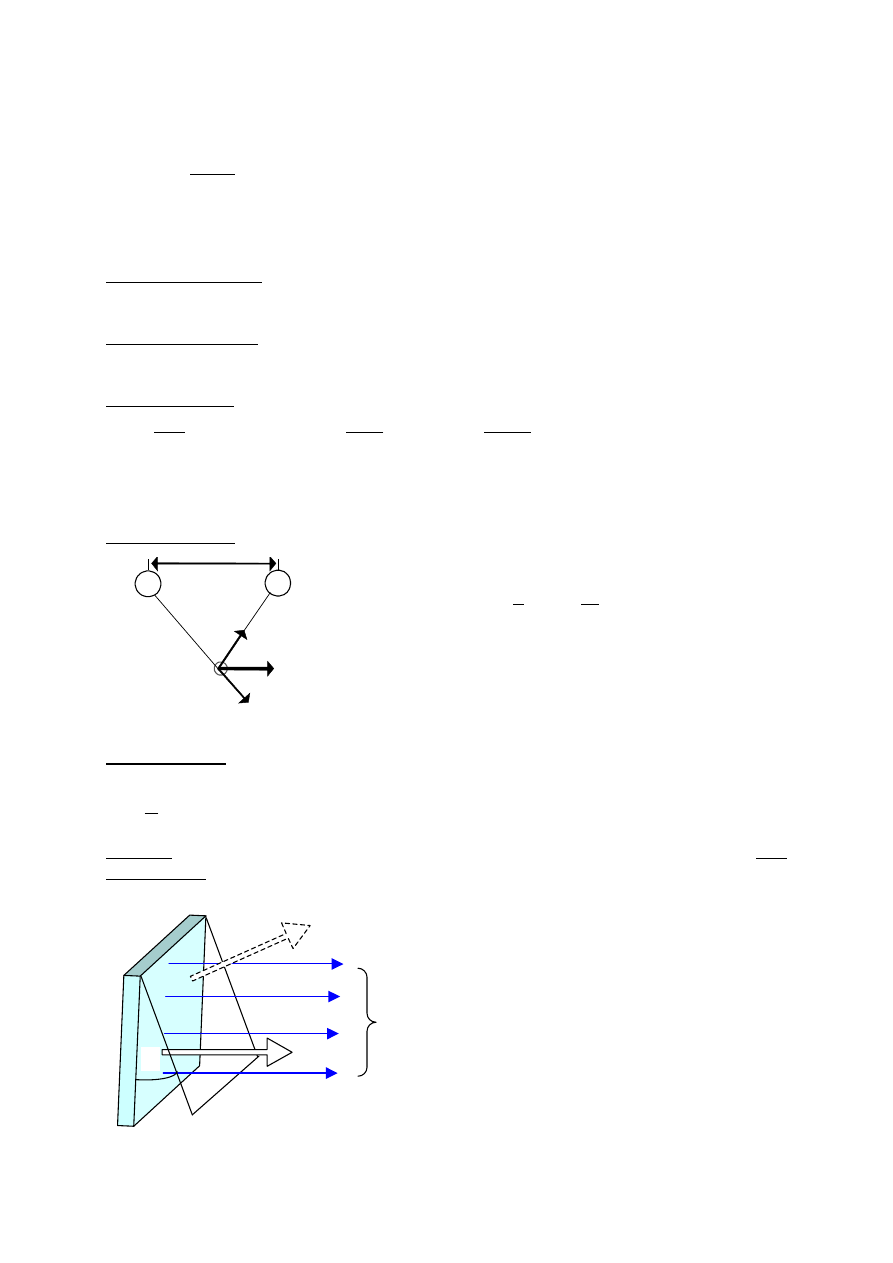
Wykres energii potencjalnej
E
p
ciała o masie
m w centralnym
polu grawitacyjnym w funkcji
odległości
r od środka masy
-GMm/R
E
p
r
R
0
21
VII. ELEKTRYCZNOŚĆ
Siła elektrostatyczna a grawitacyjna między elektronem i protonem
N
R
m
m
G
F
H
e
p
G
47
2
10
61
,
3
−
⋅
=
=
F
E
= 8,19·10
-8
N,
czyli
2,27·10
39
razy większa od
F
G
= 3,61·10
-47
N
Kwantyzacja ładunku - Wszystkie ładunki są wielokrotnością e.
Ładunek elementarny e = 1,6·10
-19
C.
w ukł. SI 1 C = 1 As.
Zachowanie ładunku - Wypadkowy ładunek w układzie zamkniętym (izolowanym) jest stały
(nie zmienia się w czasie).
Prawo Coulomba
2
2
1
r
q
q
k
F
=
0
4
1
πε
=
k
, ogólnie
ε
πε
0
4
1
=
k
ε
0
= 8,854·10
-12
C
2
/(Nm
2
) - przenikalność elektryczna próżni (stała dielektryczna próżni),
ε
- stałą dielektryczna substancji lub względną przenikalnością elektryczna ośrodka
Dipol elektryczny
+Q
-Q
l
q
F
F
2
F
1
r
r
Pole elektryczne - Ładunek próbny jest dodatni (umowa). Kierunek E jest taki sam jak F (na
ładunek dodatni).
q
F
E
r
r
=
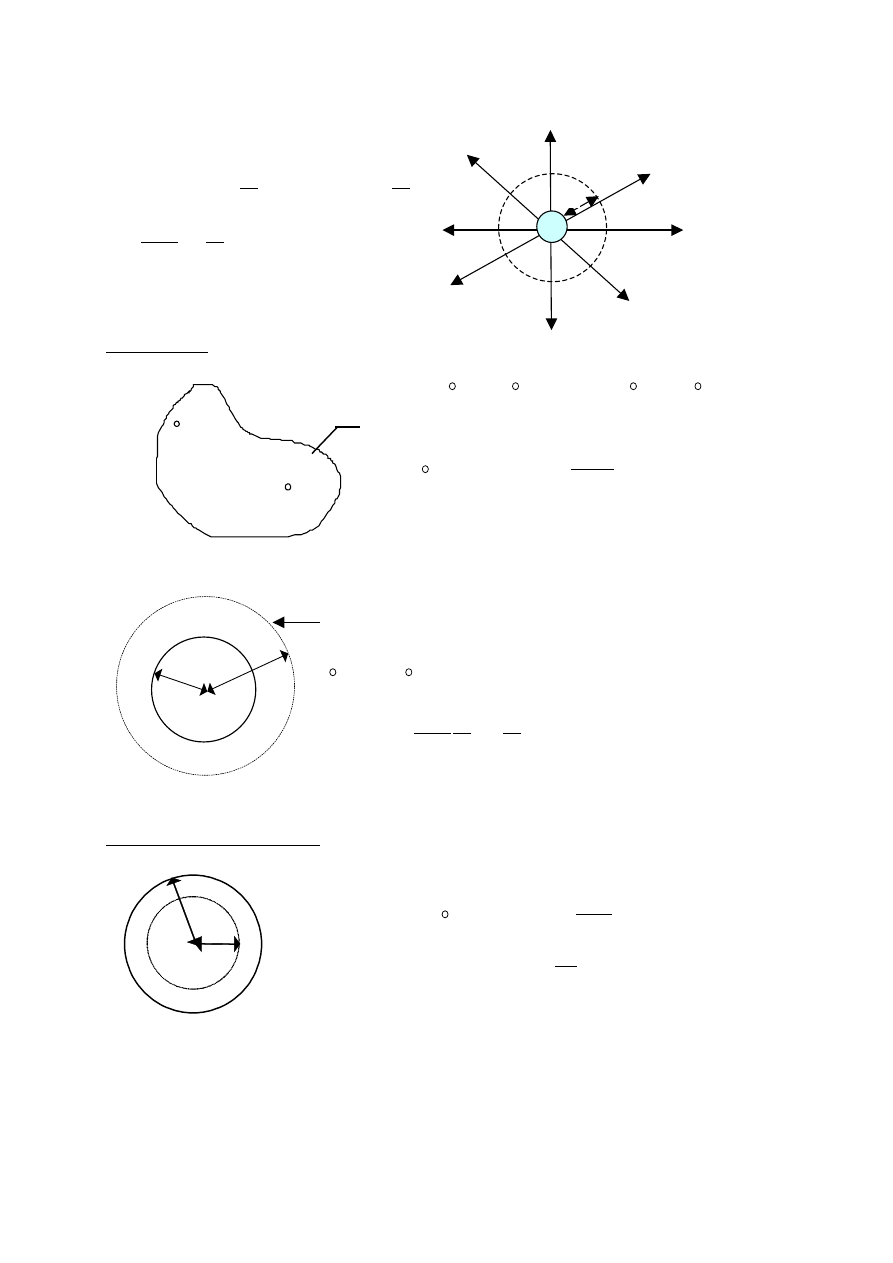
Strumień
pola
elektrycznego
∆
φ
=
E
∆
S = E
∆
S cos
α
α
- kąt pomiędzy wektorem powierzchni
∆
S i wektorem E
∆∆∆∆
S
∆∆∆∆
S’
∆
Φ
E
αααα
3
1
r
p
qk
F
r
l
F
=
=
gdzie
p = Ql jest momentem
dipolowym.
S
E
d
r
r
d
=
φ
∑
∆
=
ia
powierzchn
S
E
r
r
φ
Suma ta przedstawia całkę
powierzchniową
∫
=
S
S
E
r
r
d
φ
Pole elektryczne od n ładunków punktowych jest
równe sumie wektorowej pól elektrycznych
(zasada superpozycji)
Natężenie
pola
elektrycznego
22
Prawo Gaussa
S
Q
1
Q
2
Jednorodnie naładowana sfera
r
R
+Q
Jednorodnie naładowana kula
R
r
Q
Q
wewn
Wykres E w funkcji odległości od środka jednorodnie naładowanej kuli.
Q
r
E
powierzchnia Gaussa
o promieniu r
k
k
Q
kQ
r
r
Q
k
r
E
π
ε
πε
ε
π
π
π
φ
4
1
4
1
4
)
4
(
)
4
(
0
0
0
2
2
2
=
⇒
=
=
=
=
=
∫
∫
∫
∫
+
=
+
=
=
S
E
S
E
S
E
E
S
E
r
r
r
r
r
r
r
r
r
d
d
d
)
(
d
2
1
2
1
calk
φ
φ
całk
= (
Q
1
/
ε
0
) + (
Q
2
/
ε
0
) = (
Q
1
+
Q
2
)/
ε
0
0
.
.
4
d
ε
π
wewn
wewn
Q
kQ
=
=
∫
S
E
r
r
Prawo Gaussa
∫
∫
=
=
)
4
(
d
2
r
E
dS
E
π
S
E
r
r
E(4
π
r
2
) = Q/
ε
0
Dla r > R
2
2
0
4
1
r
Q
k
r
Q
E
=
=
πε
Dla r < R,
E = 0
=
=
=
∫
0
2
)
4
(
Q
r
E
S
d
E
wew
ε
π
r
r
r
R
Q
k
E
3
=
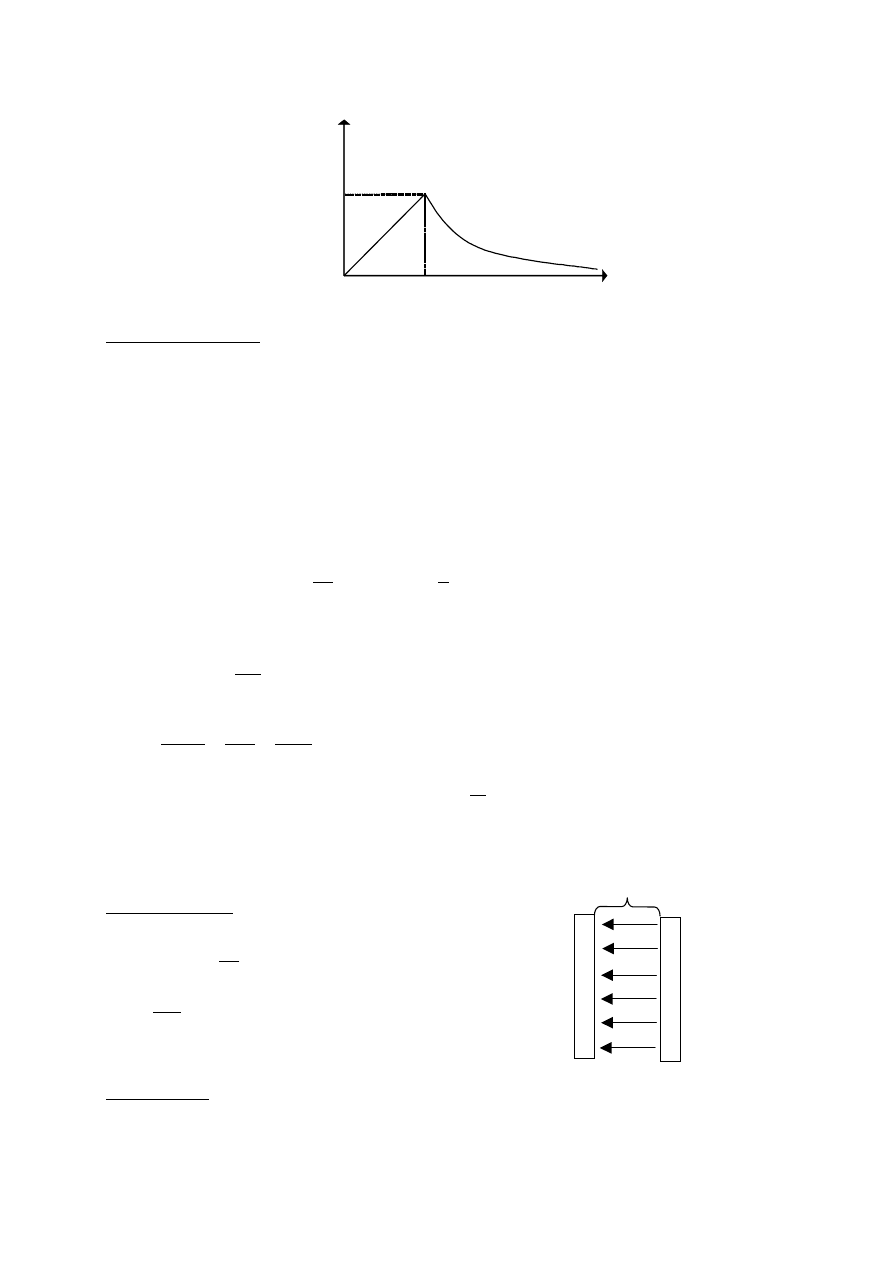
23
kQ/R
2
R
E
r
Potencjał elektryczny
Różnica energii potencjalnych
∫
−
=
−
B
A
pA
pB
E
E
r
F d
∫
∫
−
=
−
=
−
=
−
B
A
B
A
pA
pB
B
A
q
E
E
U
U
r
E
r
F
r
r
r
r
d
d
Elektryczną energię potencjalną
F – siła elektrostatyczna działająca na ładunek q.
∫
∞
−
=
=
r
p
q
r
E
r
U
r
E
r
r
d
)
(
)
(
Energia potencjalna jest równa pracy wykonanej przeciw sile elektrycznej
∫
∞
∞
∞
−
−
=
−
=
=
=
r
r
r
p
r
qQk
r
r
Q
k
q
W
r
E
r
U
1
d
)
(
)
(
2
U(r) jest energią potencjalną ładunków q i Q
r
k
r
E
r
U
p
=
=
)
(
)
(
Potencjał elektryczny
q
r
U
q
W
q
r
E
r
V
r
p
)
(
)
(
)
(
=
=
=
∞
Jedn. [J/C]=[V]
Potencjał dla ładunku punktowego
r
Q
k
V
=
∫
−
=
=
=
−
B
A
AB
A
B
W
U
V
V
r
E d
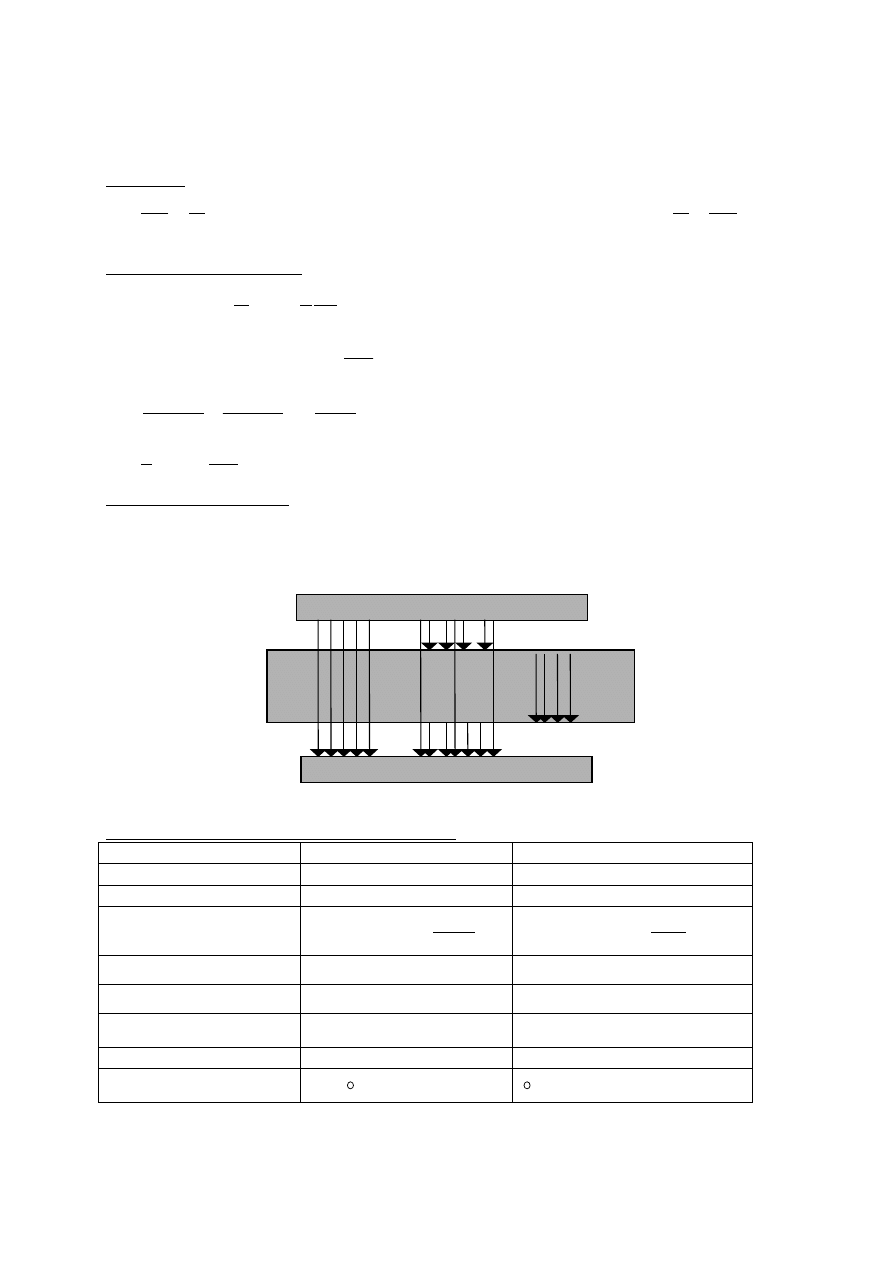
Płyty równoległe
∆
V = – Ed
0
4
ε
σ
σ
π
−
=
−
=
k
E
stąd
∆
V =
σ
d/
ε
0
S
Qd
V
0
ε
=
∆
Elektronowolt
∆
E
k
= e∆V = (1,60·10
-19
C)(1 V) = 1,60·10
-19
J =>
1 eV = 1,60·10
-19
J
0
Różnica
potencjałów
d
+
σ
-
σ
24
Powierzchnia każdego przewodnika jest powierzchnią stałego potencjału (powierzchnią
ekwipotencjalną).
Pojemność
U
Q
V
Q
C
=
∆
=
Jedn. farad. 1F = 1C/1V. Dla kondensatora płaskiego
d
S
U
Q
C
0
ε
=
=
Energia pola elektrycznego
C
Q
q
C
q
q
U
W
Q
Q
2
0
0
2
1
d
d
=
=
=
∫
∫
Energia zgromadzone w kondensatorze
Dla kondensatora płaskiego
ES
Q
czyli
S
Q
E
0
0
,
ε
ε
=
=
oraz C = ε
0
S/d i
(
)
Sd
E
d
S
S
E
C
ES
W
2
2
2
2
0
0
2
2
0
2
0
ε
ε
ε
ε
=
=
=
,
Sd - objętość kondensatora
2
2
0
8
1
2
1
E
k
E
w
π
ε
=
=
Gęstość energii pola elektrycznego
Trzy wektory elektryczne
P
E
D
r
r
r
+
=
0
ε
D, E, P są wektorami: indukcji elektrycznej, natężenia pola, polaryzacji.
D - ładunek swobodny,
ε
0
E - wszystkie ładunki, P - ładunek polaryzacyjny
+ + + + + + + + + + +
- - - - - - - - - - -
- - - - - - - - - - -
+ + + + + + + + + + +
D
ε
0
E
P
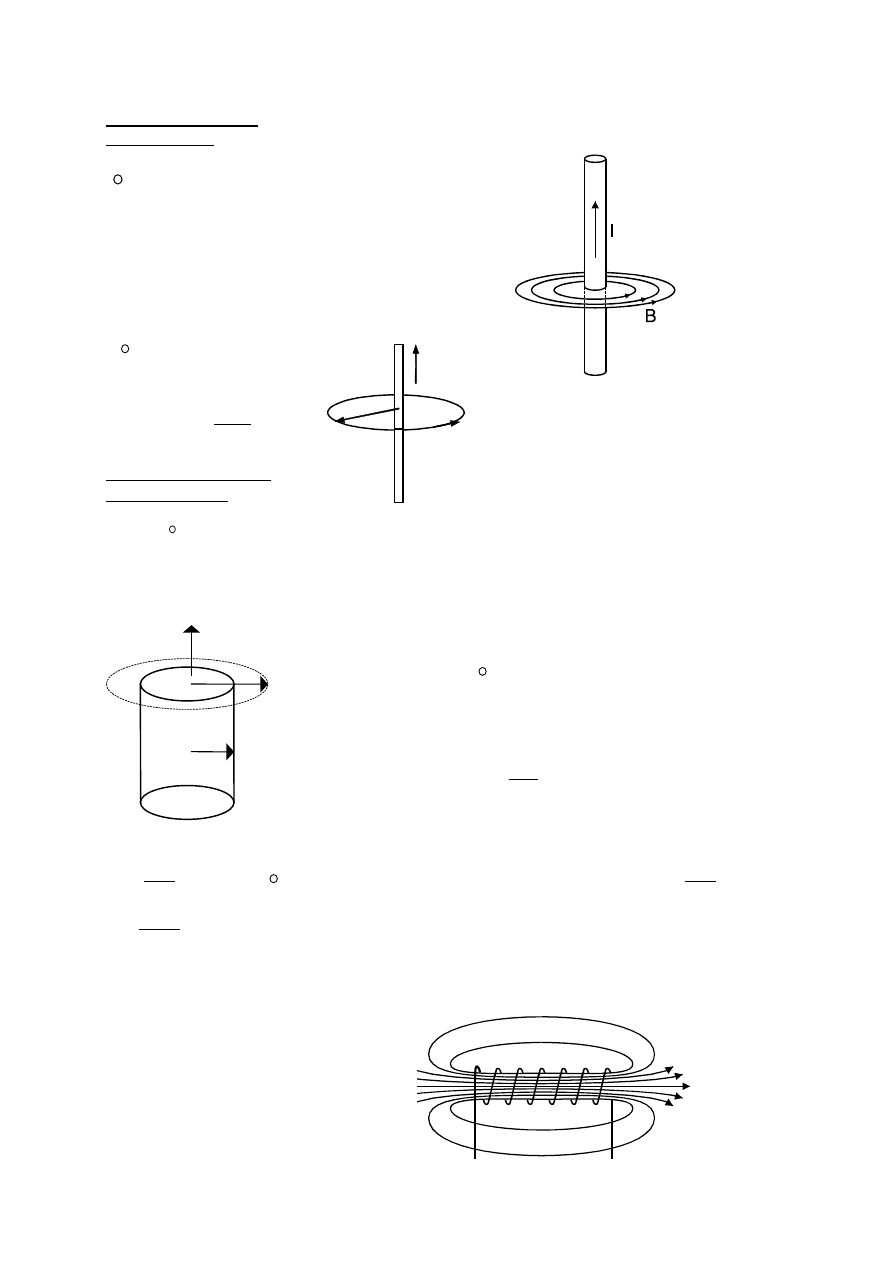
Porównanie pola grawitacyjnego i elektrycznego
Pole grawitacyjne
g
Pole elektryczne
E
1. źródło pola
Masa m>0
Ładunek q>0, q<0
2. stosowalność
Obowiązuje, gdy v<<c
Obowiązuje zawsze
3. siła
Newtona
r
r
m
m
G
F
r
r
3
2
1
=
Coulomba
r
r
q
q
k
F
r
r
3
2
1
=
4. natężenie pola
r
r
Gm
m
F
g
r
r
r
)
/
(
/
2
=
=
r
r
kq
q
F
E
r
r
r
)
/
(
/
2
=
=
5. energia potencjalna
r
m
Gm
U
g
/
2
1
−
=
r
q
kq
U
E
/
2
1
=
6. potencjał pola
r
Gm
m
U
V
g
g
/
/
=
=
∫
⋅
−
=
=
=
r
d
E
r
kq
q
U
V
E
E
r
r
/
/
7. praca
W
g
= U
g
= mV
g
W
E
= U
E
= qV
E
8. pole zachowawcze
Gdy
∫
=
⋅
0
r
d
F
g
r
r
∫
=
⋅
0
r
d
F
E
r
r
25
IX. MAGNETYZM
Prawo Ampera
Strumień magnetyczny
(
Prawo Gaussa)
Na zewnątrz pręta o promieniu R (
r > R)
I
r
R
2
2
R
r
I
i
π
π
=
∫
=
i
0
d
µ
l
B
r
r
B2
π
r =
µ
0
i
2
2
0
2
R
r
I
r
B
π
π
µ
π
=
czyli
r
R
I
B
2
0
2
π
µ
=
dla r<R
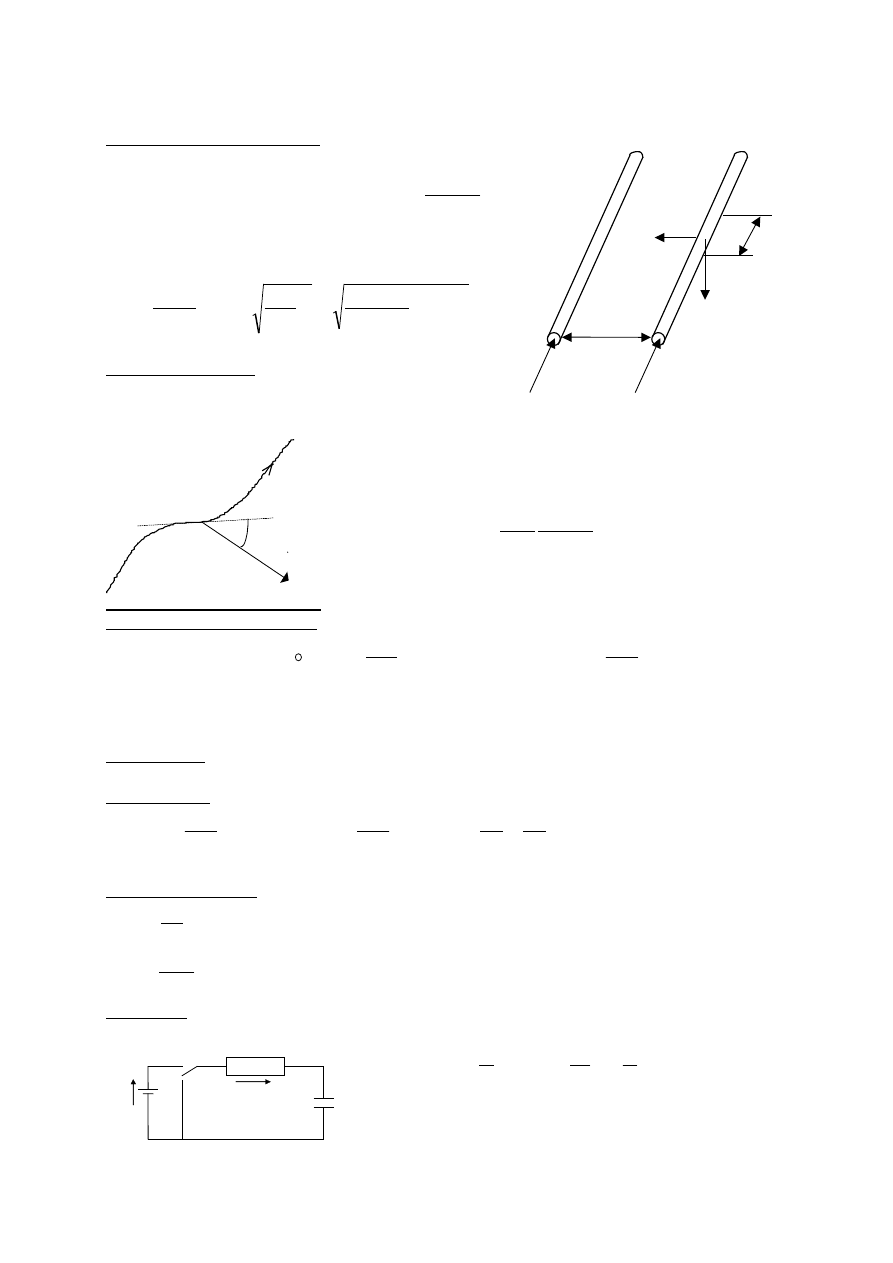
Cewka (solenoid)
d
l
||
B
∫
=
=
S
B
0
d
s
B
r
v
φ
∫
=
I
0
d
µ
l
B
r
r
dl – element konturu,
µ
0
= 4
π
k/c
2
= 4
π
·10
-7
Tm/A -
przenikalnością magnetyczną próżni.
Pole wokół nieskończenie długiego prostoliniowego
przewodnika w odległości
r od niego.
∫
=
I
0
d
µ
l
B
r
r
B2
π
r =
µ
0
I,
r
I
B
π
µ
2
0
=
dla r>R
∫
=
I
0
d
µ
l
B
r
r
B2
π
r =
µ
0
I
r
I
B
π
µ
2
0
=
I
r
dl
Z prawa Ampera
Bh =
µ
0
I
0
nh czyli
B =
µ
0
I
0
n
B - pole wewnątrz długiego solenoidu.
Pole wewnątrz solenoidu jest
jednorodne i nie zależy od kształtu
cewki, jeśli tylko jest ona bardzo długa.
26
Dwa przewodniki równoległe
Prawo Biota-Savarta
r
dl
I
θ
dB
Indukcja elektromagnetyczna
Prawo Faradaya
t
l
d
E
B
d
d
φ
ε
−
=
=
∫
r
r
dla
N zwojów
t
N
B
d
d
φ
ε
−
=
ε
- SEM pracą na jedn. ład. wykonaną przy przeniesieniu ład. wokół zamkniętej pętli (
ε
=
W/q), Φ
B
– strumień magnetyczny przechodzący przez tę pętlę.
Reguła Lenza
Prąd indukowany ma taki kierunek, że przeciwstawia się zmianie, która go wywołała.
Transformator
t
N
U
B
d
d
2
2
φ
−
=
oraz
t
N
U
B
d
d
1
1
φ
−
=
1
2
1
2
N
N
U
U
=
Indukcyjność własna
t
I
L
d
d
−
=
ε
Jednostką
L jest henr. [1H] = [1Vs/A] lub [1H] = [1
Ω
s]
0
2
0
l
S
N
L
µ
=
Indukcyjność cewki (
L zależy tylko od czynników geometrycznych)
Obwód
RC
Włącznik pozycja a
C
q
IR
+
=
ε
C
q
R
t
q
+
=
d
d
ε
rozwiązanie
)
1
(
/
RC
t
e
C
q
−
−
=
ε
Siła elektrodynamiczna
d
I
I
l
lB
I
F
b
a
a
b
b
π
µ
2
0
=
=
Założenie:
l = 1m, d = 1m, F = 2·10
-7
N,
I
a
= I
b
= I, stąd
A
F
l
d
I
d
I
l
F
1
10
2
10
4
2
2
2
7
7
0
2
0
=
⋅
⋅
⋅
=
=
⇒
=
−
−
π
π
µ
π
π
µ
3
0
4
r
r
l
d
I
dB
r
r
×
=
π
µ
ε
R
C
a
b
+
-
d
i
a
i
b
F
B
a
l
a
b
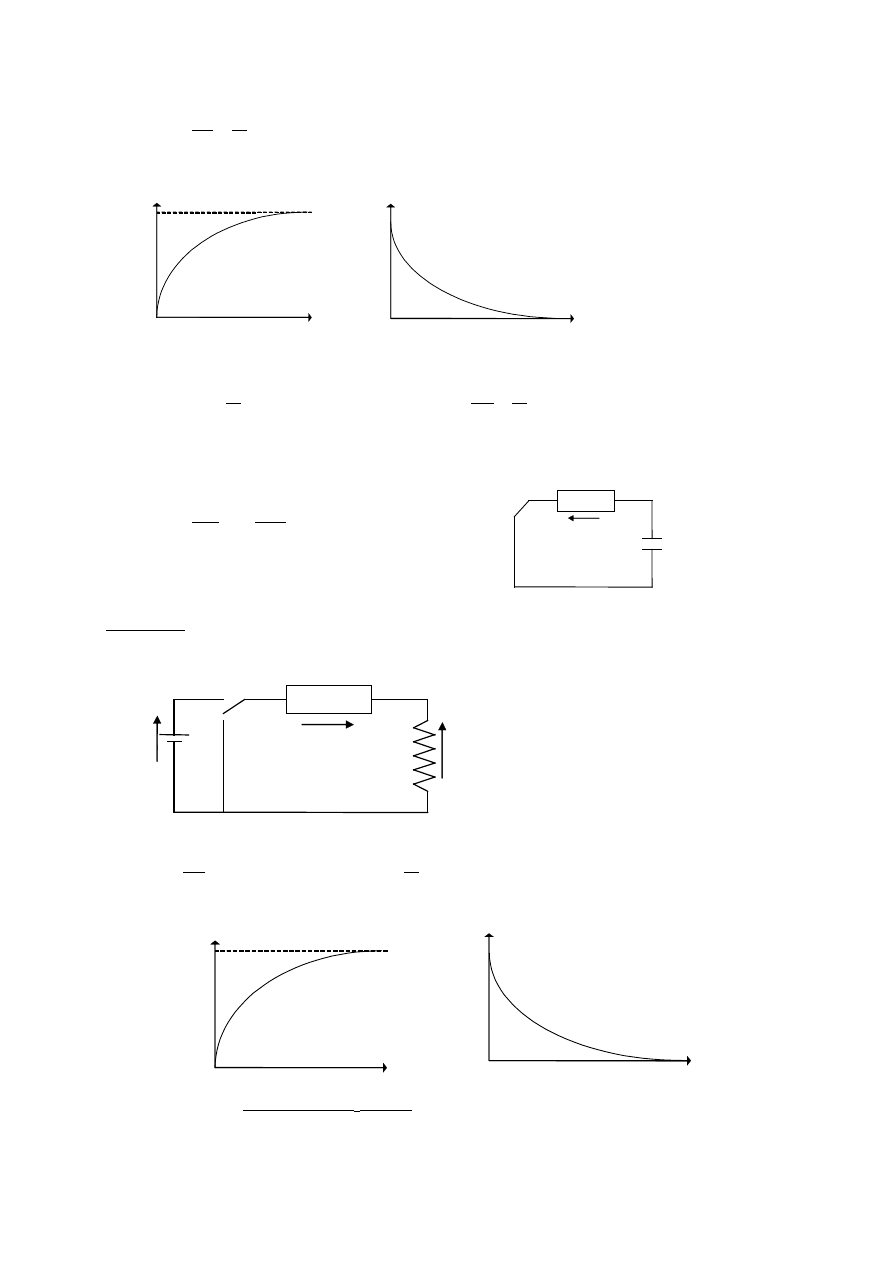
27
Prąd
RC
t
RC
t
e
I
e
R
t
q
I
/
0
/
d
d
−
−
=
=
=
ε
Zależności
q(t) oraz I(t).
q
t
C
ε
I
ε
/R
t
Wyłącznik pozycja b - rozładowanie kondensatora
0
=
+
C
q
IR
czyli
0
d
d
=
+
C
q
t
q
R
RC
t
e
q
q
/
0
−
=
gdzie
q
0
jest ładunkiem początkowym na kondensatorze.
Obwód
RL
+
-
εεεε
L
I
ε
R
L
a
b
0
d
d
=
−
−
t
I
L
IR
ε
rozwiązanie
)
1
(
)
1
(
)
1
(
/
0
/
0
/
L
t
L
Rt
L
Rt
e
I
e
I
e
R
I
τ
ε
−
−
−
−
=
−
=
−
=
Napięcie na oporniku i cewce – rys.
V
t
ε
R
V
ε
t
L
Narastanie prądu - stała czasowa
τ
L
= L
/R.
Natężenie prądu przy rozładowaniu wynosi
C
t
RC
t
e
I
e
RC
q
t
q
I
τ
/
0
/
0
d
d
−
−
=
−
=
=
τ
C
= RC -
stała czasowa obwodu.
I
R
C
+q
+
-q
-
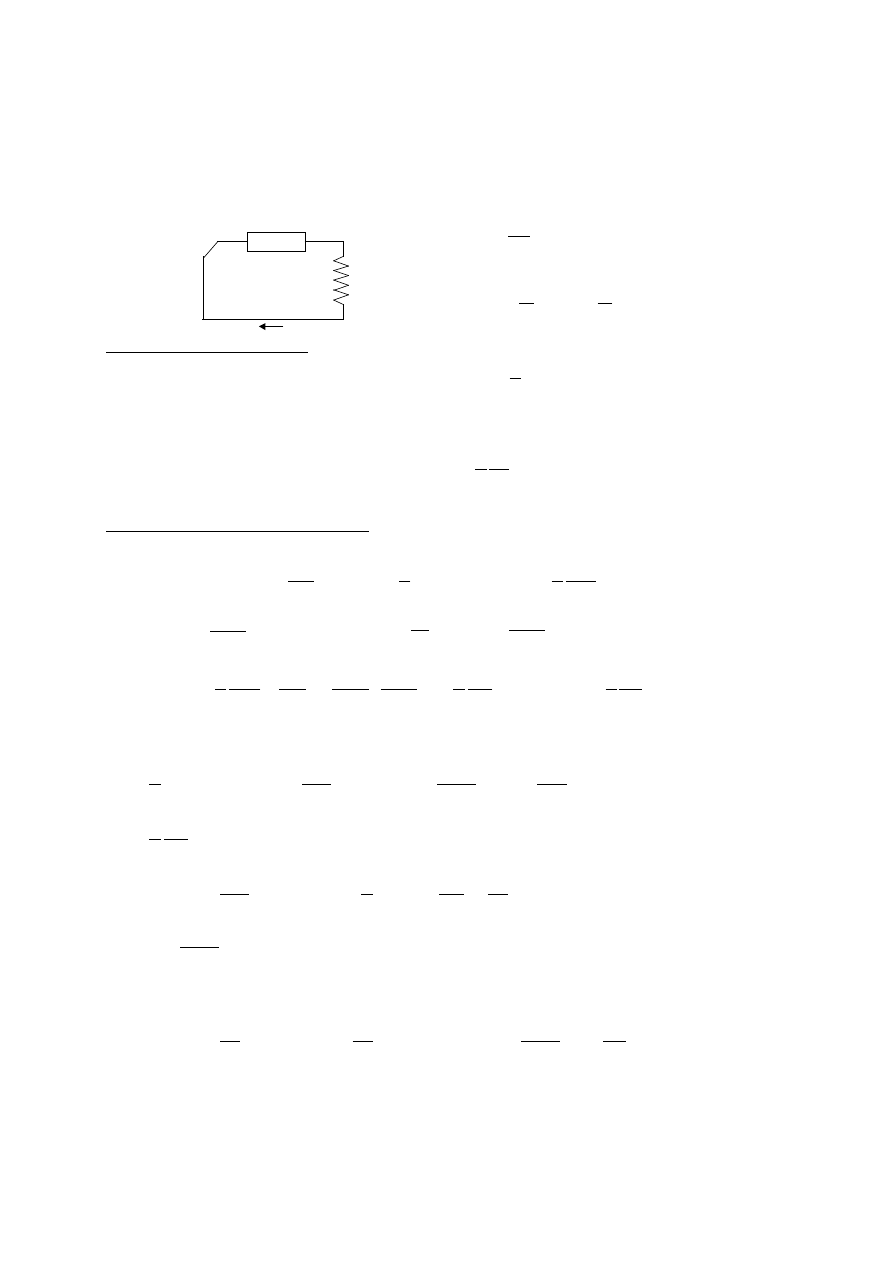
28
Przełącznik w pozycji (b)
Energia a pole magnetyczne
2
2
1
d
d
LI
I
LI
W
W
W
B
B
L
=
=
=
=
∫
∫
Całkowitą energię magnetyczną zawartą w cewce o indukcyjności L przez którą płynie prąd I.
Energią naładowanego kondensatora
C
q
W
W
C
E
2
2
1
=
=
Gęstość energii pola magnetycznego
Solenoid o długości
l i powierzchni przekroju S, czyli o objętości lS.
Gęstość energii
lS
W
w
B
B
=
2
2
1
LI
W
B
=
więc
lS
LI
w
B
2
2
1
=
oraz
l
S
N
L
2
0
µ
=
i
0
0
0
µ
µ
µ
N
Bl
I
l
N
I
In
B
=
⇒
=
=
zatem
0
2
2
0
2
0
2
2
1
2
1
2
1
µ
µ
µ
B
N
Bl
l
S
N
lS
lS
LI
w
B
=
=
=
0
2
2
1
µ
B
w
B
=
Całkowita gęstość energii pola elektromagnetycznego
0
0
2
2
2
2
0
0
2
2
0
2
2
2
0
2
0
0
2
2
0
1
)
(
2
)
(
2
1
)
(
8
1
2
1
4
1
4
1
8
1
lub
2
1
ε
µ
ε
µ
ε
π
µ
π
ε
πε
π
ε
=
+
=
+
=
+
=
+
=
=
=
⇒
=
=
=
c
bo
B
c
E
B
E
B
c
E
k
w
w
w
B
w
k
k
bo
E
k
w
E
w
B
E
B
E
E
Fala elektromagnetyczna wypromieniowana przez zmieniający się prąd ma E = cB.
Energia promieniowania
2
0
2
0
0
0
2
2
2
2
0
2
2
2
0
1
1
)
(
2
)
(
2
B
B
B
c
B
c
B
c
E
w
w
w
B
E
µ
ε
µ
ε
ε
ε
=
=
+
=
+
=
+
=
0
d
d
=
+
IR
t
I
L
rozwiązanie
L
t
L
Rt
e
R
e
R
I
τ
ε
ε
/
/
−
−
=
=
I
R
L
+
-
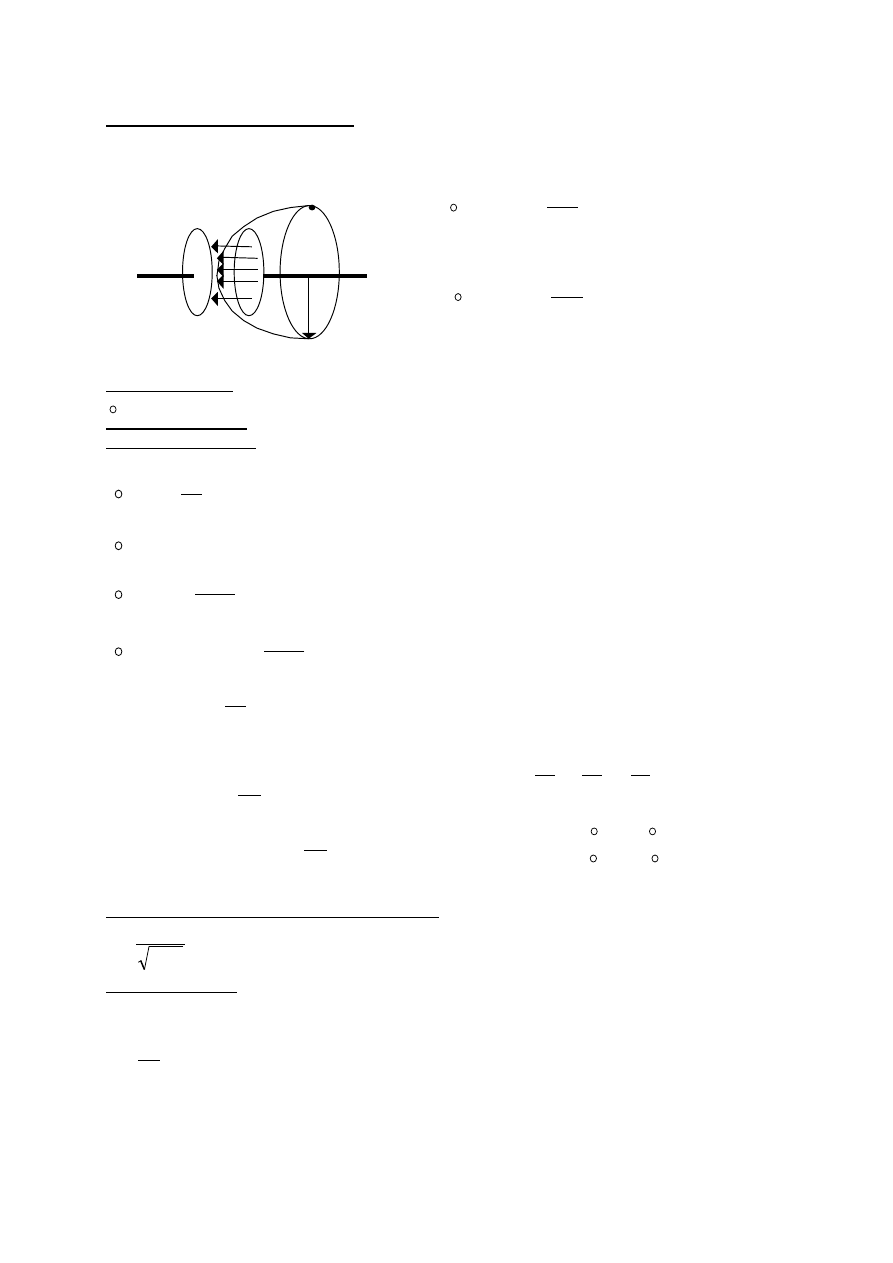
29
X. RÓWNIANIA MAXWELLA
Indukowane pole magnetyczne - w kondensatorze (cylindrycznym) powstaje tam pole
magnetyczne wytworzone przez zmieniające się pole elektryczne.
S
S'
E
i
i
r
P
Prąd przesunięcia
∫
+
=
)
(
d
0
I
I
P
µ
l
B
r
r
Równania Maxwella
Fale elektromagnetyczne
–
prędkość w próżni
0
0
1
ε
µ
=
c
Wektor Poyntinga
Szybkość przepływu energii przez jednostkową powierzchnię płaskiej fali
elektromagnetycznej można opisać wektorem S zwanym wektorem Poyntinga.
B
E
S
r
r
r
×
=
0
1
µ
W układzie SI jest on wyrażony w W/m
2
, kierunek S pokazuje kierunek przenoszenia energii.
Wektory E i B - chwilowe wartości pola elektromagnetycznego w rozpatrywanym punkcie.
∫
=
t
E
d
d
d
0
0
φ
ε
µ
l
B
r
r
prawo Ampera
po modyfikacji ma
postać
∫
+
=
I
t
E
0
0
0
d
d
d
µ
φ
ε
µ
l
B
r
r
Pole magnetyczne jest wytwarzane
przez przepływ prądu i/lub przez
zmieniające się pole elektryczne.
∫
∫
∫
∫
=
Φ
=
•
=
Φ
=
Φ
=
•
=
Φ
s
d
B
d
S
B
s
d
E
d
S
E
B
B
E
E
r
r
r
r
r
r
r
r
k
z
j
y
i
x
r
r
r
r
∂
∂
+
∂
∂
+
∂
∂
=
∇
)
(
0
0
0
0
0
P
E
B
I
I
t
I
l
d
B
t
l
d
E
s
d
B
q
s
d
E
+
=
∂
Φ
∂
+
=
∂
Φ
∂
−
=
=
=
∫
∫
∫
∫
µ
ε
µ
ε
r
r
r
r
r
r
r
r
∂
∂
+
=
×
∇
=
∂
∂
−
=
×
∇
=
=
•
∇
=
=
•
∇
=
t
E
J
B
B
rot
t
B
E
E
rot
B
B
div
E
E
div
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
0
0
0
0
ε
µ
ε
ρ
E
– natężęnie pola elektrycznego
B
– indukcja magnetyczna
ρ
- gęstość ładunku
ε
0
– przenikalność dielektryczna
µ
0
– przenikalność magnetyczna
J
– gęstość prądu
I – natężenie prądu
I
p
– prąd przesunięcia
ds
– element powierzchni
dl
– element przewodnika
Φ
B
– strumień pola magnetycznego
Φ
E
– strumień pola elektrycznego
∇
∇
∇
∇
- operator Nabla
Wyszukiwarka
Podobne podstrony:
drPera miedzynarodowe stosunki gospodarcze notatki do wykladow
MATERIALY DO WYKLADU CZ VIII i Nieznany
MATERIALY DO WYKLADU CZ V id 2 Nieznany
H.G. - wykład 10, Notatki do wykładów z Historii Gospodarczej (dr M
Materialy do wykladu (cz 1) id Nieznany
NOTATKI do wykładów, III, IV, V ROK, SEMESTR II, WPROWADZENIE DO PSYCHOFIZJOLOGII, notatki
Materialy do wykladu (cz 2) id Nieznany
Materialy do wykladu (cz 3) id Nieznany
Materialy do wykladu 5 (02 11 2 Nieznany
Algebra notatki do wykładu all
notatki do wykładów dla kursantów
Metody numeryczne dla inżynierów (notatki do wykładów)
Materialy do wykladu 1 (06 10 2 Nieznany
dynamika budowli notatki do wykładów[1] (1)
JPPO Wstep do wykladu id 228827 Nieznany
H.G. - wykład 11, Notatki do wykładów z Historii Gospodarczej (dr M
H.G. - wyklad 4, Notatki do wykładów z Historii Gospodarczej (dr M
7 Materialy do wykladow id 4529 Nieznany (2)
materialy do wykladow w 06 Samo Nieznany
więcej podobnych podstron