
Józef Szymczak
Politechnika Opolska
MACIERZE I WYZNACZNIKI (notatki z wykładu)
I. Macierze.
Niech
}
,...,
3
,
2
,
1
{
},
,...,
3
,
2
,
1
{
2
1
n
N
m
N
=
=
. Iloczyn kartezjański tych zbiorów oznaczamy symbolem
2
1
N
N
×
i definiujemy w następujący sposób:
}
,
:
)
,
{(
2
1
2
1
N
j
N
i
j
i
N
N
∈
∈
=
×
. Odwzorowanie iloczynu
kartezjańskiego
2
1
N
N
×
na pewien zbiór A nazywamy macierzą i zapisujemy ją w postaci prostokątnej tablicy
składającej się z m wierszy i n kolumn:
mn
m
m
n
n
a
a
a
a
a
a
a
a
a
A
...
.
...
.
.
...
...
=
2
1
2
22
21
1
12
11
.
Elementami macierzy mogą być liczby rzeczywiste, zespolone bądź funkcje.
Macierz możemy też zapisać w skróconej formie:
n
m
ij
a
A
×
=
]
[
,
gdzie indeks
n
m
×
oznacza wymiar (typ) macierzy. Zapis
ij
a
oznacza element macierzy należący do i-tego
wiersza oraz j-tej kolumny. Jeśli
n
m
=
, to mówimy, że macierz jest macierzą kwadratową n-tego stopnia.
Definicja 1. Dwie macierze są równe gdy mają ten sam wymiar i na tych samych miejscach te
same elementy, tzn.:
b
a
B
A
ij
ij
=
⇔
=
dla każdej pary
2
1
)
,
(
N
N
j
i
×
∈
.
Przykłady macierzy:
[
]
n
n
... a
a
a
A
1
12
11
1
=
×
– macierz wierszowa (mająca jeden wiersz i n kolumn);
=
×
1
21
11
1
.
m
m
a
.
.
a
a
A
– macierz kolumnowa (mająca jedną kolumnę i m wierszy);
n
m
...
.
...
.
.
...
...
×
=
0
0
0
0
0
0
0
0
0
Θ
– macierz zerowa wymiaru
n
m
×
,
Macierz diagonalna to macierz kwadratowa, której elementy poza główną przekątną są zerami:
nn
a
...
.
...
.
.
...
a
...
a
0
0
0
0
0
0
22
11
.
Główną przekątną tej macierzy stanowią elementy o równych indeksach pierwszym i drugim.

Macierz jednostkowa to macierz diagonalna, która na głównej przekątnej ma same jedynki. Oznaczamy ją
symbolem I
n
, gdzie indeks n oznacza stopień tej macierzy:
=
1
...
0
0
.
...
.
.
0
...
1
0
0
...
0
1
n
I
.
≠
=
1,2,...,
=
,
,
dla
0
dla
1
n
j
i
j
i
i=j
a
ij
.
Macierz transponowana do macierzy A wymiaru m
×
n to macierz wymiaru n
×
m, która powstaje z danej
macierzy przez zamianę wierszy z kolumnami (bez zmiany ich kolejności). Oznaczamy ją symbolem
T
A
. Na
przykład:
jeśli
f
e
d
c
b
a
A=
, to
=
f
c
e
b
d
a
T
A
.
Jeżeli spełniona jest równość
T
A
A
=
, to macierz A jest kwadratową macierzą symetryczną (w takiej
macierzy mamy
ji
ij
a
a
=
). Na przykład:
=
3
4
5
4
0
2
5
2
1
,
3
4
5
4
0
2
5
2
1
-
-
-
-
=
T
A
A
.
Zachodzi oczywista równość:
( )
A
A
T
T
=
.
Jeśli dla macierzy A zachodzi równość
A
A
T
−
=
, to mówimy, że A jest macierzą antysymetryczną.
II. Działania na macierzach.
Dodawanie macierzy jest określone tylko dla macierzy tego samego wymiaru:
n
m
ij
ij
n
m
ij
n
m
ij
b
a
b
a
A+B=
×
×
×
+
=
+
]
[
]
[
]
[
.
Na przykład
=
+
0
1
1
5
2
3
1
0
1
3
1
-
2
1
-
1
0
2
3
1
.
Dodawanie macierzy ma następujące własności:
−
jest działaniem łącznym:
C
B
A
C
B
A+
+
+
=
+
)
(
)
(
,
−
jest działaniem przemiennym:
A
B
A+B
+
=
,
−
elementem neutralnym dodawania macierzy jest macierz zerowa danego wymiaru:
A
A+Θ
=
,
−
do każdej macierzy A istnieje macierz przeciwna
A
−
tego samego wymiaru taka, że
Θ
A
A+
=
−
)
(
.
Na przykład
=
+
0
0
0
0
0
0
1
1
0
2
3
1
1
1
0
2
3
1
-
-
-
-
-
.
Mówimy, że ze względu na powyższe własności zbiór wszystkich macierzy danego wymiaru
n
m
×
M
z
działaniem dodawania stanowi
grupę przemienną.
Mnożenie macierzy przez liczbę (rzeczywistą lub zespoloną) polega na wymnożeniu przez tę liczbę
każdego elementu macierzy:
n
m
n
m
ij
ij
ka
a
k
A
k
×
×
=
⋅
=
⋅
]
[
]
[
.
Na przykład

=
⋅
15
-
20
0
30
5
-
10
3
-
4
0
6
1
-
2
5
.
Mnożenie macierzy przez liczbę ma następujące własności:
1
o
.
B
A
B
A
⋅
+
⋅
+
⋅
α
α
α
=
)
(
,
2
o
.
(
)
A
A
A
⋅
+
⋅
⋅
+
β
α
β
α
=
,
3
o
.
( )
(
)
A
A
⋅
⋅
⋅
β
α
αβ
=
,
4
o
. 1
⋅
A = A.
Ć
wiczenie 1. Obliczyć
B
A 4
3
−
jeśli
1
0
1
2
1
-
i
, B=
i
-i
i
A=
.
Mnożenie macierzy przez macierz.
Działanie to jest wykonalne tylko wtedy, gdy liczba kolumn pierwszej macierzy jest równa liczbie wierszy
drugiej macierzy. W wyniku mnożenia tych macierzy otrzymujemy macierz mającą tyle samo wierszy co
pierwsza macierz i tyle kolumn, ile ma druga macierz:
p
m
ij
p
n
ij
n
m
ij
c
C
B
A
b
B
a
A
×
×
×
=
=
=
=
⋅
]
[
]
[
]
[
,
,
,
gdzie elementy
ij
c
iloczynu wyznaczane są według wzoru:
nj
in
b
a
b
a
b
a
b
a
c
j
i
j
i
kj
n
k
ik
def
ij
⋅
+
+
⋅
+
⋅
=
⋅
=
∑
=
...
2
2
1
1
1
,
a więc element
ij
c
otrzymujemy sumując iloczyny odpowiednich elementów i-tego wiersza macierzy A i j-tej
kolumny macierzy B.
Przy mnożeniu macierzy wygodnie jest stosować tzw. schemat Falka, sporządzając prostą tabelę.
W lewym dolnym polu tabeli wpisujemy macierz A, a w prawym górnym
polu wpisujemy macierz B. Wynik otrzymujemy w prawym dolnym polu
tabeli, mając zawsze element
ij
c
na przedłużeniu
i
-tego wiersza macierzy A
oraz
j
-tej kolumny macierzy B.
Przykład. Pomnóżmy macierze
=
4
1
3
-
2
-
0
2
1
-
3
1
5
4
1
-
3
2
=
,
B
A
.
Stosując schemat Falka mamy:
4
11
8
13
16
2
11
-
11
-
12
7
11
-
0
1
5
4
1
-
3
2
4
1
3
-
2
-
0
2
1
-
3
−
⋅
B
A
, a więc
−
⋅
4
11
8
13
16
2
11
-
11
-
12
7
11
-
0
=
B
A
.
Przykład. Niech
=
3
-
2
-
3
2
4
2
-
6
-
3
=
,
B
A
. Wtedy
⋅
18
-
12
-
27
18
=
B
A

(sprawdzić). Zauważmy ponadto, że w tym przypadku możemy też wyznaczyć iloczyn B
⋅
A. Otrzymamy tutaj
⋅
0
0
0
0
=
A
B
(zauważmy, że iloczyn dwóch niezerowych macierzy może być macierzą zerową).
Uwaga. Mnożenie macierzy jest na ogół działaniem
nieprzemiennym.
Ć
wiczenie 2. Obliczyć A
⋅
B i B
⋅
A jeśli
[
]
6
5
4
,
3
2
1
=
=
B
A
.
Jeśli macierz A ma wymiar m
×
n, wtedy
A
A
I
I
A
=
m
n
⋅
=
⋅
(macierz jednostkowa jest elementem neutralnym mnożenia macierzy).
Iloczyn macierzy przy założeniu jego wykonalności ma własność łączności oraz własność rozdzielności
względem dodawania:
(
)
(
)
(
)
(
)
C .
B
C
C=A
A+B
C ,
A
B
A
B+C
A
,
C
B
C=A
B
A
⋅
+
⋅
⋅
⋅
+
⋅
=
⋅
⋅
⋅
⋅
⋅
Ć
wiczenie 3. Sprawdzić na wybranych przykładach, że zachodzą wzory:
(
)
(
)
.
T
T
T
T
T
T
,
A
B
B
A
B
A+B
A
⋅
=
⋅
+
=
Sprawdzić, że macierz
T
A+A jest symetryczna, a macierz
T
A
A
−
jest antysymetryczna, w przypadku, gdy
A jest macierzą kwadratową.
III. Wyznacznik macierzy kwadratowej.
Definicja 2.
Wyznacznikiem macierzy kwadratowej A (o elementach rzeczywistych lub zespolonych)
nazywamy funkcję, oznaczoną symbolem
A
A
lub
det
, przypisującą danej macierzy liczbę (rzeczywistą
lub zespoloną) w następujący sposób:
o
1
jeśli
[ ]
11
=
a
A
, to
11
det
a
A
=
,
o
2
jeśli A jest stopnia
2
n
≥
, to
n
n
n
A
a
A
a
A
a
A
1
1
1
12
12
2
1
11
11
1
1
det
(-1)
...
det
(-1)
det
(-1)
=
det
+
+
+
+
+
+
gdzie
k
A
1
oznacza macierz otrzymaną z macierzy A przez skreślenie 1-go wiersza i k-tej kolumny.
W szczególności, gdy
d
c
b
a
A=
, to
ad-bc
A
d
c
b
a
=
=
det
.
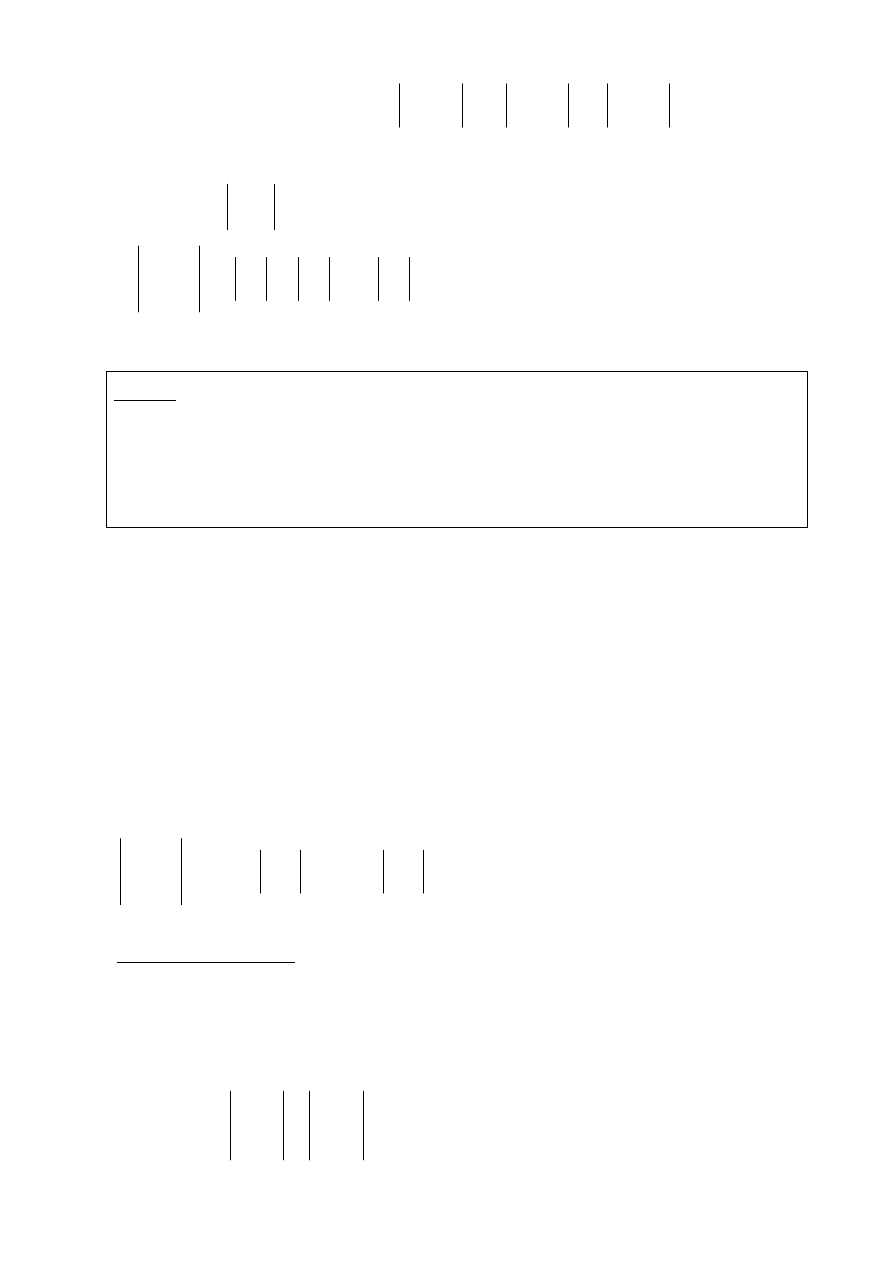
Gdy
33
32
31
23
22
21
13
12
11
=
a
a
a
a
a
a
a
a
a
A
, to
32
31
22
21
13
33
31
23
21
12
33
32
23
22
11
=
det
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
A
+
−
.
Na przykład: a)
23
4
)
2
(
5
3
5
2
4
3
=
⋅
−
−
⋅
=
−
,
b)
29
4
15
40
)
2
)(
2
(
5
3
10
4
4
3
2
1
-2)
(
5
3
0
1
3
5
4
0
2
4
5
4
3
0
2
1
2
-
3
4
=
+
−
=
−
−
+
⋅
−
⋅
=
⋅
+
⋅
−
⋅
=
.
c) Dla wyznacznika stopnia trzeciego, wygodną do obliczeń jest też tzw. metoda Sarrusa.
Definicja 3.
Dopełnieniem algebraicznym elementu
ij
a
macierzy kwadratowej
A stopnia
2
≥
n
nazywamy liczbę:
ij
i+j
A
ij
D
det
-1)
(
=
,
gdzie
ij
A jest macierzą stopnia n-1 powstałą z macierzy A przez skreślenie i-tego wiersza oraz j-tej
kolumny.
Jeżeli więc macierz A jest macierzą kwadratową stopnia n
≥
2, wtedy jej wyznacznik możemy obliczać
według wzoru:
(1)
=
det
2
2
1
1
in
in
i
i
i
i
D
a
...
D
a
D
a
A
+
+
+
lub według wzoru:
(2)
=
det
2
2
1
1
D
...+a
D
a
D
a
A
nj
nj
j
j
j
j
+
+
Wzór (1) nazywamy rozwinięciem Laplace’a wyznacznika względem
i-tego wiersza, a wzór (2) rozwinięciem
Laplace’a wyznacznika względem
j-tej kolumny.
Obliczymy przykładowo wyznacznik stopnia 3 dokonując rozwinięcia Laplace’a względem drugiego
wiersza:
29
52
23
5
3
2
-
4
2
+
2
-1)
(
2
5
4
2
-
3
1
2
)
1
-
(
1
5
4
3
0
2
1
2
-
3
4
=
+
−
=
⋅
+
+
⋅
=
.
Własności wyznaczników:
1.
A
A
det
det
T
=
.
2.
B
A
B
A
det
det
)
det(
⋅
=
⋅
.
3. Jeśli w macierzy kwadratowej przestawimy dwa dowolne wiersze (lub kolumny), to wartość jej wyznacznika
zmieni się na przeciwną.
Na przykład
1
3
2
2
2
0
0 - 1 2
-
= −
2
2
0
1
3
2
0
1 2
(zamieniono tu miejscami wiersze I oraz II).
4. Wspólny czynnik występujący w pewnym wierszu (lub kolumnie) można wyłączyć przed wyznacznik.

Na przykład
1
3 4
2
6
4
0
1
2
2
1
3 4
1
3 2
0 1 2
2 2
1
3 2
1
3 1
0 1
1
1
3
2
1
3
1
0
4
4
= ⋅
= ⋅ ⋅
=
.
5. Wyznacznik jest równy zero jeżeli:
a) elementami pewnego wiersza (kolumny) są same zera,
b) dwa wiersze (dwie kolumny) są identyczne,
c) dwa wiersze (dwie kolumny) mają odpowiednie elementy proporcjonalne.
Na przykład
2
1
3
0
0
0
1
2
4
0,
0,
4
0
=
=
=
1
2
7
4
3
2
1
2
7
- 4
- 3
2
4
3
- 2
8
6
-
.
6. Jeżeli w wyznaczniku do elementów pewnego wiersza dodamy odpowiednie elementy innego wiersza
pomnożone przez liczbę różną od zera, to wartość wyznacznika nie zmieni się (to samo dotyczy kolumn).
Na przykład
)
k
(k
))
2
-
(
w
w
(
.
1
0
1
1
2
(-1)
=
1
-
0
0
2
-
0
1
1
1
2
=
1
-
0
0
2
-
1
1
1
3
2
=
1
2
2
3
5
-
2
2
2
-
1
1
1
3
2
−
+
=
⋅
7. Jeżeli w wyznaczniku wszystkie elementy znajdujące się pod główną przekątną są równe zero, to wartość
wyznacznika jest równa iloczynowi wyrazów z głównej przekątnej.
Na przykład
2
5
1
7
0
3 2
4
0
0
1
2 3 1 2
12
- 8
0
0
0
2
= ⋅ ⋅ ⋅ =
.
Uwaga. Korzystając z przedstawionych własności wyznaczników, a szczególnie z własności (6), możemy
uprościć ich obliczanie przez uzyskanie w wybranym wierszu (lub kolumnie) możliwie jak największej ilości
zer.
Jeżeli detA = 0, to macierz kwadratową A nazywamy osobliwą. Jeżeli natomiast detA
≠
0, to mówimy, że
macierz A jest nieosobliwa.
IV. Macierz odwrotna.
Definicja 4. Niech macierz A będzie kwadratową macierzą nieosobliwą stopnia n. Macierzą odwrotną
do macierzy A nazywamy taką macierz B, która spełnia warunek:
n
A
B
B
A
I
=
⋅
=
⋅
.
Macierz odwrotną do
A
oznaczamy symbolem
A
-1
.
Istnieje kilka sposobów wyznaczania macierzy odwrotnej. Jeden z nich określa następujący wzór:
T
=
nn
n
n
n
n
D
...
D
D
.
...
.
.
D
...
D
D
D
...
D
D
A
A
2
1
2
22
21
1
12
11
det
1
1
-
,
gdzie elementy
ij
D
oznaczają dopełnienia algebraiczne elementów
ij
a
macierzy A. Aby więc wyznaczyć
macierz odwrotną do A należy utworzyć macierz dopełnień algebraicznych macierzy A, następnie ją
transponować i pomnożyć przez odwrotność wyznacznika macierzy A.
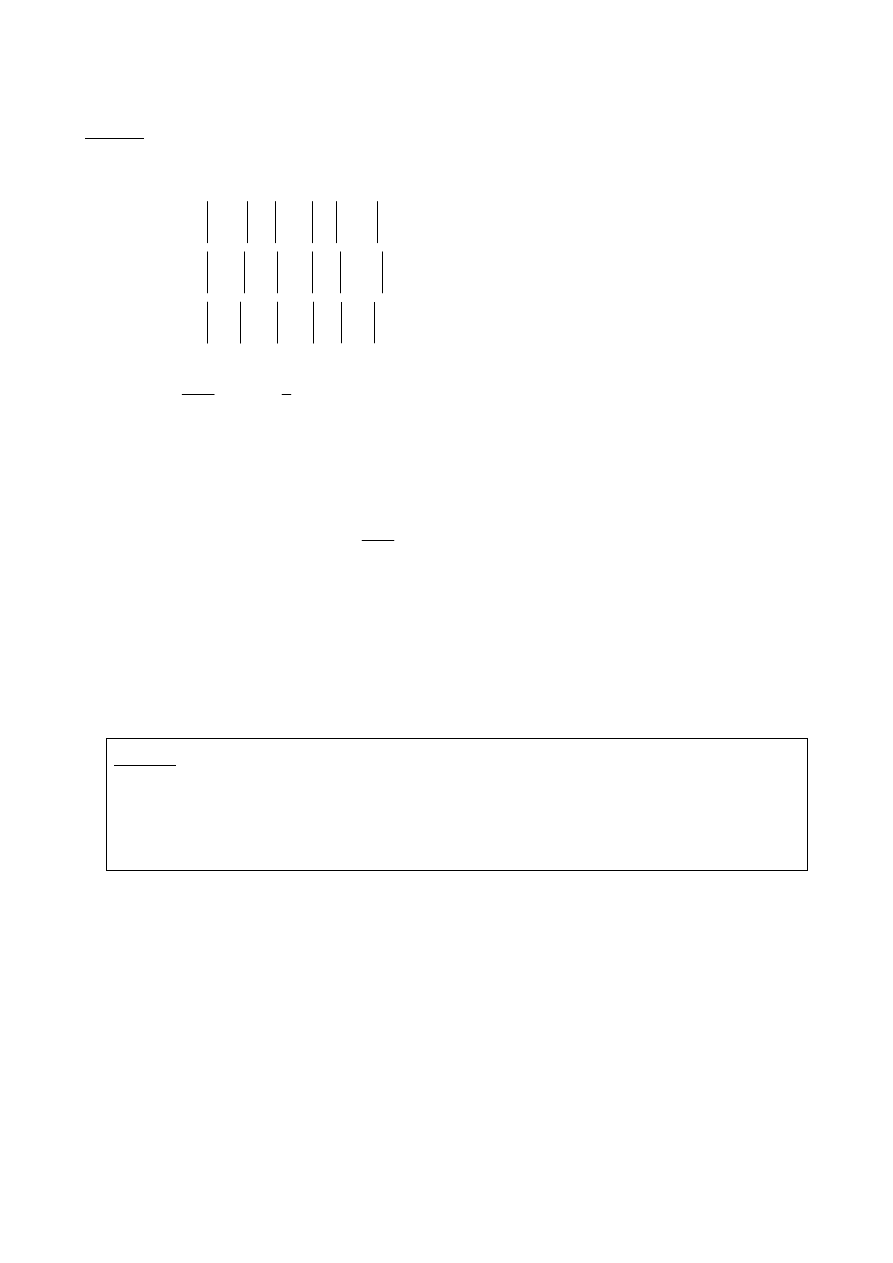
Przykład. Niech
1
2
-
1
-
0
1
2
1
1
0
=
A
. Zauważmy, że
5
det
−
=
A
. Oznaczmy przez
]
[
ij
D
macierz dopełnień
algebraicznych macierzy
A. Mamy zatem:
[ ]
,
,
2
-
1
-
3
-
2
1
2
-
1
-
3
-
1
2
-
2
1
-
1
-
1
3
-
3
-
2
-
1
1
2
1
0
0
2
1
0
0
1
1
1
2
-
1
-
1
0
1
1
-
1
0
1
2
-
1
1
2
-
1
-
1
2
1
1
-
0
2
1
2
-
0
1
T
-
-
-
-
]
[
=
=
=
ij
ij
D
D
[ ]
=
=
=
0,4
0,2
0,6
0,4
-
0,2
-
0,4
0,2
0,6
0,2
-
2
-
1
-
3
-
2
1
2
-
1
-
3
-
1
5
1
-
det
1
1
-
T
ij
D
A
A
.
Poprawność obliczeń sprawdzamy wymnażając otrzymaną macierz odwrotną przez macierz A. Powinniśmy
otrzymać macierz jednostkową.
Dla macierzy nieosobliwych drugiego stopnia można łatwo zapamiętać procedurę jej odwracania:
jeżeli
=
d
c
b
a
A
, to
=
a
c
b
d
A
A
-
-
det
1
-
1
Dla macierzy nieosobliwych zachodzi równość:
(
)
1
1
1
-
-
A
B
B
A
⋅
=
⋅
−
.
Sprawdzić tę równość na przykładzie macierzy:
.
1
1
2
0
1
2
3
1
=
i
=
B
A
Definicja 5.
Przekształceniami elementarnymi macierzy są
1. Pomnożenie dowolnego wiersza (kolumny) przez liczbę różną od zera.
2. Zamiana miejscami dwóch dowolnych wierszy (kolumn).
3. Dodanie do dowolnego wiersza (kolumny) elementów innego wiersza (innej kolumny)
pomnożonych przez liczbę różną od zera.
Macierz B otrzymaną z macierzy A przez wykonanie skończonej ilości przekształceń elementarnych
nazywamy macierzą
równoważną macierzy A, co zapisujemy symbolicznie: A
∼
B.
W każdej macierzy A wymiaru m
×
n możemy wyodrębnić pewną liczbę tzw.
minorów, czyli
podwyznaczników stopnia s
≤
min(m, n). Na przykład w macierzy wymiaru 3
×
4 możemy wyodrębnić 4 minory
stopnia trzeciego (wykreślając za każdym razem inną kolumnę), 18 minorów stopnia drugiego i 12 minorów
stopnia pierwszego (są to poszczególne elementy tej macierzy).
s
r
q
p
h
g
f
e
d
c
b
a

Definicja 6. Rzędem macierzy A wymiaru m
×
n nazywamy liczbę równą maksymalnemu ze stopni
minorów danej macierzy różnych od zera.
Rząd macierzy A będziemy zapisywali symbolicznie:
)
( A
r
(lub też
)
( A
rank
).
Na przykład jeśli
3
0
0
5
2
0
1
3
2
=
A
, to
3
)
(
=
A
r
, ponieważ
0
12
det
≠
=
A
(jest niezerowy minor stopnia
trzeciego i nie ma niezerowych minorów wyższego stopnia). Łatwo zauważyć z kolei, że
[
]
1
4,
1,
1,
,
2
0
0
0
0
0
1
2
3
2
0
0
0
1
2
0
0
1
2
3
0
1
2
2
2
5
0
2
1
4
3
2
1
0
0
1
=
=
=
=
=
r
r
r
r
r
Uwaga. Przekształcenia elementarne nie zmieniają rzędu macierzy, stąd też macierze równoważne mają ten
sam rząd.
W celu wyznaczenia rzędu dowolnej macierzy, dogodnie jest przekształcić ją do postaci diagonalnej w
pierwszym najwyższym stopniem minorze. Robimy to za pomocą przekształceń elementarnych, nie
zmieniających rzędu macierzy.
Przykładowo wyznaczmy rząd macierzy
6
-
3
-
0
1
-
3
0
6
2
3
1
2
1
=
A
.
Przekształcając ją, mamy:
)
y w
(wykreslam
)
w
(w
)
w
,
2
(w
0
0
0
0
3
-
2
-
2
0
3
1
2
1
3
-
2
-
2
0
3
-
2
-
2
0
3
1
2
1
6
-
3
-
0
1
-
3
0
6
2
3
1
2
1
3
2
3
1
3
1
2
=
=
=
=
)
(
−
+
−
w
w
r
r
A
r
r
/2)
(w
)
w
(w
.
1,5
-
1
-
1
0
6
3
0
1
3
-
2
-
2
0
6
3
0
1
3
-
2
-
2
0
3
1
2
1
2
2
1
2
=
=
=
−
=
r
r
r
(W ostatniej macierzy, równoważnej poprzednim, pierwszy minor
1
0
0
1
jest niezerowym minorem stopnia
drugiego, stąd r(A) = 2).
Uwaga.
Wykorzystując przekształcenia elementarne macierzy, możemy w dość prosty sposób wyznaczyć macierz
odwrotną do każdej macierzy nieosobliwej. Należy po prostu po napisaniu danej macierzy dopisać jeszcze obok
niej macierz jednostkową tego samego stopnia. Będziemy mieli więc blokową macierz wymiaru
n
n 2
×
.
Następnie wykonujemy na takiej macierzy przekształcenia elementarne –
tylko na wierszach – postępując w
ten sposób, aby daną macierz doprowadzić do postaci jednostkowej. Wówczas pierwotny blok jednostkowy
przekształci się do macierzy odwrotnej względem wyjściowej macierzy.
[ ]
⇒⇒⇒⇒⇒⇒
1
-
A
I
I
A
ch
na wiersza
wykonywane
e
elementarn
cenia
przeksztal

Zadanie. Rozwiązać dane równanie macierzowe:
.
1
3
5
2
1
1
2
0
1
2
3
4
T
X
=
+
⋅
Rozwiązanie: Na początek wykonujemy transponowanie po obu stronach równości i otrzymujemy
+
⋅
=
=
1
5
3
2
1
3
5
2
1
1
2
0
1
2
3
4
T
X
. Z kolei przenosimy na prawą stronę wolną macierz znajdującą się po
lewej stronie równości i odejmujemy od macierzy znajdującej się z prawej strony:
⋅
=
−
=
0
4
1
2
1
1
2
0
1
5
3
2
1
2
3
4
X
. Mamy zatem równanie
⋅
=
0
4
1
2
1
2
3
4
X
z niewiadomą macierzą X,
która jest macierzą wymiaru
2
2
×
i którą w tym przypadku wyliczymy mnożąc obie strony równania przez
macierz odwrotną do macierzy znajdującej się przy X. Mnożenie to należy wykonać z prawej strony po obu
stronach równania ze względu na nieprzemienność mnożenia macierzy. Macierzą odwrotną do macierzy
1
2
3
4
jest macierz
=
2
-
1
5
,
1
5
,
0
-
4
2
-
3
-
1
2
1
-
.
⋅
=
0
4
1
2
1
2
3
4
X
,
⋅
⋅
⋅
=
0
4
1
2
2
-
1
5
,
1
5
,
0
-
1
2
3
4
2
-
1
5
,
1
5
,
0
-
X
,
⋅
−
+
+
=
⋅
=
0
1
8
-
2
0
0,5
-
6
1
-
0
4
1
2
2
-
1
5
,
1
5
,
0
-
X
I
,
=
1
6
-
0,5
-
5
X
.
Wyszukiwarka
Podobne podstrony:
macierze i wyznaczniki, wyklad Nieznany
Macierze wyznaczniki Wykład 3
2 Zadania do wykladu Macierze wyznaczniki
2 Zadania do wykladu Macierze wyznaczniki
Prawo cywilne notatki z wykładów prof Ziemianin
macierze i wyznaczniki lista nr Nieznany
prof łaszczyca przwo administracyjne notatki z wykładów5
Filozofia Notatki z wykładów Zdrenka
Teoria kultury - Socjologiczna teoria kultury, Kulturoznawstwo, Teoria kultury - notatki z wykładów
Marketing społeczny notatki z wykładów, notatki - pedagogika, edukacja
Wykład 4 ewolucja, EWOLUCJA, notatki wykład
Macierze i wyznaczniki, Politechnika Poznańska, Elektrotechnika, Matematyka, semestr 2
szacka notatki z wykładów, socjologia
Podstawy marketingu notatki z wykładów
etyka w rachunkowości notatki z wykładu 1
Notatki wykład 1
Marketing w turystyce notatki z wykładów
więcej podobnych podstron