Wykład 4                                                                                                                             24.03.2013r.

MECHANICZNE WŁASNOŚCI SKAŁ

Są to własności, które charakteryzują zachowanie się skał przy oddziaływaniu na nie 
mechanicznych obciążeń. W zależności od typu, wielkości i czasu działania obciążenia powstają 
różnorodne związki pomiędzy naprężeniami i odkształceniami. Wyróżniamy następujące grupy 
własności:

–

Własności sprężyste (odkształceniowe) skał:charakteryzują one związki pomiędzy 
naprężeniami i odkształceniami sprężystymi (odwracalnymi).

–

Własności wytrzymałościowe skał: charakteryzują związki pomiędzy naprężeniami i 
odkształceniami niszczącymi (nieodwracalnymi).

–

Własności plastyczne skał: charakteryzują związek pomiędzy naprężeniami i 
odkształceniami nieodwracalnymi zachodzącymi bez naruszenia ciągłości skały.

–

Własności reologiczne skał: charakteryzują zmiany podanych wyżej własności przy 
długotrwałym oddziaływaniu obciążeń.

SPRĘŻYSTE (ODKSZTAŁCENIOWE) WŁASNOŚCI SKAŁ

Naprężenie – jest miarą sił wewnętrznych wywiązujących się w ciele stałym w rezultacie działania 
przyłożonych doń sił, lub innych czynników dążących do odkształcenia ciała. Naprężenie jest 
wielkością tensorową, którą można sobie uzmysłowić jako całość sił działających wzdłuż krawędzi 
nieskończenie małego sześcianu wpisanego w to ciało. W przybliżeniu wartość danego naprężenia 
określamy jako graniczną wartość stosunku siły działającej na nieskończenie mały element pola 
przekroju ciała do wymiaru tego pola. W obliczeniach praktycznych wartość naprężenia przyjmuje 
się jako wartość stałą określoną przez stosunek siły do powierzchni w dowolnym punkcie 
przekroju. 

Odkształcenie (deformacja – na większą skalę, deformacja terenu) – to zmiana kształtu, objętości 
lub jednocześnie kształtu i objętości ciała. Zmiana kształtu to tzw. odkształcenie postaciowe. 
Zmiana objętości to tzw. odkształcenie objętościowe. Każde odkształcenie powoduje zmianę 
ustawienia cząstek elementarnych, co w przypadku skały wiąże się z powstaniem sił wewnętrznych 
przeciwdziałających tej zmianie. Odkształcenie skały jest więc nierozerwalnie związane z 
wywiązywaniem się naprężeń. 

Własności odkształceniowe – określane są modułami sprężystości, czyli współczynnikami 
proporcjonalności pomiędzy naprężeniami i odkształceniami. Wyróżniamy następujące moduły 
sprężystości:

➔

moduł Younga (sprężystości podłużnej) 

E

σ=

E ⋅ε

Jest to współczynnik proporcjonalności między wielkością naprężeń normalnych 
(ściskających/rozciągających) i odkształceniem względnym występującym wzdłuż osi próbki. 

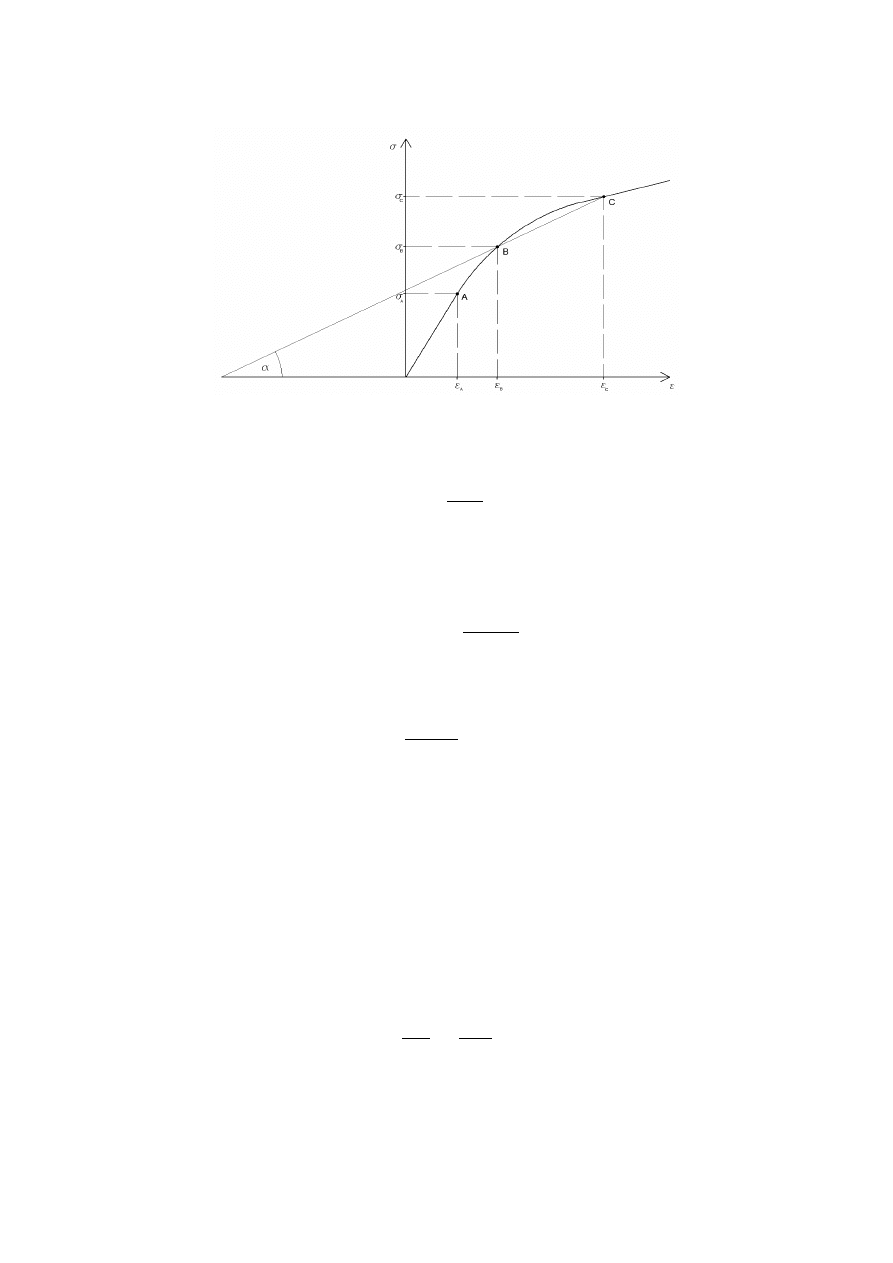
Wartość modułu zmienia się w zależności od obciążenia:

W punkcie A wykresu wartość modułu 

E

określana jest pochodną funkcji naprężenia względem 

odkształcenia:

E

A

=

d σ

A

d E

A

w pewnym przedziale naprężeń moduł sprężystości określa się za pomocą tangensa kąta nachylenia 
cięciwy łączącej dwa punkty krzywej.

E

BC

=

tg α =

σ

C

– σ

B

σ

C

−σ

B

Praktycznie moduł sprężystości podłużnej określa się z zależności:

E=

Δ

F ⋅h

S ⋅Δh

,[ Pa ]

Δ

F

 – różnica obciążeń końcowego i początkowego (wstępnego) Δ

F= F

K

−

F

W

przy czym: 

F

K

=

R

C

⋅

S ⋅ 75%

F

W

=

R

C

⋅

S ⋅ (0,10~0,15)%

h

 – wysokość początkowa próbki

S

 – pole przekroju początkowego próbki

Δ

h

 – uśrednione skrócenie próbki

W wyniku ściskania, materiał skalny zagęszcza się. Zwiększa się powierzchnia kontaktu ziarn, a 
zmniejsza zdolność skały do odkształceń. Powoduje to wzrost modułu sprężystości podłużnej

E

.

➔

współczynnik Poisssona,  ν

Δ

d

d

=ν

⋅Δ

l

l

jest to współczynnik proporcjonalności między względnymi odkształceniami poprzecznymi oraz 
względnymi odkształceniami wzdłużnymi. Wartość odwrotności współczynnika Poissona zmienia 
się od głębokości zalegania skał, a tym samym zmienia się od ciśnienia pionowego pochodzącego 
od skał nadległych.

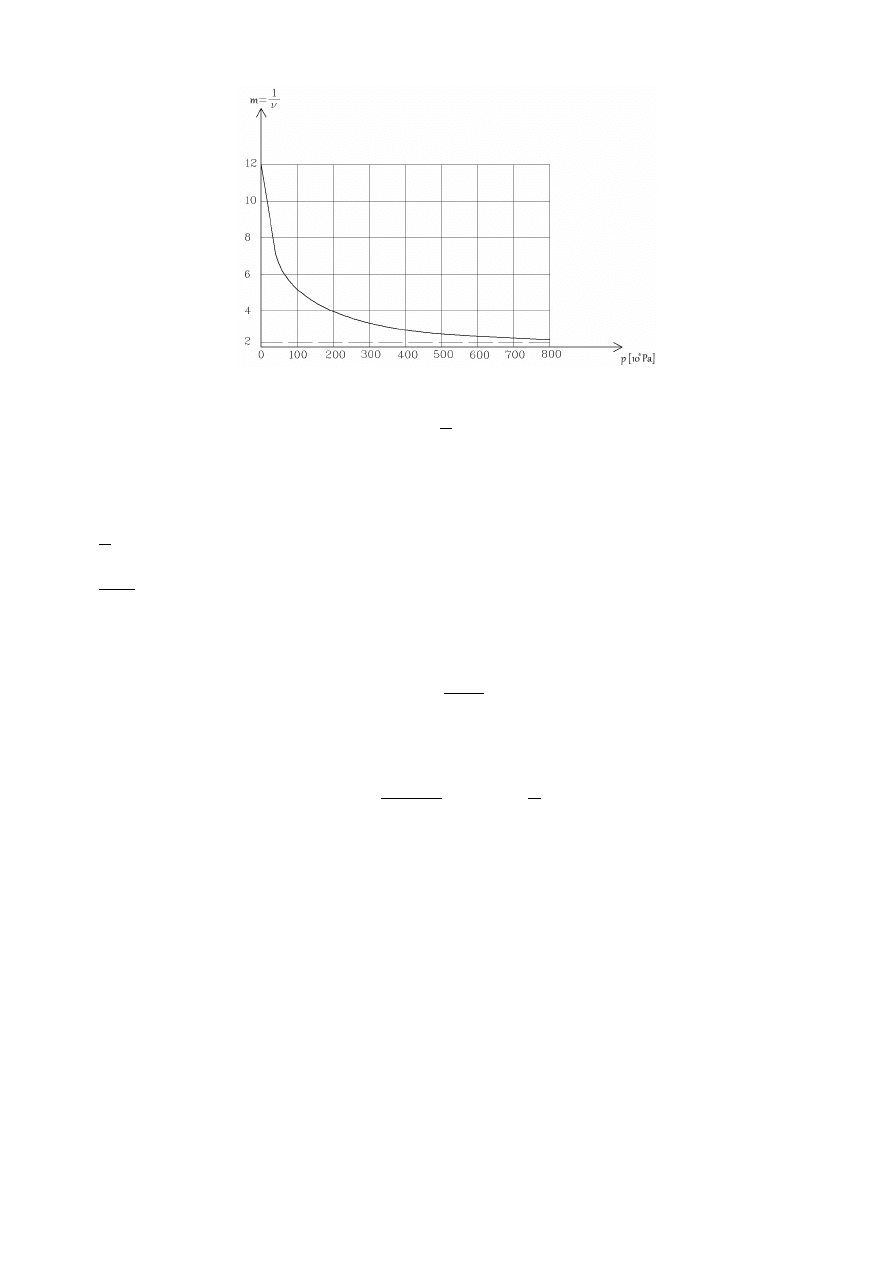
Dla danego piaskowca przy małym obciążeniu 

1

ν =m=12  ze wzrostem obciążenia maleje, 

zdążając asymptotycznie do granicy  m=2 , co odpowiada nieściśliwości materiału. Materiał 
nieściśliwy to taki, który zachowuje swoją objętość przy ściskaniu i rozciąganiu. 
Wprowadzamy następujące oznaczenia:

1

ν =m

ν

1−ν

=λ

r

 , gdzie λ

r

to współczynnik rozporu bocznego.

Dla górotworu sprężystego (odpowiadającego prawu Hooka):

  λ

r

=

1

m−1

Dla górotworu ziarnisto-sypkiego (bez kohezji):

  λ

r

=

1−sin φ

1+sin φ

=

tg

2

(

45

o

−

φ

2

)

φ

– kąt tarcia wewnętrznego (charakterystyczny dla ośrodka ziarnisto–sypkiego)

Wartość współczynnika Poissona zawarta jest w granicach

0<ν<0,5

, dolna granica 

charakterystyczna jest dla ośrodka doskonale ściśliwego, górna charakterystyczna dla ośrodka 
absolutnie nieściśliwego. Teoretycznie można przyjąć również i wartości 

2<m<∞

,

0<λ

r

<

1

. 

Duże wartości m dotyczą małej głębokości, natomiast małe wartości m dotyczą głębokości 
dużych. Ze wzrostem głębokości rośnie składowa pozioma ciśnienia pierwotnego, wraz ze zmianą 
współczynnika rozporu bocznego. 

➔

moduł Kirchoffa (sprężystości postaciowej)  G

τ=

G ⋅γ

Jest to współczynnik proporcjonalności między wielkością naprężeń stycznych τ
i odpowiadającym im odkształceniom postaciowym  γ  charakteryzującym zmianę kształtu ciała. 

➔

moduł sprężystości objętościowej  K

σ=

K

⋅Δ

V

V

Jest to współczynnik proporcjonalności między naprężeniami ściskającymi  σ  i względną zmianą 

objętości 

Δ

V

V

.

➔

moduł jednostronnego ściskania M , tzw. edometryczny moduł ściśliwości

σ=

M

⋅Δ

l

l

Jest to współczynnik proporcjonalności między naprężeniami podłużnymi i odpowiadającymi im 
odkształceniami względnymi podczas ściskania próbki skalnej w nieodkształcalnym cylindrze. 
Edometryczny moduł ściśliwości jest wielkością charakterystyczną dla skał sypkich i spoistych, 
czyli gruntów.

Wszystkie moduły sprężystości, zwane też stałymi materiałowymi związane są między sobą 
zależnościami matematycznymi. W skałach liniowo-sprężystych izotropowych wystarcza 
znajomość jedynie dwóch stałych materiałowych. Pozostałe mogą być wyznaczane na podstawie 
związków teorii sprężystości. 

Skały nie są ciałami doskonale sprężystymi, jednak dla uproszczenia matematycznego opisu 
procesów mechanicznych zachodzących w ośrodku skalnym niejednokrotnie przyjmuje się 
założenie o sprężystości liniowej skał, a charakterystyki naprężeniowo-odkształceniowe 
aproksymuje się liniami prostymi. 

WŁASNOŚCI WYTRZYMAŁOŚCIOWE SKAŁ 

Przez wytrzymałość skał rozumie się ich zdolność do przeciwstawiania się zewnętrznym 
obciążeniom niszczącym. Inaczej, jest to największa wartość naprężeń jaką dana skała może 
przenieść nie ulegając zniszczeniu. Każde działanie sił zewnętrznych powoduje powstanie w skale 
naprężeń, które rosną w miarę zwiększania się tych sił. Z chwilą przekroczenia wartości sił 
międzycząsteczkowych następuje zmiana pierwotnego kształtu skały, czyli odkształcenie.

Własności odkształceniowe charakteryzowane są przez wytrzymałości doraźne. Wyróżniamy:

➔

wytrzymałość doraźną na ściskanie

R

c

R

c

=

F

S

,

N

m

2

Jest to stosunek największej krytycznej siły ściskającej niszczącej próbkę  F  do pola 
powierzchni jej początkowego przekroju poprzecznego S .

➔

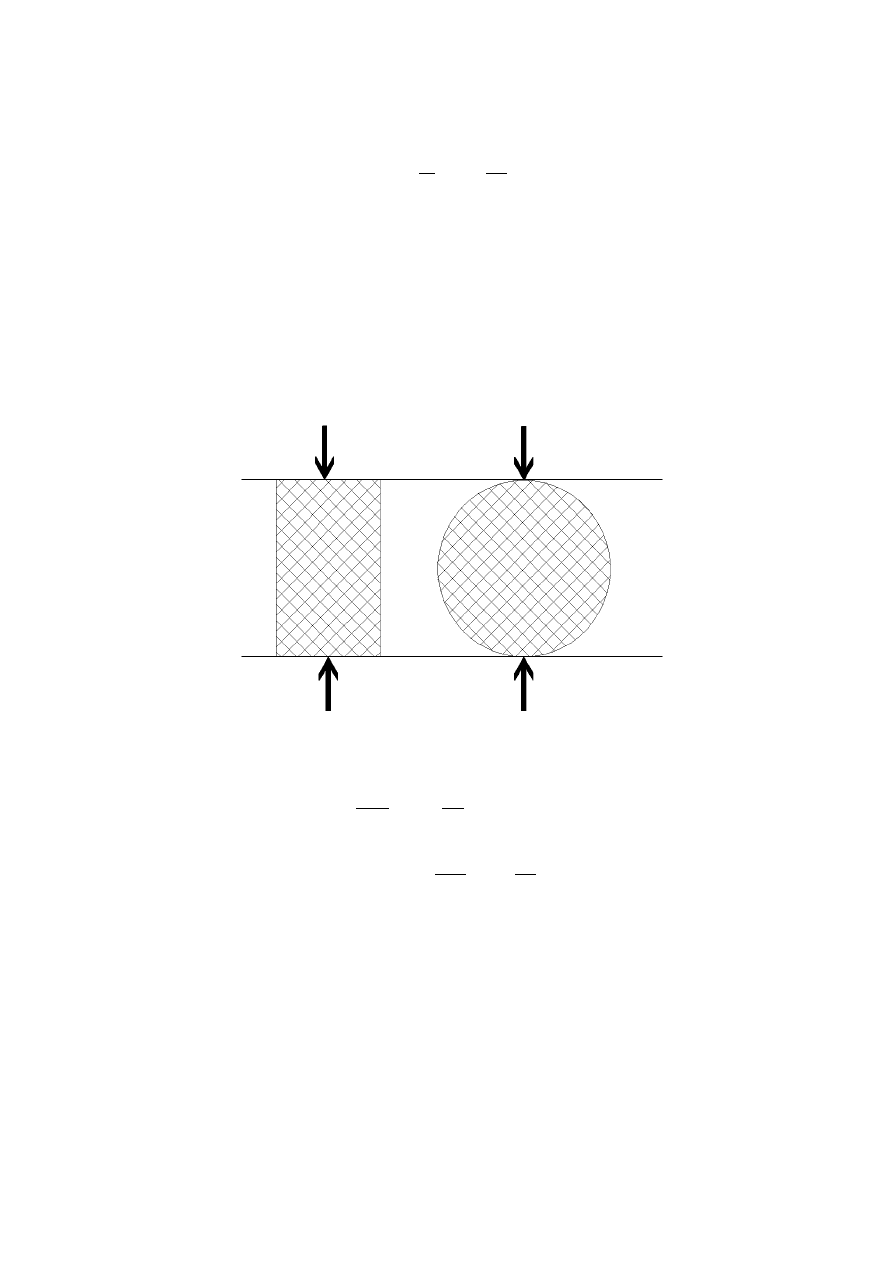
wytrzymałość doraźną na rozciąganie

R

r

R

r

=

F
S

,

N

m

2

Jest to stosunek największej siły rozciągającej przy której próbka ulega zniszczeniu, do pola 
powierzchni jej początkowego przekroju poprzecznego. 

Najwygodniejszą metodą badania

R

r

jest metoda poprzecznego ściskania. Polega ona na 

obciążaniu próbki skalnej w kształcie walca lub prostopadłościanu siłą ściskającą równomiernie 
rozłożoną wzdłuż tworzącej walca, lub wzdłuż podłużnej krawędzi prostopadłościanu. 

Wykorzystujemy w tym przypadku zależności:

Dla próbek walcowych:   R

r

=

0,637

F

d ⋅h

,

[

N

m

2

]

Dla próbek prostopadłościennych:    R

r

=

0,734

F

b ⋅h

, [

N

m

2

]

F

– siła krytyczna

d

– średnica próbki

h

– wysokość próbki

b

– przekątna podstawy prostopadłościanu 

➔

wytrzymałość doraźną na ścinanie 

R

t

R

t

=

F

S

, [

N

m

2

]

Przy czystym ścinaniu wytrzymałość R

t

definiowana jest jako stosunek krytycznej siły F

do pola powierzchni ścięcia

S

. Na ogół wytrzymałość na ścinanie charakteryzowana jest przez 

dwa parametry: spójność i kąt tarcia wewnętrznego wg zależności:

τ=σ

n

⋅

tg φ+c

τ

– graniczne naprężenie ścinające

σ

n

– naprężenie normalne

φ

– kąt tarcia wewnętrznego

c

– spójność

➔

wytrzymałość doraźną na zginanie R

g

Jest to krytyczna wartość naprężenia przy którym próbka skalna poddana obciążeniu zginajacemu 
ulega zniszczeniu. Dla próbki skalnej w kształcie beleczki swobodnie podpartej na końcach a 
obciążonej siłą skupioną w połowie długości beleczki wytrzymałość na zginanie obliczamy z 
zależności:

R

g

=

M

g

W

x

=

3 ⋅F ⋅l

2 ⋅b ⋅h

2

, [

N

m

2

]

gdzie:

F – siła łamiąca beleczki

l – odstęp podpór beleczki
h – wysokość tego przekroju
b – szerokość przekroju poprzecznego beleczki

Najczęściej, ze względu na wygodę, określamy wytrzymałość doraźną na ściskanie. 

Orientacyjne zależności pomiędzy wytrzymałościami są następujące:

R

C

>

R

t

>

R

g

>

R

r

Dokonuje się pomiarów

R

C

i

R

r

, resztę liczy się ze wzorów. 

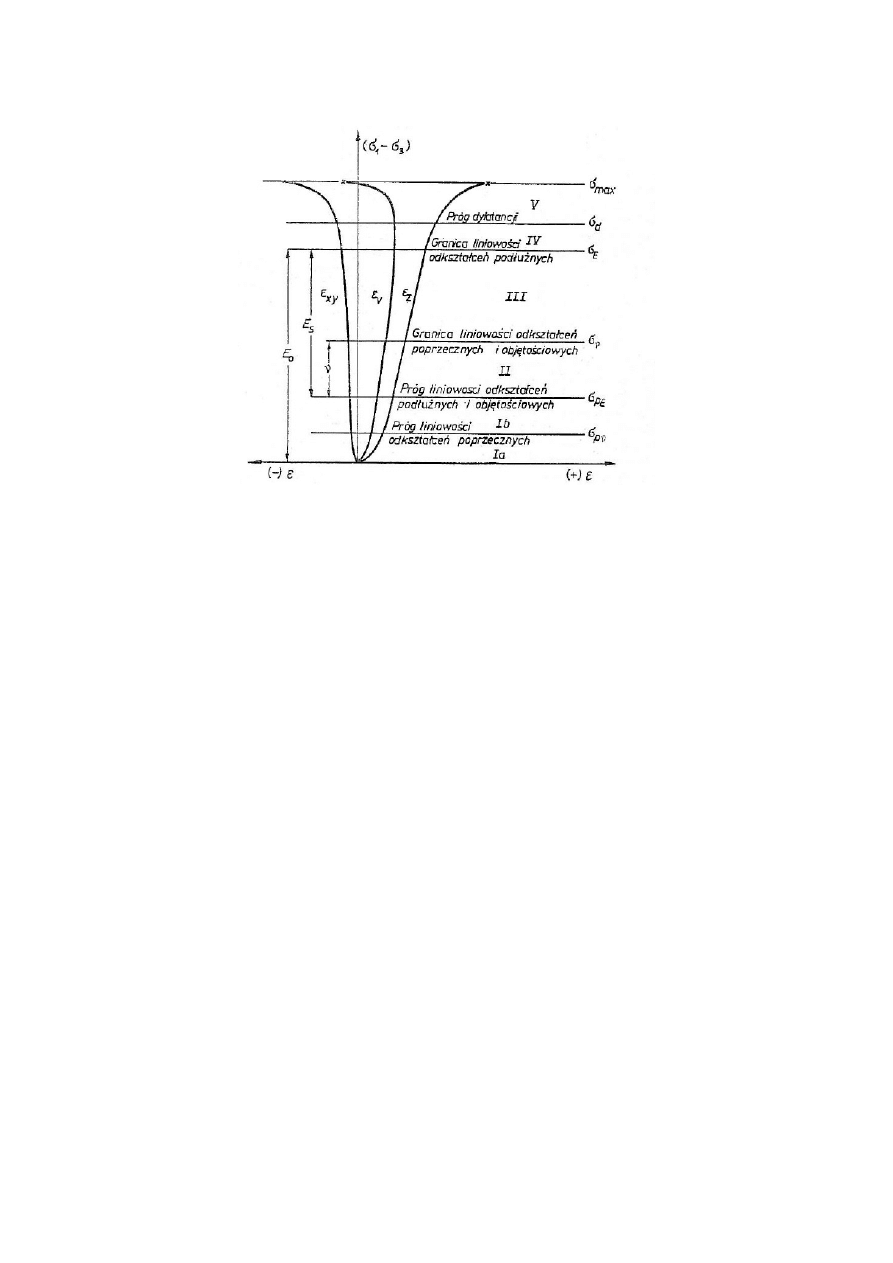
MECHANIZM ZNISZCZENIA SKAŁY KRUCHEJ

Na charakterystykę odkształceniowo – naprężeniową uzyskaną przy ściskaniu próbki skały kruchej 
można wyróżnić:

–

krzywą ε

Z

– jest to krzywa odkształcenia podłużnego

–

krzywą ε

xy

– jest to krzywa odkształcenie poprzecznego

–

krzywą ε

V

– jest to krzywa odkształcenia objętościowego

Na wyżej wymienionej charakterystyce można wyróżnić następujące stadia odkształcenia i 
zniszczenia skały: 

–

( I ) stadium nieliniowego odkształcania się skały: pod wpływem działania naprężenia 
następuje zamykanie mikroszczelin, mikroporów. Krzywa odkształceń podłużnych wygięta 
jest zwykle w kierunku osi  ε  – im skała bardziej zbita, tym krzywizna mniejsza, 
odkształcenia poprzeczne wzrastają, zwiększa się więc wartość współczynnika Poissona i 
modułu sprężystości.

–

( II ) stadium liniowego odkształcania się skały: w tym stadium przyrosty odkształceń są 
proporcjonalne do przyrostów naprężeń. Stosunek poprzecznego i podłużnego odkształcenia 
jest stały. 

–

( III ) stadium liniowości odkształceń podłużnych ε

z

 i nieliniowości odkształceń 

poprzecznych i objętościowych. W stadium tym rozpoczyna się propagacja mikroszczelin 
pierwotnych, towarzyszy jej względny wzrost objętości skały. Moduł sprężystości podłużnej 
jest jeszcze stały, natomiast współczynnik Poissona rośnie.

–

( IV ) stadium nieliniowego odkształcania się skały: następuje tu wzrost odkształceń 
poprzecznych, moduł sprężystości podłużnej maleje, natomiast współczynnik Poissona 
rośnie. 

–

( V ) stadium dylatacji (stadium nieliniowego odkształcania się skały i bezwzględnego 
wzrostu objętości): następuje tu niekontrolowana i niestabilna propagacja makrospękań, 
stadium kończy się osiągnięciem przez próbkę granicy wytrzymałości. 

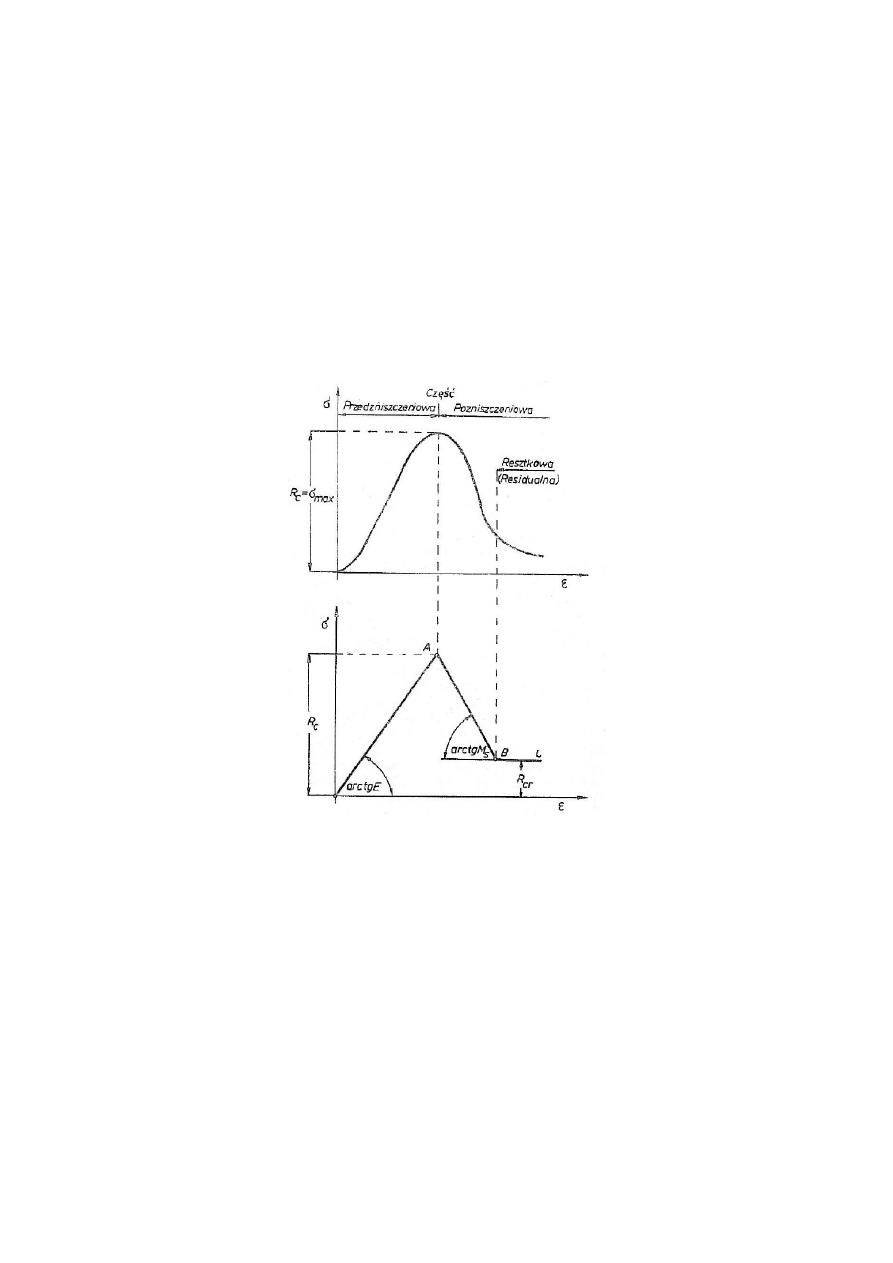
Przy ściskaniu próbek skalnych w tzw. miękkich maszynach wytrzymałościowych otrzymuje się 
informacje o wznoszącej części charakterystyki naprężenie-odkształcenie, gdyż w chwili 
zniszczenia próbka ulega dynamicznemu rozpadowi. Z chwilą skonstruowania tzw. sztywnych 
maszyn wytrzymałościowych uzyskano pełną charakterystykę naprężenie-odkształcenie, na której 
wyróżniamy: 

–

część wznoszącą, identyczną jak w przypadku prowadzenia badań w maszynie miękkiej

–

część opadającą cechującą się tym, że mimo rozpoczęcia procesu zniszczenia próbka w 
miarę wzrostu odkształceń posiada pewną nośność, przy czym nośność ta jest funkcją 
malejącą odkształceń. Badania na maszynach sztywnych pozwalają stwierdzić, że po 
przekroczeniu wytrzymałości skały powstające w niej naprężenia znajdują się w stałej 
równowadze z przyłożonym obciążeniem. 

Dysponując sztywnymi maszynami wytrzymałościowymi można określić:

–

moduł sprężystości

E

, określany jako tangens kąta nachylenia wznoszącej części 

krzywej do osi odciętych.

–

moduł spadu M

s

określany jako tangens kąta nachylenia opadającej części krzywej do 

osi odciętych. 

Maksymalne naprężenie w charakterystyce nieliniowej lub zlinearyzowanej trzema odcinkami linii 
prostej przyjmuje się za granicę wytrzymałości na ściskanie.

Najmniejsze naprężenie, jakie występuję w części pozniszczeniowej przyjmuje się za wytrzymałość 
resztkową (rezydualną).