Wykład 3 23.03.2013r.
STRUKTURALNE WŁASNOŚCI SKAŁ I GRUNTÓW
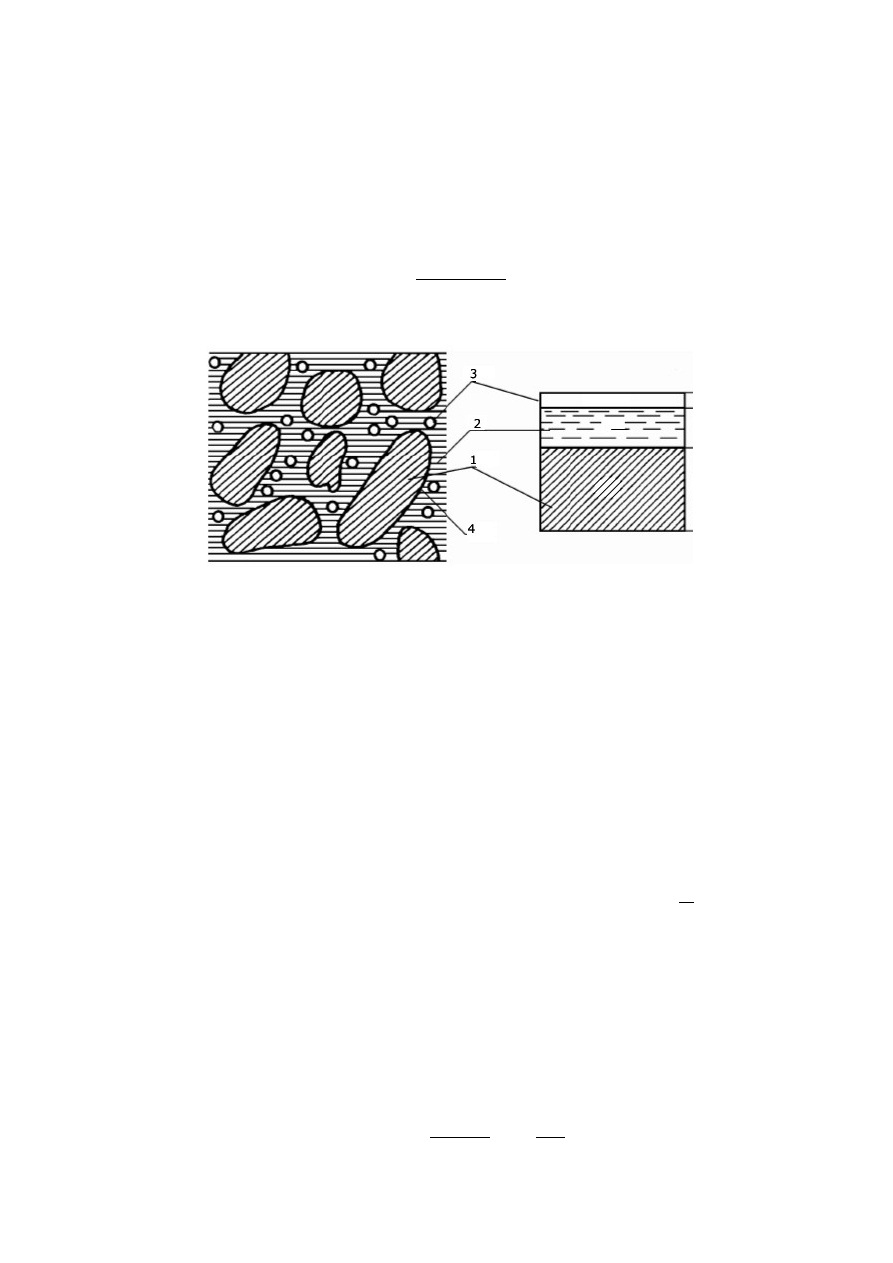
Podstawowym magnetem charakteryzującym własności strukturalne ośrodka skalnego jest gęstość.
W ogólnym przypadku określona jest ona jako stosunek sumy mas fazy stałej m
1
, ciekłej m
2
i
gazowej
m
3
do sumy objętości tych faz:
ϱ
r
=
m
1
+
m
2
+
m
3
V
1
+
V
2
+
V
3
Składniki gruntów i skał:
1. Cząstki mineralne.
2. Woda.
3. Powietrze.
4. Woda błonkowa.
W praktyce objętość i masę dowolnego elementu wyciętego z warstwy skalnej przedstawiamy
następująco:
V =V
1
+
V
2
+
V
3
m=m
1
+
m
2
Wyróżniamy:
–
gęstość objętościową: stosunek masy próbki skalnej do jej objętości ρ =
m
V
można ją
określać następującymi metodami:
•
w pierścieniu (badamy grunty o strukturze nienaruszonej): pierścień należy wcisnąć w
grunt, tym sposobem wypełniając pierścień w całości, wyrównujemy brzegi pierścienia,
ważymy wytarowaną próbkę (przy znanych wymiarach), określamy jego objętość.
•
w cylindrze (badamy grunty sypkie, niespoiste)
Badanie w pierścieniu lub cylindrze wypełnionym gruntem przeprowadza się
wykorzystując następującą zależność:
ρ =
m
mt
−
m
t
V
P
, [
g
cm
3
]

m
mt
– masa pierścienia/cylindra wraz z gruntem
m
t
– masa samego pierścienia/cylindra
V
P
– objętość próbki
•
w wodzie: próbkę skalną po określeniu jej masy zanurzamy w roztopionej parafinie w
celu uzyskania powłoki zamykającej z zewnątrz pory skalne w tej próbce, następnie
próbkę waży się w powietrzu oraz w wodzie (wykonuje ważenie hydrostatyczne)
ρ =
m
m
V
=
m
m
m
p
−
m
pw
ρ
w
−
m
p
−
m
m
ρ
p
m
m
– masa próbki w stanie naturalnym
m
p
– masa próbki oparafinowanej
m
pw
– masa próbki oparafinowanej zanurzonej w wodzie
V – objętość próbki
ρ
w
– gęstość wody
ρ
p
– gęstość parafiny
•
w rtęci: próbkę waży się, a następnie zanurza w naczyniu pomiarowym wypełnionym
rtęcią. Wypartą przez próbkę rtęć zbiera się, waży, a następnie oblicza gęstość
objętościową wg zależności: ρ =
m
m
V
=
m
m
⋅
ρ
h
m
r
m
m
– masa próbki
m
r
– masa rtęci wypartej przez próbkę
ρ
h
– gęstość właściwa rtęci
–
gęstość właściwą: stosunek masy cząstek stałych próbki skalnej do ich poszczególnych
objętości ρ
0
=
m
1
V
1
Miernikami gęstości są:
–
ciężar objętościowy: stosunek ciężaru fazy stałej wraz z zawartymi w nich porami do jej
objętości: γ =
G
V
,
[
N
m
3
]
–
ciężar właściwy: stosunek ciężaru fazy stałej w stanie sproszkowanym i wysuszonym do jej
objętości: γ
0
=
G
1
V
1
,
[
N
m
3
]
Pomiędzy ciężarami zachodzą następujące zależności:
γ =ρ ⋅
g
γ
0
=
ρ
0
⋅
g
dla gruntów parametrem charakteryzującym własności strukturalne są:
–
gęstość objętościowa szkieletu gruntowego: jest to stosunek masy ziarn i cząstek stałych
szkieletu gruntowego do objętości całej próbki ρ
d
=
m
1
V
1
+
V
2
+
V
3
. Gdy znana jest

wilgotność, tzn. gdy znany jest stosunek masy wody zawartej w próbce m
2
do masy
szkieletu gruntowego
m
1
to gęstość objętościową szkieletu gruntowego można
przedstawić następująco:
W =
m
2
m
1
⋅
100
ρ =
m
V
=
m
1
+
m
2
V
=
m
1
+
W ⋅m
1
100
V
=
ρ
d
+
W
100
⋅
ρ
d
ρ
d
=
ρ
100+W
⋅
100
–
ciężar objętościowy szkieletu gruntowego: jest to stosunek ciężaru próki skalnej
wysuszonej do jej objętości przed wysuszeniem γ
d
=
G
s
V
γ
d
=
ρ
d
⋅
g
γ
d
=
γ
100+W
⋅
100
Gęstość właściwa szkieletu gruntowego: jest to stosunek masy szkieletu gruntowego do jego
objętości. Wyraża się go wzorem:
ρ
od
=
m
1
V
1
[
g
cm
3
]
, [
kg
m
3
]
Najczęściej wykorzystywane metody badania:
–
Metoda piknometru
–
kolba Le Chateliera
Najczęściej wykorzystuje się, ze względu na prostotę badania metodę piknometru:
ρ
od
=
(
m
g
+
m
t
) ⋅
ρ
W
m
wt
+(
m
g
– m
t
)
– m
wg
m
g
– masa piknometru
m
t
– masa piknometru z wysuszonym gruntem
m
wt
– masa piknometru wypełnionego do kreski wodą destylowaną w temperaturze badanej
m
wg
– masa piknometru z gruntem i wodą wypełniającą piknometr do kreski na szyjce
ρ
w
– gęstość właściwa wody
(piknometr)
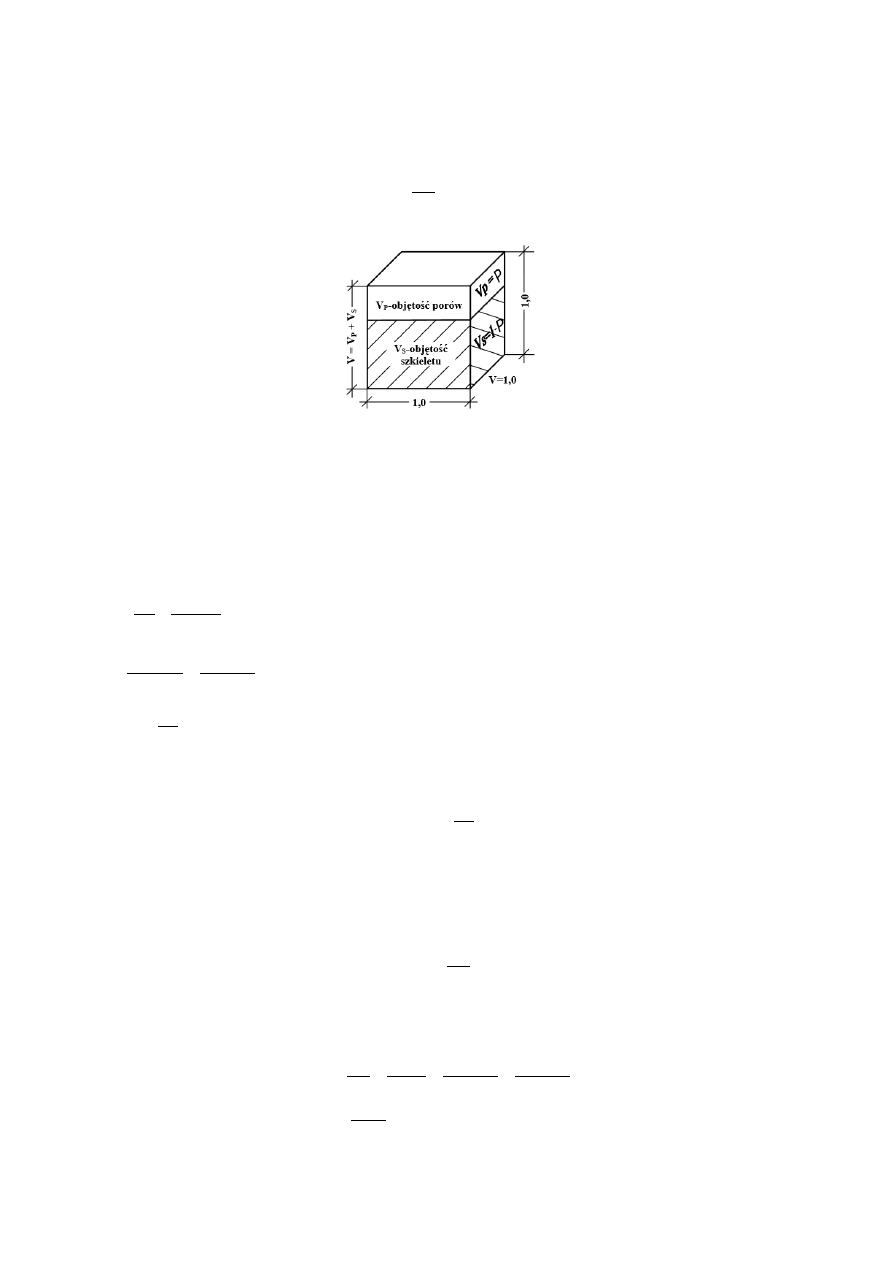
POROWATOŚĆ
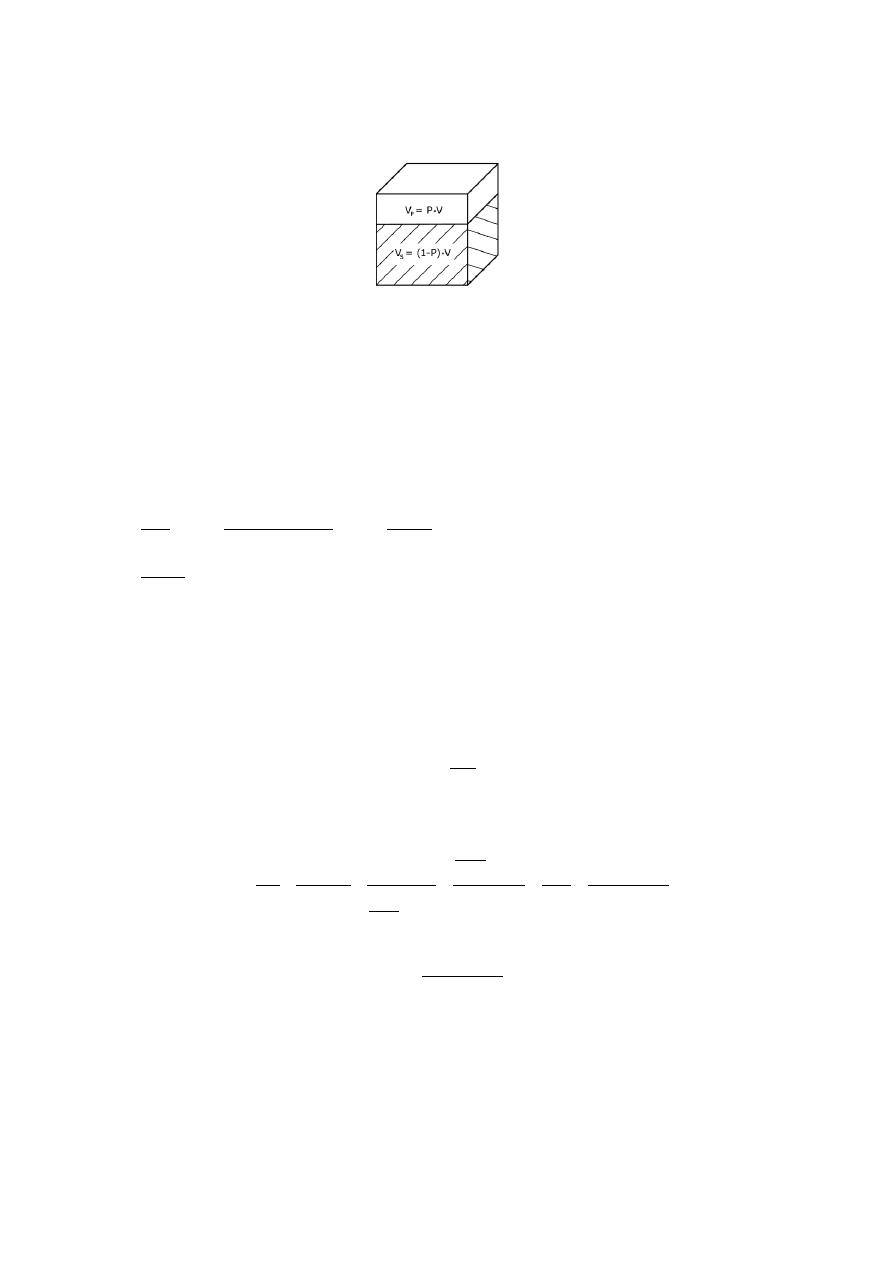
Jest to stosunek objętości porów w próbce skały do objętości całej próbki
P=
V
p
V
⋅
100 , [%]
(elementarny sześcian – wymiary 1x1x1, V=1)
Ponieważ sześcian jest elementarny i jego V wynosi 1, zatem:
P=V
P
, a więc
V
s
=
1−P
m
1
=
V
S
⋅
ρ
0
(gęstość właściwa)
ρ
d
=
m
1
V
=
V
s
⋅
ρ
o
V
=
V
s
ρ
0
=(
1−P )⋅ρ
o
⋅
γ
d
=(
1−P)⋅γ
0
P=
ρ
0
−
ρ
d
ρ
0
=
γ
0
−
γ
d
γ
0
P=(1−
γ
γ
0
) ⋅
100
Stosunek ciężaru objętościowego do ciężaru właściwego zwany jest współczynnikiem szczelności:
k
s
=
γ
γ
0
Gęstość jest podstawowym parametrem charakteryzującym właściwości strukturalne, drugim
podstawowym jest porowatość. Dla scharakteryzowania porowatości wykorzystuje się pojęcie
wskaźnika porowatości. Jest to stosunek objętości porów do objętości materiału skalnego w
próbce skalnej.
e=
V
p
V
s
Pomiędzy porowatością a współczynnikiem porowatości istnieje następująca zależność:
e=
V
p
V
s
=
P
1−P
=
ρ
0
−
ρ
d
ρ
d
=
γ
0
−
γ
d
γ
d
P=
e
1+e
⋅
100
W odniesieniu do skały urobionej lub rozdrobnionej w wyniku jakiegoś procesu technologicznego
wykorzystuje się pojęcia:
–
współczynnik rozluzowania: jest to stosunek objętości rozluzowanej skały do jej objętości
w stanie nienaruszonym (w masywie) k
r
=
V
r
V
.
–
gęstość nasypowa: jest to stosunek gęstości objętościowej skały w masywie do
współczynnika rozluzowania ρ
n
=
ρ
k
r
Współczynnik rozluzowania i gęstość nasypowa zależą od:
–
składu granulometrycznego luźnej masy,
–
wzajemnego ułożenia kawałków rozdrobnionej skały,
–
stopnia zagęszczenia,
–
wysokości słupa luźnej skały,
–
pojemności i kształtu naczynia, w którym umieszczona jest skała
W ocenie gruntów sypkich wykorzystuje się parametr nazywany stopniem zagęszczenia. Jest to
stosunek zagęszczenia istniejącego w naturze do największego możliwego zagęszczenia danego
gruntu.
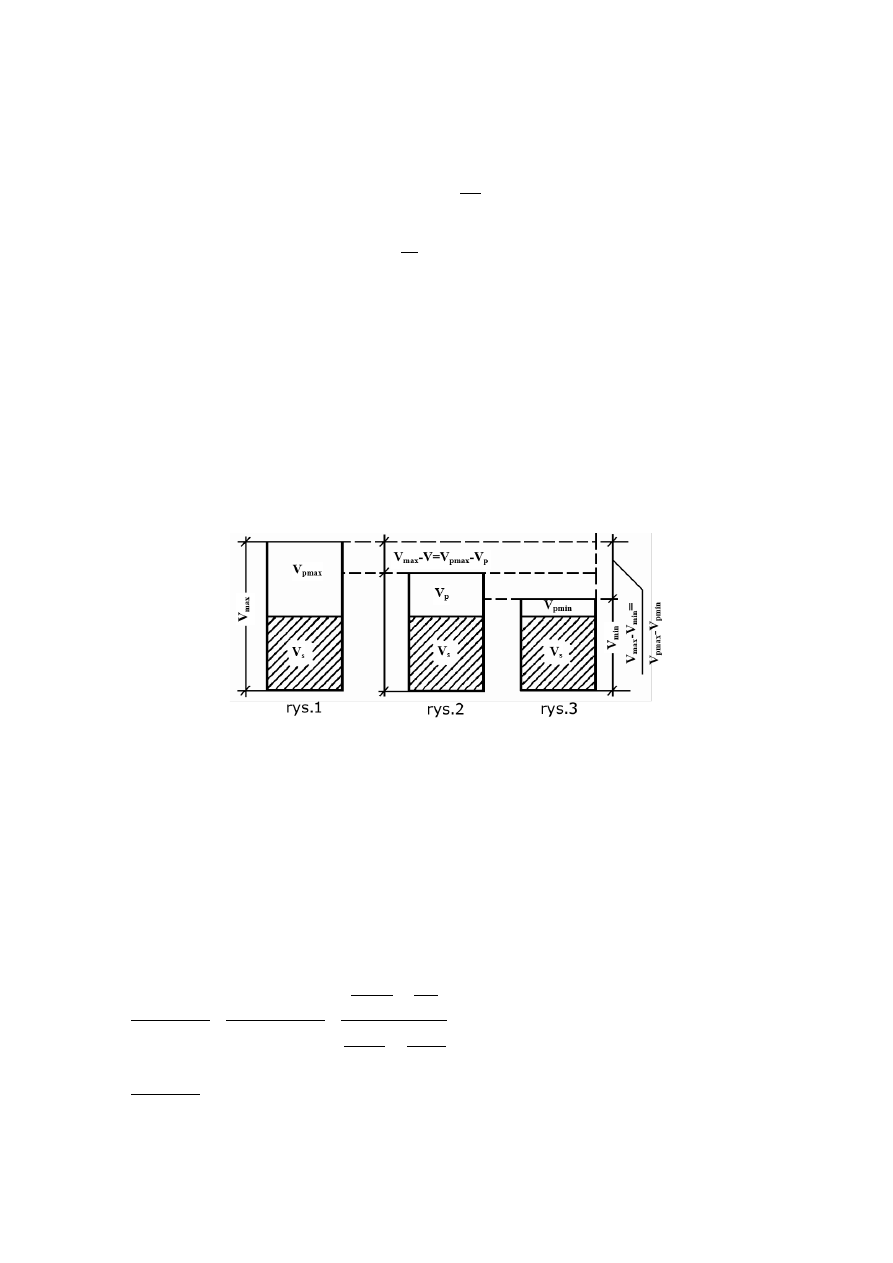
1 – objętość piasku najbardziej luźnego
2 – objętość w naturze
3 – objętość piasku najbardziej zagęszczonego
Przeprowadzenie badania: wsypujemy do cylindra luźny piasek, wypełniając go do pewnej
objętości. V
max
będzie stanowił piasek i pory między ziarnami (rys.1). Następnie przenosimy
cylinder na zewnątrz, gdzie jest poddany warunkom otoczenia, pod wpływem których naturalnie się
zagęści ( V
s
pozostaje stałe, V
p
się zmniejsza, rys.2). Cylinder przenosimy do laboratorium,
gdzie pod wpływem wstrząsów materiał zawarty w cylindrze jest zagęszczany (rys. 3).
Stopień zagęszczania określamy z zależności:
I
d
=
V
max
−
V
V
max
−
V
min
=
V
Pmax
−
V
P
V
Pmax
−
V
Pmin
=
V
Pmax
V
S
−
V
P
V
S
V
Pmax
V
S
−
V
Pmin
V
S
I
d
=
e
max
−
e
e
max
−
e
min
e
max
– wskaźnik porowatości maksymalnej

e – wskaźnik porowatości naturalnej
e
min
– wskaźnik porowatości minimalnej
W zależności od stopnia zagęszczenia wyróżniamy stany gruntów sypkich:
–
grunt jest luźny, tzn I
d
<
0,33
–
grunt jest średnio zagęszczony, 0,33< I
d
<
0,67
–
grunt jest zagęszczony, 0,67< I
d
<
1
Klasyfikacja zagęszczenia gruntów wg PN-EN ISO 14688-2:
Nazwa:
Stopień zagęszczenia
I
D
grunty bardzo luźne
0 – 15
grunty luźne
15 – 35
grunty średnio zagęszczone
35 – 65
grunty zagęszczone
65 – 85
grunty bardzo zagęszczone
85 – 100
HYDROGAZOMECHANICZNE WŁASNOŚCI SKAŁ
Własności te charakteryzują zdolność skał do przepuszczania, pochłaniania i zatrzymywania
różnych cieczy i gazów oraz skłonność skał do zmiany swego stanu mechanicznego podczas
oddziaływania cieczami, względnie gazami.
Wilgotność: jest podstawowym parametrem własności hydro-gazo-mechanicznych, wyrażana jest
procentowym stosunkiem masy wody w porach skały do masy suchej próbki:
W =
M
W
M
d
⋅
100
%
Praktycznie, w laboratorium wilgotność określamy w parowniczce, z zależności:
W =
m
mt
– m
st
m
st
– m
t
⋅
100 %
m
mt
– masa parowniczki z próbką wilgotną
m
st
– masa parowniczki z próbką wysuszoną
m
t
– masa parowniczki
W celu określenia stanu zawilgocenia skały, należy wyznaczyć wilgotność całkowitą i stopień
wilgotności.
M
w
=
P ⋅V ⋅ρ
W
, M
d
=
V
s
⋅
ρ
s
=(
1 −P )⋅V ⋅ρ
s
M
w
– masa wody
M
d
– masa szkieletu gruntowego, równa objętości szkieletu gruntowego pomnożonej przez jego
gęstość
Wilgotność całkowita: jest to największa względna ilość wody, gdy pory skały są całkowicie
wypełnione wodą. Określamy ją zależnościami wynikającymi z rysunku, wstawionymi do wzoru:
W
sr
=
M
w
M
d
⋅
100=
P ⋅V ⋅
ρ
W
(
1 −P)⋅V ⋅
ρ
S
⋅
100=
e ⋅
ρ
W
ρ
S
⋅
100
W
sr
=
e ⋅γ
W
γ
S
⋅
100
γ
S
– ciężar właściwy szkieletu gruntowego
γ
W
– ciężar właściwy wody
V – objętość całej próbki (szkieletu gruntowego łącznie z porami)
Stopień wilgotności: jest to stosunek objętości wody znajdującej się w porach i pustkach skały do
ich objętości całkowitej.
S
r
=
V
W
V
p
Znając wilgotność naturalną
W
n
, stopień wilgotności możemy określić następująco:
S
r
=
V
w
V
p
=
V
w
⋅
ρ
w
V
p
⋅
ρ
w
=
M
W
W
sr
100
⋅
M
d
=
M
W
M
d
⋅
100
W
sr
=
W
n
W
sr
=
W
n
⋅
ρ
S
100 ⋅e ⋅ρ
W
S
r
=
W
n
⋅
γ
s
100 ⋅e ⋅γ
w
W zależności od wartości stopnia wilgotności wyróżniamy stany zawilgocenia gruntów sypkich:
S
r
=
0
– grunt suchy
0<S
r
<
0,4 – grunt mało wilgotny
0,4<S
r
<
0,8
– grunt wilgotny
0,8<S
r
<
1 – grunt mokry

Obecność wody wpływa na kształtowanie się własności gruntów spoistych, czyli na kształtowanie
się ich konsystencji. Wyróżniamy następujące konsystencje gruntów spoistych:
–
płynną, gdy grunt zachowuje się jak ciecz i nie ma prawie żadnej wytrzymałości na
ścinanie,
–
plastyczną, gdy grunt poddany pewnemu naciskowi nie ulega spękaniom i zachowuje
nadany mu kształt,
–
zwartą, gdy grunt odkształca się przy dużych naciskach, czemu towarzyszą spękania
Poszczególne konsystencje rozdzielone są granicami konsystencji:
–
granicą płynności: jest to wilgotność w procentach, jaką ma masa gruntowa umieszczona w
miseczce aparatu Casagrande'a, gdy wykonana w niej bruzda zlewa się przy 25tym
uderzeniu miseczki o podstawę aparatu {rysunek 6: uproszczony schemat aparatu
Casagrande'a}, opis przebiegu badania granicy płynności, wilgotności i wykresy na
podstawie których wyznaczamy wilgotność dla 25. uderzenia
–
granicą plastyczności: jest to wilgotność w procentach, jaką ma grunt, gdy przy kolejnym
wałeczkowaniu bryłki gruntu wałeczek pęka po osiągnięciu średnicy
3 mm
. Tok
postępowania: próbkę 'wałeczkujemy' między dłońmi, w momencie gdy ma średnicę około
3 mm sprawdzamy, czy występują pęknięcia, następnie próbkę suszymy, ważymy,
wyznaczamy wilgotność i granicę plastyczności W_P
–
granicą skurczalności: wilgotność w procentach, jaką ma grunt, gdy przy suszeniu bryłka
gruntu przestaje zmniejszać swoją objętość. Granicę skurczalności określamy też z
zależności:
W
S
=
ρ
W
⋅(
1
ρ
d
−
1
ρ
s
) ⋅
100 %
ρ
W
– gęstość właściwa wody
ρ
S
– gęstość właściwa gruntu
ρ
d
– gęstość objętościowa szkieletu gruntowego
Plastyczne własności gruntów charakteryzowane są przez stopień plastyczności i wskaźnik
plastyczności.
I
L
=
W
n
−
W
p
W
L
−
W
p
W
n
– wilgotność naturalna
W
p
– granica plastyczności
W
L
– granica płynności
Ze względu na wartość stopnia plastyczności, oraz wilgotność naturalną wyróżnia się stany
gruntów spoistych:
I
L
≤
0 W
n
≤
W
s
– grunt zwarty
I
L
≤
0
W
s
<
W
n
≤
W
P
– grunt półzwarty
0<I
L
≤
0,25 – grunt twardoplastyczny
0,25< I
L
≤
0,5
– grunt plastyczny
0,5< I
L
≤
1 – grunt miękkoplastyczny
I
L
=
1
– grunt płynny
Wskaźnik plastyczności: różnica pomiędzy granicą płynności W
L
i granicą plastyczności W
p
I
p
=
W
L
– W
p
[%]

Zdolność skał porowatych do przepuszczania cieczy lub gazu siecią kanalików utworzonych z
porów nazywa się przepuszczalnością.
Miarą przepuszczalności jest współczynnik przepuszczalności:
k
prz
=
Q
F ⋅τ ⋅grad p
⋅
μ
, [m
2
]
Q
– ilość cieczy lub gazu przechodzącego przez próbkę
[
m
3
]
F – powierzchnia przekroju poprzecznego próbki [m
2
]
τ
– czas przepływu [s]
μ
– lepkość dynamiczna
[
Pa ⋅s]
grad p – spadek ciśnienia na pewnej drodze:
grad p=
P
1
– P
2
L
gdzie L - droga przepływu (długość próbki)
Współczynnik przepuszczalności charakteryzuje wielkość powierzchni przekroju poprzecznego
porów skały przez którą odbywa się przepływ.
Jednostka: m^2 bądź mD gdzie 1D = 1.02^10^-12 m^2
powolne przesączanie się cieczy poprzez system kanalików i porów pod wpływem ciśnienia
nazywa się filtracją. Miarą jej jest współczynnik filtracji:
k
f
=
Q
F ⋅τ ⋅i
, [
m
s
]
gdzie:
Q – ilość przepływającej cieczy [m
3
]
F
– pole powierzchni przekroju próbki
[
m
2
]
τ
– czas przepływu [s ]
i – spadek hydrauliczny, różnica poziomów cieczy na drodze przepływu: i=
Δ
H
L
Pomiędzy współczynnikiem filtracji a przepuszczalności istnieje następująca zależność:
k
f
=
k
prz
⋅
γ
0
η
, [
m
s
]
Zdolność skał do zwiększenia swej objętości przy nasycaniu wodą nazywa się pęcznieniem.
Zjawisko to jest charakteryzowane przez współczynnik pęcznienia:
P
V
=
V
k
−
V
0
V
0
P
h
=
h
k
−
h
0
h
0
V
k
– objętość końcowa próbki
V
0
– objętość początkowa próbki
h
k
– wysokość końcowa próbki
h
0
– wysokość początkowa próbki

Zdolność skał do utraty spójności i przekształcenia się w pulchną masę z częściowym lub
całkowitym zanikiem nośności pod wpływem wody stojącej nazywamy rozmakalnością.
Zjawisko rozmakalności charakteryzowane jest przez wskaźnik rozmakalności. Określamy go
w teście trzydobowym:
–
1 doba: próbka w naczyniu z wodą
–
2 doba: próbka w stanie powietrzno-suchym (po wyciągnięciu z naczynia)
–
3 doba: próbka w naczyniu z wodą
Określone wartości wskaźnika rozmakalności:
1,0
– próbka nie zmienia formy ani konsystencji
0,8
– próbka pęka wzdłuż uwarstwienia
0,6
– próbka pęka wzdłuż powierzchni uwarstwienia oraz rzadko w kierunku prostopadłym do
uwarstwienia
0,4
– próbka pęka gęsto w wielu kierunkach
0,2
– próbka rozkłada się na rumosz z mulem
0,1
– próbka rozkłada się całkowicie na muł
Wyszukiwarka
Podobne podstrony:
nowe kamyki wyklad5
nowe kamyki wyklad4
nowe kamyki wykład3
Wykład - Opioidowe leki przeciwbólowe oraz leki przeciwkaszlowe i wykrztuśne, farma - nowe pliki, wy
DIAGNOSTYKA APARATU RUCHU--8 nowe, diagnostyka wykłady prof ronikier
Wykład - Cukrzyca i leki przeciwcukrzycowe, farma - nowe pliki, wykłady
ściąga chemia wykład, Studia, Sem 1,2 +nowe, ALL, szkoła, Chemia
9 ASYMILACJA WYKŁAD piAGET swps, ASYMILACJA - PROCES POZNAWCZY, DZIĘKI KTÓREMU NOWE TREŚCI PERCEPCYJ
Farmacja wykład Nowe postaci leków
Kopia Mechanika[1].wyklady, Studia, Sem 1,2 +nowe, Semestr1, 2 semestr, mechanika
Psychoterapia. Wykład 5 (2), nowe, wykłady(1)
więcej podobnych podstron