POCHODNA FUNKCJI
Definicja
Niech funkcja f będzie określona na przedziale (a, b), -
a < b
oraz niech x
0
(a, b),
x
0
+
x
(a, b). Pochodną właściwą funkcji f w punkcie x
0
nazywamy granicę skończoną
0
0
0
0
lim
x
x
x
f
x
f
x
f
x
x
def
Jeżeli istnieje pochodna właściwa funkcji f w punkcie x
0
, to mówimy, że funkcja f jest
różniczkowalna w tym punkcie.
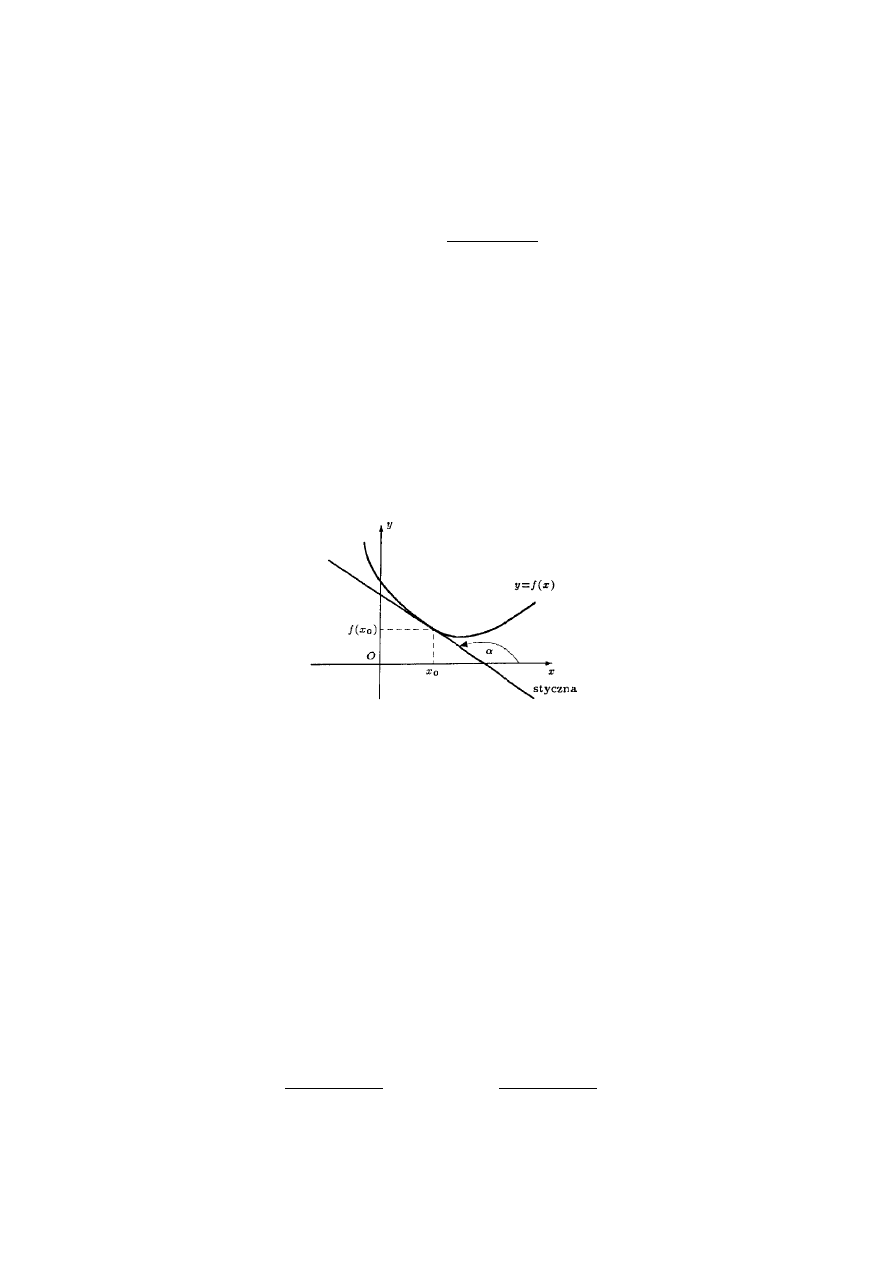
I
NTERPRETACJA GEOMETRYCZNA POCHODNEJ
Niech
oznacza kąt między styczną do wykresu funkcji f w punkcie (x
0
, f(x
0
)) i dodatnią
częścią osi Ox. Wtedy
tg
)
(
0
/
x
f
Równanie stycznej do wykresu funkcji f w punkcie (x
0
, f(x
0
)) ma postać:
)
)(
(
)
(
0
0
/
0
x
x
x
f
x
f
y
Twierdzenie (warunek konieczny różniczkowalności funkcji)
Jeżeli funkcja jest różniczkowalna w punkcie, to jest ciągła w tym punkcie.
Implikacja odwrotna nie jest prawdziwa!
Definicja
Funkcja jest różniczkowalna na przedziale wtedy i tylko wtedy, gdy jest różniczkowalna
w każdym punkcie tego przedziału.
Funkcję określoną na przedziale, której wartości w punktach x tego przedziału są równe
f
x
nazywamy pochodną funkcji f na przedziale i oznaczamy przez
f
.
Definicja
Niech funkcja f będzie określona na przedziale (a,b), -
a < b
oraz niech będzie ciągła
w punkcie x
0
(a,b). Funkcja f ma w punkcie x
0
pochodną niewłaściwą wtedy i tylko wtedy,
gdy
0
0
)
(
)
(
lim
0
x
x
x
f
x
f
x
x
albo
0
0
)
(
)
(
lim
0
x
x
x
f
x
f
x
x
W tym przypadku styczna do wykresu funkcji f w punkcie (x
0
, f(x
0
)) ma postać x=x
0
.

27
Twierdzenie (o pochodnej sumy, różnicy, iloczynu i ilorazu funkcji)
Jeżeli funkcje f i g są różniczkowalne w punkcie x
0
, to
1)
)
(
)
(
)
(
)
(
0
/
0
/
0
/
x
g
x
f
x
g
f
2)
/
/
0
0
(
) ( )
( )
c f
x
c f
x
gdzie
R
c
3)
)
(
)
(
)
(
)
(
)
(
)
(
0
/
0
0
0
/
0
/
x
g
x
f
x
g
x
f
x
g
f
4)
)
(
)
(
)
(
)
(
)
(
)
(
0
2
0
/
0
0
0
/
0
/
x
g
x
g
x
f
x
g
x
f
x
g
f
o ile g(x
0
)
0
Twierdzenie (o pochodnej funkcji złożonej)
Jeżeli
1. funkcja f jest różniczkowalna w punkcie x
0
,
2. funkcja g jest różniczkowalna w punkcie f(x
0
),
to funkcja złożona
f
g
jest różniczkowalna w punkcie x
0
oraz
)
(
)
(
)
(
0
/
0
/
0
/
x
f
x
f
g
x
f
g
Twierdzenie (o pochodnej funkcji odwrotnej)
Jeżeli
1. funkcja f jest ciągła na przedziale (a,b),
2. funkcja f jest malejąca albo rosnąca na przedziale (a,b),
3. istnieje
)
,
(
,
0
)
(
0
0
/
b
a
x
x
f
.
Wtedy funkcja odwrotna
1
f
jest różniczkowalna w punkcie y
0
= f(x
0
) oraz
)
(
1
)
(
)
(
0
/
0
/
1
x
f
y
f
Definicja
Pochodną n-tego rzędu funkcji f w punkcie x
0
definiujemy indukcyjnie:
2
)
(
)
(
0
/
)
1
(
0
)
(
n
dla
x
f
x
f
n
def
n
,
gdzie
)
(
)
(
0
/
0
)
1
(
x
f
x
f
def
. Ponadto przyjmujemy
)
(
)
(
0
0
)
0
(
x
f
x
f
def
.
Jeżeli istnieje pochodna właściwa
)
(
0
)
(
x
f
n
, to mówimy, że funkcja f jest n-krotnie
różniczkowalna w punkcie x
0
.
Funkcję określoną na przedziale, której wartości w punktach x tego przedziału są równe
)
(
)
(
x
f
n
, nazywamy pochodną n-tego rzędu funkcji f na tym przedziale.
Dla istnienia n-tej pochodnej funkcji w punkcie x
0
konieczne jest istnienie pochodnej
)
1
(
n
f
(i co za tym idzie także wszystkich poprzednich pochodnych) na pewnym otoczeniu
punktu x
0
.
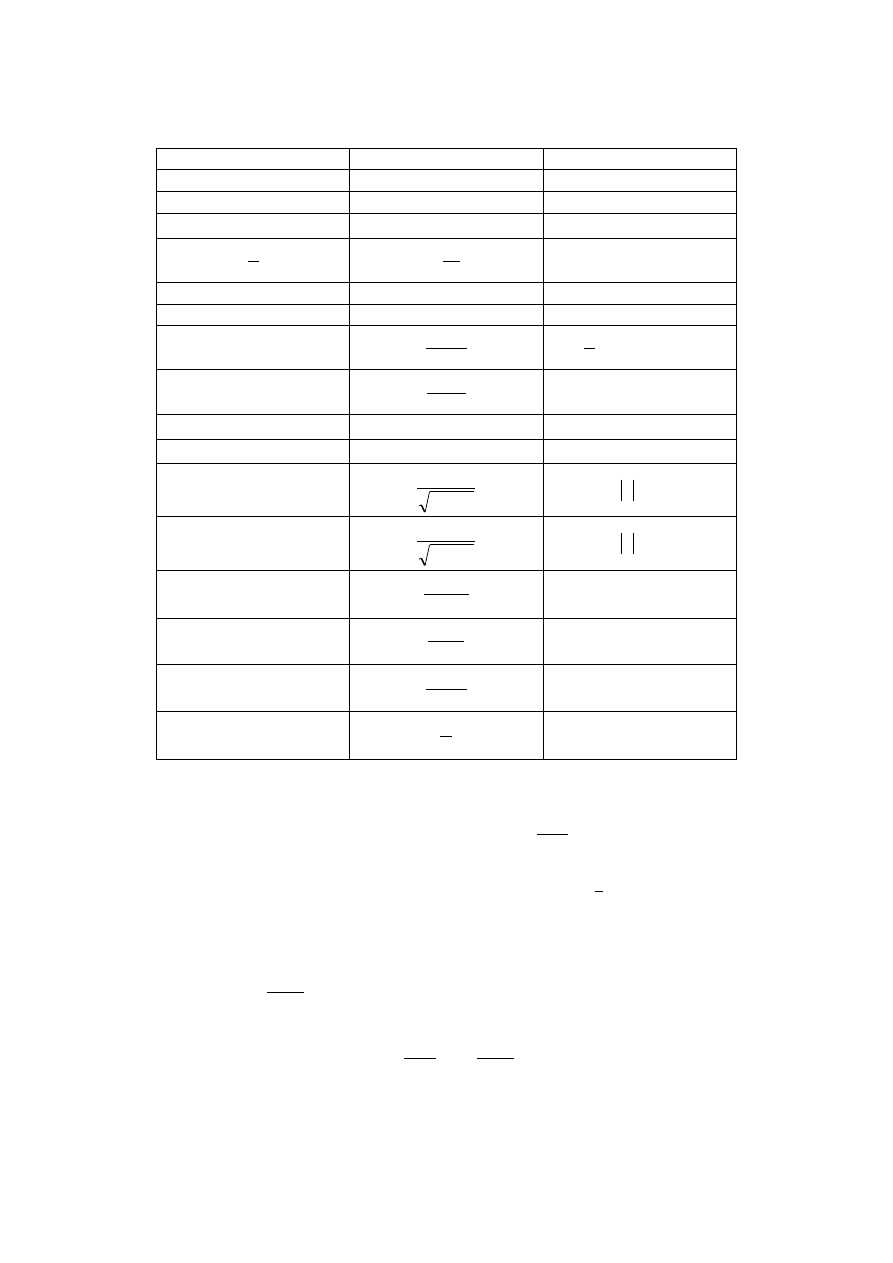
28
P
OCHODNE WAŻNIEJSZYCH FUNKCJI ELEMENTARNYCH
Funkcja
Pochodna
Zakres zmienności
c (funkcja stała)
0
R
c
x
1
R
x
x
1
x
R, x > 0
1
x
2
1
x
x
0
x
sin
x
cos
R
x
x
cos
x
sin
R
x
x
tg
2
1
cos x
Z
k
gdzie
k
x
,
2
x
ctg
2
1
sin x
Z
k
gdzie
k
x
,
x
a
a
a
x
ln
0 < a
1, x
R
x
e
x
e
R
x
x
sin
arc
2
1
1
x
1
x
x
arccos
2
1
1
x
1
x
x
arctg
2
1
1
x
R
x
x
arcctg
2
1
1 x
R
x
x
a
log
a
x ln
1
0 < a
1, x > 0
x
ln
x
1
x > 0
Aby obliczyć pochodne funkcji postaci
g
f
oraz
g
f
l o g
zapisujemy te funkcje
w następujących postaciach:
f
g
g
e
f
ln
oraz
f
g
g
f
ln
ln
log
Twierdzenie (reguła de L’Hospitala dla nieoznaczoności
0
0
)
Jeżeli funkcje f i g spełniają warunki:
1)
0
0
lim
( )
lim ( )
0
x
x
x
x
f x
g x
, przy czym
0
x
g
dla
0
x
S
x
2) istnieje granica
0
/
/
( )
lim
( )
x
x
f
x
g x
(właściwa lub niewłaściwa)
to:
0
0
/
/
( )
( )
lim
lim
( )
( )
x
x
x
x
f x
f
x
g x
g x
Powyższe twierdzenie jest prawdziwe także dla granic jednostronnych w punkcie x
0
oraz
w –
lub w +
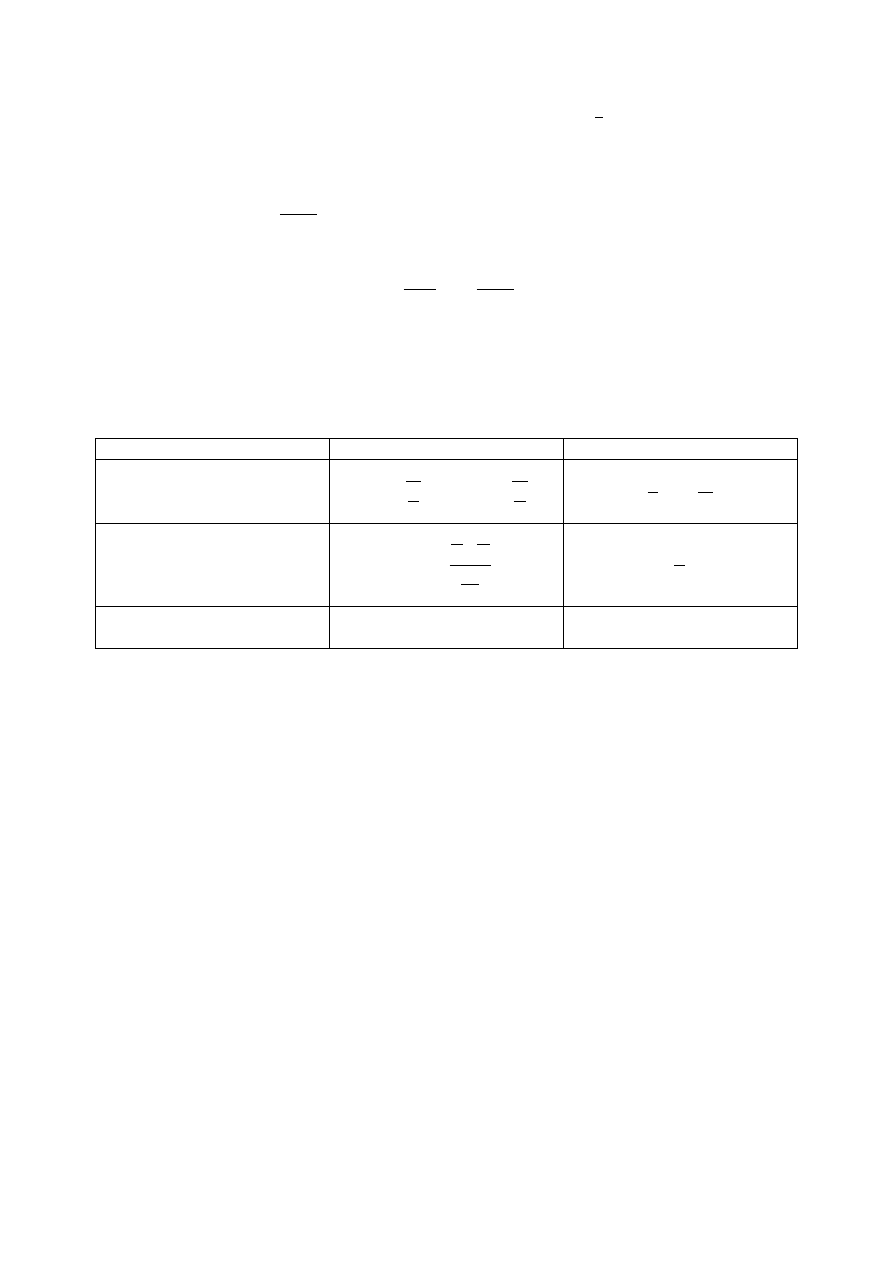
29
Twierdzenie (reguła de L’Hospitala dla nieoznaczoności
)
Jeżeli funkcje f i g spełniają warunki:
1)
0
0
0
0
lim
( )
lub lim
( )
oraz lim ( )
lub lim ( )
x
x
x
x
x
x
x
x
f x
f x
g x
g x
2) istnieje granica
0
/
/
( )
lim
( )
x
x
f
x
g x
(właściwa lub niewłaściwa)
to:
0
0
/
/
( )
( )
lim
lim
( )
( )
x
x
x
x
f x
f
x
g x
g x
Powyższe twierdzenie jest prawdziwe także dla granic jednostronnych w punkcie x
0
oraz
w –
lub w +
T
OŻSAMOŚCI ZMIENIAJĄCE RODZAJE NIEOZNACZONOŚCI
Nieoznaczoność
Stosowana tożsamość
Otrzymana nieoznaczoność
0
1
f
f g
g
lub
1
g
f g
f
0
0
lub
1
1
1
g
f
f
g
fg
0
0
0
0
0
,
,
1
f
g
g
e
f
ln
0
Literatura
1. M. Gewert, Z. Skoczylas: Analiza matematyczna 1. Definicje, twierdzenia, wzory.
2. M. Gewert, Z. Skoczylas: Analiza matematyczna 1. Przykłady i zadania.
3. W. Krysicki, L. Włodarski: Analiza matematyczna w zadaniach, część I.
Wyszukiwarka
Podobne podstrony:
pochodne wyzszych rzedow id 364 Nieznany
pochodne wyzszych rzedow id 364 Nieznany
LOGIKA wyklad 5 id 272234 Nieznany
ciagi liczbowe, wyklad id 11661 Nieznany
AF wyklad1 id 52504 Nieznany (2)
Neurologia wyklady id 317505 Nieznany
ZP wyklad1 id 592604 Nieznany
CHEMIA SA,,DOWA WYKLAD 7 id 11 Nieznany
or wyklad 1 id 339025 Nieznany
II Wyklad id 210139 Nieznany
cwiczenia wyklad 1 id 124781 Nieznany
BP SSEP wyklad6 id 92513 Nieznany (2)
MiBM semestr 3 wyklad 2 id 2985 Nieznany
algebra 2006 wyklad id 57189 Nieznany (2)
olczyk wyklad 9 id 335029 Nieznany
Kinezyterapia Wyklad 2 id 23528 Nieznany
AMB ME 2011 wyklad01 id 58945 Nieznany (2)
AWP wyklad 6 id 74557 Nieznany
więcej podobnych podstron