1. Geometria stropu

Rozpiętość belek stropowych

:

B

8.6 m





Rozstawienie belek stropowych

:

a

2.3 m





Liczba belek:

n

6



Rozpiętość dźwigarów:

L

n a



13.8 m





2. Zebranie obciążeń na belkę stropową

-obciążenie stale: ciężar płyty 120 mm, ciężar warstw wykończenia 0,3 kN/m

2

, ciężar

własny belki IPE 300

-obciążenia zmienne: użytkowe 3,5 kN/m

2

3. Obliczenia belki stropowej

3.1 Warunek nośności belki przy zginaniu:

Moment zginający w belce:

MyEd

197.38 kN



m





Wybieram przekrój: dwuteownik równoległościenny IPE360 ze stali S235

h

360 mm





Wysokość:

b

170 mm





Szerokość:

tf

12.7 mm





tw

8.0 mm





Grubość części:

Promień zaokrąglenia:

r

18 mm





Szerokość środnika:

hw

h

2 tf





0.3346 m





fy

235 MPa





1



Granica plastyczności:

Współczynniki częściowe:

M0

1.0



M1

1.0



Klasa przekroju:

Środnik :

h

2 r





2 tf





tw

37.325



72



72





Stopka :

b

tw



2 r





2 tf



4.961



9



9





Zatem przekrój jest klasy 1 przy zginaniu.

Wskaźnik plastyczny przekroju:

Wpl.y

b tf



h

tf









hw

2

tw



4



2 r

2



hw r











r

2



4

3



3

r



hw

2



















1.019 





Nośność plastyczna przekroju:

Mc.y.Rd

Wpl.y fy



M0

239.5 kN·m







Belka jest stężona pasem górnym (ściskanym) bocznie na całej długości.
Pominięto zwichrzenie.

LT

1



Nośność zwichrzeniowa belki:

Mb.y.Rd

LT

Wpl.y fy



M1



239.5 kN·m







Warunek stateczności elementu:

MyEd

Mb.y.Rd

0.824



1



Zatem warunek jest spełniony.

3.2 Warunek nośności przekroju przy ścinaniu.

Siła tnaca przy podporze

Vz.Ed

70.1 kN





Sprawdzam wrażliwość na miejscową utratę stateczności.

współczynnik

1.2



środnik

hw

tw

41.825



72



60





Środnik nie jest wrażliwy na utratę stateczności miejscowej.

Pole brutto przekroju:

A

2 tf



b



h

2 tf









tw





4 

(

) r

2





72.729 cm

2







Pole czynne przy ścinaniu:

AV

max A

2 b

 tf





tf 2 r



tw











hw



tw









35.137 cm

2







Nośność plastyczna przekroju:

Vc.z.Rd

AV fy



3

1

3

M0



572.526 kN







Warunek wytrzymałości przekroju:

Vz.Ed

Vc.z.Rd

0.122



1.0



Warunek jest spełniony

3.3 Sprawdzenie ugięć granicznych:

Ugięcie belki w środku rozpiętosci:

Ugięcie dopuszczalne belki:

wmax

26.7mm





B

250

34.4 mm





Warunek jest spełniony

3.4 Warunki nośności belki w miejscu połączenia z dźwigarem

Reakcja podporowa belki:

R

Vz.Ed

70.1 kN







Połączenie zakładkowe dociskowe (kategorii A). Przyjmuję 3 śruby M18 kl.8.8

Siła tnąca na jeden łącznik:

FEd

1

2

R



35.05 kN







Nośność śruby na ścinanie:

Fv.Rd

0.6 200



mm

2



800



MPa



1.25

76.8 kN







FEd

Fv.Rd

0.456



1.0



Warunek jest spełniony.

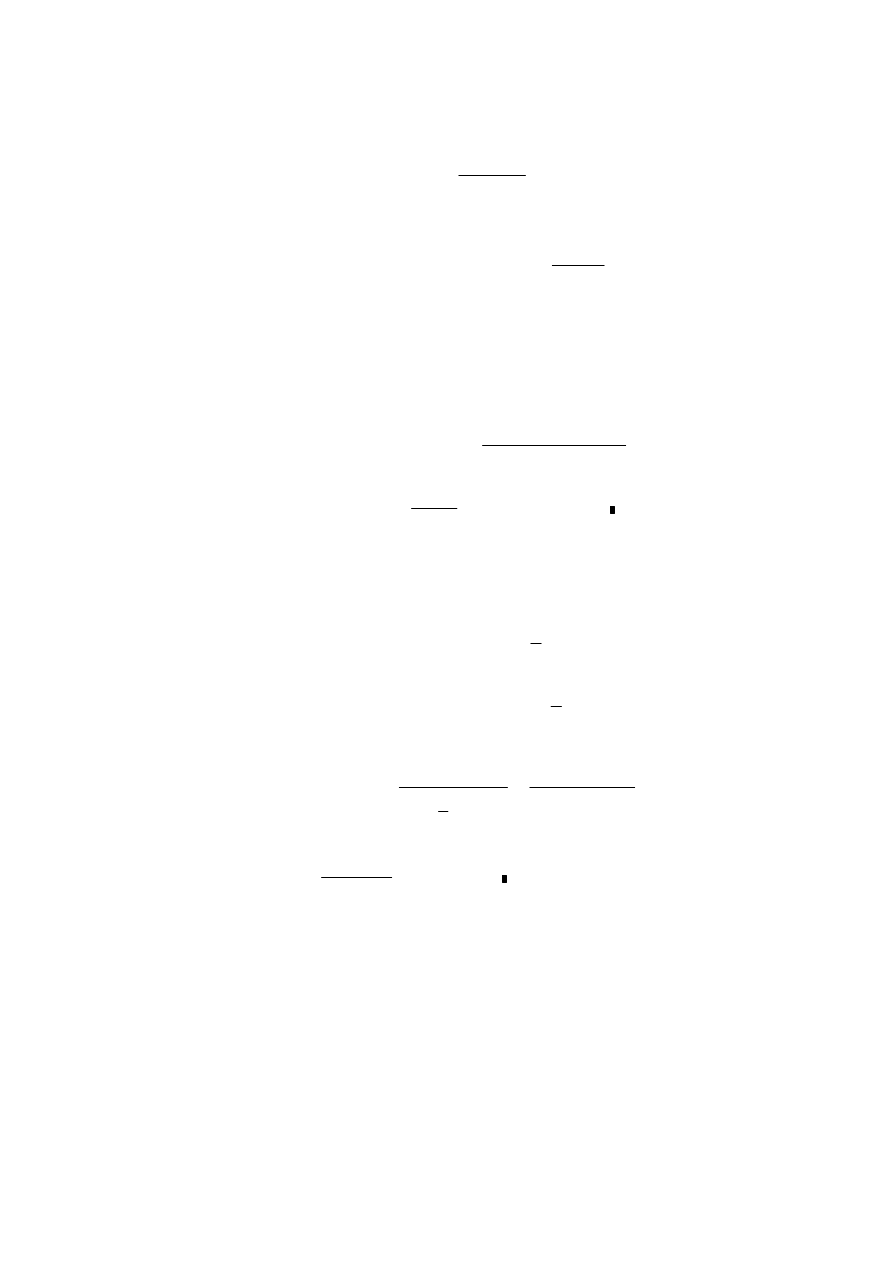
Nośność otworu na docisk:

d

40 mm



3 20



mm



0.667





b

min 1

d







0.667





k1

min 2.5 2.8

40 mm



20 mm





1.7

















2.5





t

tw

8 mm







d

18 mm





Fb.Rd

k1 b



d

 t

 360



MPa



1.25

69.12 kN







FEd

Fb.Rd

0.507



1.0



Warunek jest spełniony.

Rozerwanie blokowe:

An.t

40 mm



d

2















tw



2.48 cm

2







An.v

40 mm



110 mm





d



d

2















tw



9.84 cm

2







Feff.1.Rd

An.v 235



MPa



3

1

3

1.0



An.t 360



MPa



1.25



231.757 kN







R

Feff.1.Rd

0.302



1.0



Warunek jest spełniony.

Złożony stan naprężeń w miejscu podcięcia:

R

70.1 kN





M1

R 110



mm

7.711 kN m









h1

h

40mm



320 mm







b1

b

2

tw

2



81 mm







zc

0.5 h1

2



tw



0.5 tf

2



b1





h1 tw



b1 tf





11.596 cm







Iy

h1

3

tw



tf

3

b1





12

h1 tw



zc



h1

2















2





b1 tf



zc



tf

2















2





3.918

10

3



cm

4







Wy

Iy

h1 zc



192.035 cm

3







R

h1 tw



27.383 MPa







M1
Wy

40.154 MPa







red

2

3

2









1

2

62.143 MPa







fy

M0



235 MPa







Warunek jest spełniony.

4. Obliczenia dźwigara

4.1 Warunek nośności dźwigara przy zginaniu

Moment zginający w dźwigarze

My.Ed

1358.6 kN



m





Przekrój: dwuteownik spawany 1000x8/250x40 ze stali S275

hw

1000 mm





Wysokość:

b

250 mm





Szerokość:

tf

40 mm





tw

8 mm





Grubość części:

Szerokość środnika:

h

hw 2 tf





0.92 m





fy

275 MPa





0.924



Granica plastyczności:

Współczynniki częściowe:

M0

1.0



M1

1.0



Klasa przekroju:

Środnik :

hw

tw

125



124



114.576





Stopka :

b

tw



2 tf



3.025



9



8.316





Więc przekrój jest klasy 4 przy zginaniu, przy czym wrażliwy na utratę stateczności
jest środnik

Cechy przekroju brutto:

Iy

1

12

h

3

b



h

2 tf









3

b

tw





















4.27

10

5



cm

4







A

2 tf



b



h

2 tf









tw





267.2 cm

2







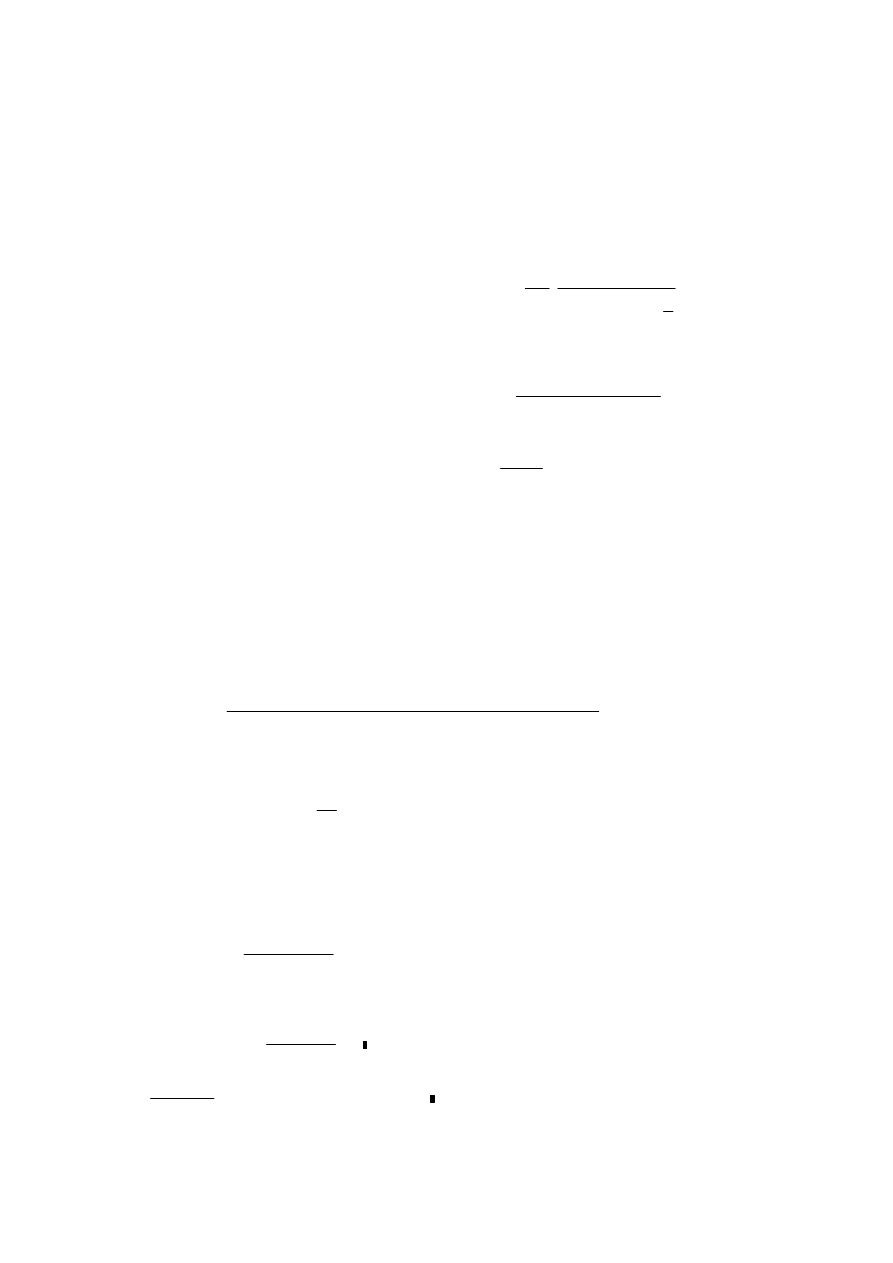
Środnik

współczynnik rozkładu naprężeń normalnych na szerokości ścianki

1





parametr niestateczności miejscowej:

k

23.9



smukłość względna

w

hw

tw

1

28.419

k

 

1

2





0.974





w

w

0.055 3 

(

)





w

2

0.911





współczynnik redukcyjny

szerokość strefy ściskanej

bc

hw

1 

500 mm







szerokości współpracujące

beff

bc w



455.489 mm







be.1

0.4 beff



182.196 mm







be.2

0.6 beff



273.294 mm







zmiana położenia środka ciężkości

zc

tw bc beff









0.5 h



tf



be.1



0.5 bc beff

















A

tw bc beff











2.911 mm







Cechy przekroju współpracującego:

Ieff.y

Iy

A

zc

2





1

12

bc beff







3



tw





1



(

) tw



bc beff









0.5 hw



zc



be.1



0.5 bc beff















2







4.238

10







Weff.y

Ieff.y

0.5 h



zc



9.156

10

3



cm

3







Nośność plastyczna przekroju

Mc.y.Rd

Weff.y fy



M0

kN m









My.Ed

Mc.y.Rd

0.54



1.0



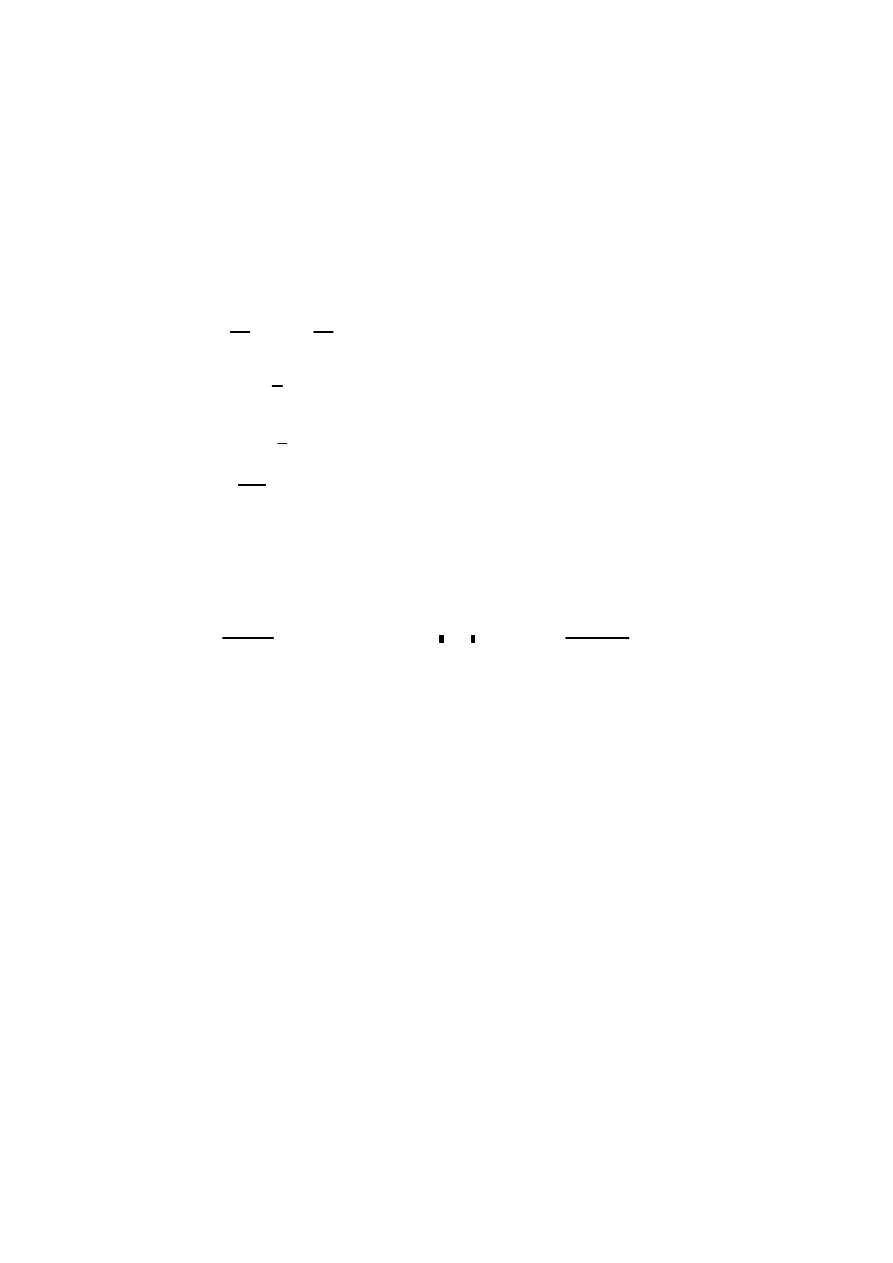
Warunek jest spełniony.

Zwichrzenie liczę metodą uproszczoną

Lc

2.1m



kc

1.0



Iz.f

1

12

b

3



tf



1

72

hw



tw

3





5.209

10

3



cm

4







Af

b tf



1

6

hw



tw





113.333 cm

2







iz.f

Iz.f

Af











1

2

6.78 cm







1

93.9

86.764





c.0

0.4



f

Lc kc



iz.f 1



0.357







c.0

Mc.y.Rd

My.Ed



0.741



Nie przekroczono granicznej wartości smukłości giętnej pasa przy wyboczeniu w
płaszczyźnie dźwigara. Zatem warunek stateczności elementu sprowadza się do
warunku wytrzymałości przekroju, Warunek zatem jest spełniony.

4.2 Warunek nośności dźwigara przy ścinaniu

Zastosuję żebra podporowe i pośrednie. Przy podporze przyjmuję rozstaw obliczeniowy
1150 mm, na długości przęsła 2300 mm.

Panel środnika przy podporze:

a

1150 mm





hw

1000 mm





Siła tnąca przy podporze

Vz.Ed.1

431.3 kN





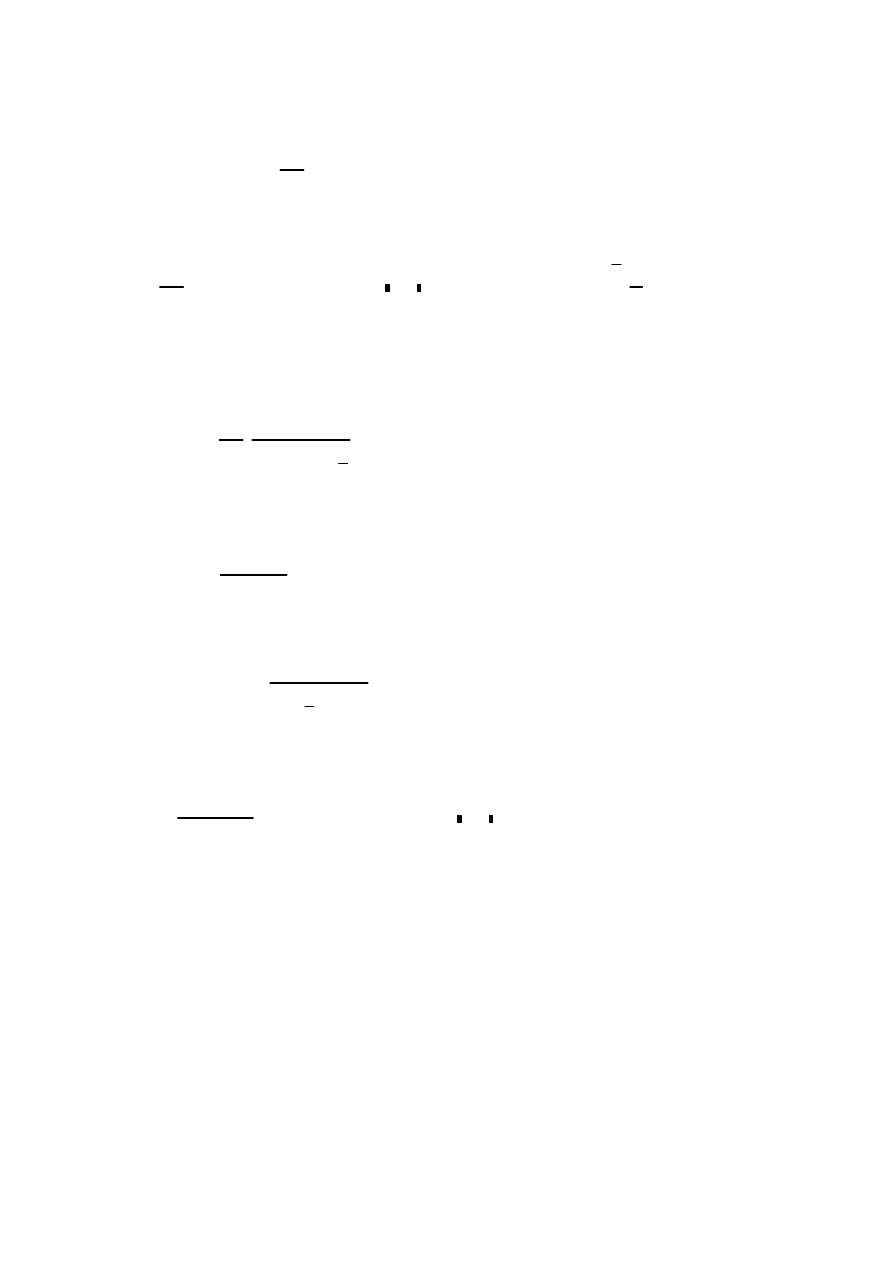
Parametr niestateczności:

k

5.34

4

hw

a













2





8.365





Sprawdzenie wrażliwości na miejscową utratę stateczności

hw

tw

125





31 k

 

1

2





69.036



Panel środnika jest wrażliwy na utratę stateczności przy ścinaniu.

Smukłość względna

w

hw

tw

1

37.4

k

 

1

2





1.251





Współczynnik redukcji niestateczności

w

1.37

0.7

w



0.702





Nośność wyboczeniowa środnika na ścinanie:

Vbw.Rd.1

w hw



tw



fy



3

( )

1

2

M1



892.067 kN







Warunek nośności na ścinanie panela:

Vz.Ed.1

Vbw.Rd.1

0.483





1.0

Warunek jest spełniony

Panel środnika za pierwszą belką

a

2100 mm





hw

990 mm





Siła tnąca za pierwszą belką

Vz.Ed.2

289.3 kN





Parametr niestateczności:

Parametr niestateczności:

k

5.34

4

hw

a













2





6.229





Sprawdzam wrażliwość na miejscową utratę stateczności

hw

tw

123.75





31 k

 

1

2





59.575



Panel środnika jest wrażliwy na utratę stateczności przy ścinaniu.

Smukłość względna

w

hw

tw

1

37.4

k

 

1

2





1.435





Współczynnik redukcji niestateczności

w

1.37

0.7

w



0.642





Nośność wyboczeniowa środnika na ścinanie:

Vbw.Rd.2

w hw



tw



fy



3

( )

1

2

M1



806.974 kN









1.0

Vz.Ed.2

Vbw.Rd.2

0.358



Warunek jest spełniony:

4.3 Sprawdzenie ugięć granicznych

Ugięcie dźwigara w środku rozpiętosci:

Ugięcie dopuszczalne dźwigara:

wmax

24.1mm





L

350

39.429 mm





Warunek jest spełniony

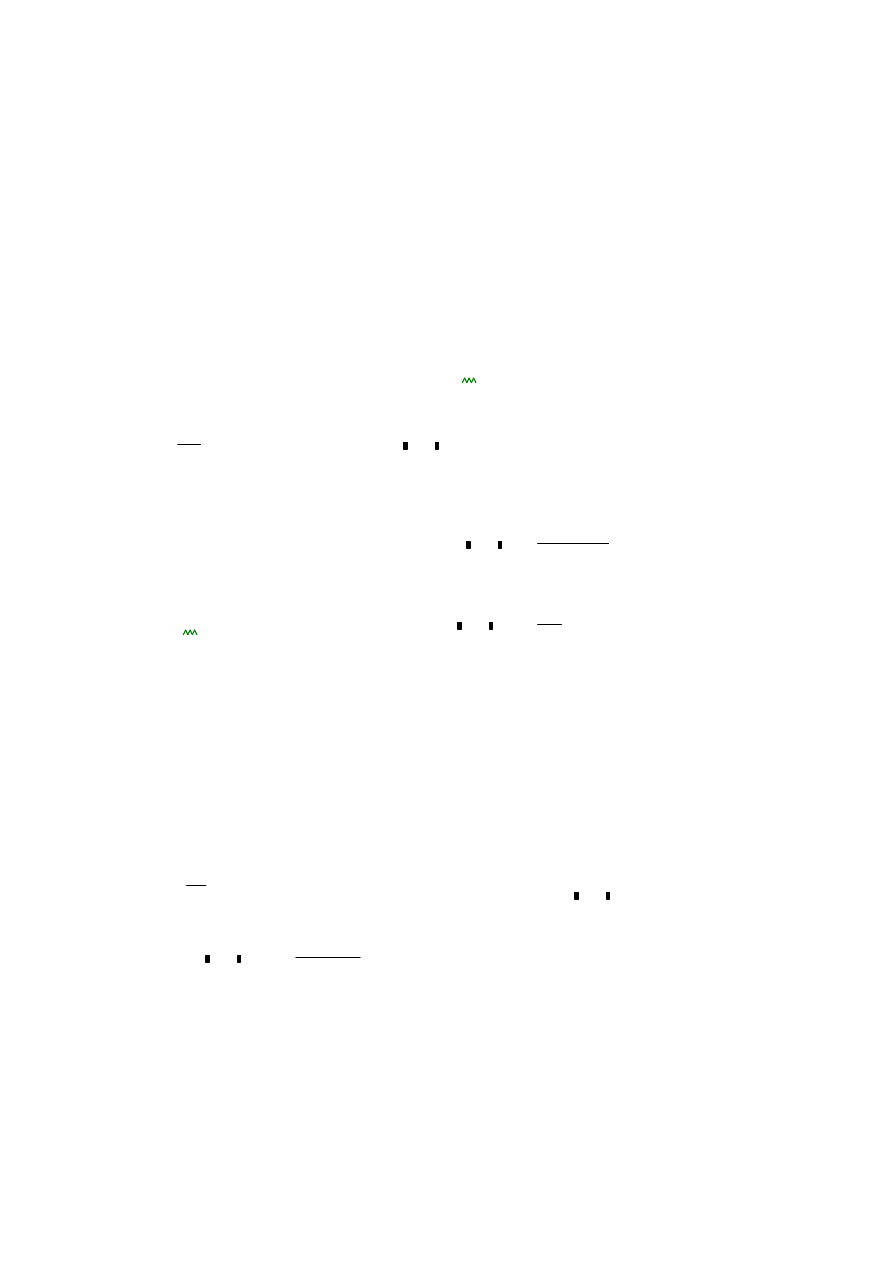
4.4 Dobór żeber ze względu na ścinanie

Żebro podporowe sztywne

Żebro podporowe przyjmuję jako zdwojone żebro dwustronne z płaskownika
120x10, w odstępie osiowo 140 mm

bst

120 mm





tst

10 mm





e

140 mm





bst

tst

12





14

12.936



Żebro jest stateczne

Ast

2 bst



tst



24 cm

2









4 hw



tw

2



e

18.103 cm

2





Warunek jest spełniony

e

140 mm







hw

10

99 mm





Warunek jest spełniony

Zatem przyjęte żebro jest właściwe.

Żebro pośrednie sztywne

Przyjęto żebro pośrednie 120x8

a

1150 mm





hw

1000 mm





Ist

1

12

2 bst



tw







3



tst



2.5 tw

4





1272.029 cm

4











1.5

hw

3

tw

3



a

2



58.072 cm

4





Warunek jest spełniony

Zatem przyjęte żebro jest właściwe.

4.5 Połączenie dźwigara ze słupem

Reakcja podporowa dźwigara:

R

Vz.Ed.1 431.3 kN







Połączenie kategorii A. Przyjęto 6 śrub M24 kl. 8.8, co 80 mm.

Siła tnąca na jeden łącznik:

FEd

1

8

R



53.913 kN







Nośność śruby na ścinanie:

Fv.Rd

0.6 354



mm

2



800



MPa



1.25

135.936 kN







FEd

Fv.Rd

0.397



1.0



Warunek jest spełniony.

d

80 mm



3 22



mm



1

4



0.962





Nośność śruby na docisk:

b

min 1

d







0.962





k1

min 2.5 2.8

40 mm



22 mm





1.7

















2.5





t

tw

8 mm







d

24 mm





Fb.Rd

k1 b



d

 t

 360



MPa



1.25

133.004 kN







FEd

Fb.Rd

0.405



1.0



Warunek jest spełniony.

10

3

cm

3



10

5

cm

4



Zastosuję żebra podporowe i pośrednie. Przy podporze przyjmuję rozstaw obliczeniowy