4.4 Wymiarowanie wsporników

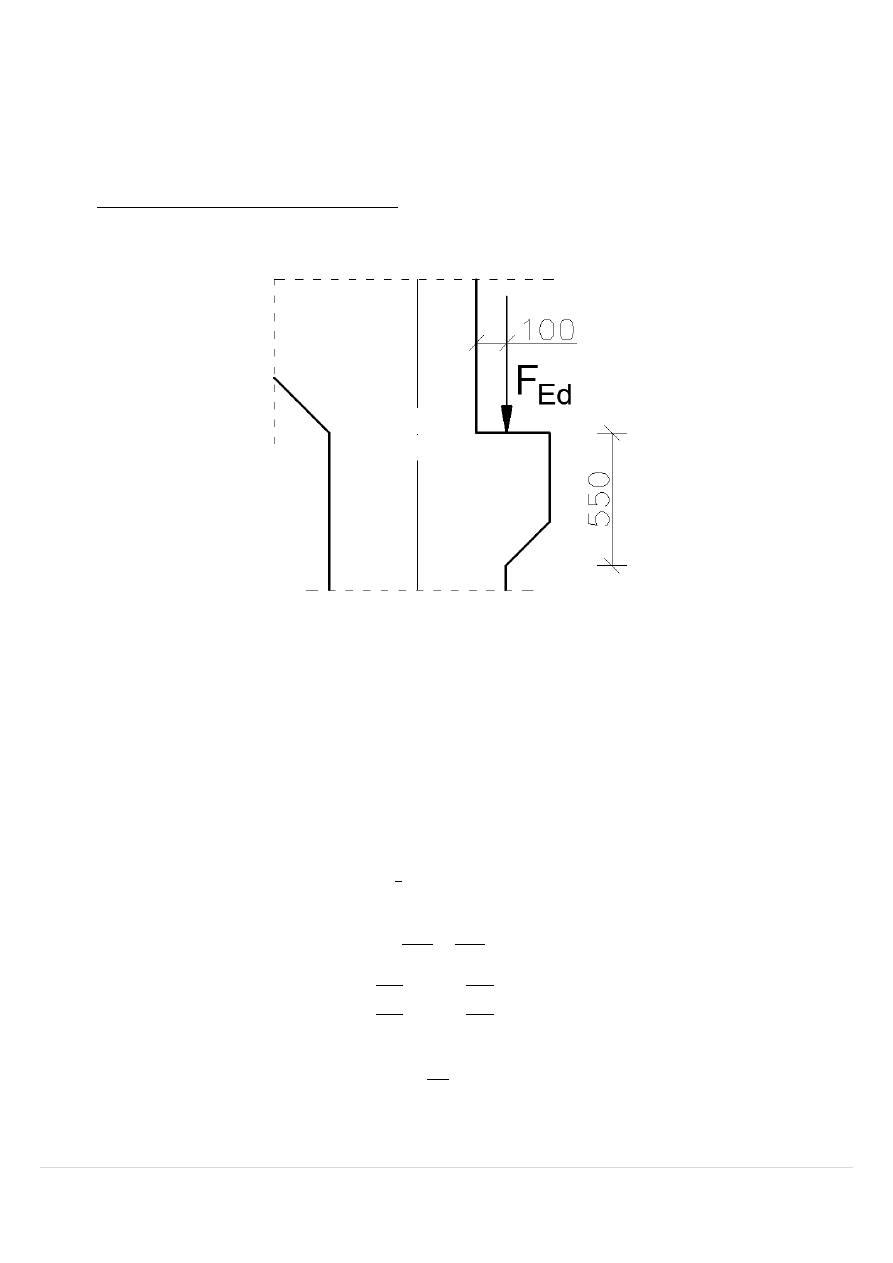
4.4.1 Wspornik pod dźwigar dachowy nawy niższej

𝐹

𝐸𝑑

= 162,24 𝑘𝑁 - Reakcja pionowa od dźwigara dachowego na wspornik

𝐻 = 0,2 ∗ 𝐹

𝐸𝑑

= 32,45 𝑘𝑁

Sprawdzam geometrię wspornika:

𝐹

𝐸𝑑

≤ 𝑉

𝑅𝑑,𝑐

𝐹

𝐸𝑑

≤ 𝐹

𝑉,𝑅𝑑

= 0,5 ∗ 𝜗 ∗ 𝑓

𝑐𝑑

∗ 𝑏 ∗ 𝑑

𝑉

𝑅𝑑,𝑐

= 𝐶

𝑅𝑑,𝑐

∗ 𝑘 ∗ 100𝜌

𝑙

∗ 𝑓

𝑐𝑘

1

3

+ 𝑘

1

∗ 𝜍

𝑐𝑝

∗ 𝑏 ∗ 𝑑 > 𝜈

𝑚𝑖𝑛

+ 𝑘

1

∗ 𝜍

𝑐𝑝

∗ 𝑏 ∗ 𝑑

𝐶

𝑅𝑑,𝑐

=

0,18

𝛾

𝑐

=

0,18

1,4

= 0,129

𝑘 = 1 +

200

𝑑

= 1 +

200
500

= 1,63 < 2,0

𝜌

𝑙

=

𝐴

𝑠𝑙

𝑏𝑑

< 0,02

𝑝𝑟𝑧𝑦𝑗ę𝑡𝑜 𝜌

𝑙

= 0,01

𝑓

𝑐𝑘

= 30 𝑀𝑃𝑎

𝑏 = 500 𝑚𝑚

𝑑 = 400 𝑚𝑚

𝜈

𝑚𝑖𝑛

= 0,035 ∗ 𝑘

3

∗ 𝑓

𝑐𝑘

= 0,035 ∗ 1,63

3

∗ 30 = 0,399

Zatem

𝑉

𝑅𝑑,𝑐

= 0,129 ∗ 1,63 ∗ 100 ∗ 0,01 ∗ 30

1

3

+ 0 ∗ 500 ∗ 500 = 164,40 𝑘𝑁

𝜈

𝑚𝑖𝑛

∗ 𝑏 ∗ 𝑑 = 0,488 ∗ 500 ∗ 500 = 99,74 𝑘𝑁

𝑉

𝑅𝑑,𝑐

> 𝜈

𝑚𝑖𝑛

∗ 𝑏 ∗ 𝑑

𝐹

𝐸𝑑

= 162,24 𝑘𝑁 < 𝑉

𝑅𝑑,𝑐

= 164,40 𝑘𝑁 𝑘𝑁 → 𝑤𝑎𝑟𝑢𝑛𝑒𝑘 𝑠𝑝𝑒ł𝑛𝑖𝑜𝑛𝑦

𝐹

𝑉,𝑅𝑑

= 0,5 ∗ 𝜗 ∗ 𝑓

𝑐𝑑

∗ 𝑏 ∗ 𝑑 = 0,5 ∗ 0,6 ∗ 1 −

𝑓

𝑐𝑘

250

∗ 𝑓

𝑐𝑑

∗ 𝑏 ∗ 𝑑 = 0,5 ∗ 0,6 ∗ 1 −

30

250

∗ 21,43 ∗ 500 ∗ 500

= 990,066 𝑘𝑁

𝐹

𝐸𝑑

= 162,24 𝑘𝑁 < 𝐹

𝑉,𝑅𝑑

= 990,066 𝑘𝑁 → 𝑤𝑎𝑟𝑢𝑛𝑒𝑘 𝑠𝑝𝑒ł𝑛𝑖𝑜𝑛𝑦

Zbrojenie główne wspornika:

𝑎

𝐹

𝑕

=

100 𝑚𝑚
550 𝑚𝑚

= 0,18 < 0,50

𝐴

𝑠,𝑚𝑎𝑖𝑛

>

1

𝑓

𝑦𝑑

∗ 0,5𝐹

𝐸𝑑

+ 𝐻 =

1

434 𝑁/𝑚𝑚

2

∗ 0,5 ∗ 162240 𝑁 + 32450 𝑁 = 261,68 𝑚𝑚

2

= 2,62 𝑐𝑚

2

Przyjęto pętlę z prętów 2



16 𝑨

𝒔,𝒑𝒓𝒐𝒗

= 𝟒, 𝟎𝟐 𝒄𝒎

𝟐

Długośd zakotwienia:

Obliczeniowa długośd zakotwienia:

𝑙

𝑏𝑑

= 𝛼

1

∗ 𝛼

2

∗ 𝛼

3

∗ 𝛼

4

∗ 𝛼

5

∗ 𝑙

𝑏,𝑟𝑞𝑑

> 𝑙

𝑏,𝑚𝑖𝑛

Podstawowa długośd zakotwienia:

𝑙

𝑏,𝑟𝑞𝑑

=

𝜙

4

∗

𝜍

𝑠𝑑

𝑓

𝑏𝑑

𝜙 = 16 𝑚𝑚

𝜍

𝑠𝑑

=

𝐴

𝑠,𝑚𝑎𝑖𝑛

𝐴

𝑠,𝑝𝑟𝑜𝑣

∗ 𝑓

𝑦𝑑

=

2,62 𝑐𝑚

2

4,02 𝑐𝑚

2

∗ 434 𝑀𝑃𝑎 = 252,63 𝑀𝑃𝑎

𝑓

𝑏𝑑

= 2,25 ∗ 𝜂

1

∗ 𝜂

2

∗ 𝑓

𝑐𝑡𝑑

𝜂

1

= 1,0 (𝑑𝑜𝑏𝑟𝑒 𝑤𝑎𝑟𝑢𝑛𝑘𝑖 𝑧𝑎𝑡𝑘𝑜𝑡𝑤𝑖𝑒𝑛𝑖𝑎)

𝜂

2

= 1,0 (𝑏𝑜 𝜙 < 32 𝑚𝑚)

𝑓

𝑐𝑡𝑑

= 𝛼

𝑐𝑡

∗

𝑓

𝑐𝑡𝑘 ,0/05

𝛾

𝑐

= 1,0 ∗

2 𝑀𝑃𝑎

1,4

= 1,43 𝑀𝑃𝑎

𝑓

𝑏𝑑

= 2,25 ∗ 𝜂

1

∗ 𝜂

2

∗ 𝑓

𝑐𝑡𝑑

= 2,25 ∗ 1,0 ∗ 1,0 ∗ 1,43 𝑀𝑃𝑎 = 3,22 𝑀𝑃𝑎

𝑙

𝑏,𝑟𝑞𝑑

=

𝜙

4

∗

𝜍

𝑠𝑑

𝑓

𝑏𝑑

=

16𝑚𝑚

4

∗

252,63 𝑀𝑃𝑎

3,22 𝑀𝑃𝑎

= 313,83 𝑚𝑚

𝑙

𝑏𝑑

= 𝛼

1

∗ 𝛼

2

∗ 𝛼

3

∗ 𝛼

4

∗ 𝛼

5

∗ 𝑙

𝑏,𝑟𝑞𝑑

= 1,0 ∗ 0,7 ∗ 1,0 ∗ 0,7 ∗ 1,0 ∗ 313,83𝑚𝑚 = 153,78 𝑚𝑚

𝑙

𝑏,𝑚𝑖𝑛

= max 0,3 ∗ 𝑙

𝑏,𝑟𝑞𝑑

; 10𝜙; 100𝑚𝑚 = max 0,3 ∗ 313,83𝑚𝑚 = 95,15 𝑚𝑚; 10 ∗ 16𝑚𝑚 = 160𝑚𝑚; 100𝑚𝑚

= 160𝑚𝑚

𝑙

𝑏𝑑

= 153,78𝑚𝑚 < 𝑙

𝑏,𝑚𝑖𝑛

= 160𝑚𝑚

Zatem przyjęto 𝑙

𝑏𝑑

= 160 𝑚𝑚

Strzemiona poziome:

𝑎

𝐹

= 100𝑚𝑚 < 0,5𝑕 = 0,5 ∗ 550𝑚𝑚 = 275 𝑚𝑚

𝐴

𝑠,𝑖𝑛𝑘

> 𝑘

1

∗ 𝐴

𝑠,𝑚𝑎𝑖𝑛

= 0,25 ∗ 2,62 𝑐𝑚

2

= 0,655 𝑐𝑚

2

Maksymalny rozstaw:

𝑠 = 𝑚𝑎𝑥

150𝑚𝑚

0,25𝑕 = 112,5𝑚

= 150𝑚𝑚

Przyjęto strzemiona dwucięte 2



8 o 𝑨

𝒔,𝒑𝒓𝒐𝒗

= 𝟏, 𝟎𝟏 𝒄𝒎

𝟐

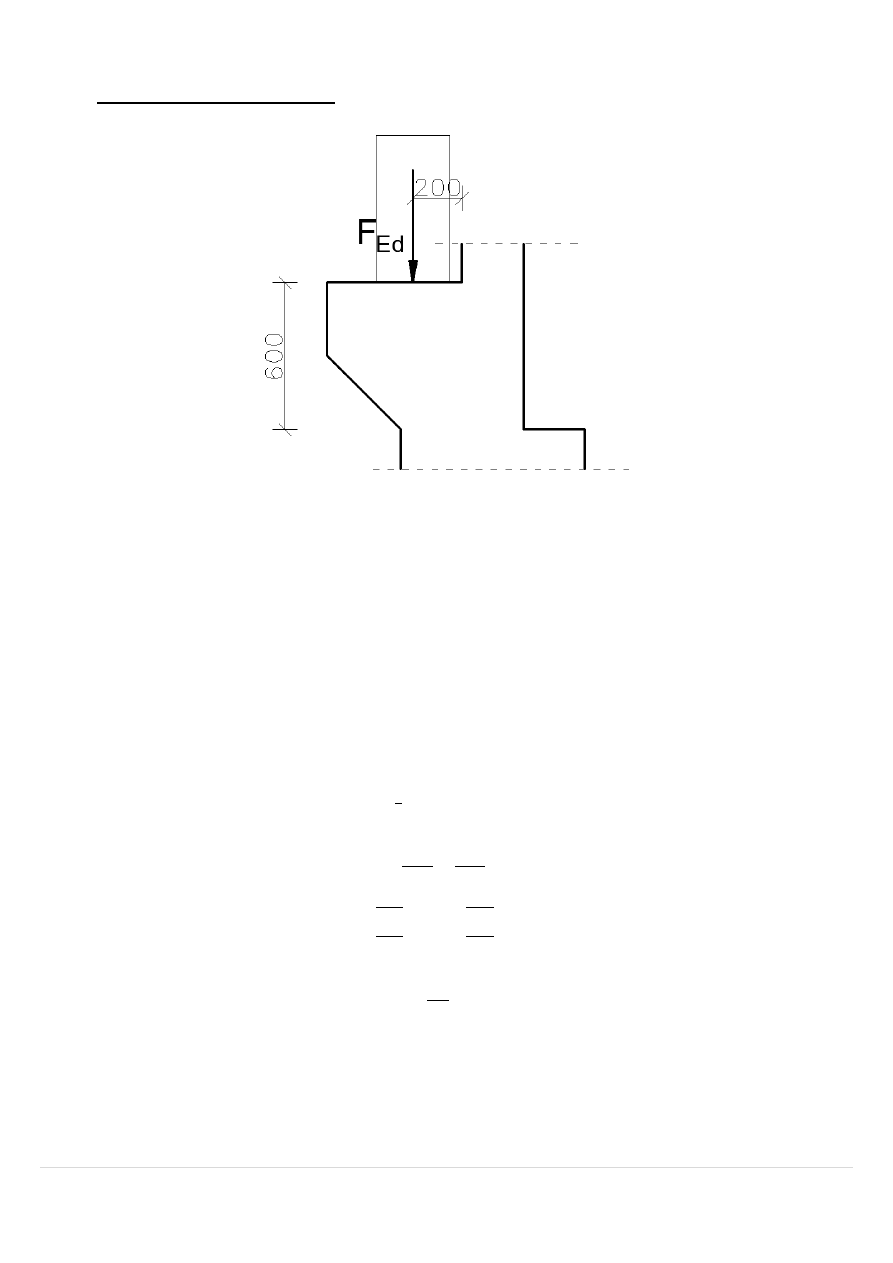
4.4.2 Wspornik pod belkę podsuwnicową

𝐹

𝐸𝑑

= 𝑃

𝑚𝑎𝑥

= 73,28 𝑘𝑁 - Reakcja pionowa od suwnicy

𝐻 = 𝐻

𝑇,2

𝑑

= 18,38 𝑘𝑁

Sprawdzam geometrię wspornika:

𝐹

𝐸𝑑

≤ 𝑉

𝑅𝑑,𝑐

𝐹

𝐸𝑑

≤ 𝐹

𝑉,𝑅𝑑

= 0,5 ∗ 𝜗 ∗ 𝑓

𝑐𝑑

∗ 𝑏 ∗ 𝑑

𝑉

𝑅𝑑,𝑐

= 𝐶

𝑅𝑑,𝑐

∗ 𝑘 ∗ 100𝜌

𝑙

∗ 𝑓

𝑐𝑘

1

3

+ 𝑘

1

∗ 𝜍

𝑐𝑝

∗ 𝑏 ∗ 𝑑 > 𝜈

𝑚𝑖𝑛

+ 𝑘

1

∗ 𝜍

𝑐𝑝

∗ 𝑏 ∗ 𝑑

𝐶

𝑅𝑑,𝑐

=

0,18

𝛾

𝑐

=

0,18

1,4

= 0,129

𝑘 = 1 +

200

𝑑

= 1 +

200
550

= 1,60 < 2,0

𝜌

𝑙

=

𝐴

𝑠𝑙

𝑏𝑑

< 0,02

𝑝𝑟𝑧𝑦𝑗ę𝑡𝑜 𝜌

𝑙

= 0,01

𝑓

𝑐𝑘

= 30 𝑀𝑃𝑎

𝑏 = 500 𝑚𝑚

𝑑 = 550 𝑚𝑚

𝜈

𝑚𝑖𝑛

= 0,035 ∗ 𝑘

3

∗ 𝑓

𝑐𝑘

= 0,035 ∗ 1,60

3

∗ 30 = 0,388

Zatem

𝑉

𝑅𝑑,𝑐

= 0,129 ∗ 1,60 ∗ 100 ∗ 0,01 ∗ 30

1

3

+ 0 ∗ 500 ∗ 550 = 176,366 𝑘𝑁

𝜈

𝑚𝑖𝑛

∗ 𝑏 ∗ 𝑑 = 0,388 ∗ 500 ∗ 550 = 106,700 𝑘𝑁

𝑉

𝑅𝑑,𝑐

> 𝜈

𝑚𝑖𝑛

∗ 𝑏 ∗ 𝑑

𝐹

𝐸𝑑

= 73,28 𝑘𝑁 < 𝑉

𝑅𝑑,𝑐

= 176,366 𝑘𝑁 → 𝑤𝑎𝑟𝑢𝑛𝑒𝑘 𝑠𝑝𝑒ł𝑛𝑖𝑜𝑛𝑦

𝐹

𝑉,𝑅𝑑

= 0,5 ∗ 𝜗 ∗ 𝑓

𝑐𝑑

∗ 𝑏 ∗ 𝑑 = 0,5 ∗ 0,6 ∗ 1 −

𝑓

𝑐𝑘

250

∗ 𝑓

𝑐𝑑

∗ 𝑏 ∗ 𝑑 = 0,5 ∗ 0,6 ∗ 1 −

30

250

∗ 21,43 ∗ 500 ∗ 550

= 1555,818 𝑘𝑁

𝐹

𝐸𝑑

= 73,28 𝑘𝑁 < 𝐹

𝑉,𝑅𝑑

= 1555,818 𝑘𝑁 → 𝑤𝑎𝑟𝑢𝑛𝑒𝑘 𝑠𝑝𝑒ł𝑛𝑖𝑜𝑛𝑦

Zbrojenie główne wspornika:

𝑎

𝐹

𝑕

=

200 𝑚𝑚
600 𝑚𝑚

= 0,33 < 0,50

𝐴

𝑠,𝑚𝑎𝑖𝑛

>

1

𝑓

𝑦𝑑

∗ 0,5𝐹

𝐸𝑑

+ 𝐻 =

1

434 𝑁/𝑚𝑚

2

∗ 0,5 ∗ 73280 𝑁 + 18380 𝑁 = 126,77 𝑚𝑚

2

= 1,26 𝑐𝑚

2

Przyjęto pętlę z prętów 2



10 𝑨

𝒔,𝒑𝒓𝒐𝒗

= 𝟏, 𝟓𝟕 𝒄𝒎

𝟐

Długośd zakotwienia:

Obliczeniowa długośd zakotwienia:

𝑙

𝑏𝑑

= 𝛼

1

∗ 𝛼

2

∗ 𝛼

3

∗ 𝛼

4

∗ 𝛼

5

∗ 𝑙

𝑏,𝑟𝑞𝑑

> 𝑙

𝑏,𝑚𝑖𝑛

Podstawowa długośd zakotwienia:

𝑙

𝑏,𝑟𝑞𝑑

=

𝜙

4

∗

𝜍

𝑠𝑑

𝑓

𝑏𝑑

𝜙 = 10 𝑚𝑚

𝜍

𝑠𝑑

=

𝐴

𝑠,𝑚𝑎𝑖𝑛

𝐴

𝑠,𝑝𝑟𝑜𝑣

∗ 𝑓

𝑦𝑑

=

1,26 𝑐𝑚

2

1,57 𝑐𝑚

2

∗ 434 𝑀𝑃𝑎 = 348,31 𝑀𝑃𝑎

𝑓

𝑏𝑑

= 2,25 ∗ 𝜂

1

∗ 𝜂

2

∗ 𝑓

𝑐𝑡𝑑

𝜂

1

= 1,0 (𝑑𝑜𝑏𝑟𝑒 𝑤𝑎𝑟𝑢𝑛𝑘𝑖 𝑧𝑎𝑡𝑘𝑜𝑡𝑤𝑖𝑒𝑛𝑖𝑎)

𝜂

2

= 1,0 (𝑏𝑜 𝜙 < 32 𝑚𝑚)

𝑓

𝑐𝑡𝑑

= 𝛼

𝑐𝑡

∗

𝑓

𝑐𝑡𝑘 ,0/05

𝛾

𝑐

= 1,0 ∗

2 𝑀𝑃𝑎

1,4

= 1,43 𝑀𝑃𝑎

𝑓

𝑏𝑑

= 2,25 ∗ 𝜂

1

∗ 𝜂

2

∗ 𝑓

𝑐𝑡𝑑

= 2,25 ∗ 1,0 ∗ 1,0 ∗ 1,43 𝑀𝑃𝑎 = 3,22 𝑀𝑃𝑎

𝑙

𝑏,𝑟𝑞𝑑

=

𝜙

4

∗

𝜍

𝑠𝑑

𝑓

𝑏𝑑

=

10𝑚𝑚

4

∗

348,31 𝑀𝑃𝑎

3,22 𝑀𝑃𝑎

= 270,43 𝑚𝑚

𝑙

𝑏𝑑

= 𝛼

1

∗ 𝛼

2

∗ 𝛼

3

∗ 𝛼

4

∗ 𝛼

5

∗ 𝑙

𝑏,𝑟𝑞𝑑

= 1,0 ∗ 0,7 ∗ 1,0 ∗ 0,7 ∗ 1,0 ∗ 270,43𝑚𝑚 = 132,51 𝑚𝑚

𝑙

𝑏,𝑚𝑖𝑛

= max 0,3 ∗ 𝑙

𝑏,𝑟𝑞𝑑

; 10𝜙; 100𝑚𝑚

= max 0,3 ∗ 270,43𝑚𝑚 = 81,129 𝑚𝑚; 10 ∗ 10𝑚𝑚 = 100𝑚𝑚; 100𝑚𝑚
= 100𝑚𝑚

𝑙

𝑏𝑑

= 132,51𝑚𝑚 > 𝑙

𝑏,𝑚𝑖𝑛

= 100𝑚𝑚

Przyjęto 𝑙

𝑏𝑑

= 140 𝑚𝑚

Strzemiona poziome:

𝑎

𝐹

= 200𝑚𝑚 < 0,5𝑕 = 0,5 ∗ 600𝑚𝑚 = 300 𝑚𝑚

𝐴

𝑠,𝑖𝑛𝑘

> 𝑘

1

∗ 𝐴

𝑠,𝑚𝑎𝑖𝑛

= 0,25 ∗ 1,26 𝑐𝑚

2

= 0,32 𝑐𝑚

2

Maksymalny rozstaw:

𝑠 = 𝑚𝑎𝑥

150𝑚𝑚

0,25𝑕 = 150𝑚

= 150𝑚𝑚

Przyjęto strzemiona dwucięte 2



8 o 𝑨

𝒔,𝒑𝒓𝒐𝒗

= 𝟏, 𝟎𝟏 𝒄𝒎

𝟐

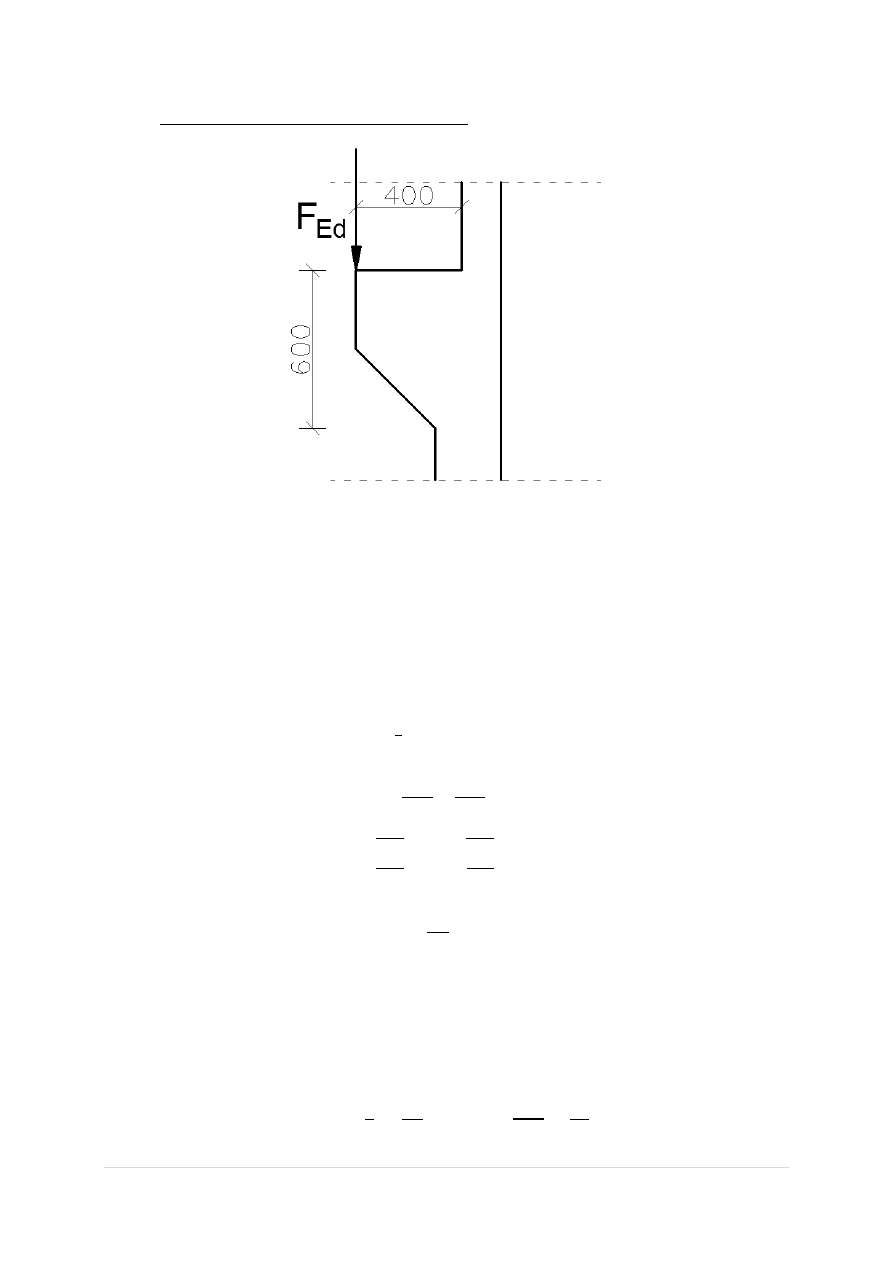
4.4.3 Wspornik pod dźwigar dachowy nawy wyższej

𝐹

𝐸𝑑

= 106,62 𝑘𝑁 - Reakcja pionowa od dźwigara dachowego na wspornik

𝐻 = 0,2 ∗ 𝐹

𝐸𝑑

= 21,33 𝑘𝑁

Sprawdzam geometrię wspornika:

𝐹

𝐸𝑑

≤ 𝑉

𝑅𝑑,𝑐

𝐹

𝐸𝑑

≤ 𝐹

𝑉,𝑅𝑑

= 0,5 ∗ 𝜗 ∗ 𝑓

𝑐𝑑

∗ 𝑏 ∗ 𝑑

𝑉

𝑅𝑑,𝑐

= 𝐶

𝑅𝑑,𝑐

∗ 𝑘 ∗ 100𝜌

𝑙

∗ 𝑓

𝑐𝑘

1

3

+ 𝑘

1

∗ 𝜍

𝑐𝑝

∗ 𝑏 ∗ 𝑑 > 𝜈

𝑚𝑖𝑛

+ 𝑘

1

∗ 𝜍

𝑐𝑝

∗ 𝑏 ∗ 𝑑

𝐶

𝑅𝑑,𝑐

=

0,18

𝛾

𝑐

=

0,18

1,4

= 0,129

𝑘 = 1 +

200

𝑑

= 1 +

200
550

= 1,60 < 2,0

𝜌

𝑙

=

𝐴

𝑠𝑙

𝑏𝑑

< 0,02

𝑝𝑟𝑧𝑦𝑗ę𝑡𝑜 𝜌

𝑙

= 0,01

𝑓

𝑐𝑘

= 30 𝑀𝑃𝑎

𝑏 = 500 𝑚𝑚

𝑑 = 550 𝑚𝑚

𝜈

𝑚𝑖𝑛

= 0,035 ∗ 𝑘

3

∗ 𝑓

𝑐𝑘

= 0,035 ∗ 1,60

3

∗ 30 = 0,388

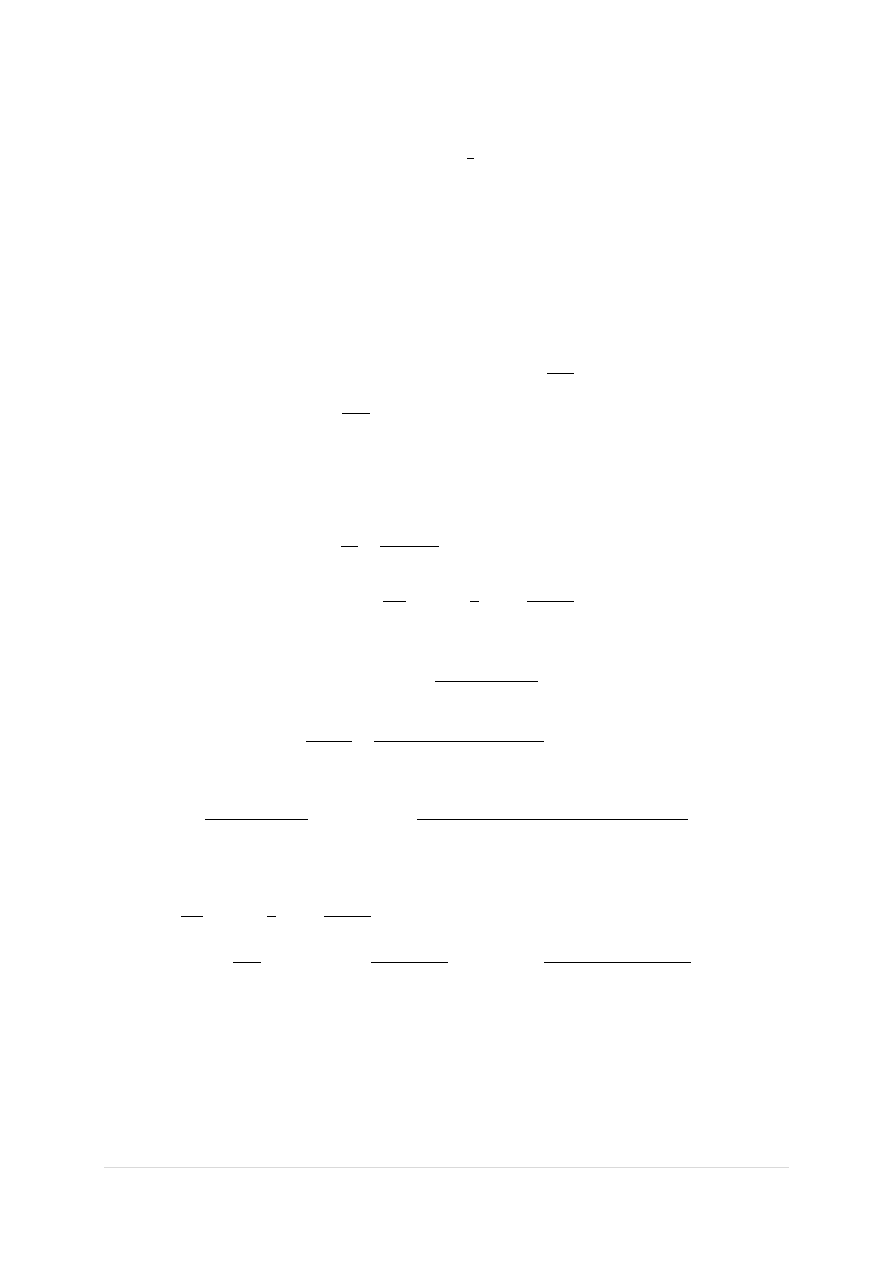
Zatem

𝑉

𝑅𝑑,𝑐

= 0,129 ∗ 1,6 ∗ 100 ∗ 0,01 ∗ 30

1

3

+ 0 ∗ 500 ∗ 550 = 176,366 𝑘𝑁

𝜈

𝑚𝑖 𝑛

∗ 𝑏 ∗ 𝑑 = 0,388 ∗ 500 ∗ 550 = 106,7 𝑘𝑁

𝑉

𝑅𝑑,𝑐

> 𝜈

𝑚𝑖𝑛

∗ 𝑏 ∗ 𝑑

𝐹

𝐸𝑑

= 106,62 𝑘𝑁 < 𝑉

𝑅𝑑,𝑐

= 176,366 𝑘𝑁 → 𝑤𝑎𝑟𝑢𝑛𝑒𝑘 𝑠𝑝𝑒ł𝑛𝑖𝑜𝑛𝑦

𝐹

𝑉,𝑅𝑑

= 0,5 ∗ 𝜗 ∗ 𝑓

𝑐𝑑

∗ 𝑏 ∗ 𝑑 = 0,5 ∗ 0,6 ∗ 1 −

𝑓

𝑐𝑘

250

∗ 𝑓

𝑐𝑑

∗ 𝑏 ∗ 𝑑

= 0,5 ∗ 0,6 ∗ 1 −

30

250

∗ 21,43 ∗ 500 ∗ 5500 = 1555,818 𝑘𝑁

𝐹

𝐸𝑑

= 106,62 𝑘𝑁 < 𝐹

𝑉,𝑅𝑑

= 1555,818 𝑘𝑁 → 𝑤𝑎𝑟𝑢𝑛𝑒𝑘 𝑠𝑝𝑒ł𝑛𝑖𝑜𝑛𝑦

Zbrojenie główne wspornika:

𝑎

𝐹

𝑕

=

400 𝑚𝑚
600 𝑚𝑚

= 0,667 > 0,50

𝐴

𝑠,𝑚𝑎𝑖𝑛

>

1

𝑓

𝑦𝑑

∗ 𝐹

𝐸𝑑

∗

𝑎

𝑧

+ 𝐻 ∗

𝑎

𝐻

+ 𝑧

𝑧

𝑧 = 𝑑 − 0,5𝑎

2

𝑎

2

= 𝑑 − 𝑑

2

− 2 ∗ 𝑎

1

∗ 𝑎

𝑎

1

=

𝐹

𝑓

𝑐𝑑

∗ 𝑏

=

106620 𝑁

21,43 𝑁/𝑚𝑚

2

∗ 500𝑚𝑚

= 9,95𝑚𝑚

𝑎 = 𝑎

𝐹

+ 0,5 ∗ 𝑎

1

= 400𝑚𝑚 + 0,5 ∗ 9,95𝑚𝑚 = 404,97 𝑚𝑚

𝑎

2

= 𝑑 − 𝑑

2

− 2 ∗ 𝑎

1

∗ 𝑎 = 550𝑚𝑚 − 550𝑚𝑚

2

− 2 ∗ 9,95𝑚𝑚 ∗ 404,97𝑚𝑚 = 7,38 𝑚𝑚

𝑧 = 𝑑 − 0,5𝑎

2

= 550𝑚𝑚 − 0,5 ∗ 7,38𝑚𝑚 = 546,31 𝑚𝑚

𝐴

𝑠,𝑚𝑎𝑖𝑛

>

1

𝑓

𝑦𝑑

∗ 𝐹

𝐸𝑑

∗

𝑎

𝑧

+ 𝐻 ∗

𝑎

𝐻

+ 𝑧

𝑧

=

1

434

∗ 106620 𝑁 ∗

404,97𝑚𝑚
546,31𝑚𝑚

+ 21330 𝑁 ∗

50𝑚𝑚 + 546,31 𝑚𝑚

546,31 𝑚𝑚

= 2,35 𝑐𝑚

2

Przyjęto pętlę z prętów 2



16 𝑨

𝒔,𝒑𝒓𝒐𝒗

= 𝟒, 𝟎𝟐 𝒄𝒎

𝟐

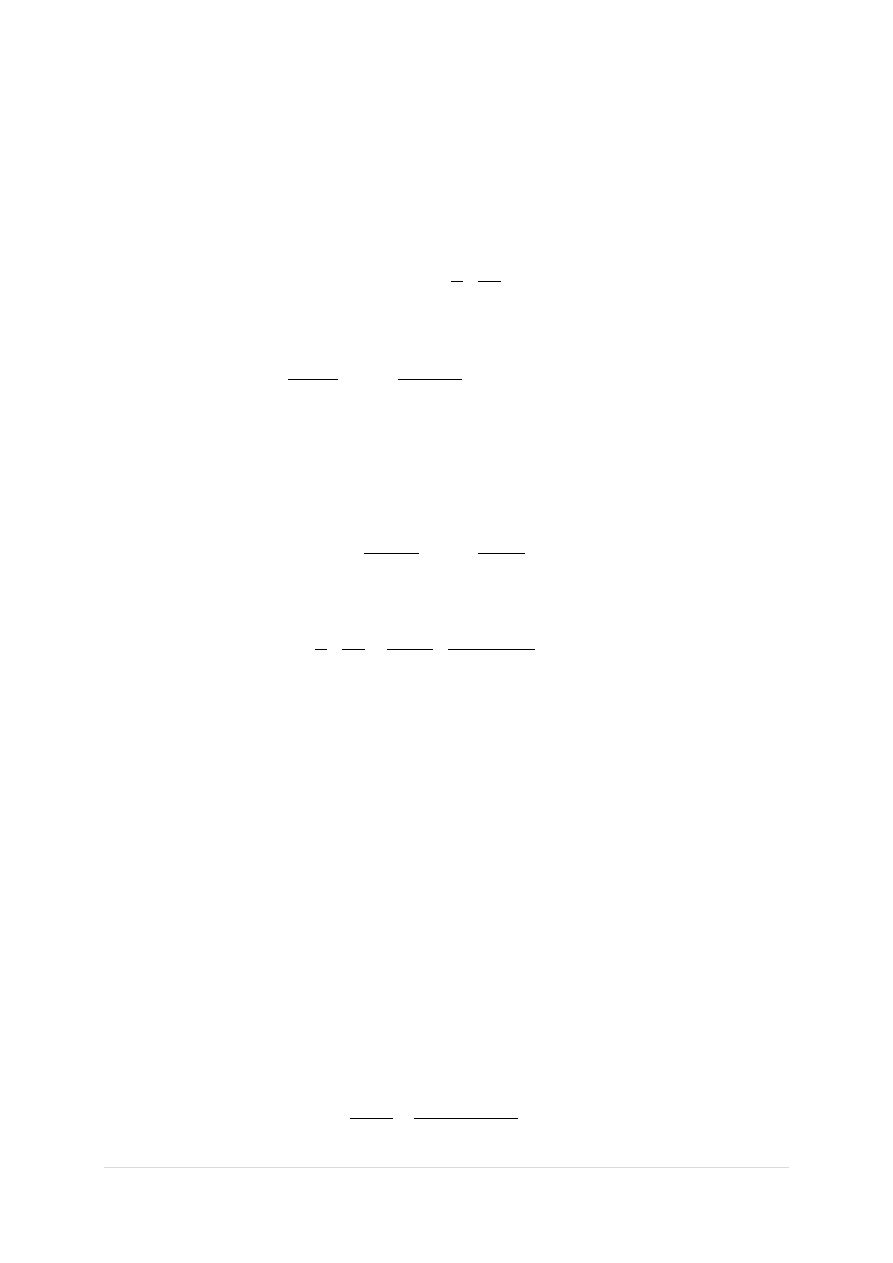
Długośd zakotwienia:

Obliczeniowa długośd zakotwienia:

𝑙

𝑏𝑑

= 𝛼

1

∗ 𝛼

2

∗ 𝛼

3

∗ 𝛼

4

∗ 𝛼

5

∗ 𝑙

𝑏,𝑟𝑞𝑑

> 𝑙

𝑏,𝑚𝑖𝑛

Podstawowa długośd zakotwienia:

𝑙

𝑏,𝑟𝑞𝑑

=

𝜙

4

∗

𝜍

𝑠𝑑

𝑓

𝑏𝑑

𝜙 = 16 𝑚𝑚

𝜍

𝑠𝑑

=

𝐴

𝑠,𝑚𝑎𝑖𝑛

𝐴

𝑠,𝑝𝑟𝑜𝑣

∗ 𝑓

𝑦𝑑

=

2,35 𝑐𝑚

2

4,02 𝑐𝑚

2

∗ 434 𝑀𝑃𝑎 = 253,71 𝑀𝑃𝑎

𝑓

𝑏𝑑

= 2,25 ∗ 𝜂

1

∗ 𝜂

2

∗ 𝑓

𝑐𝑡𝑑

𝜂

1

= 1,0 (𝑑𝑜𝑏𝑟𝑒 𝑤𝑎𝑟𝑢𝑛𝑘𝑖 𝑧𝑎𝑡𝑘𝑜𝑡𝑤𝑖𝑒𝑛𝑖𝑎)

𝜂

2

= 1,0 (𝑏𝑜 𝜙 < 32 𝑚𝑚)

𝑓

𝑐𝑡𝑑

= 𝛼

𝑐𝑡

∗

𝑓

𝑐𝑡𝑘 ,0/05

𝛾

𝑐

= 1,0 ∗

2 𝑀𝑃𝑎

1,4

= 1,43 𝑀𝑃𝑎

𝑓

𝑏𝑑

= 2,25 ∗ 𝜂

1

∗ 𝜂

2

∗ 𝑓

𝑐𝑡𝑑

= 2,25 ∗ 1,0 ∗ 1,0 ∗ 1,43 𝑀𝑃𝑎 = 3,22 𝑀𝑃𝑎

𝑙

𝑏,𝑟𝑞𝑑

=

𝜙

4

∗

𝜍

𝑠𝑑

𝑓

𝑏𝑑

=

16𝑚𝑚

4

∗

253,71 𝑀𝑃𝑎

3,22 𝑀𝑃𝑎

= 315,16 𝑚𝑚

𝑙

𝑏𝑑

= 𝛼

1

∗ 𝛼

2

∗ 𝛼

3

∗ 𝛼

4

∗ 𝛼

5

∗ 𝑙

𝑏,𝑟𝑞𝑑

= 1,0 ∗ 0,7 ∗ 1,0 ∗ 0,7 ∗ 1,0 ∗ 315,16𝑚𝑚 = 154,43 𝑚𝑚

𝑙

𝑏,𝑚𝑖𝑛

= max 0,3 ∗ 𝑙

𝑏,𝑟𝑞𝑑

; 10𝜙; 100𝑚𝑚

= max 0,3 ∗ 315,16𝑚𝑚 = 92,32 𝑚𝑚; 10 ∗ 12𝑚𝑚 = 120𝑚𝑚; 100𝑚𝑚 = 120𝑚𝑚

𝑙

𝑏𝑑

= 154,43𝑚𝑚 > 𝑙

𝑏,𝑚𝑖𝑛

= 120𝑚𝑚

Przyjęto 𝑙

𝑏𝑑

= 160 𝑚𝑚

Strzemiona poziome:

𝑎

𝐹

= 400𝑚𝑚 > 0,5𝑕 = 0,5 ∗ 600𝑚𝑚 = 300 𝑚𝑚

𝐴

𝑠,𝑖𝑛𝑘

> 𝑘

1

∗ 𝐴

𝑠,𝑚𝑎𝑖𝑛

= 0,25 ∗ 1,72 𝑐𝑚

2

= 0,43 𝑐𝑚

2

Przyjęto strzemiona dwucięte 2



8 o 𝑨

𝒔,𝒑𝒓𝒐𝒗

= 𝟏, 𝟎𝟏 𝒄𝒎

𝟐

Strzemiona pionowe:

𝐴

𝑠,𝑖𝑛𝑘

>

𝑘

2

∗ 𝐹

𝑓

𝑦𝑑

=

0,5 ∗ 106620𝑁

434 𝑁/𝑚𝑚

2

= 1,23 𝑐𝑚

2

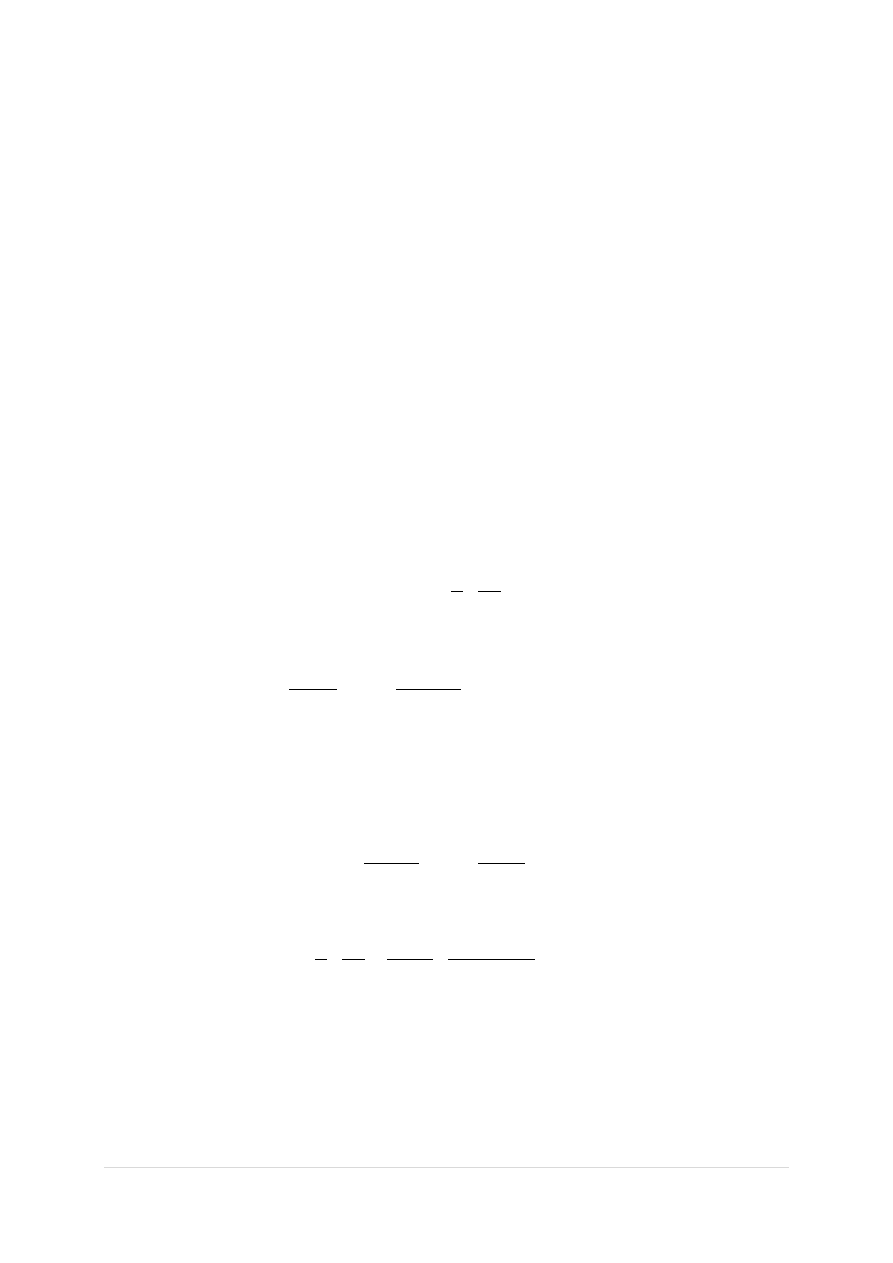
Przyjęto strzemiona dwucięte 2



10 o 𝑨

𝒔,𝒑𝒓𝒐𝒗

= 𝟏, 𝟓𝟕 𝒄𝒎

𝟐

Maksymalny rozstaw:

𝑠 = 𝑚𝑎𝑥

150𝑚𝑚

0,25𝑕 = 112,5𝑚

= 150𝑚𝑚

4.5 Długości zakładu prętów głównych

Częśd od punktu 1 do 4

Obliczeniowa długośd zakładu:

𝑙

0

= 𝛼

1

∗ 𝛼

2

∗ 𝛼

3

∗ 𝛼

4

∗ 𝛼

5

∗ 𝑙

𝑏,𝑟𝑞𝑑

> 𝑙

0,𝑚𝑖𝑛

Podstawowa długośd zakotwienia:

𝑙

𝑏,𝑟𝑞𝑑

=

𝜙

4

∗

𝜍

𝑠𝑑

𝑓

𝑏𝑑

𝜙 = 20 𝑚𝑚

𝜍

𝑠𝑑

=

𝐴

𝑠,𝑟𝑒𝑞

𝐴

𝑠,𝑝𝑟𝑜𝑣

∗ 𝑓

𝑦𝑑

=

8,72 𝑐𝑚

2

9,43 𝑐𝑚

2

∗ 434 𝑀𝑃𝑎 = 401,32 𝑀𝑃𝑎

𝑓

𝑏𝑑

= 2,25 ∗ 𝜂

1

∗ 𝜂

2

∗ 𝑓

𝑐𝑡𝑑

𝜂

1

= 1,0 (𝑑𝑜𝑏𝑟𝑒 𝑤𝑎𝑟𝑢𝑛𝑘𝑖 𝑧𝑎𝑡𝑘𝑜𝑡𝑤𝑖𝑒𝑛𝑖𝑎)

𝜂

2

= 1,0 (𝑏𝑜 𝜙 < 32 𝑚𝑚)

𝑓

𝑐𝑡𝑑

= 𝛼

𝑐𝑡

∗

𝑓

𝑐𝑡𝑘 ,0/05

𝛾

𝑐

= 1,0 ∗

2 𝑀𝑃𝑎

1,4

= 1,43 𝑀𝑃𝑎

𝑓

𝑏𝑑

= 2,25 ∗ 𝜂

1

∗ 𝜂

2

∗ 𝑓

𝑐𝑡𝑑

= 2,25 ∗ 1,0 ∗ 1,0 ∗ 1,43 𝑀𝑃𝑎 = 3,22 𝑀𝑃𝑎

𝑙

𝑏,𝑟𝑞𝑑

=

𝜙

4

∗

𝜍

𝑠𝑑

𝑓

𝑏𝑑

=

20𝑚𝑚

4

∗

401,32 𝑀𝑃𝑎

3,22 𝑀𝑃𝑎

= 623,17 𝑚𝑚

𝑙

0

= 𝛼

1

∗ 𝛼

2

∗ 𝛼

3

∗ 𝛼

4

∗ 𝛼

5

∗ 𝑙

𝑏,𝑟𝑞𝑑

= 1,0 ∗ 0,7 ∗ 1,0 ∗ 0,7 ∗ 1,0 ∗ 623,17 𝑚𝑚 = 305,35 𝑚𝑚

𝑙

0,𝑚𝑖𝑛

= max 0,3 ∗ 𝑙

𝑏,𝑟𝑞𝑑

; 10𝜙; 100𝑚𝑚

= max 0,3 ∗ 401,32 𝑚𝑚 = 120,35 𝑚𝑚; 15 ∗ 20𝑚𝑚 = 300𝑚𝑚; 200𝑚𝑚
= 300𝑚𝑚

𝑙

0

= 305,35𝑚𝑚 > 𝑙

0,𝑚𝑖𝑛

= 300𝑚𝑚

Przyjęto 𝑙

0

= 350 𝑚𝑚

Częśd przekroju od punktu 5 do 6

Obliczeniowa długośd zakładu:

𝑙

0

= 𝛼

1

∗ 𝛼

2

∗ 𝛼

3

∗ 𝛼

4

∗ 𝛼

5

∗ 𝑙

𝑏,𝑟𝑞𝑑

> 𝑙

0,𝑚𝑖𝑛

Podstawowa długośd zakotwienia:

𝑙

𝑏,𝑟𝑞𝑑

=

𝜙

4

∗

𝜍

𝑠𝑑

𝑓

𝑏𝑑

𝜙 = 20 𝑚𝑚

𝜍

𝑠𝑑

=

𝐴

𝑠,𝑟𝑒𝑞

𝐴

𝑠,𝑝𝑟𝑜𝑣

∗ 𝑓

𝑦𝑑

=

8,84 𝑐𝑚

2

9,43 𝑐𝑚

2

∗ 434 𝑀𝑃𝑎 = 406,85 𝑀𝑃𝑎

𝑓

𝑏𝑑

= 2,25 ∗ 𝜂

1

∗ 𝜂

2

∗ 𝑓

𝑐𝑡𝑑

𝜂

1

= 1,0 (𝑑𝑜𝑏𝑟𝑒 𝑤𝑎𝑟𝑢𝑛𝑘𝑖 𝑧𝑎𝑡𝑘𝑜𝑡𝑤𝑖𝑒𝑛𝑖𝑎)

𝜂

2

= 1,0 (𝑏𝑜 𝜙 < 32 𝑚𝑚)

𝑓

𝑐𝑡𝑑

= 𝛼

𝑐𝑡

∗

𝑓

𝑐𝑡𝑘 ,0/05

𝛾

𝑐

= 1,0 ∗

2 𝑀𝑃𝑎

1,4

= 1,43 𝑀𝑃𝑎

𝑓

𝑏𝑑

= 2,25 ∗ 𝜂

1

∗ 𝜂

2

∗ 𝑓

𝑐𝑡𝑑

= 2,25 ∗ 1,0 ∗ 1,0 ∗ 1,43 𝑀𝑃𝑎 = 3,22 𝑀𝑃𝑎

𝑙

𝑏,𝑟𝑞𝑑

=

𝜙

4

∗

𝜍

𝑠𝑑

𝑓

𝑏𝑑

=

20𝑚𝑚

4

∗

406,85 𝑀𝑃𝑎

3,22 𝑀𝑃𝑎

= 631,75 𝑚𝑚

𝑙

0

= 𝛼

1

∗ 𝛼

2

∗ 𝛼

3

∗ 𝛼

4

∗ 𝛼

5

∗ 𝑙

𝑏,𝑟𝑞𝑑

= 1,0 ∗ 0,7 ∗ 1,0 ∗ 0,7 ∗ 1,0 ∗ 631,75 𝑚𝑚 = 309,56 𝑚𝑚

𝑙

0,𝑚𝑖𝑛

= max 0,3 ∗ 𝑙

𝑏,𝑟𝑞𝑑

; 10𝜙; 100𝑚𝑚

= max 0,3 ∗ 406,85 𝑚𝑚 = 122,055 𝑚𝑚; 15 ∗ 20𝑚𝑚 = 300𝑚𝑚; 200𝑚𝑚
= 300𝑚𝑚

𝑙

0

= 309,56𝑚𝑚 > 𝑙

0,𝑚𝑖𝑛

= 300𝑚𝑚

Przyjęto 𝑙

0

= 350 𝑚𝑚

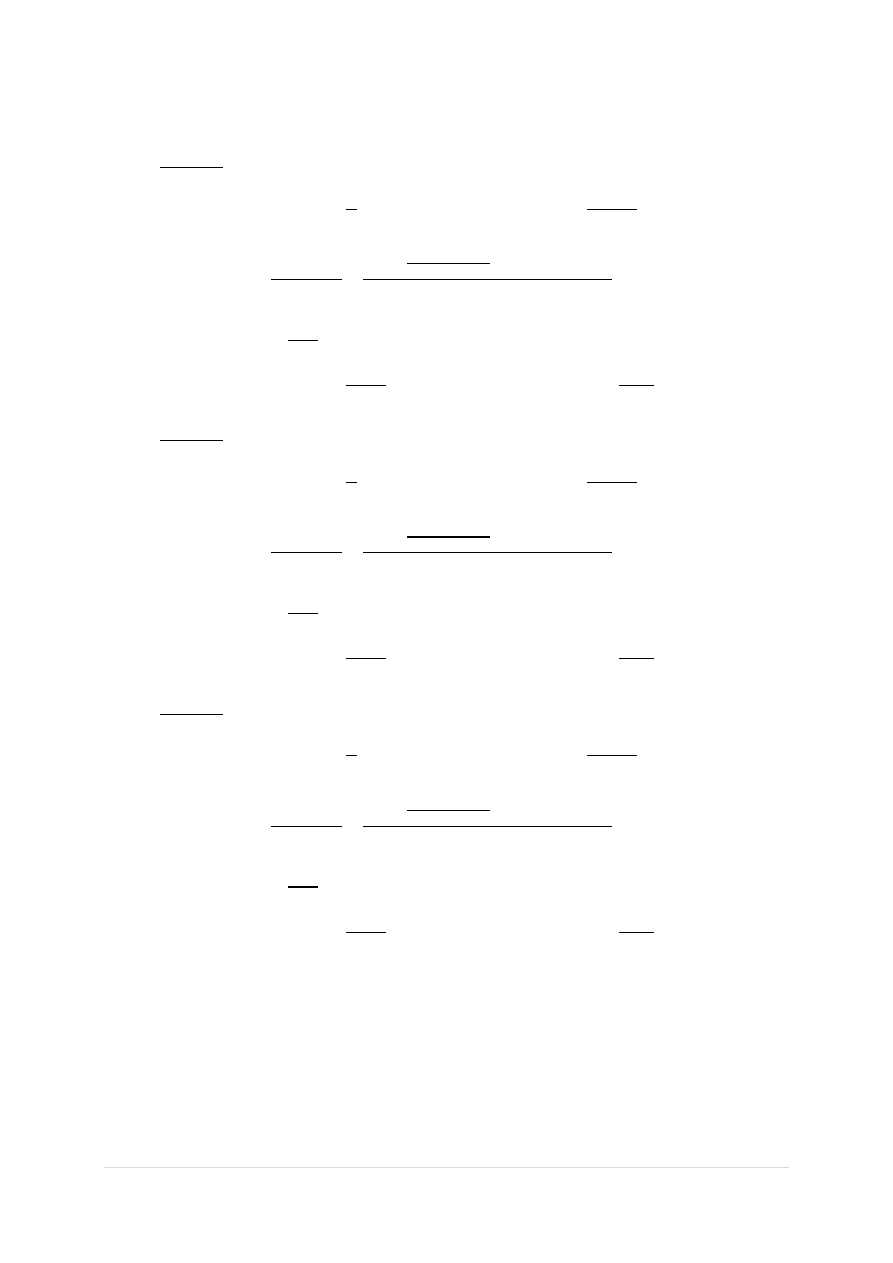
4.6 Sprawdzenie nośności słupa

4.6.1 Częśd 1-2

𝑑 = 𝑕 − 𝑐

𝑛𝑜𝑚

− 𝜙

𝑠𝑡𝑟𝑧

−

𝜙

2

= 500 𝑚𝑚 − 50 𝑚𝑚 − 8 𝑚𝑚 −

20 𝑚𝑚

2

= 432 𝑚𝑚

𝜉

𝑒𝑓𝑓

=

𝐴 ∗ 𝑓

𝑦𝑑

𝑏 ∗ 𝑑 ∗ 𝑓

𝑐𝑑

=

2 ∗

𝜋 ∗ 20 𝑚𝑚

2

4

∗ 434 𝑁/𝑚𝑚

2

600 𝑚𝑚 ∗ 432 𝑚𝑚 ∗ 21,43 𝑁/𝑚𝑚

2

= 0,049

𝑀

𝑅𝑑,1−2

= 𝜉

𝑒𝑓𝑓

∗ 1 −

𝜉

𝑒𝑓𝑓

2

∗ 𝑑

2

∗ 𝑏 ∗ 𝑓

𝑐𝑑

= 0,049 ∗ 1 −

0,049

2

∗ (432 𝑚𝑚)

2

∗ 600𝑚𝑚 ∗ 21,43

𝑁

𝑚𝑚

2

= 114,70 𝑘𝑁𝑚

4.6.2 Częśd 3-4

𝑑 = 𝑕 − 𝑐

𝑛𝑜𝑚

− 𝜙

𝑠𝑡𝑟𝑧

−

𝜙

2

= 500 𝑚𝑚 − 50 𝑚𝑚 − 8 𝑚𝑚 −

20 𝑚𝑚

2

= 432 𝑚𝑚

𝜉

𝑒𝑓𝑓

=

𝐴 ∗ 𝑓

𝑦𝑑

𝑏 ∗ 𝑑 ∗ 𝑓

𝑐𝑑

=

2 ∗

𝜋 ∗ 20 𝑚𝑚

2

4

∗ 434 𝑁/𝑚𝑚

2

500 𝑚𝑚 ∗ 432 𝑚𝑚 ∗ 21,43 𝑁/𝑚𝑚

2

= 0,059

𝑀

𝑅𝑑,3−4

= 𝜉

𝑒𝑓𝑓

∗ 1 −

𝜉

𝑒𝑓𝑓

2

∗ 𝑑

2

∗ 𝑏 ∗ 𝑓

𝑐𝑑

= 0,059 ∗ 1 −

0,059

2

∗ (432 𝑚𝑚)

2

∗ 500𝑚𝑚 ∗ 21,43

𝑁

𝑚𝑚

2

= 114,50 𝑘𝑁𝑚

4.6.3 Częśd 5-6

𝑑 = 𝑕 − 𝑐

𝑛𝑜𝑚

− 𝜙

𝑠𝑡𝑟𝑧

−

𝜙

2

= 500 𝑚𝑚 − 50 𝑚𝑚 − 8 𝑚𝑚 −

20 𝑚𝑚

2

= 432 𝑚𝑚

𝜉

𝑒𝑓𝑓

=

𝐴 ∗ 𝑓

𝑦𝑑

𝑏 ∗ 𝑑 ∗ 𝑓

𝑐𝑑

=

2 ∗

𝜋 ∗ 20 𝑚𝑚

2

4

∗ 434 𝑁/𝑚𝑚

2

250 𝑚𝑚 ∗ 432 𝑚𝑚 ∗ 21,43 𝑁/𝑚𝑚

2

= 0,117

𝑀

𝑅𝑑,5−6

= 𝜉

𝑒𝑓𝑓

∗ 1 −

𝜉

𝑒𝑓𝑓

2

∗ 𝑑

2

∗ 𝑏 ∗ 𝑓

𝑐𝑑

= 0,117 ∗ 1 −

0,117

2

∗ (432 𝑚𝑚)

2

∗ 250𝑚𝑚 ∗ 21,43

𝑁

𝑚𝑚

2

= 110,14 𝑘𝑁𝑚

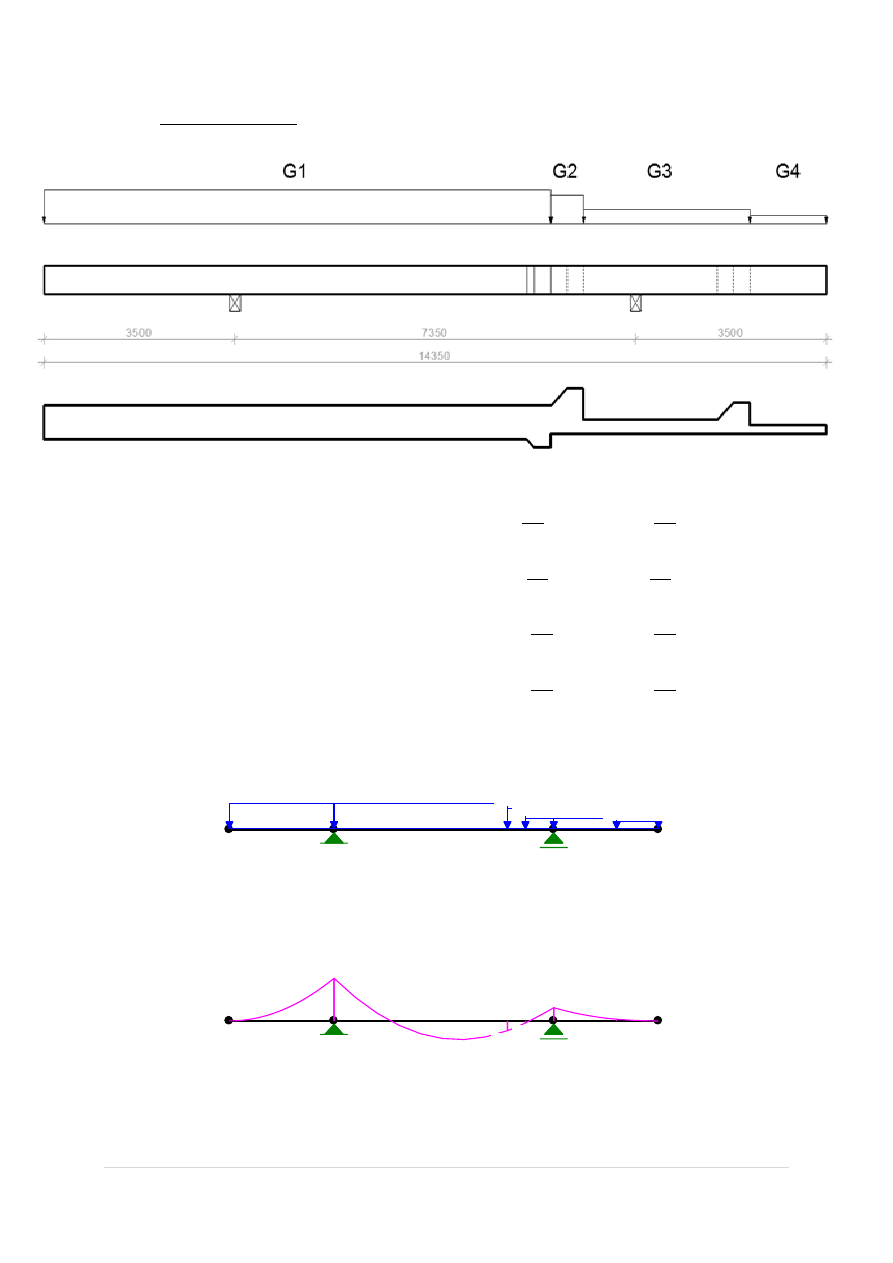
4.6.4 W fazie składowania

𝐺1 = 𝑏 ∗ 𝑕 ∗ 𝛾

𝑏

∗ 1,35 = 0,6 𝑚 ∗ 0,5 𝑚 ∗ 25

𝑘𝑁

𝑚

∗ 1,35 = 10,13

𝑘𝑁

𝑚

𝐺2 = 𝑏 ∗ 𝑕 ∗ 𝛾

𝑏

∗ 1,35 = 0,5 𝑚 ∗ 0,5 𝑚 ∗ 25

𝑘𝑁

𝑚

∗ 1,35 = 8,44

𝑘𝑁

𝑚

𝐺1 = 𝑏 ∗ 𝑕 ∗ 𝛾

𝑏

∗ 1,35 = 0,25 𝑚 ∗ 0,5 𝑚 ∗ 25

𝑘𝑁

𝑚

∗ 1,35 = 4,22

𝑘𝑁

𝑚

𝐺1 = 𝑏 ∗ 𝑕 ∗ 𝛾

𝑏

∗ 1,35 = 0,15 𝑚 ∗ 0,5 𝑚 ∗ 25

𝑘𝑁

𝑚

∗ 1,35 = 2,53

𝑘𝑁

𝑚

Obciążenia:

Momenty:

Siły tnące:

1

2

3

10,130

10,130

10,130

10,130

8,440

8,440

4,2204,220

4,220

4,220

2,530

2,530

1

2

3

-62,046

-62,046 -62,046

14,176

14,176

2,916

2,916

-19,223

27,182

-62,046

-19,223

-2,479

-2,479

-19,223

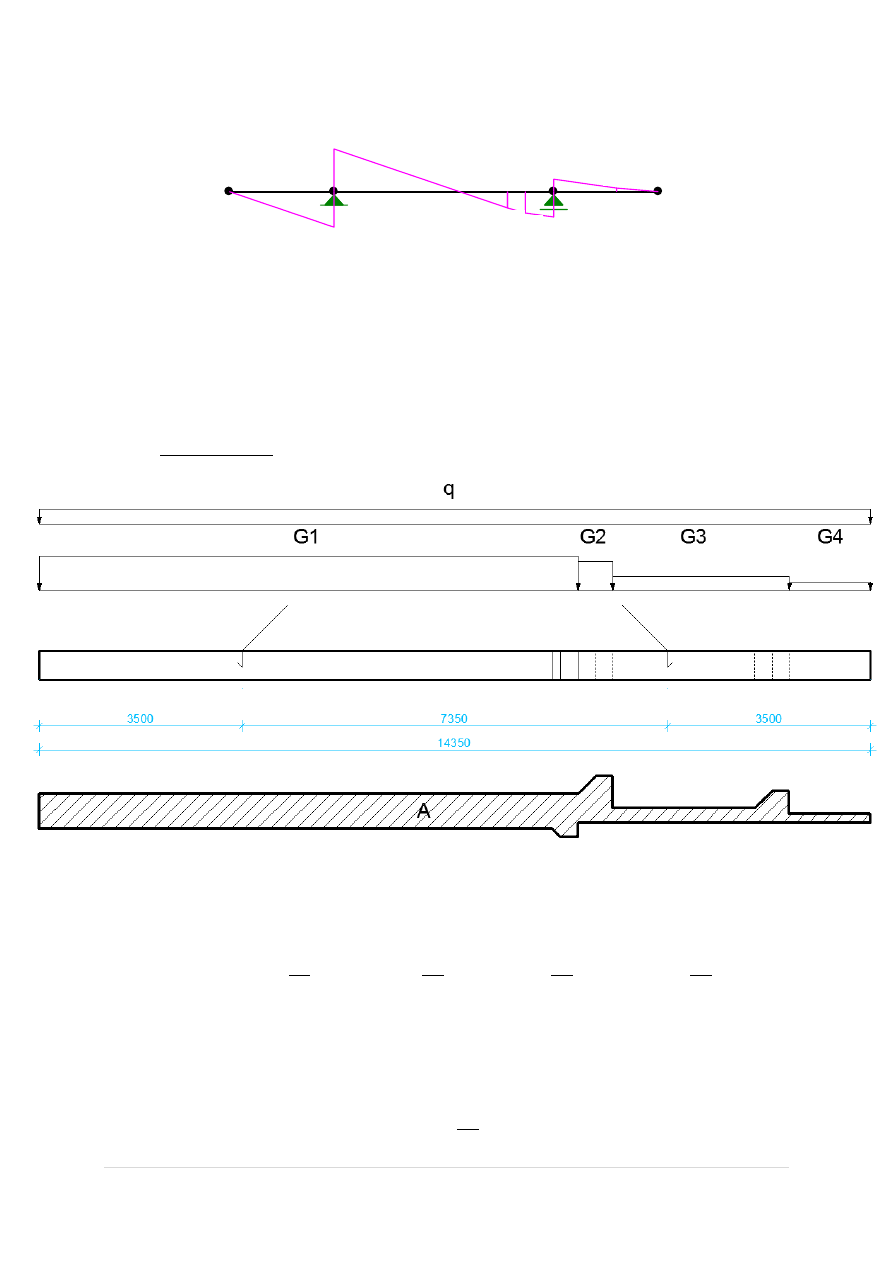
𝑀

𝐸𝑑,𝑚𝑎𝑥

= 62,05𝑘𝑁𝑚 <

𝑀

𝑅𝑑,5−6

𝑀

𝑅𝑑,3−4

𝑀

𝑅𝑑,1−2

Warunek spełniony

4.6.5 W fazie montażu

𝑃 = 𝐺

𝑠ł

+ 𝑄 ∗ 𝛽 ∗ 0,5

𝐺

𝑠ł

= 𝐺

1

∗ 9,3 𝑚 + 𝐺

2

∗ 0,6 𝑚 + 𝐺

3

∗ 3,05 𝑚 + 𝐺

4

∗ 1,40𝑚

= 10,13

𝑘𝑁

𝑚

∗ 9,3 𝑚 + 8,44

𝑘𝑁

𝑚

∗ 0,6𝑚 + 4,22

𝑘𝑁

𝑚

∗ 3,05𝑚 + 2,53

𝑘𝑁

𝑚

∗ 1,40𝑚

= 115,70 𝑘𝑁

𝑄 = 𝐴 ∗ 1 𝑘𝑁/𝑚

2

- przyczepnośd betonu do stali

𝐴 = 7,20 𝑚

2

𝑄 = 7,20 𝑚

2

∗ 1

𝑘𝑁
𝑚

2

= 7,20𝑘𝑁

1

2

3

-35,455

-35,455

42,519

-16,235

-16,235

-21,299

-21,299

-25,308

42,519

-25,308

12,404

3,542

3,542

12,404

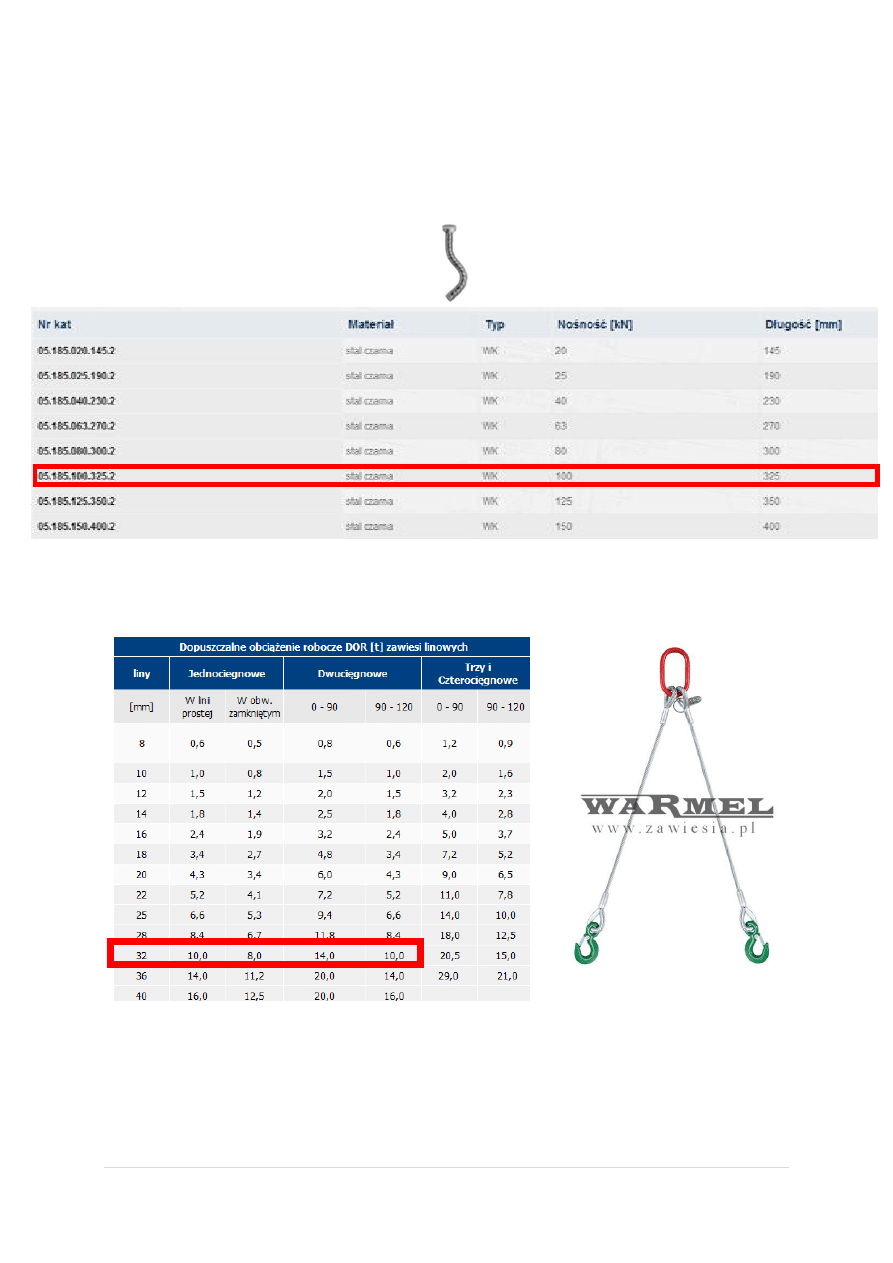
𝑃 = 𝐺

𝑠ł

+ 𝑄 ∗ 𝛽 ∗ 0,5 = 115,7 𝑘𝑁 + 7,20 𝑘𝑁 ∗ 1,5 ∗ 0,5 = 92,18 𝑘𝑁

Dobrano kulowy hak falowy typu WK firmy JORDAHL – PFEIFER o długości 325 mm.

Dobrano również zawiesie dwucięgnowe linowe firmy WARNEL o dopuszczalnym obciążeniu 10 ton.

Rozstaw strzemion konstrukcyjnych:

𝑠

𝑙𝑡,𝑚𝑎𝑥 ,1−2

= min 20𝜙; 400𝑚𝑚; min 𝑏; 𝑕

= min 20 ∗ 20𝑚𝑚 = 40𝑚𝑚; 400𝑚𝑚; 500mm = 400 𝑚𝑚

𝑠

𝑙𝑡,𝑚𝑎𝑥 ,5−6

= min 20 ∗ 20𝑚𝑚 = 400𝑚𝑚; 400𝑚𝑚; 250mm = 250 𝑚𝑚