
Wykład 8
Zmienne zerojedynkowe
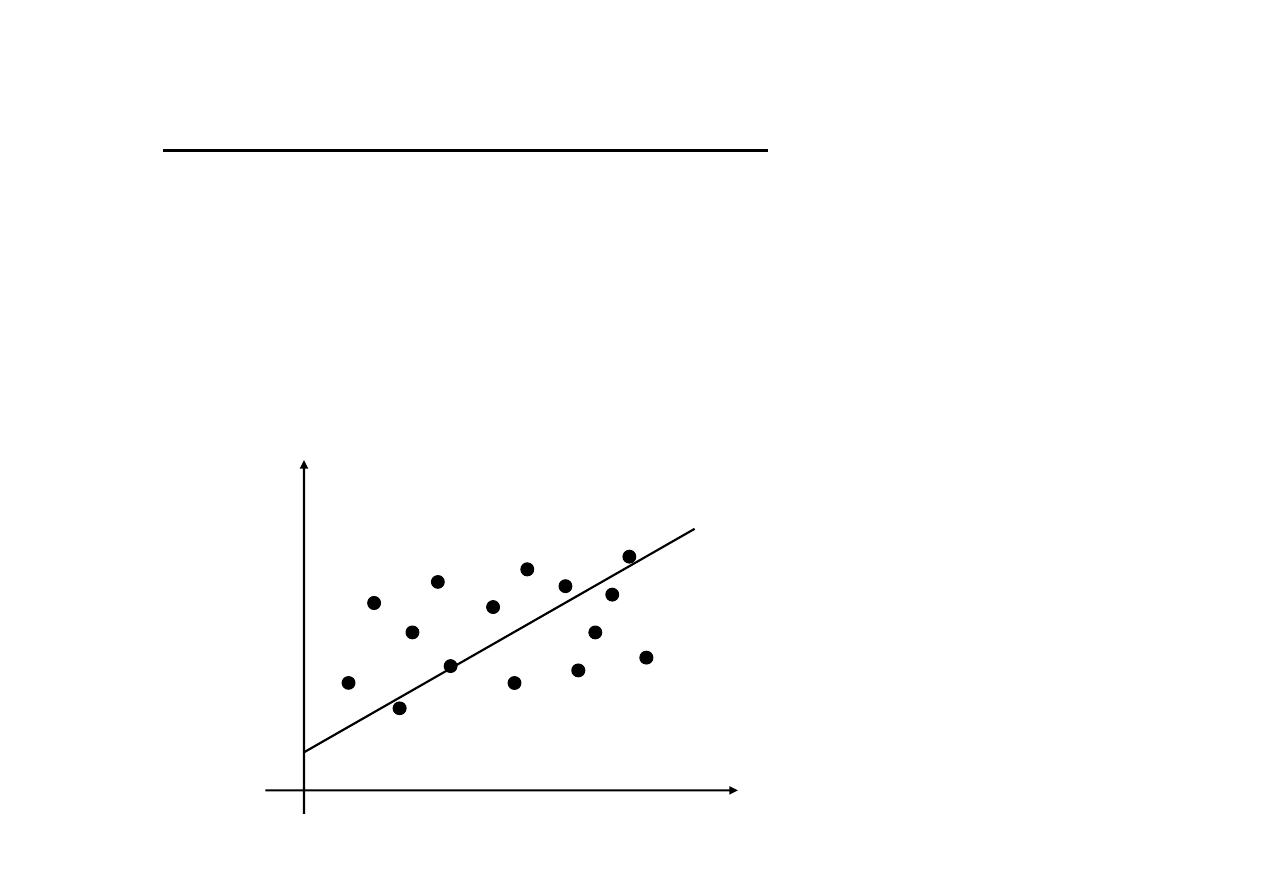
Model z jako
ś
ciowymi zmiennymi obja
ś
niaj
ą
cymi
t
t
t
Y
X
,
= α + β + ξ
= α + β + ξ
= α + β + ξ
= α + β + ξ
(Maddala (2005), rozdz. 8.1-8.2)
t
Y
- dochód
t
X - wykształcenie (lata sp
ę
dzone w szkole)
Y
X
α
αα
α
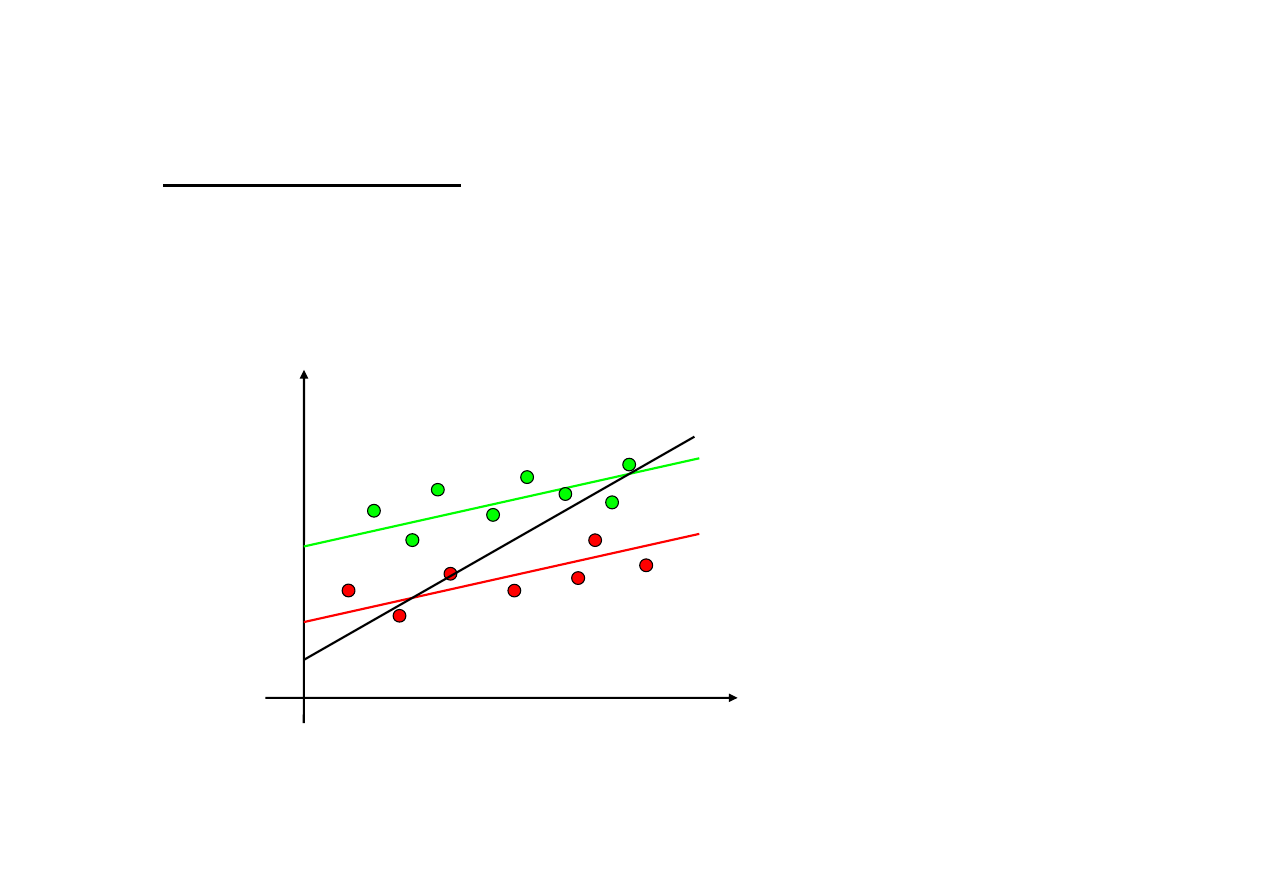
Zmiana wyrazu wolnego (jeden czynnik ró
ż
nicuj
ą
cy)
1
t
t
t
2
t
t
X
dlapierwszej grupy
Y
X
dla drugiej grupy
α + β + ξ
α + β + ξ
α + β + ξ
α + β + ξ
====
α + β + ξ
α + β + ξ
α + β + ξ
α + β + ξ
Y
X
α
αα
α
1
α
αα
α
2

t
1
2
1
t
t
t
Y
(
)D
X
= α + α − α
+ β + ξ =
= α + α − α
+ β + ξ =
= α + α − α
+ β + ξ =
= α + α − α
+ β + ξ =
1
2
t
t
t
D
X
′′′′
= α + α
+ β + ξ
= α + α
+ β + ξ
= α + α
+ β + ξ
= α + α
+ β + ξ
2
2
1
′′′′
α = α − α
α = α − α
α = α − α
α = α − α
t
1 dla drugiej grupy
D
0 dla pierwszej grupy
====

1
t
t
t
2
t
t
3
t
t
X
dla pierwszej grupy
Y
X
dla drugiej grupy
X
dla trzeciej grupy
α + β + ξ
α + β + ξ
α + β + ξ
α + β + ξ
= α + β + ξ
= α + β + ξ
= α + β + ξ
= α + β + ξ
α + β + ξ
α + β + ξ
α + β + ξ
α + β + ξ
t
1
2
1
1t
3
1
2t
t
t
Y
(
)D
(
)D
X
= α + α − α
+ α − α
+ β + ξ =
= α + α − α
+ α − α
+ β + ξ =
= α + α − α
+ α − α
+ β + ξ =
= α + α − α
+ α − α
+ β + ξ =
1
2
1t
3
2t
t
t
D
D
X
′
′
′
′
′
′
′
′
= α + α
+ α
+ β + ξ
= α + α
+ α
+ β + ξ
= α + α
+ α
+ β + ξ
= α + α
+ α
+ β + ξ
,
2
2
1
′′′′
α = α − α
α = α − α
α = α − α
α = α − α
,
3
3
1
′′′′
α = α − α
α = α − α
α = α − α
α = α − α
1t
1
dla grupy drugiej
D
0
dla gruppierwszej i trzeciej
====
2t
1
dla grupy trzeciej
D
0
dla gruppierwszej i drugiej
====

Zmiana wyrazu wolnego (wiele czynników ró
ż
nicuj
ą
cych)
t
t
1
1t
2
2t
3
3t
4
4 t
5
5t
t
Y
X
D
D
D
D
D
= α + β + γ
+ γ
+ γ
+ γ
+ γ
+ ξ
= α + β + γ
+ γ
+ γ
+ γ
+ γ
+ ξ
= α + β + γ
+ γ
+ γ
+ γ
+ γ
+ ξ
= α + β + γ
+ γ
+ γ
+ γ
+ γ
+ ξ
,
1t
1 M
D
0 K
====
(płe
ć
),
2t
1 wiek
25
D
0 wiek
25
<<<<
====
≥≥≥≥
(wiek),
3t
1 wiek
(25,50)
D
0 wiek
(25,50)
∈
∈
∈
∈
====
∉
∉
∉
∉
(wiek),
4 t
1
W
D
0 inne
====
(wykształcenie),
5 t
1
S
D
0 inne
====
(wykształcenie),
m
ęż
czyzna,30 lat, wykształcenie wy
ż
sze:
1t
2t
3t
4t
5 t
D
1,D
0,D
1,D
1,D
0
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
; st
ą
d
4
3
1
γγγγ
++++
γγγγ
++++
γγγγ
++++
αααα
====
αααα′′′′
kobieta, 60 lat, wykształcenie
ś
rednie:
1t
2t
3t
4t
5t
D
0,D
0,D
0,D
0,D
1
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
; st
ą
d
5
′′′′
α = α + γ
α = α + γ
α = α + γ
α = α + γ

Przykład (Lovell, AER 1986)
t
t
ˆ
Y
7,952
0,693X
=
+
=
+
=
+
=
+
,
2
R
0,74
====
(1,735) (0,061)
t
t
t
t
t
ˆ
Y
22,008
0,002W
2,76K
3,28P
0, 415X
=
−
−
+
+
=
−
−
+
+
=
−
−
+
+
=
−
−
+
+
,
2
R
0,82
====
(5,349)
(0,001)
(0,708)
(1, 413)
(0,097)
t
Y
- ilo
ść
mil przejechanych z 1 galona paliwa wg
stowarzyszenia konsumentów
t
X - zu
ż
ycie paliwa podawane przez producentów
t
W - waga pojazdu (funty)
t
K - 1 (zm. biegów automat.), 0 (zm. biegów r
ę
czna)
t
P - 1 (silnik diesla), 0 (silnik benzynowy)
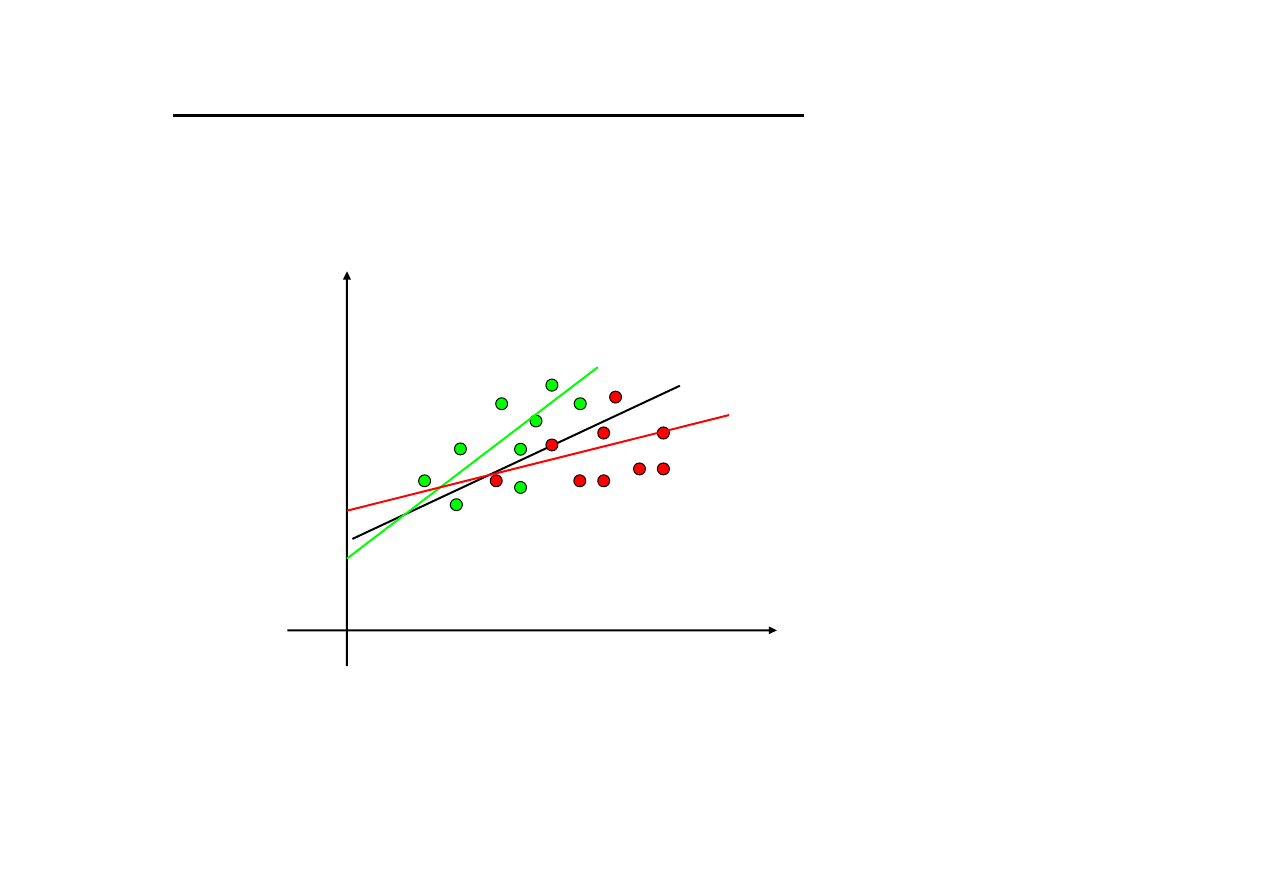
Zmiana wyrazu wolnego i współczynnika kierunkowego
1
1
t
t
t
2
2
t
t
X
dlapierwszej grupy
Y
X
dla drugiej grupy
α + β
+ ξ
α + β
+ ξ
α + β
+ ξ
α + β
+ ξ
====
α + β
+ ξ
α + β
+ ξ
α + β
+ ξ
α + β
+ ξ
X
Y
t
1
2
1
1t
1
t
2
1
1t
t
t
Y
(
)D
X
(
)D X
= α + α − α
+ β
+ β − β
+ ξ =
= α + α − α
+ β
+ β − β
+ ξ =
= α + α − α
+ β
+ β − β
+ ξ =
= α + α − α
+ β
+ β − β
+ ξ =
1
2
1t
1
t
2
1t
t
t
1
2
1t
1
t
2
t
t
D
X
D X
D
X
Z
′
′
′
′
′
′
′
′
′
′
′
′
′
′
′
′
= α + α
+ β
+ β
+ ξ = α + α
+ β
+ β
+ ξ
= α + α
+ β
+ β
+ ξ = α + α
+ β
+ β
+ ξ
= α + α
+ β
+ β
+ ξ = α + α
+ β
+ β
+ ξ
= α + α
+ β
+ β
+ ξ = α + α
+ β
+ β
+ ξ
,
2
2
1
′′′′
α = α − α
α = α − α
α = α − α
α = α − α
,
2
2
1
′′′′
β = β − β
β = β − β
β = β − β
β = β − β
,
t
1t
t
Z
D X
====
,
1t
1
dla drugiejgrupy
D
0
dla pierwszej grupy
====
Uwaga:
Testowanie stabilno
ś
ci współczynników regresji
0 1 0 0
R
0 0 1 0
====
,
1
2
1
2
αααα
′′′′
αααα
β =
β =
β =
β =
ββββ
′′′′
ββββ
,
0
q
0
====
;
0
H : R
q
β =
β =
β =
β =
(
2
2
0,
0
′
′
′
′
′
′
′
′
α = β =
α = β =
α = β =
α = β =
)

ˆ
d R
q
= β −
= β −
= β −
= β −
,
T
2
T
1
T
ˆ
ˆ
Var(d) Var(R
q) R(Var( ))R
R(X X) R
−−−−
ξξξξ
=
β − =
β
= σ
=
β − =
β
= σ
=
β − =
β
= σ
=
β − =
β
= σ
T
2
T
1
T
1
ˆ
ˆ
ˆ
(R
q) (
R(X X) R ) (R
q)
F
~ F(J,T (K 1))
J
−
−
−
−
−
−
−
−
ξξξξ
β −
σ
β −
β −
σ
β −
β −
σ
β −
β −
σ
β −
=
−
+
=
−
+
=
−
+
=
−
+
2
T
2
T
1
T
1
2
ˆ
ˆ
ˆ
(R
q) (
R(X X) R ) (R
q) ~
(j)
−
−
−
−
−
−
−
−
ξξξξ
χ = β −
σ
β −
χ
χ = β −
σ
β −
χ
χ = β −
σ
β −
χ
χ = β −
σ
β −
χ

Efekty sezonowe
7
t
i
it
t
i 1
Y
D
====
=
β
+ ξ
=
β
+ ξ
=
β
+ ξ
=
β
+ ξ
∑
∑
∑
∑
,
6
t
0
i
it
t
i 1
Y
D
====
= β +
β
+ ξ
= β +
β
+ ξ
= β +
β
+ ξ
= β +
β
+ ξ
∑
∑
∑
∑
,
t
Y - wielko
ść
przewozu w i-tym dniu tygodnia,
it
1 dla i
tegodnia tygodnia
D
0
dla innego dnia
−−−−
====
i
i
E(Y )
β =
β =
β =
β =
-
ś
redni przewóz w i-tym dniu tygodnia
i
0
i
′′′′
β = β + β
β = β + β
β = β + β
β = β + β
-
ś
redni przewóz w i-tym dniu tygodnia
0
7
E(Y )
β =
β =
β =
β =
-
ś
redni przewóz w niedziel
ę
i
i
0
′′′′
β = β − β
β = β − β
β = β − β
β = β − β
Wyszukiwarka
Podobne podstrony:
ekonomika w8
ekonometria W8
ekonomika w8
Ekonomia Drdrozdrowski, w8 motywowanie
EKONOMIKA MIAST I REGIONÓW W8
Ekonomia Drdrozdrowski w8 motywowanie
eko w8, Ekonomia, Ekonometria
Ekonomia Drdrozdrowski, w8 motywowanie
W8 globalizacja, ekonomia
w8 VLAN oraz IP w sieciach LAN
Spoleczno ekonomiczne uwarunkowania somatyczne stanu zdrowia ludnosci Polski
Ekonomia konspekt1
EKONOMIKA TRANSPORTU IX
Ekonomia II ZACHOWANIA PROEKOLOGICZNE
W8 kwas glutaminowy
Ekonomia9
więcej podobnych podstron