zasady statyki

 

Statyka jako dział mechaniki ogólnej wykorzystuje następujące zasady 
(aksjomaty), których się nie udowadnia, a przyjmuje jako pewniki. 
 
  

Zasada pierwsza (zasada równoległoboku). Działanie dwóch sił P

1 

i P

2

 

można zastąpić działaniem jednej siły R, działającej na ten sam punkt, 

będącej przekątną równoległoboku ABCD zbudowanego na wektorach sił P

1 

i 

P

2

. 

      

 

Wypadkową R wyznaczamy ze wzoru  
 

          

 

W przypadku, gdy siły P

1 

i P

2

 działają wzdłuż jednej prostej i są zgodnie 

skierowane, wartość wypadkowej wynosi 

          

 

Natomiast, gdy siły są przeciwnie skierowane i P

2 

=P

1

 , to  

          

 

  Zasada druga. 

Jeżeli do ciała przyłożone są dwie siły, to równoważą się one 

tylko w

tedy, gdy mają tę samą linię działania, te same wartości liczbowe i 

przeciwne zwroty. Aby siły te równoważyły się, muszą być spełnione 
zależności 

          

 

  Zasada trzecia. 

Skutek działania dowolnego układu sił przyłożonego do 

ciała nie zmieni się, jeśli do tego układu dodamy lub odejmiemy dowolny 
układ równoważących się sił, czyli tzw. układ zerowy. Wynika stąd 
następujący wniosek: każdą siłę działającą na ciało sztywne można 
przesunąć dowolnie wzdłuż jej linii działania.  
 
  Zasada czwarta (zasada zesztywnienia). 

Jeżeli ciało odkształcalne 

znajduje się w równowadze pod działaniem pewnego układu sił, to również 
pozostanie w równowadze ciało doskonale sztywne (nieodkształcalne), 
identyczne z poprzednim, pod działaniem tego samego układu sił. Wynika 
stąd wniosek, że warunek konieczny i wystarczający do równowagi ciała 
sztywnego jest tylko warunkiem koniecznym, ale nie wystarczającym do 
równowagi ciała odkształcalnego. 
 
  

Zasada piąta (zasada działania i przeciwdziałania). Każdemu działaniu 

towarzyszy równe co do wartości, o przeciwnym zwrocie i leżące na tej samej 
prostej przeciwdziałanie. 
 
  

Zasada szósta (zasada oswobodzenia od więzów). Każde ciało 

nieswobodne można myślowo oswobodzić z więzów, zastępując ich działanie 
reakcjami, a następnie rozważać jako ciało swobodne znajdujące się pod 
działaniem sił czynnych i biernych (reakcji więzów). 
 

S

TOPNIE SWOBODY WIĘZY I ICH ODDZIAŁYWANIE

 

Każde ciało doskonale sztywne mogące poruszać się w przestrzeni 
nazywamy 

ciałem swobodnym. 

Stopniem swobody 

nazywa się możliwość wykonania ruchu ciała 

niezależnego od innych ruchów. 
Punkt materialny 

ma na płaszczyźnie dwa, a w przestrzeni trzy stopnie 

swobody. 
Ciało doskonale sztywne ma na płaszczyźnie trzy, a w przestrzeni sześć 
stopni swobody. 
Trzy stopnie swobody ciała sztywnego na płaszczyźnie oznaczają możliwość 
dwóch przesunięć niezależnych w kierunku osi x i y oraz możliwość obrotu 
ciała w płaszczyźnie Oxy. Sześć stopni swobody ciała w przestrzeni oznaczają 
możliwość trzech niezależnych przesunięć w kierunku osi x, y i z oraz 

możliwość niezależnego obrotu ciała wokół tych osi. Więzami nazywamy 
warunki ograniczające ruch ciała w przestrzeni. 
 
Wprowadzenie więzów jest równoznaczne z działaniem na ciało sił biernych, 
czyli reakcji. Najczęstszymi sposobami podparcia ciał sztywnych są: przegub 
walcowy, przegub kulisty, podpora przegubowa stała, zawieszenie na 
cięgnach wiotkich, oparcie o gładką i chropowatą powierzchnię, utwierdzenie 
całkowite, podparcie na prętach zamocowanych przegubowo na obu końcach.  
 
Przegub walcowy. 

            

 

Ciało sztywne jest osadzone na walcowym sworzniu przechodzącym przez 
kołowy otwór wykonany w tym ciele. Po pominięciu siły tarcia jako małej w 

porównaniu z siłą normalną R do powierzchni styku linia działania tej reakcji 
będzie przechodziła przez oś sworznia. Występujące dwie reakcje R

x

 i R

y

 

stanowią dwie niewiadome i umożliwiają wyznaczenie wartości reakcji R i jej 
kierunku.  
 
 
 
 
 
 
 
 
 

 
Przegub kulisty. 

                     

 

W celu unieruchomienia punktu podparcia w przestrzeni stosuje się przeguby 
kuliste, które krępują swobodę przesunięć, ale umożliwiają obrót wokół 
dowolnej osi. Ich zakończenie jest wykonane w kształcie kuli, która jest 
osadzona w łożysku kulistym. W wyniku pominięcia sił tarcia w przegubie 
kulistym powstaje reakcja R o dowolnym kierunku w przestrzeni, 

przechodząca przez środek kuli i mająca trzy niezależne składowe R

x

, R

y 

i R

z

.  

 
Podpora przegubowa przesuwna (rolkowa). 

 

Ponieważ opór przy przesuwaniu takiej podpory w kierunku poziomym jest 
bardzo mały, przyjmuje się, że linia działania reakcji jest prostopadła do 
płaszczyzny poziomej (przesuwu). 
 
Podpora przegubowa stała. 

 

W przypadku zastosowania podpory przegubowej stałej koniec podparcia 
ciała sztywnego może się obracać dookoła osi przegubu, ale nie może się 
przemieszczać w dwóch kierunkach. Przy założeniu, że w przegubie nie ma 
tarcia, linia działania reakcji R przechodzi przez punkt A. Powstają dwie 

niezależne od siebie składowe reakcje R

x

 iR

y

. Rozważając podporę 

przegubową stałą w przestrzeni należy zauważyć, że koniec podparcia B nie 
może się przemieszczać w trzech kierunkach i dlatego występują trzy 
niezależne składowe reakcje R

x

, R

y 

iR

z

.  

 

Zawieszenie na cięgnach wiotkich.               

 

Podwieszenie ciała za pomocą wiotkich cięgien stwarza tzw. podpory 
kierunkowe jednost

ronne, bo cięgna mogą być tylko rozciągane. Reakcje S

1

 i 

S

2

 

działają na ciało wzdłuż tych cięgien, zgodnie z rysunkiem. 

 

Oparcie o gładką i chropowatą powierzchnię. 
 

 

W przypadku oparcia ciała o gładką powierzchnię (styk punktowy) występuje 
jedna reakcja R

A

, prostopadła do powierzchni styku. Jeżeli powierzchnia 

będzie chropowata, to wystąpią dwie składowe reakcji R

A

: normalna do 

powierzchni N i styczna siła tarcia T.  
 
Utwierdzenie całkowite. 

 

Gdy chodzi o zupełne unieruchomienie ciała, wtedy stosuje się utwierdzenie 
całkowite. Ciało sztywne na płaszczyźnie ma trzy stopnie swobody, a więc 
wystąpi reakcja R o dwóch składowych R

x

 i R

y

 oraz moment utwierdzenia M. 

Rozważając całkowite unieruchomienie ciała w przestrzeni, należy 
zastosować takie utwierdzenie, które przedstawia sześć więzów. Wystąpi 
wtedy reakcja R o trzech składowych R

x

, R

y 

i R

z 

oraz moment utwierdzenia M o 

trzech składowych M

x

, M

y 

i M

z 

.  

 

Ciało podparte na prętach zamocowanych przegubowo na obu końcach 
(prętach przegubowych). 

                

 

Ciało sztywne można także unieruchomić przez podparcie na prętach 
zakończonych przegubami. Jeżeli pominiemy ciężary własne prętów i tarcie w 
przegubach, to reakcje na ciało będą działać wzdłuż tych prętów S

A

, S

B 

i S

C 

, 

zgodnie z rysunkiem. 
 

ZBIEŻNY UKŁAD SIŁ

 

P

ŁASKI I PRZESTRZENNY UKŁAD SIŁ ZBIEŻNYCH

 

Układy sił, w których linie działania przecinają się w jednym punkcie 
nazywamy 

zbieżnymi układami sił. Takie układy mogą być płaskie lub 

przestrzenne. 
 
Płaski układ sił zbieżnych P

1

, P

2

,..., P

n 

przyłożonych do punktu O można 

zastąpić siłą wypadkową P równą sumie geometrycznej tych sił i przyłożoną 
również w punkcie O. 
 

                   

 

 

W analitycznym sposobie wyznaczania wypadkowej korzystamy z twierdzenia 
o rzucie sumy wektorów, według którego rzut sumy geometrycznej wektorów 
na dowolną oś jest równy sumie rzutów tych wektorów na tę samą oś. 
Przyjmując układ współrzędnych Oxy, oznaczamy odpowiednio przez 



1

, 



2

,..., 



n 

kąty nachylenia poszczególnych sił do osi Ox. Wypadkowa tych sił 

działa wzdłuż prostej l przechodzącej przez punkt O i nachylonej do osi Ox 
pod kątem 



.  

 

Składowe wypadkowej P

x 

i P

y

 

mają postać 

 

                  

 

 
Wartość liczbową wypadkowej P i kąt 



, który tworzy ona z osią Ox, 

wyznaczamy ze wzorów 

                  

 

W geometrycznym sposobie wyznaczania wypadkowej 

należy zbudować 

wielobok sił, w którym wektory sił odkładamy równolegle do ich linii działania. 
Z punktu O odkładamy wektor P

1

, a z jego końca wektor P

2

 i tak kolejne 

wektory aż do P

n

. 

 

Wektor poprowadzony z początku wektora P

1

 

do końca wektora P

n

 jest 

wypadkową rozpatrywanego układu sił zbieżnych.  
 

Przestrzenny układ sił zbieżnych P

1

, P

2

,..., P

n

 

przyłożonych do punktu O 

można zastąpić siłą wypadkową P równą sumie geometrycznej tych sił i 
przyłożoną również w punkcie O 

             

[ 

Analityczny sposób wyznaczenia wypadkowej przestrzennego układu sił 
zbieżnych polega na wyznaczeniu składowych wypadkowej P

x

, P

y 

i P

z

 w 

prostokątnym układzie współrzędnych Oxyz  

                  

 

Wartość liczbową wypadkowej P oraz jej cosinusy kierunkowe wyznaczamy 
ze wzorów  

                  

 

W geometrycznym sposobie wyznaczania wypadkowej 

należy zbudować 

wielobok sił, w którym wektory sił odkładamy równolegle do ich linii działania. 

Wektor poprowadzony z początku wektora P

1

 

do końca wektora P

n

 jest 

wypadkową rozpatrywanego układu sił zbieżnych. 
 

równowaga płaskiego i przestrzennego 

układu sił 

zbieżnych

 

Analityczny warunek równowagi (metoda analityczna) płaskiego układu sił 
zbieżnych (czynnych i reakcji więzów) brzmi następująco: aby siły zbieżne 
leżące w jednej płaszczyźnie były w równowadze, sumy rzutów tych sił na 
osie układu współrzędnych muszą być równe zeru 

                        

 

 
      

Geometryczny warunek równowagi (metoda geometryczna) płaskiego 

układu sił zbieżnych brzmi: aby układ sił zbieżnych działających w jednej 

płaszczyźnie znajdował się w równowadze, wielobok utworzony ze wszystkich 
sił tego układu musi być zamknięty. 
 
Wskazówki metodyczne przy wyznaczaniu reakcji więzów ciała sztywnego 
poddanego działaniu płaskiego układu sił zbieżnych:  

a. 

wydzielić ciało sztywne, którego równowagę rozpatrujemy,  

b. 

narysować siły czynne i reakcje więzów,  

c. 

sprawdzić, czy układ sił jest statycznie wyznaczalny,  

d. 

obrać układ współrzędnych Oxy, napisać równania równowagi według 
powyższych wzorów i rozwiązać je ze względu na niewiadome (metoda 
analityczna),  

e. 

narysować zamknięty wielobok sił utworzony ze wszystkich sił 
rozpatrywanego układu i wyznaczyć poszukiwane niewiadome (metoda 
geometryczna).  

      

Analityczny warunek równowagi (metoda analityczna) przestrzennego 

układu sił zbieżnych sprowadza się do trzech równań rzutów sił na dowolne 
trzy nierównoległe do jednej płaszczyzny osie. Po przyjęciu rzutowania na 
osie prostokątnego układu współrzędnych Oxyz otrzymamy następujące 
równania równowagi 

                        

 

      

Geometryczny warunek równowagi (metoda geometryczna) 

przestrzennego układu sił zbieżnych jest spełniony, gdy wypadkowa tych sił 
będzie równa zeru. Wielobok sił jest wtedy zamknięty i ma zgodny obieg 
wektorów sił.  
 
Wskazówki metodyczne przy wyznaczaniu reakcji więzów ciała sztywnego 
poddanego działaniu przestrzennego układu sił zbieżnych są podobne jak w 
przypadku płaskiego układu sił zbieżnych. 

PŁASKI UKŁAD SIŁ

 

REDUKCJA PŁASKIEGO UKŁADU SIŁ

 

Dowolny układ sił, działających na ciało sztywne, o liniach działania leżących 
w jednej płaszczyźnie możemy zastąpić wektorem głównym R, przyłożonym 
do dowolnie wybranego środka redukcji O oraz momentem głównym M

o

 

względem środka redukcji O. Wektor główny R jest równy sumie 
geometrycznej wszystkich sił układu                 

 

      

Wartość wektora głównego oraz kąt 



, jaki wektor ten tworzy z osią Ox, 

wyznaczamy ze wzorów 

                 

 

      

Moment główny M

o

 względem środka redukcji O jako początku układu 

współrzędnych Oxy jest równy sumie momentów danych sił układu względem 
punktu O 

                  

 

      

Wektor momentu głównego M

o

 jest wektorem o jednej składowej w 

kierunku wersora k, czyli prostopadły do płaszczyzny Oxy i wektora głównego 
R. 
      

Wyrażenie  

                

 

gdzie F jest siłą działającą wzdłuż prostej l, a r jej ramieniem nazywamy 
momentem siły względem dowolnego punktu O.                       

 

Jest to wektor mający następujące cechy: 



 

wartość liczbową równą iloczynowi (F · r) wartości siły F i jej ramienia r  



 

Kierunek prostopadły do płaszczyzny wyznaczonej przez linię działania 
siły oraz biegun 



 

Zwrot momentu przyjmujemy zgodnie z regułą śruby prawoskrętnej  

 

                 

 

 

      

Wzór na moment główny w prostszej postaci przedstawia się następująco: 

 

                

 
gdzie M

1

, M

2

,



, M

n  

to poszczególne momenty sił.  

 
      

Parą sił nazywamy układ dwóch sił równej wartości i równoległych (o 

jednakowych kierunkach), lecz o przeciwnych zwrotach. 
Iloczyn 

wartości jednej z sił i ramienia pary nazywamy momentem pary sił. 

               

 

              

 

 
      

Warunek równowagi par sił. 

Dowolna liczba par sił działających w jednej płaszczyźnie lub w płaszczyznach 
równoległych jest w równowadze wtedy, gdy algebraiczna suma ich momentów 
jest równa zeru. 

               

 

      

Każdą parę sił możemy zastąpić wektorem momentu sił i odwrotnie 



 

każdy 

wektor momentu sił możemy zastąpić parą sił, jeśli tylko iloczyn wartości siły i 
odległości między siłami wynosi M. 
 
      

Moment pary sił uważamy za dodatni, jeżeli para dąży do obrócenia swego 

ramienia w stronę przeciwną do ruchu wskazówek zegara. Jeżeli para dąży do 
obrócenia swego ramienia w stronę zgodną z ruchem wskazówek zegara, to jej 
moment uważamy za ujemny. 
 

               

 

RÓWNOWAGA DOWOLNEGO PŁASKIEGO UKŁADU SIŁ

 

Płaski dowolny układ sił znajduje się w równowadze, jeżeli sumy rzutów 
wszystkich sił na osie układu są  równe zeru i moment wszystkich sił względem 
dowolnego punktu O płaszczyzny działania sił jest równy zeru. 

                  

 

Jeżeli moment układu sił względem dwóch punktów A i B jest równy zeru oraz 
rzut sił na oś nieprostopadłą do odcinka AB łączącego te punkty jest równy zeru, 
to płaski układ sił jest w równowadze 

                  

 

Dla równowagi płaskiego układu sił sumy momentów wszystkich sił względem 
trzech punktów nie leżących na jednej prostej muszą być równe zeru  

                  

 

 
Wskazówki metodyczne przy wyznaczaniu reakcji więzów ciała sztywnego 
poddanego działaniu dowolnego płaskiego układu sił:  

a. 

wydzielić ciało sztywne, którego równowagę rozpatrujemy,  

b. 

narysować siły czynne i reakcje więzów,  

c. 

sprawdzić, czy układ sił jest statycznie wyznaczalny,  

d. 

w metodzie analitycznej napisać równania równowagi i rozwiązać je ze 
względu na niewiadome,  

e. 

w metodzie geometrycznej narysować zamknięty wielobok sił, utworzony ze 
wszystkich sił rozpatrywanego układu i wyznaczyć poszukiwane 
niewiadome.  

 
Szczególnym przypadkiem dowolnego płaskiego układu sił jest płaski układ sił 
równoległych. Zatem płaski równoległy układ sił znajduje się w równowadze, jeżeli 
spełnione są dwa równania równowagi 

                  

 

 

REDUKCJA PŁASKIEGO UKŁADU SIŁ

 

Zagadnieniami statycznie wyznaczalnymi 

nazywamy takie zagadnienia, które 

dotyczą równowagi układu sił działających w jednej płaszczyźnie na jedno lub 
kilka ciał sztywnych (układ mechaniczny), w których istnieje możliwość 
wyznaczenia niewiadomych sił. Niewiadome siły stanowią zwykle reakcje podpór 
albo siły wzajemnego oddziaływania wewnątrz rozważanego układu 
mechanicznego. 
 
      

W przypadku układu statycznie wyznaczalnego liczba reakcji zastępujących 

działanie więzów jest równa liczbie równań równowagi. Jeżeli więzów jest za 
mało, to dany układ mechaniczny jest niesztywny. Równowaga takiego układu 
może być zapewniona w przypadku spełnienia dodatkowych warunków, które 
zapewniają układowi odpowiednią postać geometryczną. 

 
      

Gdy więzów jest więcej niż potrzeba do unieruchomienia danego układu 

mechanicznego, dany układ jest przesztywniony. Wówczas niewiadomych reakcji 
jest więcej niż mamy równań równowagi i dlatego niektórych reakcji nie można 
wyznaczyć metodami stosowanymi w statyce. Zagadnienia takie nazywamy 
zagadnieniami statycznie niewyznaczalnymi. 
 

TARCIE

 

Tarciem 

nazywa się zjawisko powstawania sił stycznych do powierzchni styku 

dwóch ciał.  

      

T

ARCIE ŚLIZGOWE

 

     

W przypadku ciała pozostającego w spoczynku na chropowatej powierzchni 

zależność między siłą tarcia T a naciskiem normalnym N wyraża się następująco 
 

                  

 

gdzie 



 

współczynnik tarcia ślizgowego (statycznego). 

 
      

Jeżeli siła tarcia osiąga swą graniczną wartość, co oznacza, że tarcie jest 

całkowicie rozwinięte, to siła tarcia przedstawia się następująco 
 

                  

 

      

Kierunek siły tarcia T, działającej na ciało znajdujące się w spoczynku, jest 

przeciwny do kierunku ruchu, który zaistniałby, gdyby tarcia nie było. 
      

Kąt tarcia jest to maksymalny kąt 



, o jaki może się odchylić linia działania 

całkowitej reakcji R od kierunku normalnej do powierzchni styku i zachodzi 
następująca zależność 
 

                  

 

      

W przypadku ciała ślizgającego się po chropowatej powierzchni siła tarcia jest 

skierowana przeciwnie do kierunku ruchu, a jej wartość jest określona 
zależnością 
 

                  

 

gdzie 



k



 

współczynnik tarcia ślizgowego (kinetycznego). 

                    

 

 
Wskazówki metodyczne przy wyznaczaniu reakcji więzów ciał sztywnych 
poddanych działaniu płaskich układów sił z tarciem  

a. 

wydzielić ciało sztywne, bądź ciała sztywne, których równowagę 
rozpatrujemy,  

b. 

narysować siły czynne, reakcje więzów obciążających te ciała i siły tarcia,  

c. 

sprawdzić, czy układ sił jest statycznie wyznaczalny i obrać układ 
współrzędnych Oxy,  

d. 

napisać równania równowagi,  

e. 

napisać równania tarcia,  

f. 

rozwiązać układ równań zestawionych w dwóch ostatnich punktach oraz 
wyznaczyć wielkości niewiadome.  

Tarcie toczenia 

powstaje przy usiłowaniu przetoczenia walca o ciężarze G po 

poziomej płaszczyźnie. 

 

     

Siła tarcia tocznego musi spełniać warunki (przy równowadze walca) 

                 

 

     

W przypadku toczenia walca wartość siły tarcia tocznego T musi być mniejsza 

od wartości siły tarcia ślizgowego 



N



rozwiniętego, co wyraża się nierównością 

                  

 

gdzie f 



 

współczynnik tarcia tocznego, r 



 

promień walca. 

 
      Tarciem c

ięgna o krążek nazywamy siły tarcia występujące między 

powierzchniami cylindrycznymi i cięgnami na nie nawiniętymi. Związek miedzy 
napięciami S

1 

i S

2 

 

w cięgnie opasującym krążek wyraża się wzorem 

 

                  

 

gdzie 



 

współczynnik tarcia ślizgowego (statycznego) między cięgnem a 

powierzchnią krążka, 



kąt opasania, na którym cięgno przylega do krążka. 

 

 

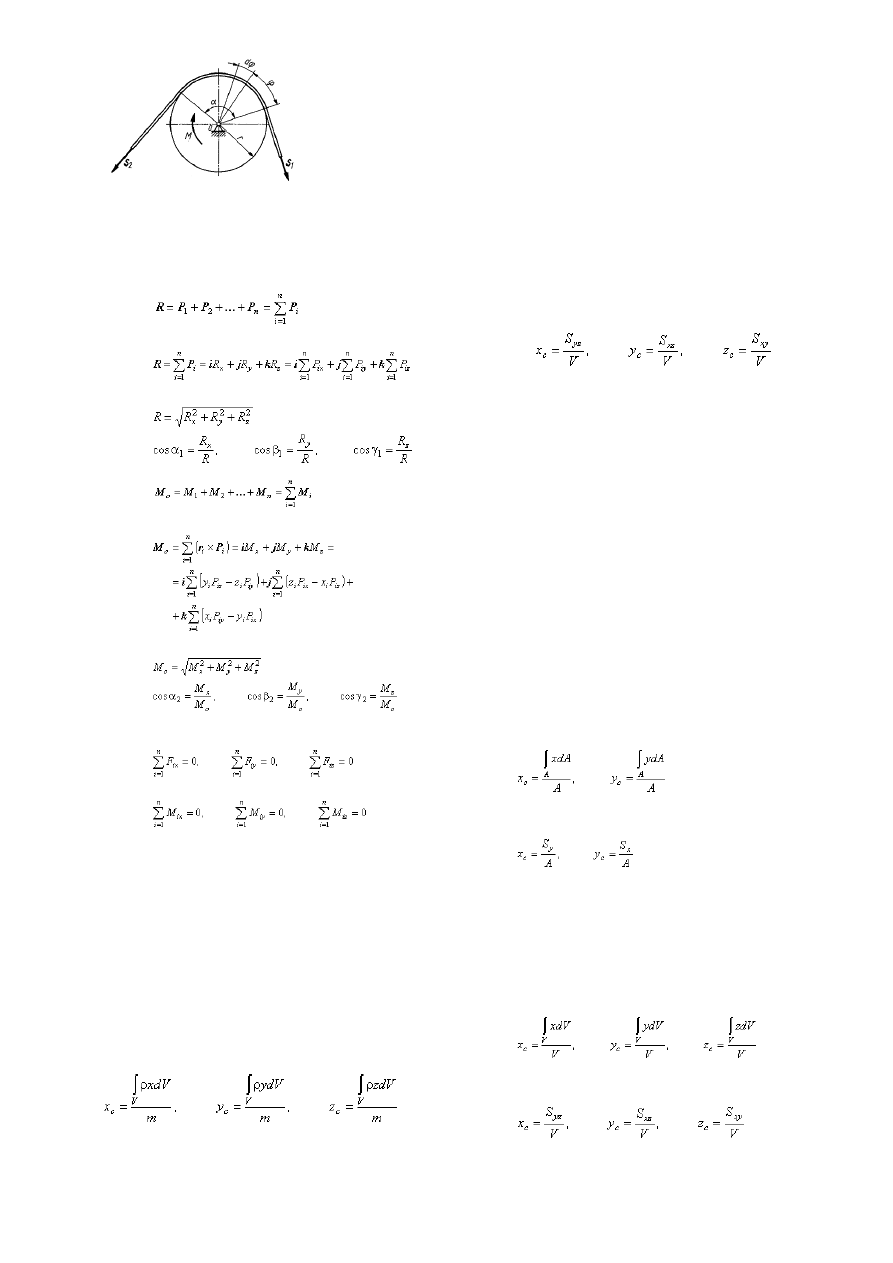
Przestrzenny układ sił 

Redukcja przestrzennego układu sił 

Dowolny przestrzenny układ sił działających na ciało sztywne możemy zastąpić 
wektorem 

głównym R, przyłożonym do dowolnie wybranego środka redukcji O, 

równym sumie geometrycznej wszystkich sił układu oraz momentem głównym 
M

o

, równym sumie geometrycznej momentów tych sił względem środka redukcji. 

Wektor główny obliczamy ze wzoru 

                   

 

lub jeżeli znane są składowe sił w prostokątnym układzie współrzędnych, wektor 
główny obliczamy ze wzoru 

                  

 

Wartość wektora głównego oraz jego cosinusy kierunkowe wyznaczamy ze 
wzorów 

                  

 

Moment główny obliczamy ze wzoru 

                   

 

lub po obraniu początku układu współrzędnych jako środka redukcji, moment 
główny obliczamy ze wzoru 

                  

 

Wartość i cosinusy kierunkowe wektora momentu głównego obliczamy ze 
wzorów 

                  

 

Przestrzenny 

układ  sił jest w równowadze, jeżeli  sumy rzutów wszystkich sił na 

trzy osie układu równe są zeru i sumy momentów wszystkich sił względem trzech 
osi układu są równe zeru. 

                  

 

Wskazówki metodyczne przy wyznaczaniu reakcji więzów ciała sztywnego 
poddanego działaniu dowolnego przestrzennego układu sił:  

a. 

wydzielić ciało sztywne bądź ciała sztywne, których równowagę 
rozpatrujemy,  

b. 

narysować siły czynne i reakcje więzów, obciążające te ciała,  

c. 

sprawdzić czy układ sił jest statycznie wyznaczalny i obrać układ 

współrzędnych Oxyz,  

d. 

napisać równania równowagi,  

e. 

rozwiązać układ równań zestawiony w poprzednim punkcie i wyznaczyć 
wielkości niewiadome.  

Srodek Ciężkości 

Ś jest to punkt, w którym jest zaczepiona siła 

przedstawiająca ciężar danego ciała, i pokrywa się on ze środkiem sił 
równoległych, które reprezentują elementarne siły ciężkości, tj. siły przyciągania 
cząstek ciała materialnego przez kulę ziemską, skierowane pionowo do środka 
ziemi. 
 
Współrzędne  x

c

, y

c 

i z

c

 

środka ciężkości C dowolnego ciała jednorodnego 

wyznaczamy ze wzorów  
                  

 

gdzie 



 

gęstość ciała, m



masa danego ciała jednorodnego.  

Z wzorów tych wynika, że współrzędne środka ciężkości C zależą od kształtu ciała 
oraz rozkładu masy. 
Wyrażenia w licznikach tych wzorów noszą nazwę momentów statycznych ciała 
materialnego względem odpowiednich płaszczyzn układu współrzędnych Oxyz. 

Twierdzenia przydatne do wyznaczania środków ciężkości ciał materialnych 
jednorodnych  



 

Jeżeli bryła ma płaszczyznę symetrii, to środek ciężkości leży w tej 
płaszczyźnie.  



 

Gdy bryła ma dwie płaszczyzny symetrii, środek ciężkości leży na linii ich 
przecięcia.  



 

Gdy bryła ma trzy płaszczyzny symetrii, środek ciężkości leży w punkcie 
przecięcia się tych płaszczyzn.  



 

Moment statyczny dowolnej figury wzgl

ędem płaszczyzny przechodzącej 

przez środek ciężkości tej figury jest równy zeru. 

 
Metody stosowane do wyznaczenia położenia środka ciał jednorodnych  



 

analityczna 



 

polegająca na zastosowaniu odpowiednich wzorów,  



 

momentów statycznych, w której korzysta się z twierdzenia, że moment 
statyczny ciała względem płaszczyzny przechodzącej przez środek 
ciężkości tego ciała jest równy zeru. Wzory do obliczenia współrzędnych 
środka ciężkości danego ciała 
 

                

 

gdzie S

yz

, S

xz 

i S

xy

 to momenty statyczne z odpowiednim indeksem, 

określającym płaszczyznę, względem której oblicza się te momenty.  



 

dzielenia

, która sprowadza się do następujących etapów:  

o 

podziału bryły na proste elementy bryłowe, których położenia 
środków ciężkości są znane,  

o 

obliczenia momentów statycznych bryły względem płaszczyzn 
przyjętego układu współrzędnych (sumując iloczyny objętości 
brył prostych i współrzędnych środków ciężkości)  

o 

obliczenia z wcześniejszych wzorów współrzędnych środka 
ciężkości bryły (dzieląc momenty statyczne bryły przez 
całkowitą objętość bryły).  

metoda ta stosowana jest również do obliczania współrzędnych środków 
ciężkości figur płaskich, powierzchni i linii.  

- 

uzupełniania (ujemnych mas), która polega na tym, że bryłę (figurę płaską, 

powierzchnię, linię) uzupełnia się inną bryłą tak dobraną, aby uzyskać bryłę 
(figurę płaską, powierzchnię, linię) o możliwie prostej postaci. Wyznaczenie 
środka ciężkości sprowadza się wówczas do metody momentów statycznych, 
odejmując od momentu statycznego otrzymanej bryły (figury płaskiej, 
powierzchni, linii) moment statyczny bryły (figury płaskiej, powierzchni, linii) 
uzupełniającej.  

środki ciężkości figur płaskich

Przyjmuje się, że grubość figury 

płaskiej jest stała i znikomo mała w porównaniu z pozostałymi wymiarami oraz 
ciężar na jednostkę pola powierzchni figury płaskiej jest stały. Położenie środka 
ciężkości figury płaskiej zależy zatem tylko od kształtu geometrycznego tej figury. 
 
Obliczanie współrzędnych środka ciężkości traktuje się jako zagadnienie 
dwuwymiarowe, gdyż współrzędna  z

c 

= 0. 

Współrzędne środka ciężkości figury płaskiej wyznaczamy ze wzorów 

                  

 

gdzie A - 

pole powierzchni figury płaskiej w m

2

. 

 
Przy wykorzystaniu definicji momentów statycznych figur płaskich współrzędne 
środka ciężkości figury płaskiej obliczymy ze wzorów 

                  

 

gdzie S

y

 - 

moment statyczny względem osi y,  S

x

 - 

moment statyczny względem 

osi x

. Przydatne twierdzenia do obliczania współrzędnych środka ciężkości figury 

płaskiej  

- 

gdy figura płaska ma oś symetrii, to środek ciężkości 
leży na tej osi,  

- 

jeżeli figura płaska ma dwie osie symetrii, to środek 
ciężkości leży w punkcie przecięcia tych osi. 

     ŚRODKI CIĘŻKOŚCI

 

BRYŁ

 

Położenie środka ciężkości bryły zależy  tylko od kształtu geometrycznego tej 
bryły. 
 
Obliczanie współrzędnych środka ciężkości traktuje się jako zagadnienie 
trójwymiarowe. 
Współrzędne środka ciężkości bryły wyznaczamy ze wzorów 

                  

 

gdzie V 



całkowita objętość danej bryły w m

3

. 

 
P

rzy wykorzystaniu definicji momentów statycznych brył współrzędne środka 

ciężkości bryły obliczymy ze wzorów 

                  

 

gdzie S

yz

, S

xz 

i S

xy

 

to momenty statyczne z odpowiednim indeksem, określającym 

płaszczyznę, względem której oblicza się te momenty