Mechanika Techniczna Opracowanie

Mechanika techniczna I

Strona 1

Zagadnienia na egzamin z mechaniki technicznej I

1) S A T Y K A

a) Pojęcie siły, rodzaje sił.
b) Zasady statyki.
c) Tarcie, model tarcia Culomba, tarcie rozwinięte, i nierozwinięte, współczynnik tarcia, tarcie

liny na krążku stałum.

d) Para sił, dodawaniw par sił.
e) Redukcja układu sił, warunki równowagi układu sił, szczególne przypadki układów sił i ich

warunki równowagi.

f) Środki mas brył, sposoby wyznaczania położenia środka masy brył.

2) K I N E M A T Y K A

a) Równanie ruchu punktu materialnego.
b) Tor punktu materialnego.
c) Równanie torowe, prędkość i przyśpieszenie punktu materialnego, ruch jednostajny

i jednostajnie przyśpieszony (złożony) punktu materialnego, ruch krzywoliniowy
i prostoliniowy, ruch punktu materialnego po okręgu prędkość i przyśpieszenie linowe i
kątowe.

d) Ruch harmoniczny punktu materialnego.
e) Ruch przestrzenny ciała sztywnego.
f) Równania ruchu, prędkość i

przyśpieszenie punktów

ciała sztywnego w ruchu przestrzennym.

g) Liczba stopni swobody, ruch translacyjny i postępowy ciała sztywnego.
h) Ruch płaski ciała sztywnego, chwilowy środek Obrowu, prędkość i przyspieszenie punktów

ciała sztywnego w ruchu płaskim.

i) Ruch obrotowy ciała sztywnego wokół osi stałej, dodawanie prędkości kątowych, prędkość i

przyśpieszenie ciała w tym ruchu.

j) Ruch złozony punktu materialnego, prędkość i przyspieszenie w tym ruchu przyśpieszenie

Corilisa

3) D Y N A M I K A

a) Zasady Newtona i prawo powszechnej grawitacji, zasada d’Alemberta
b) Wahadło matematyczne i oscylator harmoniczny.
c) Pęd punktu materialnego i układu punktów materialnych.
d) Prawo zmienności pędu, prawo zachowania pędu.
e) Kręt punktu materialnego i układu punktów materialnych,

prawo zmienności krętu

i prawo

zachowania krętu.

f) Zasada ruchu układu punktów materialnych, moment bezwładności układu punktów

materialnych i ciał sztywnych, definicje, podstawowe wnioski, twierdzenie Szteinera.

g) Energia kinetyczna i potencjalna, energia mechaniczna, prawo zachowania energii,

twierdzenie Koeniga dla układu punktów materialnych i ciał sztywnych.

h) Prawo zmienności energii kinetycznej dla układu punktów materialnych.
i) Płaski ruch ciała sztywnego, wahadło fizyczne.
j)

Ruch kulisty ciała sztywnego,

równanie Eulera.

Mechanika techniczna I

Strona 2

S T A T Y K A

a) Pojecie siły, rodzaje siły

a. Siła – wielkość fizyczna będąca miarą mechanicznego i wzajemnego oddziaływania ciał

na siebie. Posiada atrybuty wektora (wartość, kierunek, zwrot, punkt przyłożenia)

b. Rodzaje sił

 Siła zachowawcza – siła dla, której można określić potencjał V, z którym

związana jest energia potencjalna U. związek siły z energią potencjalną
wyraża wzór:

⃗ = −∇

Do takich sił stosuje się zasadę zachowania energii

 Siła centralna – siła, której wartość zależy od odległości od źródła. Siły

centralne są zawsze zachowawcze, mają potencjał zależny tylko od odległości
od żródła i spełniają zasadę zachowania momentu pędu. Siłami centralnymi
są np. siła grawitacji kuli lub siła elektrostatyczna ładunku punktowego.

b) Zasady statyki

a. I zasada (I zasada Newtona)

Jeżeli na układ mechaniczny nie działają żadne siły lub działające siły stanowią układ
sił będący w równowadze to układ mechaniczny pozostaje w spoczynku lub porusza
się ruchem jednostajnym prostym prostoliniowym

, … ,

~ 0

b. II zasada

Układ dwóch sil równoważnych co do wartości i przeciwnego zwrotu działających w
tym samym punkcie i wzdłuż tej samej prostej jest w równowadze.

⇒

~ 0

c. III zasada

Gdy na ciało sztywne działą układ dwóch sił równoważnych co od wartości i
przeciwnego zwrotu działających w dwóch różnych punktach ciała sztywnego wzdłuż
tej samej prostej to ciało sztywne pozostaje w równowadze.
S

~ 0

Mechanika techniczna I

Strona 3

d. IV zasada

Układ dwóch sił działających w jednym punkcie jest równoważny jednej sile
działającej w tym punkcie i będącej sumą dwóch pozostałych.

e. V zasada

Każdy układ sił można zastąpić innym układem sił równoważnym jemu.

f. VI zasada

Dwa układy sił różniące się miedzy sobą, układem równoważnym (układem
zrównoważonym) są równoważne sobie

−

~ 0 ⇒

g. VII zasada (zasada więzów)

Jeżeli ruch zrównoważonego układu mechanicznego jest ograniczony innym układem
mechanicznym to te inne układy nazywamy więzami założonymi na zrównoważony
układ mechaniczny. Układ mechaniczny, który nie jest skrępowany żadnymi więzami
nazywamy układem mechanicznym swobodnym. W przeciwnym wypadku rozważany
układ mechaniczny jest skrępowany. Rozważany układ można uwolnić od więzów
zastępując je siłami reakcji (reakcji więzów).

c) Tarcie, model tarcia Culomba, tarcie rozwinięte i nie rozwinięte, współczynnik tarcia, tarcie

liny na krążku stałym.

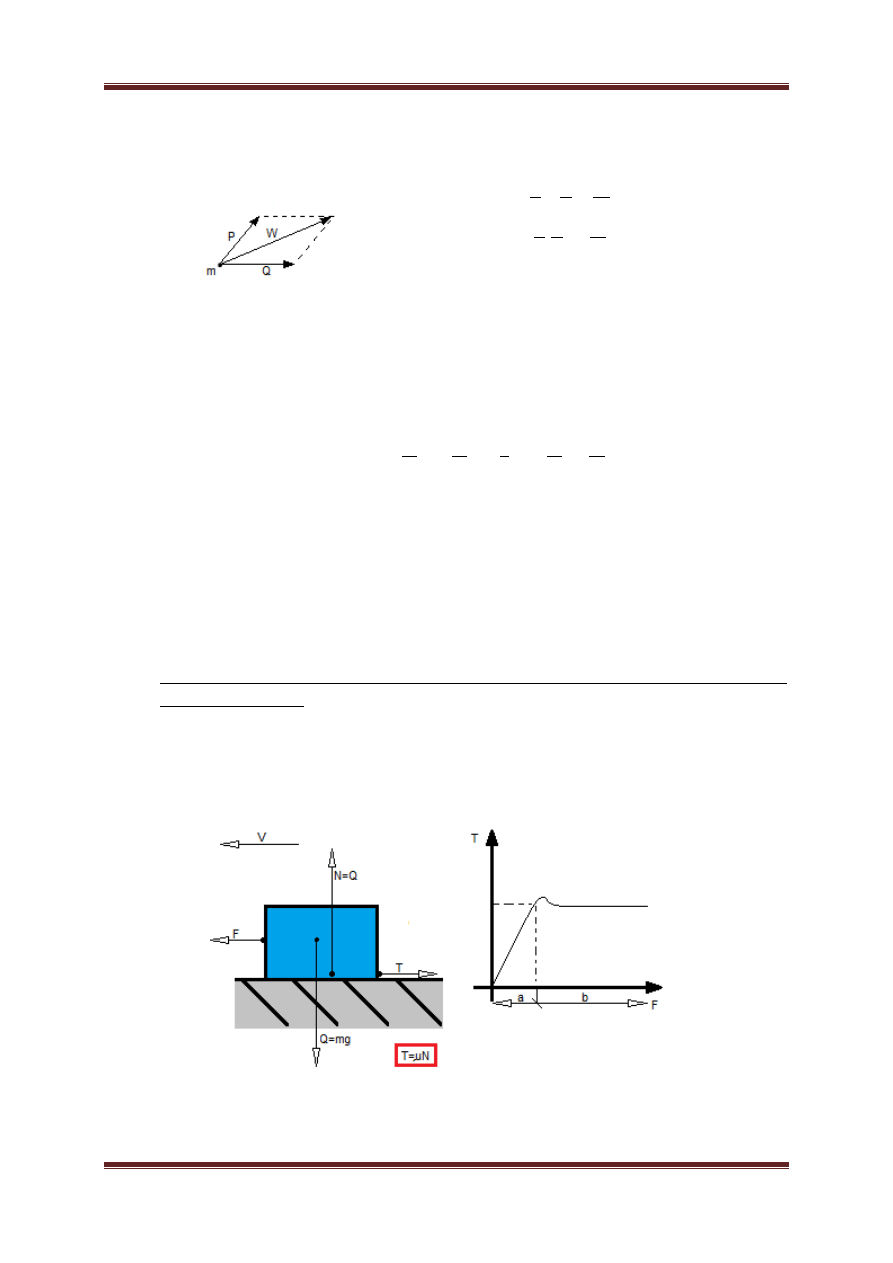
a. Tarcie – Dwa ciała, które są ze sobą w kontakcie stykowym, do, których przyłożono

siłę sprawczą próbującą porzesunąć te ciała, powoduje poślizg na styku i przesunięcie
się tych ciał. Te dwa ciała nazywamy parą cierną. Na ich styku działają siły tarcia. Do
momentu gdy siły tarcia nie pozwalają na poślizg, tarcie nazywamy nie rozwiniętym.
Po przekroczeniu sił tarcia następuje poślizg. W tedy tarcie nazywamy rozwiniętym.

b. Własności tarcia:

 Zależy od rodzaju powierzchni pary ciernej
 Niezależny od pola powierzchni styku i prędkości wzajemnego poślizgu

Mechanika techniczna I

Strona 4

c. Współczynnik tarcia – wielkość charakteryzująca siłę tarcia
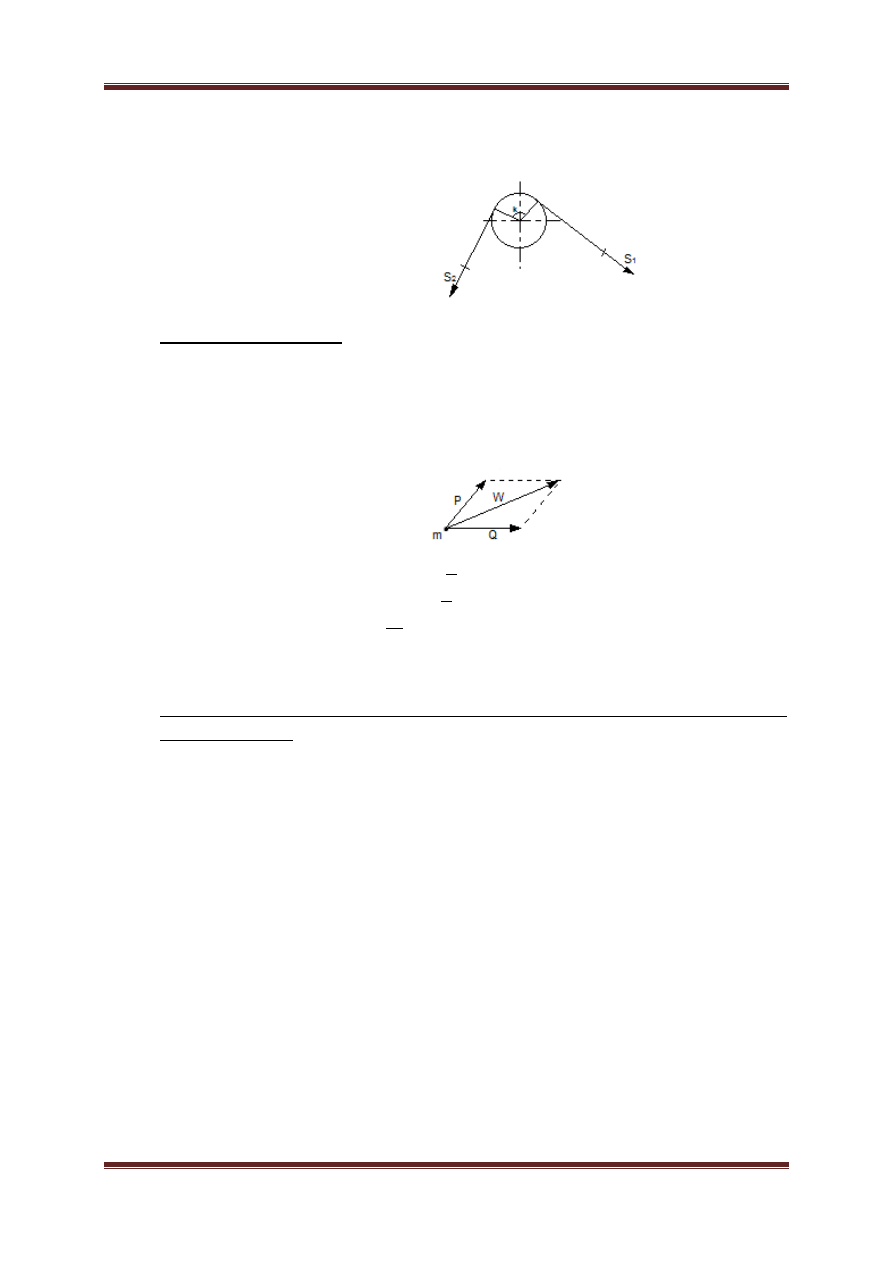
d. Tarcie liny na krążku stałym

k – kąt opasania

d) Para sił, dodawanie pary sił

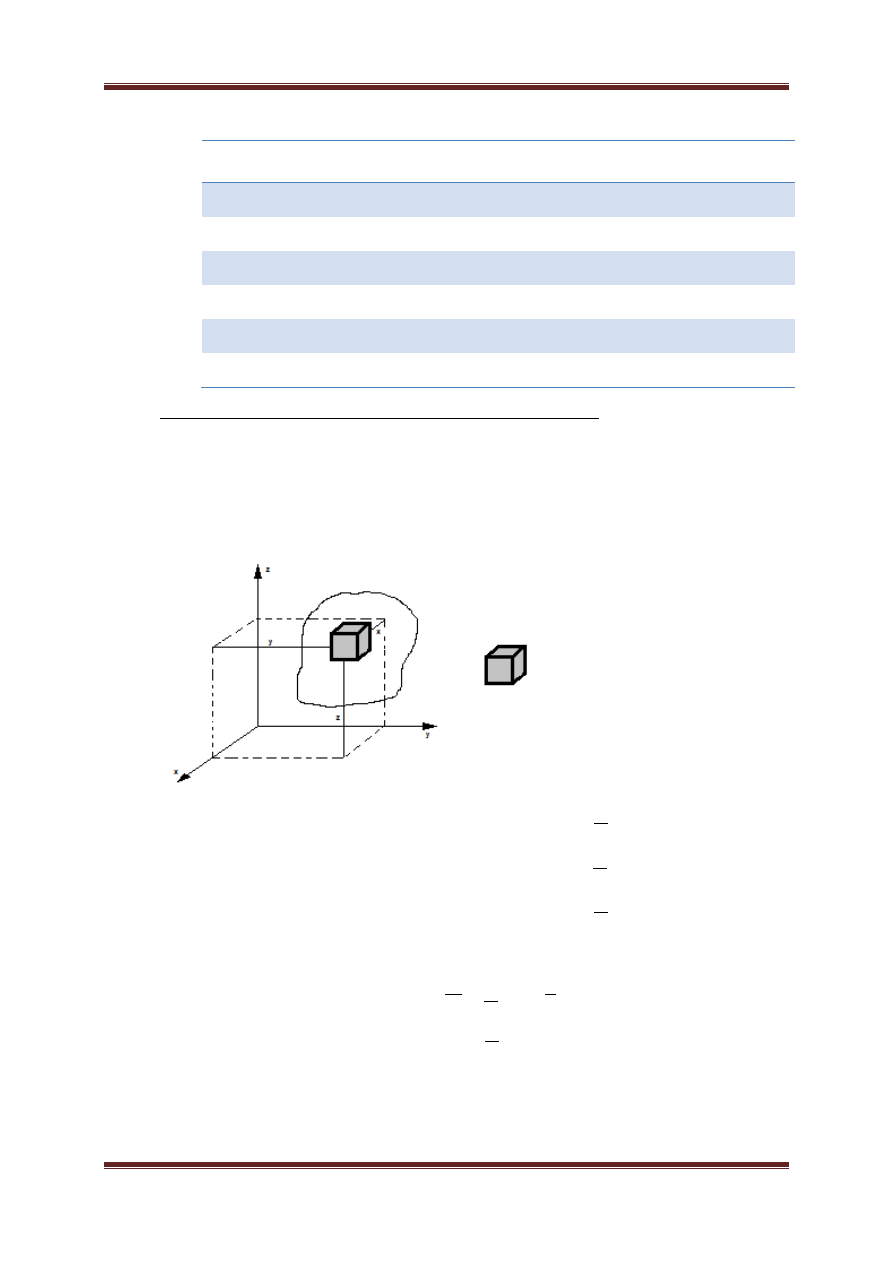
a. Para sił – diwe siły równej wartości, tego samego kierunku, przeciwnych zwrotów

przeciwnym zwrocie i różnych liniach działania.

Moment pary sił względem punktu to suma momentów tych sił względem tego
punktu

b. Dodawanie pary sił

e) Redukcja układu sił, warunki równowagi układu sił, szczególne przypadki układów sił i ich

warunki równowagi

a. Redukcja dowolnego układu sił P

, P

, …, P

działających na ciało sztywne można

zastąpić siłą R przyłożoną do dowolnie wybranego środka redukcji O, równą sumie
geometrycznej wszystkich sił układu oraz parą sił o momencie M

równej sumie

geometrycznej momentów tych sił względem środka redukcji.

b. Dowolny układ sił jest w równowadze jeżeli suma rzutów wszystkich sił na osie

przyjętego układu odniesienia jest równa zeru i suma momentów względem trzech osi
układu jest równa zeru.

c. Szczególne przypadki układów sił:

 Płaski układ sił – to taki układ sił, którego wszystkie wektory sił leżą na jednej

płaszczyźnie.

 Zbieżny układ sił – to taki układ sił, w którym linie działania sił przecinają się

w jednym punkcie (mogą być układy zbieżne płaskie i przestrzenne)

 Układ równoległy – to taki układ, w którym wszystki siły mają ten sam

kierunek działania (układ sił przestrzenny lub płaski)

 Układ jednowymiarowy (liniowy) – to taki układ sił w którym wszystkie siły

mają wspólną linię działania.

Mechanika techniczna I

Strona 5

d. Warunki równowagi sił w szczególnych przypadkach

f) Środki mas brył, Sposoby wyznaczania położeń środków mas brył.

a. Środek mas brył to taki punkt o współrzędnych (x

, y

, z

), że:

⎩

⎪

⎨

⎪

⎧

= dx, dy, dz => dV

Warunek

równowagi

Ogólny

Zbieżny

Liniowy

3D Oz

Zbieżny

Równo.

Liniowy

2D Ox

Ogólny

Mechanika techniczna I

Strona 6

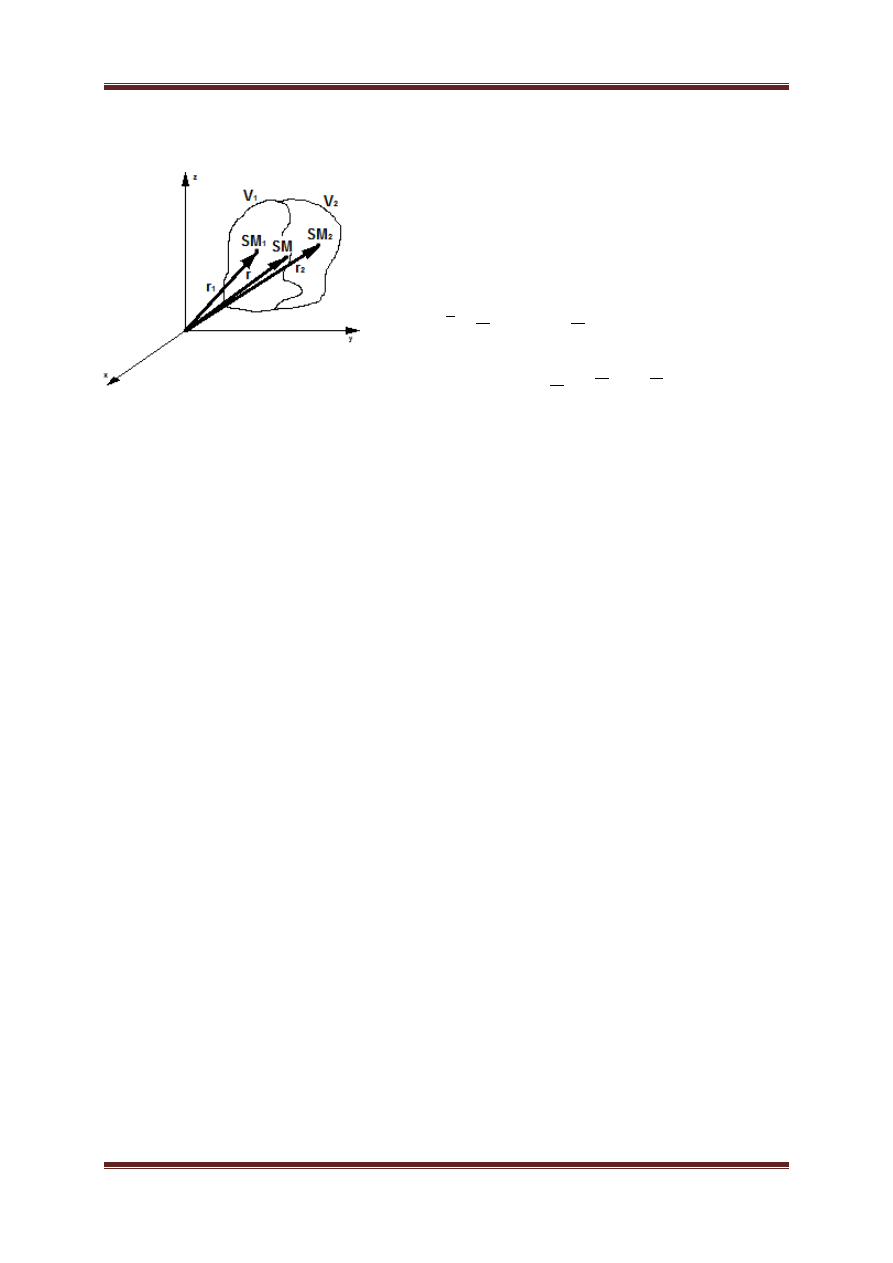
b. Sposoby wyznaczania położenia środka masy brył

 Metoda grupowania

Jeżeli ciało sztywne da się podzielić na dwa ciała takie
że:

∪

∧

∩

= ∅

(

)

 Metoda symetrii geometrycznej (dla ciał jednorodnych)

Jeżeli jednorodne ciało sztywne ma płaszczyznę symetrii to środek
masy tego ciał leży na tej płaszczyźnie

II.

Jeżeli jednorodne ciało sztywne ma oś symetrii to środek masy tego
ciał leży na tej osi

III.

Jeżeli ciało ma środek symetrii to jest on jednocześnie środkiem
masy tego ciała

Mechanika techniczna I

Strona 7

K I N E M A T Y K A

A. Równanie ruchu punktu materialnego

a. Równanie ruchu punktu materialnego – równanie opisujące drogę po jakiej

porusz się punkt materialny

⎩

⎪

⎨

⎪

⎧ =

(1 + cos )

sin

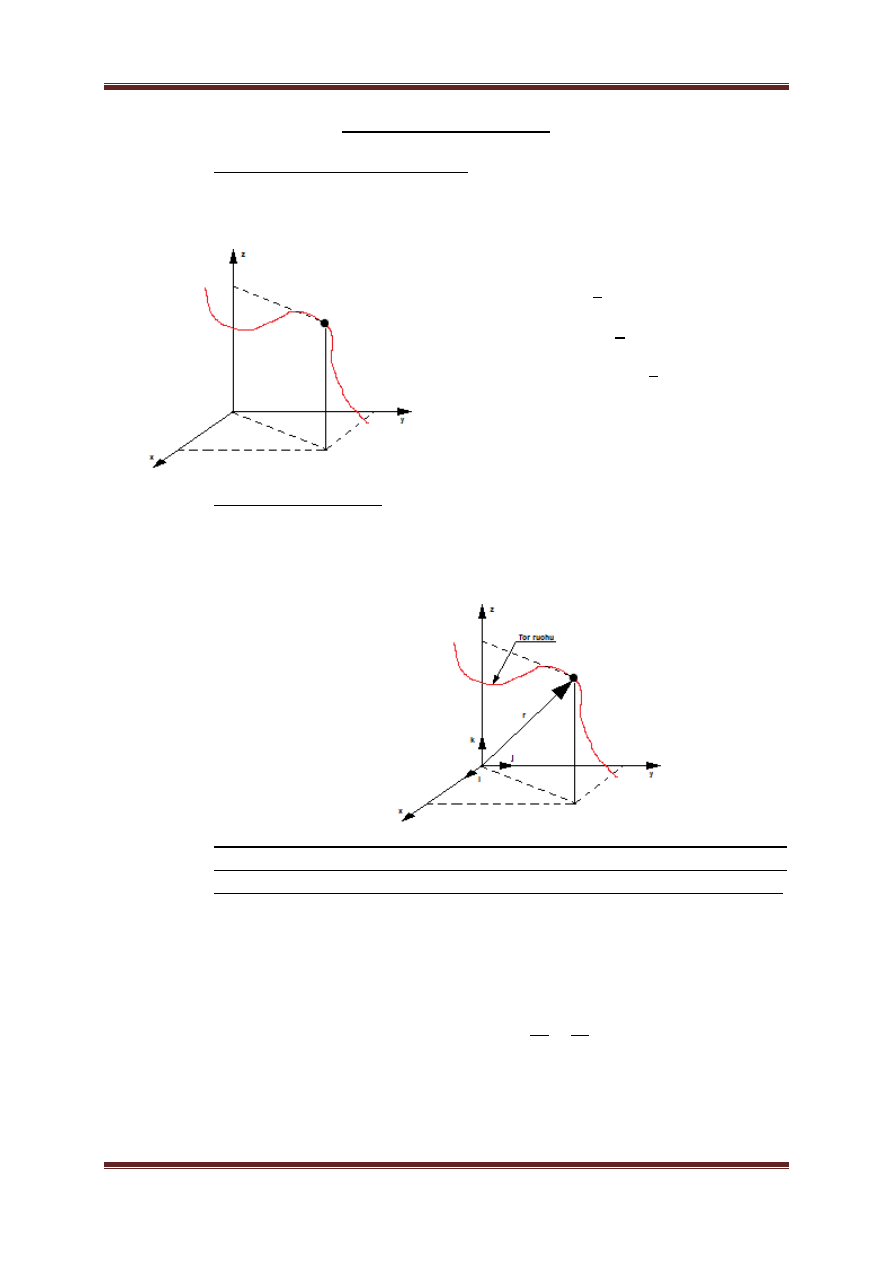
B. Tor punktu materialnego

a. Tor punktu materialnego – krzywa opisana w czasie przez koniec wektora r.

Tor ruchu punktu materialnego nazywany jest również trajektorią. Są to
kolejne punkty położenia punktu w przestrzeni na którym punkt był jest lub
będzie.

C. Równanie torowe, prędkość i przyśpieszenie punktu materialnego, ruch jednostajny i

jednostajnie przyśpieszony (zmienny) punktu materialnego, ruch krzywoliniowy i
prostoliniowy, ruch punktu materialnego po okręgu, przyśpieszenie liniowe i kątowe.

a. Równanie toru – zależnośc pomiędzy wsółżednymi x, y, z, z których usunięto

czas

b. Prędkość – prędkość punktu materialnego to wektor styczny do toru ruchu

punktu materialnego charakteryzująca zmianę przebytej drogi.

= lim

∆ →

∆

c. Przyśpieszenie – wektorowa wartość fizyczna określająca zmianę prędkości w

czasie. Przyspieszenie definiuje się jako pochodna prędkości po czasie, czyli
jest szybkością zmiany prędkości w czasie. Jeżeli przyspieszenie ma zwrot

Mechanika techniczna I

Strona 8

przeciwny do prędkości to wartość prędkości w danym ruchu,
a przyśpieszenie nazywane jest opóźnieniem.

d. Ruch jednostajny punktu materialnego – ruch w którym punkt materialny w

takich samych przedziałach czasu punkt pokonuje takie same odcinki drogi.

e. Ruch jednostajnie przyspieszony (zmienny) punktu materialnego –

prostoliniowy ruch w którym wartość przyśpieszenia jest stała

Jest to ogólny przypadek ruchu jednostajnie przyśpieszonego (a>0) i
opóźniony (a<0).

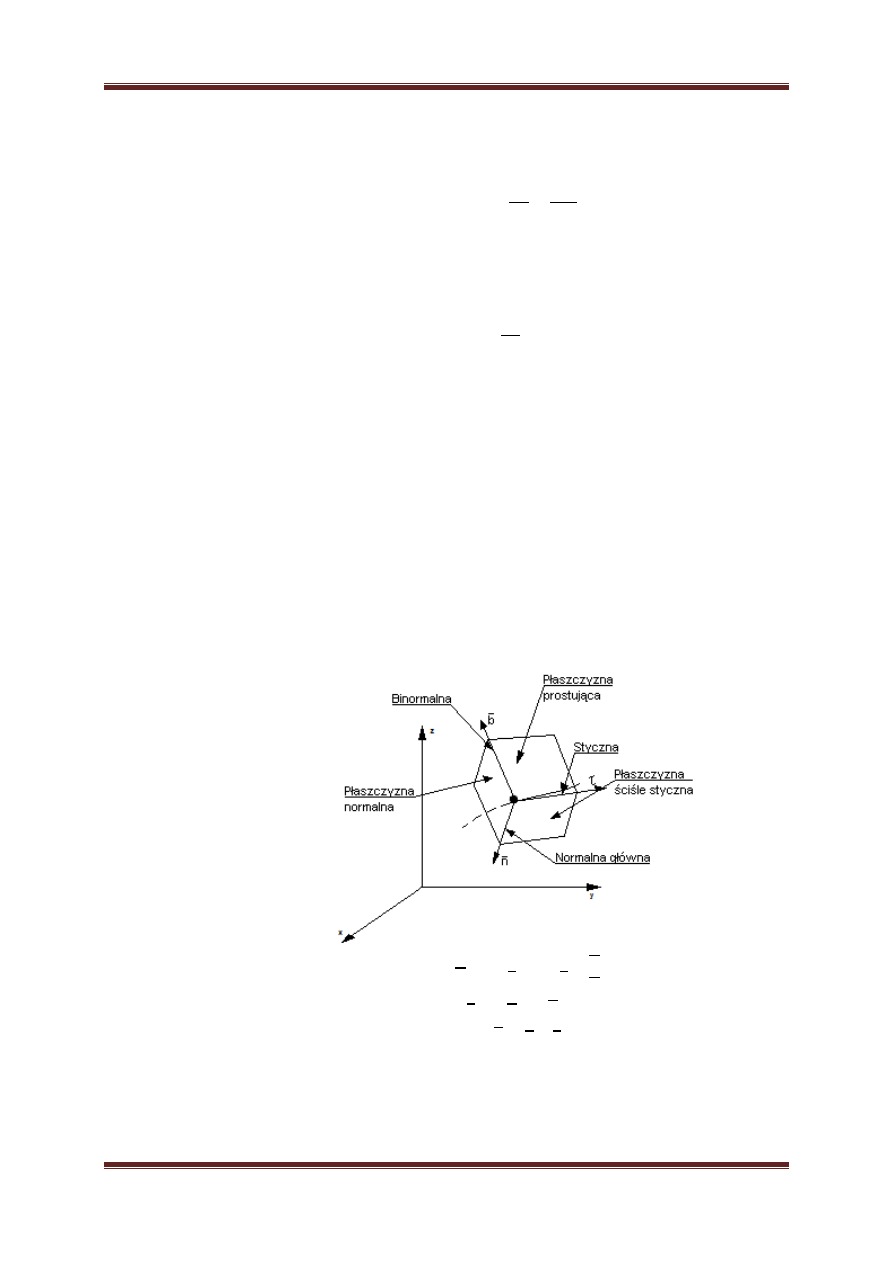
f. Ruch krzywoliniowy – ruch punktu materialnego po linii krzywej. gdy tor jest

krzywą przestrzenną, kierunkami naturalnymi są krawędzie tak zwanego
Trójścianu Freneta, które tworzą wzajemnie prostopadłe płaszczyzny
związane z punktem materialnym poruszającym się po krzywej.

∙ =

| | = | | =

= 1

g. Ruch po okręgu punktu materialnego – jest szczególnym przypadkiem ruchu

krzywoliniowego.

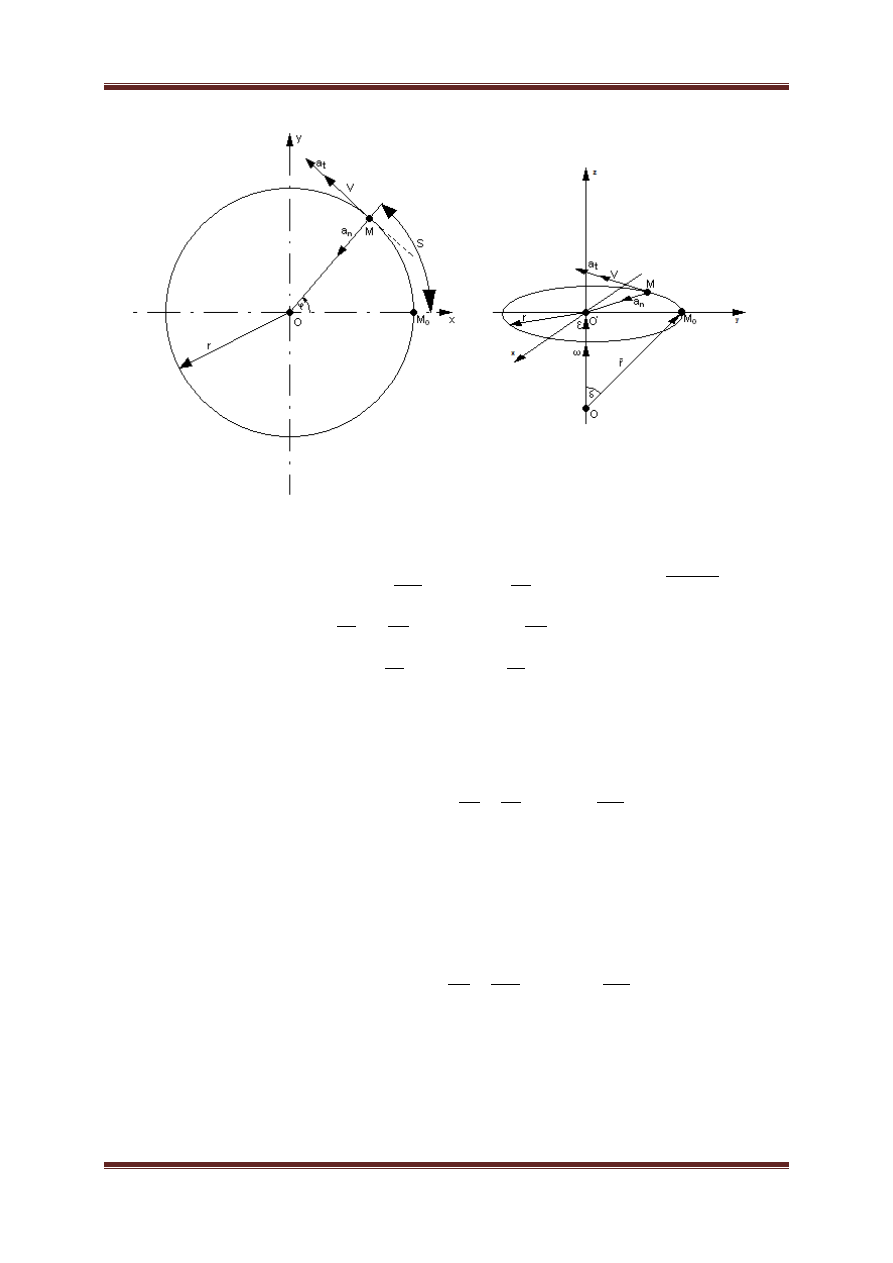
Mechanika techniczna I

Strona 9

= 2

360

−

h. Prędkośc kątowa – wielkość opusująca ruch obrotowy. Jest wektorem

leżącym na osi obrotu i skierowany zgornie z regółą śruby prawoskrętnej.

[ ] =

i. Przyśpieszenie kątowe – równe co do wartości pochodnej względem czasu

prędkości kątowej, lub drugiej pochodnej względem czasu kąta obrotu. Jest
wektorem leżącym na osi obrotu i skierowany zgornie z regółą śruby
prawoskrętnej.

[ ] =

Mechanika techniczna I

Strona 10

D. Ruch charmoniczny punktu maerialnego

a. Jeżeli punkt porusza się ruchem jednostajnym po okręgu to rzut tego punktu

na oś średnicy porusz się ruchem charmonicznym

sin(

+ ),

cos(

+ )

sin(

+ )

= −

E. Ruch przestrzenny ciała sztywnego

a. Ciało sztywne – zbór punktów, których wzajemne odległości są stałe
b. Ruch ciała sztywnego w przestrzeni jest jednozmnacznie określony przez

równania róchu trzech punktów nieleżących na jednej prostej.

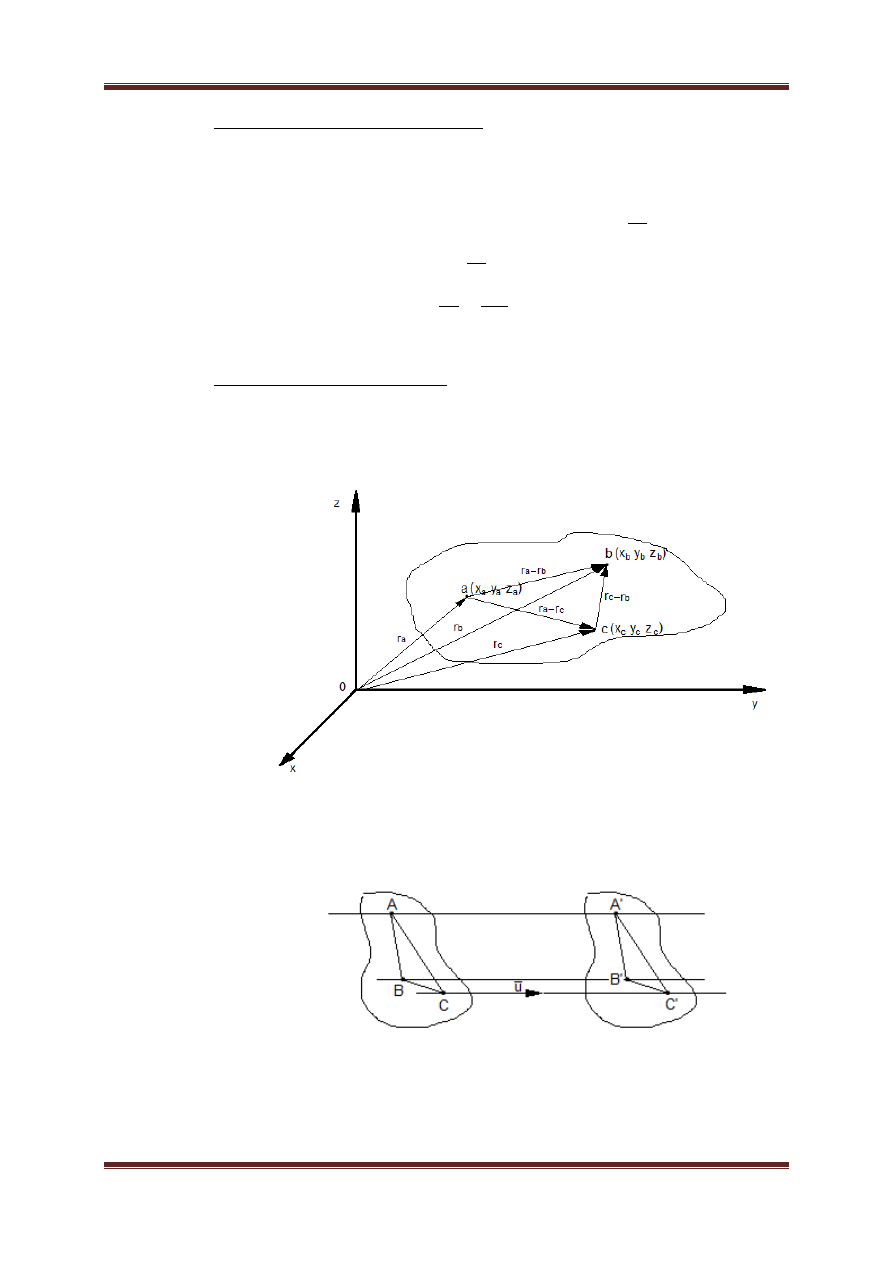
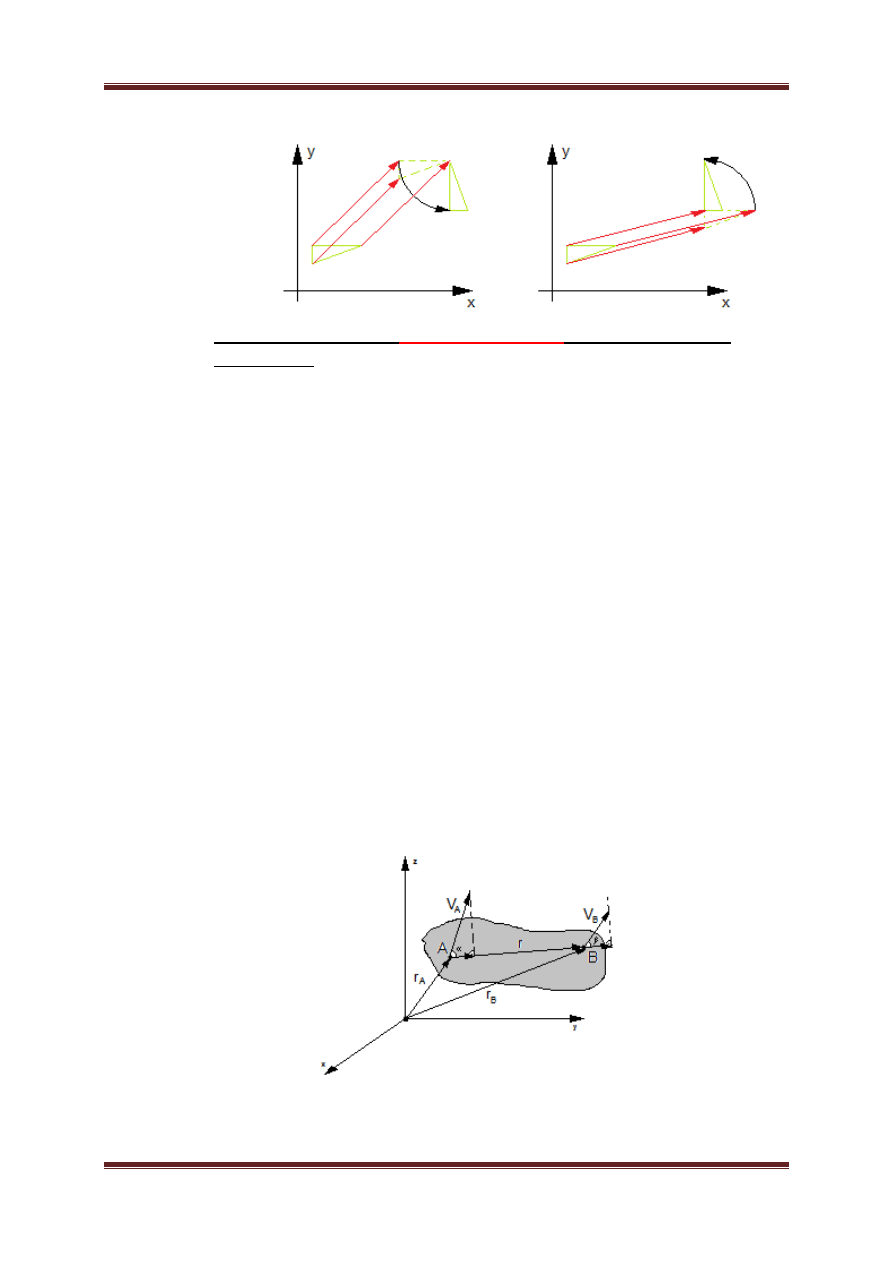
c. Translacja – ruch postępowy w przestrzeni którego kierownice są liniami

prostymi

Wprowadza się wektor translacji u o który wszystkie punkty są przesunięte.

d. Każdą figurę F można przeksztacić w fifurę F’ bez oderwania od płaszczyzny

na której leży, za pomocą jednej tranclacji i jednego obrotu, na wiele
sposobów.

Mechanika techniczna I

Strona 11

F. Równania ruchu, prędkość i

przyśpieszenie punktów

ciała sztywnego w ruchu

przestrzennym

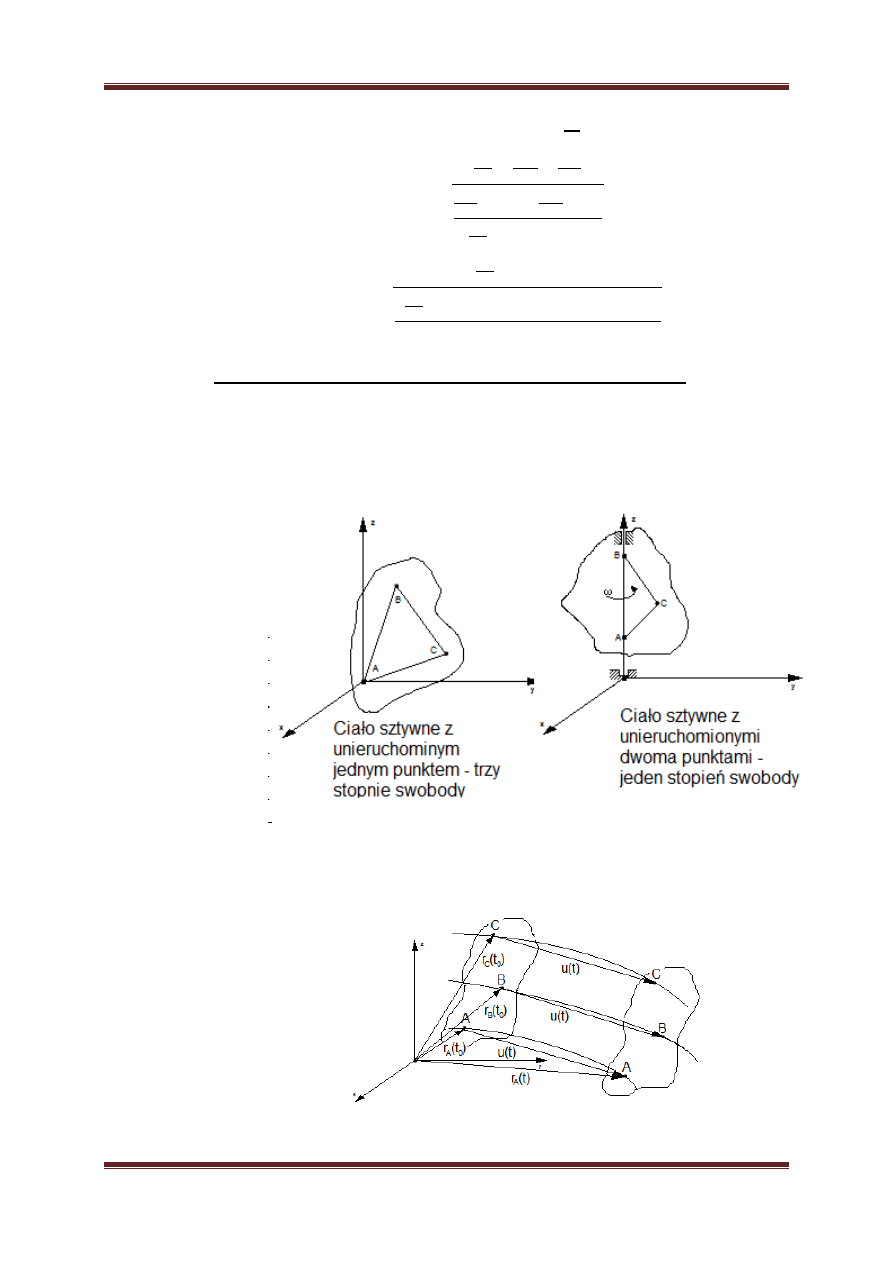
a. Ruch ciała sztywnego może być określony wektorowymi równaniami ruchu

trzech punktów A, B, C.

( )

Warunek aby rozpatrywane trzy punkty nie leżały na jednej prostej, można
zapisać następująco

(

−

) × (

−

) ≠ 0

Równanie ruchu trzech punktów można obrać dowolnie

−

| = , |

−

| = , |

−

| = ,

b. W ciele sztywnym, podczas dowolnego ruchu, rzuty wektorów prędkości

dwóch jej dowolnych punktów na prostą łączącą te punkty są równe.

Mechanika techniczna I

Strona 12

−

/∙

= (

−

)

= 0

(

−

) × (

−

) ≠ 0

∙ =

∙ ⇒

cos

sin

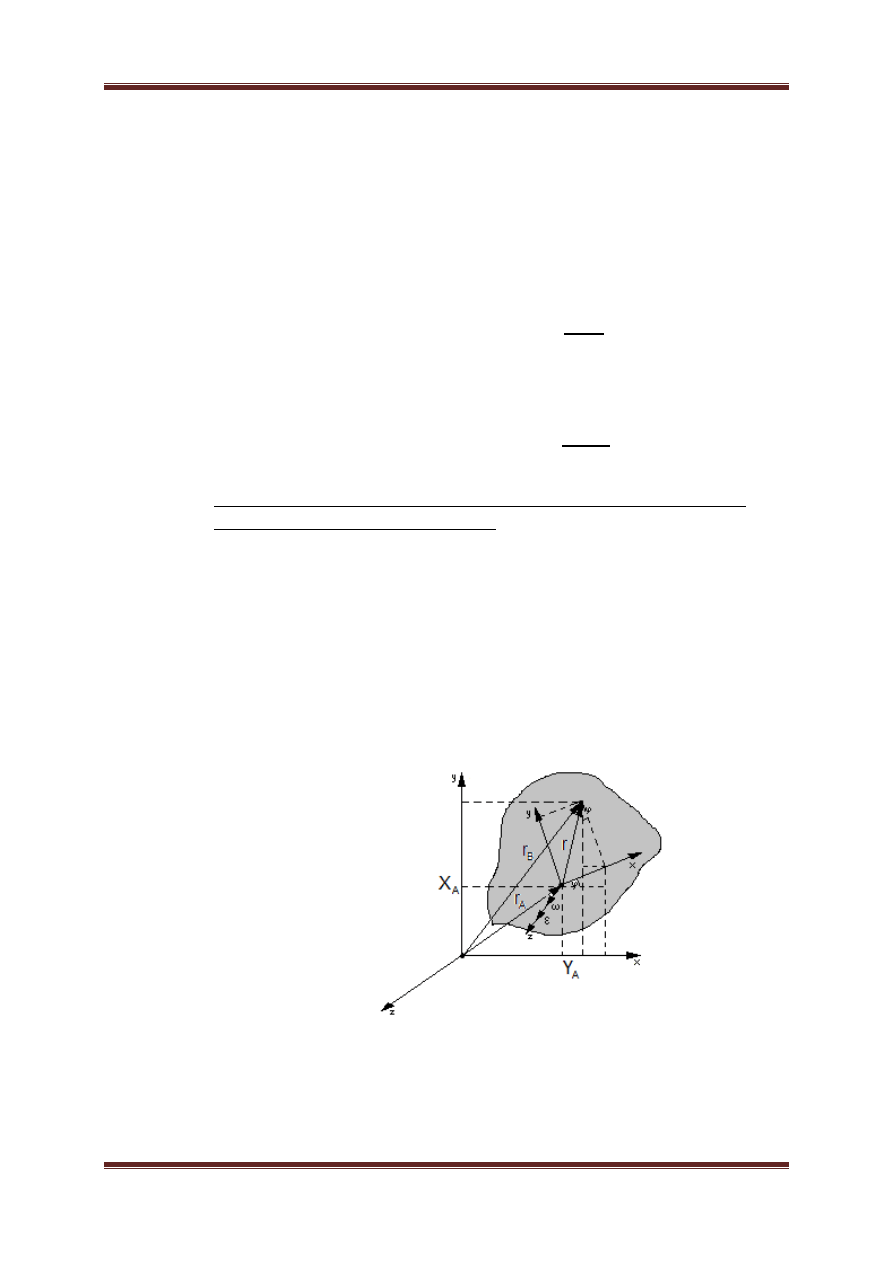
G. Liczba stopni swobody, ruch translacyjny i postępowy ciała sztywnego.

a. Ciało sztywne w przestrzeni posiada sześć stopni swobody

Po nałozeniu na ciało sztywne pewnych ograniczeń ruchu (więzów)
zmaniejszamy liczbę stopni swobody
Stopnie swobody to możliwości ruchu ciała (trzy ruchy postępowe, trzy
oborty).

G
h
j
g
h
j
g
h
j

b. Ruch postępowy ciała sztywnego – najprostrzy przypadek ruchu ciała

sztywneg w którym wszystkie jego punkty doznają tych samych przesunięć.

Mechanika techniczna I

Strona 13

c. Równania ruchu

( ) =

( ) + ( )

( ) =

( ) + ( )

( ) =

( ) + ( )

Po zróżniczkowaniu powyższych równań otrzymujemu równania prędkości

d. Prędkość

( )

e. Przyśpieszenia

( )

H. Ruch płaski ciała sztywnego, chwilowy środek obrotu, prędkość i przyśpieszenie

punktów ciała sztywnego w ruchu płaskim

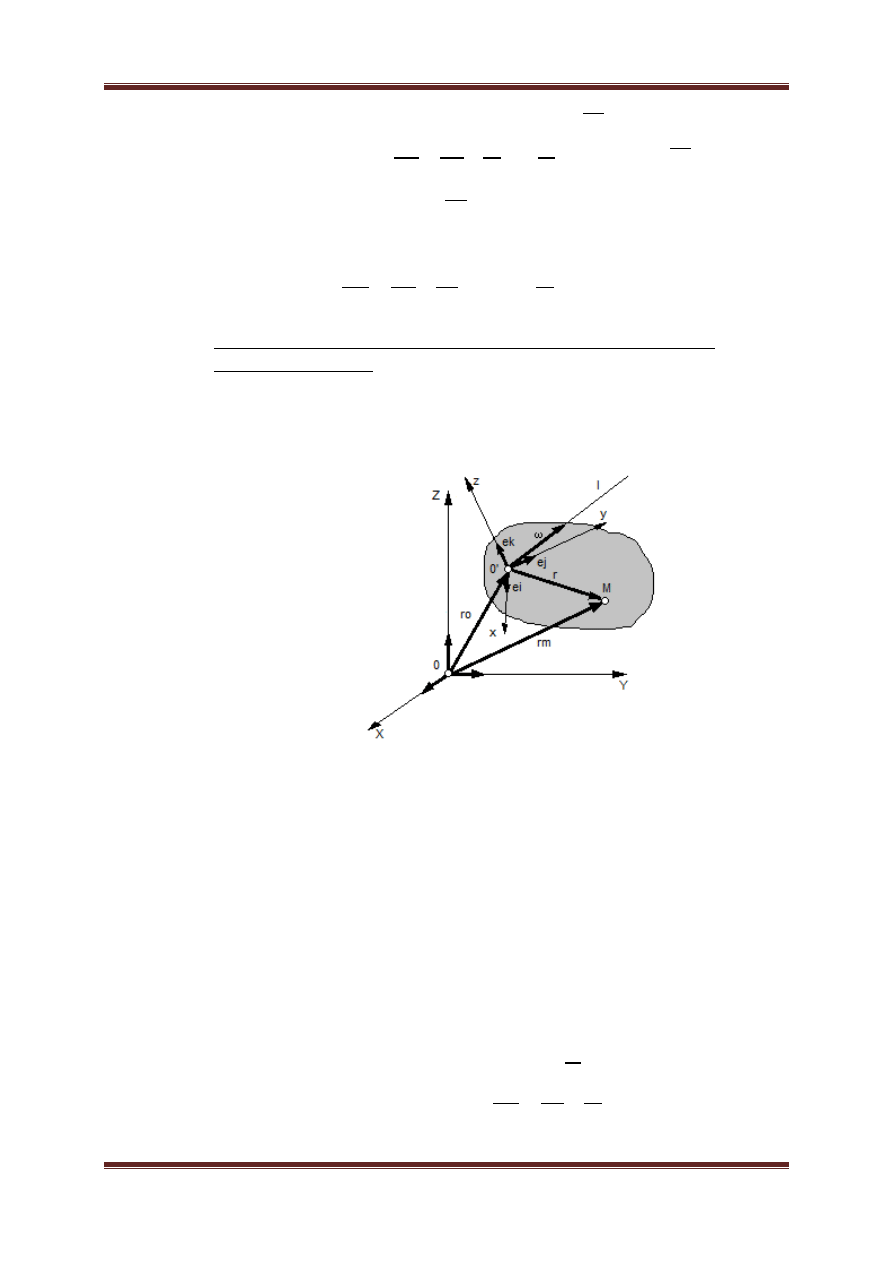
a. Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie

punkty ciała poruszają się w płaszczyznach równoległych do pewnej
płaszczyzny zwanej płaszczyzną ruchu płaskiego (płaszczyzną kierującą).

Dowolne przesunięcie figury płaskiej w jej płaszczyźnie może być dokonane
za pomocą przesunięcia równoległego, równego przesunięciu dowolnie
obranego punktu A tej figury oraz obrotu wokół punktu zwanego chwilowym
środkiem obrotu.

Mechanika techniczna I

Strona 14

(

−

) (

−

)

× +

+ × +

× ( × )

I. Ruch złożony punktu materialnego, prędkość i przyśpieszenie w tym ruchu,

przyspieszenie Coriolisa

a. Ruch punktu M względem układu nieruchomego OXYZ nazywamy ruchem

bezwzględnym. Ruch punktu M względem układu ruchomego Oxyz
nazywamy ruchem względnym. Ruch układu ruchomego O’xyz względem
układu nieruchomego OXYZ nazywamy ruchem unoszenia.

Ruch unoszenie można określić inaczej, że jest to ruch punktu M, jaki
wykonałby on względem układu nieruchomego OXYZ, gdyby go w danej
chwili sztywno związać z układem O’xyz.

Położenie punktu M jest określone wektorem r

, który jest sumą wektorów

i r

Gdzie

Prędkość w ruchu złożonym punktu
Badany układ ruchomy dodatkowo obraca się wokół prostej l

+ /

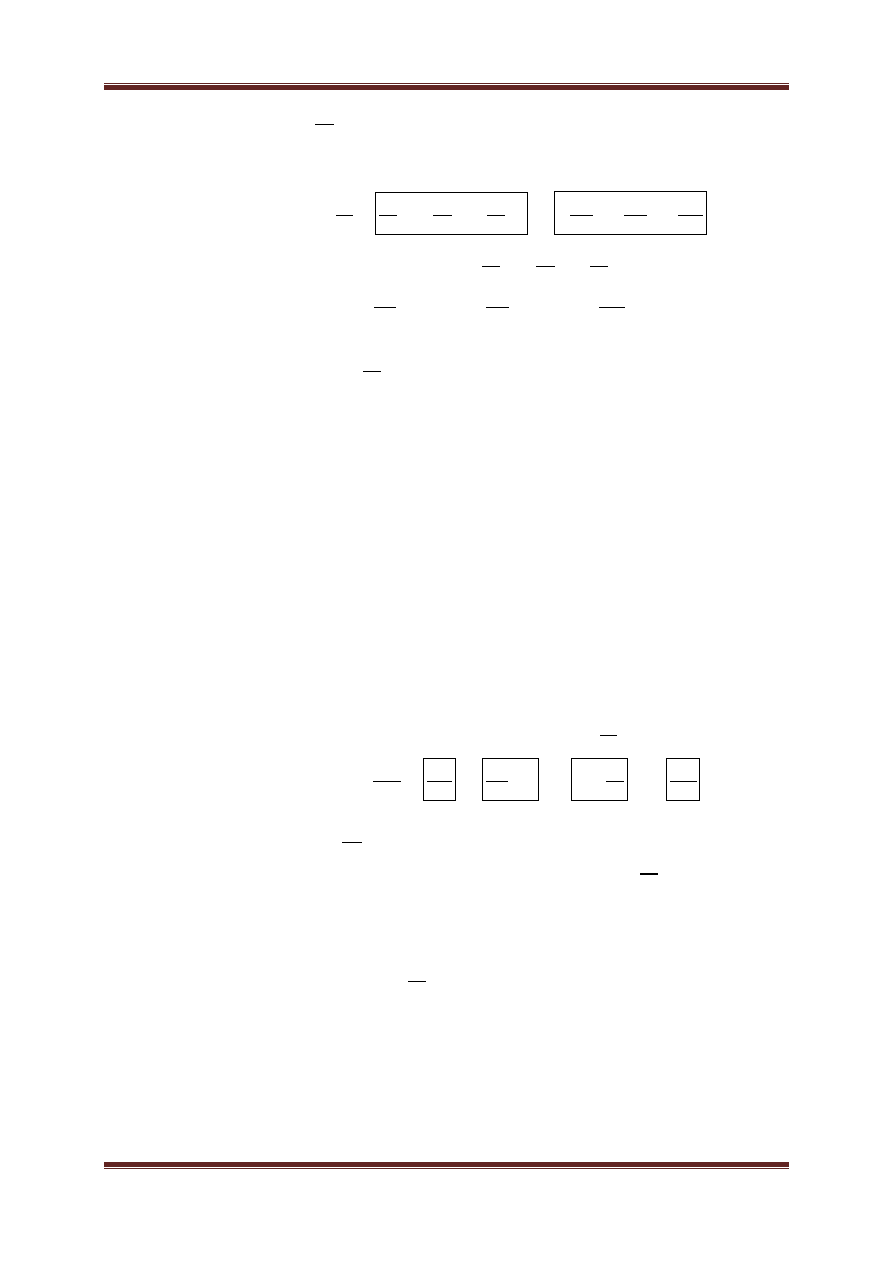
Mechanika techniczna I

Strona 15

Gdzie

jest to prędkość unoszenie w ruchu postępowym układu

ruchomego O’xyz.

∗

∗∗

_________________________________________________________________

∗

∗∗

Więc

Po podstawieniu do zależności na V

uzyskujemy prędkość bezwzględną

punktu M w ruchu złożonym

× +

Ponieważ

jest całkowitą prędkością unoszenie punktu M

(w ruchu postępowym i obrotowym).

Prędkość bezwzględna punktu M w ruchu złożonym jest wypadkową
prędkości unoszenia V

i prędkości względnej V

Przyśpieszenie w ruchu złożonym

× +

∗

∗∗

∗∗∗

∗∗∗∗

Gdzie (*)

jest składową przyspieszenie unoszenia w ruchu

postępowym układu ruchomego O’xyz, natomiast (**)

× = × =

jest kładową styczną przyspieszenia unoszenia w ruchu obrotowym układu
ruchomego

∗∗∗ ×

× ( × ) =

Gdzie a

jest składową normalną przyspieszenia unoszenia, wynikającą z

ruchu obrotowego układu ruchomego.

Mechanika techniczna I

Strona 16

∗∗∗∗

∗∗∗∗∗

∗∗∗∗∗∗

Gdzie pierwsze trzy wyrazy (*****) są składowymi przyspieszenia
względnego a

Natomiast trzy (******) ostatnie wyrazy, przedstawiają iloczyn wektorowy

× . Po uwzględnieniu dotychczasowych rozważań wzór na przyspieszenie

bezwzględne punktu M wygląda następująco:

= [

+ × +

× ( × )] +

+ 2 ×

Gdzie wyrażenie w nawiasie kwadratowym przedstawia przyśpieszenie
unoszenia a

. Ostatni wyraz przedstawia

przyspieszenie Coriolisa.

= 2 ×

Po uwzględnieniu wszystkich zależności wynika, że:

Przyspieszenie bezwzględne a

punktu M w ruchu złożonym równa się sumie

wektorowej przyspieszeń unoszenia a

, względnego a

i Coriolisa a

b. Przyśpieszenie Coriolisa jest związane z obrotem badanego układu.

Przyśpieszenie Coriolisa jest podwojonym iloczynem wektorowym prędkości
kątowej i prędkości względnej.

= 2 ×

Przyśpieszenie Coriolisa jest równe zeru, jeżeli ω=0, albo V

=0 , lub jeżeli

wektor ω jest równoległy do V

. Przyśpieszenie to jest wektorem

prostopadłym do płaszczyzny utworzonej przez wektory ω oraz V

. Wartość

wektora wynosi

= 2

sin ∢( ,

)

Zwrot wektora ustalmy zgodnie z regułą śruby prawoskrętnej

Mechanika techniczna I

Strona 17

Przyspieszenie Coriolisa wywołane obrotem kuli ziemskiej jest bardzo małe i
dlatego zwykle się je pomija, uważając Ziemię na nieruchomy układ
odniesienia. Na przykład przy prędkości pociągu V

= 108 m/s = 30 m/s

jadącego po południku z południa Ana północ naszerokości geograficznej
Radomia ϕ=51

, mamy:

= 2

sin 51 = 2 ∙ 0,7288 ∙ 10

∙ 30 ∙ 0,777 = 34 ∙ 10

Co stanowi znikomy procent przyśpieszenia ziemskiego g (a

=0.034% g)

Mechanika techniczna I

Strona 18

D Y N A M I K A

a) Zasady Newtona, prawo powszechnej grawitacji, zasada d’Alemberta

a. I zasada Newtona (Zasada bezwładności)

W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub
siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza
się ruchem jednostajnym prostoliniowym.

(Philosophiae Naturalis Principia Mathematica, 1726 edition):

Lex I. Corpus omne perseverare in statu suo quiescendi vel movendi

uniformiter in directum, nisi quatenus illud a viribus impressis cogitur

statum suum mutare.

Każde ciało trwa w swym stanie spoczynku lub ruchu prostoliniowego

jednostajnego, jeżeli siły przyłożone nie zmuszą ciała do zmiany tego

stanu.

b. II zasada Newtona

Jeśli siły działające na ciało nie równoważą się (czyli siła wypadkowa F

jest różna od zera), to ciało porusza się z przyspieszeniem wprost
proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do
masy ciała

(Philosophiae Naturalis Principia Mathematica, 1726 edition):

Lex II. Mutationem motus proportionalem esse vi motrici impressae, et

fieri secundum lineam rectam qua vis illa imprimitur.

Zmiana ruchu jest proporcjonalna do przyłożonej siły poruszającej i

odbywa się w kierunku prostej, wzdłuż której siła jest przyłożona.

Zmiana pędu ciała jest proporcjonalna do działającej siły wypadkowej

⃗

= ⃗

c. III Zasada Newtona (Zasada akcji i reakcji)

Oddziaływania ciał są zawsze wzajemne. Siły wzajemnego oddziaływania
dwóch ciał mają takie same wartości, taki sam kierunek, przeciwne
zwroty i różne punkty przyłożenia (każda działa na inne ciało).

Mechanika techniczna I

Strona 19

(Philosophiae Naturalis Principia Mathematica, 1726 edition):

Lex III. Actioni contrariam semper et aequalem esse reactionem; sive

corporum duorum actiones in se mutuo semper esse aequales et in partes

contrarias dirigi.

Względem każdego działania istnieje przeciwdziałanie zwrócone

przeciwnie i równe, to jest wzajemne działania dwóch ciał są zawsze

równe i zwrócone przeciwnie.

d. Prawo powszechnego ciążenia.

Między dowolną parą ciał posiadających masę pojawia się siła
przyciągająca, która działa na linii łączącej ich środki, a jej wartość rośnie
z iloczynem ich mas i maleje z kwadratem odległości.

∙

≈ 6,67 ∙ 10

∙

e. Zasada d’Alemberta

Każdy problem dynamiki może być sprowadzony do problemu statyki po
dodaniu fikcyjnych siła d’Alemberta, które równoważy układ sił

−

= 0

b) Wahadło matematyczne, oscylator harmoniczny.

a. Wahadło matematyczne to punkt materialny zawieszony na

nierozciągliwej i nieważkiej nici w polu grawitacyjnym. Jest to idealizacja
wahadła fizycznego.

Okres drgań dla małych ϕ

= 2

Mechanika techniczna I

Strona 20

Okres drgań dla dużych ϕ (wahania o
dużej amplitudzie)

= 2

∙

(2 )!

(2 ∙ !)

∙ sin

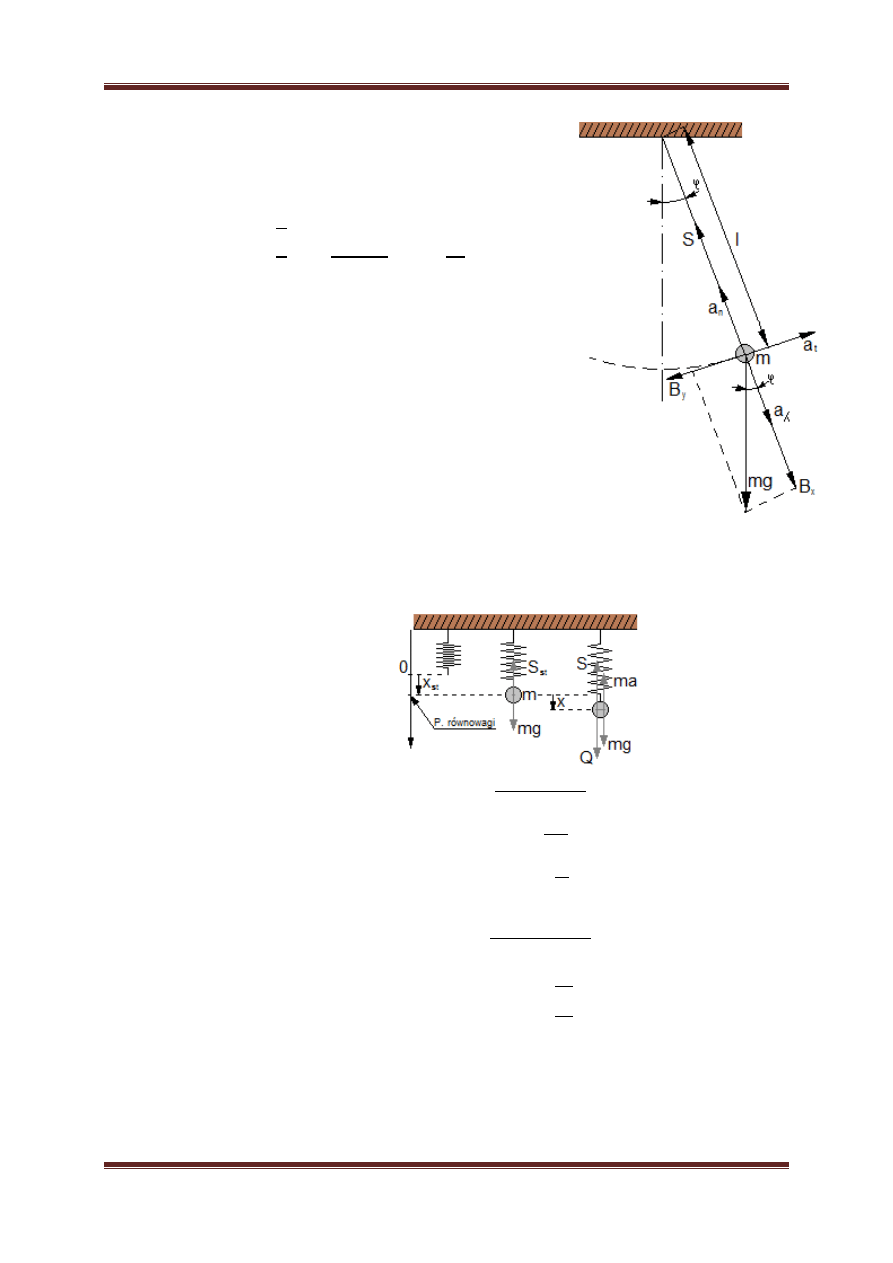
b. Oscylator harmoniczny to model

teoretyczny służący opisowi drgań
wykonywanych

przez

punkt

materialny o masie m pod wpływem
działania sił proporcjonalnych (np.
sprężystości i lub grawitacji) do
chwilowego

wychylenia

pewnego położenia równowagi. W
mechanice klasycznej jednym z wielu
przedstawień tego modelu jest masa na sprężynie wykonujące drgania
swobodne nie tłumione.

P. równowagi

[ ] =

W czasie drgań

̈ +

= 0 − ó

sin

Mechanika techniczna I

Strona 21

c) Pęd punktu materialnego i układu punktu materialnego

a. Pęd w mechanice to wielkość fizyczna opisująca ruch obiektu fizycznego.

Pęd mogą mieć wszystkie formy materialne; np. ciała o niezmiennej
masie spoczynkowej, pole elektromagnetyczne, pole grawitacyjne. Pęd
punktu materialnego jest równy iloczynowi masy m i prędkości V. Pęd
jest wielkością wektorową; kierunek i zwrot pędu jest zgodny z
kierunkiem i zwrotem wektora prędkości.

[ ] =

∙

[ ∙ ]

W odniesieniu do II zasady Newtona
Dla m = const.

b. Pęd układu punktów materialnych jest równy sumie wektorowej pędów

wszystkich punktów układu. Można łatwo udowodnić, że pęd układu jest
równy całkowitej masie pomno0żonej przez prędkość środka masy
układu

Pęd układu punktów materialnych zmienia się tylko wtedy gdy działa na
nie siła zewnętrzna. Jeżeli układ rozpada się w wyniku działania sił
wewnętrznych na części to suma pędów części jest równa pędowi układu
przed rozpadem. Podobnie się dzieje przy łączeniu się części w układ.
Zderzenie ciał możemy traktować jako złączenie i rozłączenie układu ciał.

d) Prawo zmienności pędu, Prawo zachowania pędu.

a. Prawo zachowania pędu

Jeżeli na punkt materialny działa samo zrównoważony układ sił (siły
działające równoważą się, F

=0), to pęd jest wektorem stałym.

= 0

= 0 ⇒

b. Prawo zmienności pędu (zasada pędu i popędu)

Przyrost pędu układu punków materialnych w skończonym przedziale
czasu jest równy popędowi wektora siła zewnętrznych działających na
ten układ

←

ę ł

Mechanika techniczna I

Strona 22

e) Kręt punktu materialnego i układu punktów materialnych,

prawo zmienności

krętu

i prawo zachowania krętu.

a. Kręt (moment pędu) punktu materialnego o pędzie P, którego położenie

opisane jest wektorem wodzącym r względem obranego układu
odniesienia definiuje się jako wektor będący rezultatem iloczynu
wektorowego wektora położenia i pędu.

= ×

= | × | = | | ∙ | | ∙ sin

= ×

−

(

−

) +

−

Gdzie:
m – masa punktu materialnego;
x

, y

, z

– współrzędne punktu materialnego;

, V

– składowe prędkości punktu materialnego;

b. Kręt układu punktów materialnych jest równy sumie wektorowej krętów

punktów wchodzących w skład układu. Kręt układu jest równy iloczynowi
pędu układu i wektora wodzącego rozpiętego pomiędzy obranym
punktem odniesienia i środka masy układu.

c. Prawo zachowania krętu – dla dowolnego izolowanego układu punktów

materialnych całkowita suma krętu jest stała.

Lub

Moment pędu bryły sztywnej pozostaje stały, gdy nie działają na nią
żaden moment siły zewnętrznej.

= 0

( ) = 0

d. Prawo zmienności krętu

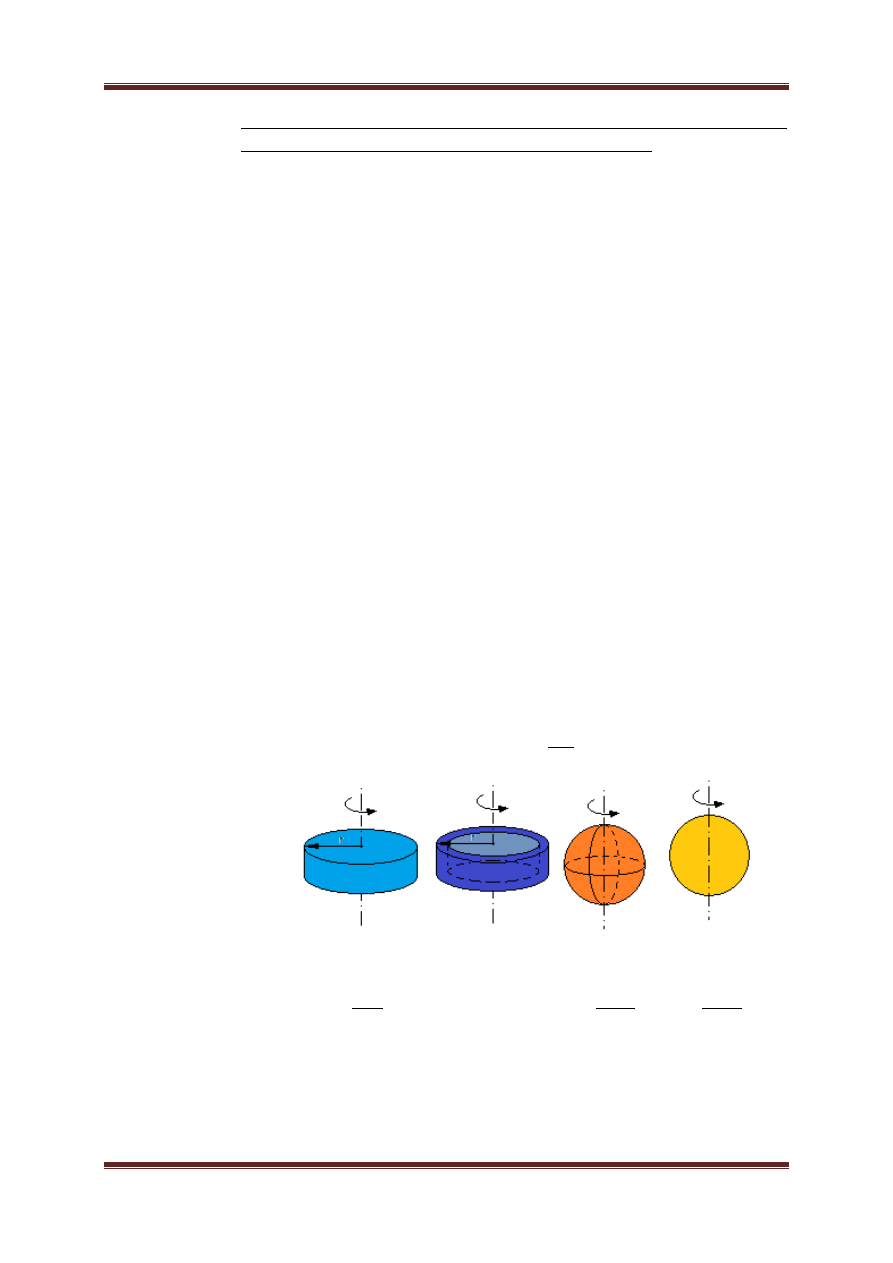
Mechanika techniczna I

Strona 23

f) Zasada ruchu układu punktów materialnych , momenty bezwładności układu

punktów materialnych i ciał sztywnych, twierdzenie Sztainera

a. Środek masy każdego układu punktów materialnych porusza się tak,

jakby była w nim skupiona cała masa układu i jakby do tego punktu przy
łożone były wszystkie siły zewnętrzne

b. Moment bezwładności to maira bezwładności ciała w ruchu obrotowym

względem określonej i ustalonej osi obrotu. Im większy momen ciała Tm
trudniej wpłynąć na ruch ciała np. zmienić prędkość kątową. Moment
ciała zależy od wyboru osi obrotu, kształtu ciała i od rozmieszczenia masy
w tym ciele.

c. Moment bezwładności punktu materialnego

Gdzie:
m – masa punktu
r – odległość punktu od osi

d. Moment bezwładności układu n punktów materialnych

Za pomocą momentu bezwładności bryły sztywnej obracającej się
względem pewnej osi, z pewną prędkością kątową ω względem tej osi
można wyznaczyć energię kinetyczną tej bryły.

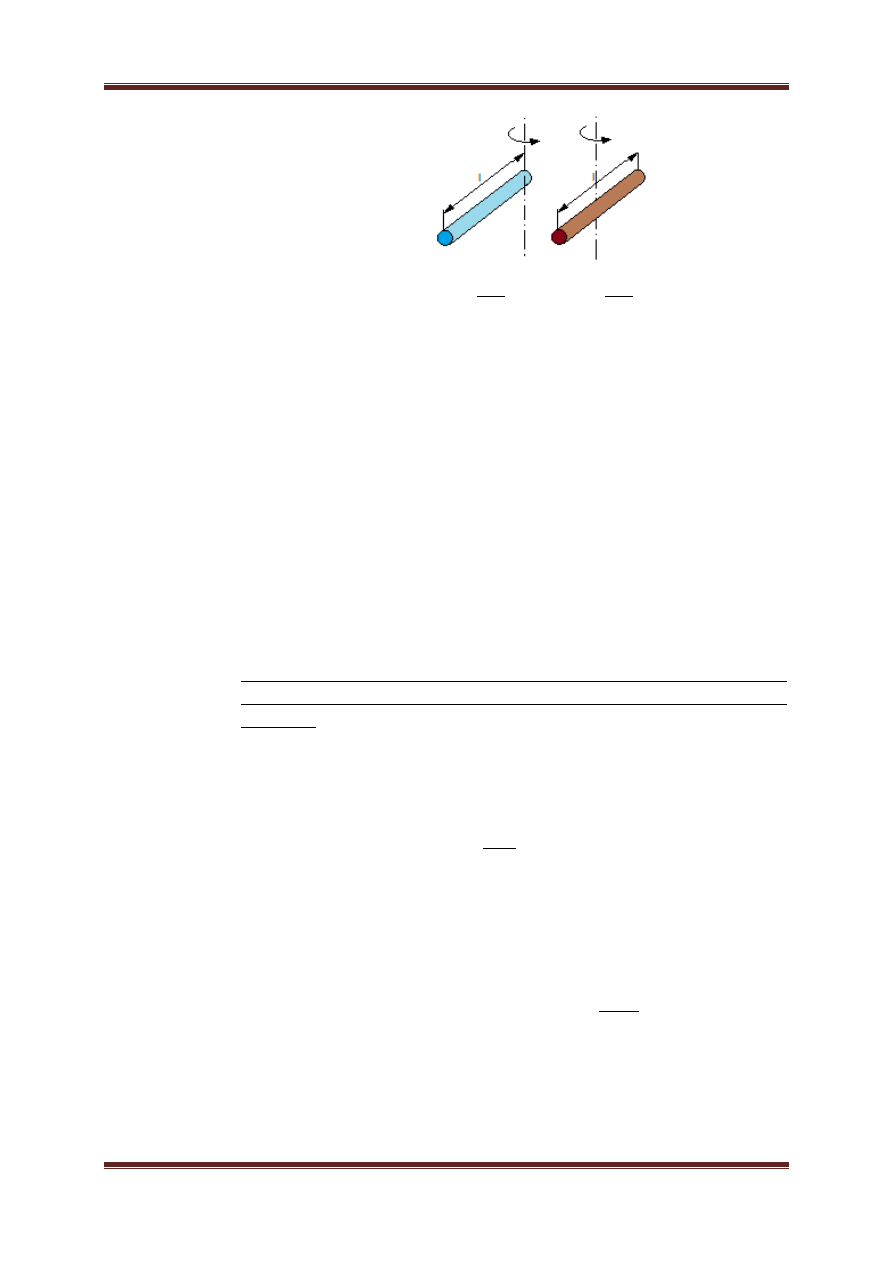
Walec Walec wydrążony Kula Sfera cienkościenna

Mechanika techniczna I

Strona 24

e. Zasada Szteinera – moment bezwładności układu punktów materialnych

względem pewnej osi równa się momentowi układu punktów
materialnych względem osi równoległej do tej wyjściowej przechodzącej
przez środek masy układu punktów materialnych w sumie z iloczynem
masy układy punktów materialnych i kwadratu odległości między osiami

Gdzie:
I

– moment bezwładności względem osi przechodzącej przez środek

masy.
I – momen względem obranej pierwotnie osi
m – masa układu punktów materialnych
r – odległość między osiami

g) Energia kinetyczna, Energia potencjalna, energia mechaniczna, prawo

zachowania energii, twierdzenie Koeniga dla układu punktów materialnych i ciała
sztywnego.

a. Energia kinetyczna to energia ciała lub układu punktów materialnych

związanych z jego ruchem. Dla obiektów o masie m i prędkości V dużo
mniejszych od prędkości światła (V<<c) energię kinetyczną wyraża wzór:

[

] = [ ] ż

Energia kinetyczna układu punktów materialnych jest równa sumie
energii kinetycznych wszystkich punktów materialnych wchodzących w
skład układu:

Mechanika techniczna I

Strona 25

b. Energia potencjalna – energia jaką ma układ ciał umieszczony w polu siłą

zachowawczych, wynikająca z rozmieszczenia tych ciał. Równa jest pracy
jaką trzeba wykonać, aby uzyskać daną konfigurację wychodząc od
innego rozmieszczenia, dla którego umownie przyjmuje się wartość
równą zero. Konfigurację odniesienia dobiera się w taki sposób aby ukła
miał t tej konfiguracji minimum energii potencjalnej. Podobnie jak
energię pracę energię potencjalną mierzymy w dżulach [J].

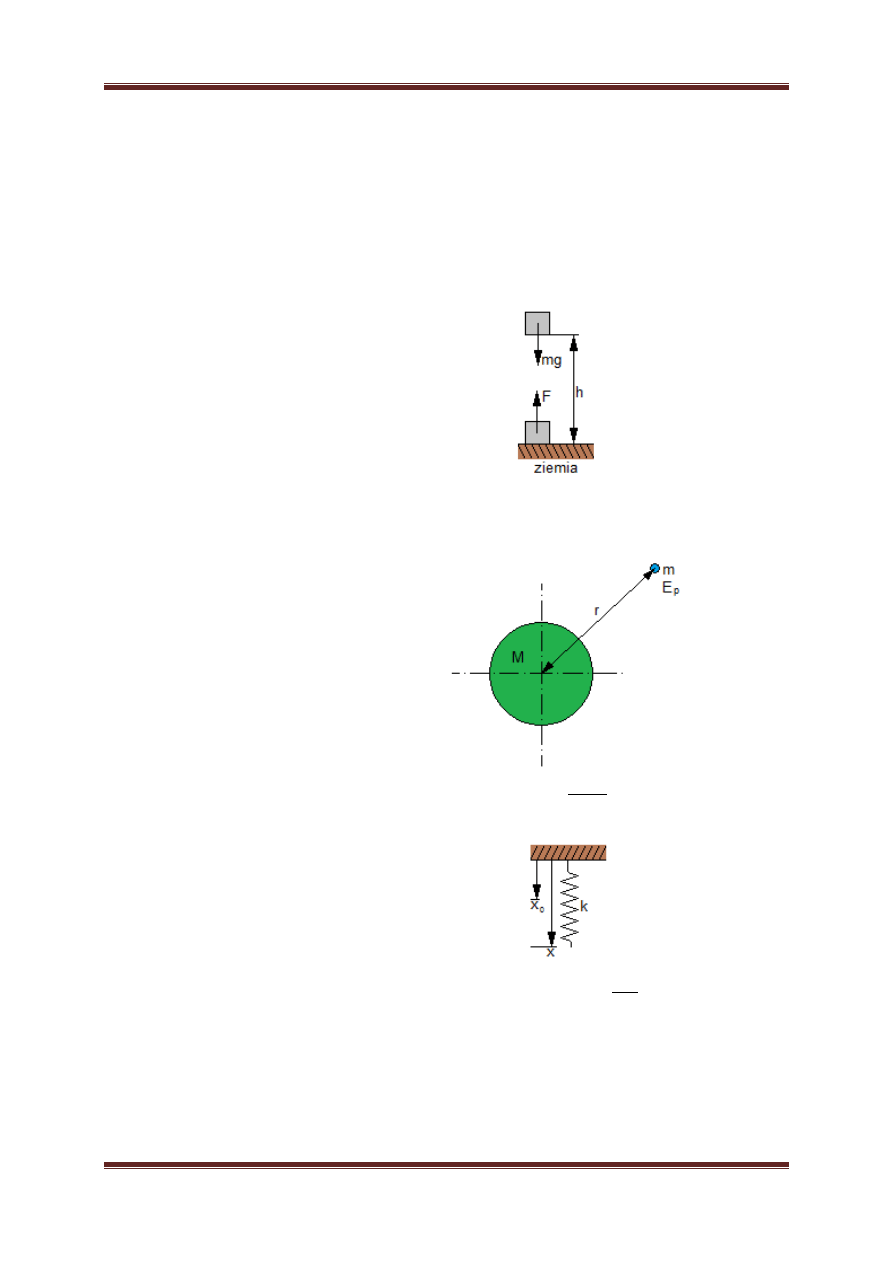
I. W pobliżu powierzchni ziemi

= ℎ =

ℎ

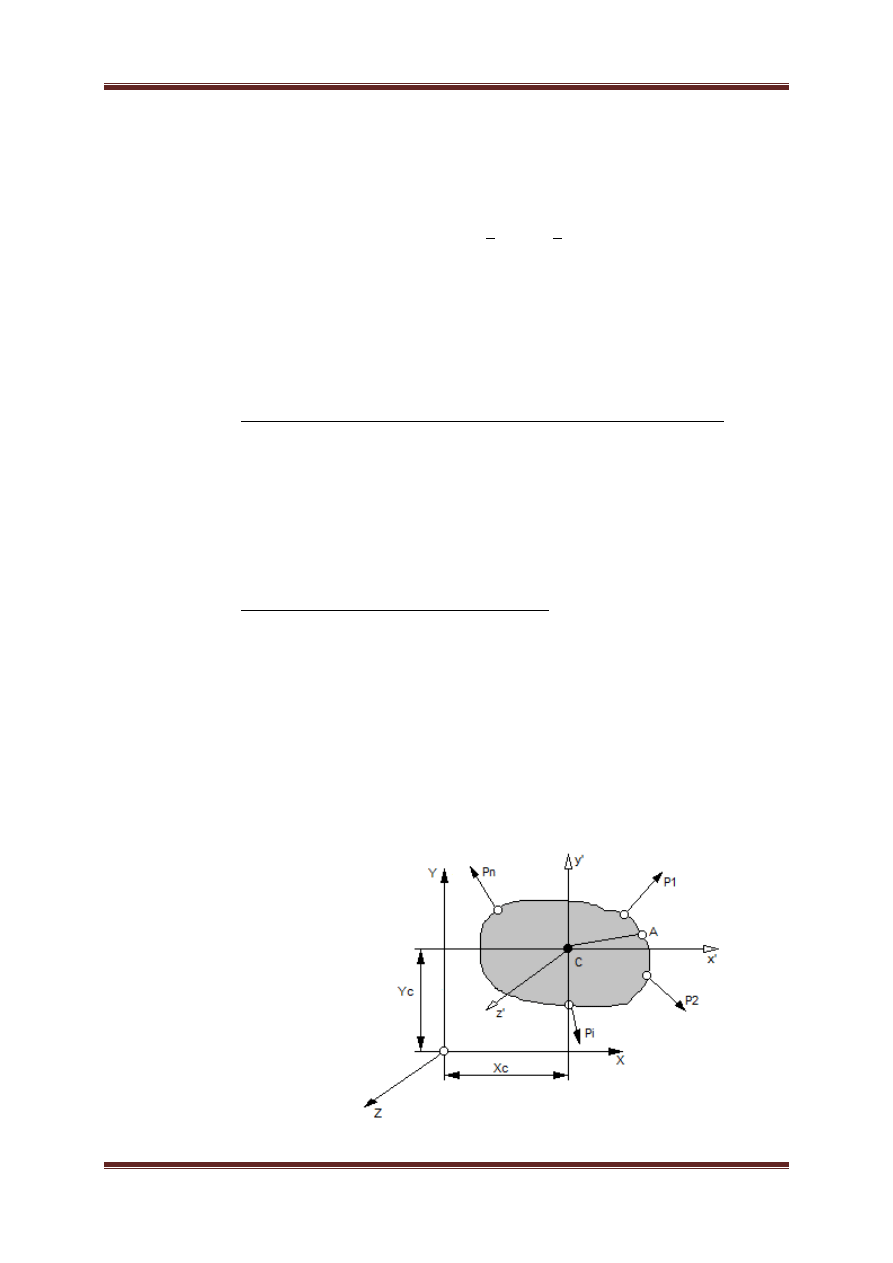
II. W centralnym polu grawitacyjnym

III. Energia potencjalna sprężystości sprężyny

c. Energia mechaniczna – suma energii kinetycznej i potencjalnej. Jest

postacią energii związanej z ruchem i położeniem obiektu fizycznego
(układu punktów materialnych , ośrodka ciągłego, itp.) względem
pewnego układu odniesienia.

Mechanika techniczna I

Strona 26

d. Twierdzenie Koeniga – energia kinetyczna układu punktów materialnych

i ciała sztywnego jest równa sumie energii kinetycznej ruchu
postępowego i energii kinetycznej w ruchu względnym dookoła środka
masy C układu.

1
2

e. Prawo zachowania energii – empiryczne prawo fizyki, stwierdzające, że w

układzie izolowanym suma wszystkich rodzajów energii układu jest stała
(nie zmienia się w czasie). W konsekwencji, energia w układzie
izolowanym nie może być ani utworzona ani zniszczona, może jedynie
zmieniać swe formy. Tak na przykład podczas spalania wodoru w tlenie
energia chemiczna zmienia się w energię cieplną.

h) Prawo zmienności energii kinetycznej dla układu punktów materialnych.

a. Różnica energii kinetycznych nie izolowanego układu punktów

materialnych między położeniem początkowym i końcowym układu jest
równa pracy sił zewnętrznych, wykonanych na drodze między
położeniami krańcowymi układu.

−

i) Płaski ruch ciała sztywnego, wahadło fizyczne.

a. Płaski ruch ciała sztywnego

Ruch swobodny ciała sztywnego jest płaski, jeżeli chwilowe osie obrotu
nie zmieniające kierunku pozostają stale w równowadze do głównej
centralnej osi bezwładności tego ciała.

W celu otrzymania dynamicznych równań ruchu ciała sztywnego podczas
działania obciążeń zewnętrznych w postaci sił P

, P

, …, P

zastosujemy

dynamiczne równanie ruchu postępowego i zasadę krętu w ruchu
obrotowym.

Mechanika techniczna I

Strona 27

̈ =

Gdzie:

̈ , ̈ - składowe przyspieszeń środka masy

- Moment bezwładności ciała względem osi z

- przyśpieszenie kątowe względem osi z

b. Wahadło fizyczne – bryła sztywna zawieszona lub zamocowana ponad

swoim środkiem ciężkości wykonujące w pionowej płaszczyźnie drgania
pod wpływem siły grawitacji. W wahadle fizycznym, bryła sztywna może
wykonywać obroty dokoła poziomej osi przechodzącej ponad środkiem
ciężkości tej bryły.

Wzór na okres drgań

= 2

Gdzie:
L

– odległość zredukowana wahadła

d – odległość od punktu zawieszenia do środka ciężkości
g – przyśpieszenie ziemskie
I – moment bezwładności ciała względem osi obrotu
m – masa ciała

c. Wahadło Foucaulta

Jest to duża masa zawieszona na długiej linie. dzięki działaniu siły
Coriolisa spowodowanej obrotem ziemi, płaszczyzna drgań wahadła
ulega powolnemu obrotowi

≈

24ℎ

sin

Gdzie:
ϕ – szerokość geograficzna na której znajduje się wahadło
h – długość liny na której wisi masa

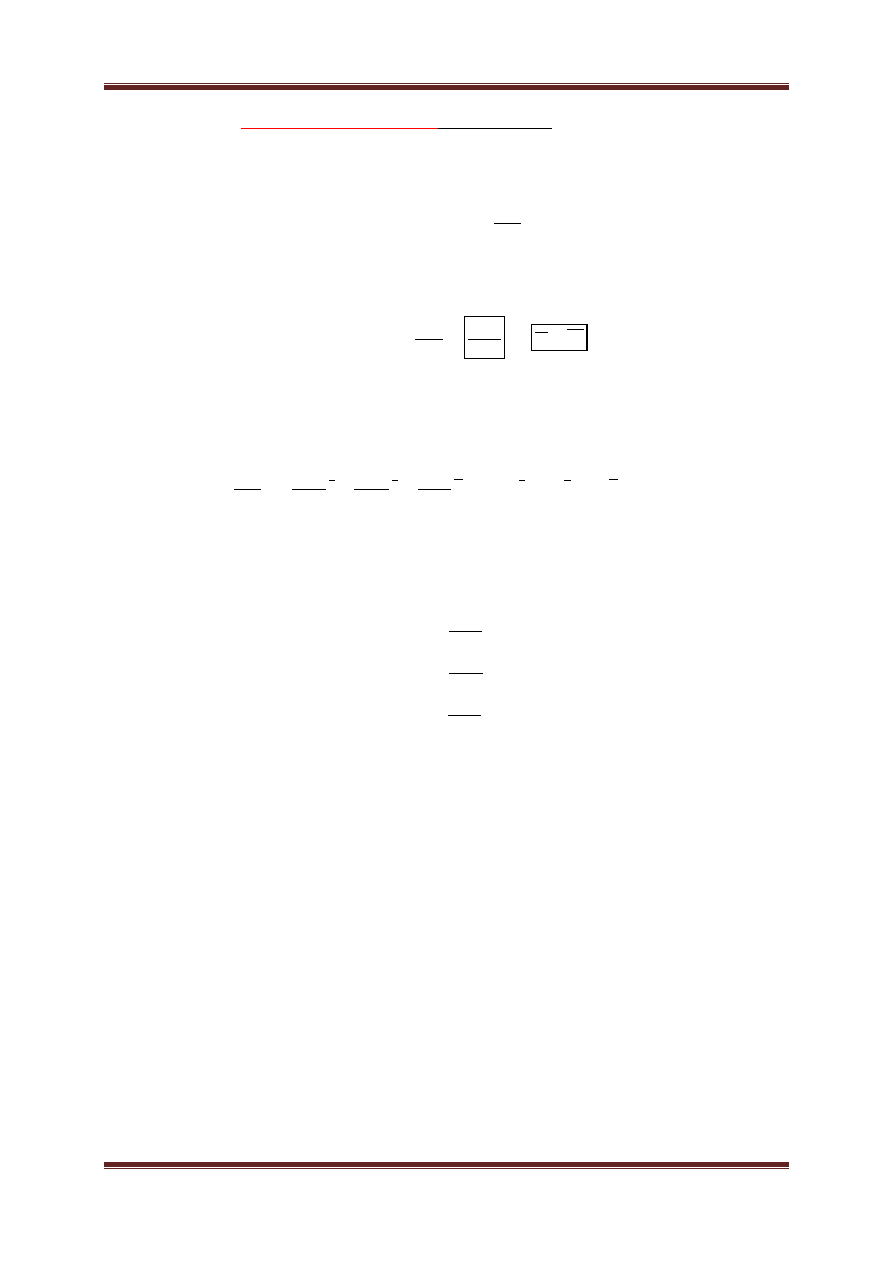
Mechanika techniczna I

Strona 28

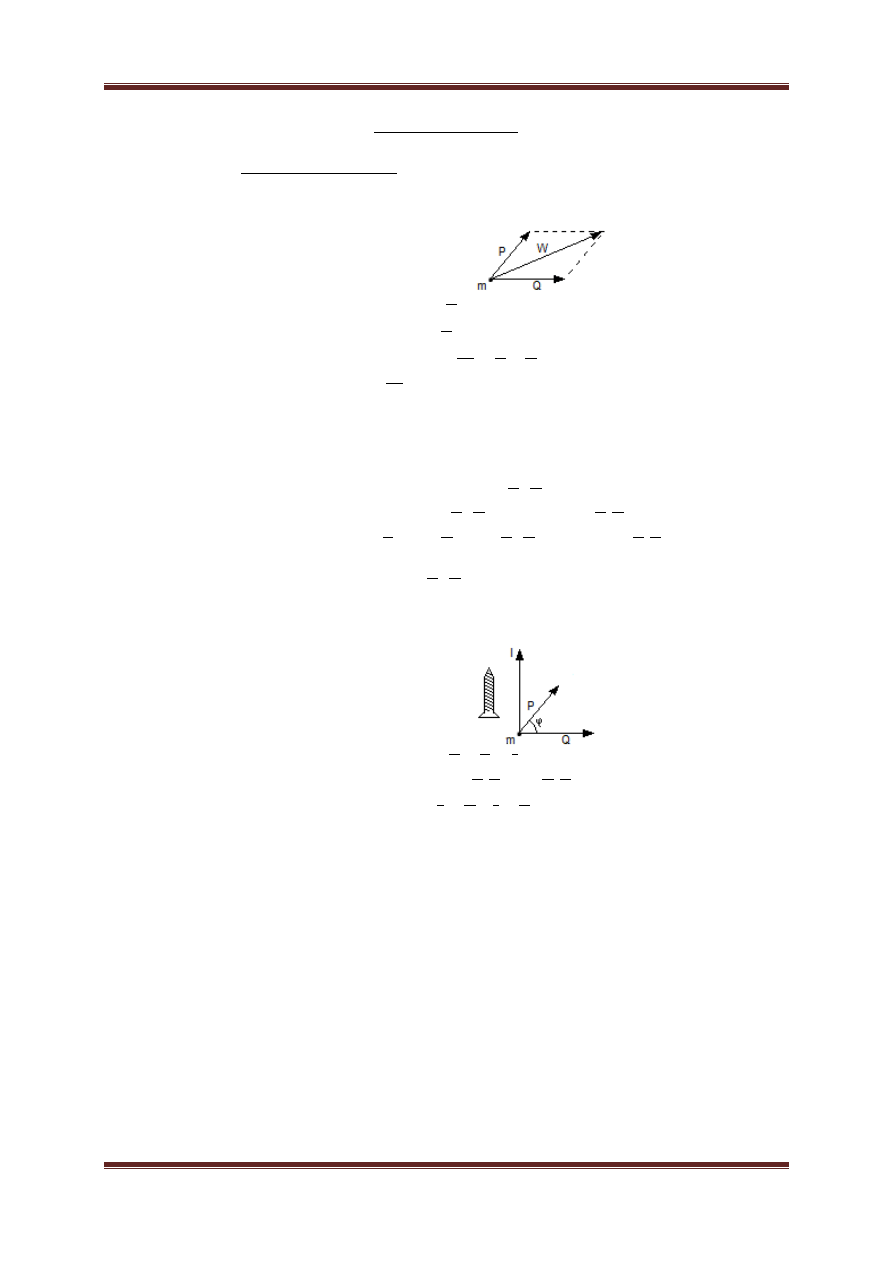
j) Ruch kulisty ciała sztywnego,

równanie Eulera.

a. Ruch kulisty ciała sztywnego

b. równanie Eulera

( )

Po uwzględnieniu układu ruchomego

∗

∗∗

( )

* pochodna krętu w układzie ruchomym
**unoszenie

Założenie: osie układu O

x’y’z’ są głównymi osiami bezwładności

′

Po przekształceniach:

′ =

′

′ − ′

′

′ =

′

′ =

′

+ ( ′ − ′ ) ′

′ =

′

′ =

′

′ − ′

′

′ =

′

Mechanika techniczna I

Strona 29

S U P L E M E N T

a) Działania na wektorach

a. Dodawanie wektorów

b. Iloczyn skalarny - jego wynikiem jest liczba

∙

∙ cos ∢( , )

≠ 0 ∧

≠ 0 ∙

= 0 ⇒ cos ∢( , ) = 0

∙

c. Iloczyn wektorowy

∙

∙ sin ∢( , ) ∢

⊥

∧ ⊥

−

+ (

−

) +

−

Wyszukiwarka

Podobne podstrony:
Mechanika Techniczna I Opracowanie 06
9048000196926-mechanika techniczna opracowane pytania maruszewski-ulepszone, 1
9496136526577-mechanika techniczna opracowane pytania maruszewski POPRAWIONE, Politechnika Poznanska
mechanika techniczna opracowane Nieznany
Mechanika Techniczna - Opracowania - Do Prof. Maruszewskiego, Politechnika Poznańska (PP), Mechanika
mechanika techniczna opracowane pytania maruszewski (1), Polibuda (MiBM), Semestr III, III semestr,
Mechanika Techniczna I Opracowanie 06
Mechanika Techniczna I Opracowanie 05
9048000196926 mechanika techniczna opracowane pytania maruszewski ulepszone
Mechanika Techniczna Opracowania Do Prof Maruszewskiego 1 semestr
opracowanie 4 mechana, Studia - Mechatronika, III semestr, Mechanika Techniczna
ZAKRES NA EGZAMIN Z MECHANIKI TECHNICZNEJ II DLA SEMESTRU III opracowanie
opracowanie 4 mt, Studia - Mechatronika, III semestr, Mechanika Techniczna
Wydymala opracowanie pytan, sem III, +Mechanika Techniczna II - Wykład.Ćwiczenia.Laboratorium, mecha

więcej podobnych podstron