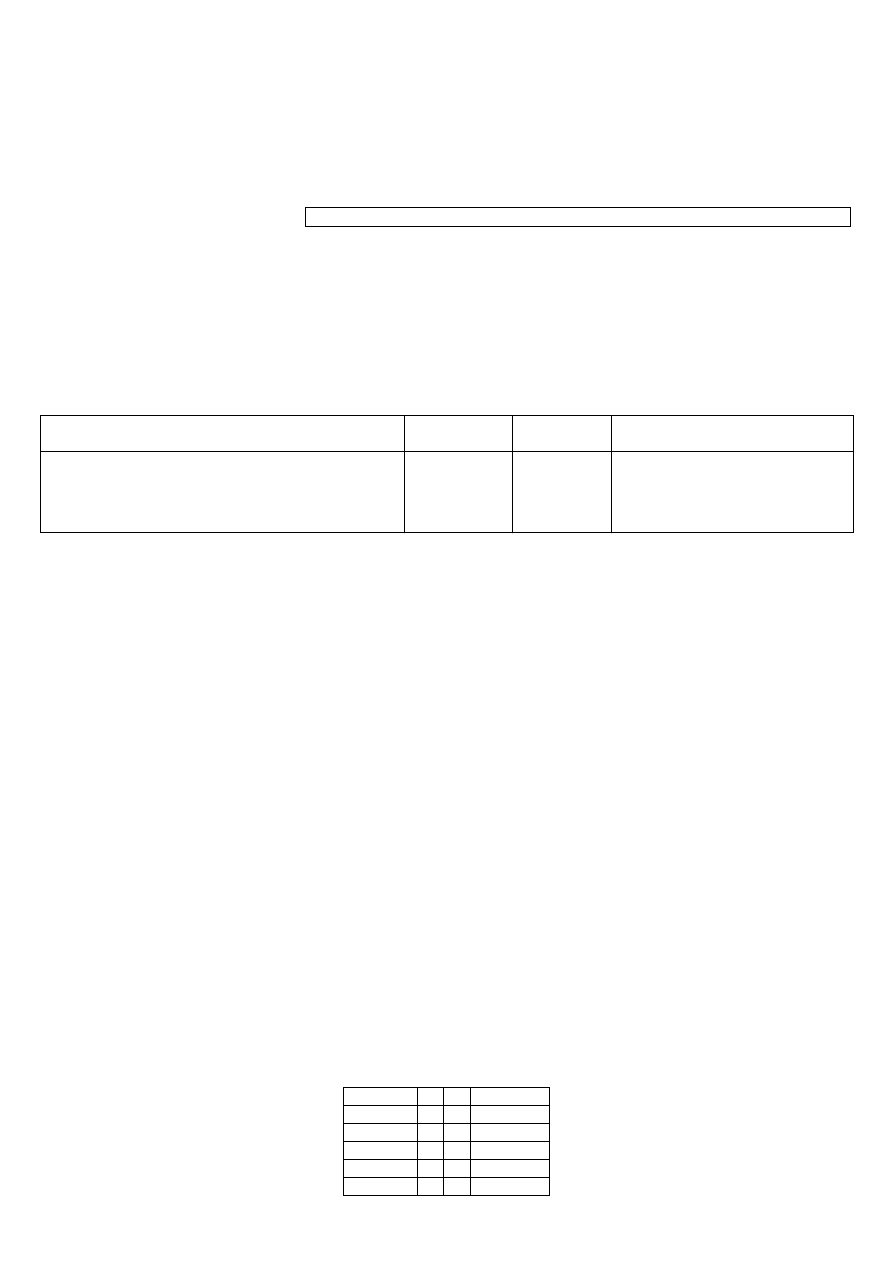
1. Zagadnienie diety.

Rozważmy następujące zagadnienie: przy dokonywaniu zakupów artykułów

żywnościowych o ustalonych cenach często bierze się pod uwagę zawartość w nich środków odżywczych.
Przy tym ilości zakupionych produktów powinny być takie, aby w sumie pokrywały minimalne
zapotrzebowanie organizmu konsumenta na poszczególne środki odżywcze. Oczywiście, zapotrzebowanie
to może być zaspokojone różnymi sposobami, gdyż poszczególne produkty mogą być zakupione w różnych
ilościach tak, aby ogólna ilość zawartych w nich środków odżywczych była w sumie ta sama. Chodzi
jednak o taki zakup produktów któremu odpowiada najmniejszy koszt i który równocześnie zaspokaja
potrzeby konsumenta. Takiego rodzaju zagadnienie nazywane jest w literaturze zagadnieniem diety.
Rozważymy to zagadnienie na prostym przykładzie, w którym bierze się pod uwagę tylko dwa produkt
żywnościowe.

Produkt A zawiera około 1000 kalorii i 25 gramów protein na jednostkę. Produkt B zawiera około 2000 kalorii i 100

gramów protein na jednostkę. Minimalne dzienne zapotrzebowanie konsumenta na środki odżywcze wynosi: 3000 kalorii
i 100 gramów protein. Ceny rynkowe zaś są następujące: produkt A kosztuje 20 zł za jednostkę, produkt B

50 zł za

jednostkę. Powyższe dane zestawiamy w tablicy.

Tablica

Na jednostkę

Na jednostkę

Zapotrzebo

produktu

A

produktu

B

wanie

Zawartość kalorii

1000

2000

3000

Zawartość protein wg

25

100

100

Koszt jednostki

20 zł

50 zł

W produktach A i B znajdują się również inne składniki potrzebne dla organizmu człowieka. Przyjmijmy na

przykład, że produkty A i B zawierają odpowiednio 25 mg i 20 mg witaminy C na jednostkę, a dzienne zapotrzebowanie
na tę witaminę wynosi co najmniej 50 mg. Czy nowe ograniczenie wpłynie na optymalną wartość funkcji celu?

2. Zagadnienie analizy działalności gospodarczej

W pewnym zakładzie produkcyjnym produkuje się dwa rodzaje produktów A i B. Do wyprodukowania

produktów A i B potrzebne są surowce X oraz Y. Surowców tych zakład nie może sprowadzić w dowolnych
ilościach. Surowca X zakład może uzyskać najwyżej 15 jednostek, a surowca Y — najwyżej 12 jednostek.
Ilości surowców X potrzebne do wyprodukowania jednostek produktów A i B wynoszą 0,5 oraz 0,3
odpowiednio oraz ilości surowców Y potrzebne do wyprodukowania jednostek produktów A i B wynoszą 0,3
oraz 0,4 odpowiednio. Ceny produktów A i B (produkty i surowce mierzone są w tych samych jednostkach)
wynoszą 800 oraz 700 PLN.

(ZESTAWIĆ DANE W TABLICY!).

Producenta interesuje, w jakich ilościach powinien produkować produkty A i B, aby zapewnić sobie największy
zysk.

PROBLEM 1:

Jacek zamierza hodować dwa gatunki albionaków (A1 i A2), ale powyższy problem związany jest z gatunkiem A1. Można

go żywić dwoma rodzajami pasz (P1, P2). Dostępne w odżywianiu pasze zawierają trzy składniki pokarmowe (S1, S2, S3). W tablicy
podano: zawartość składników pokarmowych S1, S2 i S3 w poszczególnych rodzajach pasz P1 i P2 (jednostki odżywcze na jednostkę
paszy). Kolumna limit dolny podaje minimalne ilości składników pokarmowych, jakie trzeba dostarczyć albionakom A1 w ciągu
cyklu rozwojowego (2 miesiące księżycowe). Wiersz limit Pi podaje minimalne ilości pasz, jakie trzeba dostarczyć w ciągu cyklu
rozwojowego (w beczkach). Wiersz cena PLN podaje koszty jednostki (beczki) poszczególnych rodzajów pasz. Jaki jest optymalny
skład mieszanki dla albionaków gatunku A1, gdy przyjmiemy kryterium – najmniejszy koszt tej mieszanki?

P1 P2 Limit dolny

S1

30 60

480

S2

40 15

240

S3

10 10

140

Limit Pi

10 2

Cena PLN 5

10

PROBLEM 2:

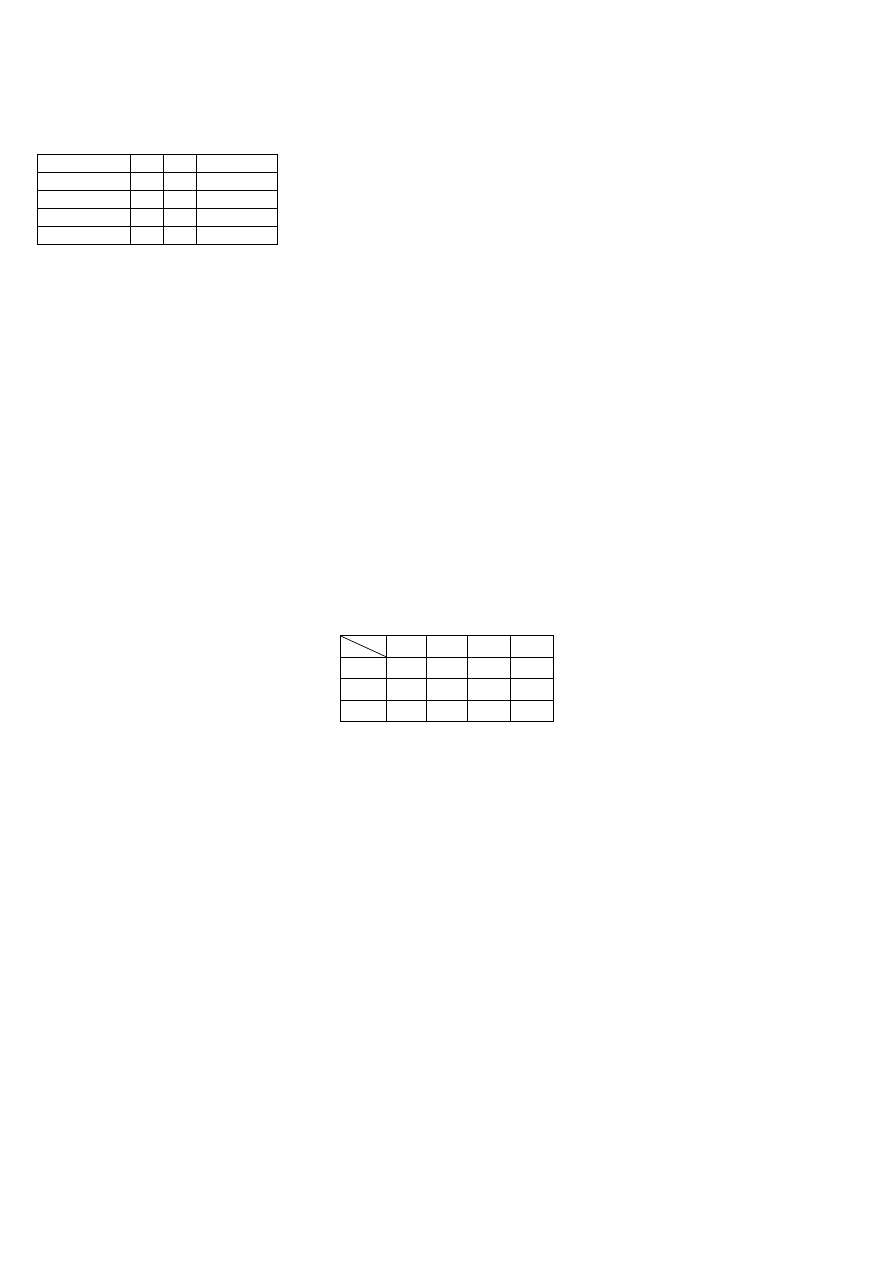
Optymalna mieszanka dla albionaków gatunku A2 składa się z 10 beczek paszy P1 oraz 1 beczki paszy P2. W tablicy

podano dane dotyczące zużycia pasz przez każdy z gatunków albionaków. Zawarte są tam także limity górne dostępności pasz
oraz ceny sprzedaży poszczególnych gatunków. Wiersz popyt (sztuki) ogranicza ilości hodowanych zwierzaków. Zaproponuj
ilości, w jakich hodować poszczególne gatunki albionaków, aby z ich sprzedaży osiągnąć maksymalny przychód.

A1 A2 Limit górny

P1

10

6000

P2

1

1000

Popyt (sztuki) 300 300

Cena PLN

180 110

Uwaga: Do komórek na przecięciu P1 i P2 oraz A1
wpisz dane uzyskane z rozwiązania problemu 1. Gdy
problem 1 nie został rozwiązany do (P1,A1) wpisz 6;
do (P2,A1) wpisz 1 i te dane wykorzystaj do budowy
modelu.

PROBLEM 3:

Ile beczek paszy P1 zjadają albionaki w jednym cyklu rozwojowym?

(wykorzystaj odpowiednie ograniczenie z problemu 2 – przy braku danych przyjmij limit górny}

Ile beczek paszy P2 zjadają albionaki w jednym cyklu rozwojowym?

(wykorzystaj odpowiednie ograniczenie z problemu 2 – przy braku danych przyjmij limit górny}

Oblicz koszty zjadanych beczek paszy P1 i P2 przez hodowane zwierzaki.

(ceny beczek paszy - dane z problemu 1}

Oblicz zysk brutto hodowli (jeden cykl) odejmując od przychodu ze sprzedaży koszty zmienne, które

obejmują koszty paszy zjadanej przez albionaki oraz pracę dwóch studentów zatrudnionych na zlecenie z gażą
1750 PLN na osobę.

PROBLEM 4:

Jacek sprzedaje albionaki gatunku A2 z trzech farm hodowlanych. Zgłosiło się czterech kupujących. W tabeli
podano ilości wystawionych na sprzedaż albionaków (a

i

), zapotrzebowanie kupujących (b

j

) oraz w lewym

górnym rogu komórek koszty transportu zwierzaków z farm do odbiorców (koszty te pokrywa Jacek).

a

i

b

j

30

40

70 100

70

2

4

2

5

150

1

7

4

3

180

2

1

8

6

Sprawdź, czy można od razu przystąpić do transakcji (podaż=popyt), jeśli nie popraw ZT.
Jakie są koszty transportu z farm do odbiorców uzyskane metodą kąta północno-zachodniego?
Spróbuj zmniejszyć koszty transportu stosując jeden raz metodę potencjałów. O ile zmniejszył się koszt
transportu? Czy koszt transportu można jeszcze zmniejszyć?
Jaki przychód uzyska Jacek z transakcji?

(wykorzystaj cenę sprzedaży z problemu 2, od ceny sprzedaży odejmij koszt transportu uzyskany metodą potencjałów}

PROBLEM 5

Przedsiębiorstwo produkuje dwa wyroby: W

1

i W

2

. W procesie produkcji tych wyrobów zużywa się wiele

środków, spośród których dwa są limitowane. Limity te wynoszą: środek I 96000 jedn., natomiast środek II

80000 jedn. Nakłady limitowanych środków na jednostkę wyrobów W

1

i W

2

podano w tablicy

Tablica

Środki

Jednostkowe nakłady

produkcji

W

1

W

2

I 16 24
II 16 10

Wiadomo także, że zdolności produkcyjne jednego z wydziałów, stanowiącego wąskie gardło procesu

produkcyjnego, nie pozwalają produkować więcej niż 3000 szt. wyrobów W

1

oraz 4000 szt. wyrobów W

2

.

Ponadto, działająca w ramach przedsiębiorstwa komórka analizy rynku ustaliła optymalne proporcje produkcji,

które kształtują się odpowiednio jak 3 :2. Cena sprzedaży (W zł) jednostki wyrobu W

1

wynosi 30, a wyrobu W

2

— 40. Ustalić rozmiary produkcji przy założeniu, że uzyskany przychód ze sprzedaży będzie maksymalny.