1

C3

Projektowanie algorytmów z blokami decyzyj-

nymi

wiczenie 1.

Skonstruowa brakuj ce schematy blokowe i opracowa algorytmy w po-
staci listy kroków dla poni szych algorytmów zapisanych w j zyku
Java.

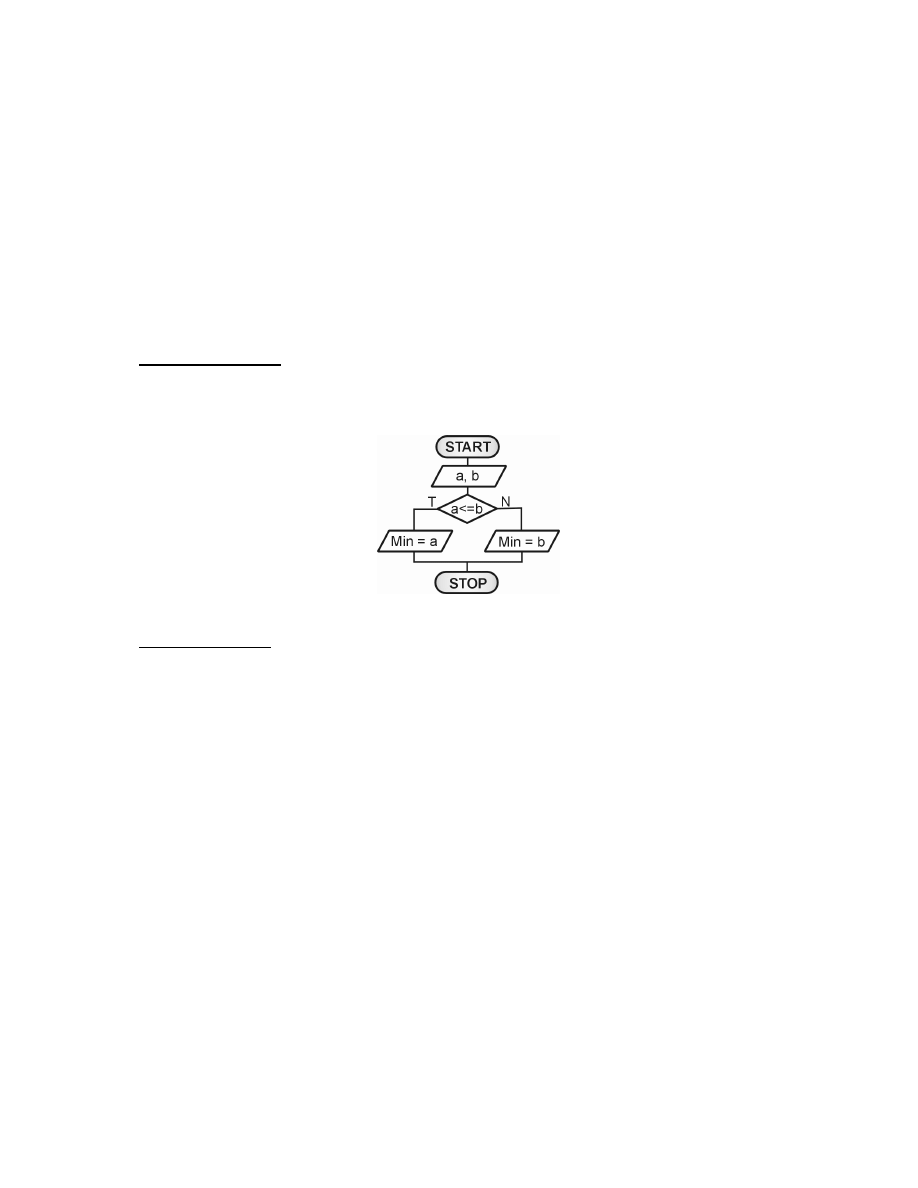
Rys. 3.1. Wyszukiwanie mniejszej spo ród dwóch liczb a, b.

Algorytm 3.1.

import javax.swing.JOptionPane;
public class BlokDecyzyjny {

public static void main(String[] args) {

double a,b;

String dane1 = JOptionPane.showInputDialog("Podaj a = ");

a = Double.parseDouble(dane1);

String dane2 = JOptionPane.showInputDialog("Podaj b = ");

b = Double.parseDouble(dane2);

System.out.println("Badane liczby:");

System.out.println(" a = " + a);

System.out.println(" b = " + b);

if(a <= b){

System.out.println("Najmniejsz liczb jest a" );

}

else{

System.out.println("Najmniejsz liczb jest b" );

}

}
}

2

Algorytm 3.2.

import javax.swing.JOptionPane;

public class LiczbaParzysta {

public static void main(String[] args) {

int r = 0;

int x;

String dane = JOptionPane.showInputDialog("Podaj liczb

naturaln wi ksz od zera x = ");

x = Integer.parseInt(dane);

System.out.print("Badana liczba x = " + x);

r = x % 2;

if(r == 0){

System.out.println(" jest parzysta.");

}

else{

System.out.println(" nie jest parzysta.");

}

}
}

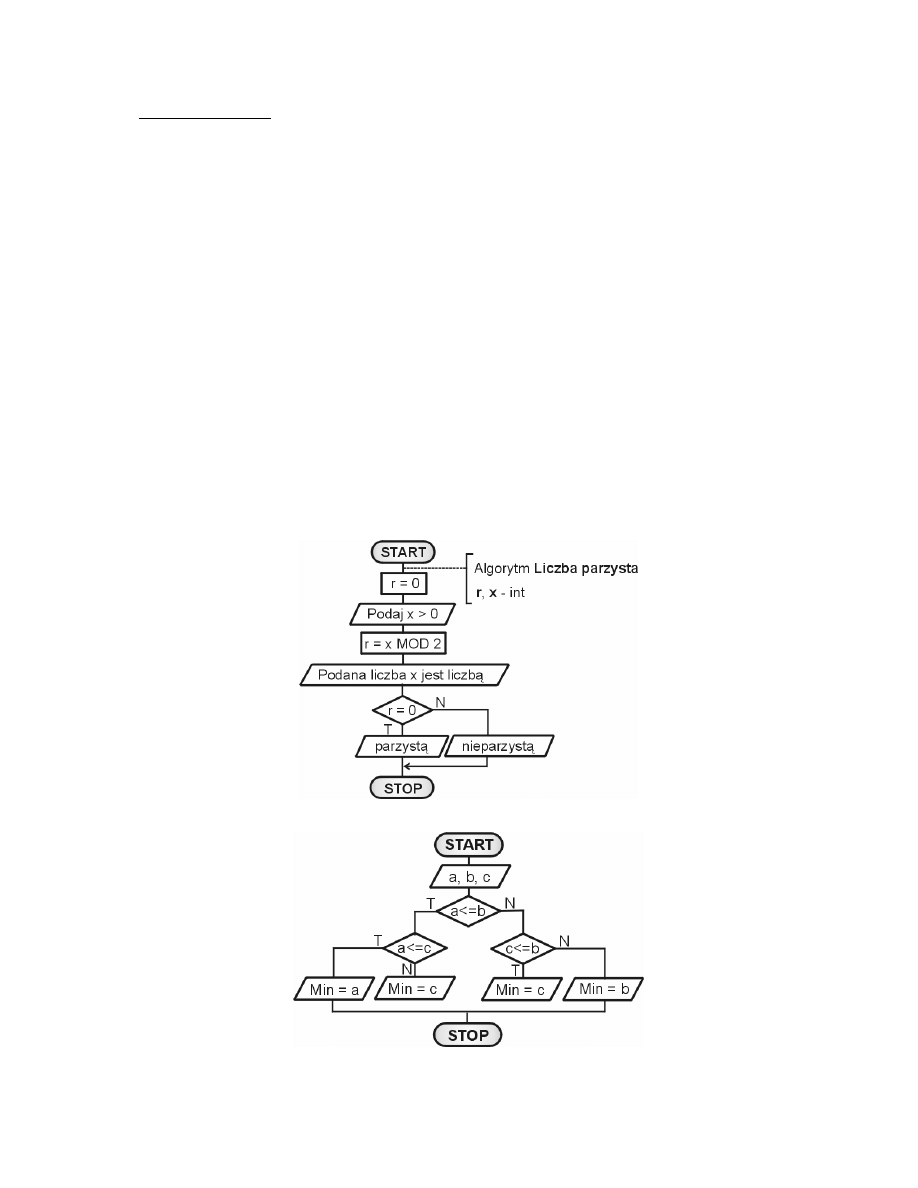
Rys. 3.2. Schemat badania parzysto ci liczb

Rys. 3.3. Wyszukiwanie najmniejszej spo ród trzech liczb a, b, c.

3

Algorytm 3.3.

import javax.swing.JOptionPane;
public class BlokDecyzyjny_1 {

public static void main(String[] args) {

double a,b,c;

String dane1 = JOptionPane.showInputDialog("Podaj a = ");

a = Double.parseDouble(dane1);

String dane2 = JOptionPane.showInputDialog("Podaj b = ");

b = Double.parseDouble(dane2);

String dane3 = JOptionPane.showInputDialog("Podaj c = ");

c = Double.parseDouble(dane3);

System.out.println("Badane liczby:");

System.out.println(" a = " + a);

System.out.println(" b = " + b);

System.out.println(" c = " + c);

if(a <= b){

if(a <= c){

System.out.println("Najmniejsz liczb jest a");

}

else{

System.out.println("Najmniejsz liczb jest c" );

}

}

else if(c <=b){

System.out.println("Najmniejsz liczb jest c" );

}

else{

System.out.println("Najmniejsz liczb jest b" );

}

}
}

Rys. 3.4. Instrukcja warunkowa IF … ELSE IF

4

Algorytm 3.4.

import javax.swing.JOptionPane;
public class BlokDecyzyjny_4 {

public static void main(String[] args) {

double a,b,c;

String dane1 = JOptionPane.showInputDialog("Podaj a = ");

a = Double.parseDouble(dane1);

String dane2 = JOptionPane.showInputDialog("Podaj b = ");

b = Double.parseDouble(dane2);

String dane3 = JOptionPane.showInputDialog("Podaj c = ");

c = Double.parseDouble(dane3);

System.out.println("Badane liczby:");

System.out.println(" a = " + a);

System.out.println(" b = " + b);

System.out.println(" c = " + c);

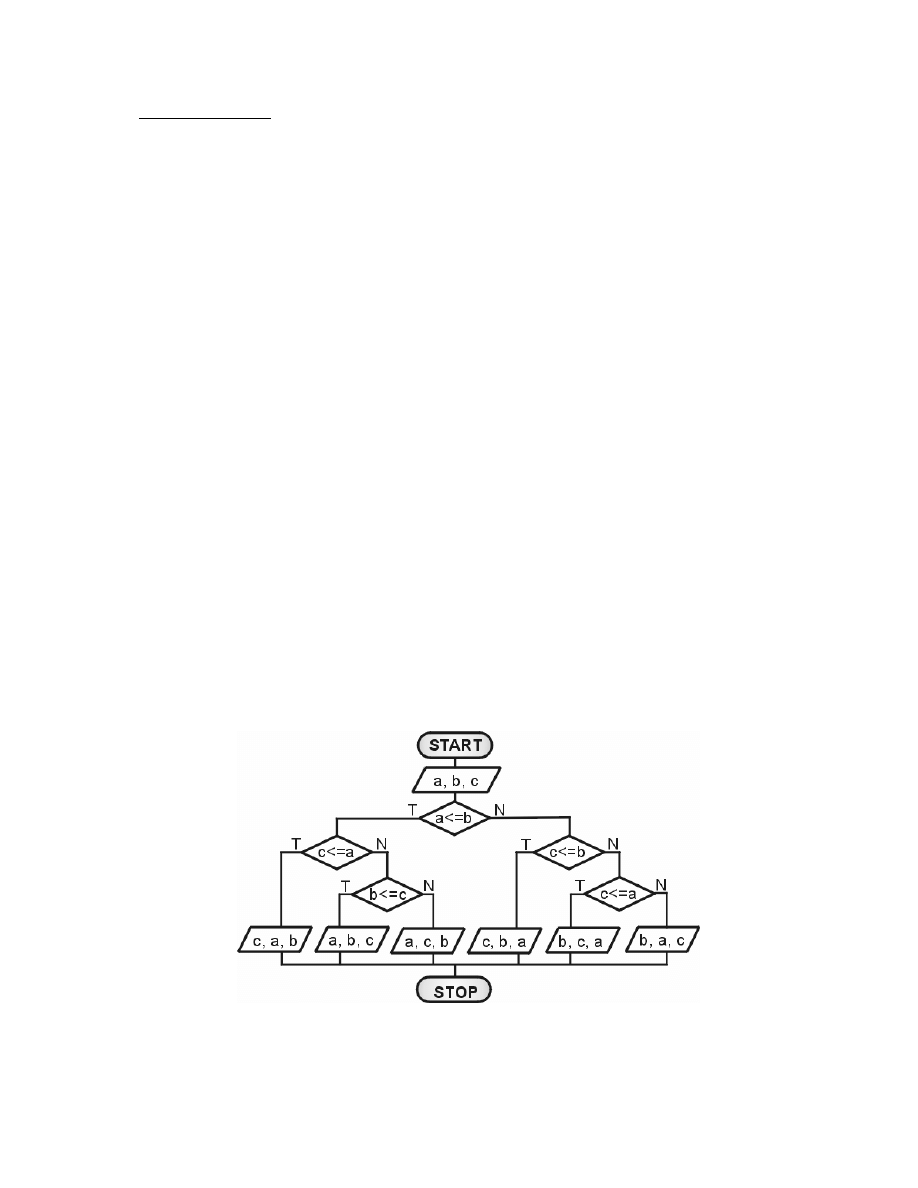
if(a <= b ){

if(c <= a){

System.out.println("Kolejno

rosn ca: c, a, b." );

}

else if(b <= c){

System.out.println("Kolejno

rosn ca: a, b, c." );

}

else{

System.out.println("Kolejno

rosn ca: a, c, b." );

}

}

else if(c <= b){

{

System.out.println("Kolejno

rosn ca: c, b, a." );

}

}

else if(c <= a){

System.out.println("Kolejno

rosn ca: b, c, a." );

}

else{

System.out.println("Kolejno

rosn ca: b, a, c." );

}

}

}

W

W

y

y

n

n

i

i

k

k

i

i

t

t

e

e

s

s

t

t

o

o

w

w

a

a

n

n

i

i

a

a

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

1

1

.

.

0

0

b

b

=

=

2

2

.

.

0

0

c

c

=

=

3

3

.

.

0

0

K

K

o

o

l

l

e

e

j

j

-

-

n

n

o

o

r

r

o

o

s

s

n

n

c

c

a

a

:

:

a

a

,

,

b

b

,

,

c

c

.

.

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

1

1

.

.

0

0

b

b

=

=

3

3

.

.

0

0

c

c

=

=

2

2

.

.

0

0

K

K

o

o

l

l

e

e

j

j

-

-

n

n

o

o

r

r

o

o

s

s

n

n

c

c

a

a

:

:

a

a

,

,

c

c

,

,

b

b

.

.

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

2

2

.

.

0

0

b

b

=

=

1

1

.

.

0

0

c

c

=

=

3

3

.

.

0

0

K

K

o

o

l

l

e

e

j

j

-

-

n

n

o

o

r

r

o

o

s

s

n

n

c

c

a

a

:

:

b

b

,

,

a

a

,

,

c

c

.

.

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

2

2

.

.

0

0

b

b

=

=

3

3

.

.

0

0

c

c

=

=

1

1

.

.

0

0

K

K

o

o

l

l

e

e

j

j

n

n

o

o

r

r

o

o

s

s

n

n

c

c

a

a

:

:

c

c

,

,

a

a

,

,

b

b

.

.

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

3

3

.

.

0

0

b

b

=

=

1

1

.

.

0

0

c

c

=

=

2

2

.

.

0

0

K

K

o

o

l

l

e

e

j

j

n

n

o

o

r

r

o

o

s

s

n

n

c

c

a

a

:

:

b

b

,

,

c

c

,

,

a

a

.

.

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

3

3

.

.

0

0

b

b

=

=

2

2

.

.

0

0

c

c

=

=

1

1

.

.

0

0

K

K

o

o

l

l

e

e

j

j

-

-

n

n

o

o

r

r

o

o

-

-

s

s

n

n

c

c

a

a

:

:

c

c

,

,

b

b

,

,

a

a

.

.

5

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

1

1

.

.

0

0

b

b

=

=

1

1

.

.

0

0

c

c

=

=

1

1

.

.

0

0

K

K

o

o

l

l

e

e

j

j

-

-

n

n

o

o

r

r

o

o

s

s

n

n

c

c

a

a

:

:

c

c

,

,

a

a

,

,

b

b

.

.

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

1

1

.

.

0

0

b

b

=

=

1

1

.

.

0

0

c

c

=

=

2

2

.

.

0

0

K

K

o

o

l

l

e

e

j

j

-

-

n

n

o

o

r

r

o

o

s

s

n

n

c

c

a

a

:

:

a

a

,

,

b

b

,

,

c

c

.

.

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

1

1

.

.

0

0

b

b

=

=

2

2

.

.

0

0

c

c

=

=

1

1

.

.

0

0

K

K

o

o

l

l

e

e

j

j

-

-

n

n

o

o

r

r

o

o

s

s

n

n

c

c

a

a

:

:

c

c

,

,

a

a

,

,

b

b

.

.

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

2

2

.

.

0

0

b

b

=

=

1

1

.

.

0

0

c

c

=

=

1

1

.

.

0

0

K

K

o

o

l

l

e

e

j

j

n

n

o

o

r

r

o

o

s

s

n

n

c

c

a

a

:

:

c

c

,

,

b

b

,

,

a

a

.

.

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

2

2

.

.

0

0

b

b

=

=

1

1

.

.

0

0

c

c

=

=

2

2

.

.

0

0

K

K

o

o

l

l

e

e

j

j

n

n

o

o

r

r

o

o

s

s

n

n

c

c

a

a

:

:

b

b

,

,

c

c

,

,

a

a

.

.

B

B

a

a

d

d

a

a

n

n

e

e

l

l

i

i

c

c

z

z

b

b

y

y

:

:

a

a

=

=

2

2

.

.

0

0

b

b

=

=

2

2

.

.

0

0

c

c

=

=

1

1

.

.

K

K

o

o

l

l

e

e

j

j

-

-

n

n

o

o

r

r

o

o

-

-

s

s

n

n

c

c

a

a

:

:

c

c

,

,

a

a

,

,

b

b

.

.

Algorytm 3.5.

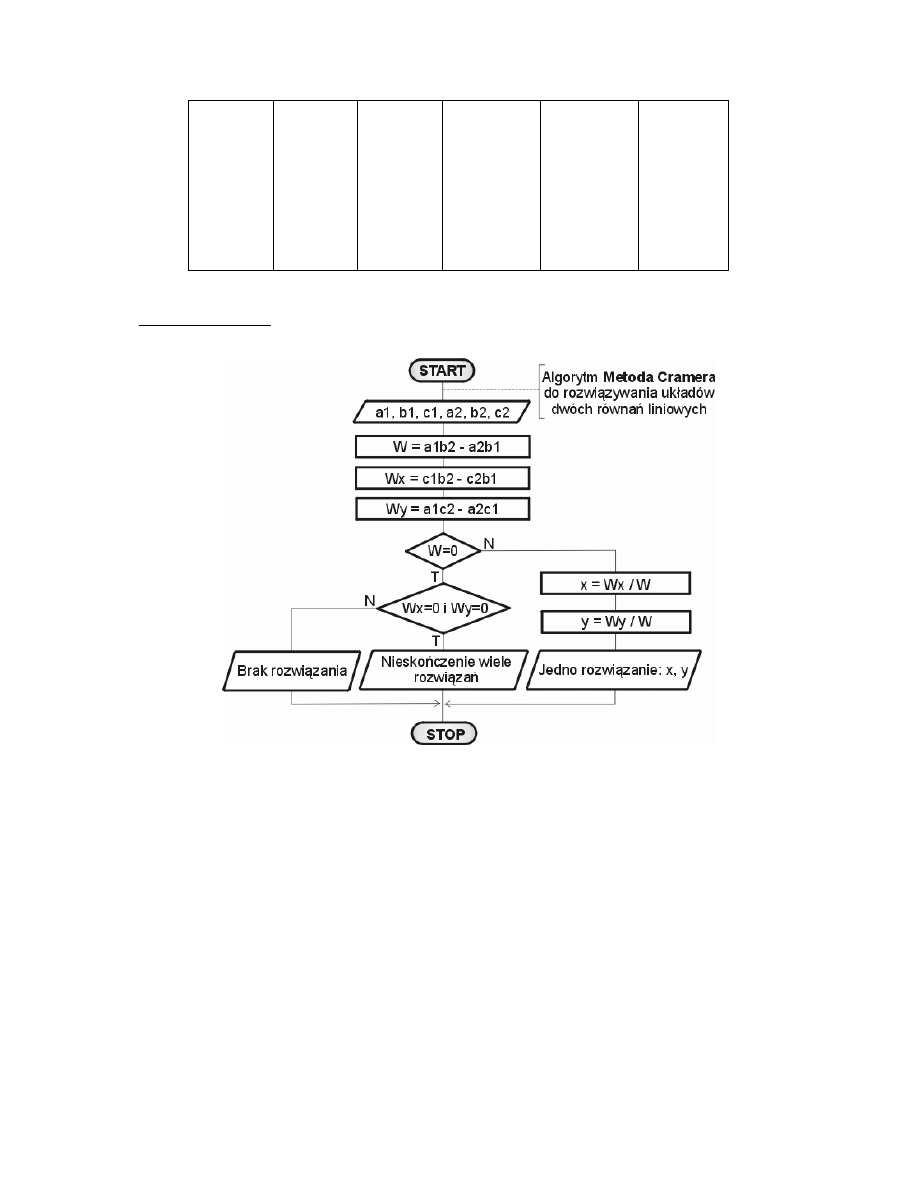
Rys. 3.5. Schemat blokowy rozwi zywania układu równa liniowych

metod wyznacznikow Cramera.

import javax.swing.JOptionPane;

public class MetodaCramera {
public static void main(String[] args) {

double a1, b1, c1, a2, b2, c2, Wx, Wy, W, x, y;

String wsp_a1 = JOptionPane.showInputDialog("a1 = ");

a1 = Integer.parseInt(wsp_a1);

String wsp_b1 = JOptionPane.showInputDialog("b1 = ");

b1 = Integer.parseInt(wsp_b1);

String wsp_c1 = JOptionPane.showInputDialog("c1 = ");

c1 = Integer.parseInt(wsp_c1);

String wsp_a2 = JOptionPane.showInputDialog("a2 = ");

a2 = Integer.parseInt(wsp_a2);

String wsp_b2 = JOptionPane.showInputDialog("b2 = ");

6

b2 = Integer.parseInt(wsp_b2);

String wsp_c2 = JOptionPane.showInputDialog("c2 = ");

c2 = Integer.parseInt(wsp_c2);

W = a1*b2 - a2*b1;

Wx = c1*b2 - c2*b1;

Wy = a1*c2 - a2*c1;

if(W == 0){

if(Wx == 0 && Wy == 0){

System.out.println("Układ równa ma niesko czenie wiele

rozwi za .");

}

else {

System.out.println("Układ równa sprzeczny - brak rozwi zania");

}

}

else{

x = Wx/W;

y = Wy/W;

System.out.println("Rozwi zaniem układu równa jest:");

System.out.println("x = " + x);

System.out.println("y = " + y);

}

}
}

Algorytm 3.6.

public class FunkcjaLiniowa {

public static void main(String[] args) {

System.out.println("Program oblicza miejsca zerowe funkcji liniowej");

double a = 1;

double b = 2;

if (a != 0) {

double x = -b / a;

System.out.println("Miejsce zerowe x = " + x);

}

else if (a ==0 && b == 0) {

System.out.println("Funkcja posiada niesko czenie wiele miejsc zerowych");

}

else if (a == 0 && b != 0) {

System.out.println("Funkcja nie posiada miejsc zerowych");

}

}

}

7

Algorytm 3.7.

public class RownaniaKwadratowe1 {

public static void main(String[] args) {

double a = 1;

if (a < 0){

System.out.println("Złe dane");

}

else{

double b = 1;

double c = 1;

double delta = b * b - 4 * a * c;

if (delta < 0){

System.out.println("Brak pierwiastków");

}

else if (delta == 0){

double x0 = -b / (2 * a);

System.out.println("Xo = " + x0);

}

else {

double x1 = (-b - Math.sqrt(delta))/(2 * a);

double x2 = (-b + Math.sqrt(delta))/(2 * a);

System.out.println("X1 = " + x1 + " X2 = " + x2);

}

}

}
}

Algorytm 3.8.

public class RownaniaKwadratowe2 {
public static void main(String[] args) {

System.out.println("Program oblicza miejsca zerowe funkcji

kwadratowej");

double a = 0;

double b = 0;

double c = 0;

double p =0;

double q = 0;

double delta = 0;

double del1 = 0;

double x0 = 0;

double x1 = 0;

double x2 = 0;

InputStreamReader strumien = new InputStreamReader(System.in);

BufferedReader wejscie = new BufferedReader(strumien);

try{

System.out.print("Podaj a = ");

a = Double.parseDouble(wejscie.readLine());

8

if (a != 0){

System.out.print("Podaj b = ");

b = Double.parseDouble(wejscie.readLine());

System.out.print("Podaj c = ");

c = Double.parseDouble(wejscie.readLine());

System.out.println("Współczynniki funkcji

kwadratowej:");

System.out.println("a= "+a+" b= " +b+" c= "+c);

}

else{

System.out.println("Funkcja liniowa");

}

}

catch(Exception e){

System.out.println("Wyst pił bł d");

return;

}

{

delta = b*b-4*a*c;

p = b/a;

q = c/a;

del1 = p*p-4*q;

System.out.println("delta = " +delta + " p= " +p + " q= "

+q + " del1 = " +del1);

}

if (delta >= 0){

if (del1 == 0){

x0 = -p/2;

System.out.println("Xo = " +x0);

if (p < 0){

x2 = (-p-Math.sqrt(del1))/2;

x1 = q/x2;

}

}

else{

x1 = (-p-Math.sqrt(del1))/2;

x2 = q/x1;

System.out.print("X1 = " +x1 + " X2 = " +x2);

}

}

else{

System.out.println("Brak miejsc zerowych");

}

}

}

9

ZADANIA DO SAMODZIELNEGO WYKONANIA

ZADANIE 1.

Skonstruowa schematy blokowe, opracowa algorytmy w postaci listy
kroków oraz w postaci kodu w j zyku C

++

dla poni szego algorytmu za-

pisanego w j zyku Java.

Algorytm 3.9.

import javax.swing.JOptionPane;
public class BlokDecyzyjny_3 {
public static void main(String[] args) {

int dzien;

String dane1 = JOptionPane.showInputDialog("Podaj dzie

tygodnia (1 - 7): ");

dzien = Integer.parseInt(dane1);

System.out.print("Wybrano ");

if(dzien == 1){

System.out.print("niedziel .");

}

else if(dzien == 2){

System.out.print("poniedziałek.");

}

else if(dzien == 3){

System.out.print("wtorek.");

}

else if(dzien == 4){

System.out.print(" rod .");

}

else if(dzien == 5){

System.out.print("czwartek.");

}

else if(dzien == 6){

System.out.print("pi tek.");

}

else if(dzien == 7){

System.out.print("sobot .");

}

}

}

ZADANIE 2.

Skonstruowa schemat blokowy, opracowa algorytmy w postaci listy

kroków oraz w postaci kodu w j zyku C

++

do:

a)

Wyznaczania miejsc zerowych funkcji liniowej.

b)

Rozwi zywania układów równa liniowych z trzema niewiadomymi.

c)

Rozwi zywania równa kwadratowych według tzw. „algorytmu szkol-
nego”.

d)

Rozwi zywania równa kwadratowych według algorytmu stabilnego
numerycznie.

e)

Porz dkowania czterech liczb.

f)

Obliczania warto ci wyra e wymiernych W(x)=P(x)/Q(x) dla zada-
nej warto ci x.