
TWIERDZENIE de l’HOSPITALA
Obliczyć granice funkcji.
1.
2
ln
lim
x
x
x
2.
1
1
1
6
lim
x
x
x
3.
4
1024
2
2
10
lim
x
x
x
4.
x
x
x
cos
1
3
0
2
lim
5.
4
2
2
1
1
cos
0
lim
x
x
x
x
6.
)
(
lim
1
sin
1
0
x
x
x
7.
tgx
x
x
ln
0
lim
8.
)
(
lim
ln
1
1
1
1
x
x
x
9.
x
x
tgx
x
cos
sin
1
4
lim
10.
x
x
x
ln
1
1
2
lim
11.
3
1
,
0
lim
x
e
x
x
12.
x
e
e
x
x
x
7
sin
0
4
lim
13.
2
2
1
1
1
0
lim
x
x
x
x
14.
x
x
x
x
sin
3
sin
5
sin
0
lim
15.
)
1
(
2
0
lim
x
e
ctgx
x
16.
3
cos
sin
0
lim
x
x
x
x
x
17.
x
x
e
e
x
x
x
x
sin
0
2
lim
18.
3
2
2
1
)
1
ln(
0
lim
x
x
x
x
x
19.
x
x
x
4
cos
1
3
cos
1
0
lim
20.
x
x
x
ln
2
0
lim
21.
)
1
1
1
0
(
lim
x
e
x
x
22.
x
x
x
x
x
cos
2
sin
1
sin
cos
2
lim
23.
x
xe
x
lim
24.
x
x
x
cos
1
0
lim
25.
x
x
x
5
1
3
0
lim
26.
2
)
(
lim
x
x
tg
x
27.
x
x
e
x
x
5
sin
1
3
0
2
3
lim
28.
x
x
x
x
3
3
0
lim
29.
tgx
x
x
)
(
lim
2
1
0
30.
ctgx
x
x)
sin
1
(
lim
0
31.
5
1
)
4
(
lim
5
x
x
x
32.
x
x
e
x
x
1
2
0
lim
33.
x
x
x
ln
2
1
8
0
lim
34.
)
3
3
5
(
)
2
sin(
0
lim
x
arctg
x
x
Odpowiedzi.
1. 0
2. 6
3. 1280
4. 6
5.
24
1
6. 0
7. 0
8.
2
1
9.
2
10. 2
11.
12.
7
3
13.
8
1
14. 2
15. 2 16.
3
1
17. 2
18.
3
1
19.
16
9
20. 0
21.
2
1
22. 1
23. 0
24.
2
1
25.
5
3
ln
26. 2
27.
50
9
28.
3
1
29. 1
30. e
31. e
32.
3
e
33.
4
e
34.
5
2
WYKRES FUNKCJI
Narysować wykres funkcji spełniającej warunki:
1.
)
(
lim
x
f
x
,
)
(
lim
0
x
f
x
,
1
)
(
lim
0
x
f
x
,
5
)
(
lim
x
f
x
2.
4
)
(
lim
x
f
x
,
)
(
lim
1
x
f
x
,
4
)
(
lim
x
f
x
3.
)
(
lim
0
x
f
x
,
1
)
)
(
(
lim
x
x
f
x
,
)
(x
f
jest parzysta
4.
0
)
(
' x
f
dla
2
x
,
)
2
(
'
f
5.
0
)
(
' x
f
dla
3
x
,
0
)
3
(
'
f
6.
0
)
(
' x
f
dla
R
x
,
2
)
(
lim
x
f
x
7.
0
)
(
' x
f
dla
1
x
,
0
)
(
' x
f
dla
1
x
,
)
1
(
'
f
nie istnieje
8.
0
)
(
' x
f
dla
2
x
,
0
)
2
(
'
f
Odpowiedzi na odwrocie (przykładowe).
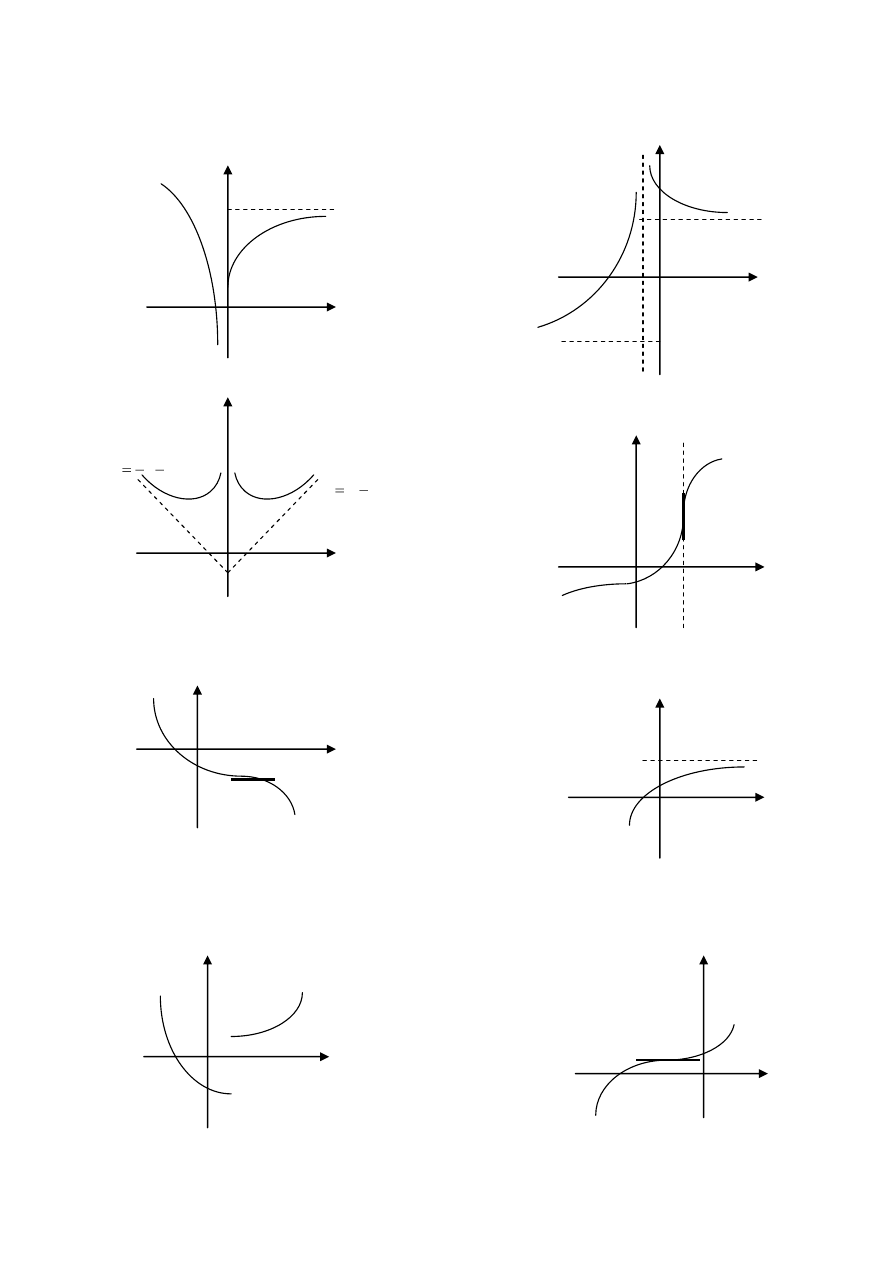
WYKRES FUNKCJI
1.
2.
5
4
1
-1
-4
3.
4.
1
x
y
1
x
y
2
5.
6.
3
2
7.
8.
1
-
2
Wyszukiwarka
Podobne podstrony:
Healthcare Karolinska Hospital Nieznany
AMI 22 Regula De L'Hospitala i Nieznany (2)
A5[1] Feuillade i pierwsze ser Nieznany (2)
Hospital Guidance document Nieznany
hospital i asymptoty id 206201 Nieznany
a5 zszywka Podajnik01 id 49836 Nieznany (2)
12 5 Energia jadrowa [v1 2] A5 Nieznany (2)
populacja hospitacja ppt
Gor±czka o nieznanej etiologii
02 VIC 10 Days Cumulative A D O Nieznany (2)
Abolicja podatkowa id 50334 Nieznany (2)
45 sekundowa prezentacja w 4 ro Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
Mechanika Plynow Lab, Sitka Pro Nieznany
katechezy MB id 233498 Nieznany
2012 styczen OPEXid 27724 Nieznany
metro sciaga id 296943 Nieznany
więcej podobnych podstron