1/4
OBLICZANIE PRZEPUSTÓW
Procedura:
1. Obliczenia hydrologiczne – dla cieku, na którym projektowane są przepusty
dla przekroju cieku w miejscu konstrukcji przepustów. Wykonuje się w celu
określenia przepływów miarodajnych i miarodajnej prędkości wody.
Obliczenia te są niezbędne do wykonania obliczeń hydraulicznych.
2. Obliczenia hydrauliczne - określenie parametrów przepustu tj. światła
przepustu (średnica przepustu kołowego, wysokość i szerokość przepustu
kwadratowego, sposobu umocnienia skarp i dna przepustu na wlocie i
wylocie.
OBLICZENIA HYDROLOGICZNE
W przypadku braku wyników obserwacji hydrologicznych (tak jest najczęściej)
stosuje się różne wzory empiryczne do obliczeń hydrologicznych.
1. Przepływy miarodajne (charakterystyczne) w obliczeniach wodno-
melioracyjnych w tym do obliczania przepustów to:
Przepływ średni normalny - Q
2
(SQ),
Przepływ wysoki roczny Q
3
(NWQ).
Przepływ (Q
2
) występuje przeciętnie w wieloleciu w okresie ok. 9 miesięcy w
roku poza przepływami wyżówkowymi okresu zimowo-wiosennego i niekiedy
letniego rzadko występujących w małych zlewniach melioracyjnych oraz
niżówkami okresu letniego. Przepływ wysoki roczny w małych zlewniach
nizinnych występuje na ogół w okresie zimowo-wiosennym (Q
3Z
) oraz
niekiedy w okresie wezbrań letnich (Q
3L
).
2. Obliczenie przepływu Q
2
wg wzorów empirycznych Iszkowskiego:
─ Obliczyć przepływ Q
s
przepływ absolutnie średni z normalnego roku na
podstawie sparametryzowanych cech zlewni.
─ Obliczyć przepływ Q
2
na podstawie wartości przepływu Q
s
(SNQ) i
sparametryzowanych cech zlewni
3. Obliczenie przepływu Q
3
wg wzoru empirycznego Lewego na podstawie
sparametryzowanych cech zlewni.
Oblicza się również przepływy o określonym prawdopodobieństwie
wystąpienia (w zależności od rodzaju budowli) np. dla przepustów 25, 10, 5,
2, 1%.
2/4
WZORY
Obliczenie przepływów miarodajnych (charakterystycznych):
1. Przepływ Q
s
przepływ absolutnie średni z normalnego roku
3
0,0317
s
s
m
Q
C
h A
s
A - Powierzchnia zlewni [km
2
]
H - normalny opad roczny m
C
s
= współczynnik empiryczny zależny od rzeźby terenu
C
s
= 0,20 (obszary równinne płaskie bagienne)
C
s
= 0,25 (obszary równinne płaskie)
C
s
= 0,30 (obszary równinne płaskie i równiny faliste)
C
s
= 0,35 (obszary równinne pagórkowate niespadziste, morenowe)
2. Przepływ Q
2
przepływ średni normalny
2
3
0,7
s
m
Q
V Q
s
Q
s
- przepływ absolutnie średni z normalnego roku
H - normalny opad roczny m
V – współczynnik empiryczny zależny od rzeźby terenu, przepuszczalności gruntu
i wielkości zlewni
V = 1,5 na równinie przy odpływie przez jeziora i stawy
V = 1,0 na równinie bez jezior i stawów
V = 0,8 teren falisty
V = 0,6-0,5 teren pagórkowaty (wybrać 0,6 do zadania)
W przypadku zlewni o powierzchni mniejszej niż 200 km2 współczynnik V
zmniejsza się o 0,25
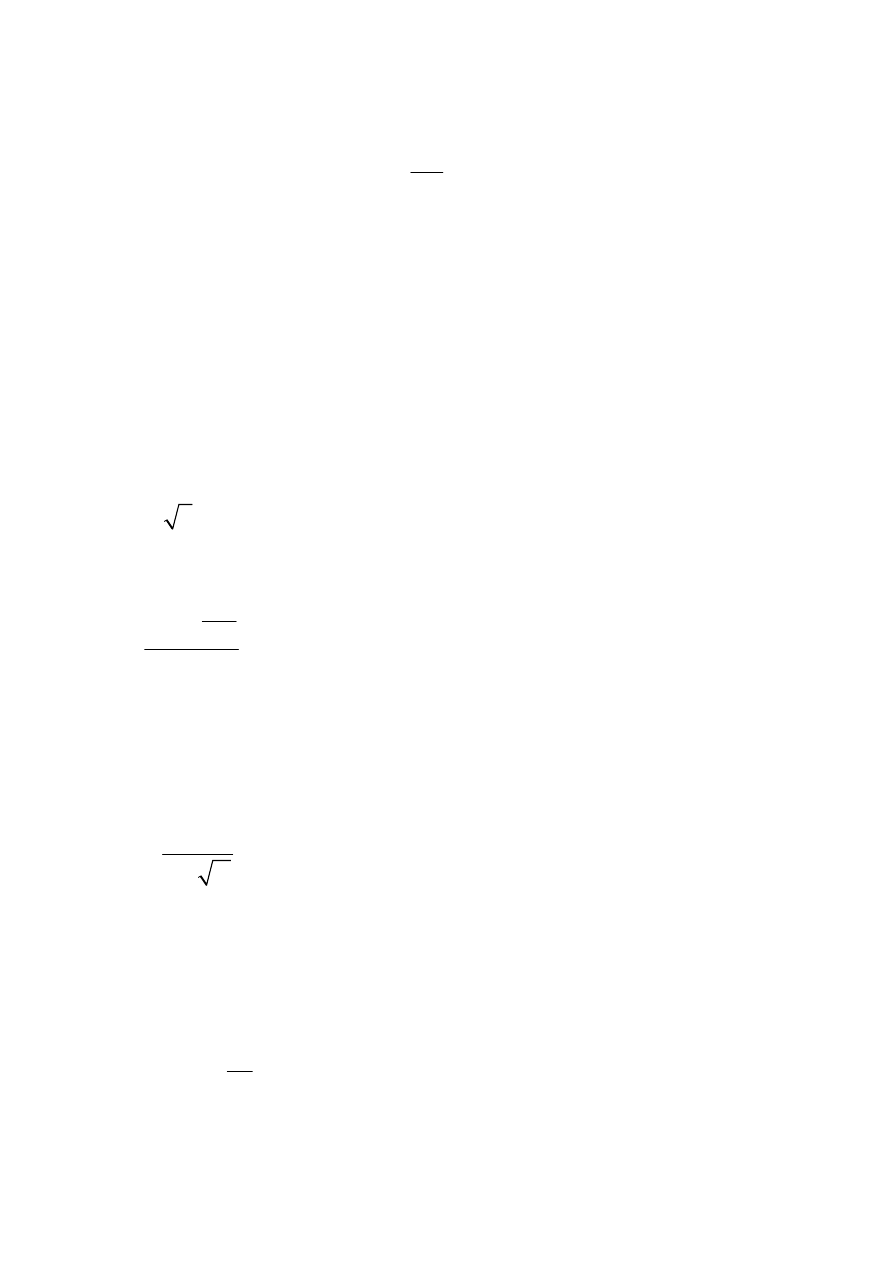
3/4
3. Przepływ Q
3
przepływ wysoki roczny (zimowy)
3
3
1
2
3
4
m
Q
K
K
K
K
h A
s
H – opady z miesięcy styczeń-marzec ok. (I-III), przyjąć 0,15 opadów rocznych
K
1-4
– współczynniki zależne od cech fizyczno-geograficznych zlewni
K
1
– współczynnik zależny od reliefu, pokrycia terenu i przepuszczalności gruntu
K
1
= 3,0 grunty piaszczyste równinne łąki, tereny zakrzaczone
K
1
= 2,0 grunty piaszczyste równinne lasy
K
1
= 3,75 grunty gliniaste faliste łąki, tereny zakrzaczone
K
1
= 3,5 grunty gliniaste faliste lasy
K
2
– zależny od przeciętnego spadku zlewni
4
2
K
I
I – przeciętny spadek w zlewni [‰]
2
pp
pd
i
i
n
I
[‰]
I
pd
– spadek podłużny
I
pp
– spadek poprzeczny
n – liczba pomiarów spadku poprzecznego
K
3
– zależny od powierzchni zlewni
3
3
10
9
K
A
A – powierzchnia zlewni [km
2
]
K
4
– współczynnik zależny od jeziorności zlewni wyrównującej przepływ dla
obszarów bezjeziornych K
4
= 1
1
4
1
A
K
A
A - powierzchnia zlewni [km
2
]
4/4
A
1
- powierzchnia zlewni jezior [km
2
]
– współczynnik zależny od stosunku powierzchni jezior w zlewni (a) i
powierzchni zlewni jezior (A
1
)
1
a
A
jest stabelaryzowany. Dla obszarów
bezjeziornych
=0.