ZASADA FERMATA
Promienie świetlne poruszają się zawsze po takich drogach, aby czas ich przejścia
pomiędzy dwoma danymi punktami był najkrótszy
Światło biegnie z punktu A do punktu B. Chcemy odnaleźć krzywą, po której się ono
porusza. Załóżmy, że mamy dwa ośrodki optyczne o bezwzględnym współczynniku
załamania N1 N2 . Wtedy prędkość światła w każdym z tych ośrodków wynosi
odpowiednio:
Oznaczmy przez x punkt, w którym światło przechodzi przez granicę dwóch ośrodków
(najszybszą drogą dotarcia do tego punktu w jednorodnym ośrodku jest linia prosta).
Czas potrzebny na przebycie tej drogi to:
gdzie a jest odległością między punktami A i B mierzoną w poziomie wzdłuż granicy
ośrodków. Stacjonarność rozwiązania wymaga zerowania się pierwszej pochodnej
czasu po x
28)Interferometr Michelsona
Interferometr składa się z
monochromatycznego źródła światła
półprzepuszczalnej
zwierciadeł A i B ,
równych odległościach
miejsca padania wiązki światła na płytkę
P .
Na ustawioną pod kątem
pada wiązka światła ze źródła
ulega rozszczepieniu na dwie wiązki
biegnące wzajemnie prostopadle do
zwierciadeł A i B .
wiązki te wracają do płytki
ponownie ulegają rozszczepieniu, i część wraca do źródła S,
razem do teleskopu T. Na drodze PT w zależności od relacji między odległościami AP i
Bp promienie interferują dając jasne i ciemne prążki. Obraz interferencyjny oglądany
jest w głównej płaszczyźnie ogniskowej detektora T . Zakładamy że zwierciadła są
idealnie prostopadłe a ogległości dokładnie równe. Wówczas w centrum obrazu w
detektorze wystąpi maksimum interferencyjne. Zmieniając położenie zwierciadła B
możemy w obszar centralny wprowadzić kolejne jasne lub ciemne prążki. Warunkiem
wystąpienia maksimum jest, to aby różnica dróg obydwóch promieni
wielokrotnością długości fali czyli:
D = 2(lb - la) = k l (k = 0, 1, 2, ..., n
gdzie: l długość fali światła monochromatycznego. f jest kątem padania (od
normalnej) promieni światła na zwierciadło B. l = 589nm, 10 prążków
Efekt halla to zjawisko fizyczne, odkryte w 1879 roku przez Edwina H. Halla).
Jest to w gruncie rzeczy recepta na okreslenie znaku ładunków
plynacych w przewodniku. W przewodniku miedzianym w formie paska,
umieszczonym w prostopadlym polu magnetycznym o indukcji B plynie prad i. Prad
ten jest przenoszony przez ladunki dodatnie (lewy pasek), lub ujemne (prawy pasek).
Sila dzialajaca na ladunki:
bedzie je odchylala w prawa
strone niezaleznie od tego, czy sa to ładunki dodatnie, czy ujemne. Odchylenie to
spowoduje powstanie poprzecznej róznicy potencjalów Halla V
X i Y. Teraz, znak ladunków bedzie okreslony przez znak róznicy potencjalów. Jesli
plynace w przewodniku ladunki maja znak dodatni, to potencjal w punkcie Y
wyzszy niz w punkcie X. Jesli ladunki maja znak ujemny, potencjal w
nizszy niz w X. Eksperymenty pokazaly, ze realizowana jest druga opcja. Stanowi to
potwierdzenie opinii, ze w metalach nosnikami pradu sa ladunki ujemne.
Promienie świetlne poruszają się zawsze po takich drogach, aby czas ich przejścia
Światło biegnie z punktu A do punktu B. Chcemy odnaleźć krzywą, po której się ono
porusza. Załóżmy, że mamy dwa ośrodki optyczne o bezwzględnym współczynniku
. Wtedy prędkość światła w każdym z tych ośrodków wynosi
punkt, w którym światło przechodzi przez granicę dwóch ośrodków
(najszybszą drogą dotarcia do tego punktu w jednorodnym ośrodku jest linia prosta).
ą w poziomie wzdłuż granicy
ośrodków. Stacjonarność rozwiązania wymaga zerowania się pierwszej pochodnej
28)Interferometr Michelsona-Morleya
Interferometr składa się z
monochromatycznego źródła światła S,
półprzepuszczalnej
płytki P, oraz dwóch
B , ustawionych w
równych odległościach PA = PB = l od
miejsca padania wiązki światła na płytkę
Na ustawioną pod kątem 45o płytkę P
pada wiązka światła ze źródła S , która
ulega rozszczepieniu na dwie wiązki
biegnące wzajemnie prostopadle do
B . Po odbiciu się od A i B,
wiązki te wracają do płytki P, gdzie
S, a pozostała część biegnie
w zależności od relacji między odległościami AP i
braz interferencyjny oglądany
Zakładamy że zwierciadła są
padłe a ogległości dokładnie równe. Wówczas w centrum obrazu w
detektorze wystąpi maksimum interferencyjne. Zmieniając położenie zwierciadła B
możemy w obszar centralny wprowadzić kolejne jasne lub ciemne prążki. Warunkiem
różnica dróg obydwóch promieni D była całkowitą
k = 0, 1, 2, ..., n)
jest kątem padania (od
l = 589nm, 10 prążków
to zjawisko fizyczne, odkryte w 1879 roku przez Edwina H. Halla).
ładunków elektrycznych
W przewodniku miedzianym w formie paska,
prostopadlym polu magnetycznym o indukcji B plynie prad i. Prad
przenoszony przez ladunki dodatnie (lewy pasek), lub ujemne (prawy pasek).
bedzie je odchylala w prawa
dodatnie, czy ujemne. Odchylenie to
róznicy potencjalów Halla V
xy
pomiedzy punktami
ladunków bedzie okreslony przez znak róznicy potencjalów. Jesli
i, to potencjal w punkcie Y będzie
wyzszy niz w punkcie X. Jesli ladunki maja znak ujemny, potencjal w punkcie Y bedzie
jest druga opcja. Stanowi to
a ladunki ujemne.
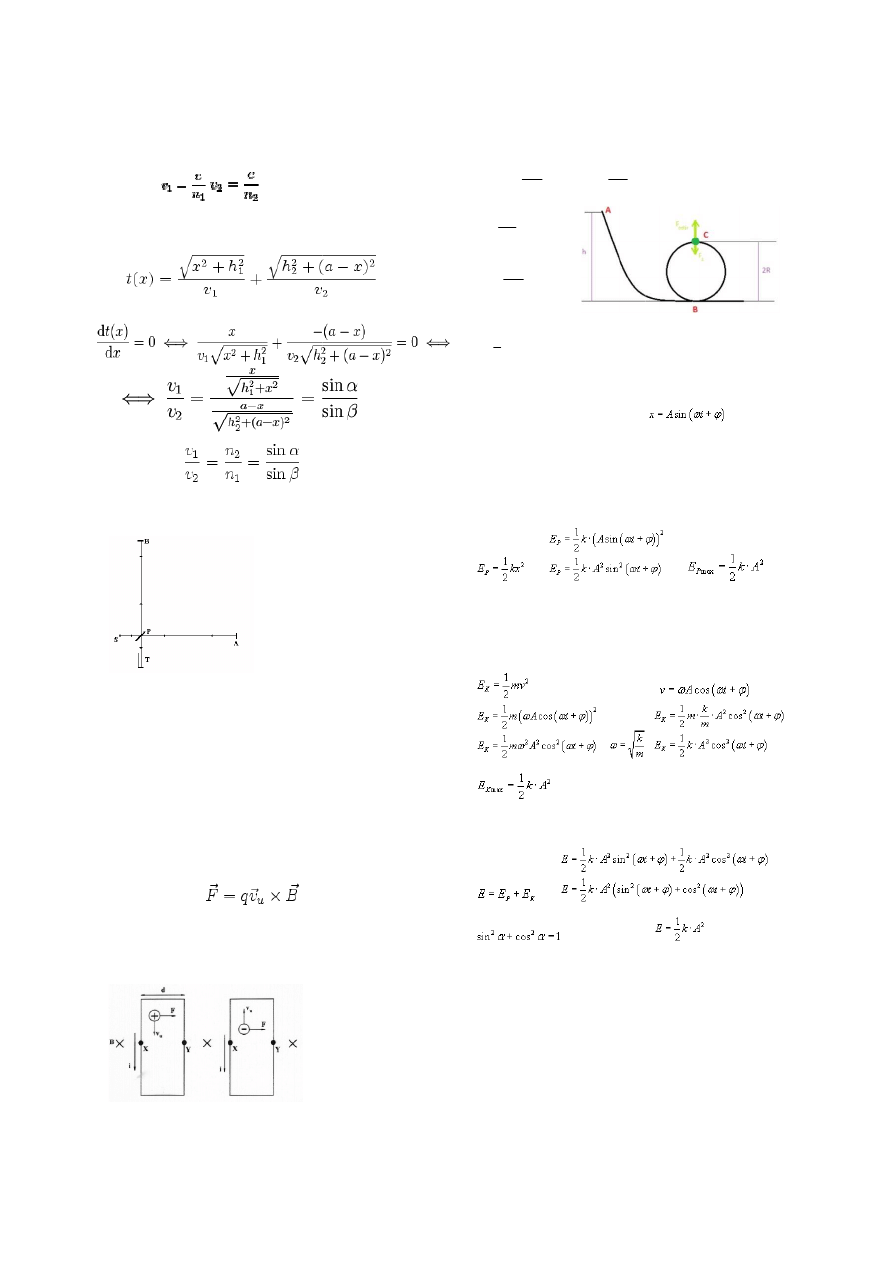
7) Zasada zachowania energii(Pętla śmierci)
W układzie izolowanym: ΔE
K
+ ΔE
P
+ Q + (zmiana innych form energii) =0
W układzie takim energia może być przekształcona z jednej formy w inną, ale nie
może być stworzona ani niszczona.
A: E
A
= E
P
= mgh
B: E
B
= E
K
=
2
2
c
mv
C: E
C
=
2
2
c
mv
+2mgR
Aby ciało w najwyższym punkcie C nie oderwało
warunek:
mg
R
mv
F
c
od
≥
=
2
(*)
Z zasady zachowania energii:
E
A
= E
C
mgh =
2
2
c
mv
+2mgR
2gh =
gR
v
c
4
2
+
gR
gh
v
c
4
2
2
−
=
wstawiamy do (*) i otrzymujemy:
R
h
2
5
≥
Wyprowadzić wzór na Ek, Ep i całkowitą energię mechaniczną w ruchu
harmonicznym sprężyny x=Acos(wt).
W ruchu harmonicznym prostym o wychyleniu
w którym nie występują żadne siły rozpraszające (np. tarcie), całkowita energia
mechaniczna jest zachowana (pozostaje stała). Całkowita energia to suma energii
potencjalnej i kinetycznej.
A. Energia potencjalna
Ciało drgające ruchem harmonicznym prostym posiada energię potencjalną wtedy,
gdy znajduje się ono w jakimś wychyleniu od stanu równowagi. Gdy ciało znajduje się
więc w położeniu równowagi, nie posiada energii potencjalnej.
Energia potencjalna jest równa energii potencjalnej sprężystości, którą możemy
wyrazić wzorem:
i ciało ma tę energię wtedy, gdy znajduje się w położeniu maksymalnego wychylenia
(amplitudy).
B. Energia kinetyczna
Ciało o masie m drgające ruchem harmonicznym pros
wtedy, gdy posiada ono jakąś prędkość v w danej chwili. Oznacza to, że ciało nie
posiada energii kinetycznej wtedy, gdy prędkość równa jest zeru, a taki moment
następuje, gdy ciało znajduje się w położeniu maksymalnego wychyl
Energię kinetyczną wyrażamy wzorem:
Ponieważ w ruchu harmonicznym:
Maksymalna wartość energii kinetycznej wynosi
i mamy z nią do czynienia, gdy drgające ciało ma największą prędkość (a jak wiemy,
ma ono ją wtedy, gdy znajduje się w punkcie równowagi
C. Energia mechaniczna
Przypominam, że energia mechaniczna w danym momencie jest równa:
Korzystając z zależności trygonometrycznej
mamy ostatecznie:
Całkowita energia punktu materialnego poruszającego się ruchem harmonicznym
prostym jest proporcjonalna do kwadratu amplitudy tego ruchu.
+ Q + (zmiana innych form energii) =0
W układzie takim energia może być przekształcona z jednej formy w inną, ale nie
+2mgR
Aby ciało w najwyższym punkcie C nie oderwało się od szyn musi być spełniony
wstawiamy do (*) i otrzymujemy:
itą energię mechaniczną w ruchu
w którym nie występują żadne siły rozpraszające (np. tarcie), całkowita energia
mechaniczna jest zachowana (pozostaje stała). Całkowita energia to suma energii
Ciało drgające ruchem harmonicznym prostym posiada energię potencjalną wtedy,
gdy znajduje się ono w jakimś wychyleniu od stanu równowagi. Gdy ciało znajduje się
więc w położeniu równowagi, nie posiada energii potencjalnej.
energii potencjalnej sprężystości, którą możemy
i ciało ma tę energię wtedy, gdy znajduje się w położeniu maksymalnego wychylenia
drgające ruchem harmonicznym prostym posiada energię kinetyczną
w danej chwili. Oznacza to, że ciało nie
posiada energii kinetycznej wtedy, gdy prędkość równa jest zeru, a taki moment
następuje, gdy ciało znajduje się w położeniu maksymalnego wychylenia (x = A).
Ponieważ w ruchu harmonicznym:
to:
Maksymalna wartość energii kinetycznej wynosi
i mamy z nią do czynienia, gdy drgające ciało ma największą prędkość (a jak wiemy,
ma ono ją wtedy, gdy znajduje się w punkcie równowagi x = 0).
Przypominam, że energia mechaniczna w danym momencie jest równa:
Całkowita energia punktu materialnego poruszającego się ruchem harmonicznym
prostym jest proporcjonalna do kwadratu amplitudy tego ruchu.
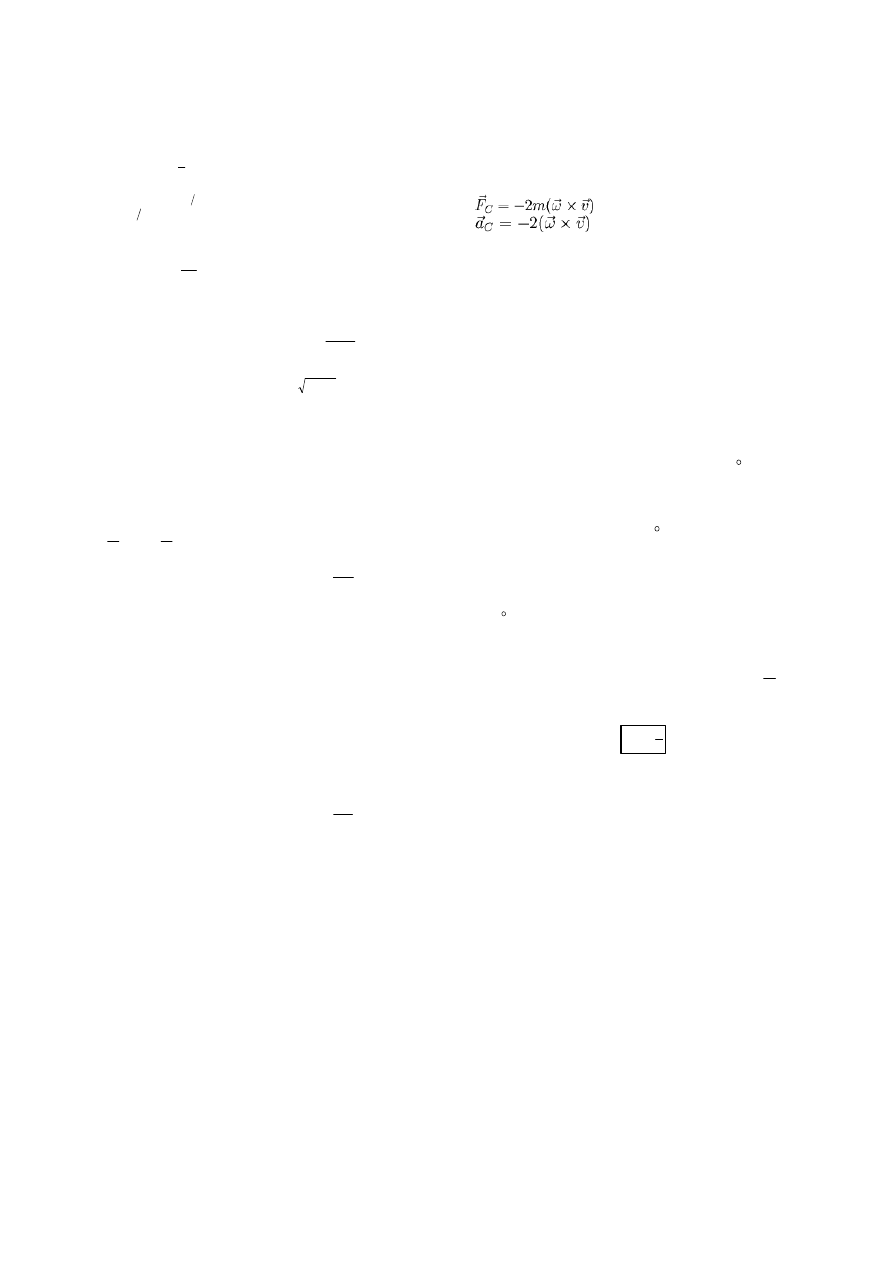
97) Równanie Schrodingera. Ogólne rozwiązanie fla atomu wodoru. Liczby
kwantowe.
Jest to równanie falowe dla cząstek. Zalozenia:
1. Równanie to powinno być zgodne z postulatami Einstaina i de Broglia:
ν
h
E
=
p
h
=
λ
2. Musi odzwierciedlać związek pomiedzy całkowitą energią E cząstki o masie m, a jej
energią kinetycznej
m
p
2
2
i jego energia potencjalną V
V
m
p
E
+
=
2
2
3. Równanie musi być liniowe względem funkcji Ψ(x,y,z,t) będącej jego rozwiązaniem.
4.Eneria potencjalna V jest w ogólności funkcją x, y, z ale może być tez funkcją t.
V(x,y,z,t,) = Vo = const
0
)
,
,
,
(
)
(
2
)
,
,
,
(
2
2
=
Ψ
−
+
Ψ
∇
t
z
y
x
V
E
m
t
z
y
x
h
Liczby kwantowe
Rozwiązanie problemu tlenu zalezy od pewnych parametrów (n, l, m) przyjmyjące
określone, dyskretne wartości. Nazywamy je liczbami kwantowymi:
- główna liczba kwantowa n = 1, 2, 3, …
Wyznacza dozwolone stany energetyczne elektronu.
2
6
,
13
n
eV
E
−
=
Stan podstawowy opisywany jest przez n = 1.
- azymutalna liczba kwantowa l = 1, 2, 3, … (n-1)
Kwantuje orbitalny moment pędu elektronu L:
h
)
1
(
+
=
l
l
L
- magnetyczna liczba kwantowa m = 0, ±1, ±2, …, ±l
Kwantuje składową „z”-etową orbitalnego momentu pędu elektronu.
Lz = mh
- magnetyczna spinowa – pokazuje w którą stronę skierowany jest spin danej
cząsteczki S = sqrt(s(s+1))h Sz = MsH
TLEN: 1s^2 2s^2 2p^4
prawo rozpadu promieniotworczego i opisac wszystkie wielkosci biorace w nim
udzial.Co to jest rozpad sukcesywny ? Co to jest równowaga izotopowa ?
Ilość jąder ulegających promieniotwórczemu rozpadowi w jednostce czasu musi być
proporcjonalna do ilości wszystkich jąder danego izotopu:
N
dt
dN
−
∝
czyli
N
dt
dN
λ
−
=
po scałkowaniu
t
e
N
N
λ
−
=
0
gdzie λ-stała rozpadu.
Odwrotność stałej rozpadu 1/ λ jest średnim czasem życia jąder danego izotopu. Stała
związana jest z czasem połowicznego zaniku T
1/2
relacją :
2
/
1
2
ln
T
=
λ
Czas połowicznego rozpadu T
1/2
jest czasem po którym połowa jąder danego izotopu
ulega rozpadowi.
Ilośc rozpadów promieniotwórczych w jednostce czasu określana jest mianem
aktywności źródła promieniotwórczego A(t)
A(t)= λ*N(t)
3 szeregi promieniotwórcze:
-szereg uranowy, rozpoczynający się od
U
238
92
a kończący stabilnym
Pb
208
82
- szereg uranowy od
U
235
92
, kończący się na
Pb
207
82
- szereg torowy, rozpoczynający się od
Th
232
90
a kończący się
Pb
237
82
Cecha charakterystyczna wszystkich szeregów to sukcesywny rozpad tzn jeden z
izotopów ulegając rozpadowi produkuje inny, który również rozpada się produkując
następny itd. Izotop1>izotop2>izotop3
Pierwszy z izotopów rozpada się według prawa
t
e
N
N
1
01
1
λ
−
=
gdzie N
1
- liczba jąder
izotopu 2 w dowolnej chwili czasu, N
01
-liczba jąder izotopu 1 w początkowej chwili
(t=0)
Zmiana ilości jąder izotopu 2 w dowolnej chwili czasu wynosi
2
2
1
1
2
λ
λ
N
N
dt
dN
−
=
Dwa izotopy w szeregu znajdują się w równowadze izotopowej, gdy ich aktywności SA
sobie równe tj: N
1
λ
1
=N
2
λ
2
=…
Poszczególne izotopy szeregów promieniotwórczych są różnymi pierwiastkami, więc
ich zachowanie w środowisku naturalnym jest różne, dlatego rzadko występuje
równowaga promieniotwórcza w obrębie szeregów, lub nawet ich części
Efekt Coriolisa – efekt występujący w obracających się układach odniesienia. Dla
obserwatora pozostającego w obracającym się układzie odniesienia, objawia się
zakrzywieniem toru ciał poruszających się w takim układzie. Zakrzywienie to zdaje się
być wywołane jakąś siłą, tak zwaną siłą Coriolisa. Siła Coriolisa jest siłą pozorną,
występującą jedynie w nieinercjalnych układach obracających się. Dla zewnętrznego
obserwatora siła ta nie istnieje. Dla niego to układ zmienia położenie a poruszające
się ciało zachowuje swój stan ruchu zgodnie z I zasadą dynamiki.
Siła ta wyrażona jest wzorem:
Z siłą tą wiąże się przyspieszenie Coriolisa:
Oznaczenia: m – masa ciała, v – jego prędkość, ω – prędkość kątowa układu,
natomiast \times – iloczyn wektorowy.
Siła Coriolisa powoduje odchylenie od linii prostej toru ruchu ciała poruszającego się
w układzie obracającym się (np. Ziemi lub płaskiej tarczy). Ponieważ Ziemia obraca
się z zachodu na wschód, zatem siła Coriolisa powoduje odchylenie w kierunku
zachodnim toru ciała poruszającego się po powierzchni Ziemi ku równikowi, a w
kierunku wschodnim, gdy ciało porusza się w stronę któregoś z biegunów, czyli ku osi
obrotu. Efekt taki występuje na obu półkulach.
Siła Coriolisa powoduje również odchylenie swobodnie spadających ciał w kierunku
wschodnim. Dzieje się tak, gdyż ciało przybliżając się do osi obrotu zachowuje większą
prędkość liniową, którą miało na większej wysokości. Jeśli np. na równiku postawimy
wysoką wieżę i puścimy z jej szczytu swobodnie kamień to przyciągany siłą grawitacji
będzie się on zbliżał do powierzchni Ziemi, która porusza się wokół osi z mniejszą
prędkością liniową niż wierzchołek wieży. Dlatego spadający kamień "wyprzedza"
powierzchnię Ziemi. Ciała swobodnie spadając odchylają się na wschód wszędzie poza
biegunami Ziemi. Siła Coriolisa nie oddziałuje na ciała pozostające w spoczynku, jak
również na ciała poruszające się równolegle do osi obrotu Ziemi (wówczas iloczyn
wektorowy prędkości ciała i prędkości kątowej Ziemi równy jest 0).
prawo Gaussa.
Strumień pola elektrycznego jest skalarem, jednostką jest [rm
2
/c]
S
d
E
r
o
r
∫
=
Φ
Strumień elektryczny Φ przenikający przez powierzchnię Gaussa jest proporcjonalny
do całkowitej liczby linii pola elektrycznego przechodzącego przez tę powierzchnię.
Prawo Gaussa opisuje związek między strumieniem Φ przenikającym przez zamkniętą
powierzchnię i całkowitym ładunkiem wewnętrznym zawartym wewnątrz tej
powierzchni
wew
q
=
Φ
0
ε
S
d
E
q
wew
r
o
r
∫
=
0
ε
Jeśli powierzchnia, przez którą liczymy strumień nie jest prostopadła do wektora E, to
trzeba to uwzględnić. Teraz element powierzchni prostopadły do wektora E przez całą
powierzchnię S wynosi:
S
E
S
E
E
∆
=
∆
=
Φ
∑
∑
r
o
r
θ
cos
*
*
Scisła definicja strumienia dla powierzchni zamkniętej dana jest granicą prawej strony
powyższego równania przy trójkąt S strzałka 0;:
=
Φ
E
S
d
E
r
o
r
∫
Z definicji wektora ds. wynika, ze strumień jest dodatni jeśli linie sił
skierowane są na zewnątrz oraz ujemny, jeśli skierowane są do wnętrza powierzchni.
Zakładamy, że powierzchnie okładzin są duże, a odległość między nimi niewielka.
Sprawia to, że pole elektryczne wytwarzane jest tylko pomiędzy okładkami i jest to
pole równomierne. Rozważając powierzchnię Gaussa zaznaczoną na rysunku możemy
napisać:
Z drugiej strony, ponieważ pole jest równomierne, możemy napisać
Uwzględniając obie zależności i dokonując przekształceń otrzymujemy wzór na
pojemność kondensatora płaskiego
q
S
E
⋅
=
⋅
=
Φ
0
1
ε
d
E
U
⋅
=
d
S
C
⋅
=
0
ε

Wyprowadzenie wzoru na energię kinetyczną
Jeśli energia potencjalna nie zmienia się (droga się nie wznosi i nie opada) cała praca
wykonana przez siłę wypadkową zostaje przekształcona w zmianę energii kinetycznej
Ponieważ siła działa wzdłuż kierunku przemieszczenia (możemy zrezygnować z zapisu
wektorowego) definicja pracy przyjmuje najprostszą postać:
Teraz dokonamy szeregu podstawień i przekształceń tak by ostatni powyżej wzór na
pracę W móc wyrazić poprzez prędkości początkową V1 i końcową
oraz jego masę m.
Zgodnie z II zasadą dynamiki Newtona wiemy, że ciało o masie
siły wypadkowej Fw będzie przyspieszać, co możemy zapisać tak:
Teraz ostatni wzór możemy podstawić w odpowiednie miejsce do tego na pracę i
otrzymamy:
. Po podstawieniu
Dodajemy do siebie dwa ułamki w dużym nawiasie:
Jeśli ze względu na równość lewych stron porównamy teraz dwa ostatnie równania
prawymi stronami uzyskamy wyrażenie:
wzór na energię kinetyczną dla ciała o masie m poruszającego się z prędkością
możemy zapisać w postaci:
Zderzenie dwóch ciał nazywamy sprężystym jeżeli suma energii zderzających się ciał
przed zderzeniem i po zderzeniu jest taka sama i suma pędów przed zderzeniem i po
zderzeniu jest taka sama.
Ruch postępowo - obrotowy
Złożenie ruchu postępowego środka masy i ruchu obrotowego względem osi
przechodzącej przez środek masy jest równoważne czystemu ruchowi obrotowemu
zachodzącemu z taką samą prędkością kątową wokół osi przechodzącej przez punkt
zetknięcia się z powierzchnią, po której może się ono toczyć bez poś
Podstawa cylindra w każdej chwili spoczywa (gdy brak poślizgu). Cylinder obraca się
wokół osi przechodzącej przez pkt. P. Liniowa prędkość każdego pkt cylindra jest w
każdej chwili prostopadła do linii łączącej go z pkt P. Ek =
2
1
Ip moment bezwładności względem osi przechodzącej przez pkt P. z tw Steinera:
Ip = I
2
.
.
MR
m
śr
+
, R
ω
=
.
.m
śr
v
zatem
Ek =
2
1
I
2
.
2
.
.
2
1
m
r
m
śr
Mv
+
ω
. Ruch postępowo-obrotowo jest równoważny
ruchowi obrotowemu zachodzącego z tą samą prędkością dookoła środka osi
przechodzącej przez pkt. zetknięcia z powierzchnią po której może się toczyc bez
poślizgu.
Szpula Równania względem środka masy:
1.F*cosα-T=m*a ruch postępowy
2.RT-rF=I*ε ruch obrotowy
Jeśli brak poślizgu to: 3.a= ε*R
Stąd:
)
cos
(
2
r
R
mR
I
FR
a
−
+
=
α
Wnioski:
Nawijanie na nić a>0 cosα>r/R
Rozwijanie na nici a<0 cosα<r/R
Spoczynek szpuli a=0 cosα=r\R
Jeśli energia potencjalna nie zmienia się (droga się nie wznosi i nie opada) cała praca
wykonana przez siłę wypadkową zostaje przekształcona w zmianę energii kinetycznej
Ponieważ siła działa wzdłuż kierunku przemieszczenia (możemy zrezygnować z zapisu
wektorowego) definicja pracy przyjmuje najprostszą postać:
Teraz dokonamy szeregu podstawień i przekształceń tak by ostatni powyżej wzór na
i końcową V2 samochodu
Zgodnie z II zasadą dynamiki Newtona wiemy, że ciało o masie m poddane działaniu
będzie przyspieszać, co możemy zapisać tak:
.
dnie miejsce do tego na pracę i
Jeśli ze względu na równość lewych stron porównamy teraz dwa ostatnie równania
poruszającego się z prędkością V
jeżeli suma energii zderzających się ciał
zderzeniem i po zderzeniu jest taka sama i suma pędów przed zderzeniem i po
i ruchu obrotowego względem osi
przechodzącej przez środek masy jest równoważne czystemu ruchowi obrotowemu
zachodzącemu z taką samą prędkością kątową wokół osi przechodzącej przez punkt
zetknięcia się z powierzchnią, po której może się ono toczyć bez poślizgu.
Podstawa cylindra w każdej chwili spoczywa (gdy brak poślizgu). Cylinder obraca się
wokół osi przechodzącej przez pkt. P. Liniowa prędkość każdego pkt cylindra jest w
Ip
2
ω
.
Ip moment bezwładności względem osi przechodzącej przez pkt P. z tw Steinera:
obrotowo jest równoważny
ruchowi obrotowemu zachodzącego z tą samą prędkością dookoła środka osi
przechodzącej przez pkt. zetknięcia z powierzchnią po której może się toczyc bez
48) Cykl Carnota.
Substancją roboczą jest gaz doskonały, zamknięty w cylindrze o podstawie wykonanej
z dobrego przewodnika ciepła oraz ściankach i tłoku wykonanych z izolatorów
cieplnych.
Otoczenie: dwa zbiorniki ciepła o dużej pojemności cieplnej i tempe
dwie nieprzewodzące podstawki.
ETAP 1: Rozprężanie izotermiczne p , V , T →
podstawę ciepło Q
1
i wykonuje pracę W
1
.
ETAP 2: Rozprężanie adiabatyczne p , V , T
ciepła z otoczeniem. Gaz wykonuje pracę W
′
.
ETAP 3: Sprężanie izotermiczne p , V , T →
podstawę ciepło Q
2
, a tłok wykonuje pracę nad układem W
ETAP 4: Sprężanie adiabatyczne p , V , T →
otoczeniem, a tłok wykonuje pracę nad układem
Wypadkowa praca układu jest równa:
W
W
W
′
– W
W
′
Wypadkowa ilość ciepła pobranego przez układ:
Q
Q – Q
Na mocy pierwszej zasady termodynamiki:
W
Q – Q – pewna ilość ciepła zostaje zamie
Cykl Carnota można przeprowadzić w obu kierunkach.
Sprawność silnika Carnota: η
T
T T
Doświadczenie Fizeau, opis aparatury i wyprowadzenie
W 1849 roku Fizeau jako pierwszy zmierzył prędkość światła metodami
nieastonomicznymi, otrzymując wielkość 3,13*108m/s
schemat aparatury używanej przez Fizeau
Nie zwracajmy na razie uwagi na koło zębate. Światło ze źródła S skupione jest przez
soczewkę L1, odbija się do zierciadła Z1 które jest zwierciadłem półprzezroczystym;
jego warstwa odbijająca jest tak cieńka, że jedynie połowa światła oadającego odbija
się, a pozostała część przechodzi przez zwierciadło.
Światło z obrazu w punkcie F pada na soczewkę L2
Po przejściu przez soczewkę L3 odbija się od zwierciadła Z2. W doświadczeniu Fizeau
odległośćl miedzy Z2 i F wynosiła 8630m. Światło padające ponownie na zwierciadło
Z1częściowo przejdzie przez nie i wpadnie do oka obserwatora poprzez soczewsk
Obserwator zobaczy obraz źródła utworzony przez światło, które przebiegło odległość
2l między kołem a zwierciadłem Z2 i wróciło. Aby określić czas przelotu wiązki
świetlnej, trzeba klzaznaczyć na niej jakieś punkty. Osiąga się to przez "pocięcie"
(przerywanie) wiązki szybko obracającym się kołem zębatym. Załóżmy, że w czasie
przelotu wiązki światła tam i z powrotem, równym
światło z danego "impulsu" wiązki wróciło do koła w momencie, gdy punkt F został
zasłonięty przez ząb koła. Światło padnie wówczas na powierzchnię koła i nie trafi do
oka obserwatora. Jeżeli prędkość obrotu koła jest odpowiednio dobrana, to
obserwator nie zobaczy żadnego "impulsu" z wiązki, gdyż każdy zostanie zasłonięty
przez któryś ząb. Obserwator może zmierzyć prędkość c przez zwiększanie prędkości
kątowej koła od zera do wartości, przy której zniknie obraz źródła ś. Niech
odległością kątową między środkiem przerwy a środkiem zęba. Czas potrzebny na to,
by koło obróciło się o kąt, ma być równy czasowi przelotu
otrzymujemy:
, czyli
Technika "przerywania wiązki", odpowiednio
zmodyfikowana jest obecnie stosowana do pomiarów prędkości neutronów i innych
cząstek.
Cyklotron składa się z elektromagnesu
wytwarzającego
próżniowej, w której umieszczono dwie półkoliste elektrody zwane
elektrodami wytwarzane jest za pomocą generatora wysokiej częstotliwości zmienne
pole elektryczne. W centrum cyklotronu znajduje się źródło cząstek (cząsteczek)
naładowanych elektrycznie lub cząsteczki te są wprowadzane z zewnątrz. Jeżeli
częstotliwość generatora jest równa częstotliwości obiegu
przyspieszane podczas przelotu między duantami. Cząstki o innym czasie przelotu są
okresowo przyspieszane i hamowane i w końcu uderzają w duanty. Cząsteczki o
większej energii poruszają się po większym promieniu. Gdy promień toru ruchu
cząstki jest odpowiednio duży, może ona opuścić akcelerator; pomocna w tym może
być dodatkowa elektroda kierująca cząstki w odpowiednią stronę.
Synchrocyklotron, fazotron - akcelerator cząstek rodzaj cyklotronu o zmiennej
częstotliwości pol elektrycznego, tak dobranej, aby kompensowało ono
relatywistyczny wzrost masy, który wywołuje w
zbliżaniu się ich prędkości do prędkości światła. Pierwszy synchrocyklotron
skonstruował Weksler w ZSRR w roku 1945.
Częstotliwość cyklotronową w mechanice relatywistycznej opisuje wzór:
,
gdzie:
f
c
- częstotliwość w przybliżeniu klasycznym, T -
masa spoczynkowa cząstki, c - prędkość światła.
Substancją roboczą jest gaz doskonały, zamknięty w cylindrze o podstawie wykonanej
z dobrego przewodnika ciepła oraz ściankach i tłoku wykonanych z izolatorów
Otoczenie: dwa zbiorniki ciepła o dużej pojemności cieplnej i temperaturach T
1
i T
2
,
→ p , V , T
. Gaz pochłania przez
→ p , V , T
. Nie ma wymiany
p , V , T
. Gaz oddaje przez
, a tłok wykonuje pracę nad układem W
2
.
p , V , T
. Nie ma wymiany ciepła z
otoczeniem, a tłok wykonuje pracę nad układem W
′
.
Wypadkowa ilość ciepła pobranego przez układ:
niona na pracę.
Cykl Carnota można przeprowadzić w obu kierunkach.
Doświadczenie Fizeau, opis aparatury i wyprowadzenie
W 1849 roku Fizeau jako pierwszy zmierzył prędkość światła metodami
3,13*108m/s. Na rysunku pokazany jest
Nie zwracajmy na razie uwagi na koło zębate. Światło ze źródła S skupione jest przez
które jest zwierciadłem półprzezroczystym;
jego warstwa odbijająca jest tak cieńka, że jedynie połowa światła oadającego odbija
się, a pozostała część przechodzi przez zwierciadło.
Światło z obrazu w punkcie F pada na soczewkę L2 i wychodzi jako wiązka równoległa.
odbija się od zwierciadła Z2. W doświadczeniu Fizeau
i F wynosiła 8630m. Światło padające ponownie na zwierciadło
Z1częściowo przejdzie przez nie i wpadnie do oka obserwatora poprzez soczewskę L4
Obserwator zobaczy obraz źródła utworzony przez światło, które przebiegło odległość
i wróciło. Aby określić czas przelotu wiązki
świetlnej, trzeba klzaznaczyć na niej jakieś punkty. Osiąga się to przez "pocięcie"
erywanie) wiązki szybko obracającym się kołem zębatym. Załóżmy, że w czasie
przelotu wiązki światła tam i z powrotem, równym 2l/c, koło obróciło siętak, by
światło z danego "impulsu" wiązki wróciło do koła w momencie, gdy punkt F został
b koła. Światło padnie wówczas na powierzchnię koła i nie trafi do
oka obserwatora. Jeżeli prędkość obrotu koła jest odpowiednio dobrana, to
obserwator nie zobaczy żadnego "impulsu" z wiązki, gdyż każdy zostanie zasłonięty
zmierzyć prędkość c przez zwiększanie prędkości
koła od zera do wartości, przy której zniknie obraz źródła ś. Niech FI będzie
odległością kątową między środkiem przerwy a środkiem zęba. Czas potrzebny na to,
ny czasowi przelotu 2l/c. W ten sposób
Technika "przerywania wiązki", odpowiednio
zmodyfikowana jest obecnie stosowana do pomiarów prędkości neutronów i innych
wytwarzającego pole magnetyczne i komory
próżniowej, w której umieszczono dwie półkoliste elektrody zwane duantami. Między
wytwarzane jest za pomocą generatora wysokiej częstotliwości zmienne
. W centrum cyklotronu znajduje się źródło cząstek (cząsteczek)
naładowanych elektrycznie lub cząsteczki te są wprowadzane z zewnątrz. Jeżeli
częstotliwość generatora jest równa częstotliwości obiegu cząstek, to są one
przyspieszane podczas przelotu między duantami. Cząstki o innym czasie przelotu są
okresowo przyspieszane i hamowane i w końcu uderzają w duanty. Cząsteczki o
większej energii poruszają się po większym promieniu. Gdy promień toru ruchu
ząstki jest odpowiednio duży, może ona opuścić akcelerator; pomocna w tym może
być dodatkowa elektroda kierująca cząstki w odpowiednią stronę.
ek rodzaj cyklotronu o zmiennej
dobranej, aby kompensowało ono
relatywistyczny wzrost masy, który wywołuje wzrost czasu obiegu cząstek przy
zbliżaniu się ich prędkości do prędkości światła. Pierwszy synchrocyklotron
mechanice relatywistycznej opisuje wzór:
- energia kinetyczna cząstki, m
0
-
prędkość światła.

katastrofa w nadfiolecie
Wzrostowi temperatury ciała doskonale czarnego towarzyszy coraz większa ilość
wypromieniowanej energii odpowiadającej falom krótkim. Przeprowadzone przez
Wiena pomiary wykazały, że dla ciała dosk. czarnego iloczyn długości fali [lambda
max] i temperatury bezwzględnej [T] ma wartosć stałą równą b
przesunięć Wiena. Analizując zjawisko emisji promieniowania na gruncie
termodynamiki klasycznej prowadzi do prawa Rayleigha-Jeansa:
I=(8*[3.14]*k*T)/([lambda]^4)
zależność 1/[lambda]^4 sprawia że nie może ono opisywać poprawnie krzywych od
strony fal krótkich - nazwano ten fakt katastrofą w nadfiolecie wzór ten został
wyprowadzony w oparciu o klaseyczne pojęcie oscylatorów, tj drgajacych atomow i
czastek wewnatrz cdc. w stanie ustalonym srednia energia drgan oscylatorow
powinna byc taka sama z analizy wykresow natezenia promieniowania w funkcji
dlugosci wynika ze wewnatrz wneki dominuja oscylatory o wiekszych
czestotliwosciach, ale ich srednia energia jest mniejsza.
W granicy niskich częstotliwości widmo klasyczne jest bliskie krzywej doświadczalnej,
natomiast dla wysokich częstotliwości wyniki teoretyczne (R
nieskończoności podczas gdy z eksperymentów wynika, że gęstość energii zawsze
pozostaje skończona i dla wysokich częstotliwości dąży do zera.
W 1900 r. Planck zalozyl ze oscylator nie zmienia swojej energii w sposob dowolny ale
kwantami - minimalnymi porcjami. moze wiec tracic/zyskiwac kwant lub dwa energii
ale nie pol czy cwierc. zalozyl dodatkowo ze kazdy oscylator ma dla siebi
charaterystyczna wielkosc kwantu proporcjonalna do swojej czestotliwosci.
Katastrofa w nad. Stała się jedną z przyczyn wykazania, że wnioski wyciągane na
podstawie mechaniki klasycznej mogą być niesłuszne i ułatwiło przyjęcie
kwantowej.
10) Zderzenia sprężyste i niesprężyste
Zderzenie można zdefiniować jako - krótkotrwałe, silne oddziaływanie wzajemne
zderzających się ciał przy ich zetknięciu się ze sobą, w wyniku czego doznają one
zmiany prędkości.
A więc pojęcie "zderzenie" opisuje zmianę ruchu zderzających się ciał (lub
przynajmniej jednej z nich). Zmiana ta zachodzi bardzo gwałtownie, więc można
oddzielić przebieg zjawiska przed zderzeniem od przebiegu zjawiska po zderzeniu.
Daje nam to możliwość badania ruchów ciał ulegających zderzeniom. Jeśli znamy ruch
ciał przed zderzeniem, i wiemy, że podczas zderzenia musi zostać spełniona zasada
zachowania pędu i zasada zachowania całkowitej energii, to potrafimy znaleźć ruch
tych ciał po zderzeniu.
Omówiony zostanie tu przykład zderzających się sprężyście kul.
Zderzenia klasyfikuje się na podstawie tego czy energia kinetyczna jest zachowana
podczas zderzenia, czy też nie.
- Zderzenie jest sprężyste, gdy energia kinetyczna jest w zderzeniu zachowana.
- Gdy energia kinetyczna układy zmienia się podczas zderzenia, to zderzenie tak
niesprężyste .
Zderzenia sprężyste jak i niesprężyste mogą być centrale lub niecentralne.
Zderzenia centralne to szczególny przypadek zderzeń, w których prędkości
zderzających się ciał skierowane są wzdłuż prostej łączącej ich środki. Wszystkie i
przypadki zderzeń będą zderzeniami niecentralnymi lub inaczej skośnymi.
Zderzenie całkowicie niesprężyste (po zderzeniu ciała stykają się ze sobą): część
energii idzie na odkształcenie ciał. Nie można w tym przypadku stosować ZZE.
ZZP: m
1
v
1p
+m
2
v
2p
=(m
1
+m2)v
k
Zderzenia sprężyste:
Przy zderzeniu sprężystym energia kinetyczna każdego ze zderzających się ciał może
się zmieniać, lecz nie może ulec zmianie całkowita energia kinetyczna układu tych
ciał.
ZZP:m
1
v
1p
+m
2
v
2p
=m
1
v
1k
+m
2
v
2k
ZZE:1/2(m
1
v
1p
2
+m
2
v
2p
2
)=1/2(m
1
v
1k
2
+m
2
v
2k
2
)
Założenia i opis metody datowania węglem c14
Przy stosowaniu tej metody musza być spełnione założenia. 2 główne z nich to:
- obiekt datowany musi stanowić w swojej historii tzw. Układ zamknięty z uwagi na
migracje izotopów „do” i „z” układu.
- aktywność (lub stopień braku równowagi izotopowej) w początkowej chwili czasu
musi być znana. W przypadku C14 początkowa aktywność w materii organicznej na
przestrzeni ostatnich 40tys lat nie była stała z uwagi na zmienność warunków
klimatycznych i szaty roślinnej. Aktualnie znamy krzywą kalibracyjną opartą na
dendrologicznej skali czasu do ok. 10tys lat wstecz. Pozwala ona na korektę
obliczonego wieku radiowęglowego na tzw. lata kalendarzowe.
t
T
e
N
w
i
2
ln
0
−
⋅
⋅
=
λ
0
0
N
w
i
⋅
⋅
=
λ
Zasięg czasowy tej metody przy wyrafinowanych metodach pomiarowych sięga około
40 tys. Lat
By określić kiedy nastąpiło pobranie węgla z atmosfery do fotosyntezy i budowy
danego organizmu, należy zmierzyć proporcję izotopu węgla
węgla w badanych pozostałościach organizmu lub materiałów pochodzących z tego
organizmu (np. drewna lub skóry). Następnie trzeba obliczyć, jak dawno temu próbka
miała proporcje izotopów równe wówczas proporcji atmosferycznej.
Udział radiowęgla w ogóle węgla występującego w atmosferze można wyrazić
wzorem:
Wzrostowi temperatury ciała doskonale czarnego towarzyszy coraz większa ilość
wypromieniowanej energii odpowiadającej falom krótkim. Przeprowadzone przez
Wiena pomiary wykazały, że dla ciała dosk. czarnego iloczyn długości fali [lambda
ezwzględnej [T] ma wartosć stałą równą b - co stanowi prawo
przesunięć Wiena. Analizując zjawisko emisji promieniowania na gruncie
Jeansa:
e nie może ono opisywać poprawnie krzywych od
nazwano ten fakt katastrofą w nadfiolecie wzór ten został
wyprowadzony w oparciu o klaseyczne pojęcie oscylatorów, tj drgajacych atomow i
energia drgan oscylatorow
powinna byc taka sama z analizy wykresow natezenia promieniowania w funkcji
dlugosci wynika ze wewnatrz wneki dominuja oscylatory o wiekszych
ości widmo klasyczne jest bliskie krzywej doświadczalnej,
natomiast dla wysokich częstotliwości wyniki teoretyczne (R-J) dążą do
nieskończoności podczas gdy z eksperymentów wynika, że gęstość energii zawsze
dąży do zera.
W 1900 r. Planck zalozyl ze oscylator nie zmienia swojej energii w sposob dowolny ale
minimalnymi porcjami. moze wiec tracic/zyskiwac kwant lub dwa energii
ale nie pol czy cwierc. zalozyl dodatkowo ze kazdy oscylator ma dla siebie
charaterystyczna wielkosc kwantu proporcjonalna do swojej czestotliwosci.
się jedną z przyczyn wykazania, że wnioski wyciągane na
podstawie mechaniki klasycznej mogą być niesłuszne i ułatwiło przyjęcie mechaniki
krótkotrwałe, silne oddziaływanie wzajemne
zderzających się ciał przy ich zetknięciu się ze sobą, w wyniku czego doznają one
A więc pojęcie "zderzenie" opisuje zmianę ruchu zderzających się ciał (lub
zynajmniej jednej z nich). Zmiana ta zachodzi bardzo gwałtownie, więc można
oddzielić przebieg zjawiska przed zderzeniem od przebiegu zjawiska po zderzeniu.
Daje nam to możliwość badania ruchów ciał ulegających zderzeniom. Jeśli znamy ruch
zeniem, i wiemy, że podczas zderzenia musi zostać spełniona zasada
zachowania pędu i zasada zachowania całkowitej energii, to potrafimy znaleźć ruch
Omówiony zostanie tu przykład zderzających się sprężyście kul.
uje się na podstawie tego czy energia kinetyczna jest zachowana
Zderzenie jest sprężyste, gdy energia kinetyczna jest w zderzeniu zachowana.
Gdy energia kinetyczna układy zmienia się podczas zderzenia, to zderzenie takie jest
Zderzenia sprężyste jak i niesprężyste mogą być centrale lub niecentralne.
Zderzenia centralne to szczególny przypadek zderzeń, w których prędkości
zderzających się ciał skierowane są wzdłuż prostej łączącej ich środki. Wszystkie inne
przypadki zderzeń będą zderzeniami niecentralnymi lub inaczej skośnymi.
Zderzenie całkowicie niesprężyste (po zderzeniu ciała stykają się ze sobą): część
energii idzie na odkształcenie ciał. Nie można w tym przypadku stosować ZZE.
Przy zderzeniu sprężystym energia kinetyczna każdego ze zderzających się ciał może
się zmieniać, lecz nie może ulec zmianie całkowita energia kinetyczna układu tych
Przy stosowaniu tej metody musza być spełnione założenia. 2 główne z nich to:
obiekt datowany musi stanowić w swojej historii tzw. Układ zamknięty z uwagi na
aktywność (lub stopień braku równowagi izotopowej) w początkowej chwili czasu
musi być znana. W przypadku C14 początkowa aktywność w materii organicznej na
przestrzeni ostatnich 40tys lat nie była stała z uwagi na zmienność warunków
h i szaty roślinnej. Aktualnie znamy krzywą kalibracyjną opartą na
dendrologicznej skali czasu do ok. 10tys lat wstecz. Pozwala ona na korektę
obliczonego wieku radiowęglowego na tzw. lata kalendarzowe.
0
ln
2
ln
i
i
T
t
−
=
Zasięg czasowy tej metody przy wyrafinowanych metodach pomiarowych sięga około
By określić kiedy nastąpiło pobranie węgla z atmosfery do fotosyntezy i budowy
zotopu węgla
14
C do całej zawartości
węgla w badanych pozostałościach organizmu lub materiałów pochodzących z tego
trzeba obliczyć, jak dawno temu próbka
miała proporcje izotopów równe wówczas proporcji atmosferycznej.
Udział radiowęgla w ogóle węgla występującego w atmosferze można wyrazić
Efekt fotoelektryczny zewnętrzny jest jednym ze sposobów
elektromagnetycznej (Np. światła) z materią, polegającym na emisji elektronów z
powierzchni metalu po naświetleniu jej promieniowaniem elektromagnetycznym (na
przykład światłem widzialnym) o odpowiedniej częstotliwości, charakterystyczne
danego materiału. Emitowane w ten sposób elektrony nazywa się czasem
fotoelektronami. Energia kinetyczna fotoelektronów nie zależy od natężenia światła
a jedynie od jego częstotliwości. Odkrycie i wyjaśnienie efektu fotoelektrycznego
przyczyniło się do rozwoju korpuskularno falowej teorii materii, w której obiektom
mikroświata przypisywane są jednocześnie własności falowe i materialne
(korpuskularne). Wyjaśnienie i matematyczny opis efektu fotoelektrycznego podał
Albert Einstein, który wykorzystał hipotezę kwantów wysuniętą w 1905 roku przez
Maxa Plancka.
Prawa efektu fotoelektrycznego
·… Efekt fotoelektryczny zachodzi gdy światło ma częstotliwość v >=
jest charakterystyczną dla każdego metalu częstotliwością graniczną. Gdy v <
efekt fotoelektryczny nie zachodzi bez względu na natężenie światła. Gdy efekt
fotoelektryczny zachodzi, to energia kinetyczna fotoelektronów wzrasta liniowo wraz
z częstotliwością i nie zależy od natężenia światła.
·… Przy ustalonej częstotliwości v >= v.gr światła liczba fotoelektronów emitowanych
przez jednostkę powierzchni metalu w jednostce czasu jest wprost proporcjonalna do
natężenia światła.
·… Nie występuje żadne mierzalne opóźnienie czasowe pomiędzy padaniem
promieniowania świetlnego a emisją fotoelektronów dla v >=
natężenie światła.
Energia pojedynczego fotonu: E = hv
Wzór Einsteina bilansujący efekt fotoelektryczny:
Energia podającego fotonu (hv) zostaje zużyta w części na pokonanie przez elektron
powierzchniowej bariery potencjału katody. Resztę energii (hv
jako energię kinetyczną. Jeśli nie straci on części tej energii wskutek zderzeń
wewnątrz katody, będzi to energia maksymalna Ekin,max.
Zwiększenie natężenia światla powoduje wzrost ilości fotonów, ale nie ich energii.
Dlatego Ekin.max nie zależy od natężenia padającego światła.
Pęd Fali elektomagnetycznej
Fale elektromagnetyczne mogą transportować również pęd, zatem mogą wywierać
ciśnienie na obiekt na który padają. Zostało ono nazwane ciśnieniem
promieniowania. W życiu codziennym nie są to jednak siły odczuwalne dla człowieka.
Maja jednak znaczenie dla cyklu życiowego gwiazd.
Pęd można zdefiniować jako:
gdzie U to energia zaabsorbowana przez dany obiekt, a c to prędkość
światła. Należy jeszcze przyjąć, że promieniowanie jest przez ten obiekt całkowicie
pochłaniane.
Kierunek wektora pędu jest taki sam jak kierunek wiązki padającej na daną
powierzchnię.
Jeśli natomiast przyjmiecie założenie, że wiązka promieniowania zostaje
odbita od powierzchni ciała to ciśnienie promieniowania przedstawia się jako:
Tak więc w przypadku całkowitego odbicia powierzchni przekazany zostaje dwa razy
większy pęd.
Natomiast jeśli część promieniowania ulegnie absorpcji, a część odbiciu
pęd będzie zawierał się w przedziale między tymi dwiema wartościami.
Ciśnienie promieniowania zmierzyli Nichols i Hull udowadniając słuszność wzorów
opisujących przekaz pędu. Dokonali tego przy pomocy skalibrowanego wahadła
torsyjnego z dwoma lustrami. Energię padającej wiązki promieniowania określili
poprzez pomiar wzrostu temp. Czarnej płytki ustawionej na drodze wiązki. Zmierzone
ciśnienie było rzędy 10e-6N/m^2
DOŚW.-Radiometr Crookesa (wiatraczek słoneczny)
pomiaru intensywności światła. Gdy na radiometr pada
wnętrzu zaczyna się obracać i prędkość obrotów zależy od intensywności oświetlenia.
Po zasłonięciu światła niewielkie opory ruchu osi powodują zatrzymanie wiatraczka.
Według koncepcji Crookesa, przyrząd ten miał wykazywać, że ś
ciśnienie na powierzchnię, na którą pada.
Urządzenie to składa się z wiatraczka umieszczonego w szklanej bańce. Skrzydła
wiatraczka z jednej strony są czarne, natomiast
umocowany jest na delikatnej osi tak, aby opory
wiatraczka były zminimalizowane. Szklana bańka wypełniona jest
znacznie obniżonym ciśnieniu.
Początkowo sądzono, że wiatraczek kręci się na skutek ciśnienia wywieranego przez
światło. Crookes sądził, że od posrebrzonej powierzchni światło odbija się, natomiast
przez czarną jest pochłaniane – stąd różnica w wywieranym ciśnieniu. Dziś można by
powiedzieć, że fotony przekazują posrebrzonej powierzchni
czarnej tylko p. Wiatraczek zatem powinien obracać się w kierunku zgodnym z
kierunkiem padania światła na posrebrzoną powierzchnię, czyli
przodu. Jednak okazało się, że wiatraczek kręci się w odwrotną stronę.
Wyjaśnienie znalazł Osborne Reynolds, a jego opis matematyczny poprawił J. C.
Maxwell. Przyczyną takich obrotów wiatraczka jest różne nagrzewanie się
powierzchni jasnej i ciemnej na skutek absorpcji promieniowania. Czarna
powierzchnia nagrzewa się silniej i powoduje wzrost temperatury gazu znajdującego
się w jej pobliżu. Gaz przepływa od zimnej strony skrzydła (srebrnej) do ciepłej
(czarnej). Ten ruch powoduje różnicę ciśnień z obu stron skrzydła i ruch wiatraczka.
Dodatkowym argumentem przemawiającym za takim mechanizmem jest fakt, że
zmniejszenie ciśnienia powietrza w bańce radiometru poni
10
–4
Pa), powoduje zaniknięcie zjawiska – wiatraczek przestaje się obracać. Gdyby
przyczyną obrotów było ciśnienie promieniowania
nawet do stanu doskonałej próżni, powinno powodować zmniejszenie oporów
powietrza i coraz lepsze działanie radiometru.
Efekt fotoelektryczny zewnętrzny jest jednym ze sposobów oddziaływania fali
elektromagnetycznej (Np. światła) z materią, polegającym na emisji elektronów z
powierzchni metalu po naświetleniu jej promieniowaniem elektromagnetycznym (na
przykład światłem widzialnym) o odpowiedniej częstotliwości, charakterystycznej dla
danego materiału. Emitowane w ten sposób elektrony nazywa się czasem
fotoelektronami. Energia kinetyczna fotoelektronów nie zależy od natężenia światła
a jedynie od jego częstotliwości. Odkrycie i wyjaśnienie efektu fotoelektrycznego
do rozwoju korpuskularno falowej teorii materii, w której obiektom
mikroświata przypisywane są jednocześnie własności falowe i materialne
(korpuskularne). Wyjaśnienie i matematyczny opis efektu fotoelektrycznego podał
potezę kwantów wysuniętą w 1905 roku przez
·… Efekt fotoelektryczny zachodzi gdy światło ma częstotliwość v >= v.gr gdzie v.gr
jest charakterystyczną dla każdego metalu częstotliwością graniczną. Gdy v < v.gr to
efekt fotoelektryczny nie zachodzi bez względu na natężenie światła. Gdy efekt
to energia kinetyczna fotoelektronów wzrasta liniowo wraz
z częstotliwością i nie zależy od natężenia światła.
światła liczba fotoelektronów emitowanych
przez jednostkę powierzchni metalu w jednostce czasu jest wprost proporcjonalna do
·… Nie występuje żadne mierzalne opóźnienie czasowe pomiędzy padaniem
oelektronów dla v >= v.gr bez względu na
Wzór Einsteina bilansujący efekt fotoelektryczny: hv = E0 + Ekin,max
Energia podającego fotonu (hv) zostaje zużyta w części na pokonanie przez elektron
powierzchniowej bariery potencjału katody. Resztę energii (hv – E0) elektron unosi
jako energię kinetyczną. Jeśli nie straci on części tej energii wskutek zderzeń
wewnątrz katody, będzi to energia maksymalna Ekin,max.
wzrost ilości fotonów, ale nie ich energii.
Dlatego Ekin.max nie zależy od natężenia padającego światła.
Fale elektromagnetyczne mogą transportować również pęd, zatem mogą wywierać
o ono nazwane ciśnieniem
promieniowania. W życiu codziennym nie są to jednak siły odczuwalne dla człowieka.
Maja jednak znaczenie dla cyklu życiowego gwiazd.
gdzie U to energia zaabsorbowana przez dany obiekt, a c to prędkość
wiatła. Należy jeszcze przyjąć, że promieniowanie jest przez ten obiekt całkowicie
Kierunek wektora pędu jest taki sam jak kierunek wiązki padającej na daną
Jeśli natomiast przyjmiecie założenie, że wiązka promieniowania zostaje całkowicie
odbita od powierzchni ciała to ciśnienie promieniowania przedstawia się jako:
Tak więc w przypadku całkowitego odbicia powierzchni przekazany zostaje dwa razy
Natomiast jeśli część promieniowania ulegnie absorpcji, a część odbiciu to przekazany
pęd będzie zawierał się w przedziale między tymi dwiema wartościami.
Ciśnienie promieniowania zmierzyli Nichols i Hull udowadniając słuszność wzorów
opisujących przekaz pędu. Dokonali tego przy pomocy skalibrowanego wahadła
a lustrami. Energię padającej wiązki promieniowania określili
poprzez pomiar wzrostu temp. Czarnej płytki ustawionej na drodze wiązki. Zmierzone
(wiatraczek słoneczny) – rodzaj radiometru, przyrząd do
. Gdy na radiometr pada światło, wiatraczek w jego
obrotów zależy od intensywności oświetlenia.
Po zasłonięciu światła niewielkie opory ruchu osi powodują zatrzymanie wiatraczka.
Według koncepcji Crookesa, przyrząd ten miał wykazywać, że światło wywiera
Urządzenie to składa się z wiatraczka umieszczonego w szklanej bańce. Skrzydła
z drugiej – posrebrzone. Wiatraczek
opory mechaniczne przy obrocie
wiatraczka były zminimalizowane. Szklana bańka wypełniona jest powietrzem o
Początkowo sądzono, że wiatraczek kręci się na skutek ciśnienia wywieranego przez
sądził, że od posrebrzonej powierzchni światło odbija się, natomiast
stąd różnica w wywieranym ciśnieniu. Dziś można by
ej powierzchni pęd 2p, podczas gdy
. Wiatraczek zatem powinien obracać się w kierunku zgodnym z
kierunkiem padania światła na posrebrzoną powierzchnię, czyli czarną stroną do
przodu. Jednak okazało się, że wiatraczek kręci się w odwrotną stronę.
, a jego opis matematyczny poprawił J. C.
Przyczyną takich obrotów wiatraczka jest różne nagrzewanie się
powierzchni jasnej i ciemnej na skutek absorpcji promieniowania. Czarna
powierzchnia nagrzewa się silniej i powoduje wzrost temperatury gazu znajdującego
mnej strony skrzydła (srebrnej) do ciepłej
(czarnej). Ten ruch powoduje różnicę ciśnień z obu stron skrzydła i ruch wiatraczka.
Dodatkowym argumentem przemawiającym za takim mechanizmem jest fakt, że
zmniejszenie ciśnienia powietrza w bańce radiometru poniżej pewnego progu (około
wiatraczek przestaje się obracać. Gdyby
ciśnienie promieniowania, wówczas zmniejszanie ciśnienia,
, powinno powodować zmniejszenie oporów
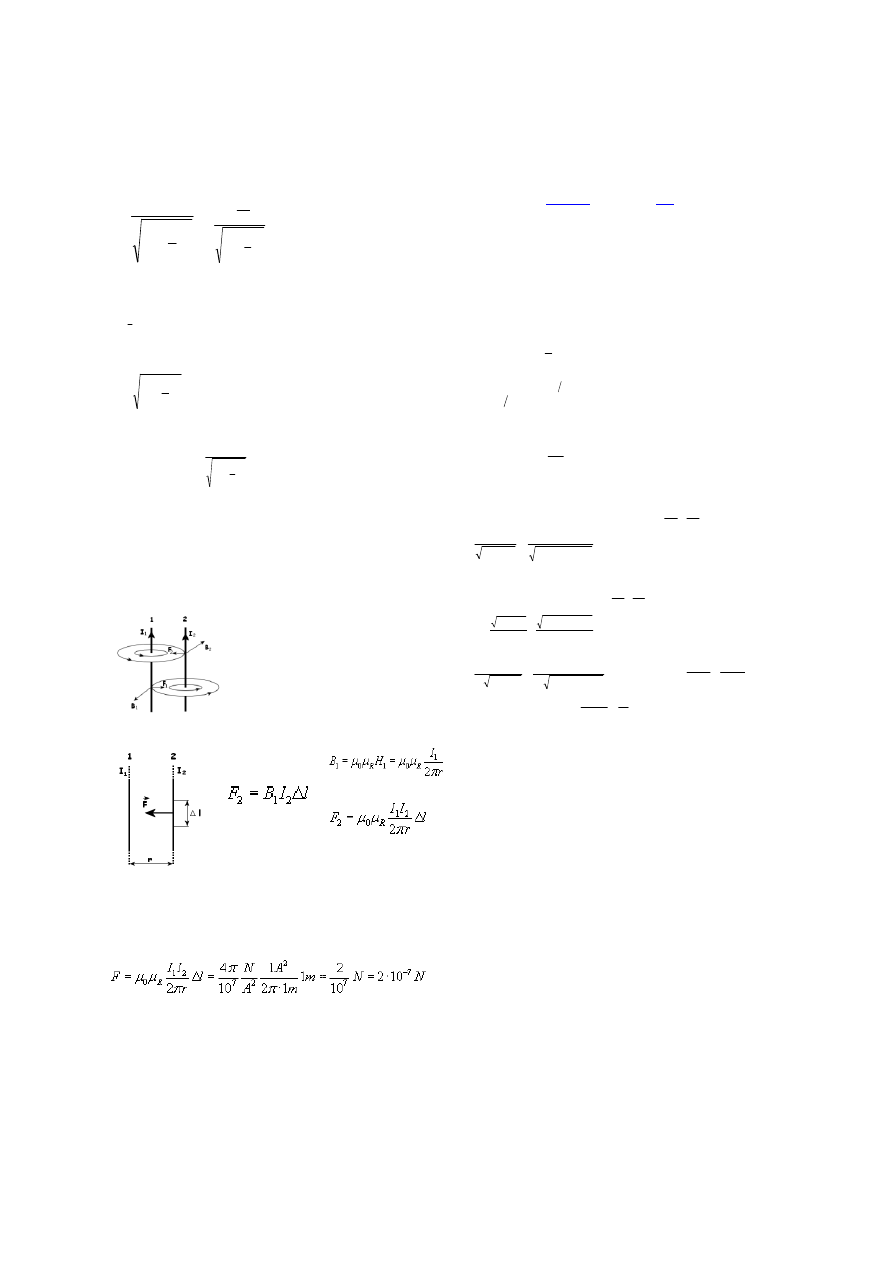
Transformacja Lorentza
Z postulatów Einsteina wynika ze prawa fizyki powinny w obydwóch układach być
takie same. Jeśli w układzie S obserwator widzi falę świetlną kulistą:
X^2 + y^2 + z^2 = c ^2 t^2 to w układzie Sprim też powinna być falą kulistą:…
Żądanie to prowadzi do tzw. transformacji Lorentza. Dla układu Sprim poruszającego
się z prędkością V wzdłuż osi x i względem układu S równania przyjmują postać:
2
1
`
−
−
=
c
v
vt
x
x
2
2
1
`
−
−
=
c
v
x
c
v
t
t
Transformacja Lorentza: (gdy jeden układ
porusza się względem drugiego wzdłuż osi x
y` = y
z` = z
Gdy
1
<<
c
v
transformacja Lorentza przechodzi w transformacje Galileusza
Skrócenie długości
Obserwator w układzie S` poruszającym się względem S z prędkością v mierzy długość
ciała z układu S. Transformacja Lorentza daje nam
2
1
`
−
=
c
v
x
x
Dylatacja czasu
Odstęp czasu mierzony w układzie poruszającym się S` dłuższy niż odstęp czasu
mierzony w układzie S.
2
1
`
−
=
c
v
τ
τ
Przykład: paradoks bliźniąt.
Wyprowadzić wzór na siłę oddziaływania dwóch równoległych przewodników z
prądem i podać definicję Ampera.
Dane są dwa równoległe prostoliniowe nieskończenie długie przewodniki z prądem.
Gdy przez te przewodniki płynie prąd to przewodniki te działają na siebie wzajemnie.
Przyciągają się, gdy prąd płynie w obu przewodnikach w jednym kierunku i odpychają
się, gdy prąd płynie w kierunkach przeciwnych. Dzieje się tak, bo wokół każdego
przewodnika istnieje pole magnetyczne i znajduje się on w polu magnetycznym
drugiego, dlatego na każdy przewodnik działa siła elektrodynamiczna.
Rozpatrzymy przewodniki z prądem płynącym w jednym kierunku.
Za pomocą reguły Fleminga stwierdzimy, że na
przewodnik 2 działa siła
płaszczyźnie rysunku i zwrócona w lewo.
Przewodnik 1 jest przekłuwany przez linie pola
przewodnika 2 od tyłu (zza rysunku). Regułą
Fleminga wyznaczamy zwrot siły działającej na
przewodnik 1. Siła F1
Rozpatrywane przewodniki przyciągają
przewodniki z prądami płynącymi w kierunkach przeciwnych odpychają się.
Będąc w tym miejscu tego wywodu, należałoby wspomnieć o definicji
absolutnego.
Niech będą zatem dane dwa przewodniki prostoliniowe nieskończenie długie z
prądami o równych natężeniach po 1A każdy, umieszczone w próżni w odległości
od siebie. Obliczmy siłę działającą na przewodniki na długości
Powyższe dane podstawiamy do wyprowadzonego powyżej wzoru:
Amper absolutny jest natężeniem prądu, który płynąc w dwóch równoległych
nieskończenie długich przewodnikach o znikomym przekroju okrągłym,
umieszczonych w próżni w odległości 1m od siebie, powoduje oddziaływanie
wzajemne tych przewodników siłą 2 . 10-7 N na każdy metr bieżący tych
przewodników.
rozpatrujemy siłę
działającą na długości
delta l.
gdzie:
B1 - indukcja
magnetyczna pola
przewodnika 1,
I2 - natężenie prądu w
przewodniku 2.
fizyki powinny w obydwóch układach być
takie same. Jeśli w układzie S obserwator widzi falę świetlną kulistą:
też powinna być falą kulistą:…
Żądanie to prowadzi do tzw. transformacji Lorentza. Dla układu Sprim poruszającego
się z prędkością V wzdłuż osi x i względem układu S równania przyjmują postać:
Transformacja Lorentza: (gdy jeden układ
transformacja Lorentza przechodzi w transformacje Galileusza
Obserwator w układzie S` poruszającym się względem S z prędkością v mierzy długość
Odstęp czasu mierzony w układzie poruszającym się S` dłuższy niż odstęp czasu
Wyprowadzić wzór na siłę oddziaływania dwóch równoległych przewodników z
Dane są dwa równoległe prostoliniowe nieskończenie długie przewodniki z prądem.
Gdy przez te przewodniki płynie prąd to przewodniki te działają na siebie wzajemnie.
Przyciągają się, gdy prąd płynie w obu przewodnikach w jednym kierunku i odpychają
ę, gdy prąd płynie w kierunkach przeciwnych. Dzieje się tak, bo wokół każdego
przewodnika istnieje pole magnetyczne i znajduje się on w polu magnetycznym
drugiego, dlatego na każdy przewodnik działa siła elektrodynamiczna.
płynącym w jednym kierunku.
Za pomocą reguły Fleminga stwierdzimy, że na
przewodnik 2 działa siła F2 leżąca w
płaszczyźnie rysunku i zwrócona w lewo.
Przewodnik 1 jest przekłuwany przez linie pola
przewodnika 2 od tyłu (zza rysunku). Regułą
aczamy zwrot siły działającej na
F1 działa w prawo.
Rozpatrywane przewodniki przyciągają się.
przewodniki z prądami płynącymi w kierunkach przeciwnych odpychają się.
Po podstawieniu
otrzymamy:
Pamiętajmy, że µR dla
przewodnika
znajdującego się w próżni
wynosi 1.
Będąc w tym miejscu tego wywodu, należałoby wspomnieć o definicji ampera
Niech będą zatem dane dwa przewodniki prostoliniowe nieskończenie długie z
każdy, umieszczone w próżni w odległości 1m
od siebie. Obliczmy siłę działającą na przewodniki na długości 1m.
amy do wyprowadzonego powyżej wzoru:
jest natężeniem prądu, który płynąc w dwóch równoległych
nieskończenie długich przewodnikach o znikomym przekroju okrągłym,
od siebie, powoduje oddziaływanie
na każdy metr bieżący tych
F. BOhra
Funkcja własna będąca rozwiązaniem równania Schrödingera
falowej. Funkcja falowa, w najogólniejszej postaci funkcja zespolona, nie ma
bezpośredniego sensu fizycznego. Dopiero jej kwadrat interpretujemy jako gęstość
prawdopodobieństwa znalezienia cząstki. Powyższa interpretacja pochodzi od
niemieckiego fizyka
Maxa Borna
, który podał ją w
F. falowe P(xyzt) będące rozwiązaniami równania Schrod. Są f. zespolonymi
stąd że w mechanice kwantowej nie możemy nadać funkcji falowej samoistnego
znaczenia fizycznego w sensie klasycznym. Przepis na opis tego podał Max Born.
Interpretacja ta stanowi zerwanie z determistycznym pojmowaniem świata. Związek
pomiędzy f. falową a zachowaniem się opisywanej przez nią cząsteczki wyraża gęstość
prawdopodobieństwa P(xyzt). Wielkośc ta określa prawdopodobieństwo znalezienia
cząstki w poblizu punktu o współ. (xyz) i ma postać P(xyzt) = FI(xyzt) * FI*(xyzt)
Gdzie: FI*(xyzt) oznacza sprzężenie zespolone f FI. W praktyce „i” trzeba Zamienic na
”-i”.
SCHRODINGHERA - Jest to równanie falowe dla cząstek. Zalozenia:
1. Równanie to powinno być zgodne z postulatami Einstaina i de Broglia:
ν
h
E
=
p
h
=
λ
2. Musi odzwierciedlać związek pomiedzy całkowitą energią E cząstki o masie m, a jej
energią kinetycznej
m
p
2
2
i jego energia potencjalną V
V
m
p
E
+
=
2
2
3. Równanie musi być liniowe względem funkcji
4.Eneria potencjalna V jest w ogólności funkcją x, y, z ale może być tez funkcją t.
V(x,y,z,t,) = Vo = const
,
,
,
(
)
(
2
)
,
,
,
(
2
2
Ψ
−
+
Ψ
∇
t
z
y
x
V
E
m
t
z
y
x
h
81) Zasada Fermata dla odbicia
Promienie świetlne poruszają się zawsze po takich drogach, aby czas ich przejścia
pomiędzy dwoma danymi punktami był najkrótszy
Aby droga APB była najkrótsza T-czasz przejścia
2
2
2
2
)
(
x
d
b
x
d
x
a
x
−
+
−
=
+
sinΦ
1
=sinΦ
1
’
Φ
1
=Φ
1
’
Co wyjaśnia prawo załamania:
2
1
v
PB
v
AP
T
+
=
2
2
2
1
2
2
)
(
v
x
d
b
v
x
a
T
−
+
+
+
=
Po obliczeniu pochodnej
2
2
2
2
2
1
)
(
x
d
b
v
x
d
x
a
v
x
−
−
−
=
+
=>
lub
21
2
1
2
1
sin
sin
n
v
v
=
=
Φ
Φ
Funkcja własna będąca rozwiązaniem równania Schrödingera nosi nazwę funkcji
falowej. Funkcja falowa, w najogólniejszej postaci funkcja zespolona, nie ma
bezpośredniego sensu fizycznego. Dopiero jej kwadrat interpretujemy jako gęstość
prawdopodobieństwa znalezienia cząstki. Powyższa interpretacja pochodzi od
, który podał ją w
1926
roku.
F. falowe P(xyzt) będące rozwiązaniami równania Schrod. Są f. zespolonymi. Wynika
stąd że w mechanice kwantowej nie możemy nadać funkcji falowej samoistnego
znaczenia fizycznego w sensie klasycznym. Przepis na opis tego podał Max Born.
Interpretacja ta stanowi zerwanie z determistycznym pojmowaniem świata. Związek
alową a zachowaniem się opisywanej przez nią cząsteczki wyraża gęstość
prawdopodobieństwa P(xyzt). Wielkośc ta określa prawdopodobieństwo znalezienia
cząstki w poblizu punktu o współ. (xyz) i ma postać P(xyzt) = FI(xyzt) * FI*(xyzt)
a sprzężenie zespolone f FI. W praktyce „i” trzeba Zamienic na
Jest to równanie falowe dla cząstek. Zalozenia:
1. Równanie to powinno być zgodne z postulatami Einstaina i de Broglia:
2. Musi odzwierciedlać związek pomiedzy całkowitą energią E cząstki o masie m, a jej
i jego energia potencjalną V
3. Równanie musi być liniowe względem funkcji Ψ(x,y,z,t) będącej jego rozwiązaniem.
4.Eneria potencjalna V jest w ogólności funkcją x, y, z ale może być tez funkcją t.
0
)
=
Promienie świetlne poruszają się zawsze po takich drogach, aby czas ich przejścia
pomiędzy dwoma danymi punktami był najkrótszy
czasz przejścia
c
PB
c
AP
T
+
=
2
2
1
1
sin
sin
v
v
Φ
=
Φ
21
czyli prawo Sneliusa

CYKL CARNOTA
Pierwsza przemiana zachodzi przy stałej temperaturze, wiec energia wewnętrzna
gazu nie ulga zmianie. Gaz pobiera ciepło Q
1
ze źródła ciepła
wykonanie pracy
W przemianie drugiej, zachodzącej pomiędzy punktami 2 i 3
adiabatycznemu. Oznacza to, że odcięty został zarówno dopływ ciepła, jak i
możliwość przekazania ciepła otoczeniu, ale rozprężanie odbywało się nadal do
objętości V
3
.
Trzeci etap jest znów przemianą izotermiczną, w której gaz zostaje sprężony od
objętości V
3
do V
4
. Gaz oddaje ciepło do chłodnicy o wielkiej pojemności cieplnej,
wiec temperatura T
2
pozostaje niezmieniona, ale wskutek rozprężania
adiabatycznego od objętości V
2
do V
3
, które zaszło wcześniej, jest niższa od
temperatury T
1
. Praca wykonana przez gaz w tym procesie wynosi
Zauważmy, że w tym przypadku obie wielkości: wykonana praca i ciepło "pobrane" z
chłodnicy są ujemne. Ciepło oddane, któremu przypisujemy wartość dodatnią,
oznacza się zwykle symbolem
. Mamy więc
Czwarty proces jest znów adiabatyczny i przeprowadza układ od punktu
początkowego punktu 1. W ten sposób cykl zostaje zamknięty. a
po wykonaniu całego cyklu ma swą pierwotną wartość. Przyrost energii wewnętrznej
układu równy jest zeru, a sumaryczna wykonana praca równa jest pobranemu przez
układ ciepłu zgodnie ze wzorem (11.4)
Indukcja elektro.
Sposoby wzbudzania prądu:
- zbliżenie lub oddalenie magnesu względem nieruchomej zwojnicy powoduje
wytworzenie w tej zwojnicy prądu
- na odwrót
Indukcja elektromagnetyczna jest to wzbudzene prądu elektrycznego w przewodniku
pod wpływem zmian pola magnetycznego obejmującego ten przewodnik.
Zwrot prądu indukcyjnego jest taki, że pole magnetyczne wytworzone przez ten prąd
przeszkadza zmianom pola magnetycznego, które wzbudza ten prąd.
Zostosowanie:
Jeśli zbliżamy magnes do zwojnicy to w zwojnicy wytwarza się prad którego pole
magnetyczne ma od strony magnesu dokladnie taki sam biegun. Przy oddalaniu ma
przeciwny S > N
SIŁA ELEKTRODYNAMICZNA-sila dzialajaca na przewodnik z pradem umieszczony w
polu magnetycznym
Fe=B*J*l*sinα [1N]
B-indukcja pola magn[1T]
J-nat pradu płynącego w przew [1A]
l-dlugosc przewodnika
α-kat miedzy kierunkiem pola magn.a przewodnikiem;
SIŁA LORENZA-
sila z jaka pole magn.dzxiala ja poruszajaca się w nimczastke
obdarzona ładunkiem El.
Fl=qVBsinα[1N]
Indukcja elektromagnetyczna - zjawisko
powstawania siły elektromotorycznej
przewodniku na skutek zmian strumienia pola magnetycznego. Zmiana ta może być
spowodowana zmianami pola magnetycznego lub względnym ruchem przewodnika i
źródła pola magnetycznego. Zjawisko to zostało odkryte w 1831
angielskiego fizyka Michała Faradaya.
Zjawisko indukcji opisuje prawo indukcji elektromagnetycznej Faradaya:
,
gdzie:
to indukowana siła elektromotoryczna (SEM) w woltach;
Φ
B
to strumień indukcji magnetycznej przepływający przez powierzchni
przewodnikiem.
Pierwsza przemiana zachodzi przy stałej temperaturze, wiec energia wewnętrzna
ze źródła ciepła i w całości zużywa go na
(13.1)
3, gaz ulega rozprężeniu
adiabatycznemu. Oznacza to, że odcięty został zarówno dopływ ciepła, jak i
możliwość przekazania ciepła otoczeniu, ale rozprężanie odbywało się nadal do
Trzeci etap jest znów przemianą izotermiczną, w której gaz zostaje sprężony od
ciepło do chłodnicy o wielkiej pojemności cieplnej,
pozostaje niezmieniona, ale wskutek rozprężania
które zaszło wcześniej, jest niższa od
. Praca wykonana przez gaz w tym procesie wynosi
.
(13.2)
Zauważmy, że w tym przypadku obie wielkości: wykonana praca i ciepło "pobrane" z
pisujemy wartość dodatnią,
(13.3)
Czwarty proces jest znów adiabatyczny i przeprowadza układ od punktu 4 do
. W ten sposób cykl zostaje zamknięty. a energia wewnętrzna
cyklu ma swą pierwotną wartość. Przyrost energii wewnętrznej
układu równy jest zeru, a sumaryczna wykonana praca równa jest pobranemu przez
oddalenie magnesu względem nieruchomej zwojnicy powoduje
Indukcja elektromagnetyczna jest to wzbudzene prądu elektrycznego w przewodniku
pod wpływem zmian pola magnetycznego obejmującego ten przewodnik.
ądu indukcyjnego jest taki, że pole magnetyczne wytworzone przez ten prąd
przeszkadza zmianom pola magnetycznego, które wzbudza ten prąd.
Jeśli zbliżamy magnes do zwojnicy to w zwojnicy wytwarza się prad którego pole
magnesu dokladnie taki sam biegun. Przy oddalaniu ma
sila dzialajaca na przewodnik z pradem umieszczony w
sila z jaka pole magn.dzxiala ja poruszajaca się w nimczastke
siły elektromotorycznej w
gnetycznego. Zmiana ta może być
lub względnym ruchem przewodnika i
1831 roku przez
Zjawisko indukcji opisuje prawo indukcji elektromagnetycznej Faradaya:
;
cy przez powierzchnię objętą
- ruch polegający na (powolnym) obrocie osi symetrii wirującego bąka symetrycznego
wokół wyróżnionego kierunku w przestrzeni. Oś symetrii bąka zatacza tzw. stożek
precesji. Ruch ten jest spowodowany działaniem zewnętrznego momentu siły,
usiłującego zmienić kierunek wektora momentu pędu (przewrócić
Wartość przyrostu krętu dla małego
przyrostu czasu Δt:
ΔL = sinϑΔφ
Wartość momentu siły ciężkości:
M = mga sin ϑ
Podstawiając powyższe równania do wzoru drugiego prawa dynamiki:
Ponieważ oś Ziemi jest nachylona pod pewnym kątem do płaszczyzny orbity
(ekliptyki), a wirująca Ziemia nie jest bąkiem kulistym (w przybliżeniu elipsoida
obrotowa), siła grawitacji Słońca i siły odśrodkowe dążą do ustawienia osi obrotu
Ziemi w kierunku prostopadłym do płaszczyzny ekliptyki. Powoduje to powolną
precesję osi ziemskiej. Okres ruchu precesyjnego wynosi T = 26 000 lat. Precesja
powoduje zmianę położenia bieguna niebieskiego, który obecnie znajduje się w
pobliżu gwiazdy - Ursae Minoris, a wczasach starożytnych znajdował się w pobliżu
gwiazdy α - Lyrae (Wega).
Ruch precesyjny powoduje, że wektor wypadkowej prędkości kątowej
i symetrii wirującego bąka symetrycznego
wokół wyróżnionego kierunku w przestrzeni. Oś symetrii bąka zatacza tzw. stożek
precesji. Ruch ten jest spowodowany działaniem zewnętrznego momentu siły,
usiłującego zmienić kierunek wektora momentu pędu (przewrócić bąka).
Wartość przyrostu krętu dla małego
Podstawiając powyższe równania do wzoru drugiego prawa dynamiki:
Ponieważ oś Ziemi jest nachylona pod pewnym kątem do płaszczyzny orbity
(ekliptyki), a wirująca Ziemia nie jest bąkiem kulistym (w przybliżeniu elipsoida
obrotowa), siła grawitacji Słońca i siły odśrodkowe dążą do ustawienia osi obrotu
stopadłym do płaszczyzny ekliptyki. Powoduje to powolną
precesję osi ziemskiej. Okres ruchu precesyjnego wynosi T = 26 000 lat. Precesja
powoduje zmianę położenia bieguna niebieskiego, który obecnie znajduje się w
h starożytnych znajdował się w pobliżu
Ruch precesyjny powoduje, że wektor wypadkowej prędkości kątowej ω
Wyszukiwarka
Podobne podstrony:
OU pytania id 342624 Nieznany
MG pytania id 297579 Nieznany
Cierpialkowska pytania id 11706 Nieznany
biogeografia pytania id 87155 Nieznany (2)
kreska pytania id 250564 Nieznany
odpowiedzi na pytania 2 id 3325 Nieznany
Pogadanka pytania id 369678 Nieznany
elektro pytania id 157897 Nieznany
Mechanika plynow PYTANIA id 291 Nieznany
opracowane pytania 2 id 337625 Nieznany
Prawo cywilne pytania id 386408 Nieznany
ODPOWIEDZI NA PYTANIA 4 id 3325 Nieznany
dyplom pytania id 145523 Nieznany
najwazniejszy pdf na HES id 313 Nieznany
braz nowe pytania id 92924 Nieznany (2)
Automatyka pytania id 73347 Nieznany
MG pytania 2 id 297580 Nieznany
Opracowane pytania 5 id 337632 Nieznany
fizjo pytania id 174178 Nieznany
więcej podobnych podstron