
Mechanika Płynów
Opracowane pytania
Strona
1/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
ZAGADNIENIA Z MECHANIKI PŁYNÓW
1. Klasyfikacja płynów.
Płynami nazywamy ciała nie wykazujące sprężystości podstawowej . Ciała takie wykazują się
wielką ruchliwością dzięki której :
-
podlegają łatwo odkształceniom postaciowym pod działaniem nawet małych sił
zewnętrznych
-
przyjmują kształt naczynia w którym się znajdują
Własności te wykazują zarówno ciecze jak i gazy . Jednakże ciecze różnią się od gazów
kilkoma istotnymi cechami (przy czym różnice te zanikają w pobliżu punktu krytycznego) .
Otóż ciecze posiadają określoną objętość w szerokim zakresie ciśnień a pozostając w
spoczynku w dużym naczyniu tworzą swobodne zwierciadło ( oczywiście w warunkach
grawitacji ) . Natomiast gazy wykazują zdolność ekspansji , dzięki której wypełniają
całkowicie naczynie , do którego zostały wprowadzone , nie tworząc swobodnego zwierciadła
. W konsekwencji ciecz w danej temperaturze posiada określoną gęstość , niezależnie od
wymiarów naczynia co odróżnia ją od gęstości gazów. Własności te tłumaczy molekularna
struktura płynów . W cieczach poszczególne cząstki utrzymane są w ciasnym upakowaniu
działaniem sił międzycząsteczkowych , natomiast cząstki gazu nie podlegają temu działaniu .
2.Pojęcie lepkości. Miary lepkości. Jednostki.
Istotną cechą każdego płynu rzeczywistego jest opór stawiany zewnętrznym siłą ścinającym.
Siły te wywołują w płynie naprężenia styczne (
τ
). Stanowią one istotę tarcia wewnętrznego,
które w przypadku płynów nazywa się lepkością. A zatem lepkością płynu nazywamy jego
zdolność przenoszenia naprężeń stycznych.
Lepkość uwarunkowana jest molekularną strukturą płynów i dlatego zależność wiążącą siłę
tarcia z rozkładem prędkości można by wyprowadzić z kinematycznej teorii gazów i cieczy.
Zmiana prędkości płynu przypadająca na jednostkę odległości w kierunku normalnym do
kierunku przepływu czyli iloraz różniczkowy:
Gradient prędkości
Newton wysuną hipotezę, w myśl której siła styczna jest proporcjonalna do gradientu
prędkości:
Przy czym znak – oznacza, że siła ta jest przeciwna do kierunku ruchu płynu.
Zatem naprężenie styczne równa się:
Wzór ten jest matematyczną formą Newtonowskiego prawa tarcia. Występujący w nim
współczynnik proporcjonalności
η
zwany jest dynamicznym współczynnikiem lepkości.
Miarą lepkości w układzie SI jest :
−
dy
dV
F
dy
dV
T
∆
−
=
∆
η
dy
dV
F
T
F
η
τ
−
=
∆
∆
=
→
∆
0
lim
2
m
Ns

Mechanika Płynów
Opracowane pytania
Strona
2/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Używa się też jednostki w układzie CGS:
Lub jednostki pochodnej, 100 razy mniejszej:
1 centypuaz=0,01P
Dwie cechy płynu, jakimi są lepkość i gęstość, można zastąpić jedną mianowicie ilorazem
lepkości dynamicznej przez gęstość. Otrzymujemy wtedy kinematyczny współczynnik
lepkości:
Zwany tak dlatego, że jego miara:
Zawiera miary długości i czasu.
Jednostką lepkości kinematycznej jest: 1 stok=1 st =1 cm/s
Ale częściej jest stosowana jednostka pochodna: 1 centystok=1cst=0,001st
3. Ciśnienie wielkość skalarna, wektorowa czy tensorowa?
Ciśnienie jest wielkością skalarną. Jeżeli siła powierzchniowa działająca na element
powierzchniowy jest zwrócona ku temu elementowi, to naprężenie normalne jest ciśnieniem,
w przeciwnym przypadku – ciągnieniem. Naprężenia normalne w cieczy są z reguły
ciśnieniami. W płynie pozostającym w równowadze względem ścian naczynia, ciśnienie na
element powierzchniowy, umieszczony w dowolnym punkcie, nie zależy od przestrzennej
orientacji tego elementu. Powyższe prawo niezależności ciśnienia o orientacji elementu
powierzchniowego, sformułowane przez Eulera, wyraża fakt że ciśnienie ma charakter
skalarowy (bezkierunkowy)
Ciśnienie wywierane przez atmosferę ziemską nazywamy ciśnieniem atmosferycznym lub
barometrycznym i oznaczamy symbolem p
b
.
Ciśnienie bezwzględne (absolutne p
a
) mierzone jest względem doskonałej próżni.
Nadciśnienie (p
n
) jest nadwyżką ciśnienia bezwzględnego ponad ciśnienie atmosferyczne :
Podciśnienie (p
w
) stanowi różnicę między ciśnieniem atmosferycznym a ciśnieniem
bezwzględnym:
Jednostką miary ciśnienia jest N/m
2
= Pa lub jednostka sto tysięcy razy większa czyli bar,
który jest prawie równy atmosferze technicznej (1 at = 1kG/cm
2
), a mianowicie:
lub
s
*
cm
g
1P
1puaz
=
=
ρ
η
ν
=
2
T
L
b
a
n
p
p
p
−
=
a
b
w
p
p
p
−
=
at
m
N
bar
019716
,
1
/
10
1
2
5
=
=
bar
at
980665
,
0
1
=
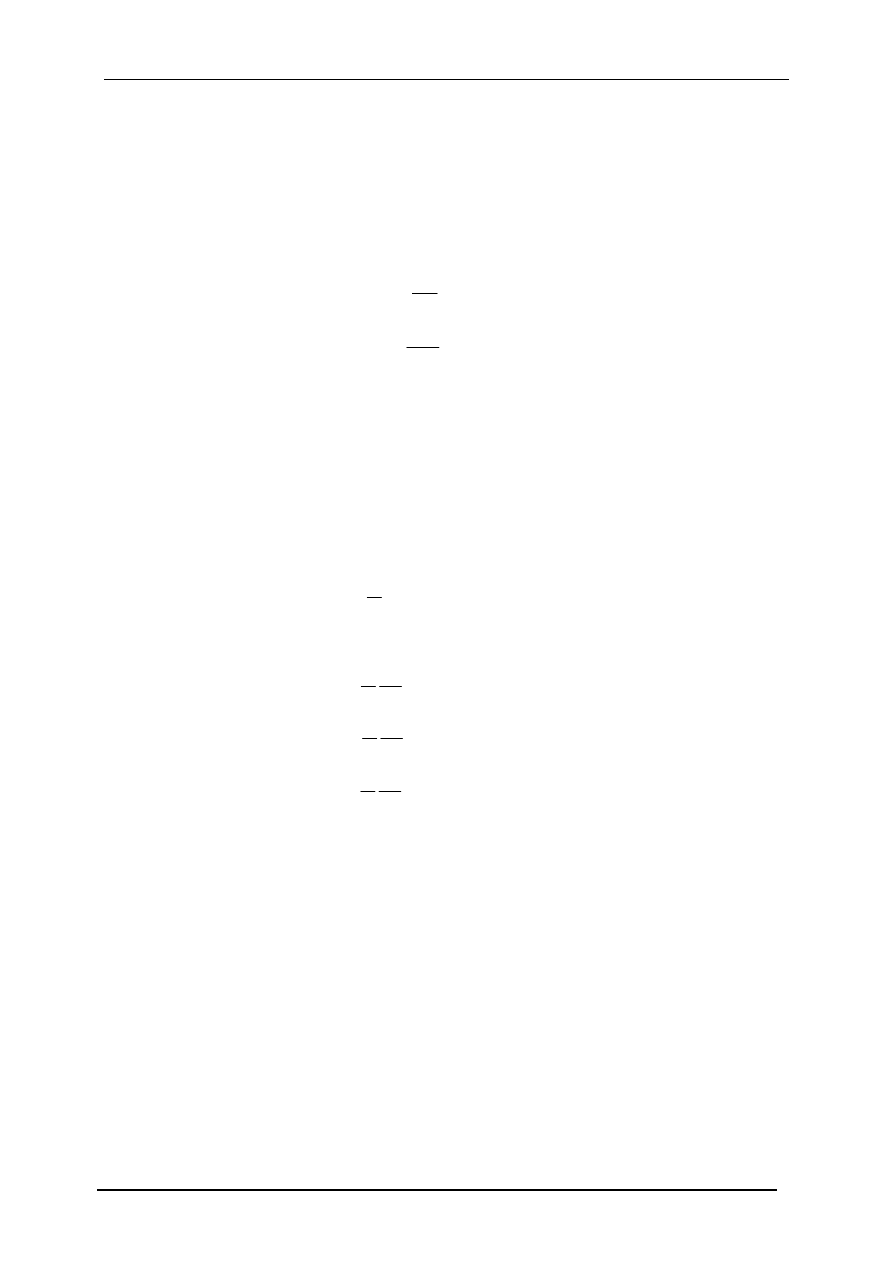
Mechanika Płynów
Opracowane pytania
Strona
3/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
4. Metody pomiaru ciśnienia. Jednostki ciśnienia.
W układzie jednostek SI jednostką ciśnienia jest Pa i bar
Ciśnienie mierzymy za pomocą :
-do pomiaru podciśnienia służy wakuometr;
-do pomiaru nadciśnienia służy manometr;
-do pomiaru ciśnień absolutnych służy barometr.
5. Warunek równowagi. Powierzchnie stałego potencjału. Paradoks hydrostatyczny.
Równanie równowagi (rów. Eulera):
Można je również zapisać w postaci współrzędnościowej:
Równanie Eulera umożliwia nam analizę równowagi cieczy poddanej działaniu sił
ciśnieniowych
(*)
a
m
N
bar
019716
,
1
/
10
1
2
5
=
=
bar
at
980665
,
0
1
=
2
1
1
m
N
Pa
=
2
1
1
cm
kG
at
=
0
1
=
−
gradp
F
ρ
r
=
∂
∂
−
=
∂
∂
−
=
∂
∂
−
0
1
0
1
0
1
z
P
z
y
P
y
x
P
x
ρ
ρ
ρ
const
p
U
dU
dp
dp
dr
gradU
gradU
F
dp
r
d
F
r
gradpd
r
d
F
dr
gradp
F
=
+
=
+
=
−
−
=
=
=
−
=
−
ρ
ρ
ρ
ρ
ρ
ρ
0
0
/*
0
r
r
r
r
r
r

Mechanika Płynów
Opracowane pytania
Strona
4/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Jedynie siły masowe-potencjalne są w stanie wywołać równowagę cieczy nieściśliwej.
W szczególności jeżeli p=const to dp=0 i z równania (*) otrzymujemy że U=const co oznacz
że powierzchnie stałego ciśnienia są zarazem powierzchniami ekwipotencjalnymi.
Paradoks hydrostatyczny.
Parcie na dno naczynia nie zależy od ciężaru zawartej w nim cieczy lub od objętości cieczy,
lecz zależy wyłącznie od ciężaru właściwego cieczy, głębokości dna pod zwierciadłem i od
pola F.
6. Równowaga względna. Przedmiot mechaniki płynów. Pojęcia podstawowe.
Równowaga względna – stan w którym ciecz przemieszcza się wraz z naczyniem ruchem
jednostajnym lub jednostajnie przyspieszonym (ciecz pozostaje w spoczynku względem
ścianek naczynia).
Mechanika płynów zajmuje się badaniem równowagi lub ruchów, a także powstawaniem
ruchów płynu pod działaniem różnego rodzaju sił.
Przedmiotem mechaniki płynów jest także określenie sił, z. jakimi płyn działa na ciało w nim
zanurzone lub na ściany ograniczające przepływ.
Mechaniką cieczy potocznie nazywa się hydromechanikę, zaś mechaniką gazów –
aeromechanikę. Hydromechanika dzieli się na hydrostatykę, która bada prawa rządzące cieczą
w spoczynku oraz hydrodynamikę, zajmującą się ruchem cieczy. Natomiast w ramach
aeromechaniki rozpatruje się na ogół wyłącznie aerodynamikę.
Przedmiotem aerodynamiki jest m.in. badanie przepływów, podczas których występują duże
różnice ciśnień, pociągające za sobą znaczne zmiany objętości, a więc i gęstości. Chodzi tu o
przepływy z dużymi prędkościami, jak np. podczas wypływu gazu ze zbiornika lub podczas
przepływu przez kanał łączący dwie przestrzenie o znacznej różnicy ciśnień, albo podczas
lotu szybkich samolotów, rakiet i pocisków.
Prawo Pascala
Gdy na płyn działają wyłącznie siły powierzchniowe, to ciśnienie ma jednakowa wartość w
każdym punkcie płynu.
Jest to prawo mówiące o rozchodzeniu ciśnienia w płynie.
8. Napór na ściany płaskie. Współrzędne środka naporu .
Parciem hydrostatycznym nazywa się siłę powierzchniowa, jaką wywiera ciecz w stanie
spoczynku na powierzchni dowolnie zorientowanej w przestrzeni. Siła ta jest skierowana
prostopadle do rozpatrywanej powierzchni.
Odległość środka naporu od osi Ox równa jest iloczynowi momentu bezwładności przez
moment statyczny figury względem tej osi
Współrzędne środka naporu.
F
z
N
S
*
*
γ
=
F
y
Js
y
z
F
y
Js
y
y
F
y
Jxy
x
S
N
N
S
S
N
S
N
*
*
*
+
=
+
=
=
Mechanika Płynów
Opracowane pytania
Strona
5/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
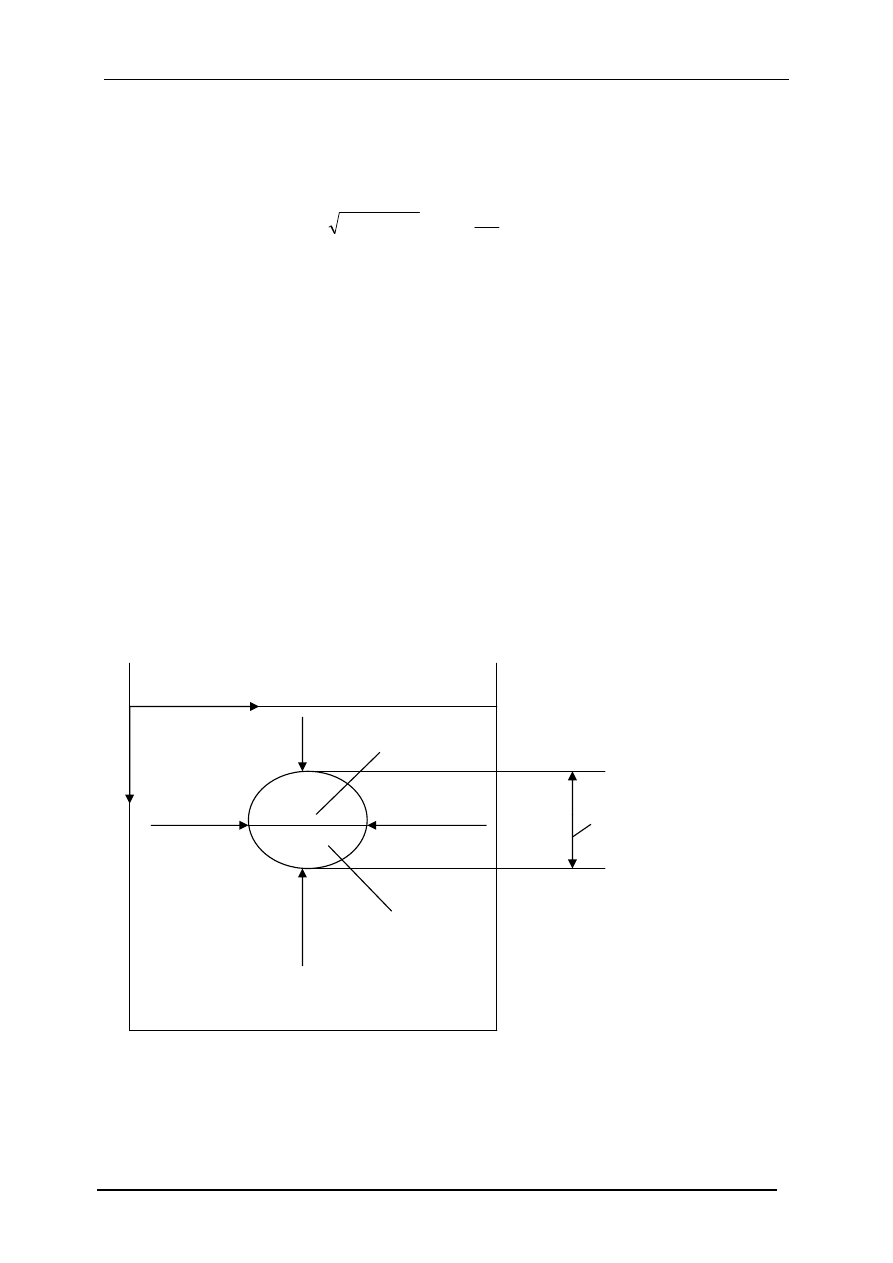
9. Napór na ściany zakrzywione. Współrzędne środka naporu.
Składowa pozioma naporu Nn na powierzchni zakrzywionej, obliczona w dowolnym
kierunku jest równa naporowi na figurę płaską, uzyskaną przez zrzutowanie powierzchni
zakrzywionej na płaszczyznę pionową, prostopadła do tego kierunku
Składowa pionowa naporu Nz na powierzchnię zakrzywioną równa się ciężarowi słupa cieczy
wznoszącego
się
nad
ta
powierzchnie,
ograniczonego
tworzącymi
pionowymi
poprowadzonymi przez kontur powierzchni i sięgającego do powierzchni Oxy
10.Zjawisko wyporu. Odkrycie Archimedesa.
Na powierzchnię zamkniętą A=A1+A2 ciała zanurzonego w cieczy działa parcie ze
wszystkich stron. Wypadkowe parcie w kierunku poziomym tj. w kierunku osi x jest równe 0,
gdyż dwa przeciwne skierowane parcia Fx dotyczą tej samej powierzchni Ax, a więc
liczbowo są równe. Wypadkowe parcie w kierunku pionowym wynosi:Fz=Fz1+Fz2.
Fz1-parcie do góry równe ciężarowi słupa cieczy nad dolną powierzchnią ciała A1,
Fz2-parcie w dół równe ciężarowi słupa cieczy nad górną powierzchnią ciała A2,
Różnica tych ciężarów jest równa ciężarowi cieczy G o tej samej objętości co objętość ciała
zanurzonego. Wypadkowe parcie działające do góry na zanurzone ciało nosi nazwę wyporu:
W=Fz=G=
ρ
gV
V
Nz
F
z
Nn
Nn
Nz
Nz
Nn
N
x
*
*
*
tg
,
2
2
γ
γ
α
=
=
=
+
=
F
Fx
Fz
1
Fz
2
A
2
A
1
X
Z
Ax

Mechanika Płynów
Opracowane pytania
Strona
6/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Gdzie V i G -objętość i ciężar wypartej cieczy,
Powyższe równanie przedstawia prawo Archimedesa, w myśl którego ciało zanurzone w
cieczy traci (pozornie) na ciężarze tyle, ile waży ciecz wyparta przez to ciało.
Archimedes żył ok.287-212 p.n.e., Syrakuzy, starożytna Grecja.
11.Stany stateczności pływania . Metacentrum i odległość matacentryczna.
Pod statecznością pływania rozumie się zdolność powrotu ciała pływającego wychylonego ze
stanu równowagi do pierwotnego położenia.
Ciała całkowicie zanurzone:
Na ciało całkowicie zanurzone działają dwie siły:
Wypór W i ciężar ciała G
1
. Punkt S oznacza środek ciała zanurzonego i w ogólnym
przypadku nie musi pokrywać się ze środkiem wyporu N, której leży w środku
geometrycznym ciała . Równowaga pływania jak wiadomo , zachodzi wówczas, gdy W=G
1
i
gdy
W
r
i
1
G
r
leżą wzdłuż tej samej osi pionowej , czyli wzdłuż osi pływania .
Możliwe są trzy przypadki :
a)
punkt S leży poniżej punktu N
b)
punkt S leży powyżej punktu N
c)
punkt S i N pokrywają się
Przy obrocie ciała dookoła osi poziomej, np. dookoła osi przechodzącej przez S, o kąt
α
,
punkt N przemieszcza się w położenie N’, przy czym W’=W. Powstaje moment pary sił
W’*l=G*l, który bądź przeciwdziała wychyleniu a), bądź wzmaga wychylenie b) bądź jest
równy 0 c).
Można zatem stwierdzić co następuje :
a)
ciała stateczne – środek ciężkości S leży poniżej środka wyporu N
b)
ciało niestateczne – S leży powyżej W
c)
równowaga obojętna – punkty S i N pokrywają się
Przy przesunięciach lub obrotach względem pozostałych osi ciało całkowicie zanurzone
pozostaje zawsze w równowadze obojętnej.
M.=-W*l
1
=-
ρ
*q*V*l
1
2
Gdzie
V – objętość wody wypartej przez ciało pływające.
Moment M.
k
wynosi :
M.
k
=W
k
*l
3
=
∫∫
∫∫
∫∫
=
=
=
A
A
A
A
J
q
dA
y
q
y
dA
y
q
y
dW
min
2
*
*
*
*
*
*
*
*
*
*
*
*
ϕ
ρ
ϕ
ρ
ϕ
ρ
3
Gdzie: J
x
=J
min
– moment bezwładności pola pływania A względem osi x.
Podstawiając równania 1,2,3 do równania 4 otrzymuje się :
V
J
l
l
min
2
1
=
+
ϕ
Z rysunku 2b wynika zależność :
l
1
+l
2
=(m.+n)*sin
ϕ
≈
(m.+n)*
ϕ
Po podstawieniu otrzymuje się ostatecznie, że odległość metacentryczna wynosi :
M.=
n
V
J
−
min
5

Mechanika Płynów
Opracowane pytania
Strona
7/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Gdzie: n – odległość środka ciężkości S ciała i środka wyporu.
Równowaga stała (m.>0) będzie zatem miała miejsce :
0<n<
V
J
min
Gdy środek ciężkości S leży poniżej środka wyporu N, wówczas:
l
1
+l
2
=(m.-n)*
ϕ
’
Równanie przyjmie postać :
M.=
n
V
J
+
min
Widać , że w tym wypadku jest zawsze m.>0, czyli ciało pływające zawsze znajduje się w
równowadze stałej. Poprawa stateczności statków jest uzyskiwana przez obniżenie środka
ciężkości S ( zmniejszeń ) . Innym sposobem jest stosowanie tzw. stabilizatorów czyli
podwodnych skrzydeł, które po wysunięciu zwiększają moment wywołany dodatkowym
wyporem.
12. Kinematyka płynów. Cele, zadania, parametry kinematyczne.
W kinematyce płynów zajmujemy się analitycznym opisem przepływów nie zależnie
od przyczyn (tzn. sił), które te przepływy wywołują. Opis ruchu jest więc czysto
geometryczny.
W kinematyce płynów posługujemy się pojęciem elementu płynu, które związane jest
w swej istocie z wcześniej omówionym pojęciem kontinuum. Przez element płynu rozumieć
będziemy bryłę na tyle małą w porównaniu z jakimś charakterystycznym wymiarem
przepływu; że można ją uważać za nieskończenie małą w sensie matematycznym. Z drugiej
jednak strony element płynu zawiera na tyle dużo cząstek (drobin) płynu, że wykazuje
makroskopowe cechy fizykalne analogiczne jak. płyn w całej swej masie. W ten sposób
rozumiemy ciągłość struktury elementu płynu przy przejściu granicznym, czyli gdy wymiary
elementu zmniejszamy do zera w sensie makroskopowym.
Ruch płynów może być opisany za pomocą metod analizy matematycznej przy założeniu
ciągłości masy i odkształceń, które to wielkości traktujemy jako ciągłe funkcje czasu. Ale
ciągłość masy sprawia, że ruchy wszystkich elementów płynu są o d siebie zależne. 0 ile
chwilowy ruch ogólny ciała sztywnego można interpretować jako skręt chwilowy wokół
odpowiedniej osi, o .tyle w ruchu ogólnym płynu, oprócz ruchu właściwego ciału sztywnemu,
występują ponadto wynikające z odkształceń (postaciowych i objętościowych) elementów
płynu. Na tym polega istotna różnica pomiędzy kinematyką ciał sztywnych i płynów. Okaże
się jednak, że zarówno pole prędkości odkształcenia związane jest ściśle z polem prędkości
ruchu postępowego.
Główne zadanie kinematyki płynów polega na określeniu prędkości (v) i
przyśpieszenia (a) dowolnego elementu płynu w dowolnej chwili t. Jak się przekonamy w
dalszym ciągu, znając prędkość i przyśpieszenie potrafimy określić pole ciśnień, a zatem i
siły działające w płynie.
W przypadku ogólnym wektorowe pole prędkości, jak również pola pozostałych
parametrów przepływu, mogą zależeć od trzech współrzędnych położenia oraz od czasu.
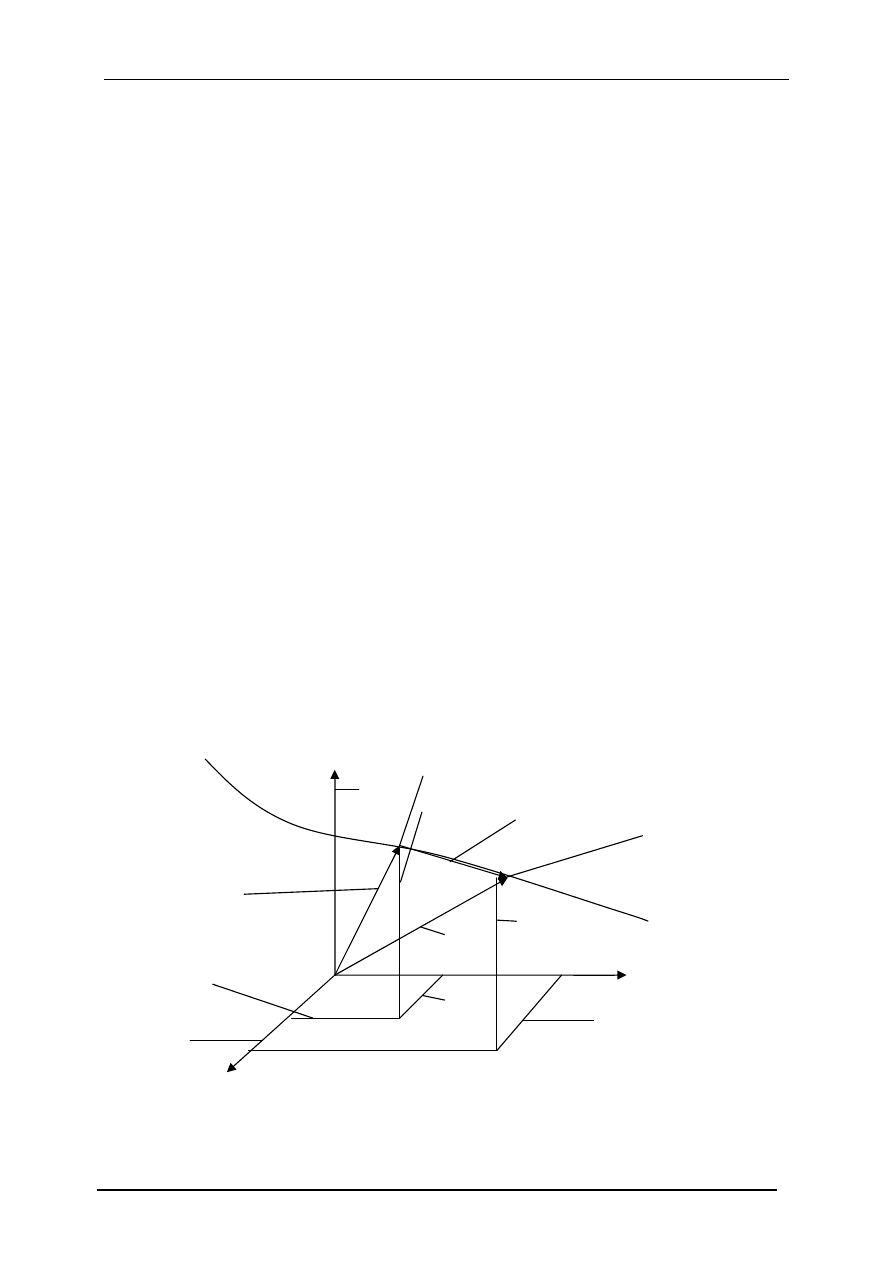
13.Metoda Eulera i Lagrange’a w kinematyce płynów.
Metoda Lagrange’a.
Mechanika Płynów
Opracowane pytania
Strona
8/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Niech Vo oznacza objętość pewnej masy płynu, którą zajmuje on w pewnej chwili
początkowej t0. Po upływie czasu
∆
t, w chwili t=to+
∆
t ta sama masa zajmuje objętość V.
Między wielkościami Vo i V jednoznaczna zależność. Dowolny element płynu
∂
V
∈
V który
w chwili to zajmował położenie Po(to), przemieści się w położenie P(to+
∆
t).Jego położenie
określamy za pomocą współrzędnych x, y, z, tego punktu w przestrzeni, w którym element
znajduje się w chwili t. Bieżące współrzędne elementu zależą nie tylko od geometrii
przepływu lecz i od położenia jakie zajmował on w chwili to. Niech to położenie początkowe
określane będzie współrzędnymi a, b, c, punktu Po. Matematycznym wyrazem tego faktu są
równości:
x= x (a, b, c, t)
y= y (a, b, c, t)
z= z (a, b, c, t)
Są to zarazem parametryczne równania toru tego elementu który został wyodrębniony,
spośród innych za pomocą współrzędnych a, b, c. Parametrem jest czas, zmieniając wartość t
określamy kolejne położenie elementu czyli jego trajektorię (tor). Zmieniając zaś trójkę liczb
a, b, c, skierujemy uwagę na inne elementy płynu .Wszystkie interesujące nas wielkości
(zmienne zależne) takie jak prędkość, ciśnienie, gęstość itd. traktujemy jako funkcję a, b, c, t
pisząc np.: V= V(a, b, c, t). Tak rozumiana czwórka zmiennych niezależnych nosi nazwę
zmiennych (współrzędnych) Lagrange’a. Przy ustalonych wartościach t, funkcja V= V(a, b, c,
t) określa prędkość różnych elementów płynu , reprezentujących ruch całej masy.
Metoda Eulera.
W przestrzeni objętej przepływem wybieramy myślowo pewien punkt „obserwacyjny” M.(x,
y, z). Przez ten punk przechodzą kolejno coraz inne elementy płynu z określonymi
parametrami v, p ,q itd. Interesuje nas zależność tych wielkości od czasu t w określonym
zbiorze punktów M. Według koncepcji Eulera ruch płynu opisuje się przez podanie funkcji:
V= v (x, y, z, t)
P= p (x, y, z, t)
Q= q (x, y, z, t)
Tak rozumiana czwórka zmiennych x, y, z, t nosi nazwę zmiennych Eulera. W metodzie
Eulera mamy okienko i rejestrujemy prędkość przelotnej cząstki. Badanie przepływów pod
względem kinematycznym polega na określeniu prędkości poruszającego się płynu, znając
prędkość można znaleźć rozkład ciśnień i siły działającej w płynie.
x
x
o
Z
c
∆
x
Po(to)
P(t)
a
b
X’
Y’
Y
X
Z’

Mechanika Płynów
Opracowane pytania
Strona
9/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
15. Pojęcie cyrkulacji. Interpretacja fizyczna i analogia.
Cyrkulacją nazywamy całkę krzywoliniową ze skalarnego iloczynu wektora prędkości przez
wektor elementarnego przemieszczenia.
Cyrkulacja prędkości jest wielkością i jeśli ma wartość dodatnią to znaczy, że element płynu
znajduje się na konturze K wykazując tendencje do poruszania się w kierunku zgodnym z
kierunkiem całkowania i na odwrót (kierunek całkowania traktujemy jako dodatni, jeśli
obszar ograniczony konturem K pozostaje przy całkowaniu po lewej stronie). Jeżeli
to znaczy, że tendencja do ruchu w kierunku dodatnim, występująca w części konturu, lub
wektory prędkości w każdym punkcie konturu są prostopadłe do elementu ds.
16. Równania toru i linii prądu, rurka i powierzchnia prądu, struga
TOR ELEMENTU PŁYNU – Linia w przestrzeni styczna do wektorów prędkości w każdym
swoim punkcie w odpowiedniej chwili.
W przepływach ustalonych tor elementu płynu pokrywa się z linią prądu
LINIA PRĄDU – Nazywamy linię pola prędkości . Jest to linia styczna w każdym punkcie do
wektora prędkości.
RURKĘ PRĄDU – Nazywamy powierzchnię utworzoną z linii prądu.
STRUGA – Jest to poruszający się płyn wypełniający rurkę prądu . Jeśli przekrój poprzeczny
strugi stanowi powierzchnię elementarną d
δ
(ma wymiar elementu płynu) to strugę
nazywamy elementarną.
Strumień masy strugi i strumień masy strugi elementarnej , zgodnie z definicją określa się
wzorami :
∫
=
Γ
k
k
ds
v *
r
0
=
Γ
k
df
w
dz
v
dy
u
dx
=
=
=
w
dz
v
dy
u
dx
=
=
δ
ρ
δ
ρ
d
V
dG
d
V
G
ń
S
ń
*
*
*
*
=
=
∫∫

Mechanika Płynów
Opracowane pytania
Strona
10/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
17. Przepływy potencjalne .
Prawie zawsze można traktować w przybliżeniu każdy przepływ przestrzenny jako przepływ
dwuwymiarowy ( płaski lub osiowo symetryczny). Takie uproszczenie jest niezmiennie
korzystne ze względów matematycznych gdyż pozwala stosować bardzo wygodną i dobrze
opracowaną teorię funkcji zmiennej zespolonej. W niniejszych rozważaniach będą omówione
wobec tego tylko płaskie przepływy potencjalne .
Równania Laplace’a dla układu płaskiego :
0
2
2
2
2
=
∂
∂
+
∂
∂
y
x
φ
φ
Cechy równania Laplace’a jest jego liniowość co jest wykorzystywane przy superpozycji
czyli nakładanych przepływów.
Przyrost potencjału prędkości może być wyrażony jako różniczka zupełna:
x
d
∂
∂
=
φ
φ
dy
y
dx
∂
∂
=
φ
Wykorzystując dwa pierwsze wyrazy równania otrzymujemy :
d
=
φ
V
x
*dx+V
y
*dy
Całkując otrzymujemy różnicę potencjałów prędkości dwóch punktów A i B ( dowolnych )
)
*
*
(
dy
V
dx
V
y
x
B
A
A
B
+
=
−
∫
φ
φ
Po uwzględnieniu równania :
∫
∫
∫
+
+
=
=
=
Γ
C
B
C
B
z
y
x
S
C
B
S
BC
dz
V
dy
V
dx
V
ds
V
ds
V
)
*
*
*
(
*
*
Otrzymujemy dla przepływu płaskiego :
A
B
AB
φ
φ
−
=
Γ
Równanie to oznacza zależność pomiędzy cyrkulacji prędkości a potencjałem prędkości w
przepływie płaskim:
dx
V
dy
V
d
y
x
*
*
−
=
ψ
gdzie
ψ
jest funkcją prądu.
Równania Cauchy – Riemanna
V
x
=
y
x
∂
∂
=
∂
∂
ψ
φ
V
y
=
x
y
∂
∂
−
=
∂
∂
ψ
φ
Różnica funkcji prądu w dwóch dowolnych punktach płaskiego przepływu potencjalnego
równa się zatem strumieniowi objętości
AB
V&
gdzie
AB
V&
[m
3
/s] jest iloczynem prędkości
normalnej V
n
i powierzchni wyobrażonej przez odcinek AB=dl
Warunki Cauchego Riemanna występują również w teorii funkcji zespolonej zmiennej
Stąd wynika , że potencjał prędkości
φ
tworzą część rzeczywistą , a funkcje prądu
ψ
część
urojoną pewnej funkcji holomorficznej zwanej potencjałem zespolonym f(z)
f(z)=
φ
+i*
ψ
Przy tym z = x + i * y
Gdzie z- zmienna zespolona
i=
1
−
- jedność urojona

Mechanika Płynów
Opracowane pytania
Strona
11/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
18. Przepływy elementarne. Superpozycja przepływów.
Przepływy elementarne są to takie przepływy, które dadzą się określić analitycznie
prostym potencjałem zespolonym. Przepływy elementarne odgrywają podstawowe znaczenie
w badaniach przepływów. Wśród przepływów elementarnych wyróżniamy:
-przepływ jednostajny;
-przepływ prostopadły do ściany;
-przepływ wzdłuż ściany;
-źródło płaskie ;
-wir płaski;
-dipol.
Bardzo ważną cechą równań Laplace’a jest jego liniowość, co jest wykorzystywane
przy super pozycji, czyli nakładaniu się dwóch lub więcej przepływów potencjalnych. W
przypadku dwóch przepływów można zatem zapisać:
skąd:
W wyniku super pozycji został otrzymany przepływ o potencjale zespolonym f(z),
którego części rzeczywiste i urojone są odpowiednio
φ
i
ϕ
, przy czym obowiązuje zależność:
Superpozycja przepływów może być wyliczona metodą analityczną lub wykreślną, a zadanie
sprowadza się do znalezienia sumarycznego (wypadkowego) potencjału zespolonego, a
zwłaszcza części urojonej.
19. Odwzorowanie konforemne
W nauce o przepływach, podobnie jak w innych naukach, wiele zagadnień jest opartych na
izomorfiźmie, czyli na tożsamości struktury układów fizycznych i matematycznych.
Szczególnie odnosi się to do przepływów z ich bardziej lub mniej sprecyzowanymi modelami
matematycznymi. Modele matematyczne zmieniają się po poddaniu ich transformacją, ale te
zmienione modele mogą być wykorzystane z racji niezmienności pewnych cech względem
transformacji.
szczególne znaczenie posiada znajomość przebiegu jakiejś funkcji wewnątrz pewnego
obszaru, gdy znana jest tylko jej wartość na brzegu tego obszaru. Dany obszar płaski można
za pomocą odwzorowania przekształcić na inny obszar płaski, dla którego rozwiązania są
znane lub łatwe do wyznaczenia. Odwzorowanie znalazło szerokie zastosowanie przede
wszystkim w aerodynamice. Ułatwia ono w oparciu o teorię funkcji zmiennej zespolonej
+
=
+
=
2
2
2
1
1
1
)
(
)
(
ϕ
φ
ϕ
φ
i
z
f
i
z
f
+
=
+
=
2
2
1
1
2
2
1
1
ϕ
ϕ
ϕ
φ
φ
φ
k
k
k
k
)
(
*
)
(
*
)
(
2
2
1
1
z
f
k
z
f
k
z
f
+
=

Mechanika Płynów
Opracowane pytania
Strona
12/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
rozwiązanie szeregu zagadnień praktycznych, do których należy między innymi
projektowanie profilów lotniczych.
Odwzorowanie polega na przyporządkowaniu punktów jednej płaszczyzny punktom drugiej
płaszczyzny. Przyporządkowanie odbywa się przy pomocy funkcji odwzorowującej. Na
przykład, punkt A’ płaszczyzny z jest przyporządkowany punktowi A płaszczyzny ξ, co
wynika z następującej funkcji zmiennej zespolonej:
z=F
1
(ξ),
gdzie: z=x+iy
ξ=ξ+iη
Funkcja F
1
(ξ) odwzorowuje zatem punkty płaszczyzny ξ na płaszczyznę z. Istnieje oczywiście
także funkcja odwrotna:
ξ=F
2
(z),
która odwzorowuje punkty płaszczyzny z na płaszczyznę ξ.
Jeżeli funkcja odwzorowująca jest holomorficzna, wówczas zachodzi ODWZOROWANIE
KONFOREMNE (podobne). Odwzorowanie konforemne polega na tym, że odpowiadające
sobie figury złożone z elementarnie małych odcinków pozostają po odwzorowaniu
geometrycznie podobne. Tak więc, dwie linie przecinające się pod pewnym kątem, również
po odwzorowaniu przecinają się pod tym samym kątem.
Warto przedstawić kilka prostych funkcji odwzorowujących. Najprostsza funkcja
odwzorowująca ma następującą postać:
z=a*ξ
jeżeli a jest liczbą rzeczywistą, wówczas powyższa funkcja powoduje zmianę skali figury
odwzorowywanej, jeżeli zaś a jest liczbą zespoloną wówczas odwzorowanie polega obrocie
tej figury. Funkcja, która powoduje przesunięcie figury odwzorowywanej ma postać:
z=ξ+a
Na podstawie powyższego można krótko scharakteryzować metodę, która jest stosowana przy
odwzorowaniu opływu profilu. Jeżeli jest znany opływ jakiegoś profilu, na przykład profilu
kołowego, wówczas znany jest również potencjał zespolony f(ξ) tego opływu w płaszczyźnie
ξ. Znając funkcję odwzorowującą F
1
, można otrzymać potencjał zespolony f(z), który
przedstawia pewien przepływ w płaszczyźnie z, a mianowicie:
f(z)=F
1
[f(ξ)].
Funkcja odwzorowująca opływ okręgu na opływ profilu lotniczego nosi nazwę funkcji
Żukowskiego:
z=ξ+a
2
/ξ,
W zależności od położenia środka okręgu O względem początku układu współrzędnych,
otrzymuje się profile o różnym kształcie.
Duże usługi oddaje wprowadzenie płaszczyzny prędkości zespolonej, zwanej płaszczyzną
hodografu V
x
, V
y
. jeżeli przepływ w płaszczyźnie x, y nie jest znany, wówczas można go
odwzorować z wyznaczonego uprzednio obszaru płaszczyzny hodografu.

Mechanika Płynów
Opracowane pytania
Strona
13/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Ciało częściowo zanurzone:
Dowolne wychylenie ciała jest, ogólnie biorąc, wypadkową trzech przesunięć i trzech
obrotów względem osi x, y, z. Najczęściej środek ciężkości S ciała pływającego leży powyżej
środka wyporu N. Jak wynika z dalszych rozważań, przy takim położeniu środka ciężkości
możliwe jest zachowanie stateczności pływania, co było wykluczone w przypadku ciała
pływającego całkowicie zanurzonego.
Ciało jest stateczne, czyli posiada równowagę stałą przy przesunięciu wzdłuż osi z. Przy
takiej wymuszonej zmianie głębokości zanurzenia, zostaje naruszona równowaga między
ciężarem ciała G
1
i wyporem W, co prowadzi do zmiany zanurzenia i powrotu do stanu
początkowego.
Równowaga obojętna ma miejsce natomiast podczas przesunięć równoległych do
zwierciadła cieczy, czyli podczas przesunięć wzdłuż osi x, y oraz podczas obrotu wokół osi z.
Pozostaje do rozważenia stateczność ciała w odniesieniu do obrotu wokół osi poziomych x i
y. W obu przypadkach postępuje się analogicznie, jednak istotniejsze znaczenie ma
stateczność wokół osi x, gdyż dotyczy obrotu wokół tej głównej osi bezwładności pola
pływania, która odpowiada minimalnemu momentowi bezwładności. Zagadnienie to ma
ważne znaczenie w teorii okrętu. Przy obrocie ciała wokół osi x o kąt φ, środek wyporu
przemieszcza się w położenie N’. Przy niewielkim kącie wychylenia φ objętość zanurzonej
części ciała nie ulega zmianie, wobec czego W=W’. Wypór W’ i ciężar ciała G
1
tworzą parę
sił o momencie prostującym G
1
*l=W’*l, gdzie l jest ramieniem stateczności. Jeżeli moment
prostujący ma zwrot przeciwny do kąta obrotu – ciało znajduje się w równowadze stałej,
jeżeli moment ma zwrot zgodny – ciało znajduje się w równowadze chwiejnej, wreszcie jeżeli
moment jest równy 0 – ciało znajduje się w równowadze obojętnej.
Te
rozważania
uzupełnić
można,
wprowadzając
pojęcie
punktu
M,
zwanego
METACENTRUM, czyli punktem przecięcia linii działania wyporu początkowego W i
wyporu chwilowego W’. Odległość punktu M od środka ciężkości ciała S nosi nazwę
ODLEGŁOŚCI (WYSOKOŚCI) METACENTRYCZNEJ m. Dla informacji można podać,
że minimalna odległość metacentryczna statków wynosi m=0,5-4,5 [m].
Położenie wzajemne punktów M i S wskazuje na znak momentu prostującego. Mianowicie,
gdy M leży powyżej S, wówczas odległość metacentryczna m jest dodatnia (m>0) i ciało jest
stateczne. Gdy M leży poniżej S, wówczas odległość m jest ujemna (m<0) i ciało jest
niestateczne. Wreszcie gdy punkty M i S pokrywają się, odległość m jest równa zero (m=0) i
równowaga ciała ma charakter obojętny. Z powyższego widać, że aby wyznaczyć warunek
stateczności pływania, wystarczy znaleźć znak odległości metacentrycznej m.
Odległość metacentryczną m można wyrazić przez parametry geometryczne ciała
pływającego. Przy wychyleniu o mały kąt φ, wypór chwilowy W’ jest równy sumie
algebraicznej wyporu początkowego W i wyporów W
k
objętości klinowych:
W’=W-W
k
+W
k
Wobec tego, warunek momentów względem osi x ma następującą postać:
M’=M+M
k
gdzie:M
k
=W
k
*l
3
- moment wywołany wyporem objętości klinowych.
Momenty M’ i M wynoszą odpowiednio:
M’=W’*l
2
=ρ*g*V*l
2

Mechanika Płynów
Opracowane pytania
Strona
14/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
21 . Zasada zachowania masy. Równanie ciągłości.
Masa układu (obszaru płynnego) pozostaje stała. Masa cząstki elementarnej jest równa ρdV,
gdzie dV jest objętością zajętą przez cząstkę, a ρ jest gęstością płynu. Wiedząc, że gęstość
może się zmieniać w rożnych punktach układu, zachowanie masy może być wyrażone przez
całkę
D/Dt*∫ ρdV=0
D/Dt - jest użyte, gdyż rozpatrujemy określony zbiór elementów materialnych.
Równanie ciągłości wynika bezpośrednio z zasady zachowania masy
dm/dt = d/dt * ∫ ρdV = 0
22. Zasada pędu w mechanice płynów. Równanie Eulera, Naviera-Stokesa.
Zasada pędu w mechanice płynów .
Poznana w mechanice ciał sztywnych zasada pędu znajduje także zastosowanie w mechanice
płynów, głównie przy obliczaniu reakcji dynamicznej strumienia na umieszczoną w nim
przeszkodę (np. na łopatkę turbiny) lub na ściany przewodu (kanału) , ograniczającego
przepływ.
Zgodnie z brzmieniem wspomnianej zasady prędkość układu materialnego równa się
geometrycznej sumie sił zewnętrznych, działających na ten układ, czyli
(1)
Aby skonkretyzować pojęcie układu materialnego, wyodrębniamy pewien obszar V, który
może zawierać nie tylko płyn lecz także ciała sztywne, ruchome lub nieruchome. Jednak tylko
płyn zawarty w obszarze stanowi układ materialny (rys.1). Otaczająca go powierzchnia
płynna przemieszcza się wraz z wyodrębnionym zbiorem cząstek płynu (Fz
→
F'z), które
zmieniają przy tym swój prąd. Ale w przepływie ustalonym obszar V można traktować jako
nieruchomy, bowiem w dowolnym jego punkcie różne elementy płynu mają zawsze te same
parametry. Będziemy go nazywać obszarem kontrolnym, a powierzchnię otaczającą go -
powierzchnią kontrolną.
∑
∏
=
i
i
P
dt
d

Mechanika Płynów
Opracowane pytania
Strona
15/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Różnica pędu masy przepływająca przez obszar kontrolny w jednostce czasu określa prędkość
zmiany pędu układu, czyli lewą stronę równania (1).
Całkę obliczamy po powierzchni kontrolnej Fz, przy czym wyrażenie podcałkowe jest różne
od zera tylko na tej części powierzchni, która jest przebijana przez linie prądu (czyli nie jest
powierzchnią prądu).
Zmiana pędu dokonuje się pod wpływem się zewnętrznych, które są oddziaływaniami ze
strony ciał nie należących do układu. Chodzi tu o ściany sztywne, na których przepływający
gaz lub ciecz zmienia swój kierunek. Również płyn znajdujący się poza obszarem kontrolnym
może działać na układ pewną siłą powierzchniową. Wreszcie pole grawitacyjne (lub inne
zewnętrzne pole sił) może zmieniać pęd układu.
Płyn uderzający o ścianę sztywną wytwarza na jej powierzchni F
w
pewne pole ciśnień
dynamicznych oraz pole się tarcia. Wypadkowa zbioru elementarnych sił (normalnych i
stycznych do F
w
nazywa się reakcją dynamiczną strugi (symbol R). Z reguły jest to
niewiadoma, którą chcemy obliczyć właśnie z pomocą zasady pędu. W równaniu (1) wystąpi
wprawdzie siła przeciwna (-R), jako oddziaływanie ściany na płyn , ale nie ma to istotnego
znaczenia.
Innego rodzaju siła powierzchniowa może powstać wskutek istnienia statycznego pola ciśnień
na powierzchni F
z
. Jeżeli odpowiedni zbiór elementarnych sił ciśnieniowych -pdF ma wektor
główny, to jest nim właśnie siła ciśnieniowa , statyczna
Siła ta występuje , np. gdy przepływ przez rurociąg o osi zakrzywionej odbywa się pod
ciśnieniem.
Trzecia z wymienionych sił zewnętrznych ma charakter siły objętościowej i jako taka, ma
wektor główny
Jeżeli ta siła jest wyłącznie pochodzenia grawitacyjnego (tzn. q=g),to Pq oznacza po prostu
ciężar płynu w obszarze kontrolnym. Może on zmieniać pęd cieczy, ale tylko w ruchu
pionowym. W przypadku gazu jest z reguły pomijalny.
dF
d
dt
d
z
z
F
n
F
∫
∫
∏
≡
Ο
≡
ρνν
ρν
∫
−
=
z
F
s
P
∫
−
=
Fz
q
qdV
P
ρ

Mechanika Płynów
Opracowane pytania
Strona
16/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Zgodnie z brzmieniem zasady pędu wyrażenie (2) równa się sumie wektorowej trzech
omawianych sił
(3)
Jest to ogólne (wektorowe) równanie zasady pędu dla przepływu ustalonego. Wprawdzie na
tej podstawie nie można określić szczegółowo pola sił na powierzchni opływanego cała, a
tylko jego wypadkową R, ale taki wynik na ogół nas zadowala. Zasadę pędu wykorzystuje się
najczęściej do obliczania dynamicznej reakcji strugi na płaty lotnicze łopatki turbin, ściany
rurociągów.
Z drugiej strony równanie (3) odznacza się ogólnością , która polega na tym , że stosuje się
ono do płynów rzeczywistych (a więc lepkich i ściśliwych) i niezależnie od tego, czy płyn
wymienia ciepło z otoczeniem, czy też nie. Różnica między reakcją strugi płynu idealnego i
lepkiego polega jedynie na nieco zmienionym module i kierunku wektora R.
Całkę przekształca się łatwo , gdy w przekrojach kontrolnych występują prostokątne
profile prędkości oraz jednorodne pole gęstości. W takim przypadku
gdzie indeksy 1,2 dotyczą przekroju wlotowego i wylotowego odpowiednio.
Jeżeli ponadto wektor główny się statycznych (ciśnieniowych i masowych). Równa się zero,
to wzór na reakcję dynamiczną strugi redukuje się do postaci
Jeżeli w obszarze kontrolnym ciśnienie statyczne ulega zmianie tak, że wektor wówczas
oprócz równania zasady pędu trzeba jeszcze wykorzystać równanie Bernouliego. Wiele zadań
technicznie ważnych rozwiązuje się tą drogą stosunkowo łatwo. Trzeba jednak podkreślić, że
łatwość ta uwarunkowana jest znajomością prędkości w przekrojach kontrolnych.
Równania Eulera.
Podstawowe równania dynamiki płynów nie lepkich wyprowadził Euler (1775r.). Punktem
wyjścia jest druga zasada dynamiki , w myśl której pochodna pędu układu względem czasu
równa się wektorowi głównemu sił zewnętrznych , działających na ten układ . Niech płyn
zawarty w pewnym ograniczonym obszarze V stanowi nasz układ . Elementarna masa p dV,
wyodrębniona w otoczeniu dowolnego punktu w tym obszarze , ma pęd p v dV.
Pęd całego układu wynosi .Siły zewnętrzne, działające na układ ,są to siły
Objętościowe i powierzchniowe .
.Druga zasada dynamiki zastosowana do układu płynnego dostarcza więc równania
q
s
Fz
n
P
P
R
dF
+
+
−
=
∫
ρνν
∫
θ
ρν
d
1
2
)
(
)
(
Θ
−
Θ
=
Θ
∫
ρν
ρν
ρν
Fz
d
1
2
)
(
)
(
Θ
−
Θ
=
ρν
ρν
R
0
≠
s
P
∫
V
dV
ρν
∫
V
dV
ρν
∫
∫
∫
=
=
V
V
V
a
dV
div
qdV
dv
dt
d
)
.(
τ
ρ
ρν
∫
V
dV
div
τ

Mechanika Płynów
Opracowane pytania
Strona
17/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Obliczając pochodną całki objętościowej z lewej strony tego równania trzeba uwzględnić , że
zmienia się w czasie nie tylko pęd p v, lecz i objętość V obszaru, który obejmuje stale tę samą
masę płynu (ściśliwego).
Wobec tego
gdzie F oznacza granicę obszaru V. Teraz wszystkie trzy równania są całkami liczonymi po
tym samym obszarze. Przenosimy je na jedną stronę i przyrównujemy do zera wyrażenie
podcałkowe .
Otrzymujemy równanie:
(b)
W płynie nie lepkim tensor naprężeń
τ
= - pI, więc div
τ
= -grad p., gdzie p oznacza ciśnienie
statyczne. Ponadto rozwijamy pochodną iloczynu w pierwszym wyrazie równania (b), które
przyjmuje postać
Wyrażenie w nawiasie równa się zero na mocy warunku ciągłości . Ostatnia operacja polega
na rozwinięciu pochodnej materialnej wektora prędkości i podzieleniu całego równania przez
p.
Otrzymujemy
Powyższe równanie wektorowe rozpiszemy w postaci trzech równań analitycznych w
prostokątnym układzie współrzędnych
Są to równania Eulera .Opisują one wyłącznie ruch płynu nie lepkiego, ponieważ przy ich
wyprowadzaniu nie uwzględniliśmy tarcia wewnętrznego .
Natomiast równania te odnoszą się zarówno do płynów nieściśliwych (tzn. cieczy), jak i do
gazów , a różnica polega na traktowaniu gęstości bądź jako wielkości stałej ,bądź te§ jako
funkcji położenia i czasu. Przytoczone równania stanowią więc teoretyczną podstawę
zarówno hydro- jak i aerodynamiki. W trzech równaniach Eulera występują cztery
,
)
(
)
*
(
)
(
dV
vdivv
dt
v
d
dF
v
dV
t
dV
dt
d
F
V
V
V
∫
∫
∫
∫
+
=
+
∂
∂
=
ρ
ρ
ρν
ρν
ρν
0
)
(
=
−
−
+
τ
ρ
ρ
ρ
div
q
vdivv
dt
v
d
gradp
q
divv
dt
d
v
dt
dv
−
=
+
+
ρ
ρ
ρ
ρ
(
)
gradp
q
v
gradv
v
t
v
ρ
1
*
−
=
+
∂
∂
,
1
x
p
q
z
v
v
y
v
v
x
v
v
t
v
X
X
Z
X
Y
X
X
X
∂
∂
−
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
ρ
,
1
y
p
q
z
v
v
y
v
v
x
v
v
t
v
Y
Y
Z
Y
Y
Y
X
Y
∂
∂
−
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
ρ
,
1
z
p
q
z
v
v
y
v
v
x
v
v
t
v
Z
ż
Z
ż
Y
Z
X
Z
∂
∂
−
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
ρ

Mechanika Płynów
Opracowane pytania
Strona
18/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
niewiadome :vţ, vy ,vz,p., gdy płynem jest ciecz lub gaz przy umiarkowanych zmianach
ciśnienia.
Równania Naviera - Stokesa.
Zasadniczą przyczyną wspomnianych mankamentów teorii Eulera jest pomijanie lepkości ,
jako
nieodłącznej cechy każdego płynu rzeczywistego . Stwierdziliśmy tam, że podczas ruchu
płynu
lepkiego powstają naprężenia styczne ,których wartość można określić za pomocą
niutonowskiego prawa tarcia . Mówiąc dokładniej na element płynu lepkiego w ruchu ,
oprócz sił objętościowych
działają siły powierzchniowe , które mają składową normalną i styczną. Głębsza analiza
zagadnienia wykazuje ,że wpływ lepkości przejawia się nie tylko w powstawaniu naprężeń
stycznych, ale również w zmianie wartości ciśnienia w porównaniu z jego wartością w płynie
idealnym. Komplikuje to znacznie postać różniczkowych równań ruchu płynu lepkiego w
stosunku do równań Eulera .
Przejdźmy do wyprowadzenie różniczkowych równań przepływu lepkiego przestrzennego. W
związku tensora naprężeń
τ
.Ponieważ każdy z tych tensorów ma sześć składowych , więc
ogólnie biorąc, związki między nimi wymagałyby wprowadzenie 36 współczynników
proporcjonalności.
Liczbę ich można jednak zredukować do jednego, jeżeli przejmie się trzy dodatkowe
postulały:
1' – Płyn jest ośrodkiem izotropowym (tzn. wszystkie kierunki w przestrzeni są
równoprawne).
2' -Związek między tensorami
τ
i
ε
nie zależy od przestrzennej orientacji
układu współrzędnych.
3' -Związek ten w przypadku stycznym (v=0), jak również w przepływie idealnym musi się
sprowadzać do postaci
τ
=-pl.
Wszystkie te postulaty, łącznie z podstawowym postulatem Newtona o proporcjonalności
naprężeń stycznych do prędkości odkształceń, spełnia następujący związek (tensorowy)
Jak widać, jedynym współczynnikiem proporcjonalności (o charakterze empirycznym)
pozostała lepkość dynamiczna
η
.
W przypadku płynu nieściśliwego (div v=0) mamy znacznie prostszy związek którym
będziemy się dalej posługiwać:
Określenie siły powierzchniowej, która występuje w równaniu hydrodynamiki, wymaga
obliczenia diwergencji tensora
τ
. Jak wiemy div(pl)=graf p. pozostaje do obliczenia div
ε
.
Otóż
ηε
η
τ
2
3
2
+
−
−
=
l
divv
p
ηε
τ
2
+
−
=
pl

Mechanika Płynów
Opracowane pytania
Strona
19/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Wykorzystując wzór na prędkość odkształceń kontynuujemy obliczenia:
A zatem
Wnioskujemy stąd, że aby otrzymać równanie dynamiki dla cieczy newtonowskiej, wystarcz
do prawej strony równania Eulera dodać człon zawierający laplasjan wektora prędkości. W
ten sposób otrzymamy:
Gdzie: v=
η
/
ρ
- lepkość kinematyczna. Jest to równanie Naiviera – Stokesa, zapisane w
postaci wektorowej. Wraz z równaniem ciągłości div v=0 tworzy ono podstawowy układ
dynamiki płynów newtonowskich, nie ściśliwych. Przy rozwiązaniu tych równań dla
konkretnego przepływu należy uwzględnić warunki brzegowe, a gdy przepływ jest
niestacjonarny – także warunki początkowe. Te ostatnie polegają na określeniu pola prędkości
w pewnej chwili (t=0), obranej za początkową, a więc wymagają sprecyzowania trzech
funkcji:
Vx(x,y,z;0), Vy (x,y,z;0), Vz (x,y,z;0);
Postać tych funkcji nie zależy od tego, czy płyn jest idealny, czy też lepki.
Różnica w analitycznym opisie ruchu płynu idealnego i lepkiego wynika nie tylko z
odmienności równań ruchu , lecz i z odmiennej postaci warunków brzegowych. Te ostatnie
formułujemy zwykle dla powierzchni ciał opływanych lub ograniczających przepływ oraz w
nieskończoności. Przyjmuje się, że w przepływie nie zaburzonym znane są prędkości i
ciśnienie, a niekiedy także natężenie przepływu.
Postać powierzchniowych warunków brzegowych zależy od tego, czy ciało sztywne porusza
się w płynie , czy też struga opływa nieruchome ciało. Omawiane warunki dotyczą prędkości,
a ściślej mówiąc składowej normalnej i stycznej wektora prędkości. Odnośnie do składowej
normalnej warunki brzegowe wyrażają oczywisty fakt, iż powierzchnia graniczna ciała
sztywnego jest dla płynu nieprzenikliwa. Wobec tego jest to jedna z powierzchni prądu. W
przepływie płaskim mówimy w takim przypadku o zerowej linii prądu, na której Vn=0 .
(
)
v
kv
jv
iv
v
v
j
z
v
y
v
x
v
x
v
i
j
x
v
z
v
z
x
v
y
v
y
x
v
x
i
div
Z
Y
X
Z
Y
ż
X
Y
X
X
Y
X
y
X
X
2
2
2
2
2
2
1
2
1
2
1
2
1
2
1
...
2
1
2
1
∇
=
+
+
∇
=
=
∇
+
∇
+
∂
∂
+
∂
∂
+
∂
∂
∂
∂
+
∇
=
=
+
∂
∂
+
∂
∂
∂
∂
+
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
ε
v
v
gradp
div
2
∇
+
−
=
τ
v
v
gradp
q
v
gradp
v
t
v
2
1
)
*
(
∇
+
−
=
+
∂
∂
ρ
(
)
(
)
(
)
(...)
(...)
k
j
z
y
x
k
j
i
z
k
j
i
y
k
j
i
x
div
ZX
YX
XX
ZZ
ZY
ZX
YZ
YY
YX
XZ
XY
XX
+
+
∂
∂
+
∂
∂
+
∂
∂
=
+
+
∂
∂
+
+
+
+
∂
∂
+
+
+
∂
∂
=
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
ε
Mechanika Płynów
Opracowane pytania
Strona
20/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Warunki brzegowe składowej stycznej wynikają z faktu , iż elementy płynu lepkiego
przywierają do ścian. W takim razie na powierzchni ciała nieruchomego prędkość płynu
równa się zero, a gdy ciało porusza się, jest ona taka sama jak prędkość jak prędkość danego
punktu ruchomej powierzchni. W ten sposób możemy zawsze ustawić tyle warunków
brzegowych , ile jest stałych całkowania.
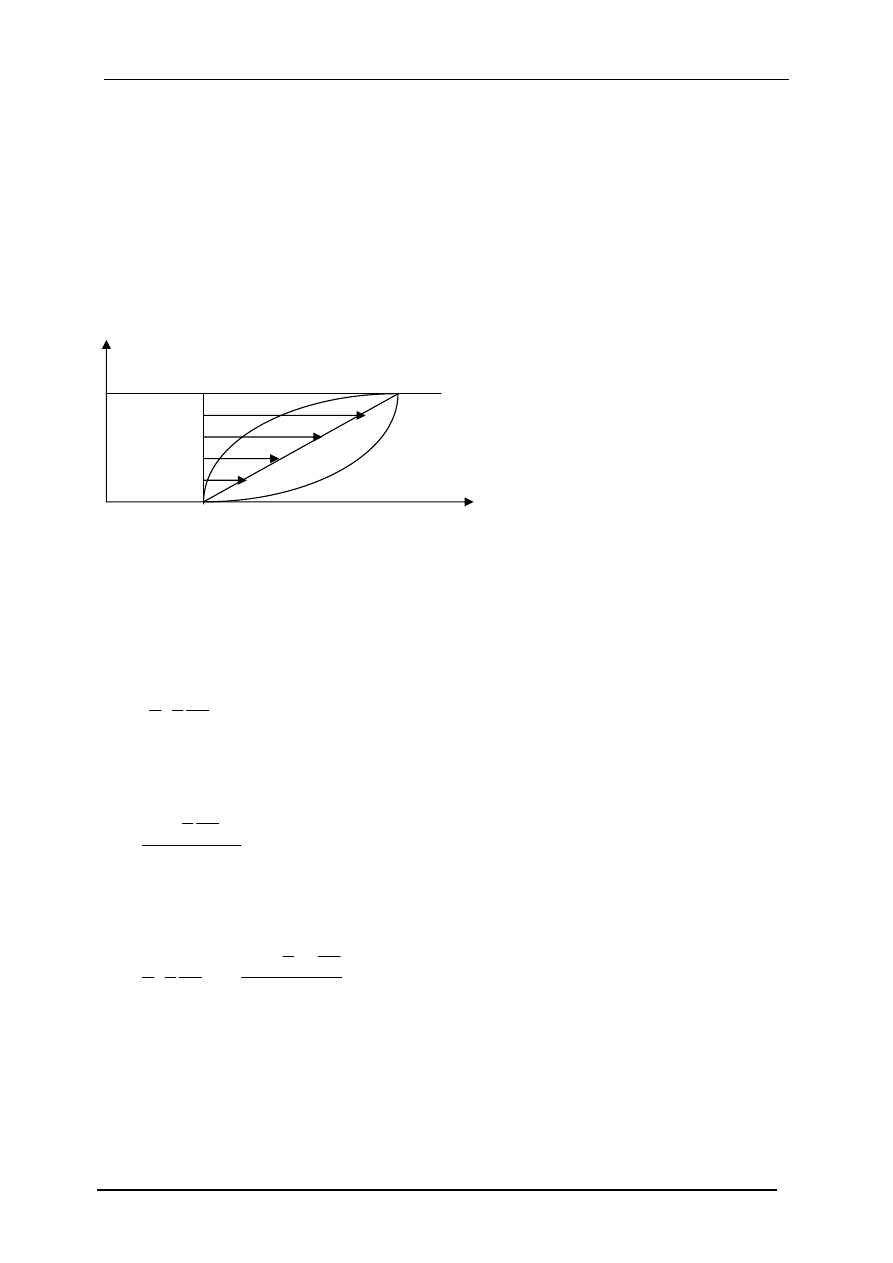
23. Przepływ Couette`a i Hagena-Poiseuillea.
Ciecz lepka płynie między dwiema równoległymi płaszczyznami, z których jedna jest
nieruchoma, druga zaś porusza się z prędkością U.
2
Warunki brzegowe pola prędkości określają zależności:
V
X
(U = 0) = 0
V
Y
(U - h) = 0
+
+
=
B
Ay
y
dx
dP
V
X
2
2
1
1
η
Wyznaczamy stałe
A i B:
h
h
dx
dP
U
n
2
2
1
−
=
A
; B = 0
zatem
−
+
=
y
h
dx
dP
h
U
y
dx
dP
2
2
2
1
2
1
1
η
η
V
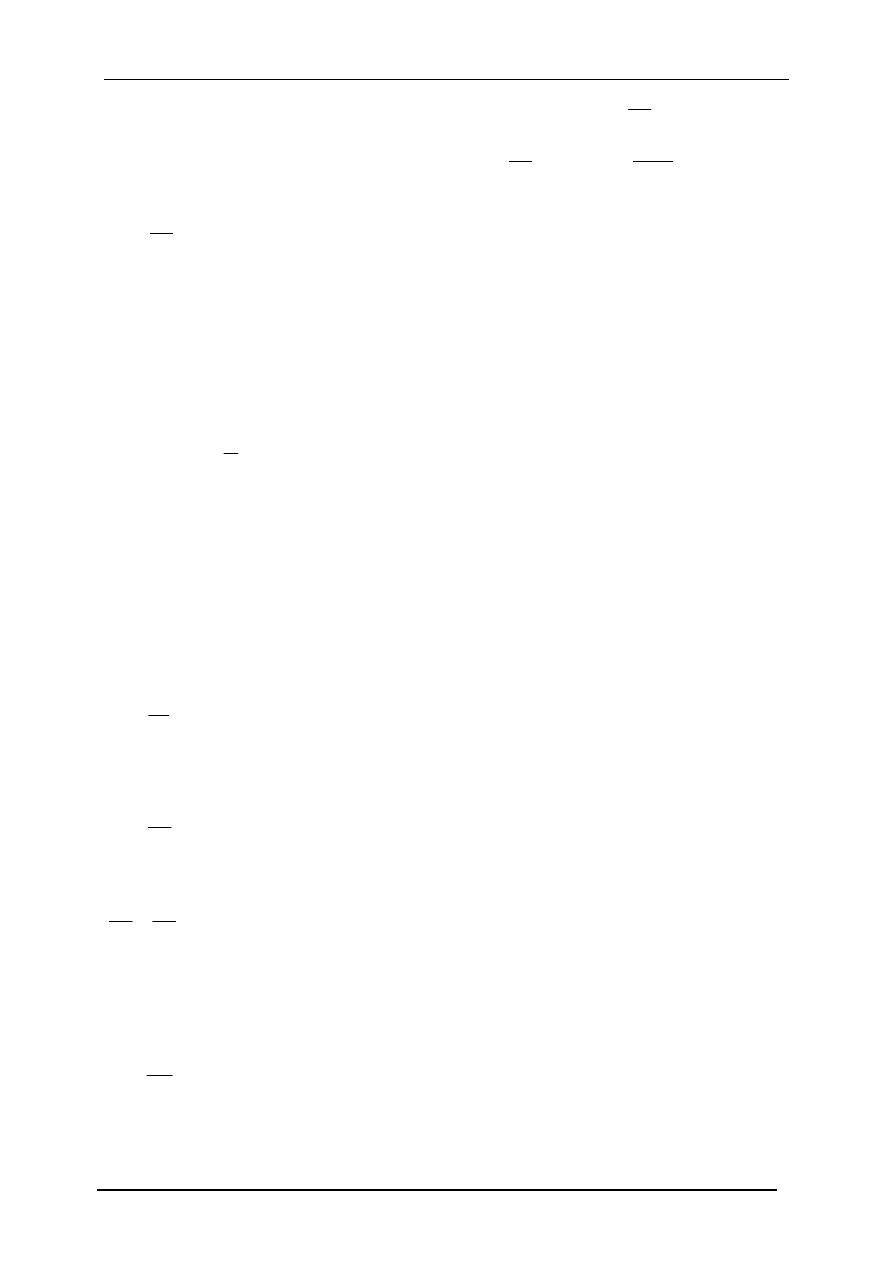
Mechanika Płynów
Opracowane pytania
Strona
21/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Profile prędkości V
X
(y) są paraboliczne i zależą od gradientu . Jeśli
0
=
dy
dP
to przebieg
V
X
(y) jest liniowy (linia 1 na rysunku). Jeśli
0
>
dx
dP
czyli
0
2
2
>
∂
∂
y
Y
X
, parabola
wklęsłością zwrócona jest w dodatnim kierunku osi X (linia 2 na rysunku).
Jeśli
0
<
dx
dP
linia wklęsłością zwrócona jest w kierunku ujemnym (linia 3 na rysunku).
Przepływy przedstawione w tym przypadku nazywają się przepływem Couette`a. Posiadają
one duże znaczenie praktyczne, gdyż stanowią model przepływu oleju w łożyskach..
Przepływ Poiseuielle`a jest to ustalony, uwarstwiony przepływ cieczy lepkiej przez
prosto osiową rurę kołową o stałym przekroju. W tym przypadku profil prędkości jest
paraboliczny czyli
−
=
2
0
1
R
v
V
V
V - prędkość na osi rury
r - odległość od osi
R - promień wewnętrzny rury
24. Liczby kryterialne i ich znaczenie w modelowaniu przepływu.
a)Liczba Reynoldsa jest wielkością bezwymiarową stanowi ona kryterium podobieństwa
częściowego z uwagi na siły lepkości i bezwładności:
b)Kryterium podobieństwa sił ciężkości.
Wielkość bezwymiarowa wyrażająca stosunek sił bezwładności do sił ciężkości, nazywamy
liczbę Froude’a:
Kryterium podobieństwa częściowego sił i zjawisk wynikających z grawitacji przedstawia
równanie:
Kryterium Frounde’a jest sprzeczne z kryterium Reynoldsa to znaczy: niemożliwe jest
równoczesne zachowanie podobieństwa oporu falowego i sił tarcia (w cieczach o tej samej
gęstości),
c)Liczba Strouhala określa stosunek składowej unoszenia do składowej lokalnej siły
bezwładności:
t*-okres rozpatrywanego zjawiska:
υ
lV
=
Re
gl
V
Fr
2
=
2
2
2
1
2
1
l
V
l
V
=
*
Vt
l
Sh
=

Mechanika Płynów
Opracowane pytania
Strona
22/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
d)Liczba Eulera wyraża stosunek sił ciśnieniowych do sił bezwładności w przepływach
nieściśliwych:
e)Liczba Macha określa stosunek prędkości v do lokalnej prędkości dźwięku ‘a’ (tzn.
występującej w danym punkcie):
Jeżeli chodzi o przepływy, to określane są one przede wszystkim polem prędkości. Dlatego
zwykle dwa przepływy uważamy za podobne, gdy ich pola prędkości są podobne.
Chodzi o to aby zjawiska zaobserwowane w przepływie modelowym umożliwiały nie tylko
jakościową ale też ilościową ocenę analogicznego zjawiska w przepływie projektowanym.
W tym celu należy zagwarantować dynamiczne podobieństwo przepływów i tylko pod tym
warunkiem wyniki uzyskane na modelu można przetransponować za pomocą odpowiednich
wzorów na projektowany obiekt.
25. Przepływ laminarny, a turbulentny.
Istnieją dwa jakościowo różne ruchy płynów lepkich:
- laminarny, w którym poszczególne warstwy płynów nie mieszają się ze sobą w
sposób makroskopowo widoczny przesuwają się względem siebie na kształt niezależnych
łusek (lamina - łuska)
- turbulentny, odznaczający się nie stacjonarnością i przypadkowością. Tory
poszczególnych elementów są różne, niepowtarzalne. Poszczególne warstwy płynu
mieszają się ustawicznie, a poszczególne elementy płynu wykazują obok ruchu głównego
również niestacjonarne ruchy w innych kierunkach.
Badania wyjaśniające naturę tych rodzajów przepływów przeprowadził w 1883 r. Osborne
Reynolds. Obserwował on zachowanie się zabarwionej strugi cieczy w strumieniu płynącym
ruchem jednostajnym w szklanej rurce. Przy bardzo małych prędkościach, barwnik układał
się
w cienką linię, równoległą do osi przewodu, co oznacza, że wszystkie cząstki poruszały się po
prostych torach równoległych. Po przekroczeniu pewnej prędkości obraz gwałtownie się
zmieniał: zabarwiona struga pulsowała, rozpływała się i zaczynała szybko zanikać.
Dowodziło to pojawienia się dodatkowych ruchów poprzecznych, powodujących wymianę
cząstek między poszczególnymi strugami i mieszanie się obu cieczy. Tory cząstek stały się
przypadkowymi liniami łamanymi, różnymi dla każdej cząstki.
Reynolds ustalił, że zmiana charakteru przepływu zależy od wartości bezwymiarowej liczby
Reynolds'a (Re) Re=vl/v, gdzie v - prędkość przepływu, 1 - wymiar charakterystyczny
przepływu. Krytyczna liczba Reynolds'a odpowiada przejściu przepływu laminarnego w
turbulentny. Jej wartość zależy od kształtu wlotu do przewodu, stopnia gładkości ścian
przewodu, wstępnych zaburzeń mechanicznych cieczy, drgań przewodu itp. Przejściu
przepływu turbulentnego w laminarny towarzyszy mniejsza wartość liczby Reynolds'a, niż
przejściu z laminarnego w turbulentny. Dla 2300<Re<50000 przepływ może być albo
laminarny albo turbulentny zależnie od pobocznych czynników zakłócających.
2
V
p
Eu
ρ
=
a
V
Ma
=
Mechanika Płynów
Opracowane pytania
Strona
23/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
26. Turbulentna warstwa przyścienna.
W efekcie przepływów turbulentnych występuje oderwanie warstw, które stykają się z
płynami. Turbulentna warstwa przejściowa ma małą skłonność do oderwania. Jeżeli
oberwanie zachodzi, to punkt oderwania jest przesunięty bardziej do tyłu. Mniejsza skłonność
do oderwania jest zrozumiała, gdyż w skutek prędkości pulsacyjnych następuje wymiana
energii kinetycznej pomiędzy poszczególnymi elementami płynu w warstwie przyściennej.
Rozkład prędkości w warstwie turbulentnej jest bardziej wypukły niż w warstwie laminarnej.
28. Charakterystyki geometryczne i aerodynamiczne profilu.
Wzór na siłę oporu ma postać:
Wzór ten w aerodynamice ma ogólniejsze znaczenie, tzn. określa on nie tylko siłę oporu lecz
ogólnie każdą siłę oddziaływania płynu na ciało. Na siłę oporu składają się dwa czynniki:
-opór kształtu;
-opór tarcia.
Siła oporu jest bezpośrednio związana z lepkością płynu. Lepkość powoduje że na
powierzchni opływanego ciała tworzy się warstwa przyścienna. Obejmuje ona jednak tylko
część powierzchni opływowej, po czym odrywa się od niej w miejscu, w którym zachodzi
gwałtowny wzrost ciśnienia. Powoduje to nie symetrie w rozkładzie ciśnień, co jest przyczyną
powstania siły w kierunku przepływu – oporu kształtu. Tarcie płynu lepkiego bezpośrednio o
powierzchnie opływową powoduje, iż oprócz oporu kształtu pojawia się opór tarcia
nazywanym również oporem powierzchniowym. Współczynnik oporu tarcia zależy od
lepkości płynu i chropowatości powierzchni, czyli od struktury warstwy przyściennej.
Najmniejszy opór kształtu stawiają ciała smukłe, czyli takie, które mają tylną część
uformowaną w sposób umożliwiający opływ bez oderwań warstwy przyściennej. Ciała o
kształtach opływowych, jak skrzydła i kadłuby samolotów oraz statków, napotkają podczas
ruchu głównie na opór tarcia.
29. Równanie Bernoulliego dla płynu doskonałego, rzeczywistego i gazów.
const
gz
p
v
=
+
+
ρ
2
2
-
dla cieczy doskonałej
const
z
p
g
v
z
p
g
v
=
+
+
=
+
+
2
2
2
2
1
1
2
1
2
2
γ
γ
-
dla płynu doskonałego
ρ
1
−
=
F
dt
V
d
grad p
-
dla płynów nieściśliwych
const
p
v
=
+
ρ
2
2
-
dla gazów nieściśliwych
2
2
(Re)
l
v
f
R
ρ
=

Mechanika Płynów
Opracowane pytania
Strona
24/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
∫
+
ρ
dp
v
2
2
-
dla gazów ściśliwych
30. Zjawisko kawitacji.
Analizując równania ruchu ustalonego i nieustalonego widać, że wraz ze wzrostem
prędkości zachodzi spadek ciśnienia. Jeżeli zjawisko to zachodzi w cieczach i ciśnienie w
pewnym punkcie spadnie poniżej ciśnienia nasycenia, to ciecz w tym miejscy będzie
parować. Wytworzone pęcherze pary przechodząc w obszar wyższego ciśnienia zanikają.
Obniżenie ciśnienia cieczy poniżej nasycenia jest warunkiem koniecznym powstania fazy
gazowej. Do cieczy parującej należy doprowadzić odpowiednią ilość ciepła - powoduje to,
że proces parowania może nastąpić jedynie w stanie przechłodzonym, tzn. w stanie, w
którym temperatura i nasycenie są mniejsze od odpowiedniej wielkości nasycenia.
Zjawisko polegające na powstaniu fazy gazowej w cieczach nazywamy kawitacją. Aby
uniknąć zjawiska kawitacji, należy tak ukształtować kanały przepływowe, aby nie
występowały w nich duże prędkości przepływowe, czyli nie wystąpiły koncentracje
prędkości. Na zjawisko kawitacji narażone są również ciecze otaczające drgające
elementy. Kawitacja jest przyczyną występowania dużych strat w przepływie oraz występują
duże straty i efekty akustyczne. Prędkość kawitacji:
ρ
p
V
K
2
=
Dla powietrza
V
K
= 2700 [km/h].
31. Straty energii w przepływie płynu. Sposoby opisu i obliczeń.
Wychodząc z równania Bernouliego mamy
Wysokość strat tarcia
gdzie :
λ
- współczynnik tarcia
Wysokość strat lokalnych
gdzie:
ξ
- współczynnik strat miejscowych
sm
strat
k
k
z
P
g
V
z
P
g
V
+
+
+
+
=
+
+
2
2
2
2
1
1
2
1
2
2
γ
γ
g
d
lv
k
strat
2
2
λ
=
g
V
P
k
sm
2
2
ξ
γ
=
∆
=
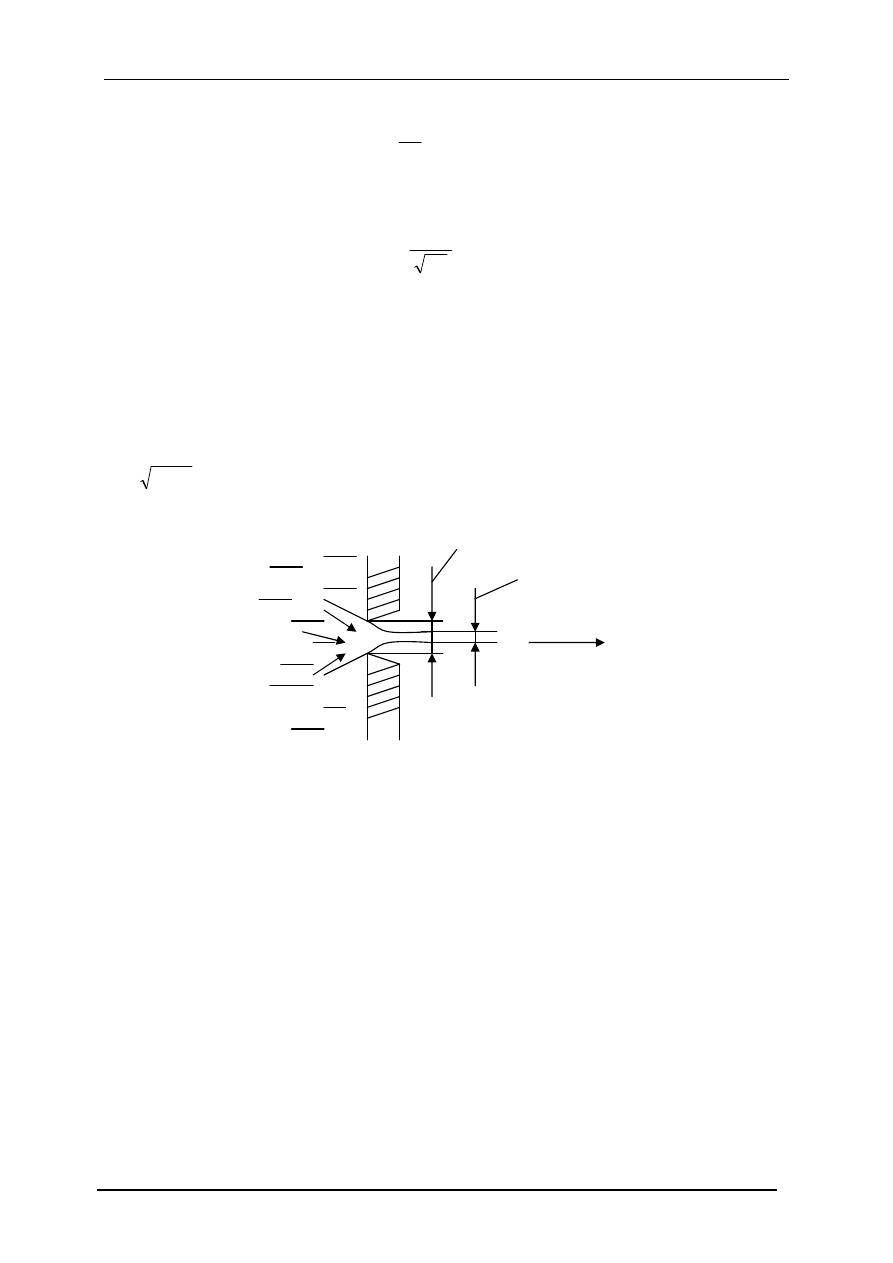
Mechanika Płynów
Opracowane pytania
Strona
25/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Dla przepływu laminarnego:
Dla przepływu burzliwego:
32.Zjawisko wypływu przez otwory i przystawki.
Przy wypływie cieczy ze zbiornika przez otwór o ostrych brzegach zauważono, że obliczony
teoretyczny wydatek według wzoru:
Qrt=Ft+Vt;
Gdzie:
Ft= pole przekroju otworu;
nie jest równy wydatkowi zmierzonemu Qvrz
Przyczyną tej różnicy jest mniejszy przekrój strugi cieczy od otworu w zbiorniku oraz
mniejszą prędkość od prędkości obliczonej Vt. Stosunek przekroju otworu do przekroju strugi
nazywamy kontrakcją i oznaczamy jako
β
=Frz/Ft, skąd Frz=
β
Ft;
β
-współczynnik kontrakcji.
W podobny sposób postąpimy z prędkością
α
=Vrz/Vt
→
Vrz=
α
Vt, gdzie
α
-współczynnik
straty prędkości.
Wydatek rzeczywisty wyrazi się wzorem Qvrz=FrzVrz.
Po podstawieniu wartości Frz i Vrz ostatecznie otrzymamy:
Q=
αβ
Qvt
Jak widać z tego wzoru, obliczony wydatek rzeczywisty równa się wydatkowi teoretycznemu
z uwzględnieniem współczynnika poprawkowego. Współczynnik ten nazywa się
współczynnikiem wydatku. Wartości liczbowe omówionych współczynników są zależne od
tzw. Przystawek. Są to odpowiednio ukształtowane krótkie kawałki rur (L
≈
3D), ustawione
współosiowo z otworem, przymocowane szczelnie do ścian zbiornika.
Re
64
=
λ
4
Re
316
,
0
=
λ
go,
Bernoullie
równania
z
obliczona
cieczy
wyplywu
pręrędko
-
2gH
V
t
=
V
F
t
F
rz

Mechanika Płynów
Opracowane pytania
Strona
26/26
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
34. Przygotować wykaz zagadnień opracowanych samodzielnie (poza wykładem i
ć
wiczeniami)
Przepływ cieczy opisany jest potencjałem (skalarnym) prędkości
Jakie warunek spełniać muszą stałe a, b, c ?
Pole wektorowe W o współrzędnych określonych trema funkcjami P,Q,R trzech zmiennych
nazywamy potencjałem jeśli wyrażenie Pdx+Qdy+Rdz jest różniczką zupełną pewnej funkcji
U (x,y,z), którą nazywamy potencjałem pola wektorowego W. Jest ona funkcją pierwotną
układu funkcji P,Q,R a więc U’x=P, U’y=Q, U’z=R
)
(
2
2
2
cz
by
ax
+
+
=
ϕ
Wyszukiwarka
Podobne podstrony:
Opracowane pytania 5 id 337632 Nieznany
Opracowane pytania id 337622 Nieznany
opracowane pytania1 id 337677 Nieznany
7 fiza opracowane pytania id 4 Nieznany (2)
biologia opracowane pytaniaa id Nieznany
OU pytania id 342624 Nieznany
MG pytania id 297579 Nieznany
opracowanie pytan id 338374 Nieznany
Nhip opracowanie pytan id 31802 Nieznany
Cierpialkowska pytania id 11706 Nieznany
Opracowanie pytan 3 id 338376 Nieznany
opracowania Ekologia id 794643 Nieznany
Opracowanie Hoffmanna id 338261 Nieznany
biogeografia pytania id 87155 Nieznany (2)
opracowanie antropologia id 338 Nieznany
Opracowanie Metrologia 2 id 338 Nieznany
kreska pytania id 250564 Nieznany
opracowanko histogram id 338711 Nieznany
opracowanie ak id 338118 Nieznany
więcej podobnych podstron