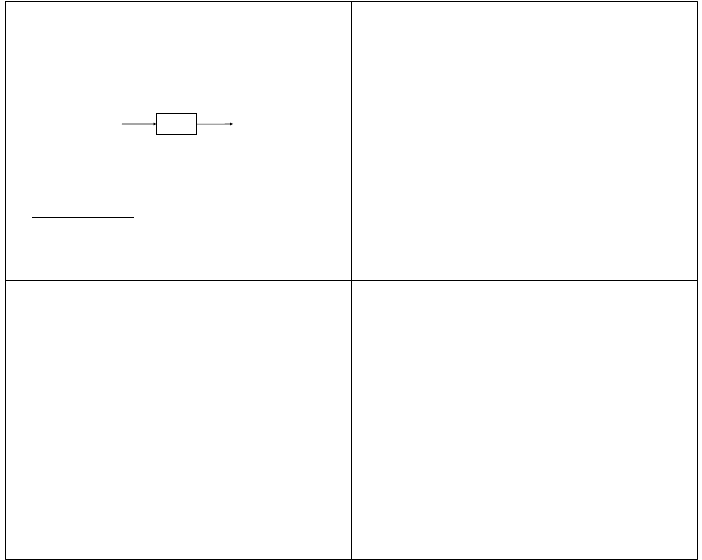
8. Liniowe układy dyskretne.doc, 1/19
UKŁADY DYSKRETNE
1
Pojęcie układu
• matematyczną definicją (modelem) układu jest jednoznaczne przekształcenie
(operator) odwzorujące sygnał wejściowy
x
w sygnał wyjściowy
y
jest to tzw. ujęcie transmisyjne
[ ]
x
T
y =
y
x
T
→
• w ogólnym przypadku układ może być wielowejściowy i wielowyjściowy
• powyższa definicja układu ma charakter uniwersalny i może odnosić się do różnych
klas sygnałów
• jeśli dziedzina
X
i przeciwdziedzina
Y
operatora
T
są zbiorami sygnałów
dyskretnych w czasie, układ nazywamy dyskretnym
1
opracowano na podstawie [1-7], wersja z dnia 02.10.2014
materiał nie jest pełnym i ścisłym pod względem formalnym opracowaniem poszczególnych tematów, stanowi
jedynie szkielet, wokół którego budowany jest wykład
y
x
T [..]
pobudzenie
odpowiedź
8. Liniowe układy dyskretne.doc, 2/19
UKŁADY DYSKRETNE (cd)
Klasyfikacja układów
• układ stacjonarny (niezmienny względem przesunięcia, inwariantny w czasie)
- operator przesunięcia w czasie sygnałów dyskretnych
( )
{
} (
)
0
0
n
n
x
n
x
P
n
−
=
- operator
T
określony w dziedzinie sygnałów dyskretnych nazywamy stacjonarnym,
jeśli dla każdych
( )
n
x
i
0
n
zachodzi przemienność
( )
[
]
{
}
( )
[
]
{
}
n
x
T
P
n
x
P
T
n
n
0
0
=
układ opisany operatorem stacjonarnym nazywamy układem stacjonarnym;
układ opisany operatorem nie spełniającym warunku stacjonarności nazywamy
układem niestacjonarnym
- dla stacjonarnych układów dyskretnych spełniona jest zależność
jeżeli
( )
( )
[
]
n
x
T
n
y
=
to
(
)
(
)
[
]
0
0
n
n
x
T
n
n
y
−
=
−
8. Liniowe układy dyskretne.doc, 3/19
UKŁADY DYSKRETNE (cd)
- operatory: mnożenia skalarnego
( )
( )
n
ax
n
y
=
oraz opóźnienia
( )
(
)
1
−
= n
x
n
y
w dziedzinie sygnałów dyskretnych są operatorami stacjonarnymi
- operator typu
( )
( )
n
x
n
n
y
=
w dziedzinie sygnałów dyskretnych jest operatorem
niestacjonarnymi
• układ liniowy
-
układ dyskretny nazywamy liniowym jeśli spełnia zasadę superpozycji, tzn.
odpowiedź układu na ważoną sumę sygnałów wejściowych równa jest sumie
ważonych odpowiednio odpowiedzi oddzielnie na każdy z sygnałów, w przeciwnym
przypadku układ nazywamy nieliniowym
( )
( )
( )
[
]
( )
[
]
( )
[
]
( )
( )
n
by
n
ay
n
x
bT
n
x
aT
n
bx
n
ax
T
n
y
2
1
2
1
2
1
+
=
+
=
+
=
w ogólnym przypadku
( )
( )
( )
( )
∑
∑
=
=
=
→
=
M
k
k
k
T
M
k
k
k
n
y
a
n
y
n
x
a
n
x
1
1
gdzie
( )
( )
[
]
M
k
n
x
T
n
y
k
k
...,
,
2
,
1
=
=
8. Liniowe układy dyskretne.doc, 4/19
UKŁADY DYSKRETNE (cd)
• układ przyczynowy
jeżeli układ opisany operatorem
T
odwzorowuje zbiór sygnałów
X
w zbiór
sygnałów
Y
i jeżeli
[ ]
1
1
x
T
y =
oraz
[ ]
2
2
x
T
y =
wówczas operator
T
określony
w zbiorze sygnałów dyskretnych
X
nazywa się operatorem przyczynowym jeśli dla
każdych
( ) ( )
X
n
x
n
x
∈
2
1
,
i każdego
0
n
z równości
( )
( )
0
2
1
,
n
n
n
x
n
x
<
=
wynika równość
( )
( )
0
2
1
,
n
n
n
y
n
y
<
=
układ opisany operatorem przyczynowym nazywamy układem przyczynowym;
w przeciwnym wypadku układ nazywamy układem nieprzyczynowym
z powyższych definicji wynika, że dla układu przyczynowego z równości
( )
0
0
n
n
n
x
<
≡
dla
, wynika równość
( )
0
0
n
n
n
y
<
≡
dla
- zatem
odpowiedź
układu przyczynowego nie może poprzedzać wymuszenia
inaczej układ dyskretny nazywamy przyczynowym jeśli wartość sygnału na jego
wyjściu
( )
n
y
w dowolnym momencie czasu
n
zależy jedynie od bieżącej
i poprzednich wartości sygnały wejściowego i nie zależy od przyszłych wartości
sygnału wejściowego w przeciwnym przypadku układ nazywamy nieprzyczynowym
układ nieprzyczynowy jest nierealizowalny praktycznie
8. Liniowe układy dyskretne.doc, 5/19
UKŁADY DYSKRETNE (cd)
• liniowość, stacjonarność i przyczynowość są immanentnymi cechami układu, zależnymi
jedynie od jego struktury wewnętrznej i niezależnymi od klasy przetwarzanych
sygnałów
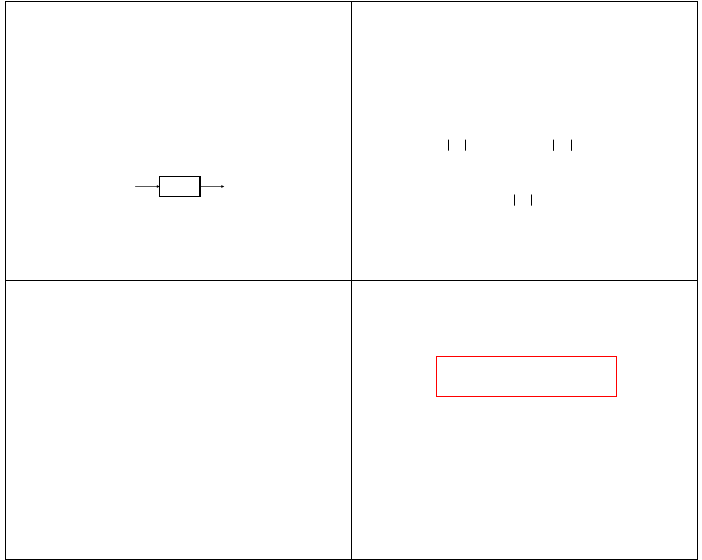
• odpowiedź układu na pobudzenie testowe (przy założeniu zerowych warunków
początkowych) jest jego charakterystyką opisującą w dziedzinie czasu relacje
„wejście -wyjście”
• rolę pobudzenia testowego pełni impuls Kroneckera
( )
n
δ
• odpowiedź impulsową
( )
n
h
układu nazywamy jego reakcję (sygnał wyjściowy) na
pobudzenie w postaci impulsu Kroneckera
( )
n
δ
przy zerowych warunkach
początkowych
znajomość odpowiedzi impulsowej pozwala wyznaczyć reakcję układu na dowolne
pobudzenie
h(n)
δ(n)
zerowe warunki
początkowe
8. Liniowe układy dyskretne.doc, 6/19
UKŁADY DYSKRETNE (cd)
• ponieważ impuls Kroneckera
( )
n
δ
przyjmuje wartości zerowe dla
0
<
n
wobec tego
dla układów przyczynowych reakcja na to pobudzenie również musi spełniać warunek
( )
0
0
<
=
n
n
h
dla
każdy układ fizyczny jest przyczynowy stąd powyższy warunek stanowi podstawowy
warunek realizowalności
• układ (system) dyskretny nazywamy stabilnym jeśli dowolny wejściowy sygnał
ograniczony w wartościach wywołuje na jego wyjściu ograniczoną w wartościach
odpowiedź, czyli istnieją skończone wartości
x
M
oraz
y
M
takie, że dla wszystkich
n
dla
( )
∞
<
≤
x
M
n
x
otrzymujemy
( )
∞
<
≤
y
M
n
y
w przeciwnym przypadku układ nazywamy niestabilnym
układy liniowe, niezmienne względem przesunięcia, są stabilne wtedy i tylko wtedy,
kiedy ich odpowiedź impulsowa spełnia warunek
( )
∞
<
∑
∞
−∞
=
n
n
h
• stacjonarne układy liniowe LS (ang. LTI Linear Time-Invariant), nazywane również
układami liniowymi niezmiennymi względem przesunięcia, są podstawową klasą
rozważanych układów i przedmiotem naszych dalszych rozważań
8. Liniowe układy dyskretne.doc, 7/19
UKŁADY DYSKRETNE (cd)
• dowolny sygnał w dyskretnej dziedzinie czasu można zapisać
( )
( ) (
)
∑
∞
−∞
=
−
δ
=
k
k
n
k
x
n
x
• odpowiedź impulsowa układu opisanego operatorem przekształcenia
T
( )
( )
[
]
n
T
n
h
δ
=
• dla układów niezmiennych względem przesunięcia (stacjonarnych)
(
)
(
)
[
]
k
n
T
k
n
h
−
δ
=
−
• odpowiedź układu na wymuszenie
( )
n
x
( )
( )
[
]
( ) (
)
−
δ
=
=
∑
∞
−∞
=
k
k
n
k
x
T
n
x
T
n
y
• z właściwości liniowości
( )
( ) (
)
[
]
∑
∞
−∞
=
−
δ
=
k
k
n
T
k
x
n
y
8. Liniowe układy dyskretne.doc, 8/19
UKŁADY DYSKRETNE (cd)
• ostatecznie na podstawie (stacjonarność)
(
)
(
)
[
]
k
n
T
k
n
h
−
δ
=
−
( )
( ) (
)
( ) (
)
∑
∑
∞
−∞
=
∞
−∞
=
−
=
−
=
k
k
k
n
x
k
h
k
n
h
k
x
n
y
powyższa operacja nazywa się operacją splotu (dyskretnego) i wyraża relację
pomiędzy sygnałem na wyjściu układu LS (odpowiedzią) a sygnałem
wejściowym (pobudzeniem) i odpowiedzią impulsową tego układu
8. Liniowe układy dyskretne.doc, 9/19
DYSKRETNY SPLOT SYGNAŁÓW
Wprowadzenie
• operacja splotu opisuje operację filtracji jednego sygnału przez drugi; w systemach
liniowych jest podstawowym narzędziem do opisu wzajemnej zależności pomiędzy
sygnałem wejściowym, odpowiedzią impulsową systemu i sygnałem wyjściowym
• w systemach cyfrowych (dyskretnych) nabiera szczególnego znaczenia – stanowi
matematyczną podstawę ich opisu
• właściwości splotu dyskretnego
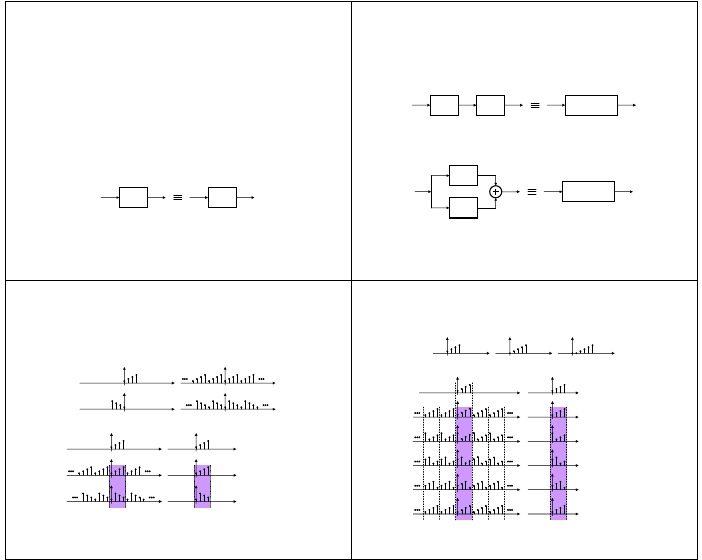
- właściwość przemienności
( )
( ) ( )
( ) ( )
n
x
n
h
n
h
n
x
n
y
∗
=
∗
=
y(n)
x(n)
h(n)
y(n)
h(n)
x(n)
8. Liniowe układy dyskretne.doc, 10/19
DYSKRETNY SPLOT SYGNAŁÓW (cd)
- właściwość łączności
( )
( )
( )
[
]
( )
( )
( )
( )
[
]
n
h
n
h
n
x
n
h
n
h
n
x
n
y
2
1
2
1
∗
∗
=
∗
∗
=
- właściwość rozdzielności względem dodawania
( )
( ) ( )
( )
( )
( )
( )
[
]
n
h
n
h
n
x
n
h
n
x
n
h
n
x
2
1
2
1
+
∗
=
∗
+
∗
y(n)
h
1
(n)
+
h
2
(n)
x(n)
y(n)
h
2
(n)
h
1
(n)
x(n)
y(n)
h
1
(n)
∗
h
2
(n)
x(n)
h
1
(n)
y(n)
h
2
(n)
x(n)
8. Liniowe układy dyskretne.doc, 11/19
DYSKRETNY SPLOT SYGNAŁÓW (cd)
• w dyskretnej dziedzinie czasu definiuje się pojęcie splotu liniowego, splotu okresowego
oraz splotu kołowego (cyklicznego); pojęcia te definiuje się w oparciu o operacji
liniowego i kołowego odwracania i przesuwania ciągu
• operacja odwracania ciągu w czasie (inwersja ciągu)
• operacja kołowego odwracania ciągu w czasie (kołowa inwersja ciągu)
x
mod N
(n)
x[(0)
mod4]=x(0)
x[(-1)
mod4]=x(3)
x[(-2)
mod4]=x(2)
x(n)
n
N=4
0 1 2 3
0 1 2 3 4 5 6 7
-4 -3 -2 -1
-8 -7 -6 -5
n
~
x
(n)
0 1 2 3
n
x
(-n)
~
0 1 2 3 4 5 6 7
-4 -3 -2 -1
8
-7 -6 -5
n
x
mod N
(-n)
0 1 2 3
n
x[(-3)
mod4]=x(1)
x
mod N
(n)
0 1 2 3
n
x
(-n)
~
x
(-n)
x(n)
n
n
N=4
0 1 2 3
0
-3 -2 -1
0 1 2 3 4 5 6 7
-4 -3 -2 -1
-8 -7 -6 -5
n
~
x
(n)
0 1 2 3 4 5 6 7
-4 -3 -2 -1
8
-7 -6 -5
n
8. Liniowe układy dyskretne.doc, 12/19
DYSKRETNY SPLOT SYGNAŁÓW (cd)
• liniowe przesunięcie ciągu
• kołowe (cykliczne) przesunięcie ciągu
0 1 2 3 4 5 6 7 8 9 10 11
-4 -3 -2 -1
-8 -7 -6 -5
n
n
x
mod N
(n-3)
x
mod N
(n-2)
x
mod N
(n-1)
x
mod N
(n)
x(n)
~
x
(n)
n
n
n
n
n
N=4
n
n
x
(n-1)
~
x
(n-2)
~
x
(n-3)
~
x
mod N
(
n)≡
≡x[(n) mod N ]
x[(0-1)
mod4]=x(3)
x[(1-1)
mod4]=x(0)
x[(2-1)
mod4]=x(1)
np.:
0 1 2 3
0 1 2 3 4 5 6 7 8 9 10 11
-4 -3 -2 -1
-8 -7 -6 -5
0 1 2 3 4 5 6 7 8 9 10 11
-4 -3 -2 -1
-8 -7 -6 -5
0 1 2 3 4 5 6 7 8 9 10 11
-4 -3 -2 -1
-8 -7 -6 -5
~
x
(n)
n
x
(n-4)
~
0 1 2 3 4 5 6 7 8 9 10 11
-4 -3 -2 -1
-8 -7 -6 -5
0 1 2 3
0 1 2 3
0 1 2 3
0 1 2 3
x
mod N
(n-4)
n
x
(n)
~
0 1 2 3
x[(3-1)
mod4]=x(2)
x
mod N
(n)
n
0 1 2 3
x(n-1)
x(n)
x(n-2)
n
N=4
0 1 2 3
n
0 1 2 3
n
0 1 2 3 4 5
4
8. Liniowe układy dyskretne.doc, 13/19
DYSKRETNY SPLOT SYGNAŁÓW (cd)
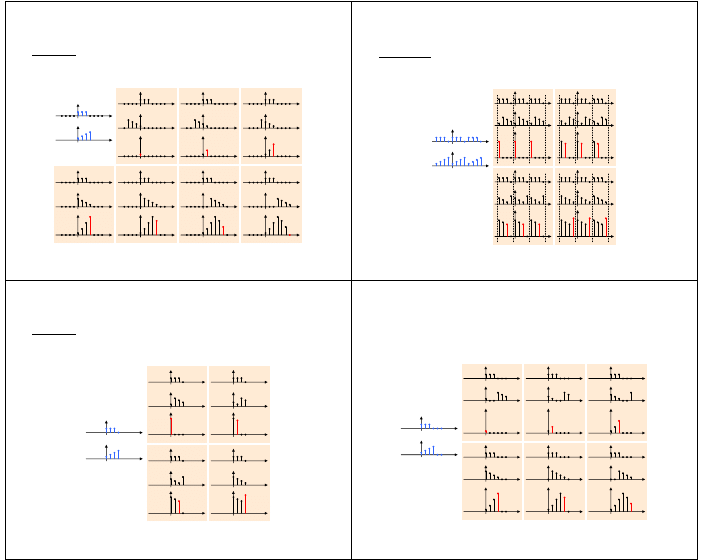
Splot liniowy ciągów
( )
n
x
i
( )
n
h
o skończonej długości odpowiednio
1
N
i
2
N
( )
( ) (
) ( ) ( )
2
,...,
0
,
2
1
2
0
2
1
−
+
=
∗
=
−
=
∑
−
+
=
N
N
n
n
h
n
x
k
n
h
k
x
n
y
N
N
k
h
(n)
x
(k)
n
n
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
h
(-k)
k
k
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
y(n)
n
0
1 2 3 4 5 6
-1
-2
-3
-4
h
(1-k)
k
k
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
y(n)
n
0
1
2 3 4 5 6
-1
-2
-3
-4
k
k
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
y(n)
n
0 1 2
3
4 5 6
-1
-2
-3
-4
k
k
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
y(n)
n
0 1 2 3
4
5 6
-1
-2
-3
-4
k
k
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
y(n)
n
0 1
2
3 4 5 6
-1
-2
-3
-4
n=0
n=1
n=2
n=3
n=4
h
(2-k)
h
(3-k)
h
(4-k)
x
(k)
x
(k)
x
(k)
x
(k)
x
(n)
N
1
=3
N
2
=4
k
k
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
y(n)
n
0 1 2 3 4
5
6
-1
-2
-3
-4
n=5
h
(5-k)
x
(k)
k
k
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
y(n)
n
0 1 2 3 4 5
6
-1
-2
-3
-4
n=6
h
(6-k)
x
(k)
8. Liniowe układy dyskretne.doc, 14/19
DYSKRETNY SPLOT SYGNAŁÓW (cd)
Splot okresowy ciągów
( )
n
x
~
i
( )
n
h
~
o jednakowych okresach
N
N
N
=
=
2
1
( )
( ) (
)
( ) ( )
n
h
n
x
k
n
h
k
x
n
y
N
k
~
~
~
~
~
1
0
∗
=
−
=
∑
−
=
n
n
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
k
k
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
n
0
1 2 3
4
5 6
-1
-2
-3
-4
n=0
N
1
=4
7
7
~
x
(n)
h
(n)
~
7
~
x
(k)
7
h
(-k)
~
7
~
y
(n)
k
k
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
n
0
1
2 3 4
5
6
-1
-2
-3
-4
n=1
7
~
x
(k)
7
7
~
y
(n)
h
(1-k)
~
k
k
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
n
0 1
2
3 4 5
6
-1
-2
-3
-4
n=2
7
~
x
(k)
7
7
~
y
(n)
h
(2-k)
~
k
k
0 1 2 3 4 5 6
-1
-2
-3
-4
0 1 2 3 4 5 6
-1
-2
-3
-4
n
0 1 2
3
4 5 6
-1
-2
-3
-4
n=3
7
~
x
(k)
7
7
~
y
(n)
h
(3-k)
~
N
2
=4
8. Liniowe układy dyskretne.doc, 15/19
DYSKRETNY SPLOT SYGNAŁÓW (cd)
Splot kołowy (splot cykliczny) dla ciągów o długości
N
N
N
=
=
2
1
( )
( )
(
)
( )
( )
1
,...,
0
,
1
0
mod
−
=
⊗
=
−
=
∑
−
=
N
n
n
h
n
x
k
n
h
k
x
n
y
N
k
N
h
.mod N
(-k)
x
(k)
k
k
0 1 2
0 1 2
y(n)
n
0
1 2
n=0
n
n
0 1 2 3
0 1 2 3
N
1
=4
N
2
=4
x
(n)
h
(n)
3
3
3
x
(k)
k
k
0 1 2
0 1 2
y(n)
n
0
1
2
n=1
3
3
3
h
.mod N
(1-k)
x
(k)
k
k
0 1 2
0 1 2
y(n)
n
0 1
2
n=2
3
3
3
h
.mod N
(2-k)
x
(k)
k
k
0 1 2
0 1 2
y(n)
n
0 1 2
n=3
3
3
3
h
.mod N
(3-k)
8. Liniowe układy dyskretne.doc, 16/19
DYSKRETNY SPLOT SYGNAŁÓW (cd)
• splot kołowy po uzupełnieniu ciągów zerami do długości
1
'
2
1
−
+
=
N
N
N
( )
( )
(
)
( )
( )
1
'
,...,
0
,
'
'
'
'
'
1
'
0
'
mod
−
=
⊗
=
−
=
∑
−
=
N
n
n
h
n
x
k
n
h
k
x
n
y
N
k
N
h'
mod N'
(-k)
x'
(k)
k
k
0 1 2 3 4
0 1 2 3 4
y'(n)
n
0
1 2 3 4
n=0
n
n
0 1 2 3
0 1 2 3
N
1
=6
N
2
=6
x'
(n)
h'
(n)
4 5
4 5
5
5
5
x'
(k)
k
k
0 1 2 3 4
0 1 2 3 4
y'(n)
n
0
1
2 3 4
n=1
5
5
5
h'
mod N'
(1-k)
x'
(k)
k
k
0 1 2 3 4
0 1 2 3 4
y'(n)
n
0 1
2
3 4
n=2
5
5
5
h'
mod N'
(2-k)
x'
(k)
k
k
0 1 2 3 4
0 1 2 3 4
y'(n)
n
0 1 2
3
4
n=3
5
5
5
h'
mod N'
(3-k)
x'
(k)
k
k
0 1 2 3 4
0 1 2 3 4
y'(n)
n
0 1 2 3
4
n=4
5
5
5
h'
mod N'
(4-k)
x'
(k)
k
k
0 1 2 3 4
0 1 2 3 4
y'(n)
n
0 1 2 3 4
n=5
5
5
5
h'
mod N'
(5-k)
8. Liniowe układy dyskretne.doc, 17/19
DYSKRETNY SPLOT SYGNAŁÓW (cd)
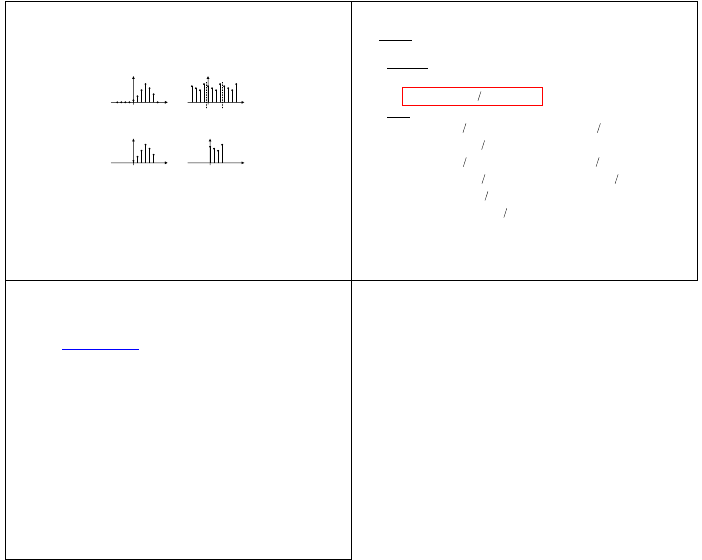
• podsumowanie
y'(n)
n
0 1 2 3 4 5
y(n)
n
0 1 2 3
n
0 1 2 3 4 5 6
-1
-2
-3
-4
7
~
y
(n)
y(n)
n
0 1 2 3 4 5 6
-1
-2
-3
-4
splot liniowy
splot okresowy
splot kołowy
splot kołowy ciągów
uzupełnionych zerami
8. Liniowe układy dyskretne.doc, 18/19
Dodatek
Funkcja 'mod' (arytmetyka modulo)
funkcja 'podłoga'
=
x
największa liczba całkowita
x
≤
( )
0
mod
≠
−
=
y
y
x
y
x
y
x
dla
,
( )
x
x
=
0
mod
(
y
- modulnik)
przykłady
( )
0
6
0
6
0
6
mod
0
=
−
=
( )
0
6
6
6
6
6
mod
6
=
−
=
( )
0
6
6
6
6
6
mod
6
=
−
−
−
=
−
( )
2
6
2
6
2
6
mod
2
=
−
=
( )
2
6
8
6
8
6
mod
8
=
−
=
( )
4
6
2
6
2
6
mod
2
=
−
−
−
=
−
( )
4
6
8
6
8
6
mod
8
=
−
−
−
=
−
( )
( )
( ) ( )
4
6
8
6
8
6
mod
8
−
=
−
−
−
=
−
( )
( )
( )
( )
2
6
8
6
8
6
mod
8
−
=
−
−
−
−
−
=
−
−
oznaczamy również w skrócie:
( )
[
]
( )
n
x
N
n
x
N
mod
mod
≡
8. Liniowe układy dyskretne.doc, 19/19
BIBLIOGRAFIA
1. Szabatin J.: Przetwarzanie sygnałów. Materiały dydaktyczne Politechniki Warszawskiej,
2003,
www.ise.pw.pl/~szabatin
.
2. Oppenheim A.V.: Cyfrowe przetwarzanie sygnałów. WKŁ, Warszawa, 1979.
3. Zieliński T.P.: Cyfrowe przetwarzanie sygnałów. Od teorii do zastosowań. WKŁ,
Warszawa 2005.
4. Izydorczyk J., Płonka G., Tyma G.: Teoria sygnałów. Kompendium wiedzy na temat
sygnałów i metod ich przetwarzania, Helion, Gliwice, 2006
5. Lyons R.G.: Wprowadzenie do cyfrowego przetwarzania sygnałów. WKŁ,
Warszawa, 2003.
6. Proakis J.G., Manolakis D.G.: Digital signal processing. Principles, Algorithms, and
Applications. Third Edition. Prentice-Hall, Inc., Upper Saddle River, New Jersey, 1996.
7. Smith S.W.: Cyfrowe przetwarzanie sygnałów. Praktyczny poradnik dla inżynierów i
naukowców. Wydawnictwo BTC, Warszawa, 2007.