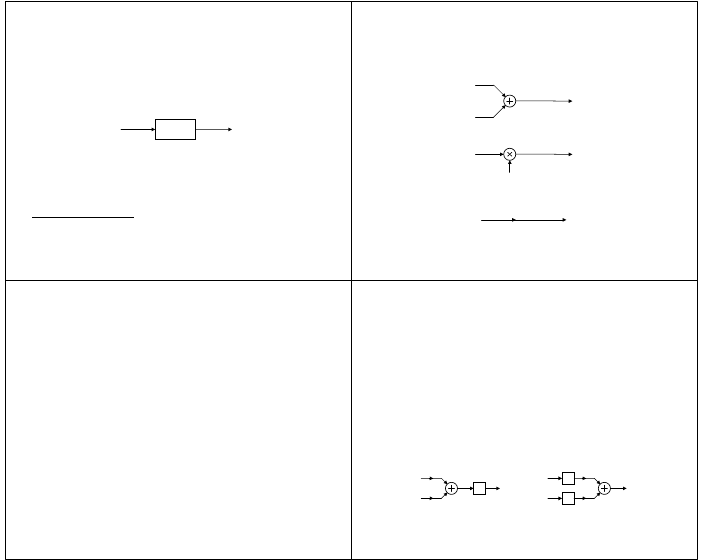
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 1/16
UKŁADY - PODSTAWOWE DEFINICJE
1
Pojęcie układu
• matematyczną definicją (modelem) układu jest jednoznaczne przekształcenie
(operator) odwzorujące sygnał wejściowy
x
w sygnał wyjściowy
y
jest to tzw. ujęcie transmisyjne
[ ]
x
T
y =
y
x
T
→
y
x
T [..]
pobudzenie
odpowiedź
• w ogólnym przypadku układ może być wielowejściowy i wielowyjściowy
• powyższa definicja układu ma charakter uniwersalny i może odnosić się do różnych
klas sygnałów
• jeśli dziedzina
X
i przeciwdziedzina
Y
operatora
T
są zbiorami sygnałów ciągłych
w czasie, układ nazywamy analogowym
1
opracowano na podstawie [1-3], wersja z dnia 02.10.2014
materiał nie jest pełnym i ścisłym pod względem formalnym opracowaniem poszczególnych tematów, stanowi
jedynie szkielet, wokół którego budowany jest wykład
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 2/16
UKŁADY - PODSTAWOWE DEFINICJE (cd)
Symbole operacji na schematach funkcjonalnych
• sumator
x
2
y= x
1
+ x
2
x
1
• układ mnożenia
y= x
1
x
2
x
1
x
2
• układ mnożenia przez stałą
y= A x
x
A
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 3/16
UKŁADY - PODSTAWOWE DEFINICJE (cd)
Klasyfikacja układów
• układ stacjonarny (niezmienny względem przesunięcia, inwariantny w czasie)
- układ nazywamy układem stacjonarnym, jeśli dla każdych
( )
t
x
i
0
t
zachodzi
przemienność
( )
[ ]
{
}
( )
[ ]
{
}
t
x
T
P
t
x
P
T
t
t
0
0
=
gdzie
0
t
P
jest operatorem przesunięcia w czasie sygnałów analogowych
( )
[ ]
(
)
0
0
t
t
x
t
x
P
t
−
=
- w przeciwnym wypadku układ nazywamy układem niestacjonarnym
- dla stacjonarnych układów analogowych spełniona jest zależność
jeżeli
( )
( )
[ ]
t
x
T
t
y
=
to
(
)
(
)
[
]
0
0
t
t
x
T
t
t
y
−
=
−
- operatory: różniczkowania, całkowania, opóźnienia w czasie, podnoszenia do
kwadratu, pierwiastkujący i logarytmujący w dziedzinie sygnałów analogowych są
operatorami stacjonarnymi
- operator typu
( )
( )
t
x
t
t
y
=
w dziedzinie sygnałów analogowych jest operatorem
niestacjonarnymi
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 4/16
UKŁADY - PODSTAWOWE DEFINICJE (cd)
• układ liniowy
-
układ analogowy nazywamy liniowym jeśli spełnia zasadę superpozycji, tzn.
odpowiedź układu na ważoną sumę sygnałów wejściowych równa jest sumie
ważonych odpowiednio odpowiedzi oddzielnie na każdy z sygnałów, w przeciwnym
przypadku układ nazywamy nieliniowym
( )
( )
( )
[
]
( )
[
]
( )
[
]
( )
( )
t
by
t
ay
t
x
bT
t
x
aT
t
bx
t
ax
T
t
y
2
1
2
1
2
1
+
=
+
=
+
=
w ogólnym przypadku
( )
( )
( )
( )
∑
∑
=
=
=
→
=
M
k
k
k
T
M
k
k
k
t
y
a
t
y
t
x
a
t
x
1
1
gdzie
( )
( )
[
]
M
k
t
x
T
t
y
k
k
...,
,
2
,
1
=
=
ilustracja graficzna
a
y
x
2
x
1
b
T
a
y
x
2
x
1
b
T
T
operator przekształcenia
T
jest liniowy wtedy i tylko wtedy kiedy
'
y
y =
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 5/16
UKŁADY - PODSTAWOWE DEFINICJE (cd)
• układ przyczynowy
- jeżeli układ opisany operatorem
T
odwzorowuje zbiór sygnałów
X
w zbiór
sygnałów
Y
i jeżeli
[ ]
1
1
x
T
y =
oraz
[ ]
2
2
x
T
y =
wówczas układ jest
układem
przyczynowym
jeśli dla każdych
( ) ( )
X
t
x
t
x
∈
2
1
,
i każdego
0
t
z równości
( )
( )
0
2
1
,
t
t
t
x
t
x
<
=
wynika równość
( )
( )
0
2
1
,
t
t
t
y
t
y
<
=
z powyższych definicji wynika, że dla układu przyczynowego z równości
( )
0
0
t
t
t
x
<
≡
dla
, wynika równość
( )
0
0
t
t
t
y
<
≡
dla
- zatem
odpowiedź układu
przyczynowego nie może poprzedzać wymuszenia
inaczej układ analogowy nazywamy przyczynowym jeśli wartość sygnału na jego
wyjściu
( )
t
y
w dowolnym momencie czasu
t
zależy jedynie od bieżącej
i poprzednich wartości sygnały wejściowego i nie zależy od przyszłych wartości
sygnału wejściowego w przeciwnym przypadku układ nazywamy nieprzyczynowym
układ nieprzyczynowy jest nierealizowalny praktycznie
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 6/16
UKŁADY - PODSTAWOWE DEFINICJE (cd)
• liniowość, stacjonarność i przyczynowość są immanentnymi cechami układu, zależnymi
jedynie od jego struktury wewnętrznej i niezależnymi od klasy przetwarzanych
sygnałów
• stacjonarne układy liniowe LS (ang. LTI Linear Time-Invariant), nazywane również
układami liniowymi niezmiennymi względem przesunięcia, są podstawową klasą
rozważanych układów i przedmiotem naszych dalszych rozważań
• z przetwarzaniem sygnału w układzie wiąże się przekształcenie jego widma, operacja
przetwarzania widma nazywa się filtracją a realizujący ją układ w teorii sygnałów
utożsamiany jest z filtrem
• układ statyczny (bez pamięci) – układ dla którego w dowolnej chwili czasu wartość
sygnału na wyjściu zależy wyłącznie od wartości sygnału wejściowego w tej samej
chwili
• jeśli wartość sygnału na wyjściu układu w dowolnej chwili zależy od wartości sygnału
wejściowego w chwilach poprzedzających lub następujących po nim to taki układ
nazywamy układem dynamicznym (z pamięcią)
• układ nazywamy stabilnym ze względu na wymuszenie jeśli dowolny ograniczony
sygnał wejściowy powoduje powstanie ograniczonego sygnału wyjściowego
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 7/16
OPIS UKŁADU W DZIEDZINIE CZASU
• odpowiedź układu na pobudzenie testowe (przy założeniu zerowych warunków
początkowych) jest jego charakterystyką opisującą w dziedzinie czasu relacje
„wejście -wyjście”
• rolę pobudzenia testowego pełnią sygnały: impuls Diraca
( )
t
δ
oraz skok jednostkowy
( )
t
1
• odpowiedź impulsową
( )
t
h
układu nazywamy jego reakcję (sygnał wyjściowy) na
pobudzenie w postaci impulsu Diraca
( )
t
δ
przy zerowych warunkach początkowych
h(t)
δ(t)
zerowe warunki
początkowe
znajomość odpowiedzi impulsowej pozwala wyznaczyć reakcję układu na dowolne
pobudzenie
impulsu Diraca
( )
t
δ
nie można wytworzyć w układzie fizycznym, zatem odpowiedź
impulsowa stanowi narzędzie służące do teoretycznego opisu układów
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 8/16
OPIS UKŁADU W DZIEDZINIE CZASU (cd)
• odpowiedź jednostkową
( )
t
r
układu nazywamy jego reakcję (sygnał wyjściowy) na
pobudzenie w postaci skoku jednostkowego
( )
t
1
przy zerowych warunkach
początkowych
r(t)
1111(t)
zerowe warunki
początkowe
znajomość odpowiedzi jednostkowej pozwala wyznaczyć reakcję układu na dowolne
pobudzenie
skok jednostkowy
( )
t
1
można z dobrym przybliżeniem wytworzyć w układzie
fizycznym, zatem odpowiedź jednostkowa stanowi narzędzie służące do badania
układów fizycznych
• ponieważ impuls Diraca
( )
t
δ
przyjmuje wartości zerowe dla
0
<
t
wobec tego dla
układów przyczynowych reakcja na to pobudzenie również musi spełniać warunek
( )
0
0
<
=
t
t
h
dla
każdy układ fizyczny jest przyczynowy stąd powyższy warunek stanowi podstawowy
warunek realizowalności układu i jest równoważny warunkowi
( )
0
0
<
=
t
t
r
dla
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 9/16
OPIS UKŁADU W DZIEDZINIE CZASU (cd)
• związek pomiędzy odpowiedzią impulsową
( )
t
h
a odpowiedzią jednostkową
( )
t
r
jeżeli
T
jest operatorem przekształcenia to
( )
( )
[ ]
t
T
t
h
δ
=
oraz
( )
( )
[ ]
t
T
t
r
1
=
wykorzystując
( )
( )
t
dt
d
t
1
=
δ
otrzymujemy
( )
( )
[ ]
( )
( )
[ ]
( )
t
r
dt
d
t
T
dt
d
t
dt
d
T
t
T
t
h
=
=
=
δ
=
1
1
oraz
( )
( )
∫
=
t
dt
t
h
t
r
0
'
'
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 10/16
OPIS UKŁADU W DZIEDZINIE CZASU (cd)
• związek pomiędzy sygnałami na wejściu i na wyjściu układu
wykorzystując właściwość splotu dystrybucji delta
( ) ( )
( )
t
x
t
x
t
=
∗
δ
na podstawie
definicji splotu możemy napisać
( )
(
) ( )
∫
∞
∞
−
τ
τ
τ
−
δ
=
d
x
t
t
x
odpowiedź układu opisanego operatorem przekształcenia
T
na sygnał
( )
t
x
( )
( )
[ ]
( ) ( )
[
]
(
) ( )
τ
τ
τ
−
δ
=
∗
δ
=
=
∫
∞
∞
−
d
x
t
T
t
x
t
T
t
x
T
t
y
uwzględniając liniowość operacji całkowania
( )
(
) ( )
[
]
(
)
[
]
( )
∫
∫
∞
∞
−
∞
∞
−
τ
τ
τ
−
δ
=
τ
τ
τ
−
δ
=
d
x
t
T
d
x
t
T
t
y
ze stacjonarności układu wynika
( )
[ ]
( )
(
)
[
]
(
)
τ
−
=
τ
−
δ
⇒
=
δ
t
h
t
T
t
h
t
T
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 11/16
OPIS UKŁADU W DZIEDZINIE CZASU (cd)
ostatecznie więc
( )
(
) ( )
( ) ( )
t
x
t
h
d
x
t
h
t
y
∗
=
τ
τ
τ
−
=
∫
∞
∞
−
ze względu na przemienność operacji splatania
( )
( ) (
)
( ) ( )
t
h
t
x
d
t
x
h
t
y
∗
=
τ
τ
−
τ
=
∫
∞
∞
−
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 12/16
OPIS UKŁADU W DZIEDZINIE CZĘSTOTLIWOŚCI
• właściwości rozważanych stacjonarnych układów liniowych w dziedzinie częstotliwości
(pulsacji) opisują ich charakterystyki amplitudowo-fazowe
• dla stacjonarnych układów liniowych opisywanych
F
-transformowalną (zarówno
w sensie zwykłym jak i granicznym) odpowiedzią impulsową
( )
t
h
ich charakterystykę
amplitudowo-fazową określa transformata Fouriera
( )
( )
∫
∞
∞
−
ω
−
=
ω
dt
e
t
h
j
H
t
j
dla układów przyczynowych
( )
( )
∫
∞
ω
−
=
ω
0
dt
e
t
h
j
H
t
j
zależność charakterystyki od argumentu
ω
j
wynika z jej związku z transmitancją
układu określoną w dziedzinie transformaty Laplace’a
( )
( )
ω
=
=
ω
j
s
s
H
j
H
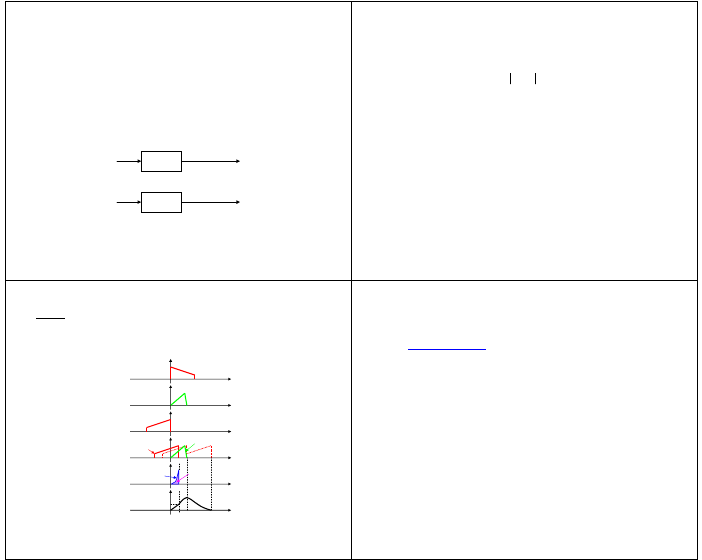
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 13/16
OPIS UKŁADU W DZIEDZINIE CZĘSTOTLIWOŚCI (cd)
• związek pomiędzy widmem sygnału na wyjściu układu a widmem pobudzenia
i charakterystyką amplitudowo-fazową określa tzw. równanie transmisyjne układu
( )
( ) ( )
ω
ω
=
ω
X
j
H
Y
wykorzystując odwrotne przekształcenie Fouriera możemy zapisać
( )
( ) ( )
[
]
ω
ω
=
−
X
j
H
F
t
y
1
• opis układu w dziedzinie czasu i częstotliwości
y(t)=h(t) ∗ x(t)
x(t)
h(t)
Y(ω)=H( j ω) ·X(ω)
X(ω)
H( jω)
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 14/16
OPIS UKŁADU W DZIEDZINIE CZĘSTOTLIWOŚCI (cd)
• charakterystykę amplitudowo-fazową można przedstawić w postaci biegunowej lub
algebraicznej
( )
( )
( )
ω
ω
=
ω
j
H
j
e
j
H
j
H
arg
( )
( )
( )
ω
+
ω
=
ω
j
H
j
j
H
j
H
Im
Re
• ponieważ charakterystyka amplitudowo-fazowa jest transformatą Fouriera funkcji
rzeczywistej, zatem jest funkcją hermitowską, tzn.
( )
(
)
ω
−
=
ω
j
H
j
H
*
co oznacza, że charakterystyka amplitudowa i charakterystyka rzeczywista są
funkcjami parzystymi, a charakterystyka fazowa i charakterystyka urojona – funkcjami
nieparzystymi
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 15/16
załącznik
wyznaczanie splotu metodą graficzną
( )
(
) ( )
∫
+
τ
τ
τ
−
=
x
h
t
t
d
x
t
h
t
y
0
h(-τ-t
1
)
h(-τ)
t
x
+t
h
t
x
t
h
t
1
0
τ
h(τ)
0
τ
x(τ)
0
τ
0
τ
x(τ)
0
τ
h(-τ-t
1
)x(τ)
P
1
t
1
0
t
y(t)
t
1
P
1
5. Przetwarzanie sygnałów analogowych przez układ liniowy.doc, 16/16
BIBLIOGRAFIA
1. Szabatin J.: Przetwarzanie sygnałów. Materiały dydaktyczne Politechniki Warszawskiej,
2003,
www.ise.pw.pl/~szabatin
.
2. Baskakow S.I.: Sygnały i układy radiotechniczne. PWN, Warszawa, 1991.
3. Proakis J.G., Manolakis D.G.: Digital signal processing. Principles, Algorithms, and
Applications. Third Edition. Prentice-Hall, Inc., Upper Saddle River, New Jersey, 1996.