Politechnika Lubelska

Wydział Elektrotechniki i Informatyki

Katedra Sieci Elektrycznych i Zabezpieczeń

Laboratorium Sieci Elektroenergetycznych

Ćwiczenie nr 4

Analiza zwarć symetrycznych w sieci elektroenergetycznej

Cel ćwiczenia:

Wyznaczanie prądów zwarciowych w sieciach elektroenergetycznych. Pomiary prądów

zwarcia symetrycznego na analizatorze prądu stałego.

1

Podstawy teoretyczne [2]

1.1

Zalecenia normatywne

1.1.1

Wiadomości wstępne

Analiza zjawisk towarzyszących zwarciom jest złożona i wymaga tworzenia opisu

matematycznego elektromagnetycznych stanów nieustalonych zachodzącego w maszynach

elektrycznych.

Z

drugiej

strony

wiele

decyzji

technicznych

dotyczących

sieci

elektroenergetycznych podejmowanych w codziennej praktyce eksploatacyjnej i projektowej

musi uwzględniać wartości prądów zwarcia i innych związanych z nimi wielkości. Stąd też

konieczność opracowania uproszczonych metod prowadzenia obliczeń zwarciowych i

traktowania ich jako swoistego inżynierskiego standardu. Powinny być to uproszczenia na

tyle istotne, aby dzięki nim ilościowa analiza stanu zwarcia ograniczyła się do analizy stanu

quasi-ustalonego, którym jest najczęściej stan podprzejściowy w chwili t=0. Wielkości

charakteryzujące dynamikę zjawisk zwarciowych powinny być wyznaczane na tej podstawie

przy wykorzystaniu pomocniczych wskaźników i współczynników. Podejście takie stosowane

jest w elektroenergetyce od kilkudziesięciu lat. W celu wyeliminowania dowolności i

niejednoznaczności

we

wprowadzanych

założeniach

upraszczających

oraz

w

celu

ujednolicenia interpretacji wyników, metody obliczeń zwarciowych są przedmiotem

uregulowań

zawartych

w

aktach

normatywnych,

zwanych

potocznie

„normami

zwarciowymi”.

Pomimo, że w tym zakresie opracowano wiele różnych dokumentów, ich podstawy

teoretyczne są podobne. Twierdzeniem z zakresu teorii obwodów, leżącym u podstaw norm

zwarciowych, jest twierdzenie Thevenina.

Poszczególne normy różnią się miedzy sobą szczegółami, dzięki którym tak uproszczony

model stanu zwarcia wystarczająco dokładnie (w opinii autorów danej normy) odwzorowuje

charakterystyczne cechy zwarcia w sieci rzeczywistej.

1.1.2

Standaryzacja obliczeń zwarciowych

Pierwszą normą wprowadzoną w Europie w 1929 r. była norma niemiecka VDE 0102, która

podlegała potem wielu aktualizacjom i stosowana jest w Niemczech także po wprowadzeniu

międzynarodowej normy IEC

1

. W Związku Radzieckim w 1944 r. ukazało się pierwsze

wydanie dokumentu „Руководящие указания по расчëту короткиж замыканий”,

aktualizowane do okresu obecnego. W USA obliczenia zwarciowe są wykonywane zgodnie z

normą ANSI/IEEE Std 399-1990 (opis z komentarzem w IEEE Buff Book).

W Polsce zalecaną metodę obliczania prądów zwarciowych podano w normie PN-52/E-05002

w 1952 r. Modyfikacje tej normy publikowano następnie w latach 1957, 1962 oraz 1974.

W latach 1990-91 zespół z Politechniki Śląskiej podjął prace nad nową wersją polskiej normy

zwarciowej polegające na tłumaczeniu i adaptacji publikacji IEC. Prace te zostały jednak

przerwane i dotychczas nie doszło do opublikowania odpowiedniego nowego dokumentu.

Przebieg prac IEC nad standaryzacją obliczeń zwarciowych był następujący. W latach

osiemdziesiątych powołano Komitet Techniczny Nr 73 (TC 73) podzielony na 2 grupy

robocze: jedną dotyczącą skutków przepływu prądów zwarciowych i drugą dotyczącą metod

wyznaczania prądów zwarciowych. W wyniku prac TC 73 IEC w latach osiemdziesiątych i

dziewięćdziesiątych powstały m.in. następujące dokumenty:

 Publication No 865/1986 “Calculation of effects of short – circuit currents”. Ma ona

polski odpowiednik PN-90/ E-05025.

 Publication No 909/1988 “Short - circuit calculation in three phase ac systems”.

Podstawowy dokument z zakresu standaryzacji obliczeń.

 Publication No 781/1989 “Application guide for calculation of short – circuit currents in

low voltage radial systems”.

Od początku swego powstania norma IEC 909 nie była jednak dobrze przyjęta przez

inżynierów elektryków z różnych krajów Europy. Bazujący na normie niemieckiej VDE 0102

bardzo obszerny dokument (ponad 100 stron) uznano za nieścisły i niewłaściwie

zredagowany. Prace nad nową wersją IEC 909 (wg aktualnych oznaczeń IEC 60909/0) trwały

do 1998 r i ich efekty są z pewnością widoczne. Aby jednak dobrze opanować i zrozumieć

proponowaną przez ten dokument metodę wyznaczania prądów i innych wielkości

charakteryzujących stan zwarcia, trzeba zapoznać się z trzema dodatkowymi dokumentami

stowarzyszonymi. Pierwszy z nich podaje i uzasadnia wartości charakteryzujące wskaźniki

wykorzystywane w obliczeniach, drugi podaje parametry modeli zwarciowych typowych

elementów sieci, trzeci zawiera przykłady obliczeniowe.

Wszystkie te dokumenty mogłyby być wydane w Polsce po przetłumaczeniu jako oddzielna

książka. Jest to jednak mało prawdopodobne z uwagi na wysokie koszty takiego

1

IEC – International Electrotechnical Commission – instytucja zajmująca się międzynarodową normalizacją w

zakresie elektrotechniki

przedsięwzięcia. Jak już jednak wspomniano, przyjęcie na grunt krajowy dokumentu

podstawowego, jest jednym z cząstkowych zadań dostosowujących polskie normy techniczne

do standardów Unii Europejskiej. W dalszych rozdziałach niniejszej książki przedstawiono

najistotniejsze (w odczuciu autorów) zagadnienia poruszane w publikacjach polskiej normy

PN-74/E-05002 oraz międzynarodowej normy IEC 60909/0.

1.1.3

Obliczenia według normy PN-74/E-05002

„Stara norma” nosi tytuł „Dobór aparatów wysokonapięciowych na warunki zwarciowe”, tak

więc metoda wyznaczania wielkości zwarciowych jest tylko jednym z poruszanych w niej

problemów.

Szczegółowy opis metody obliczania prądów zwarciowych zawiera załącznik 1 do omawianej

normy. Czynnością wstępną jest budowa schematów zastępczych analizowanego systemu dla

składowych symetrycznych. Rodzaj schematów (zgodny, przeciwny i zerowy) powinien być

dostosowany

do

rodzaju

rozpatrywanego

zwarcia

(np.

dla

zwarcia

trójfazowego

wystarczający jest schemat zgodny, dla zwarcia z ziemią konieczne są wszystkie trzy

schematy).

W budowie schematów zastępczych omawiana norma dopuszcza stosowanie uproszczeń –

pomijanie pojemności w schematach linii, impedancji magnesowania w schematach

transformatorów, przyjmowanie współczynników sprowadzania napięć na podstawie napięć

znamionowych sieci, przyjmowanie identyczności schematu zgodnego i przeciwnego

systemu, pomijanie lub zastępowanie impedancjami zwarciowymi jego fragmentów nie

mających istotnego wpływu na wartość prądów zwarcia. Szereg sformułowań związanych z

dopuszczalnymi uproszczeniami ma charakter fakultatywny – liczący może z nich skorzystać,

ale w sytuacjach gdzie wiedza inżynierska i doświadczenie podpowiadają konieczność

zastosowania modeli o większej dokładności, norma tego nie zabrania. Można powiedzieć, że

jest ona przeznaczona dla osób posiadających już w tym zakresie pewne umiejętności.

Drugą czynnością jest wyznaczenie (dowolną metodą przekształcania obwodów liniowych)

zastępczych impedancji zwarciowych widzianych w węźle odpowiadającym miejscu zwarcia

Z

1

, Z

2

, Z

0

. Kolejne dwie, najważniejsze operacje obliczeniowe to wyznaczenie składowej

zgodnej prądu początkowego w miejscu zwarcia oraz na jej podstawie prądu początkowego,

który w tej normie oznaczany jest symbolem

p

I

Nie opisując zatem szczegółowo normy, z uwagi na spotykane w praktyce częste pytania o

relacje między wielkościami w niej zawartymi a omawianymi w dokumencie IEC 60909,

warto zapoznać Czytelnika z nazewnictwem i symbolami tych wielkości wprowadzonymi

przez te obydwa dokumenty – przedstawia je tabl. 1.

Tablica 1.

Zestawienie najważniejszych wielkości zwarciowych i symboli używanych do ich opisu wg

normy IEC 60909 oraz wg dotychczas obowiązującej normy zwarciowej PN-74/E-05002

Wielkość zwarciowa

Oznaczenie

wg IEC 60909

Oznaczenie wg

PN-74/E-05002

Prąd początkowy

"

K

I

P

I

Prąd udarowy

p

i

u

i

Współczynnik udaru



u

k

Prąd wyłączeniowy symetryczny

b

I

2

ws

I

Współczynnik zanikania składowej okresowej



ws

k

Prąd nieokresowy

dc

i

nok

i

Cieplny prąd zastępczy

th

I

tz

I

Prąd wyłączeniowy niesymetryczny

asym

b

I

wns

I

Moc zwarciowa obliczeniowa

"

K

S

z

S

Czas trwania zwarcia

K

T

3

z

t

1.1.4

Ogólna charakterystyka normy IEC 60909

Podstawowe definicje, symbole i założenia

Na podstawie normy IEC 60909 mogą być wyznaczane prądy zwarcia w sieciach wysokiego i

niskiego napięcia. Dokładność obliczeń gwarantuje możliwość ich wykorzystania w praktyce

inżynierskiej. Norma nie wyklucza stosowania innych metod obliczeniowych, o ile uzyskane

dzięki nim wyniki będą wiązały się z błędem nie większym niż wprowadzony przez metodę w

niej opisaną.

Podstawowe definicje i pojęcia przedstawione w rozdz. 1 normy IEC 60909 nie różnią się

istotnie od wprowadzonych w normie PN-74/E-05002. Symbole wielkości zwarciowych są

specyficzną kompilacją języka angielskiego i niemieckiego, co czasami sprawia trudności w

określeniu znaczenia takiego symbolu. Przykładowo, podstawowym symbolem wielkości

zwarciowej wykorzystywanym jako dolny indeks, także jako oznaczenie miejsca i rodzaju

2

w tekście zastosowano indeks dolny B rezerwując indeks b dla wielkości bazowych jednostek względnych

3

z uwagi na jednolite oznaczenie czasu symbolem t autorzy stosowali w niniejszej książce oznaczenie t

K

zwarcia jest litera K, co pochodzi od niemieckiego słowa Kurzschluss – czyli zwarcie. Z kolei

parametry znamionowe elementów systemu (prąd znamionowy, napięcie znamionowe)

oznacza się indeksem r (np. I

r

, U

r

) od angielskiego przymiotnika rated – czyli nominalny.

Prąd

Górna obwiednia - 1

Składowa zanikająca (aperiodyczna) i

dc

Czas

Dolna obwiednia - 2

2

2

I

K

2

2

I

K

A

i

p

Prąd

Górna obwiednia - 1

Składowa zanikająca (aperiodyczna) i

dc

Czas

Dolna obwiednia - 2

2

2

I

K

2

2

I

K

2

2

I

K

A

i

p

=

a)

b)

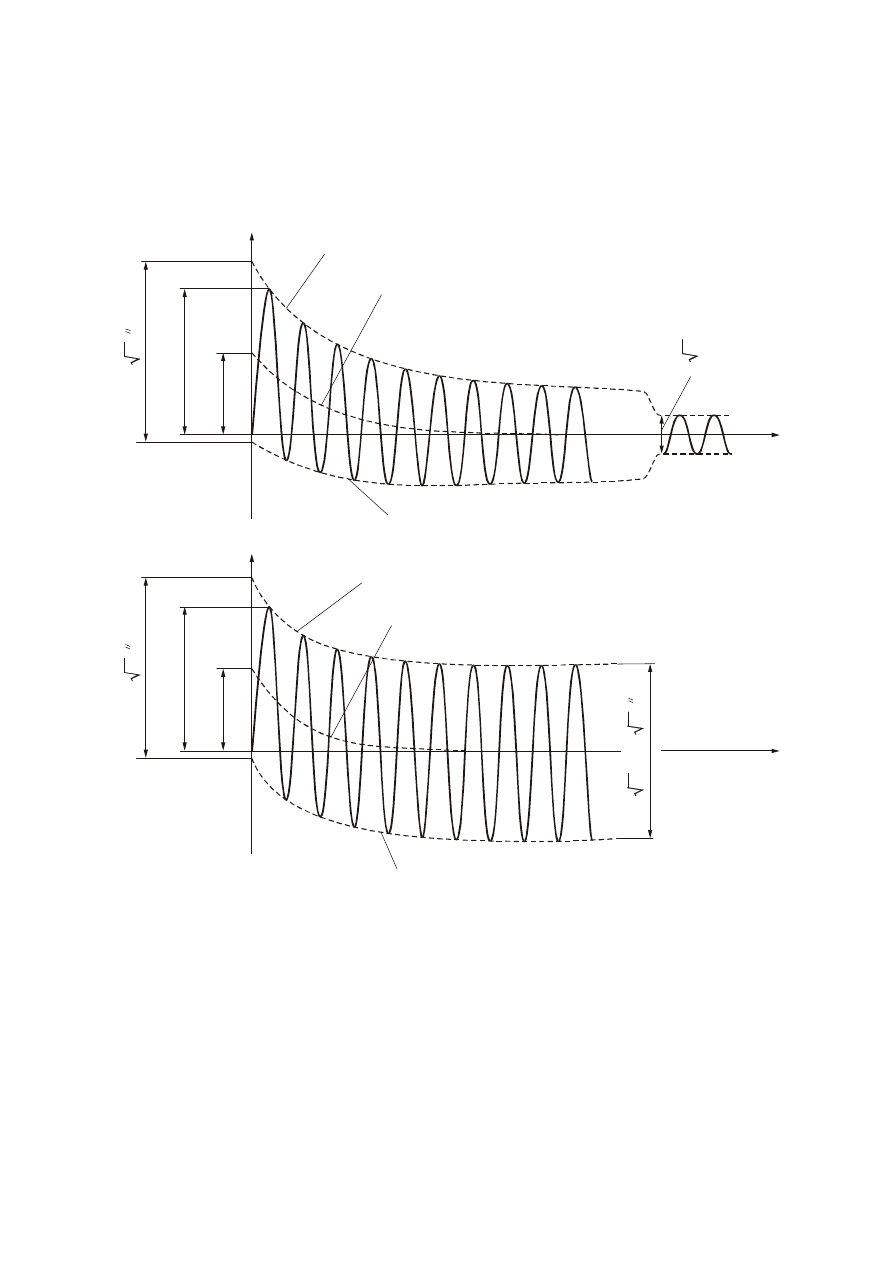
Rys. 1. Przebiegi wielkości zwarciowych wraz z oznaczeniami wprowadzonymi w normie IEC 60909; a)
zwarcie w pobliżu generatora, b) zwarcie odległe od generatora, oznaczenia: I

K

” – prąd zwarciowy

początkowy, i

p

- prąd udarowy, I

K

- ustalony prąd zwarciowy, i

dc

- składowa nieokresowa zanikająca

prądu zwarciowego, A - wartość początkowa składowej nieokresowej, 1 - obwiednia górna, 2- obwiednia
dolna

Sens najważniejszych wielkości zwarciowych wprowadzonych w normie widoczny jest na

rys. 1. W przypadku a) zwarcie ma miejsce w pobliżu generatora (widoczne zanikanie

składowej okresowej), w przypadku b) jest to zwarcie odległe (zanikanie składowej

okresowej nie występuje).

W normie podkreśla się, że rozpatrywane zwarcia mają charakter modelowy – traktuje się je

jako całkowicie bezimpedancyjne (pomija się rezystancję łuku elektrycznego w miejscu

zwarcia), zwarcia wielofazowe traktowane są jako jednoczesne (nie jest to zgodne z

rzeczywistością).

Podstawowy wzór służący do obliczeń symetrycznego, początkowego prądu zwarcia

trójfazowego ma postać

K

n

2

K

2

K

n

"

K

3

3

Z

cU

X

R

cU

I









(1)

w którym:

3

/

n

cU

- napięcie źródła zastępczego; Z

K

– zastępcza impedancja zwarciowa

(domyślnie dla sieci składowej symetrycznej zgodnej).

Stałą c dobiera się w zależności od napięcia znamionowego sieci, w której rozważa się

zwarcie oraz od tego czy chodzi o maksymalny czy minimalny prąd zwarcia. Szczegóły

związane z doborem przedstawia tabl. 2.

Tablica 2.

Dobór współczynnika c zastępczego źródła napięciowego

Napięcie znamionowe

U

n

Współczynnik napięciowy c do obliczania

maksymalnego prądu zwarcia

minimalnego prądu zwarcia

Niskie napięcie (100

1000)

a) 230/400 V

b) inne napięcia

1,00

1,05

0,95

1,00

Średnie napięcie (1

35) kV

1,10

1,00

Wysokie napięcie >35 kV

1,10

1,00

W celu wyznaczenia maksymalnych wartości prądów zwarcia (oprócz różnic w doborze stałej

c) obliczenia powinno się prowadzić dla konfiguracji systemu innych niż obliczenia

prowadzone w celu wyznaczenia wartości minimalnych. Norma IEC 60909 zaleca również

aby rezystancje odcinków linii w pierwszym przypadku były wyznaczane dla temperatury 20˚

C, a w drugim dla temperatury osiągniętej pod koniec stanu zwarcia (chodzi o większą

wartość tej rezystancji, a tym samym o mniejszą wartość prądu).

Na podstawie wartości prądu początkowego I

K

”, którą w najprostszym przypadku wylicza się

na podstawie wzoru (1), wyznaczane są pozostałe wielkości charakteryzujące przebieg prądu

zwarcia. Szczegóły związane z tymi obliczeniami przedstawiono w pkt. 5.

Specyfika modelowania elementów sieci

Norma IEC 60909 oraz związane z nią dokumenty dokładnie omawiają sposób modelowania

elementów sieci w obliczeniach zwarciowych. Poszczególne ich rodzaje – transformatory,

linie napowietrzne i kablowe, generatory oraz dławiki ograniczające prądy zwarcia są opisane

w formie podręcznikowej, z uwzględnieniem modeli dla poszczególnych składowych

symetrycznych (zgodnej, przeciwnej i zerowej). Specyfika normy ujawnia się w dwóch

zagadnieniach:

 konsekwentnym pomijaniu w modelach elementów gałęzi poprzecznych
 wprowadzenie współczynników korygujących impedancje transformatorów i

generatorów.

Poprzez elementy poprzeczne rozumie się pojemności i upływności linii, impedancje

magnesowania transformatorów oraz fikcyjne gałęzie poprzeczne wchodzące w skład ich

modeli rezonansowych, modele kompensatorów statycznych i dławików kompensacyjnych.

Modele odbiorów niewirujących (piece, oświetlenie) są także rozumiane jako elementy

poprzeczne. W niektórych przypadkach w obliczeniach modelowane są silniki indukcyjne, we

wszystkich przypadkach modelowane są silniki i kompensatory synchroniczne.

Istota współczynników korygujących wartości impedancji transformatorów i generatorów jest

trudna do zrozumienia. Są one wynikiem prac prowadzonych przez zespół profesora Oedinga

w

latach

osiemdziesiątych.

Dokładniejsze

omówienie

znaczenia

współczynników

korygujących przedstawiono w pkt. 7. Uproszczona interpretacja wynika z twierdzenia, że

przyjmowanie wartości napięcia w miejscu zwarcia jako

3

/

n

cU

(przy c ustalonym zgodnie

z tabl. 2) oraz pomijanie elementów poprzecznych modeli, jest według autorów cytowanych

prac oraz normy IEC 60909 zbyt dużym uproszczeniem. Z drugiej jednak strony prostotę

wzoru (1) uznają oni za tak znaczącą zaletę, że proponują alternatywny sposób ograniczania

wielkości błędów wynikających z przyjmowania nieodpowiedniej wartości napięcia. Polega

on na utrzymaniu postaci wzoru (1), przy równoczesnym korygowaniu znajdującej się z

mianowniku impedancji Z

K

. Modyfikacje te są przeprowadzane na etapie budowy modelu

zwarciowego sieci. Współczynniki korygujące oznaczane są literą K w połączeniu z indeksem

dolnym, odpowiadającym typowi elementu, którego impedancja jest modyfikowana. Dla

podkreślenia, że impedancja danego elementu podlega skorygowaniu dodaje się do jej opisu

również literę K jako indeks dolny. Dla poszczególnych przypadków postać impedancji

skorygowanych i współczynników korygujących jest następująca:

 transformatory dwuuzwojeniowe (z podobciążeniową regulacją zaczepów lub bez, za

wyjątkiem transformatorów blokowych)





T

T

T

T

T

TK

jX

R

K

Z

K

Z









(2)

p.u.

T

max

T

6

,

0

1

95

,

0

X

c

K





(3)

gdzie:

K

T

współczynnik korygujący impedancję transformatora;

c

max

współczynnik napięciowy wg tabl. 2(największa wartość);

p.u.

T

X

reaktancja zwarciowa transformatora w jednostkach względnych.

 transformatory dwuuzwojeniowe w przypadku możliwych do określenia ich

warunków pracy w stanie ustalonym poprzedzającym zwarcie





b

T

I

I

X

c

U

U

K



sin

1

rT

o

mT

p.u.

T

max

o

m

n

T







(4)

gdzie:

o

m

U

najwyższe napięcie w sieci w stanie przedzwarciowym;

o

I

mT

największa wartość prądu obciążenia transformatora w stanie przedzwarciowym;

o

T



kąt obciążenia transformatora w stanie przedzwarciowym.

 transformatory trójuzwojeniowe – korygowane są impedancje par uzwojeń, które w

normie IEC oznaczane są literami A,B,C (licząc od uzwojenia o napięciu najwyższym
do uzwojenia o napięciu najniższym)

p.u.

TAB

max

TAB

6

,

0

1

95

,

0

X

c

K





(5a)

p.u.

TAC

max

TAC

6

,

0

1

95

,

0

x

c

K





(5b)

p.u.

TBC

max

TBC

6

,

0

1

95

,

0

X

c

K





(5c)

 generatory synchroniczne przyłączone bezpośrednio do sieci





"

d

G

G

G

G

GK

jX

R

K

Z

K

Z







(6)

rG

"

d

max

rG

n

G

sin

1



X

c

U

U

K





(7)

gdzie:

U

rG

-

napięcie znamionowe generatora;



rG

-

kąt fazowy odpowiadający warunkom pracy generatora;

X

d

” - reaktancja generatora w jednostkach względnych.

 silniki synchroniczne i kompensatory traktowane są w większości przypadków tak

samo jak generatory

 bloki generator – transformator (transformator blokowy z podobciążeniową regulacją

przekładni)





THV

G

2

r

S

S

Z

Z

t

K

Z





(8)

rG

p.u.

T

"

d

max

2

rTVL

2

rTLV

2

rG

2

nQ

S

sin

1



X

X

c

U

U

U

U

K











(9)

gdzie:

Z

THV

-

nieskorygowana impedancja transformatora blokowego;

U

nQ

-

wartość napięcia uznana za normalną w tym miejscu przyłączenia bloku do

sieci (na ogół U

nQ

>>U

n

);

t

r

-

znamionowa przekładnia transformatora blokowego (U

rTHV

/U

rTLV

).

Jeśli napięcie generatora utrzymywane jest w sposób ciągły na poziomie wyższym niż

U

rG

, do wzoru podstawiana jest wartość odpowiednio wyższa, np. o 5 %.

 szczególny przypadek pracy bloku – praca generatora w stanie niedowzbudzenia, np.

w elektrowniach szczytowo-pompowych

"

d

p.u.

T

max

2

rTHV

2

rTLV

2

rG

2

nQ

S

8

,

1

1

X

X

c

U

U

U

U

K











(10)

 blok z transformatorem bez regulacji przekładni pod obciążeniem





THV

G

2

r

SO

SO

Z

Z

t

K

Z





(11)





rG

d

T

G

X

c

p

U

U

p

U

U

K



sin

1

)

1

(

1

"

max

rTHV

rTLV

rG

nQ

SO













(12)

gdzie:

1+p

G

-

mnożnik zwiększający napięcie generatora ponad wartość U

rG

;

1±p

T

-

mnożnik zwiększający (zmniejszający) napięcie znamionowe U

rTHV

transformatora blokowego.

Specyfika obliczeń dla zwarć w pobliżu generatorów

Przebieg prądu zwarcia, które wystąpiło w pobliżu generatorów cechuje (jak wiadomo z

wcześniejszych

rozważań)

zmniejszanie

się

amplitudy

składowej

okresowej.

W

przeciwieństwie do pierwotnej wersji normy IEC 909 (z 1988 r.) obecna wersja nie wymaga

od liczącego osobnego budowania schematów sieci jeśli zwarcie zlokalizowane jest w pobliżu

generatorów. Współczynniki korygujące wartość impedancji trzeba wprowadzać bez względu

na to, czy miejsce zwarcia jest odległe od generatora, czy też nie. Jeśli jednak zwarcie jest

uznane za odległe, wtedy upraszczają się obliczenia innych wielkości zwarciowych.

W przypadkach prostych układów zasilanych z systemu za pośrednictwem transformatora

norma z góry uznaje, że zwarcie jest zlokalizowane daleko od generatorów, jeśli spełniony

jest warunek X

TK

>2X

Q

(skorygowana reaktancja transformatora jest większa od podwojonej

wartości reaktancji systemu zasilającego).

Uwzględnianie wpływu silników indukcyjnych na prąd zwarcia

Podobnie jak norma PN-74/E-05002 również norma IEC 60909 zaleca uwzględnianie

silników indukcyjnych w obliczeniach zwarciowych. Obligatoryjnie dotyczy to silników

wysokiego napięcia, zaś w przypadku silników niskiego napięcia ma to znaczenie w

przypadku licznych grup silników dużej mocy (układy potrzeb własnych elektrowni, sieci w

niektórych zakładach przemysłowych).

Kryterium pozwalające na pominięcie silników to sytuacja gdy ich sumaryczny prąd

znamionowy nie przekracza 1% prądu zwarciowego wyznaczonego bez udziału tych

silników, tzn.





rM

"

K

01

,

0

I

I

(13)

Jeśli obliczenia dotyczą sieci publicznej niskiego napięcia - silników jest tam niewiele, są

zlokalizowane w sposób rozproszony, to również ich udział w prądzie zwarcia może być

pominięty.

W przypadku występowania w sieci grup silników, których jednoczesne załączenie jest

niemożliwe (np. ze względów technologicznych), w obliczeniach uwzględnia się tylko jedną z

tych grup.

Inne kryterium dotyczące uwzględniania silników wysokiego i niskiego napięcia, które są

przyłączone

do

sieci

dotkniętej

zwarciem

za

pośrednictwem

transformatorów

dwuuzwojeniowych (rys. 2) ma postać

3

,

0

100

8

,

0

"

kQ

rT

rT

rM













S

S

c

S

P

(14)

gdzie:



rM

P - suma mocy znamionowych silników niskiego i wysokiego napięcia;



rT

S -

suma mocy znamionowych transformatorów bezpośrednio zasilających silniki;

"

KQ

S

- moc

zwarciowa obliczeniowa w miejscu zasilania Q (rys.2). Ostatni warunek zawarty w normie

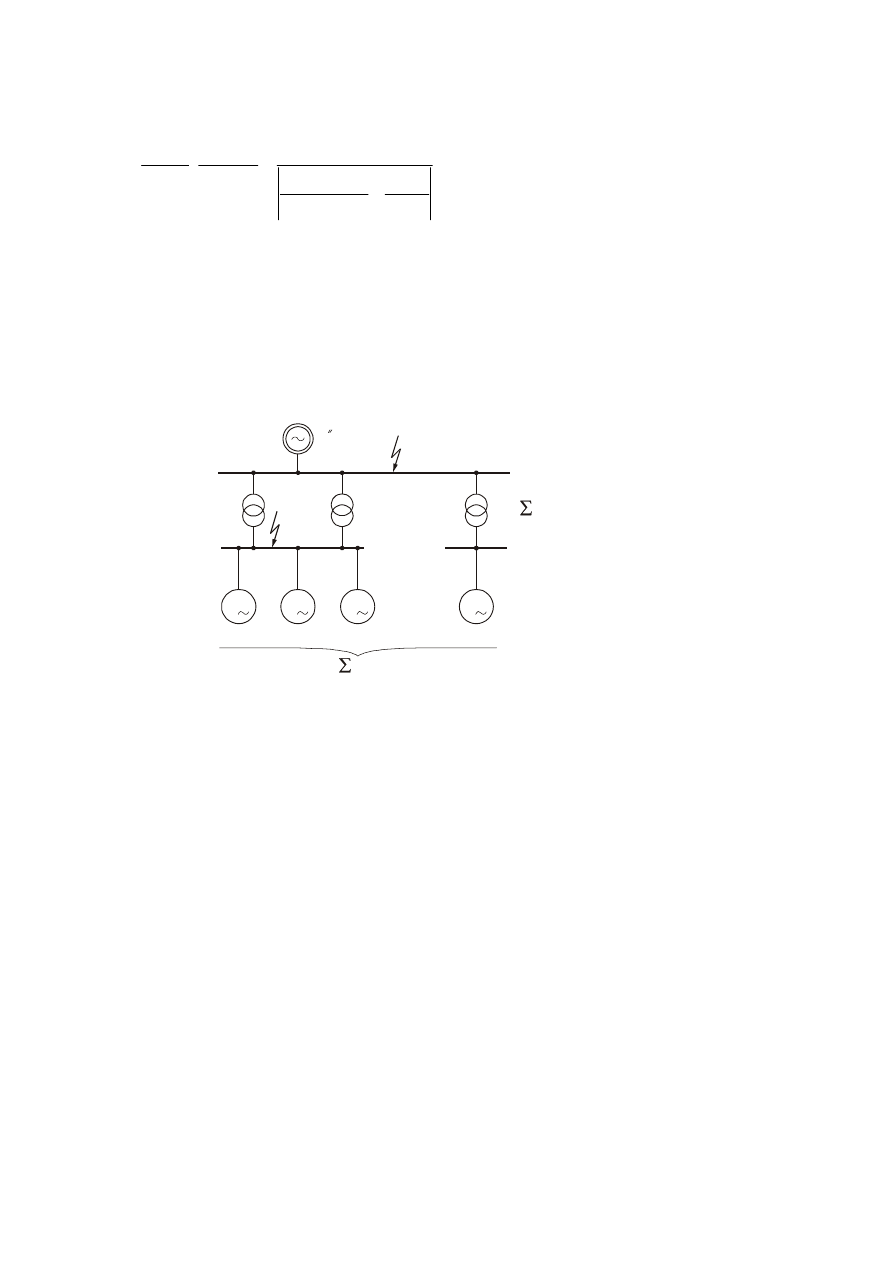
jest uproszczoną postacią warunku podanego w pracy

100

5

100

8

,

0

5

/

KT

"

KQ

rT

rM

LR

rT

rM

u

S

S

c

I

I

S

P

















(15)

Przejście od (15) do wzoru o postaci (14) podanego w normie, odbywa się przy założeniu, że

krotność prądu rozruchowego

%

6

oraz

5

/

KT

rM

LR





u

I

I

(napięcie zwarcia transformatora).

W warunkach krajowych szczególnie to ostatnie założenie jest problematyczne- częściej dla

transformatorów małej mocy SN/nn

%

5

,

4

KT



u

. Zależność (14) podana w normie nie

obowiązuje w przypadku zasilania silników z transformatorów trójuzwojeniowych.

M

3

Q

A

15 kV

6 kV

0,38 kV

S

rT1

S

rT2

S

rT3

B

M

3

M1

M

3

M2

M

3

M3

M4

Silnik zastępczy

S

KQ

P

rM

rT1

S

= S

+ S

+ S

rT

rT2

rT3

Rys. 2. Ilustracja do przykładu na wyznaczanie udziału silników indukcyjnych w prądzie zwarciowym

Ogólna idea przedstawionej w normie IEC 60909 metody uwzględniania silników

indukcyjnych w obliczeniach zwarciowych polega na modelowaniu ich w postaci źródeł siły

elektromotorycznej, a następnie traktowaniu ich w sposób równoprawny z innymi źródłami

istniejącymi w sieci. Z uwagi na zanikanie składowej okresowej prądu do zera, w

obliczeniach ustalonego prądu zwarcia trójfazowego silniki nie są uwzględniane. Traktowanie

silników tak samo jak innych źródeł przy obliczaniu prądu I

K

” stanowi istotną różnicę w

stosunku do "starej" normy zwarciowej - PN-74/E-05002.

Dla uproszczenia obliczeń można zastąpić grupę silników niskiego napięcia wraz z ich

liniami zasilającymi jednym silnikiem równoważnym. W przypadku zwarcia w miejscu Q lub

A (rys. 2) zamiast prądu silnika równoważnego M4 można przyjmować prąd znamionowy

transformatora zasilającego tę grupę silników. Impedancję Z

M

silnika zastępczego wyznacza

się wtedy przyjmując

rT3

rM4

S

S



, ponadto przyjmuje się

42

,

0

/

oraz

5

/

M

M

rM

LR





X

R

I

I

;

przy braku innych danych moc znamionowa na jedną parę biegunów wynosi m=0,05 MW.

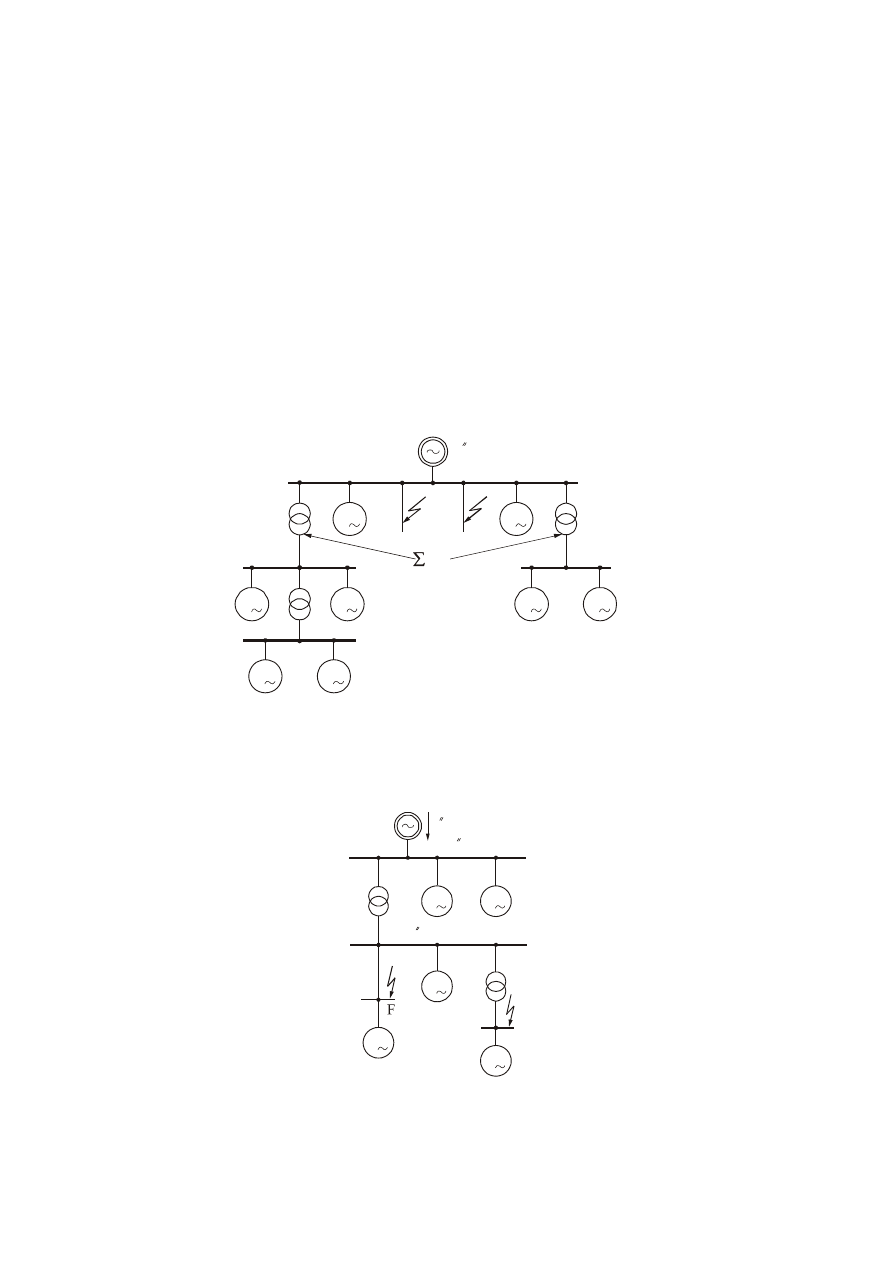
Rys. 3 ilustruje kolejny przykład uwzględniania silników w obliczeniach zwarciowych.

Inny przykład przedstawiono na rys. 4. Przy obliczaniu wielkości zwarciowych na szynach A

(10 kV) należy uwzględnić wpływ silników zasilanych z szyn 10 kV (M1 i M2), natomiast

wpływ pozostałych silników (M3, M4) w zależności od wyników kryterium (3). Dla zwarć na

szynach B (0,66 kV) należy uwzględnić wpływ silników równoważnych (M3, M4), a wpływ

grupy M5 uzależnić od wyników kryterium (14). Podobnie przy zwarciu w p. F

1

. Przy

zwarciu w p. F

2

należy uwzględnić udział grupy M5, a udział M3, M4 w zależności od

kryterium (14). Silniki przedstawione w powyższych schematach są silnikami zastępczymi

(równoważnymi), zastępującymi rzeczywistą grupę silników(∑P

rM

). Dopuszczalne jest

przyjmowanie zamiast mocy silników – mocy transformatorów zasilających te silniki.

M

3

M1

M2

M3

M4

3

3

3

3

M

3

M

3

Q

A

F

F

T1

T2

10 kV

6 kV

0,66 kV

0,38 kV

B

B

M

3

S

KQ

S

rT

a

a

a

b

c

c

b

a

Rys. 3. Podział silników indukcyjnych wg udziału w obliczeniach zwarciowych przy zwarciu w p. F: a)

silniki uwzględnione w obliczeniach; b) silniki uwzględnione w obliczeniach dotyczących potrzeb własnych

elektrowni i sieci przemysłowych; c) silniki nie uwzględniane w obliczeniach

M3

3

F

T1

T2

10 kV

0,66 kV

0,66 kV

0,38 kV

B

C

1

2

S

KQ

S

KA

S

KB

M2

3

M4

3

M5

3

M1

3

A

Rys. 4. Ilustracja do uwzględniania wpływu silników indukcyjnych przy zwarciach na szynach niskiego

napięcia

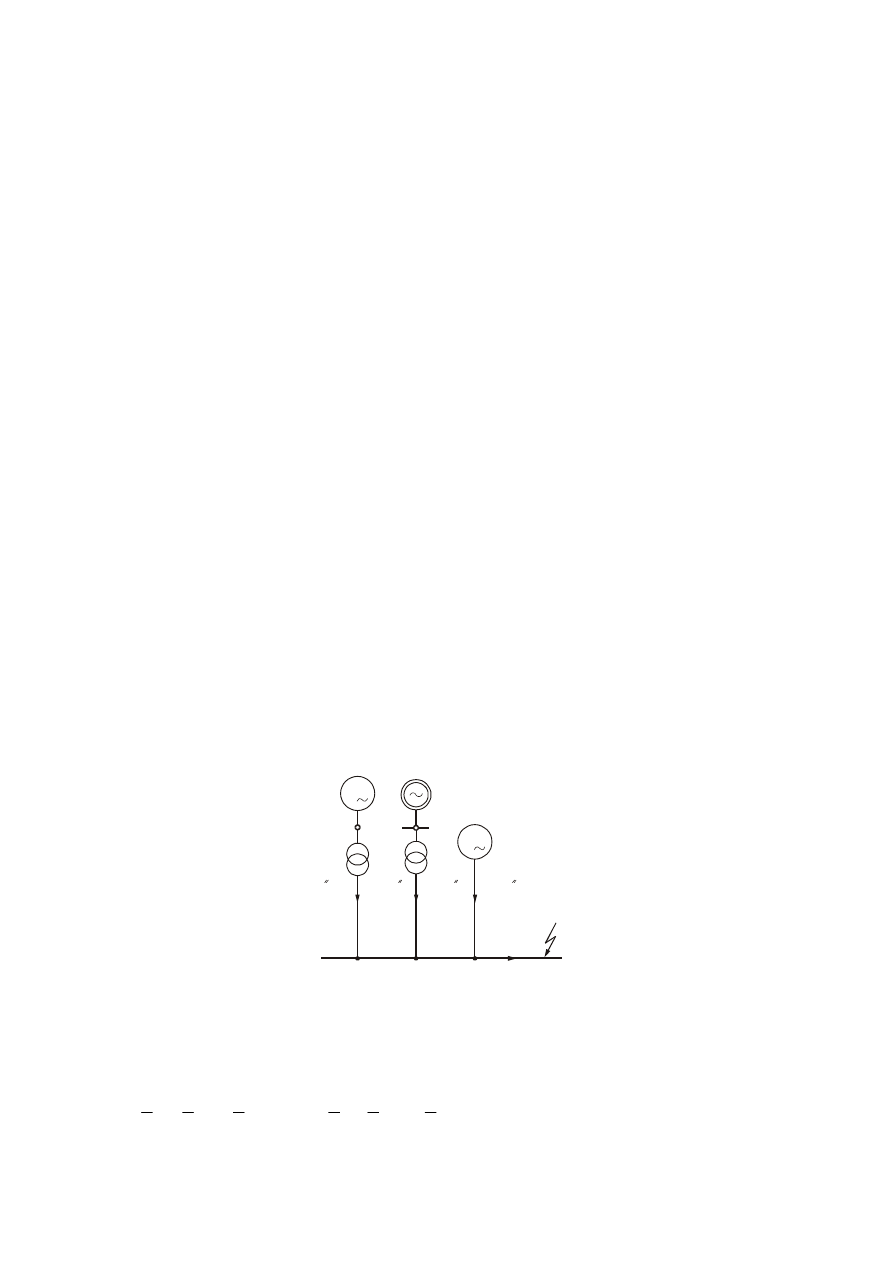
Z uwagi na fakt komputeryzacji procesu obliczeniowego często dogodniej jest uwzględnić w

obliczeniach wszystkie silniki występujące w danej sieci (np. zakładu przemysłowego),

traktując je jak równoprawne (z generatorami) źródła i nie dokonując wielokrotnego

sprawdzania kryterium (14). Postępowanie takie jest zgodne z główną ideą metody IEC - tzn.

ideą jednego źródła zastępczego, natomiast moc obliczeniowa komputera eliminuje jego

uciążliwość i pracochłonność. Należy jednak w tym przypadku liczyć się z możliwością

otrzymania prądów zwarciowych o wartościach nieco zawyżonych w stosunku do

rzeczywistych.

1.2

Obliczanie wielkości zwarciowych według zaleceń normy IEC 60909

Początkowy symetryczny prąd zwarcia

W normie IEC 60909 podobnie jak w innych standardach obliczeniowych wyznaczanie tej

wielkości I

K

” przy wykorzystaniu wzoru (1) ma znaczenie podstawowe. Norma wprowadza

jednak cztery charakterystyczne przypadki obliczeń, nadając im pewną specyfikę. Poniżej

zostały one kolejno omówione.

Zwarcie w układzie o konfiguracji zbliżonej do promieniowej

W przypadku, gdy układ ma konfigurację promieniową, lub taką, którą można sprowadzić do

konfiguracji promieniowej za pomocą prostych przekształceń, zaleca się, aby symetryczny

prąd zwarcia wyznaczać indywidualnie dla każdego elementu przyłączonego do miejsca

zwarcia stanowiącego źródło prądu zwarcia – rys. 5. Korzysta się przy tym ze wzoru (1), przy

czym za Z

K

podstawia się kolejno impedancje zastępcze poszczególnych źródeł.

G

3

M

3

Q

F

I
i
I

KPSU

pPSU

bPSU

I
i

KT

pT

I
i
I

KM

pM

bM

I
i
I
I

K

K

p

b

K3

Rys. 5. Przykład obliczania symetrycznego prądu zwarcia I

K

” w układzie o konfiguracji promieniowej

Dla przykładu widocznego na rys. 5 impedancje te wynoszą odpowiednio

 generator z transformatorem blokowym i linią





L

THV

G

2

r1

PSU

L

PSU

K

Z

Z

Z

t

K

Z

Z

Z











(16a)

 system zastępczy z transformatorem i linią

L

THV

T

2

r2

Q

K

Z

Z

K

t

Z

Z







(16b)

 silnik (grupa silników) wysokiego napięcia i linia

L

M

K

Z

Z

Z





(16c)

W miejscu zwarcia (F) prąd I

K

” wyznaczany jest jako suma zespolonych wartości prądów

cząstkowych tj.





i

i

I

I

"

K

"

K

(17)

Norma dopuszcza jednak wyznaczenie modułu tego prądu jako sumy modułów, co nie

powoduje błędów wykraczających poza dopuszczalny margines.

Zwarcie pomiędzy generatorem a transformatorem blokowym z regulacją zaczepów pod

obciążeniem

W celu wyznaczenia cząstkowych prądów zwarciowych

"

KG

I

oraz

"

KT

I

(rys. 6) dla zwarcia w

węźle F1 należy skorzystać z następujących wzorów

G

GS

rG

"

KG

3

Z

K

cU

I



(18a)

















Qmin

1

TLV

rG

"

KT

2

r

3

Z

Z

cU

I

t

(18b)

przy czym K

GS

jest współczynnikiem korygującym wyznaczanym ze wzoru

rG

"

d

max

GS

sin

1



X

c

K





(19)

a

min

Q

Z

jest minimalną wartością impedancji systemu zasilającego wynikającą z

maksymalnej wartości jego mocy zwarciowej.

W przypadku lokalizacji miejsca zwarcia na odpływie do układu potrzeb własnych (np. węzeł

F2) całkowity prąd zwarcia należy wyznaczyć ze wzoru







































Qmin

1

TLV

TS

G

GS

rG

"

KF2

2

r

1

1

3

Z

Z

K

Z

K

cU

I

t

(20)

przy czym współczynnik korygujący K

TS

wyznacza się jako

rG

Tp.u.

max

TS

sin

1



X

c

K





(21)

a współczynnik K

GS

zgodnie ze wzorem (19).

Widoczna we wzorze (20) impedancja Z

TLV

może być traktowana jako impedancja

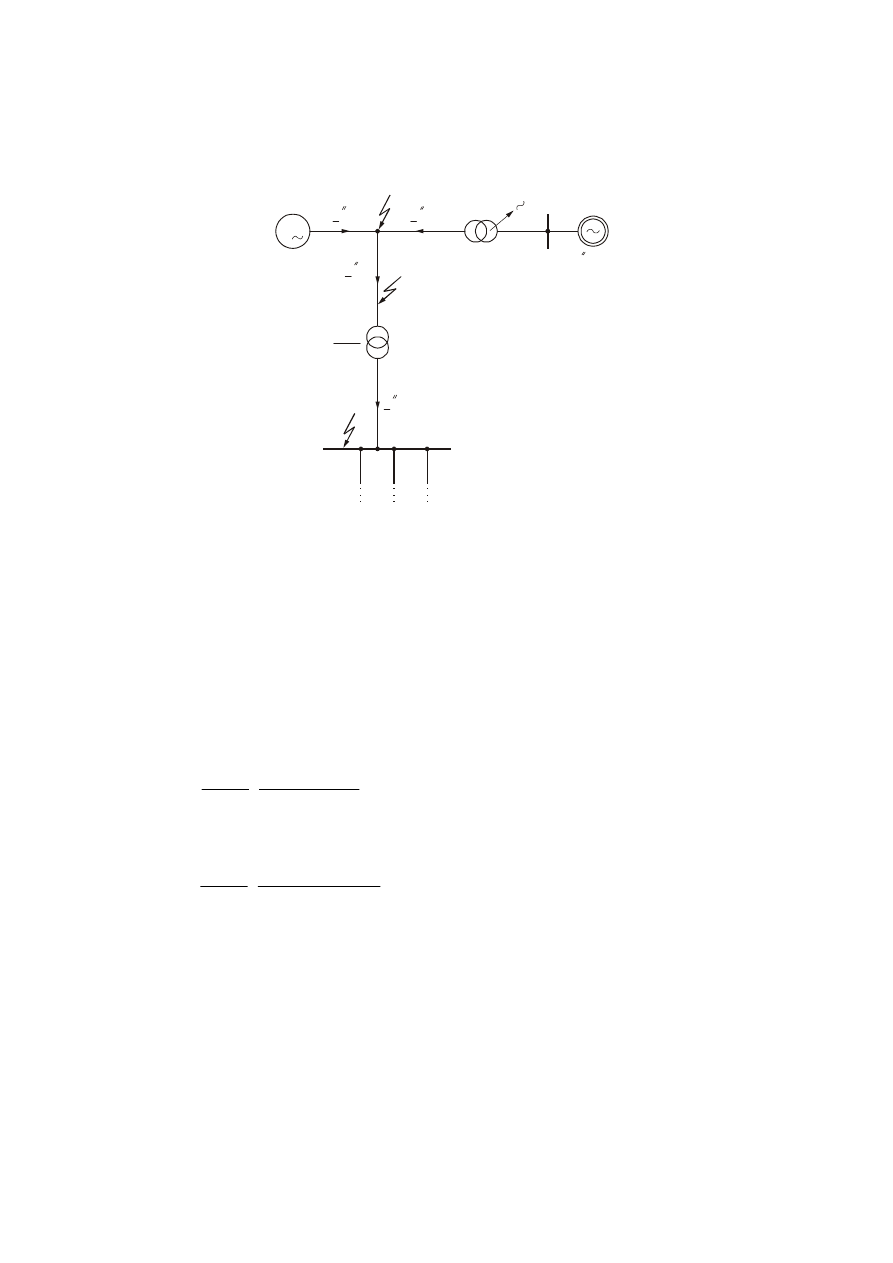
zastępczego źródła, w przypadku zwarcia po stronie dolnego napięcia autotransformatora AT

(węzeł F3 na rys. 6).

Q

G

G

3

T

F1

AT

A

F3

K3

K3

K3

t

rAT

1

F2

KF2

I

KG

I

KQmax

I

KT

I

KAT

I

1:t

nQ

U

Q

U

Rys. 6. Ilustracja metody wyznaczania prądów w przypadku zwarć zachodzących pomiędzy generatorem

a transformatorem blokowym

Zwarcie pomiędzy generatorem a transformatorem blokowym bez regulacji zaczepów pod

obciążeniem

W przypadku zwarć pomiędzy generatorem a transformatorem blokowym nie posiadającym

regulacji pod obciążeniem odpowiednie prądy wylicza się z takich samych wzorów jak (18a)

(18b) (20),

ale współczynniki

korekcyjne

wyznaczane są nieco

inaczej.

Zamiast

współczynnika K

GS

współczynnik K

GSO

wyznaczany jest jako

rG

"

d

max

G

GSO

sin

1

1

1



X

c

p

K









(22)

i zamiast K

TS

współczynnik K

TSO

wyznaczany jest ze wzoru

rG

p.u.

T

max

G

TSO

sin

1

1

1



X

c

p

K









(23)

przy czym 1+p

G

oznacza względną wartość przekładni transformatora blokowego na górnym

zaczepie. Należy także pamiętać, że w przypadku wyznaczania prądu zwarcia po stronie

dolnego napięcia transformatora potrzeb własnych uwzględnia się impedancję zastępczą Z

rsl

oraz skorygowaną wartość impedancji transformatora (współczynnik korekcyjny wyznaczony

według wzoru (3)).

Zwarcia w sieciach zamkniętych

Przykład sieci o strukturze zamkniętej przedstawiono na rys. 7. Zalecenie normy odnośnie

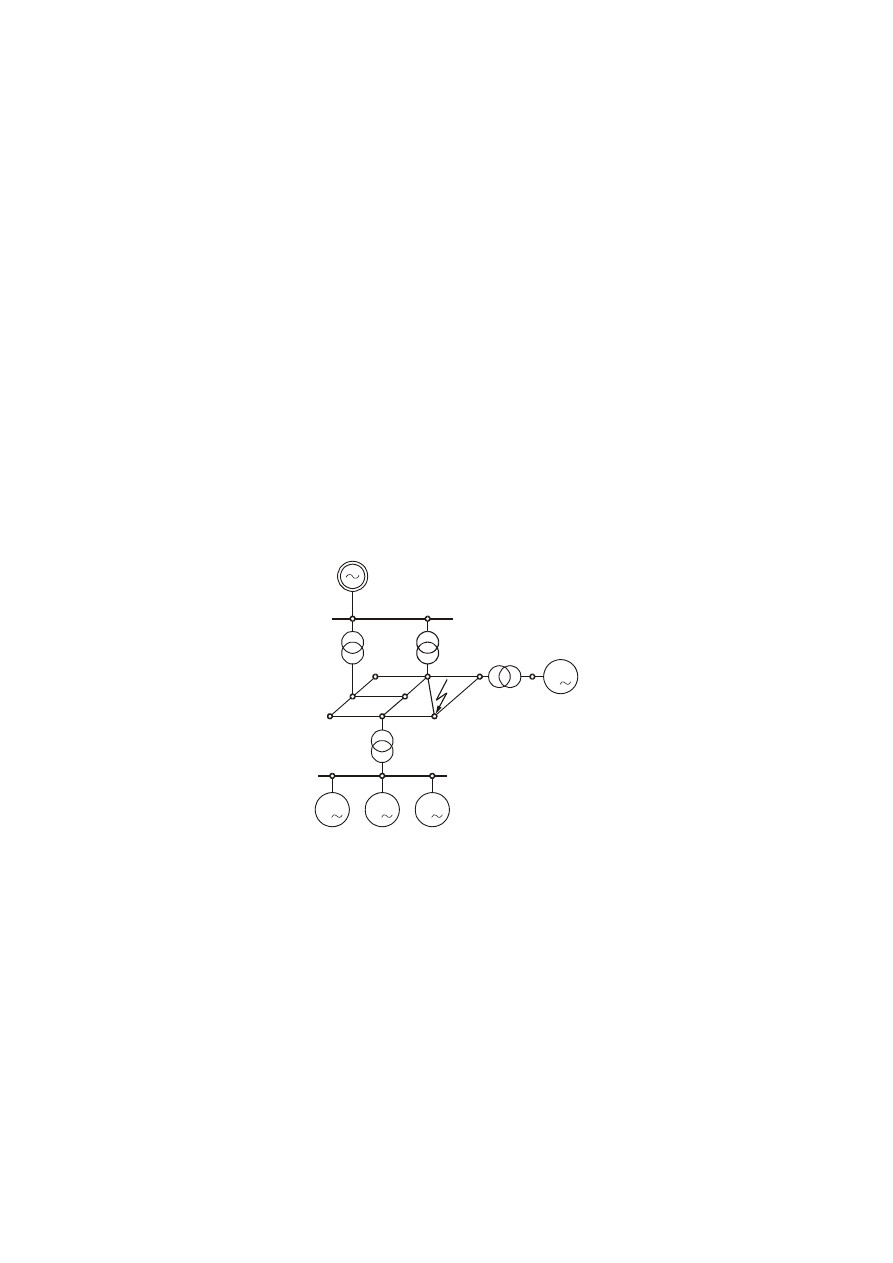
sieci zamkniętej polega w tym przypadku na wyznaczeniu zastępczej impedancji zwarciowej

Z

K

za pomocą sekwencji przekształceń topologicznych (łączenie równoległe, szeregowe,

przekształcenia trójkąt-gwiazda itd.). Możliwe jest także zastosowanie innych metod

przekształcania sieci wykorzystujących jej model węzłowy. Jeżeli pomiędzy miejscem

zwarcia a danym elementem sieci znajduje się transformator (na rys. 7 takimi elementami są –

generator G, system zastępczy Q oraz grupa silników M) jego impedancja powinna być

oczywiście sprowadzona na poziom napięcia tej sieci z uwzględnieniem przekładni

transformatora. Jeśli pomiędzy danym elementem (lub podsystemem) znajduje się więcej niż

jeden transformator, a przekładnie tych transformatorów różnią się między sobą, norma zaleca

przyjęcie za współczynnik sprowadzenia średniej arytmetycznej przekładni transformatorów

(na rys. 7 pomiędzy podsystemem Q a siecią objętą zwarciem występują dwa transformatory).

Pamiętać należy jednak, że także w sieci o strukturze zamkniętej, w obliczeniach są

wykorzystywane impedancje elementów (transformatorów, generatorów), których wartości są

pomnożone przez odpowiednie współczynniki korygujące.

G

3

M

3

M

3

M

3

F

Q

Rys. 7. Przykład sieci o strukturze zamkniętej

Udarowy prąd zwarcia

Termin prąd udarowy jest zwyczajowym (choć właściwie niepoprawnym) tłumaczeniem

nazwy wielkości zwarciowej określonej w normie jako peak current i oznaczonej symbolem

i

p

. Poprawne tłumaczenie to raczej prąd szczytowy (wartość maksymalna w przebiegu prądu

zwarcia), jednak ten termin w polskim słownictwie technicznym jest zarezerwowany dla

wielkości określającej wytrzymałość dynamiczną aparatów elektrycznych, stąd propozycja

tłumaczenia zapewniająca zgodność z normą IEC 60909.

Warto zwrócić uwagę, że wyznaczenie maksymalnej wartości, którą osiąga prąd zwarcia

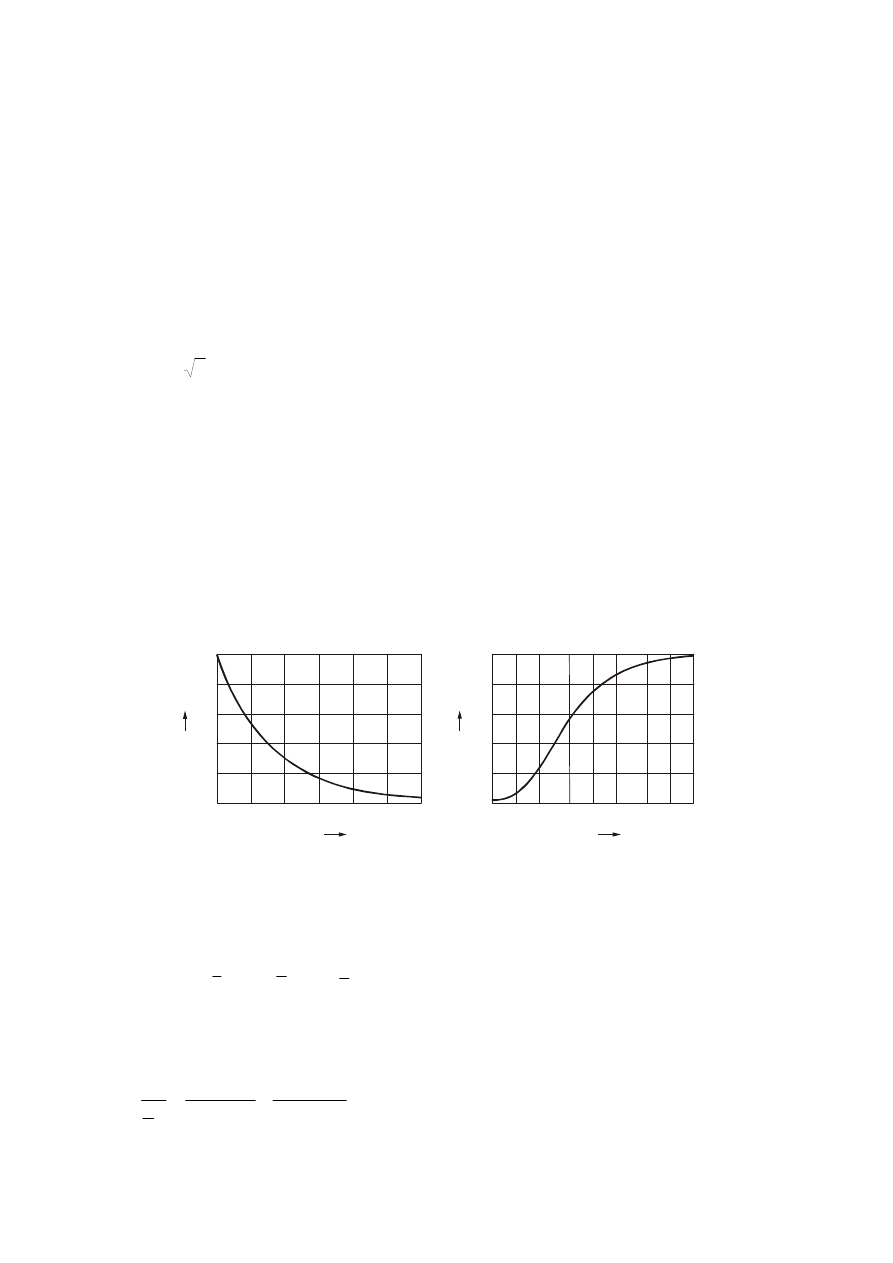
(czyli maksymalnej wartości osiąganej przez przebiegi widoczne rys. 1) nie jest z punktu

widzenia analizy matematycznej zadaniem łatwym. Rozpatrując uproszczoną opisu prądu

zwarcia w funkcji czasu w postaci (2) zadanie określenia maksymalnej wartości prądu (a więc

prądu i

p

) sprowadza się do znalezienia jej maksimum. Jednak klasyczne podejście polegające

na wyznaczeniu funkcji pochodnej i przyrównania jej do zera zawodzi, z uwagi na wyraźną

nieliniowość otrzymanego równania. Dlatego w obliczeniach inżynierskich stosuje się

podejście jeszcze bardziej uproszczone, polegające na przyjęciu zależności liniowej pomiędzy

wartością prądu udarowego a wartością początkowego prądu zwarcia tj.

"

K

p

2 I

i





(24)

przy czym wartość współczynnika udaru

 w zależności od R/X lub X/R podano w formie

graficznej na rys. 8. Współczynnik ten można również wyliczyć ze wzoru

3R/X

e

98

,

0

02

,

1









(25)

Dokładne wyznaczenie maksymalnej wartości prądu zwarcia w przypadku układu zasilanego

z kilku źródeł (konfiguracja promieniowa) oraz w sieci zamkniętej jest jeszcze bardziej

złożonym zagadnieniem. Ilustruje to rys. 9.

0

0,2 0,4 0,6 0,8 1,0 1,2

1,0

1,2

1,4

1,6

1,8

2,0

x

R X

/

1,0

1,2

1,4

1,6

1,8

2,0

0,5 1 2

5 10 20

50 100 200

x

R X

/

a)

b)

Rys.8.

Współczynnik



dla obwodów szeregowych w zależności od wartości: a)

X

R /

oraz b)

R

X /

Na podstawie analizy obwodów liniowych w stanie nieustalonym można stwierdzić, że

widoczna na rysunku składowa nieokresowa prądu i(t) może być wyrażona jako

 

t

t

t

Lz

z

R

L

R

L

R

e

i

e

i

e

i

t

i













G

G2

G1

2

2

1

1

(26)

Przebieg nieustalony zanika zatem w sposób określony poprzez dwie stałe czasowe T

1

=L

1

/R

1

oraz T

2

=L

2

/R

2

. Wyznaczając zastępczą impedancję obwodu

2

2

1

1

K

1

1

1

L

j

R

L

j

R

Z













(27)

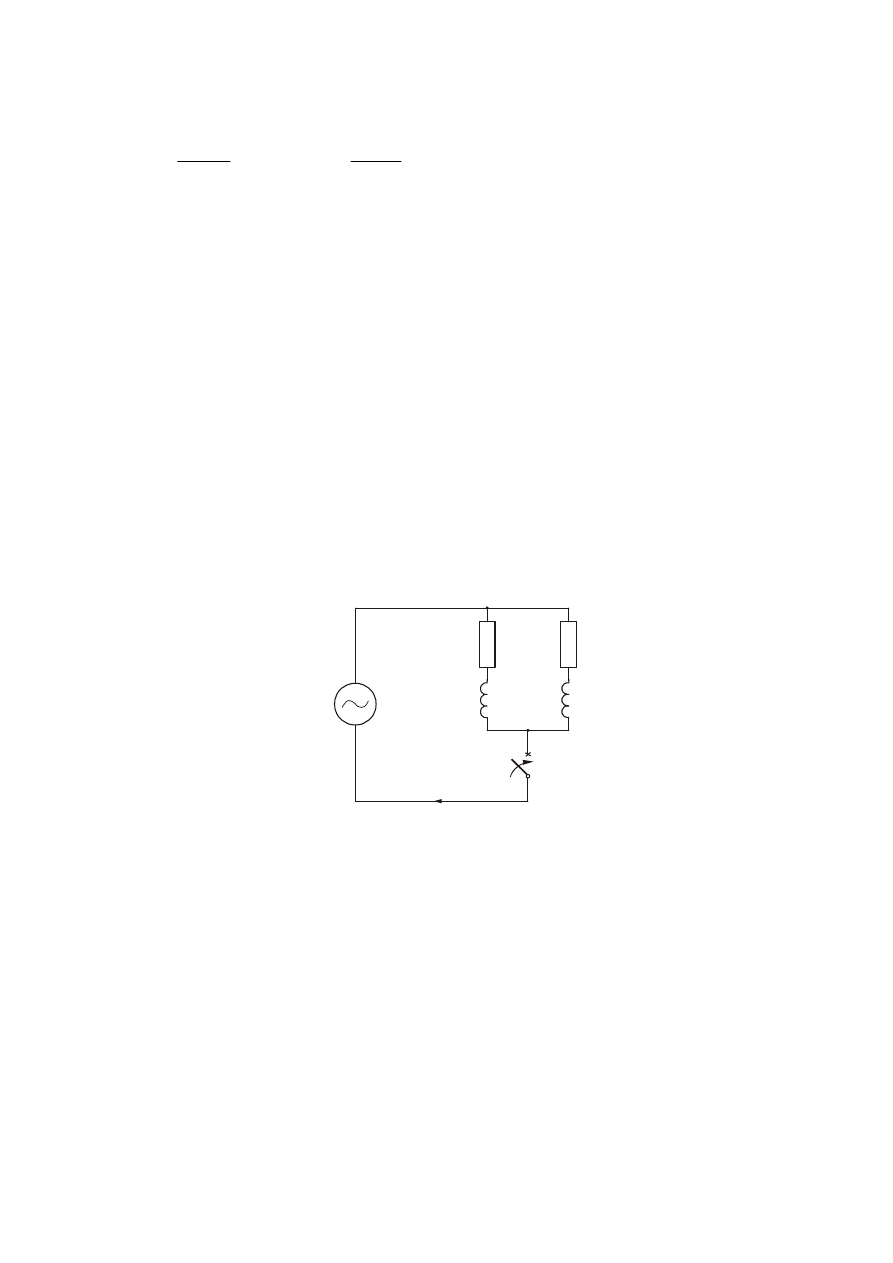
bądź też wyznaczając osobno zastępczą rezystancję i reaktancję

2

1

2

1

2

1

2

1

z

,

L

L

L

L

X

R

R

R

R

R

z











(28)

nie można dobrać zastępczej stałej czasowej charakteryzującej zanikanie składowej

nieokresowej, co wynika ze wzoru (26). Mniemanie o istnieniu takiej zastępczej stałej

czasowej jest równocześnie częstym błędem popełnianym przez mniej doświadczone osoby

zajmujące się problematyka zwarciową.

Jeżeli jednak poszukiwana jest maksymalna wartość przebiegu prądu zwarcia, to nawet przy

dość dużym rozrzucie wartości stałych czasowych (np. T

1

/T

2

=10) błąd popełniany w wyniku

zastosowania zależności

2

p

1

p

p

i

i

i





(29)

(wartość maksymalna prądu w obwodzie o dwóch stałych czasowych jest równa sumie

wartości maksymalnych wyznaczonych dla poszczególnych składowych) jest niewielki.

Takie

postępowanie,

polegające

na

sumowaniu

wartości

prądów

udarowych

w

poszczególnych elementach przyłączonych do miejsca zwarcia zaleca norma IEC 60909.

G

i t

( )

R

1

L

1

R

2

L

2

Rys. 9. Obwód zawierający dwie gałęzie równoległe o różnych wartościach stosunku R/X

W przypadku sieci zamkniętych wyznaczenie przebiegu składowej nieokresowej prądu

zwarcia wymagałoby zastosowania złożonych metod rachunku operatorowego. Dlatego też

norma podaje w tym zakresie 3 alternatywne rozwiązania uproszczone (metody A,B,C)

wykorzystujące wzór (24), a różniące się sposobem wyznaczania współczynnika

 .

Jeżeli nie jest wymagana duża dokładność obliczeń, to wystarcza metoda A. Poniżej

omówiono w skrócie tę metodę oraz metody B i C.

Metoda A

.

Przy jednakowej wartości R/X lub X/R przyjmuje się

a



 

. Współczynnik

a

 jest

określony jako najmniejsza wartość stosunku R/X (lub największa X/R) spośród wszystkich

gałęzi sieci. Wystarczające jest uwzględnienie gałęzi, przez które przepływa łącznie co

najmniej 80% prądu w miejscu zwarcia.

Metoda B.

Dla zastępczej impedancji zwarciowej

K

K

K

jX

R

Z





wyznacza się

b

 wg rys. 8

lub wzoru (25). Do obliczeń prądu udarowego przyjmuje się

b

15

,

1



 

, nie przekraczając

jednak wartości 1,8 (sieć niskiego napięcia) lub 2,0 (sieć SN i WN).

Metoda

C.

Wprowadza się pojęcie częstotliwości zastępczej

,

c

f

której wartość dla

częstotliwości sieciowej f=50 Hz wynosi

c

f =20 Hz. Dla częstotliwości tej wyznacza się

impedancję zastępczą

c

c

c

jX

R

Z





, a następnie stosunek

f

f

X

R

X

R

c

c

c





(30)

Współczynnik

c

 wyznacza się z tego właśnie stosunku (rys. 8 lub wzór (25)), a do

wyznaczenia prądu udarowego przyjmuje się

.

c



 

W przypadku wyznaczania impedancji

Z

c

wartości impedancyjnych współczynników korekcyjnych (chociaż wyznaczone dla sieci

50 Hz) nie należy przeliczać na poziom częstotliwości f

c

. Uzasadnienie dla zastosowania

częstotliwości

c

f =20 Hz ma charakter empiryczny. Zauważono bowiem, że w przypadku

sieci o strukturze zamkniętej przyjmowanie do wzoru (24) współczynnika

 wyznaczonego

na podstawie stosunku R

K

/X

K

zaniża wartość prądu i

p

. Okazało się, że przyjęcie obniżonej o

60% częstotliwości obniżające wartość reaktancji wszystkich elementów wpływa na

zadowalające skorygowanie wartości współczynnika

 . Trudno jednak dla tego faktu podać

spójne wyjaśnienie poza doświadczeniem wynikającym z wielu analiz obliczeniowych

układów zbudowanych z gałęzi typu R,L.

Symetryczny prąd wyłączeniowy

Zmniejszanie się składowej okresowej prądu zwarciowego uwzględnia się w normie IEC

60909 przy wyznaczaniu prądu wyłączeniowego I

B

za pomocą współczynnika





1







"

K

B

I

I





(31)

przy czym wartość

 zależy od stosunku

rG

"

K

/ I

I

oraz czasu własnego minimalnego

min

t

,

który jest sumą minimalnego opóźnienia czasowego przekaźnika bezzwłocznego i

najmniejszego czasu otwierania wyłącznika. Nie uwzględnia się opóźnienia czasowego

nastawianego w układach wyłączających. Wartości

 określone poniżej odnoszą się do

turbogeneratorów średniego napięcia, generatorów jawnobiegunowych oraz kompensatorów

synchronicznych ze wzbudzeniem zasilanym z maszyny wirującej lub prostownika (przy

założeniu, że w przypadku wzbudzenia prostownikowego czas własny minimalny jest

mniejszy niż 0,25 s i maksymalne napięcie wzbudzenia jest mniejsze niż 1,6 napięcia

wzbudzenia przy obciążeniu znamionowym). W innych przypadkach przyjmuje się

 =1.

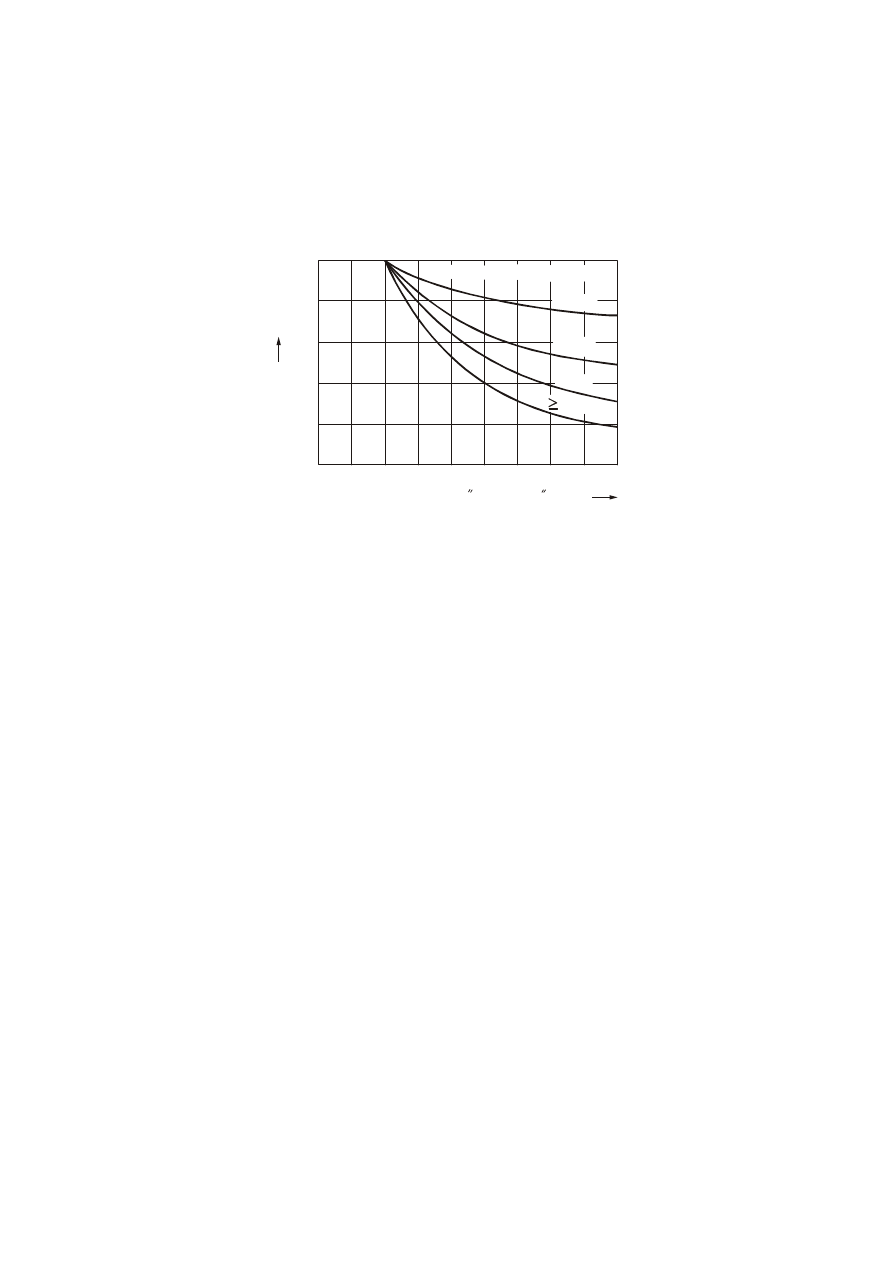
1,0

0,9

0,8

0,7

0,6

0,5

0

1

2

3

4

5

6

7

8

9

Zwarcie trójfazowe

lub

I

/I

I

/I

KG rG

KM rM

Czas własny minimalny t

min

0,02 s

0,05 s

0,1 s

0,25 s



Rys. 10. Współczynnik



do obliczania prądu zwarciowego wyłączeniowego

B

I

Wartość współczynnika

 =1 przyjmuje się także dla zwarć odległych od generatora i dla

większości przypadków obliczeń dotyczących sieci zamkniętych. Miarą odległości od

generatora jest w tym przypadku wartość stosunku

rG

"

K

/ I

I

. Jeśli jest ona mniejsza niż 2

zwarcie traktowane jest jako odległe. W pozostałych przypadkach wartość współczynnika



wyznaczana jest ze wzorów:

rG

"
KG

rG

"
KG

rG

"

KG

rG

"

KG

/

38

0

min

/

32

0

min

/

30

0

min

/

26

0

min

e

0,94

0,56

s

0,25

dla

-

e

72

,

0

62

,

0

s

10

,

0

dla

-

e

51

,

0

71

,

0

s

05

,

0

dla

-

e

26

,

0

84

,

0

s

02

,

0

dla

-

I

I

,

-

I

I

,

-

I

I

,

-

I

I

,

-

t

t

t

t

































(32)

Wartość

"

KG

I

(składowa prądu zwarciowego od generatora) i

rG

I

(prąd znamionowy

generatora) są odniesione do tego samego napięcia. Pamiętać o tym należy wyznaczając prąd

b

I w przypadku zwarć zasilanych za pośrednictwem transformatorów blokowych. Za pomocą

przekładni

r

 (znamionowa przekładnia transformacji) należy doprowadzić do tego, aby

obydwa prądy były określone na tym samym poziomie napięcia. Współczynnik

 można

również określić z rys. 10 w zależności od prądu początkowego, a dla pośrednich wartości

czasu własnego można stosować interpolację liniową pomiędzy krzywymi.

Przy zwarciu zasilanym z kilku niezależnych źródeł (rys. 5) w celu wyznaczenia prądu

wyłączeniowego, dodaje się poszczególne prądy wyłączeniowe wyznaczone oddzielnie dla

każdego ze źródeł czyli

M

B

"

KT

PSU

B

B

I

I

I

I







(33)

Z uwagi na szybkie zanikanie prądu zwarciowego silników indukcyjnych, przy obliczaniu

prądu wyłączeniowego I

bM

wprowadza się dodatkowy współczynnik q, zależny od mocy

silnika przypadającej na parę biegunów i minimalnego czasu własnego. Szybkość zanikania

prądu zwarciowego jest tym większa, im moc przypadająca na parę biegunów jest mniejsza

(

p

P

m

/

rM



). Wartości współczynnika q oblicza się następująco:

m

q

s

t

m

q

s

t

m

q

s

t

m

q

s

t

ln

10

,

0

26

,

0

25

,

0

dla

ln

12

,

0

57

,

0

10

,

0

dla

ln

12

,

0

79

,

0

05

,

0

dla

ln

12

,

0

03

,

1

02

,

0

dla

min

min

min

min

































(34)

(gdzie m oznacza moc znamionową silnika w megawatach przypadającą na jedną parę

biegunów) lub wyznacza z wykresu na rys. 11.

Tak więc

"

KM

BM

I

q

I





(35)

W sieciach zamkniętych, w obliczeniach przybliżonych można pomijać efekt zanikania

składowej okresowej prądu zwarcia i przyjmować

"

K

B

I

I



(36)

W celu uzyskania większej dokładności norma proponuje zastosowanie następującego wzoru









"

KM

n

"

M

"

KG

n

"

G

"

K

B

1

3

1

3

j

j

j

j

j

i

i

i

i

I

q

cU

U

I

cU

U

I

I























(37)

przy czym: prąd początkowy

"

K

I

wyznacza się z uwzględnieniem wszystkich źródeł;

wielkości ze wskaźnikiem i dotyczą generatorów, a ze wskaźnikiem j silników indukcyjnych.

Postać i sens wzoru (37) można wyjaśnić za pomocą rys. 12 oraz następującego

rozumowania.

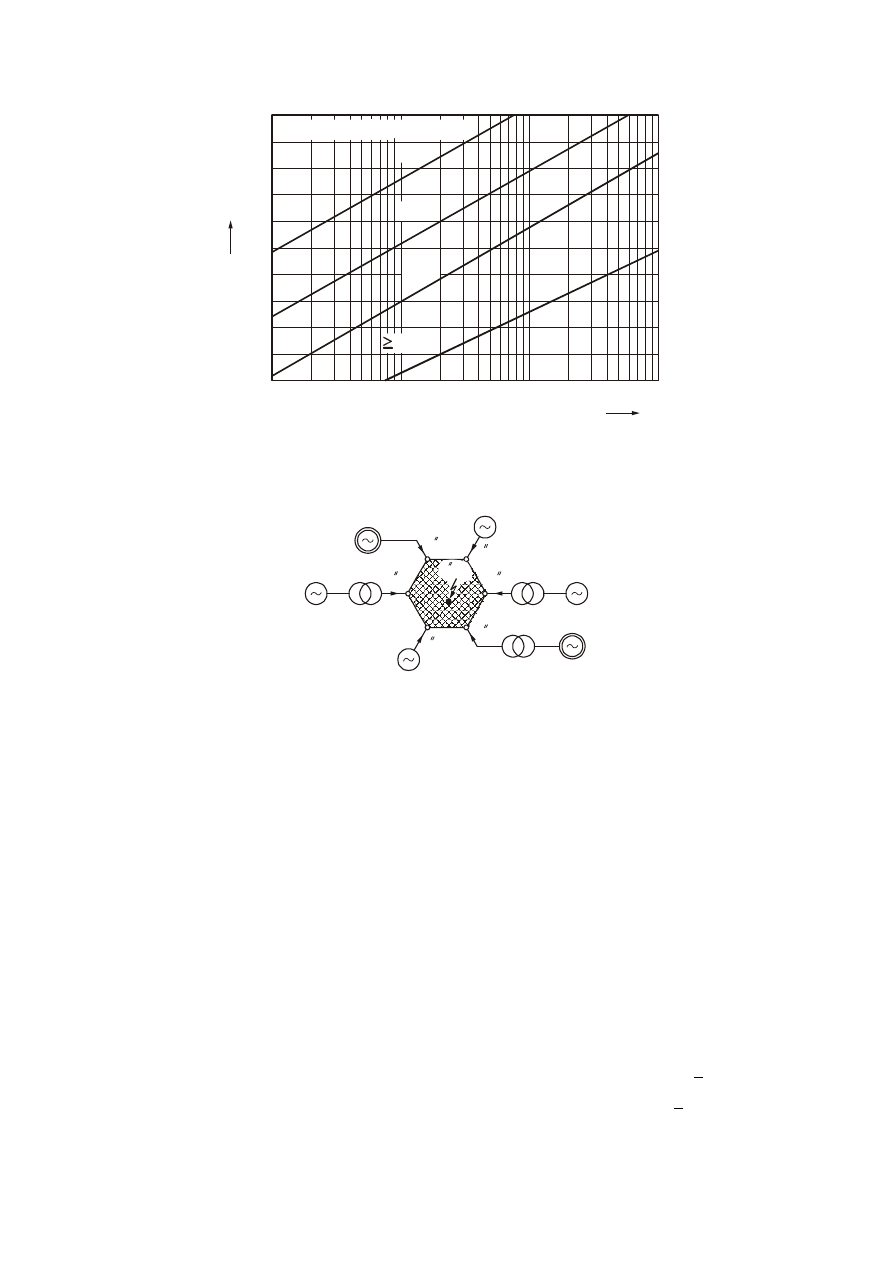
0,01 0,02 0,04

0,1

0,2

0,4

1

2

4

10

MW

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

Moc czynna silnika na jedną parę biegunów m

q

Czas własny minimalny t

min

0,02 s

0,05 s

0,1 s

0,25 s

Rys. 11. Wyznaczanie współczynnika q do obliczeń prądu zwarciowego wyłączeniowego silników

indukcyjnych

I

K1

I

K2

I

K3

I

K4

I

K5

I

K6

I ,I

K b

Rys. 12. Wyznaczanie prądu wyłączeniowego I

b

w sieci zamkniętej

Prąd wyłączeniowy I

B

dla zwarcia w sieci zamkniętej może być traktowany jako prąd

"

K

I

pomniejszony o sumę wielkości określonych poglądowo jako prądy zanikania, czyli











i

j

j

i

I

I

I

I

zM

zG

"

K

B

(38)

Gdyby zwarcie miało miejsce na zaciskach i-tego generatora (j- tego silnika) wtedy prąd

zanikania, na podstawie wcześniej wprowadzonych definicji, mógłby być wyznaczony ze

wzoru









"

KM

zM

"

KG

zG

1

,

1

j

j

j

j

i

i

i

I

q

I

I

I













(39a)

Ponieważ zwarcie jest oddalone od generatora, dynamika procesu zmniejszania się składowej

okresowej prądu zwarcia zmienia się, co omówiono szczegółowo w rozdz. 2. Można przyjąć,

że wartość prądu zanikania w zmienionych warunkach określa współczynnik α

i

, który ma

wartość bezwzględną mniejszą od 1 (dla silników odpowiednio współczynnik α

j

), pomnożony

przez wartość tego prądu wyznaczoną dla zwarcia na zaciskach generatora, czyli









"

KM

zM

"

KG

zG

1

,

1

j

j

j

j

j

i

i

i

i

I

q

I

I

I

















(39b)

Współczynnik α

i

powinien być miarą odległości pomiędzy miejscem zwarcia a zaciskami

generatora (dla zwarcia bliskiego jego moduł powinien być zbliżony do jedności, dla zwarcia

odległego do zera). W przypadku sieci promieniowej wartość tego współczynnika mogłaby

być związana z impedancją linii łączącej miejsce zwarcia z generatorem. W przypadku sieci

zamkniętej nie da się wyróżnić takiej linii. Dlatego też jako miarę odległości miejsca zwarcia

od zacisków generatora przyjęto stosunek spadku napięcia na skorygowanej reaktancji

generatora (silnika) do standardowej wartości napięcia fazowego sieci, czyli

3

"

dK

"

KG

3

"

G

n

n

cU

i

cU

i

i

X

I

U









(40a)

3

3

"

n

n

cU

M

kMj

cU

Mj

j

X

I

U









(40b)

Uwzględnienie zależności (38)-(40) prowadzi do przedstawionej postaci wzoru (37).

W przypadku większej liczby źródeł wyznaczanie

b

I

prądu jest najbardziej efektywne przy

zastosowaniu metod komputerowych.

Ustalony prąd zwarcia

Amplituda ustalonego prądu zwarciowego I

K

(rys. 1) zależy od warunków nasycania

obwodów magnetycznych maszyny oraz od łączeń dokonywanych w sieci w czasie trwania

zwarcia. Tym samym jego wartość wyliczona wg wskazówek zawartych w normie jest mniej

dokładna niż w przypadku prądu

"

K

I . Proponowana metoda obliczeń może być uznana jako

zapewniająca wystarczającą dokładność wyznaczenia maksymalnych i minimalnych wartości

K

I

w przypadku, gdy zwarcie jest zasilane z jednej maszyny synchronicznej.

Maksymalny ustalony prąd zwarciowy

max

K

I

, występujący przy maksymalnym wzbudzeniu

generatora wyznacza się ze wzoru

rG

max

max

K

I

I





(41)

przy czym stałą

max



określa się z wykresu (rys. 13 - dla turbogeneratorów, rys. 14 - dla

maszyn jawnobiegunowych). Widoczny na tych rysunkach parametr

sat

d

X

jest odwrotnością

innego,

znanego

z

teorii

maszyn

synchronicznych

współczynnika

z

k ,

zwanego

współczynnikiem zwarcia.

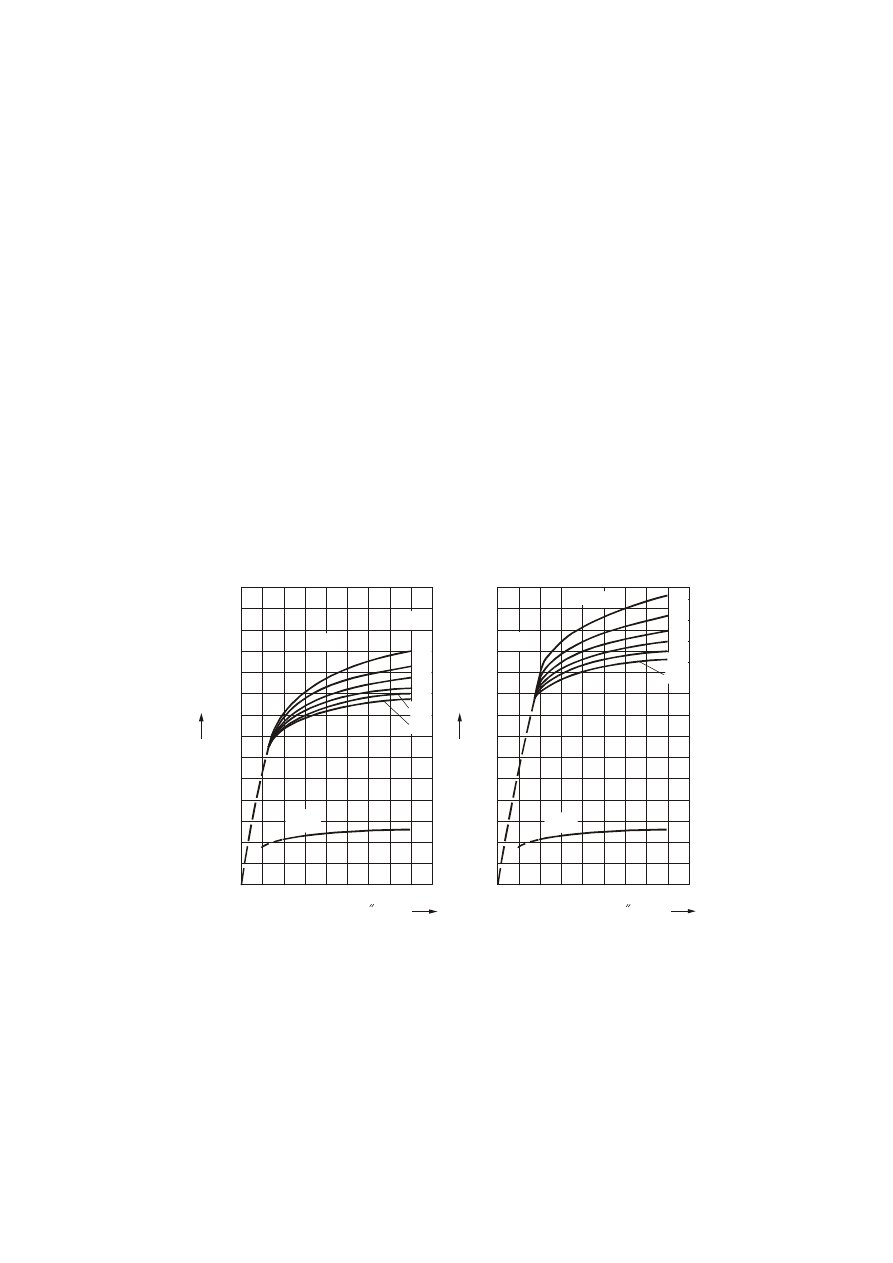
Dla widocznej na rys. 13a pierwszej serii krzywych wyznaczających

max



przyjęto najwyższy

poziom wzbudzenia turbogeneratorów występujący przy pracy w warunkach znamionowych

jako 1,3, a dla serii drugiej (rys 13b) poziom ten wynosi 1,6.

Dla widocznej na rys. 14a pierwszej serii krzywych wyznaczających

max



przyjęto najwyższy

poziom wzbudzenia maszyn jawnobiegunowych występujący przy pracy w warunkach

znamionowych jako 1,6, a dla serii drugiej (rys 14b) poziom ten wynosi 2,0.

Minimalny ustalony prąd zwarciowy

min

K

I

występuje przy stałym wzbudzeniu maszyny

synchronicznej w stanie biegu jałowego

rG

min

min

K

I

λ

I



(42)

przy czym stałą

min

 wyznacza się z rys. 13 oraz rys. 14.

Należy pamiętać, że w przypadku wzbudzenia statycznego zasilanego z szyn, do których jest

przyłączony generator, minimalny ustalony prąd zwarciowy jest równy zeru (przy zwarciu

trójfazowym na tych szynach).

1,2

1,4

1,6
1,8
2,0
2,2

1,2
1,4

1,6

1,8
2,0
2,2

min



min



max



max



d sat

X

d sat

X

0 1 2 3 4 5

7 8

0

0,2

0,4

0,6

0,8

1,0

1,2

1,4

1,6

1,8

2,0

2,2

2,4

2,6

2,8

6

0 1 2 3 4 5

7 8

0

0,2

0,4

0,6

0,8

1,0

1,2

1,4

1,6

1,8

2,0

2,2

2,4

2,6

2,8

6

Zwarcie trójfazowe I

/I

KG

rG

Zwarcie trójfazowe I

/I

KG

rG





a) seria pierwsza

b) seria druga

Rys. 13. Wyznaczanie ustalonego prądu zwarciowego – współczynniki

min

max

i





dla turbogeneratorów

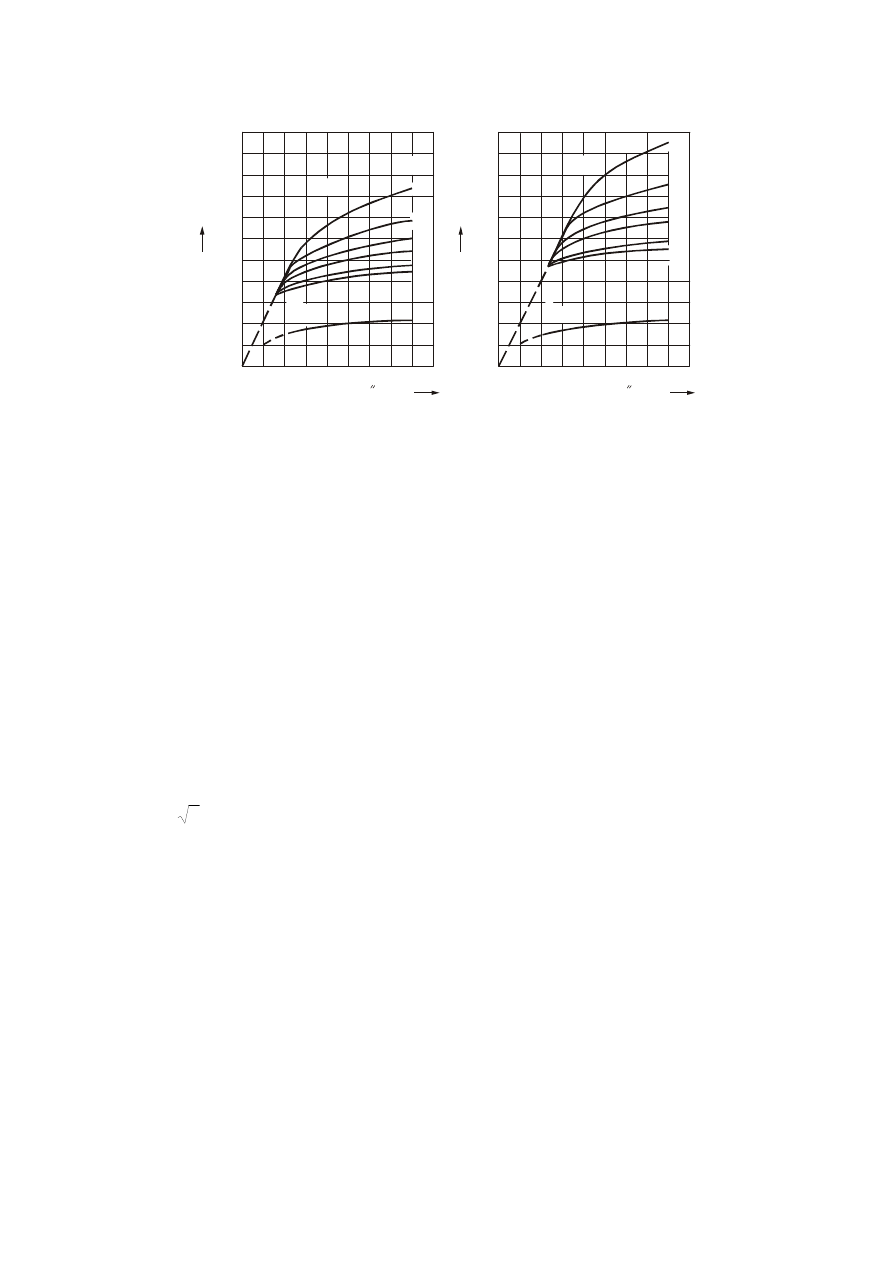
rG

Zwarcie trójfazowe I

/I

KG

rG





a) seria pierwsza

b) seria druga

2,0

2,5

3,0

3,5

4,0

4,5

5,0

5,5

6

Zwarcie trójfazowe I

/I

KG

6

0 1 2 3 4 5

7 8

0

0,5

1,0

1,5

4 5

7 8

0

0,5

1,0

1,5

2,0

2,5

3,0

3,5

4,0

4,5

5,0

5,5

min



min



max



max



d sat

X

d sat

X

0 1 2 3

0,6

0,6

0,8

0,8

1,0

1,0

1,2

1,2

2,0

1,7

1,7
2,0

Rys. 14. Wyznaczanie ustalonego prądu zwarciowego – współczynniki

min

max

,





dla generatorów

jawnobiegunowych

W przypadku zwarcia ustalonego zasilanego z bloku generator-transformator obliczenia

wykonuje się w analogiczny sposób, pamiętając o konieczności przeliczenia prądu generatora

na poziom napięcia sieci z wykorzystaniem przekładni

r

 .

Udział silników indukcyjnych w ustalonym prądzie zwarcia nie występuje, gdyż z uwagi na

brak wzbudzenia składowa okresowa zanika do zera.

Składowa nieokresowa prądu zwarcia

Decydująca o wartości prądu udarowego składowa nieokresowa prądu zwarcia i

dc

występuje

w nim niejako w sposób niejawny. Jeśli zachodzi potrzeba wyznaczenia jej wartości w chwili

t

K

, norma zaleca korzystanie ze wzoru

X

R

ft

e

I

i

/

2

"

K

dc

K

2







(43)

Zwarcia niesymetryczne

W dotychczasowych rozważaniach związanych z obliczeniami prowadzonymi według normy

IEC 60909 skoncentrowano się na zwarciach symetrycznych. Wyznaczanie prądów zwarć

niesymetrycznych wiąże się z koniecznością uwzględniania ich specyfiki. Specyfika ta

rozpoczyna się już na etapie budowy modeli sieci dla składowej przeciwnej i zerowej. Norma

wprowadza współczynników korekcyjnych o takich samych wartościach jak w przypadku

modelu zgodnego. Elementy poprzeczne w modelu zerowym nie powinny być pomijane tam

gdzie decydują o wartości impedancji zastępczej (np. sieć SN z izolowanym punktem

neutralnym).

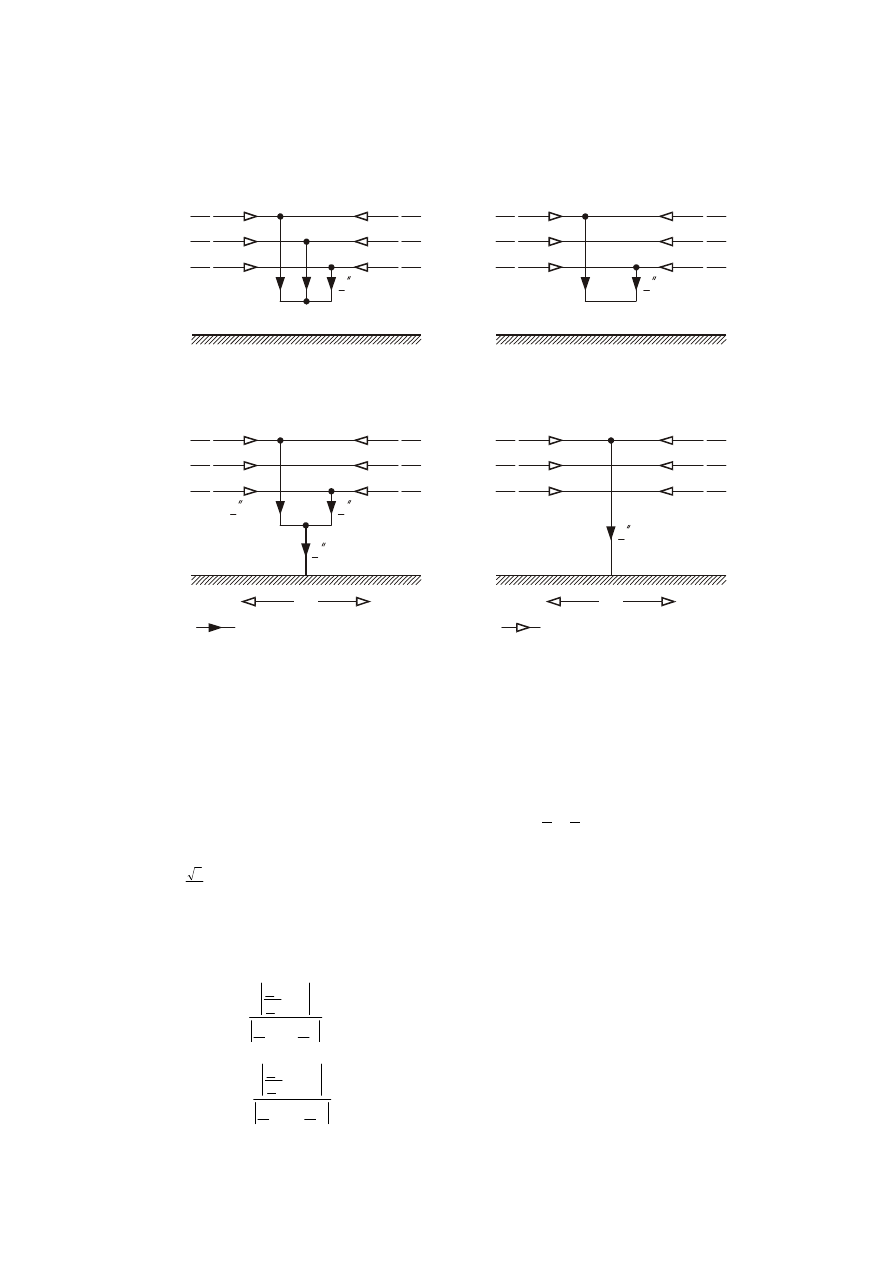
Wyznaczanie prądów dla zwarć niesymetrycznych rozpoczęto poniżej od prezentacji

oznaczeń wprowadzonych przez normę IEC 60909 – rys. 15.

L1

L2

L3

I

K3

L1

L2

L3

I

K2

L1

L2

L3

I

L1 K2E

I

E K2E

I

L3 K2E

prąd zwarcia

L1

L2

L3

I

K1

cząstkowy prąd zwarcia
w przewodach fazowych
i ziemi

a)

b)

c)

d)

Rys. 15. Sposób oznaczania prądów dla zwarć niesymetrycznych i zwarcia trójfazowego wg normy IEC

60909

Początkowy prąd zwarcia dla zwarć niesymetrycznych.

Poniżej przedstawiono jedną z zależności opisującej moduły i wyprowadzone przy założeniu

identyczności impedancji zwarciowej zgodnej i przeciwnej (Z

1

=Z

2

).

 Zwarcie dwufazowe

"

K

2

3

"

K2

I

I



(44)

gdzie

"

K

I

jest początkowym prądem zwarcia trójfazowego (wzór (1)).

 Zwarcie dwufazowe z ziemią

0

1

n

"

K2E

L2

2

1

0

Z

Z

a

cU

I

Z

Z







(45a)

0

1

2

n

"

K2E

L3

2

1

0

Z

Z

a

cU

I

Z

Z







(45b)

0

1

n

"

K2E

E

2

Z

3

Z

cU

I





(45c)

 Zwarcie jednofazowe z ziemią

0

1

n

K1

2

3

Z

Z

cU

I





"

(46)

Warto pamiętać, że prądy zwarć niesymetrycznych mogą być większe od prądu zawarcia

trójfazowego. Zależy to od stosunku Z

0

/Z

1

≈X

0

/X

1

. Odpowiednią analizę przedstawiono w [2].

Prąd udarowy.

Pomimo, że stosunek R/X w sieci przeciwnej i zerowej (szczególnie) może być

inny niż w sieci zgodnej, norma nie wymaga indywidualnego ustalania wartości

współczynnika

 dla poszczególnych składowych. Prąd udarowy jest zatem wyznaczany ze

wzorów analogicznych do (24) tj.

"

2

K

2

p

2 I

i







(47a)

"

K2E

p2E

2 I

i







(47b)

"

1

K

1

2 I

i

p







(47c)

przy czym prąd początkowy dla poszczególnych rodzajów zwarć określają wzory (44)-(45),

(46), a sposób wyznaczania współczynnika

 jest zgodny z przedstawionym pkt 5.2.

W przypadku

prądu wyłączeniowego

oraz

ustalonego prądu zwarcia

w przypadku zakłóceń

niesymetrycznych przyjmuje się, że ich wartości są takie same jak wartości prądów

początkowych. Jest to słuszne założenie, gdyż jak wykazano w [2] efekt zanikania

składowych okresowych prądu dla zwarć niesymetrycznych jest znacznie wolniejszy.

Warto również wspomnieć, że w przypadku rozważania zwarć niesymetrycznych, wpływ

silników indukcyjnych charakteryzuje się również pominięciem efektu zanikania składowej

okresowej, tj

 Dla zwarcia dwufazowego

"

K3M

2

3

B2M

I

I



(48a)

"

K3M

2

3

K2M

I

I



(48b)

 Dla zwarcia jednofazowego z ziemią

"

K1M

B1M

I

I



(49a)

"

K1M

K1M

I

I



(49b)

1.3

OBLICZANIE CIEPLNEGO EFEKTU ZWARCIA

Zgodnie z rozważaniami przedstawionymi w [2] można określić prąd przemienny I

th

dający

taki sam efekt cieplny, jaki w czasie trwania zwarcia

K

t

daje rzeczywisty prąd zwarcia.

Ponieważ nie jest znany dokładnie przebieg prądu zwarcia, więc prąd

th

I wyznacza się jako

funkcję prądu początkowego

"

K

I

oraz dwóch parametrów m, n, charakteryzujących w sposób

przybliżony dynamikę zmian przebiegu zwarciowego.

10

-2

-1

10

2 4 6

2 4 6 s1

t

K

0

0,4

0,8

1,2

1,6

2,0

m

a)





1,8

1,7

1,6

1,5

1,4

1,3

1,2

1,1

10

-2

-1

10

2 4 6

2 4 6 1 2 4 6 s 10

t

K

0

0,4

0,8

1,2

1,6

2,0

n

b)

I I

/ =10

K K

1,25

1,5

2,0

3,0

4,0

5,0

6,0

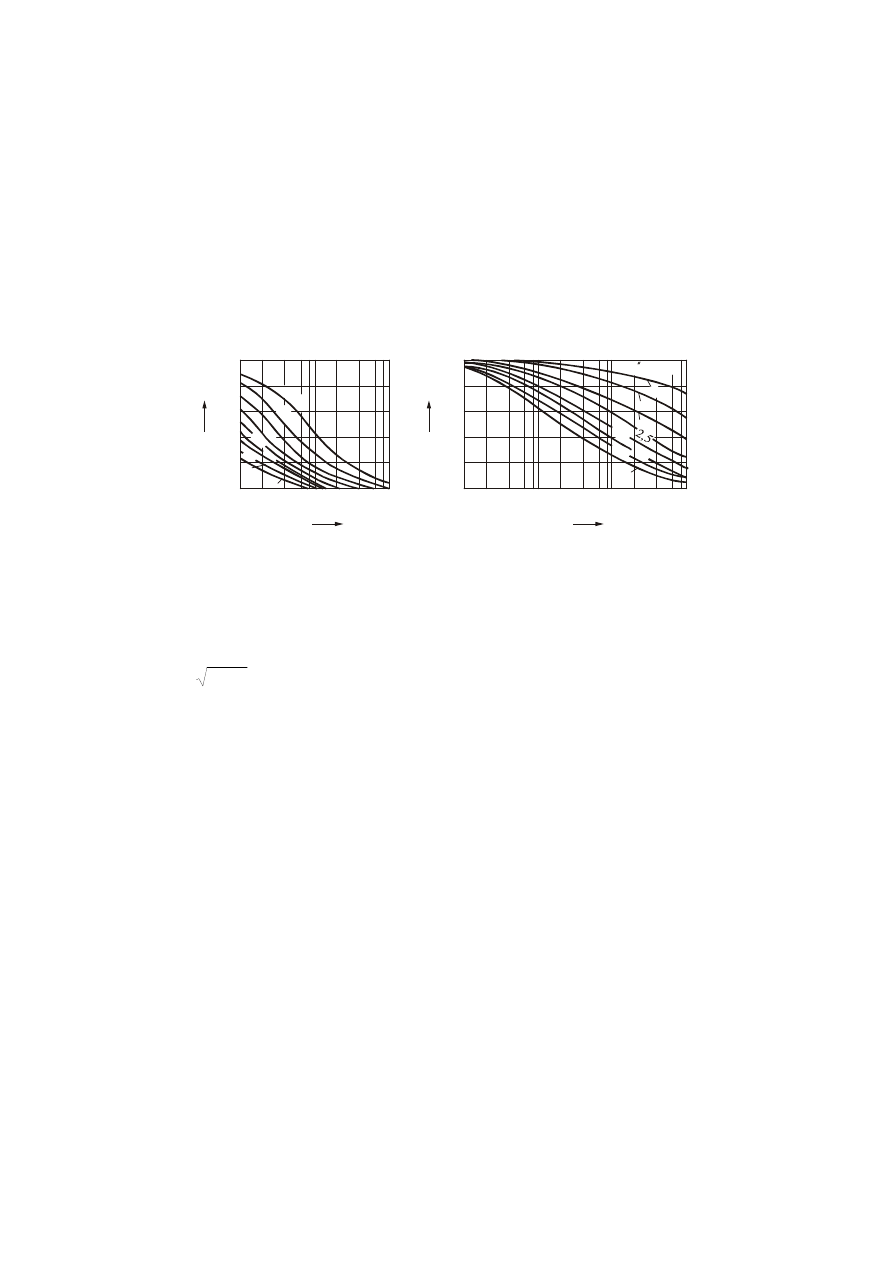
Rys. 16. Wyznaczanie współczynników do obliczania prądu zwarciowego cieplnego

th

I

w funkcji czasu

trwania zwarcia

K

t

: a) współczynnik

m

(stała



jak dla prądu udarowego); b) współczynnik

n

Zgodnie z publikacją IEC 865 oraz jej polskim tłumaczeniem PN-90/E-05025

n

m

I

I





"

K

th

(50)

Autorzy nie potrafią wytłumaczyć Czytelnikowi, dlaczego ta norma została przetłumaczona i

ustanowiona pomimo nieustanowienia polskiego odpowiednika normy IEC 60909. Jest to

przypuszczalnie wynik braku koordynacji w skomplikowanym procesie ujednolicania aktów

normatywnych.

Parametr m, który wyznacza się z wykresu (rys. 16a) w funkcji

K

t

(czas trwania zwarcia),

oraz przy wykorzystaniu współczynnika udaru

 jako parametru, charakteryzuje efekt cieplny

wywołany składową nieokresową prądu zwarciowego. Parametr n, który wyznacza się także z

wykresu (rys. 16b) w funkcji

K

t

oraz przy wykorzystaniu stosunku

K

"

K

/ I

I

jako parametru,

charakteryzuje efekt cieplny wywołany zanikającymi składowymi podprzejściową i

przejściową prądu zwarciowego. Dla sieci o złożonej konfiguracji należy przyjmować n=1,

gdyż stosunek

K

"

K

/ I

I

ma dla tych sieci również taką wartość. Norma zawiera także wzory do

wyznaczania wartości współczynników m oraz n, są one jednak bardzo złożone i nadają się do

stosowania tylko w obliczeniach wspieranych komputerowo.

W przypadku kilkakrotnego przepływu prądu zwarciowego (np. podczas nieudanego cyklu

samoczynnego ponownego załączania automatyki SPZ), należy korzystać ze wzoru







n

i

i

i

t

I

t

I

1

K

th

K

th

1

(51)

gdzie:







n

i

i

t

t

1

K

K

Należy podkreślić, że w przypadku wyznaczania prądu

th

I

w układzie o konfiguracji

promieniowej (rys. 5) niepoprawne jest zastosowanie sumowania zastępczych prądów

cieplnych cząstkowych, tak jak miało to miejsce w przypadku cząstkowych prądów

udarowych i

pi

oraz cząstkowych prądów wyłączeniowych I

Bi

. Konieczne jest wyznaczenie

całkowitego prądu początkowego

"

K

I oraz związanych z nim współczynników m, n.

Prawidłowość ta wynika z prostej matematycznej zależności, że suma kwadratów liczb nie

jest równa kwadratowi ich sumy, a przecież efekty cieplne związane są z kwadratami wartości

prądów.

G

3

F

U

I

rG

U

rG

n

K3

Rys. 17. Korekta impedancji generatora przy zwarciu zlokalizowanym na jego zaciskach

1.4

Podstawy teoretyczne metody korygowania wartości impedancji elementów

Jak kilkakrotnie podkreślano specyfika normy IEC 60909 polega na zastosowaniu

współczynników korygujących wartości impedancji elementów sieci. Poniżej przedstawiono

podstawy teoretyczne metody korygowania impedancji dla wybranych przypadków. Dla

odróżnienia reaktancji podprzejściowej wyrażonej w jednostkach mianowanych i w

jednostkach względnych tę ostatnią oznaczono wyjątkowo jako

"

.

p.u

d

X

.

Na rys. 17 przedstawiono sieć zastępczą i przyłączony do niej bezpośrednio generator.

Konieczność korekty impedancji generatora wynika z faktu, że maksymalny prąd zwarciowy

generatora wyznaczony ze wzoru podstawowego (1)

G

n

max

KG

n

max

"

KG

3

3

Z

U

c

Z

U

c

I





(52)

jest obarczony zbyt dużym błędem. Znacznie bardziej dokładną wartość tego prądu można

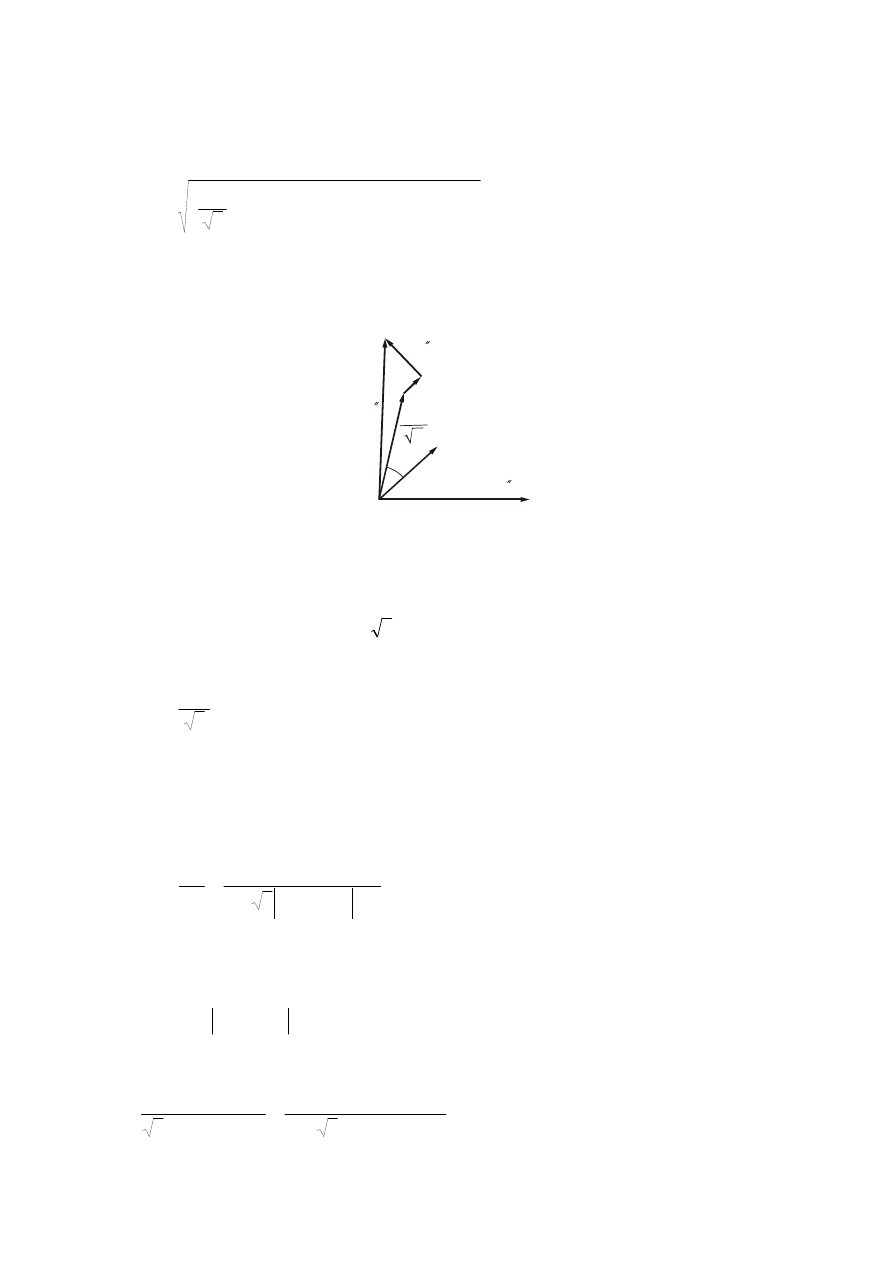
wyznaczyć biorąc pod uwagę wartość siły elektromotorycznej podprzejściowej wyznaczonej

zgodnie z rys. 18 przy założeniu, że

"

d

G

X

R



:





2

rG

"

d

rG

2

rG

"

d

rG

rG

"

cos

sin

3





X

I

X

I

U

E



















(53)

przy czym wielkości

rG

rG

rG

,

,



I

U

charakteryzują znamionowe warunki pracy generatora

(obowiązuje założenie, że warunki przedzwarciowe są właśnie takimi warunkami).

I

I

KG

rG

rG

G

E

jX I

r

d

R I

rG

U



rG



Rys. 18. Uproszczony wykres wektorowy maszyny synchronicznej do wyznaczania podprzejściowej siły

elektromotorycznej

Uwzględniając fakt, że reaktancja podprzejściowa jest wyrażana w jednostkach względnych

(jednostka podstawowa

 

rG

rG

b

3

/

I

U

Z



) oraz dokonując rozwinięcia wyrażenia pod

pierwiastkiem w szereg Taylora, otrzymuje się ostatecznie





rG

"

p.u.

d

rG

"

sin

1

3



X

U

E





(54)

przy czym

"

p.u.

d

X

jest reaktancją podprzejściową generatora wyrażoną w jednostkach

względnych.

Jeśli prąd zwarciowy wyznaczony ze wzoru









"

d

G

rG

"

p.u

d

rG

G

"

"

K

j

3

sin

1

X

R

X

U

Z

E

I











(55)

uznaje się za wyznaczony z satysfakcjonującą dokładnością, to aby uzyskać taką samą

wartość ze wzoru (3), koryguje się impedancję

G

Z za pomocą współczynnika

G

K , tzn.





"

d

G

G

KG

jX

R

K

Z





(56)

Wartość tego współczynnika wyznacza się z równania













"

d

G

rG

"

p.u.

d

rG

"

d

G

G

n

max

j

3

sin

1

j

3

X

R

X

U

X

R

K

U

c











(57)

otrzymując ostatecznie wyrażenie o postaci zgodnej z (7)

rG

"

p.u.

d

max

rG

n

G

sin

1



X

c

U

U

K







(58)

przy czym zwykle indeksy oznaczające jednostki względne są pomijane. Można zatem

powiedzieć, że dzięki skorygowaniu impedancji korzystanie z podstawowego wzoru normy,

tj. (1) nie będzie obarczone błędem.

Korekta impedancji bloków generator - transformator jest nieco bardziej złożona. Należy

bowiem wziąć pod uwagę nie tylko stan przedzwarciowy generatora, ale także napięcia

znamionowe i rzeczywistą przekładnię transformatora blokowego.

1.5

Inne aspekty normalizacji obliczania wielkości zwarciowych

Czytelnika może interesować porównanie wyników obliczeń wykonywanych za pomocą

normy PN-74/E-05002 oraz normy IEC 60909. Można stwierdzić, że im dalej od źródeł tym

wyniki obliczeń wykonywane według obydwu norm są bardziej zbliżone. Do „starej” normy

nie należy podchodzić z lekceważeniem. Z pewnością podejście w niej przedstawione nie

zawiera znaczących błędów. Pośrednim, ale ważnym tego dowodem jest fakt wieloletniego

wykorzystywania tej normy w praktyce. Należy jednak podkreślić następujące problemy

wiążące się z jej stosowaniem:

 symbole wielkości zwarciowych nie są zgodne z przyjętymi przez IEC, co z pewnością

utrudnia wykonywanie dokumentacji projektowej przy eksporcie inwestycyjnym i
odczytywaniu w kraju dokumentacji zagranicznej.

 odczytywanie charakterystycznych współczynników k

u

, k

tz

, k

nok

z wykresów utrudnia

obliczenia i ich komputeryzację

 brak wskazówek metodycznych w zakresie budowy modeli elementów dla składowej

zerowej (linii, transformatorów, generatorów)

 proponowany

w

PN-74/E-05002

sposób

uwzględniania

wpływu

silników

asynchronicznych na prąd zwarciowy na ogół prowadzi do zawyżenia wartości tych
prądów,

powodując

potwierdzone

negatywne

skutki

ekonomiczne

związane

przewymiarowaniem konstrukcji rozdzielni i doborem aparatury

 trudności z wyznaczaniem stosunku R/X dla sieci o wielu źródłach (szacowanie wartości

składowej nieokresowej), brak w tym zakresie wskazówek metodycznych

 potwierdzone pomiarowo i obliczeniowo zaniżenie wartości składowej okresowej, dla

zwarć w pobliżu generatorów

 brak wskazówek odnoście wyznaczania prądu zwarcia ustalonego.

Wydaje się, że już pierwsza niedogodność, uzasadnia wprowadzenie zmian powodujących

ujednolicenie oznaczeń wielkości zwarciowych proponowanych przez IEC i stosowanych w

Polsce. Jak już stwierdzono, ustanowienie jako obowiązującej w Polsce normy IEC 60909 jest

kwestią najbliższych lat.

Problematyka wyznaczania prądu zwarcia pojawia się także w normie PN IEC 60364

Instalacje elektryczne w obiektach budowlanych, m.in. w arkuszach dotyczących ochrony

przeciwporażeniowej oraz ochrony przed skutkami oddziaływania cieplnego. Wymagana jest

tam znajomość ...wartości skutecznej prądu zwarcia. Chodzi jednak o zwarcie pomiędzy

przewodem fazowym a neutralnym. Wobec dużych wartości stosunku R/X w instalacjach

elektrycznych wartość tego prądu wyznaczana jest po prostu jako stosunek maksymalnej

wartości fazowego napięcia znamionowego sieci do impedancji pętli zwarcia wyznaczonej

pomiarowo lub obliczeniowo. W przypadku obliczeń nie wykorzystuje się metody

składowych

symetrycznych,

gdyż

sprzężenia

magnetyczne

pomiędzy

przewodami

instalacyjnymi są pomijane. Negatywnie należy ocenić brak koordynacji w zakresie

terminologii normy IEC 60909 z normą cytowaną.

2

Analizator prądu stałego

Najprostszym urządzeniem pozwalającym na zamodelowanie sieci elektroenergetycznej i

wykonanie pomiarów na modelu jest analizator sieciowy rezystancyjny.

Pierwsza konstrukcja analizatora rezystancyjnego była wykonana w 1916r., a

impedacyjnego w 1929r. w USA. Pierwsze konstrukcje analizatorów rezystancyjnych w

Polsce powstały w 1949r. w Instytucie Elektrotechniki, zaś analizatora impedancyjnego w

1951r. w Politechnice Wrocławskiej, a następnie w Politechnice Warszawskiej. Jak zostało

wspomniane na analizatorze odwzorowuje się w odpowiedniej skali jej parametry tworząc

schemat sieci z odbiorami, źródłami i liniami przesyłowymi, które przedstawiają sieć o

skończonej liczbie węzłów i oczek sieciowych.

Do obliczania rozpływu prądów w takiej sieci, jej elementy składowe są charakteryzowane

przez podanie wartości wielkości tych elementów. Napięcie jest wielkością podstawową

charakteryzującą źródła /teoretycznie o nieskończenie dużej mocy/.

Rezystancja charakteryzuje gałęzie, prąd – odbiory sieci.

Obliczenie rozpływu prądów polega na znalezieniu prądów płynących we wszystkich

gałęziach sieci.

-

w sieci kablowej niskiego napięcia, dla której reaktancje gałęzi są pomijalnie małe w

stosunku do rezystancji,

-

w sieciach o wyższym napięciu znamionowym i większych przekrojach przewodów,

dla której rezystancje gałęzi R są pomijalnie małe wobec reaktancji /R

 0,3X/,

-

w sieci o jednym napięciu znamionowym, której gałęzie mają zbliżony stosunek R/X.

Analizatory rezystancyjne służą również do badania przepływu cieczy, wymiany ciepła,

rozkładu temperatur itp.

2.1

Wybór skali odwzorowania

W sieciach prądu stałego występuje tylko jeden rodzaj oporu – rezystancja /R/, za pomocą

którego można odwzorować układ sieci zakładając, że układ jest jednorodny i napięcia są w

fazie z prądami lub przeciwfazie. Do odwzorowania takiego układu sieci należy wybrać trzy

skale odwzorowania, dla trzech wielkości występujących w sieci. Skale te są od siebie

wzajemnie zależne i nie można wszystkich trzech obierać dowolnie.

Zasadnicze równanie odwzorowania można wyprowadzić w oparciu o prawo Ohma

dla sieci rzeczywistej i sieci analizatorowej.

Oznacza się:

w sieci rzeczywistej

w sieci analizatorowej

U – napięcie

- U

a

I – natężenie prądu

- I

a

Z – impedancja

- R

a

Z

%

- impedancja względna w procentach

- R

a%

Z

p

– impedancja podstawowa

-R

ap

P

p

– moc podstawowa

- P

ap

Umieszczając we wzorach powyższe oznaczenia możemy napisać:

dla sieci rzeczywistej

dla sieci analizatorowej

Z

U

I

f



I

a

=

a

a

Z

U

%

100

*

%

p

Z

Z

Z



%

100

*

%

ap

a

a

R

R

R



100

*

%

p

Z

Z

Z



100

*

%

ap

a

a

R

R

R



Po podstawieniu tych wielkości do równań /1/ otrzyma się:

p

f

Z

Z

U

I

*

100

*

%



/2.1

ap

a

a

a

R

R

U

I

*

100

*

%



2.2

Przy założeniu, że napięcie podstawowe jest napięciem międzyfazowym

f

p

U

U

U

*

3





a

ap

U

U

*

3



i po wprowadzeniu tych wartości do równań /2/ otrzyma się:

p

p

Z

Z

U

I

*

*

3

100

*

%



ap

a

ap

a

R

R

U

I

*

*

3

100

*

%



ponieważ

p

p

p

Z

U

I

*

3



ap

ap

ap

R

U

I

*

3



dlatego

%

100

*

Z

I

I

p



%

100

*

a

ap

a

R

I

I



Ze stosunku prądu w sieci rzeczywistej do prądu w sieci analizatorowej otrzyma się:

ap

p

a

ap

a

p

a

I

I

Z

R

I

Z

R

I

I

I

*

100

*

*

*

100

*

%

%

%

%





Oznaczając stosunek oporów względnych C

R

%

%

Z

R

a

C

R



/2.3

otrzyma się obecnie dwa równania odwzorowania

R

a%

= C

R

* Z

%

równanie odwzorowania oporów, oraz

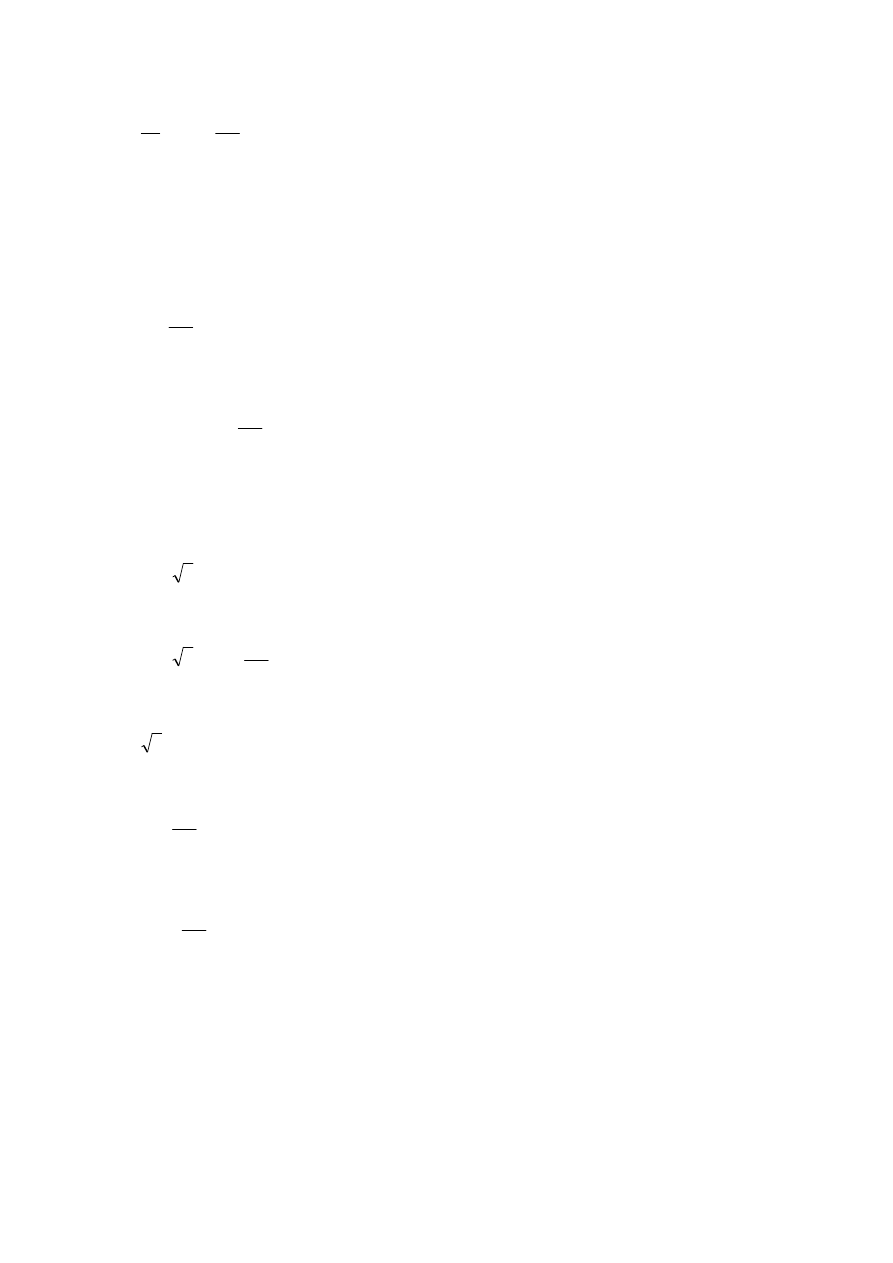
ap

p

R

a

I

I

C

I

I

*



/2.4

równanie odwzorowania prądów.

Współczynnik C

R

należy przyjmować o takiej wartości, aby wszystkie rezystancje względne

analizatora mieściły się w granicach możliwych do odwzorowania na analizatorze.

Skalę prądową C

I

określić można z równania /2.4

a

I

a

R

ap

p

I

C

I

C

I

I

I

*

*

*





/2.5

gdzie skala prądowa:

ap

p

R

I

I

I

C

C

*



Jest to skala bezpośrednia. W niektórych przypadkach wskazane jest posługiwanie się skalą

pośrednią, na przykład przy określaniu mocy.

I

U

P

p

*

*

3



Podstawiając I określone równaniem /5/, otrzyma się:

a

R

ap

p

p

I

C

I

I

U

P

*

*

*

*

3



ale

p

p

p

P

I

U



*

*

3

stąd

a

p

a

R

ap

p

I

C

I

C

I

P

P

*

*

*





/2.6

gdzie skala mocowa pośrednia wynosi

R

ap

p

p

C

I

P

C

*



Należy jeszcze przeanalizować skalę napięciową, którą będziemy utożsamiać ze skalą

spadków napięć. Stratę napięcia w sieci rzeczywistej można wyrazić ogólną zależnością:

U = I*ZS

/7/

/We wzorze I może być prądem o charakterze czynnym, biernym, pozornym lub sztucznie

dobranym w zależności od metody odwzorowania, podobnie Z

s

/.

Spadek napięcia w sieci analizatorowej, na elemencie R

as

, odpowiadającemu

oporności Z

s

, wyniesie:

Ua = Ia*Ras

Z dzielenia powyższych równań przez siebie przy wyrażeniu oporów Z

s

o R

as

w procentach

odpowiednich wielkości podstawowych otrzyma się:

ap

s

a

a

p

S

a

R

R

I

Z

Z

I

U

U

*

*

*

*

%

%







stąd po uwzględnieniu wyrażenia /5/

s

a

s

ap

a

ap

p

a

p

a

R

Z

R

I

I

Z

I

I

U

U

%

%

*

*

*

*

*



/2.8

Nakładając współczynnik odwzorowania oporów wzdłużnych

s

s

a

C

Z

R



%

%

/2.9

oraz pamiętając, że

3

*

p

p

p

U

Z

I



3

*

ap

ap

ap

U

R

I



otrzymuje się trzecie równanie odwzorowania

ap

p

S

R

a

f

a

U

U

C

C

U

U

U

U

*









/2.10

równanie odwzorowania napięć.

Z tego równania można określić skalę napięciową

a

u

a

ap

P

S

R

U

C

U

U

U

C

C

U









*

*

*



/2.11

gdzie skala napięciowa bezpośrednia

ap

p

S

R

u

U

U

C

C

C

*



Jeżeli pomiaru spadku napięcia w sieci analizatorowej nie dokonuje się w woltach,

lecz przy pomocy kompensującego miernika napięcia, w procentach napięcia zasilania

analizatora, wówczas do wzoru /2.11/ należy wprowadzić następujące wyrażenia:

3

*

100

*

%

n

U

U

U







100

*

%

a

a

a

U

U

U







100

*

*

*

3

*

100

*

%

%

a

a

ap

S

p

R

n

U

U

U

C

U

C

U

U









po przekształceniu

%

%

*

*

3

*

*

a

ap

a

n

P

S

R

U

U

U

U

U

C

C

U







/2.12

po wprowadzeniu współczynników

n

p

U

U

k



1

oraz

ap

a

U

U

k

*

3

2



otrzymamy ostatecznie

%

2

1

%

*

*

*

a

S

R

U

C

C

k

k

U







/2.13

W przypadku gdy k

1

= k

2

= 1

%

%

*

a

S

R

U

C

C

U







3

Opis analizatora

Analizator jest przeznaczony do pomiaru wartości prądów zwarciowych jakie będą płynęły w

sieci rozdzielczej danego zakładu przemysłowego. Jako podstawowe parametry analizatora

przejęte zostały napięcie i rezystancja.

RA = 1000 = 100%

UA = 2V = 100%

mA

R

U

I

A

A

A

2





Część elementów została zamodelowana na stałe, są to: linie zasilające, transformatory,

generatory i dławiki.

Pozostałe elementy będące odpływami od rozdzielni głównej należy wyznaczyć w

jednostkach względnych przyjmując za wartości podstawowe S

P

= 39,69 MVA, U

P

= 1,05 U

n

.

Linie kablowe zasilające oddziałowe rozdzielnice przedstawione zostały na analizatorze za

pomocą jednego opornika dekadowego /dwu, lub trójdekadowego/. Opornik dwudekadowy

posiada zakres nastawianej rezystancji od 18 – 23,9% co 0,1%, natomiast trójdekadowy od

10% - 49,9% co 0,1%; każdy rezystor stały oraz dekadowe posiadają w szereg włączone

boczniki o rezystancji 2 /0,2%/. Końce boczników są wyprowadzone do gniazd wtyczkowych

telefonicznych na płycie analizatora; rezystancji bocznika w trakcie modelowania nie należy

uwzględniać. Pomiar rozpływu prądów zwarciowych odbywa się za pomocą amperomierzy

przyłączonych do odpowiednich zacisków analizatora i wtyczki telefonicznej. Zasilanie

analizatora jest realizowane poprzez przyłączenie do zacisków U

A

zasilacza stabilizowanego.

4

Pomiary wykonywane na analizatorze

Badany

w

laboratorium

analizator

umożliwia

pomiar

prądu

w

miejscu

zwarcia

(miliamperomierz A

Z

) oraz prądów płynących w stanie zwarcia w poszczególnych

elementach sieci: liniach, transformatorach, generatorach, dławikach (miliamperomierz A

R

).

Jako modelowane miejsce zwarcia może być wybrany każdy punkt na płycie czołowej

analizatora, w którym znajduje się gniazdo typu "radiowego". Punkty takie (oznaczone

literą z) odpowiadają w sieci rzeczywistej szynom wszystkich rozdzielni badanego zakładu

przemysłowego t.j. rozdzielni o napięciu 220,30 i 6 kV. Włączenie wtyczki radiowej do tak

oznaczonego gniazda powoduje zamknięcie źródła zasilającego analizator przez układ

rezystorów modelujących sieć i miliamperomierz A

Z

. Prąd zwarciowy płynący w sieci

rzeczywistej, a mówiąc dokładniej składowa okresowa początkowego prądu zwarcia

(oznaczenie I

P

wg PN/E-5002) może być wyznaczona ze wzoru;

]

[

1

*

]

[

*

"

kA

I

i

i

I

p

Z

K





/4.1

gdzie:

 = 1 dla zwarcia na szynach 6 kV

 = 30/6 dla zwarcia na szynach 30 kV

 = 30/6 dla zwarcia na szynach 220 kV

i

Z

- prąd mierzony przez miliamperomierz A

Z

i

P

- prąd podstawowy analizatora (2 mA)

[I] - prąd podstawowy sieci rzeczywistej (3,64 kA) wynikający z mocy

podstawowej [S] = 39.69 MVA i napięcia podstawowego [U] = 6,3 kV

Pomiary prądów płynących w stanie zwarcia w liniach i transformatorach odbywają się wg

innej zasady. Miejscami pomiarów są umieszczone na płycie czołowej analizatora gniazda

typu "telefonicznego" (oznaczone literą P). Wtyczka telefoniczna wetknięta do takiego

gniazda powoduje bocznikowanie rezystora o rezystancji R

B

= 2 poprzez rezystancję

miliamperomierza. Tak więc prąd zwarciowy płynący przez element sieci rzeczywistej

wyznacza się ze wzoru:

]

[

*

1

*

]

[

*

"

kA

a

I

i

i

I

B

p

pu

Ku





/4.2

gdzie: i

pu

– prąd zmierzony miliamperomierzem A

p

a

B

– stała przeliczeniowa uwzględniająca rezystancję wewnętrzną miliamperomierza

(R

w

) wyznaczona ze wzoru:

b

w

b

B

R

R

R

a





/4.3

Dla zakresów miliamperomierza wykorzystywanych w pomiarach t.j. 150, 75, 30, 15, 7,5

mA, stałe a

B

wynoszą odpowiednio: 1.08 , 1.15 , 1.65 , 1.76 , 2.53.

Wyznaczone pomiarowo składowe okresowe początkowych prądów zwarcia odpowiadające

sieci rzeczywistej (po przeliczeniu wg (4.1) i (4.2) pozwalają na obliczenie innych wielkości

zwarciowych określonych w PN/E - 5002 t.j. prądów udarowych, prądów wyłączeniowych

I

Wg

, prądów zastępczych t

Z

sekundowych itp.

5

Przebieg ćwiczenia

Dla sieci zakładu przemysłowego pracującej w układzie zamodelowanym na płycie czołowej

przez prowadzącego ćwiczenia należy:

A. odwzorować zamodelowany przez prowadzącego układ sieci, zapisać potrzebne do

obliczeń zwarciowych dane znamionowe elementów sieci ;

B. obliczyć w jednostkach względnych (dla [U]=6,3 kV i [S] = 36,69 MVA) reaktancje

tych elementów sieci, które są zamodelowane na stałe;

C. zgodnie z techniką przeprowadzania pomiarów opisaną w p. 4 należy zmierzyć

składowe okresowe początkowego prądu zwarcia w punktach R-1-220, R-2-220, R-1,

R-2, R-3, RG1, RG2, RG3 oraz dodatkowo w punktach wskazanych przez

prowadzącego ćwiczenia. Dla tych miejsc należy wyznaczyć także tzw. "rozpływy

pierwszego rzędu" tzn. prądy płynące w elementach sieci połączonych bezpośrednio z

miejscem, w którym wystąpiło zwarcie. Wyniki pomiarów należy wpisać do tab.1.

Uwaga: dla miliamperomierza A

R

może zachodzić kolejność zmiany biegunowości;

D. wartości prądów zmierzone na modelu sieci należy przeliczyć wg (4.1) i (4.2) oraz

zapisać w tablicy 2 identycznej pod względem układu z tab. 1;

E. dla podanych przez prowadzącego ćwiczenia punktów sieci należy określić prąd I

K

”

oraz prądy udziałowe metodą rachunkową.

Sprawozdanie powinno zawierać schemat badanej sieci, tab. 1 i tab. 2 obliczenia reaktancji

sieci, obliczenia wykonywane w p. d oraz porównanie wyników otrzymanych metodą

pomiarową i obliczeniową.

6

Literatura

1. Kacejko P., Machowski J.: Zwarcia w sieciach elektroenergetycznych. Podstawy

obliczeń. WNT, Warszawa 1993.

2. Kacejko P., Machowski J.: Zwarcia w systemach elektroenergetycznych. WNT 2002.

3. Strojny J., Strzałka J.: Zbiór zadań z sieci elektrycznych. Część II. Wyd. AGH,

Kraków 2000.

Tablica 1

L. p.

Miejsce

zwarcia

Prąd

I

K

”

Prądy udziałowe od szyn [mA]

K1

K2

R

A

R1-220

R2-220

R1

R2

R3

RG1

RG2

RG3

........

1.

R-1-220

2.

R-2-220

3.

R1

4.

R2

5.

R3

6.

RG1

7.

RG2

8.

RG3

9.

.........

10.

11.