Magdalena Górajska, CMF

1

Elementy rachunku prawdopodobieństwa

Rachunek prawdopodobieństwa to dział matematyki zajmujący się zdarzeniami losowymi.

Doświadczenie jest losowe, jeżeli można je wielokrotnie powtarzać w tych samych warunkach i

wyniku doświadczenia nie potrafimy z góry przewidzieć. Warunki doświadczenia można podzielić

na warunki zdeterminowane, czyli systematyczne oraz warunki losowe.

Podstawowymi pojęciami rachunku prawdopodobieństwa są:

• zdarzenie elementarne oraz przestrzeń zdarzeń elementarnych,

• zdarzenie losowe,

• prawdopodobieństwo zajścia określonego zdarzenia.

Jeśli chcemy opisać jakieś zdarzenie losowe z punktu widzenia rachunku prawdopodobieństwa, to

musimy najpierw określić zbiór jego możliwych wyników.

Przykłady doświadczenia losowego

1. D

1

- rzut monetą, zbiór obserwacji to orzeł, reszka,

2. D

2

- rzut kostką do gry, zbiór obserwacji to liczba oczek na górnej ścianie kostki (1,2,...,6).

3. D

3

- zdawanie egzaminu, zbiór obserwacji "zdano", "niezdano",

1.1

Zdarzenie elementarne oraz przestrzeń zdarzeń elementarnych

Najprostsze wyniki doświadczenia nazywa się zdarzeniami elementarnymi i oznacza symbolem

ω.

Zbiór wszystkich zdarzeń elementarnych związanych z danym doświadczeniem losowym nazywamy

przestrzenią zdarzeń elementarnych PZE i oznaczamy go grecką literą Ω, a elementy PZE

oznaczamy symbolem ω, czyli ω ∈ Ω. Liczbę elementów PZE oznaczamy ¯

¯

Ω i czytamy moc zbioru.

Jeśli Ω = {ω

1

, ω

2

, ..., ω

n

}, to ¯

¯

Ω = n.

Zdarzenie elementarne i PZE są pojęciami pierwotnym teorii prawdopodobieństwa.

1.2

Zdarzenie losowe

Zdarzeniem losowym nazywamy każdy podzbiór zbioru PZE Ω. Zdarzenia losowe oznaczamy

wielkimi A, B, C, ....

Zdarzenia elementarne ω

i

, z których składa się zdarzenie A (ω

i

∈ A) nazywamy zdarzeniami

sprzyjającymi zdarzeniu A.

1

Magdalena Górajska, CMF

• Zdarzenie, dla którego zbiorem zdarzeń elementarnych sprzyjających mu jest zbiór pusty

nazywamy zdarzeniem niemożliwym i oznaczamy symbolem ∅,

• Zdarzenie, któremu sprzyja cała przestrzeń zdarzeń elementarnych (zbiór Ω) nazywamy zda-

rzeniem pewnym.

• Zdarzenie przeciwne do zdarzenia A oznaczamy przez A

0

oraz A ∩ A

0

= ∅, A ∪ A

0

= Ω.

Przykład 1

Rozważmy jednokrotny rzut kostką do gry. Kostka do gry posiada 6 możliwych wyników, więc

w tym doświadczeniu zdarzeniami elementarnymi są: ω

1

= {1}, ω

2

= {2}, ω

3

= {3}, ω

4

= {4},

ω

5

= {5}, ω

6

= {6}, Ω = {{1}, {2}, {3}, {4}, {5}, {6}}. Moc zbioru (liczba elementów) Ω wyno-

si 6, czyli ¯

¯

Ω = 6. Niech A

1

oznacza zdarzenie polegające na wyrzuceniu parzystej liczby oczek,

wówczas zdarzeniami elementarnymi sprzyjającymi A

2

jest ω

2

= {2}, ω

4

= {4}, ω

6

= {6}, zatem

A

1

= {2, 4, 6} ⊂ Ω, A

0
1

= {1, 3, 5}.

Przykład 2

Rozważmy dwukrotny rzut monetą. Możliwymi wynikami w tym doświadczeniu są cztery zdarzenia

elementarne: ω

1

= {OO}, ω

2

= {OR}, ω

3

= {RO}, ω

4

= {RR}, Ω = {{OO}, {OR}, {RO}, {RR}},

czyli ¯

¯

Ω = 4. Niech A

2

oznacza zdarzenie polegające na wyrzuceniu za drugim razem reszki,

wówczas zdarzeniami elementarnymi sprzyjającymi A

2

jest ω

2

= {OR}, ω

4

= {RR}, zatem

A

2

= {{OR}, {RR}} ⊂ Ω, A

0
2

= {{OO}, {RO}} ⊂ Ω.

Przykład 3

Rozważmy wynik egzaminu. Możliwe wyniki to ω

1

= {zdany} i ω

2

= {niezdany},

Ω = {{zdany}, {niezdany}}, czyli ¯

¯

Ω = 2 lub ω

1

= {2}, ω

2

= {3}, ω

3

= {4}, ω

4

= {5},

Ω = {{2}, {3}, {4}, {5}}, zatem ¯

¯

Ω = 4. Niech A

3

oznacza zdarzenie polegające na zdaniu egza-

minu, wówczas zdarzeniami elementarnymi sprzyjającymi A

3

jest ω

2

= {3}, ω

3

= {4}, ω

4

= {5},

stąd A

3

= {{3}, {4}, {5}}, A

0
3

= {2}.

Przykład 4

Rozważmy eksperyment polegając na pomiarze czasu oczekiwania w przychodni na wizytę u le-

karza (mierzony np. w godzinach). Przestrzeń Ω jest tu przedziałem liczb rzeczywistych [0; 8]. W

tym przypadku Ω jest zbiorem nieskończonym, ponieważ w przedziale [0; 8] mieści się nieskończe-

nie wiele liczb rzeczywistych. Ponadto, zbiór Ω jest nieprzeliczalny.

Przykład 5

Rozważmy eksperyment polegając na pomiarze wagi u noworodka (mierzony w gramach). Prze-

2

Magdalena Górajska, CMF

strzeń Ω jest tu przedziałem liczb rzeczywistych [0, 500; 5000]. W tym przypadku Ω jest zbiorem

nieprzeliczalnym.

1.3

Prawdopodobieństwo zajścia określonego zdarzenia

Aksjomatyczna definicja prawdopodobieństwa(Andriej Kołmogorow 1933r.)

Prawdopodobieństwem nazywamy funkcję P , która każdemu zdarzeniu A przyporządkowuje do-

kładnie jedną liczbę P (A) tak, aby spełnione były warunki:

(P1) P (A) ­ 0 dla każdego A,

(P2) P (Ω) = 1,

(P3) dla dowolnego ciągu parami rozłącznych zdarzeń A

1

, A

2

, ...

P (A

1

∪ A

2

∪ A

3

∪ ...) = P (A

1

) + P (A

2

) + P (A

3

) + ...

Własności prawdopodobieństwa

1. 1 = P (Ω) = P (A ∪ A

0

) = P (A) + P (A

0

), zatem P (A

0

) = 1 − P (A),

2. P (∅) = 0,

3. P (A \ B) = P (A) − P (A ∩ B),

4. Prawdopodobieństwo P jest funkcją niemalejącą tzn. jeżeli A ⊂ B to P (A) ¬ P (B),

5. P (A) ∈ [0; 1] dla każdego zdarzenia A,

6. Jeżeli A

1

, A

2

, ..., A

n

są parami rozłączne, to

P (A

1

∪ A

2

∪ ... ∪ A

n

) = P (A

1

) + P (A

2

) + ... + P (A

n

),

7. Jeżeli A

1

, A

2

, ..., A

n

tworzą układ zupełny tzn. A

1

, A

2

, ..., A

n

są parami rozłączne oraz A

1

∪

A

2

∪ ... ∪ A

n

= Ω, to

P (A

1

∪ A

2

∪ ... ∪ A

n

) = P (A

1

) + P (A

2

) + ... + P (A

n

) = 1,

8. P (A ∪ B) = P (A) + P (B) − P (A ∩ B).

3

Magdalena Górajska, CMF

Klasyczna definicja rachunku prawdopodobieństwa (Pierre Simon de Laplace 1812)

Jeżeli przestrzeń zdarzeń elementarnych Ω jest skończona (czyli ¯

¯

Ω = n) i wszystkie zdarzenia

elementarne {ω

i

} są jednakowo prawdopodobne (tzn. P ({ω

1

}) = P ({ω

2

}) = ... = P ({ω

n

}) =

1

n

), to prawdopodobieństwo dowolnego zdarzenia A składającego się z k zdarzeń (czyli ¯

¯

A = k)

jest ilorazem liczby zdarzeń elementarnych sprzyjających temu zdarzeniu przez liczbę wszystkich

zdarzeń elementarnych, co wyrażamy wzorem

P (A) =

¯

¯

A

¯

¯

Ω

=

k

n

.

Przykłady Obliczyć prawdopodobieństwa zdarzeń A

1

, A

2

, A

3

.

1.4

Prawdopodobieństwo warunkowe

W wielu przypadkach, informacja o zajściu zdarzenia B ma pewien wpływ na wartość obliczonego

prawdopodobieństwa zdarzenia A.

Zdarzenie polegające na zajściu zdarzenia A przy założeniu, że zaszło zdarzenie B, oznacza-

my symbolem A|B. Prawdopodobieństwo takiego zdarzenia nazywamy prawdopodobieństwem

warunkowym i oznaczamy symbolem P (A|B). Prawdopodobieństwem to definiujemy wzorem

P (A|B) =

P (A ∩ B)

P (B)

, gdzie A, B ⊂ Ω, P (B) > 0.

Przykład

Załóżmy, ze wśród górników wyróżniamy osoby narażone na wpływ czynnika szkodliwego i

osoby nienarażone na jego działanie. Niech

A- oznacza, ze losowo wybrany pracownik jest narażony na działanie substancji szkodliwej,

A

0

- oznacza, ze losowo wybrany pracownik jest nienarażony na działanie substancji szkodliwej,

B

1

- oznacza, ze losowo wybrany pracownik choruje na chorobę zawodową,

B

2

- oznacza, ze losowo wybrany pracownik nie choruje na chorobę zawodową.

Wśród 100 losowo wybranych pracowników przeprowadzono badanie lekarskie. Otrzymane wyniki

przedstawia poniższa tabela.

A narażony

A

0

nie narażony

Razem

B

1

choruje

30

15

45

B

2

nie choruje

12

43

55

Razem

42

58

100

4

Magdalena Górajska, CMF

Obliczamy prawdopodobieństwo, ze losowo wybrany górnik cierpi na chorobę zawodową, jeśli

wiadomo, ze jest narażony na działanie substancji szkodliwych, czyli

P (B

1

|A) =

P (B

1

∩ A)

P (A)

=

30

100

:

42

100

=

30

42

.

1.5

Niezależność zdarzeń

Kiedy rzucamy dwa razy monetą, to wynik pierwszego rzutu w żadnym stopniu nie wpływa na

wynik drugiego. Takie zdarzenia możemy nazwać zdarzeniami niezależnymi. Ogólnie brak wpływu

informacji o zajściu zdarzenia na prawdopodobieństwo drugiego jest istotą tak zwanej stochastycz-

nej niezależności zdarzeń.

Dwa zdarzenia są niezależne, jeśli zajście jednego ze zdarzeń nie ma wpływu na prawdopodo-

bieństwo zajścia drugiego z nich. Symbolicznie możemy to zapisać w postaci P (A|B) = P (A) lub

P (B|A) = P (B). Tak więc dla zdarzeń niezależnych mamy

P (A ∩ B) = P (A) · P (B).

1.6

Schemat Bernoulliego

Wśród doświadczeń wieloetapowych na szczególną uwagę zasługuję te, które polegają na n-

krotnym powtórzeniu, w tych samych warunkach i niezależnie od siebie doświadczenia losowego,

kończącego się tylko jednym z dwóch możliwych wyników sukcesem lub porażka. Takie doświadcze-

nie nazywamy próbą Bernoullioego. Przykładem próby Bernoulliego jest: rzut monetą (orzeł,

reszka), kupno losu na loterii (los wygrany, los przegrany), wynik egzaminu (zdany, niezdany).

Schemat Bernoullego

Jeżeli przeprowadzimy n niezależnych i identycznych doświadczeń, w których są tylko dwa możliwe

wyniki, to taki ciąg powtórzeń tego samego doświadczenia nazywamy schematem Bernoullego. W

schemacie tym jedno ze zdarzeń elementarnych nazywamy sukcesem, a drugie porażką. W schema-

cie n prób Bernoullego prawdopodobieństwo P (n = k) otrzymania dokładnie k sukcesów wyraża

się wzorem:

P (n = k) =

n

k

!

p

k

q

n−k

,

gdzie p jest prawdopodobieństwem sukcesu, zaś q = 1 − p prawdopodobieństwem porażki, przy

czym 0 < p < 1, k = 0, 1, 2, ..., n oraz

n

k

!

=

n!

k!(n − k)!

,

jest symbolem Newtona (czytamy "n po k"), a n! = 1 · 2 · 3... · n (czytamy "n silnia").

5

Magdalena Górajska, CMF

2

Zmienna losowa ZL

Funkcję X : Ω → R przyporządkowującą każdemu zdarzeniu elementarnemu jedną i tylko jedną

liczbę rzeczywistą x, czyli X(ω) = x nazywamy zmienną losową. Zmienna losowa to funkcja

odwzorowująca PZE Ω w zbiór liczb rzeczywistych R.

Zmienne losowe (ZL) oznaczamy X, Y, Z, a ich wartości (realizacje) X(ω), Y (ω), Z(ω) małymi

literami x, y, z.

Przykład 6

Rozważmy grę polegającą na rzucie kostką do gry. Jeśli gracz wyrzuci 6 oczek, to wygrywa 10 zł, w

przeciwnym razie płaci 1 zł. W ten sposób określiliśmy zmienną losową X, która przyporządkowuje

zdarzeniom elementarnym ω

1

, ω

2

, ..., ω

6

wartości rzeczywiste −1 lub 10 następująco:

X(ω

1

) = X(ω

2

) = X(ω

3

) = X(ω

4

) = X(ω

5

) = −1;

X(ω

6

) = 10,

gdzie ω

1

= {1}, ω

2

= {2}; ..., ω

6

= {6}.

2.1

Podział zmiennych losowych

Ze względu na zbiór wartości przyjmowanych przez ZL wyróżniamy dwa typy zmiennych: zmienne

losowe ciągłe i zmienne losowe skokowe (dyskretne).

• Jeżeli zbiór wartości ZL jest zbiorem przeliczalnym (lub skończonym) to ZL nazywamy

skokową. Zmienną losową skokową jest np. dobowa liczba urodzeń, zgonów, małżeństw w

Polsce, liczba koni w gospodarstwach województwa łódzkiego itp.

• Jeżeli ZL możne przyjmować wszystkie wartości z pewnego przedziału liczbowego to nazywa-

my ją ZL ciągła. ZL typu ciągłego jest np. wzrost, waga, wiek poszczególnych osób, długość

liścia, opór przewodnika, czas oczekiwania na wizytę u lekarza.

2.2

Dystrybuanta zmiennej losowej

Niezależnie od typu, każdą ZL X można jednoznacznie określić przy pomocy dystrybuanty teore-

tycznej.

Dystrybuantą zmiennej losowej X nazywamy funkcję F (x), zmiennej rzeczywistej x, zdefiniowa-

ną następująco

F (x) = P (X < x).

6

Magdalena Górajska, CMF

Własności dystrybuanty

• 0 ¬ F (x) ¬ 1,

• F (x) jest funkcją niemalejącą,

• F (x) jest funkcją przynajmniej lewostronnie ciągłą,

• lim

x→−∞

F (x) = 0 oraz lim

x→∞

F (x) = 1,

• P (a ¬ X < b) = F (b) − F (a).

Zmienne losowe są opisywane również za pomocą funkcji (rozkładów). W zależności od rodzaju

zmiennej są to:

(1) funkcja prawdopodobieństwa (zmienne losowe skokowe),

(2) funkcja gęstości (zmienne losowe ciągłe).

1 Zmienna losowa skokowa

Przypuśćmy, ze ZL X przyjmuje wartości x

1

, x

2

, ..., x

n

z prawdopodobieństwami odpowiednio

p

1

, p

2

, ..., p

n

. Wówczas funkcja prawdopodobieństwa ZL X przedstawia się następująco:

P (X = x

i

) = p

i

dla i = 1, 2, ..., n oraz

n

X

i=1

p

i

= 1,

gdzie drugi warunek jest nazywany warunkiem unormowania. Zestawienie wszystkich

możliwych par (x

i

, p

i

) nazywamy rozkładem prawdopodobieństwa ZL dyskretnej X. Funkcję

prawdopodobieństwa można przedstawić w postaci tabeli.

Wartość zmiennej dyskretnej x

i

x

1

x

2

x

3

...

x

n

suma

Prawdopodobieństwo P (X = x

i

) = p

i

p

1

p

2

p

3

...

p

n

1

Dla tak określonej ZL dyskretnej X dystrybuanta ma postać

F (x) =

X

x

i

<x

p

i

x

(−∞, x

1

]

(x

1

, x

2

]

(x

2

, x

3

]

...

(x

n

, ∞)

F (x) = P (X < x)

0

p

1

p

1

+ p

2

...

1

2 Zmienna losowa ciągła

W przypadku zmiennej losowej ciągłej odpowiednikiem funkcji rozkładu jest funkcja gestości

f (x). Funkcja gestości ZL ciągłej X jest określona na zbiorze liczb rzeczywistych i spełnia

warunki:

7

Magdalena Górajska, CMF

1. f (x) ­ 0,

2.

R

∞

−∞

f (x)dx = 1.

Dystrybuantę ZL X ciągłej definiujemy następująco

F (x) = P (X < x) =

Z

x

−∞

f (t)dt.

Dystrybuanta zmiennej ciągłej jest funkcją ciągłą. Jeżeli gęstość f (x) ZL X jest funkcją

ciągłą, to zachodzi związek

F

0

(x) = f (x),

gdzie F

0

(x) oznacza pochodną dystrybuanty F (x).

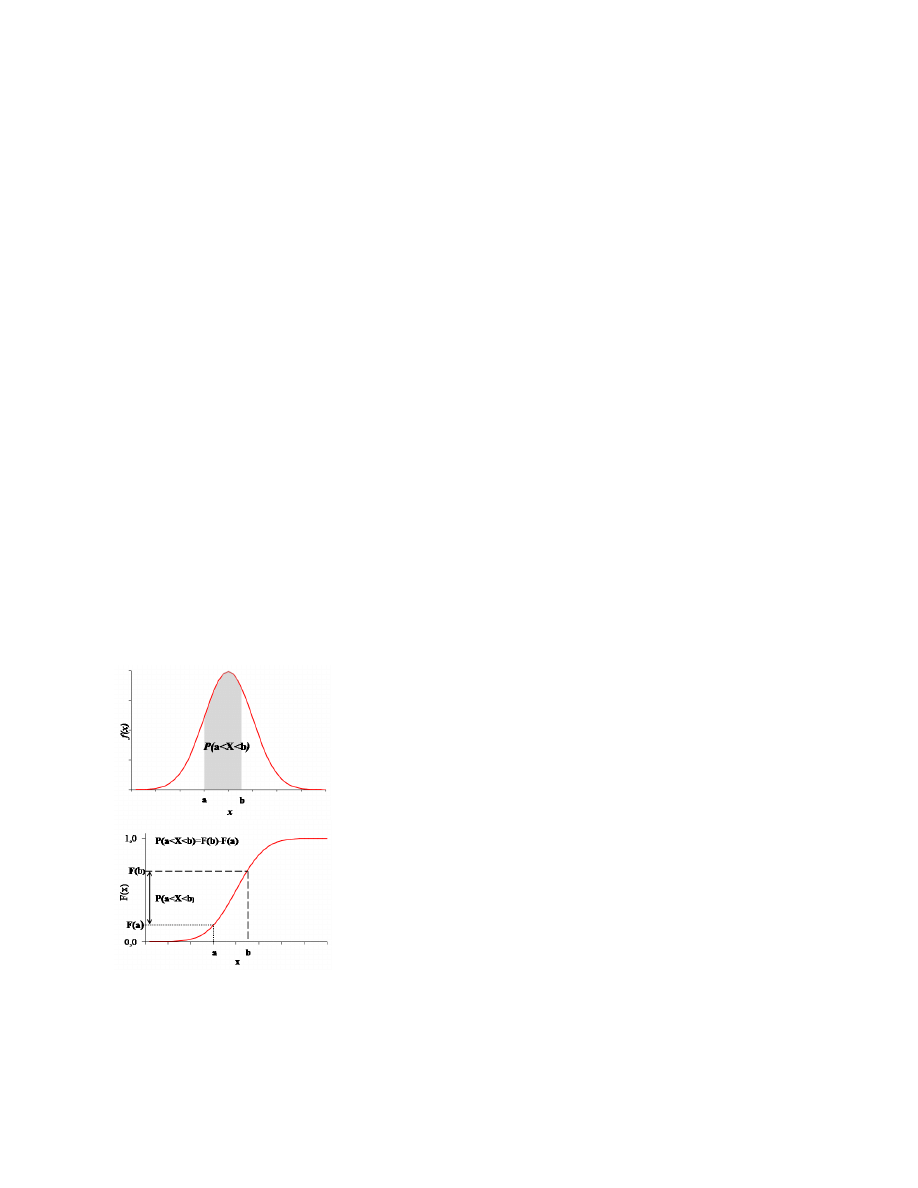
Dla ZL ciągłej prawdziwe są następujące wzory:

(1) P (X = a) = 0,

(2) P (a ¬ X ¬ b) = P (a < X < b) =

R

b

a

f (x)dx = F (b) − F (a), gdzie a, b są to stałe i

a < b,

(3) P (X < a) =

R

a

−∞

f (x)dx = F (a),

(4) P (X ­ a) =

R

+∞

a

f (x)dx = 1 − F (a).

Wyznaczanie prawdopodobieństwa dla ZL ciągłej

2.3

Charakterystyki zmiennej losowej

Z rozkładem zmiennej losowej związane są pewne, charakteryzujące go, wielkości liczbowe. Charak-

terystyki te nazywamy parametrami rozkładu ZL. Do najważniejszych parametrów ZL należą

8

Magdalena Górajska, CMF

wartość oczekiwana i wariancja.

Wartosc oczekiwana (nadzieja matematyczna) E(X) = m. Wartość m jest to taka wartość

zmiennej losowej X, wokół której skupiają się wyniki wielokrotnych realizacji tej zmiennej. Innymi

słowy, oczekuje się (ma się nadzieje), że wielokrotne realizacje zmiennej losowej X będą skupiały

się wokół liczby m.

Wariancja ZL to miara rozproszenia wartości zmiennej wokół wartości średniej, którą obliczamy

ze wzoru Var(X) = E(X − EX)

2

lub Var(X) = EX

2

− (EX)

2

.

Odchylenie standardowe ZL to pierwiastek z wariancji.

Wzory

1. Wartość oczekiwana i wariancja dla ZL dyskretnej wyrażają się wzorami:

E(X) =

n

X

i=1

x

i

p

i

,

E(X

2

) =

n

X

i=1

x

2
i

p

i

,

Var(X) =

n

X

i=1

(x

i

− E(X))

2

p

i

,

lub

Var(X) = E(X

2

) − (EX)

2

.

2. Wartość oczekiwana i wariancja dla ZL ciągłej wyrażają się wzorami:

E(X) =

Z

∞

−∞

xf (x)dx

E(X

2

) =

Z

∞

−∞

x

2

f (x)dx

VarX =

Z

∞

−∞

[x − E(X)]

2

f (x)dx

lub

VarX = E(X

2

) − [E(X)]

2

.

Przykład 7

W przykładzie 6, dotyczącym wygranej X w wysokości 10 lub −1 zł, rozkład prawdopodobieństwa

ma postać:

P (X = −1) =

5

6

P (X = 10) =

1

6

lub tabelarycznie

Wartość zmiennej x

i

−1

10

suma

Prawdopodobieństwo P (X = x

i

) = p

i

5
6

1
6

1

EX = (−1) ·

5

6

+ 10 ·

1

6

= −

5

6

+

10

6

=

5

6

,

EX

2

= (−1)

2

·

5

6

+ 10

2

·

1

6

=

5

6

+

100

6

=

105

6

,

V ar(X) = E(X

2

) − (EX)

2

=

105

6

−

25

6

=

80

6

.

9

Magdalena Górajska, CMF

2.4

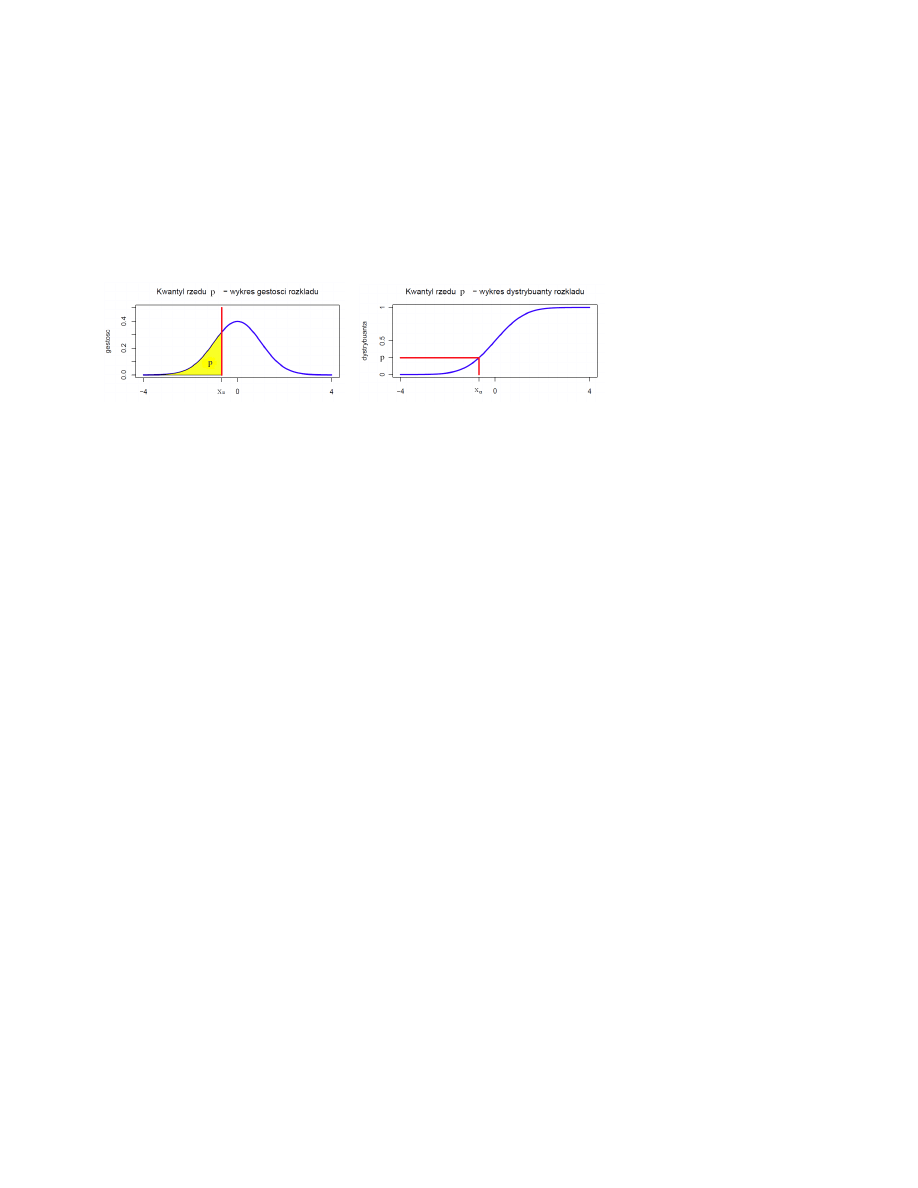
Kwantyl

Kwantylem rzędu p Kwantylem rzędu p ZL ciągłej X o dystrybuancie F i gestości prawdopo-

dobieństwa f nazywany liczbę x

p

, która spełnia jeden z równoważnych warunków:

F (x

p

) = p,

P (X < x

p

) = p,

Z

x

p

−∞

f (x)dx = p.

Kwantyl

W interpretacji geometrycznej kwantyl x

p

ZL ciągłej X o dystrybuancie F i gestości prawdopo-

dobieństwa f jest:

• odcięta x

p

takiego punktu na osi 0X, ze pole pod krzywą gestości prawdopodobieństwa

y = f (x) na przedziale (−∞, x

p

) jest równe p,

• odcięta x

p

punktu przecięcia prostej y = p z wykresem dystrybuanty y = F (x), czyli

pierwiastkiem równania F (x) = p.

10