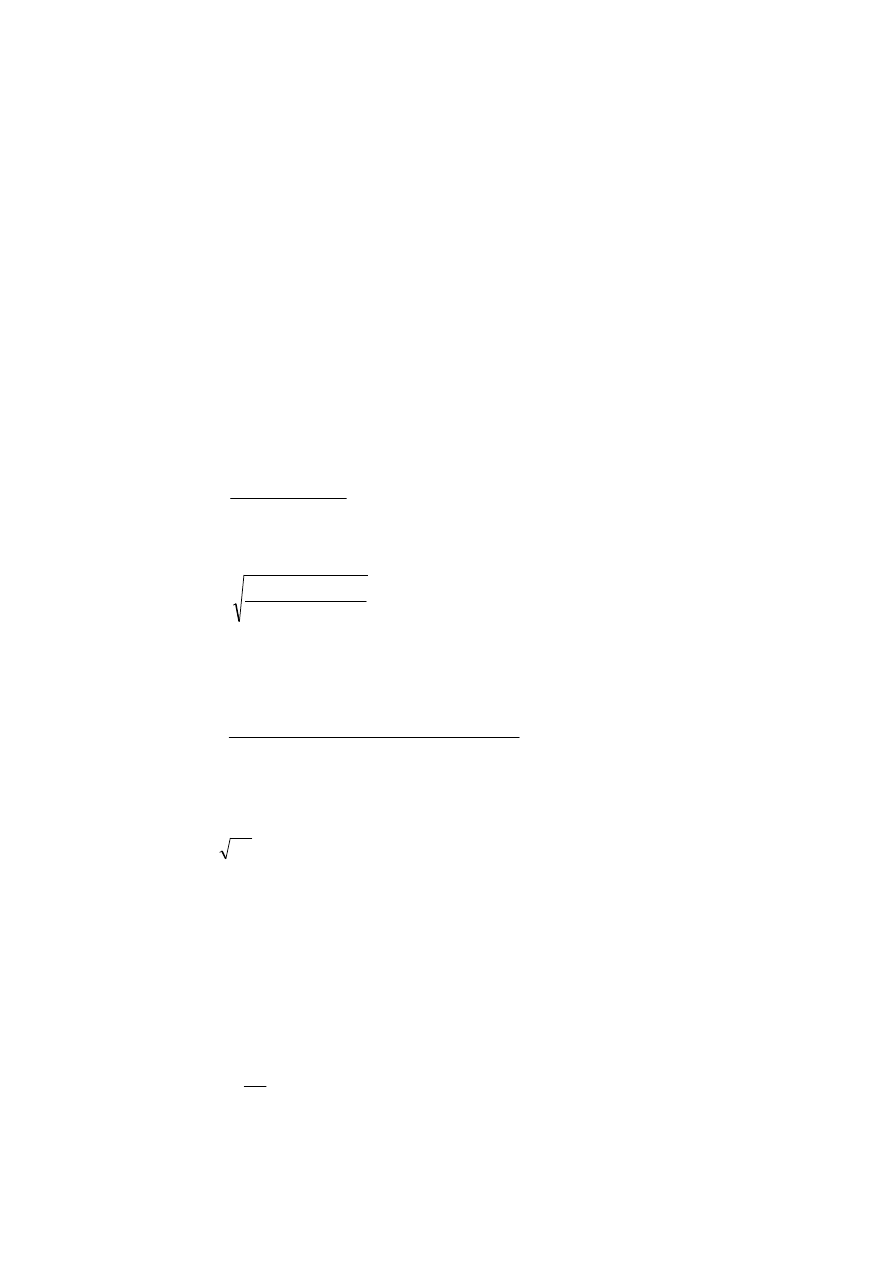
Sprawozdanie z laboratorium

„Analizy Sygnałów i Identyfikacji”

nr 1,2,3

Olsza Szymon, Olchawski Tomasz

Rok III, AiR, gr. 13A

1.1. Definicje parametrów sygnałów

• Średnia arytmetyczna (iloraz sumy wszystkich wartości i ich liczby)

n

a

a

a

a

n

sr

+

+

+

=

...

2

1

• Średnia kwadratowa (iloraz pierwiastka z sumy kwadratów wszystkich

wartości i ich liczby

n

a

a

a

a

n

kw

2

2

2

2

1

...

+

+

+

=

• Wariancja (iloraz sumy kwadratów różnic wartości i średniej

arytmetycznej oraz ich liczby)

(

)

(

)

(

)

n

a

a

a

a

a

a

sr

n

sr

sr

2

2

2

2

1

2

...

−

+

+

−

+

−

=

δ

• Odchylenie standardowe (pierwiastek z wariancji)

2

δ

δ

=

• Mediana (wartość w szeregu uporządkowanym powyżej i poniżej której

znajduję się taka sama liczba obserwacji, jeżeli ilość pomiarów jest

parzysta to mediana jest średnia arytmetyczną dwóch środkowych

wyrazów szeregu uporządkowanego)

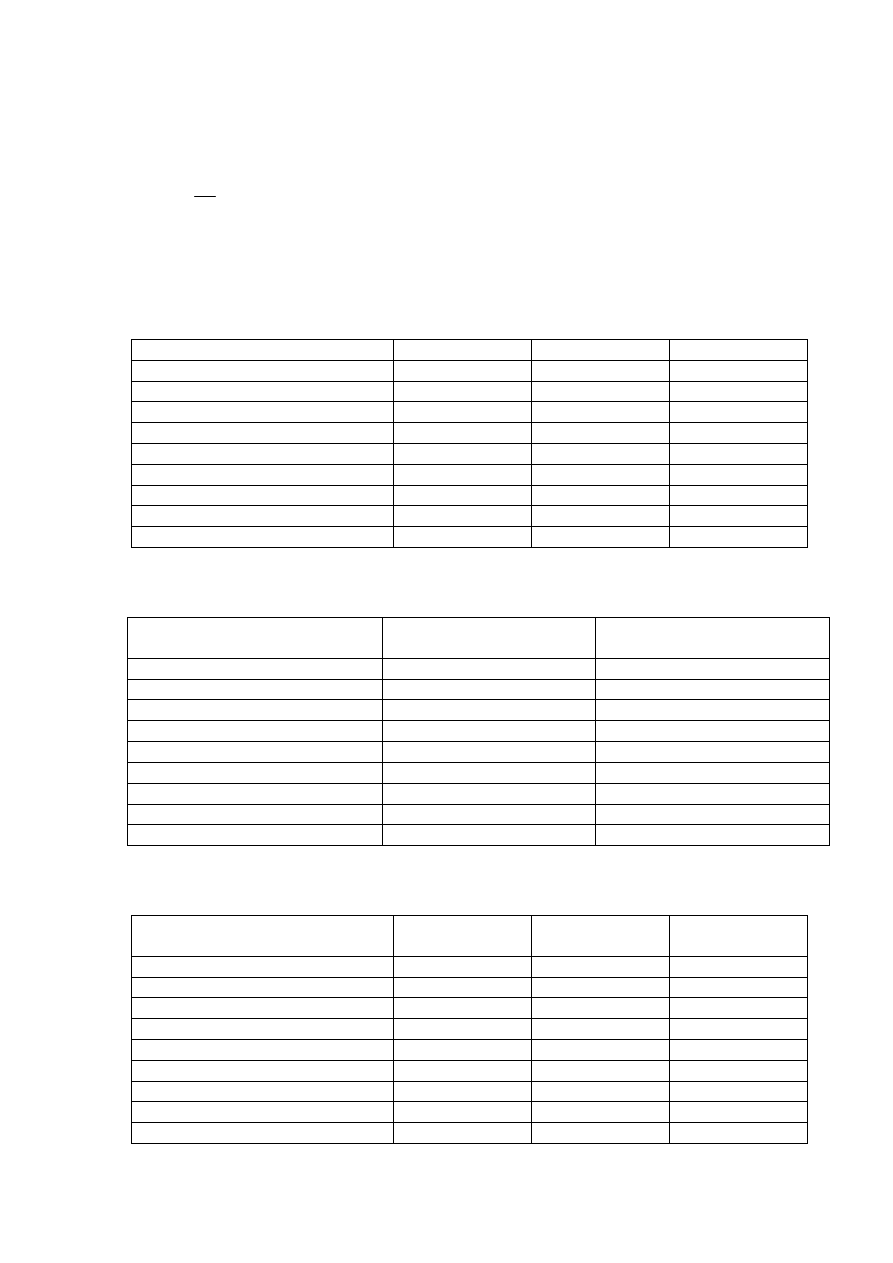
• Kurtoza (różnica ilorazu czwartego momentu centralnego i odchylenia

standardowego w czwartej potędze oraz liczby 3)

3

4

4

−

=

δ

µ

Kurt

• Współczynnik asymetrii (iloraz trzeciego momentu centralnego i

odchylenia standardowego w trzeciej potędze)

3

3

δ

µ

=

A

1.2. Wartości parametrów sygnałów

• Sygnały podstawowe

Parametr \ Sygnał

Sinusoidalny

Prostokątny

Piłokształtny

Wartość maksymalna

-0,21

-0,02

0,6

Wartość minimalna

-10,65

-10,65

-10,65

Średnia arytmetyczna

-6,05

-4,38

-5,3

Średnia kwadratowa

7,1

6,85

6,32

Wariancja

14,04

27,63

11,96

Odchylenie standardowe

3,75

5,25

3,46

Mediana

-6,5

-0,02

-5,2

Kurtoza

1,51

1,11

1,75

Współczynnik asymetrii

0,19

-0,36

-0,04

• Szumy

Sygnał

Parametr

Szum 1

(jednostajny)

Szum 2 (rozkład

Gaussa)

Wartość maksymalna

0,99

3,06

Wartość minimalna

-0,99

-2,78

Średnia arytmetyczna

0,01

-0,06

Średnia kwadratowa

0,56

1,03

Wariancja

0,32

1,06

Odchylenie standardowe

0,56

1,03

Mediana

0,03

-0,04

Kurtoza

1,87

2,77

Współczynnik asymetrii

0,002

0,03

• Sygnały zakłócone

Sygnał

Parametr

Sinusoidalny

+ szum 1

Prostokątny

+ szum 1

Piłokształtny

+ szum 2

Wartość maksymalna

-0,23

0,004

0,61

Wartość minimalna

-10,65

-10,65

-10,65

Średnia arytmetyczna

-6,2

-5,12

-5,54

Średnia kwadratowa

7,29

7,38

6,49

Wariancja

14,86

28,57

11,51

Odchylenie standardowe

3,85

5,36

3,39

Mediana

-6,76

-0,009

-5,61

Kurtoza

1,46

0,98

1,81

Współczynnik asymetrii

0,22

-0,07

0,08

1.3. Wnioski

Porównanie wartości parametrów sygnałów zakłóconych i niezakłóconych
pokazuje, że zarówno szum o rozkładzie jednostajnym jak i szum o
rozkładzie Gauss’a nie wpływają w znacznym stopniu na badane
parametry. Przyczyną mogą być niskie wartości parametrów szumów,
znacząco mniejsze niż wartości parametrów sygnałów niezakłóconych.

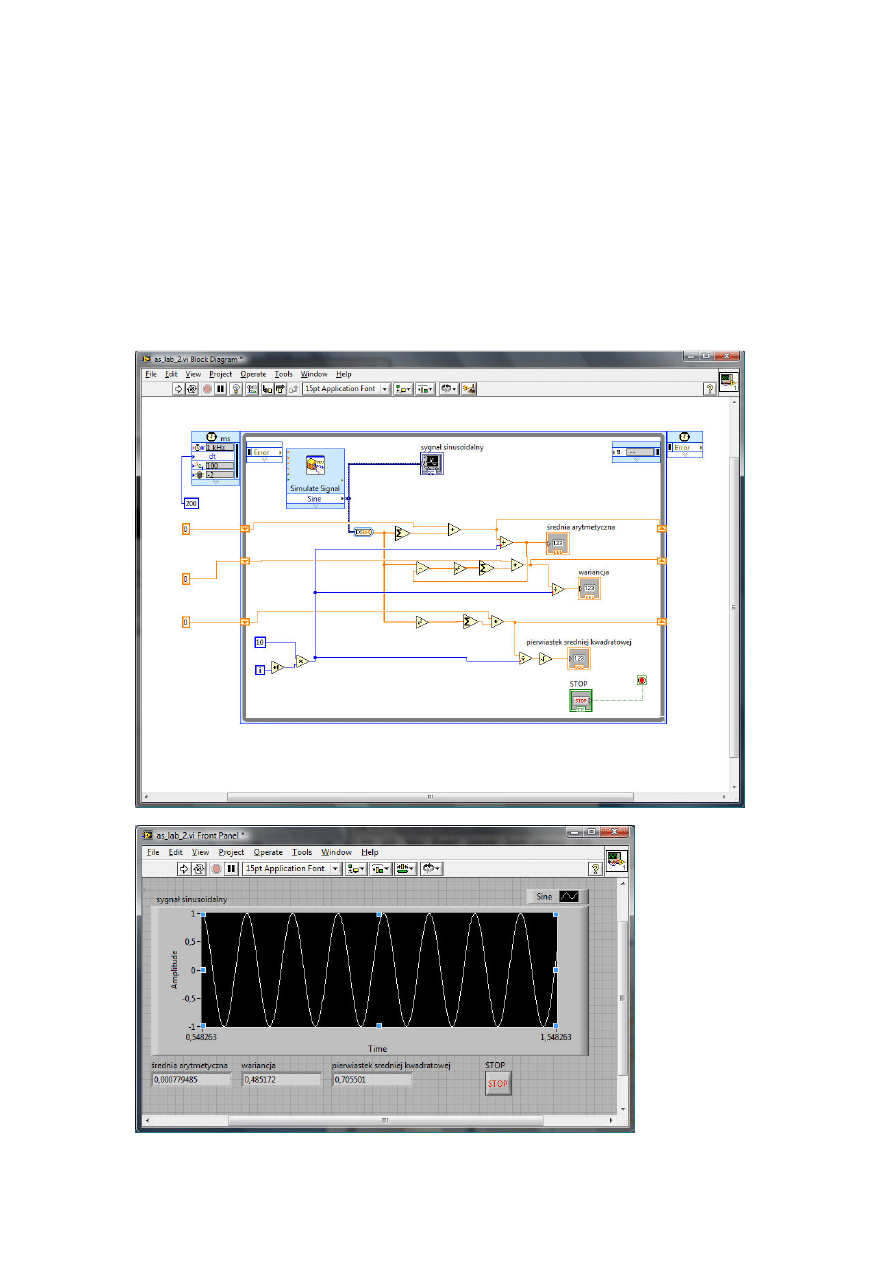
2.1. Układ liczący parametry sygnału na bieżąco.

Układ symuluje zadaną ilość próbek (w tym przypadku 10) w zadanych
odstępach czasu (200 milisekund). Przy każdym wykonaniu pętli
zapamiętywana jest wartość licznika parametrów i za pomocą SHIFT
REGISTER przekazywana do następnej iteracji. W kolejnych iteracjach liczniki
dzielone są przez całkowitą ilość próbek, które zostały zasymulowane od
początku działania programu.

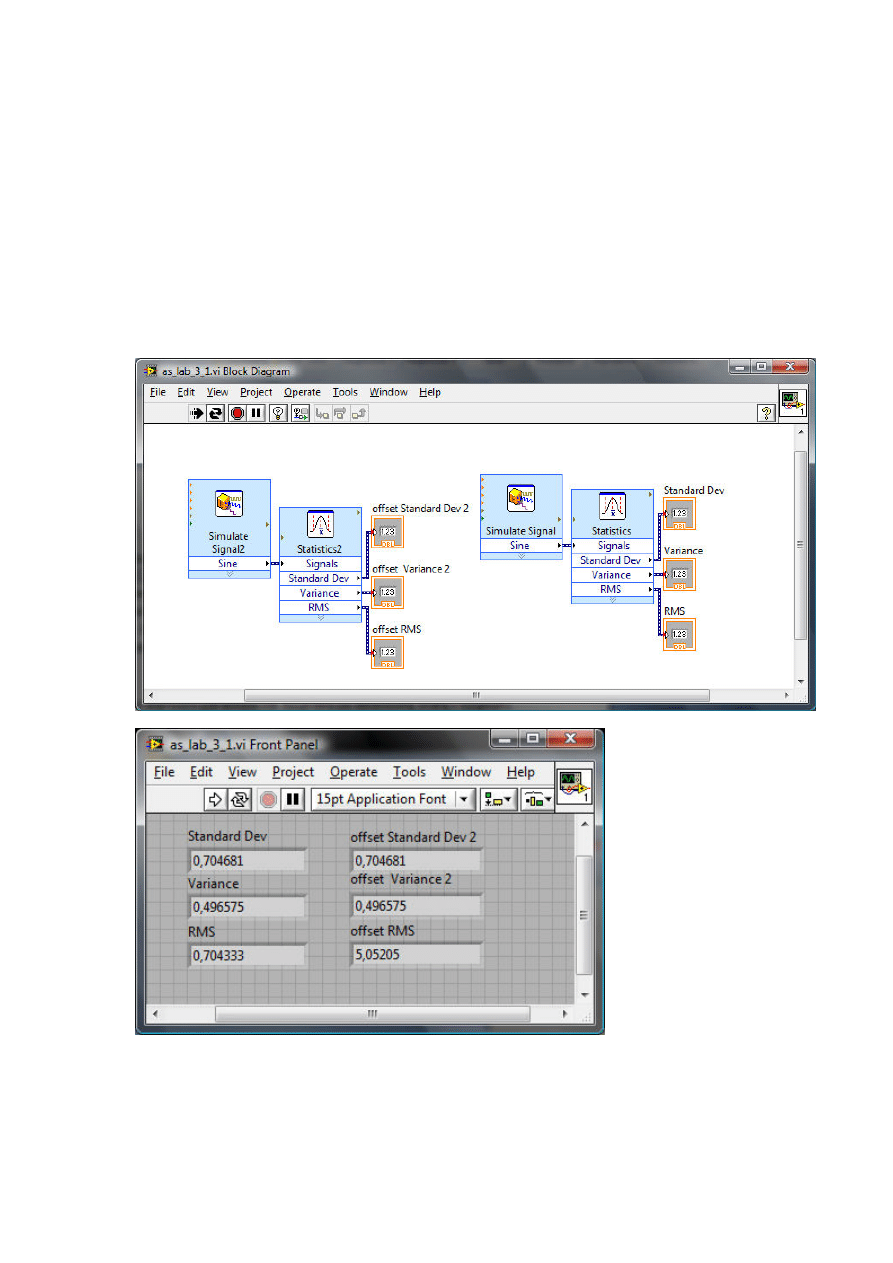
3.1. Porównanie wartości parametrów sygnału ze składową stałą i sygnału

bez składowej stałej.

Wyniki pokazują, że wariancja i co za tym idzie odchylenie standardowe nie
zależą od wartości składowej stałej. Zmianie ulega między innymi wartość
skuteczna. (w podanym przykładzie OFFSET=5)

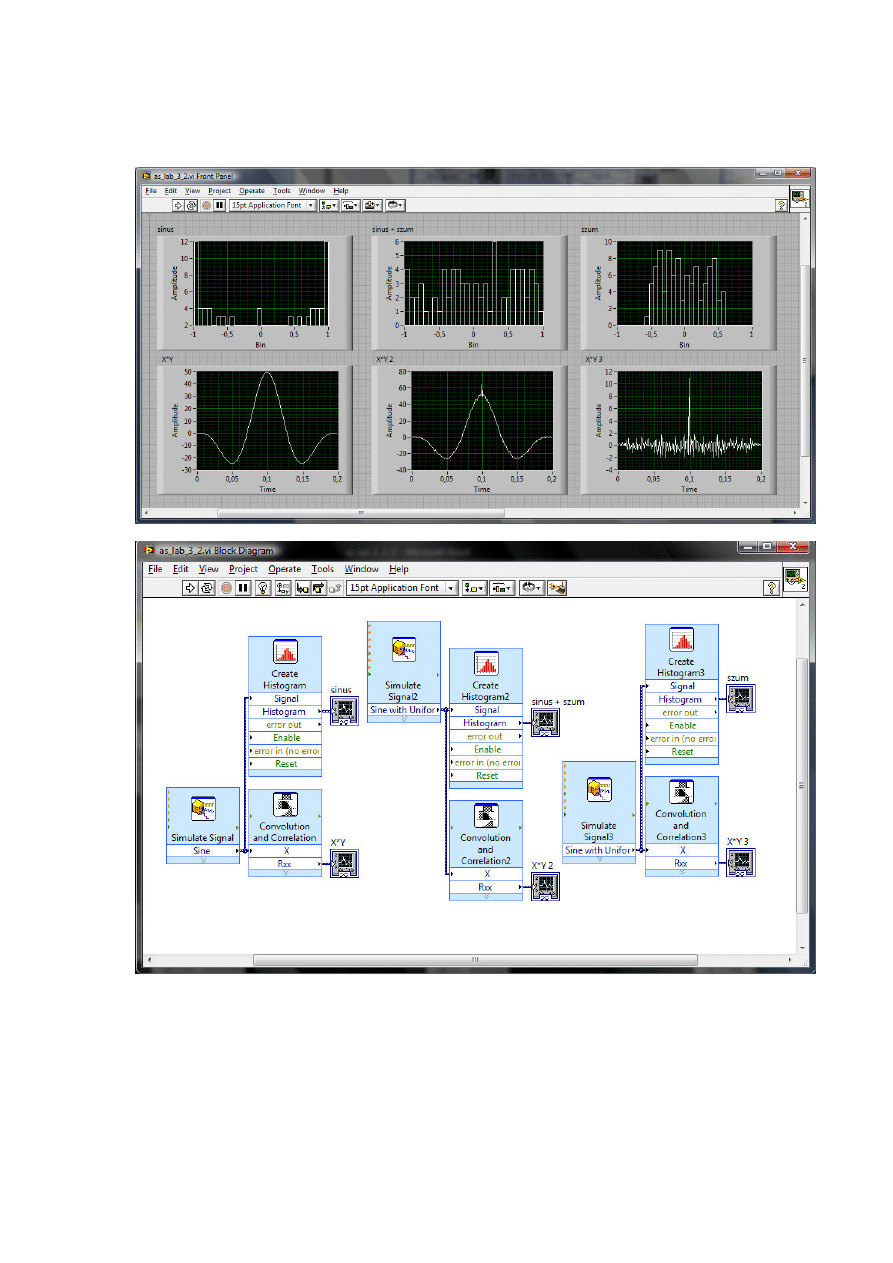
3.2. Wpływ szumu na prawdopodobieństwo wystąpienia wartości w zbiorze

wartości sygnału.

W przypadku niezakłóconego sygnału sinusoidalnego najbardziej
prawdopodobnymi wartościami są wartości największa i najmniejsza. W
przypadku zakłóconego sygnału prawdopodobieństwo bardzo odbiega od
oryginału. Wykresy autokorelacji sygnałów nie są poprawne, ponieważ ich
wartości maksymalne powinny występować dla przesunięcia równego zero.
Niestety nie udało nam się wyeliminować tego błędu.

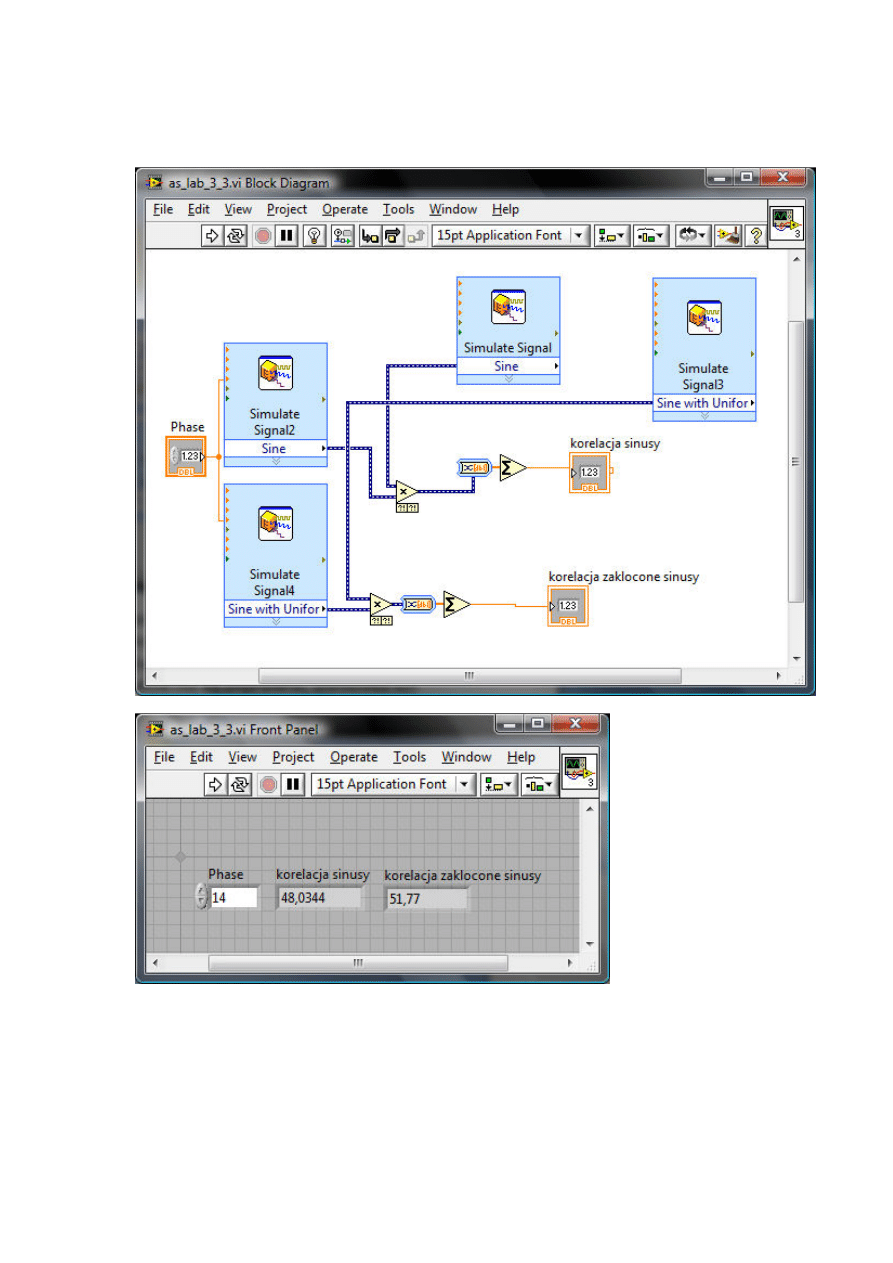
3.3. Porównanie korelacji sygnałów sinusoidalnych zakłóconych i

niezakłóconych

Program pozwala porównać wartość korelacji sygnału sinusoidalnego
zakłóconego i niezakłóconego w dla zadanego przesunięcia fazowego.
Sprawdzono, że najwyższa wartość korelacji została osiągnięta dla fazy
równej zero.