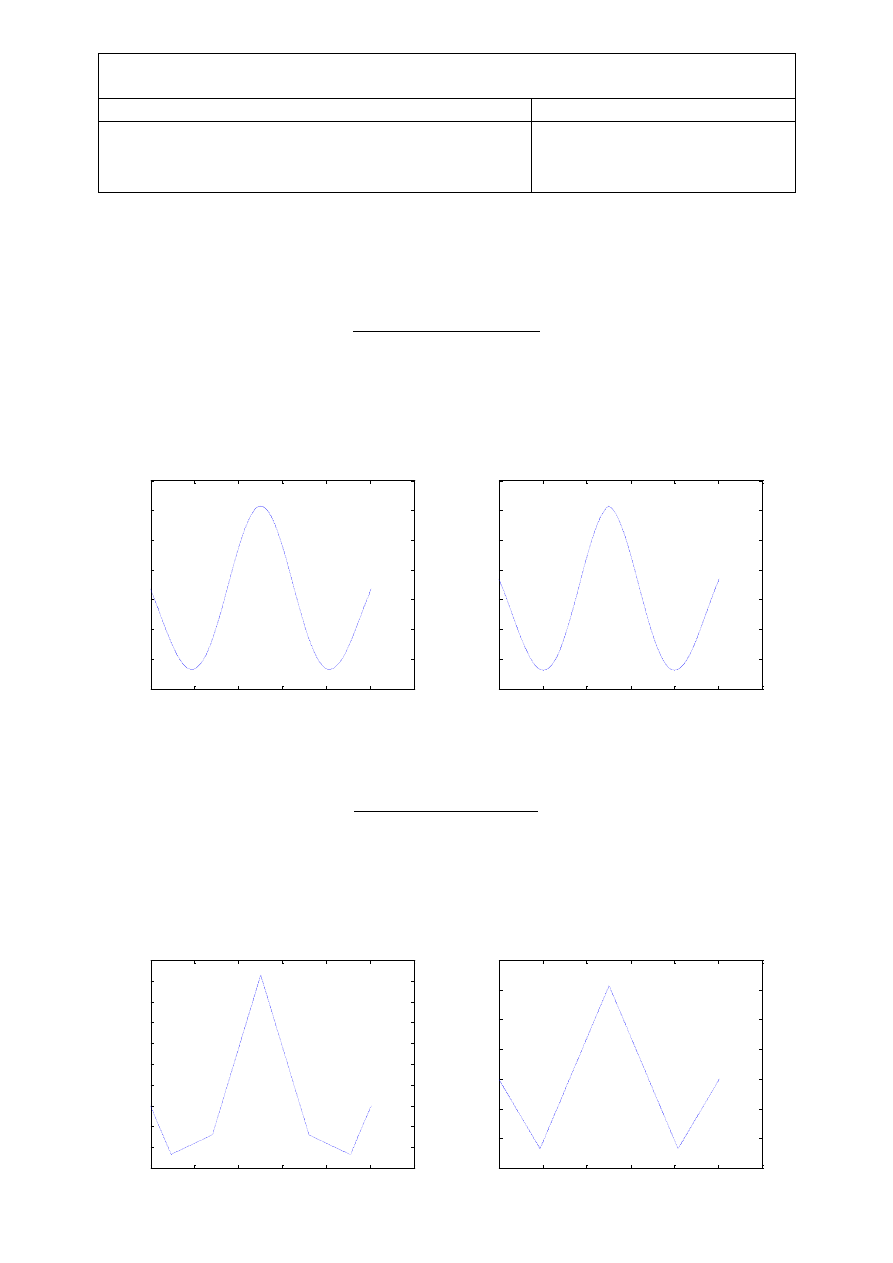
1
Politechnika Wrocławska
Teoria sygnałów, laboratorium - sprawozdanie
Temat: Autokorelacja i korelacja wzajemna sygnałów
16.11.2010
Michał Kaczara (181132),
Marek Karpioski (181172),
Wydział Elektroniki, Informatyka
Wtorek/TP, 13:15-15:00
Prowadzący:
dr inż. Paweł Biernacki
1. Autokorelacja
a) Czy faza wpływa na funkcję autokorelacji
Dla sygnału sinusoidalnego:
% faza = 10
t=0:0.001:2*pi;
Tmax=ceil(length(t)*0.4);
x=sin(2*t+(10*pi)/180);
k=xcorr(x,x,Tmax);
plot(k);
% faza = 120
t=0:0.001:2*pi;
Tmax=ceil(length(t)*0.4);
x=sin(2*t+(120*pi)/180);
k=xcorr(x,x,Tmax);
plot(k);
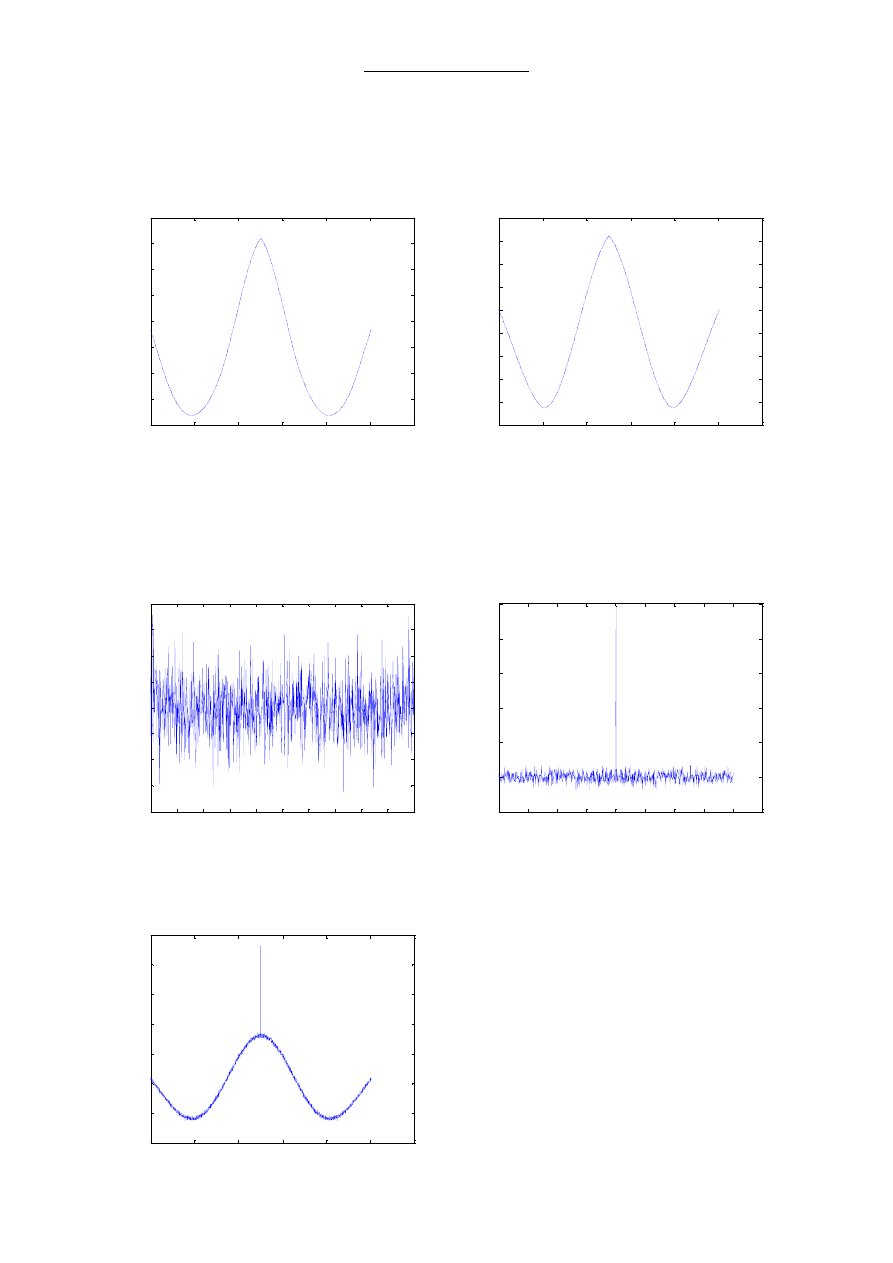
b) Czy wypełnienie wpływa na funkcję autokorelacji
Dla sygnału prostokątnego:
% wypełnienie 35%
t=0:0.001:2*pi;
Tmax=ceil(length(t)*0.4);
x=square(2*t,35);
k=xcorr(x,x,Tmax);
plot(k);
% wypełnienie 50%
t=0:0.001:2*pi;
Tmax=ceil(length(t)*0.4);
x=square(2*t,50);
k=xcorr(x,x,Tmax);
plot(k);
0
1000
2000
3000
4000
5000
6000
-3000
-2000
-1000
0
1000
2000
3000
4000
0
1000
2000
3000
4000
5000
6000
-3000
-2000
-1000
0
1000
2000
3000
4000
0
1000
2000
3000
4000
5000
6000
-3000
-2000
-1000
0
1000
2000
3000
4000
5000
6000
7000
0
1000
2000
3000
4000
5000
6000
-6000
-4000
-2000
0
2000
4000
6000
8000
2
Dla sygnału trójkątnego:
% wypełnienie 30%
t=0:0.001:2*pi;
Tmax=ceil(length(t)*0.4);
x=sawtooth(2*t,0.3);
k=xcorr(x,x,Tmax);
plot(k);
% wypełnienie 50%
t=0:0.001:2*pi;
Tmax=ceil(length(t)*0.4);
x=sawtooth(2*t,0.5);
k=xcorr(x,x,Tmax);
plot(k);
c) Jak wygląda funkcja autokorelacji dla szumu białego
% szum biały
x=randn (1,1000);
plot(x);
% autokorelacja dla szumu białego
k=xcorr(x,x,400);
plot(k);
d) Jak wygląda funkcja autokorelacji dla sygnału x = sinus + szum
t=0:0.001:2*pi;
Tmax=ceil(length(t)*0.4);
x=sin(2*t);
y = randn(1, length(t));
z=x+y;
k=xcorr(z,z,Tmax);
plot(k);
0
1000
2000
3000
4000
5000
6000
-1500
-1000
-500
0
500
1000
1500
2000
2500
0
1000
2000
3000
4000
5000
6000
-2000
-1500
-1000
-500
0
500
1000
1500
2000
2500
0
100
200
300
400
500
600
700
800
900
1000
-4
-3
-2
-1
0
1
2
3
4
0
100
200
300
400
500
600
700
800
900
-200
0
200
400
600
800
1000
0
1000
2000
3000
4000
5000
6000
-4000
-2000
0
2000
4000
6000
8000
10000
3
2. Korelacja wzajemna
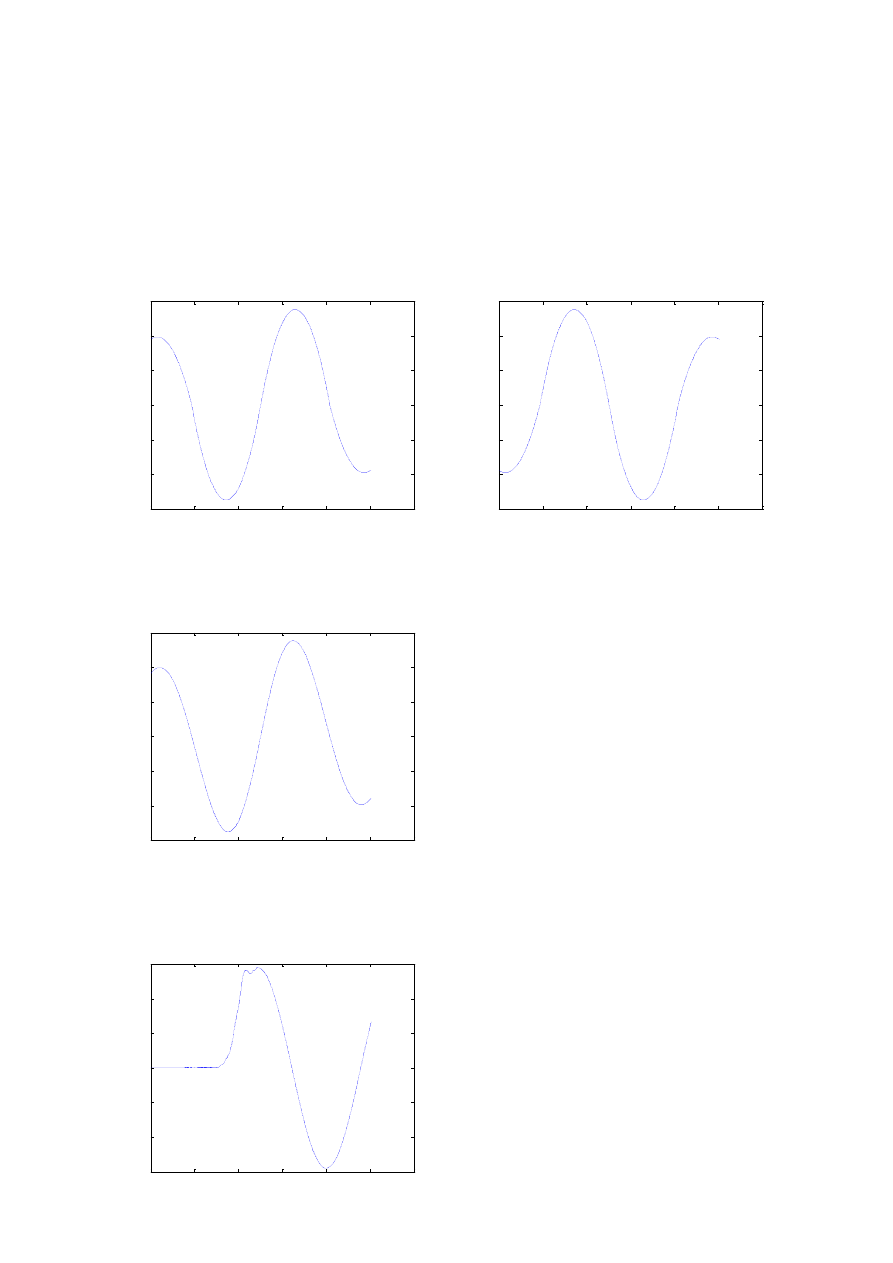
a) Czy istnieje różnica pomiędzy
)
(
),
(
yx
xy
R
R
:
)
(
xy
R
t=0:0.001:2*pi;
Tmax=ceil(length(t)*0.4);
x=sawtooth(2*t,0.5);
y=square(2*t,50);
k=xcorr(x,y,Tmax);
plot(k);
:
)
(
yx
R
t=0:0.001:2*pi;
Tmax=ceil(length(t)*0.4);
x=sawtooth(2*t,0.5);
y=square(2*t,50);
k=xcorr(y,x,Tmax);
plot(k);
b) Jak wygląda funkcja korelacji wzajemnej dla sinusa i cosinusa
t=0:0.001:2*pi;
Tmax=ceil(length(t)*0.4);
x=sin(2*t);
y=cos(2*t);
k=xcorr(x,y,Tmax);
plot(k);
c) Jak wygląda funkcja korelacji wzajemnej dla sinusa i szumu
t=0:0.001:2*pi;
Tmax=ceil(length(t)*0.4);
x=sin(2*t);
y=randn (1,1000);
k=xcorr(x,y,Tmax);
plot(k);
0
1000
2000
3000
4000
5000
6000
-3000
-2000
-1000
0
1000
2000
3000
0
1000
2000
3000
4000
5000
6000
-3000
-2000
-1000
0
1000
2000
3000
0
1000
2000
3000
4000
5000
6000
-3000
-2000
-1000
0
1000
2000
3000
0
1000
2000
3000
4000
5000
6000
-15
-10
-5
0
5
10
15
4
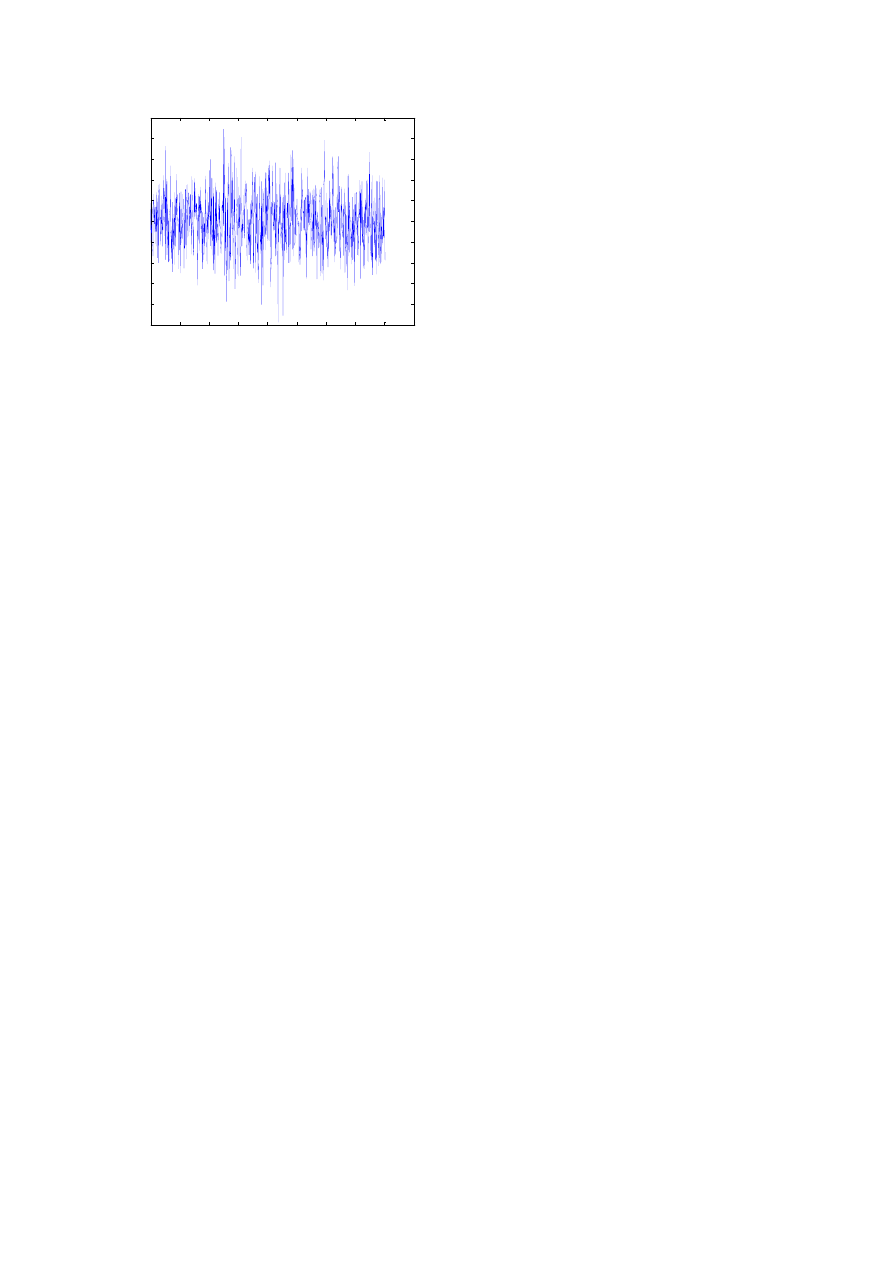
d) Jak wygląda funkcja
)
(
2
1
x
x
R
gdy
2
)
1000
,
1
(
1
x
randn
x
x1=randn (1,1000);
x2=randn (1,1000);
k=xcorr(x1,x2,400);
plot(k);
3. Wnioski
Dla przebiegu sinusoidalnego wraz ze zmianą fazy sygnału funkcja autokorelacji nie zmienia się. Dla
przebiegu prostokątnego i trójkątnego dla współczynnika wypełnienia w=0.5 (50%) funkcja
autokorelacji jest symetryczna względem wartości 0. Podczas zmniejszania lub zwiększania wartości
współczynnika funkcja autokorelacji zmienia się (rosną wartości ujemne), chociaż kształt jest bardzo
podobny.
Funkcja korelacji wzajemnej dwóch sygnałów nie jest przemienna. Przebieg funkcji korelacji
wzajemnej dla sinusa i cosinusa ma przebieg sinusoidalny. Funkcja korelacji wzajemnej dla sinusa i
szumu przyjmuje przez jakiś czas wartośd 0 (czas ten jest uzależniony od ilości próbek szumu), a
następnie przyjmuje przebieg sinusoidalny. Widad, że po pewnym czasie możemy wyodrębnid sygnał,
względem którego następuje korelacja. Funkcja korelacji wzajemnej dwóch sumów przypomina szum
biały.
0
100
200
300
400
500
600
700
800
900
-100
-80
-60
-40
-20
0
20
40
60
80
100