1

Obliczenia wytrzymałościowe elementów maszyn – materiały pomocnicze

oprac. dr inż. Ludomir J.Jankowski

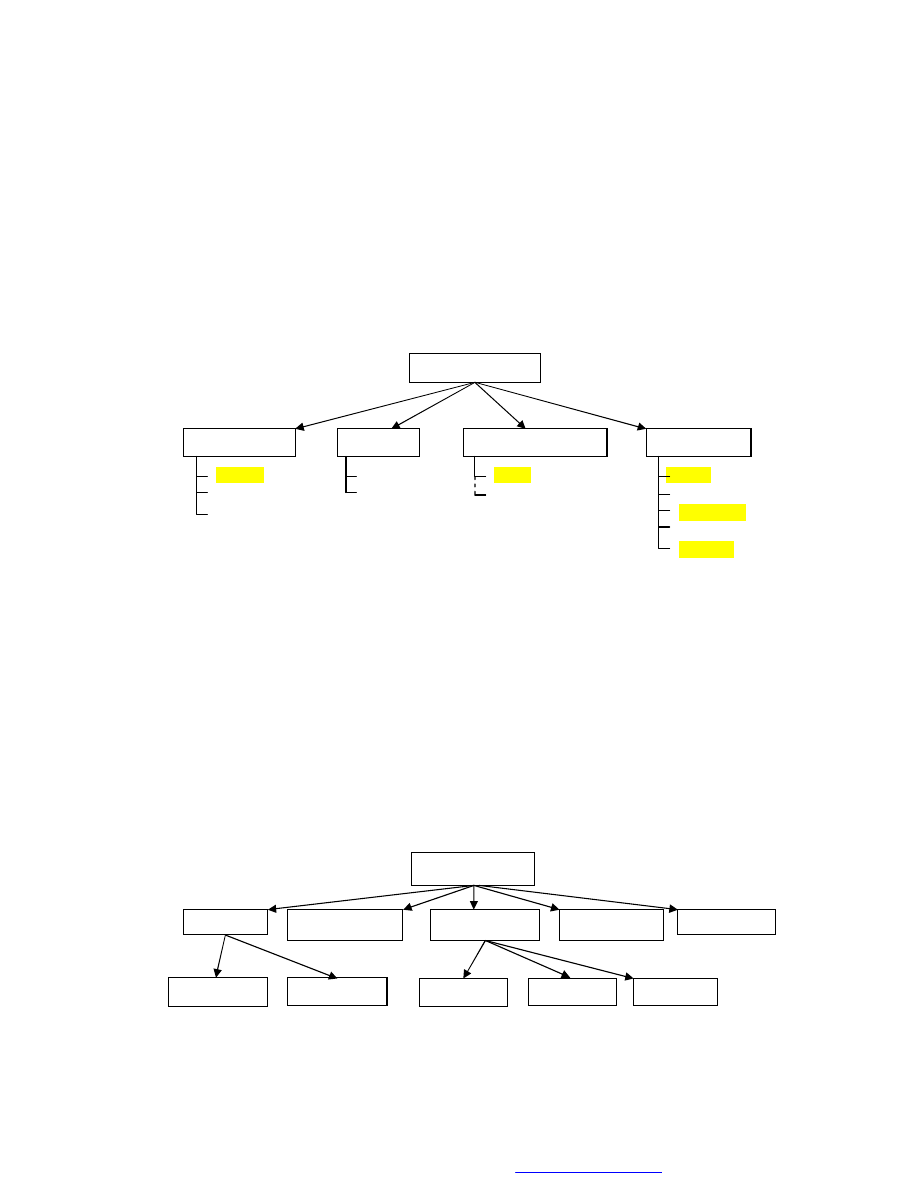
1. Obliczenia wytrzymałościowe połączeń

W budowie maszyn występują różnego rodzaju połączenia, które ogólnie można

zakwalifikować do grupy połączeń nierozłącznych lub rozłącznych. Ze względu na
występowanie pośrednich elementów łączących, połączenia dzieli się także na
bezpośrednie i pośrednie. Jeśli przyjąć, jako podstawowe kryterium podziału, sposób
przekazywania sił pomiędzy łączonymi elementami, to połączenia dzielimy wg schematu
pokazanego na rys. 1.

spawane skurczowe nitowe klinowe

zgrzewane wtłaczane klinowe wpustowe

spajane

sworzniowe

kołkowe

gwintowe

Rys. 1. Rodzaje połączeń

Często, ze względu na specyfikę, wyróżnia się dodatkowo połączenia rurowe i

sprężyste.

We wszystkich przypadkach stosowania danej postaci konstrukcyjnej połączenia,

konieczne jest przeprowadzenie obliczeń wytrzymałościowych uwzględniających warunki
jego pracy.

1.1.

Obliczanie połączenia spawanego obciążonego statycznie

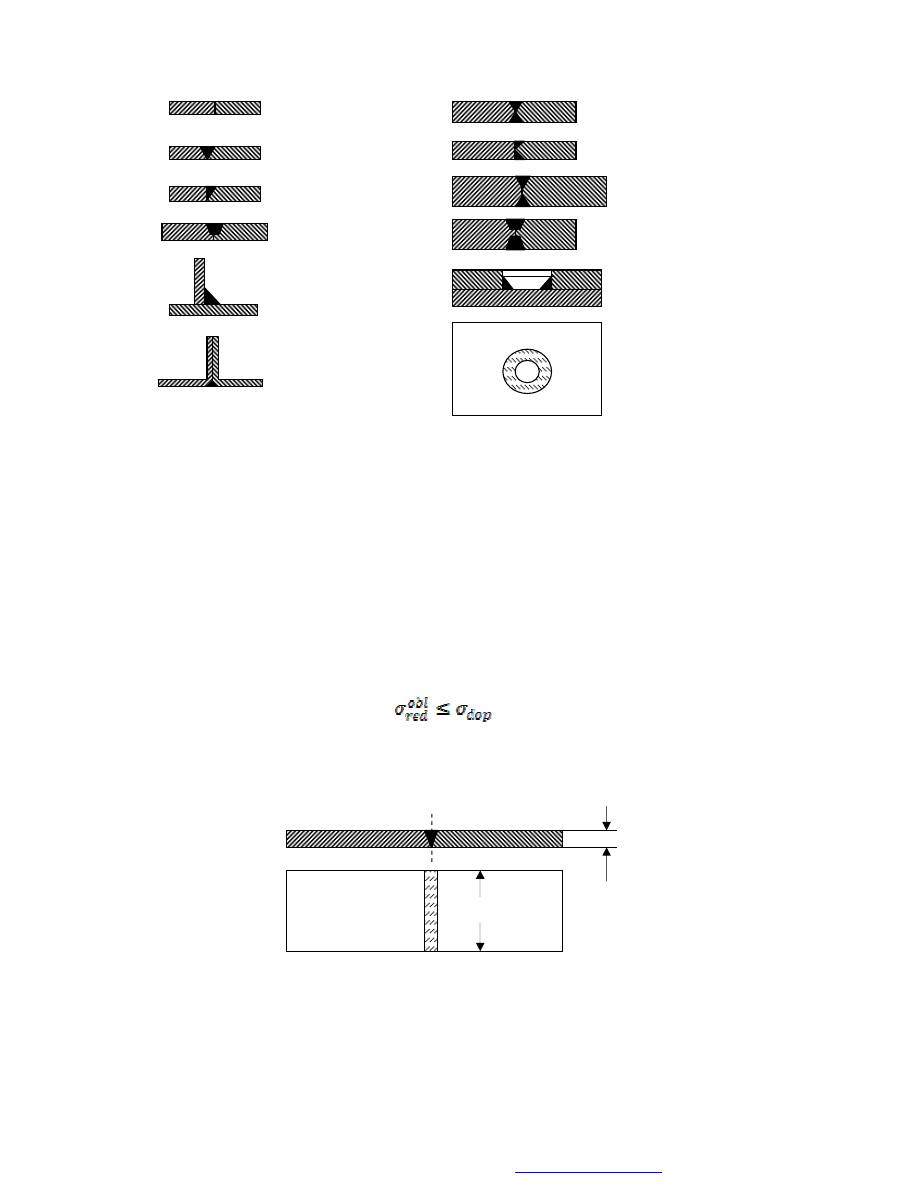
Spawanie, to łączenie metali (i niektórych tworzyw sztucznych) polegające na ich

miejscowym stopieniu. Nie wnikając w zagadnienia technologiczne, rozróżnia się
następujące rodzaje spoin (rys. 2):

Rys. 2. Rodzaje spoin

Połączenia

kohezyjne

cierne

cierno-kształtowe

kształtowe

płaskie

wklęsłe

jednostronne

dwustronne

Rodzaje spoin

czołowe

krawędziowe

pachwinowe

grzbietowe

otworowe

wypukłe

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

2

Spoina jednostronna typu I

Spoina dwustronna typu X

Spoina jednostronna typu V

Spoina dwustronna typu K

Spoina jednostronna typu ½ V

Spoina dwustronna typu 2V

Spoina jednostronna typu U

Spoina dwustronna typu 2U

Spoina pachwinowa płaska

Spoina otworowa

Spoina grzbietowa

Rys. 2. Przykładowe postacie spoin

Obliczenia spoin, z punktu widzenia wytrzymałości materiałów, to często przypadek

tzw. ścinania technicznego. Jak wiadomo, w praktyce czyste ścinanie jest niezwykle
trudne do zrealizowania, ze względu na zakłócenie momentem gnącym powstającym na
skutek występowania skończonej odległości pomiędzy siłami tnącymi. Jeśli przyjąć, że w
przekroju poprzecznym panuje jednorodny stan naprężenia tnącego, a zginanie jest
pomijalnie małe, to taki przypadek jest nazywany ścinaniem technicznym.

Podstawową zasadą obliczeń wytrzymałościowych połączeń jest określenie wartości

naprężenia zredukowanego w niebezpiecznym przekroju, a następnie porównanie go z
wartością naprężenia dopuszczalnego. Powinien być przy tym spełniony warunek:

(1)

W przypadku spoin czołowych przyjmuje się, że wartość naprężenia występuje w

przekroju N-N, pokazanym na rys. 3.

t

Rys. 3. Połączenie czołowe – schemat obliczeniowy

Do obliczeń przyjmuje się powierzchnię przekroju niebezpiecznego wynoszącą:

b

N

N

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

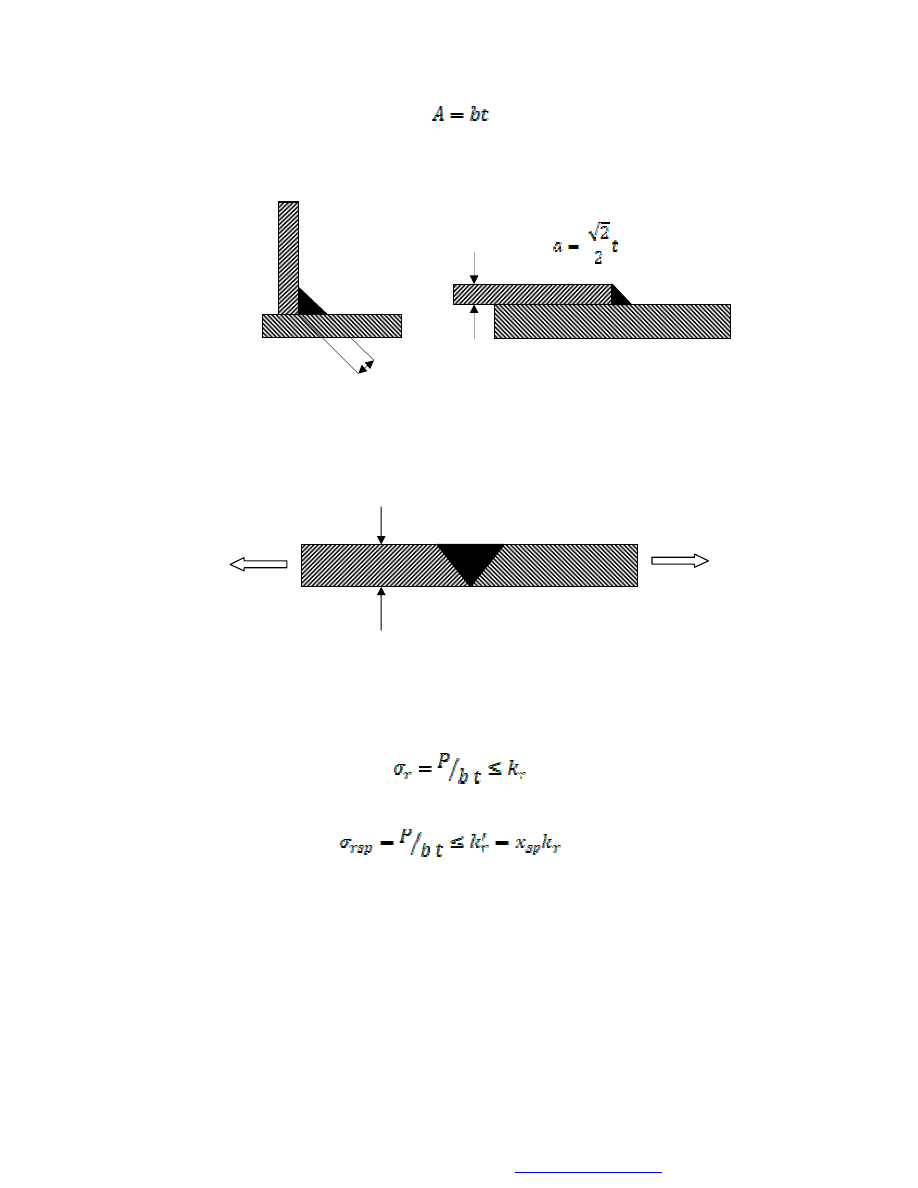
3

przy czym skośne usytuowanie spoiny nie jest uwzględniane w obliczeniach.

W przypadku spoin pachwinowych i połączeń zakładkowych, do obliczeń przyjmuje

się grubość obliczeniową spoiny a wg schematu pokazanego na rys. 4.

a) b)

Rys. 4. Grubość obliczeniowa spoiny: a) pachwinowej, b) w połączeniu zakładkowym

Należy przy tym podkreślić, że wartość dopuszczalna naprężeń powinna uwzględniać

rodzaj obciążenia działającego na spoinę. Ogólnie, może ona być ścinana, rozciągana,
ściskana lub zginana.

Rys. 5. Schemat rozciąganego połączenia spawanego typu V

W przypadku pokazanym na rys. 5, płaskowniki o grubości t

i szerokości b są

połączone spoiną typu V. W płaskowniku musi być spełniony warunek:

natomiast w spoinie:

Naprężenie dopuszczalne k

r

uwzględnia współczynniki bezpieczeństwa x

e

(ze

względu na granicę plastyczności R

e

) lub x

m

(ze względu na granicę wytrzymałości na

rozciąganie R

m

). Ogólnie, współczynniki te ujmują obniżanie się granicy plastyczności i

granicy wytrzymałości doraźnej wraz ze wzrostem wymiarów poprzecznych obciążanych
elementów. Przykładowo, w przypadku obciążeń statycznych współczynniki te wynoszą:
x

e

= 2.0÷2.3 dla stali konstrukcyjnych, x

e

= 1.6 dla stali sprężynowej, oraz x

m

= 3.5 dla

żeliwa. Ze względu na lokalne zmiany wytrzymałości w rejonie spoiny (wywołane strefą
wpływu ciepła powodującą zmiany struktury materiału konstrukcji, koncentracją

a

t

P

P

t

(2)

(3)

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

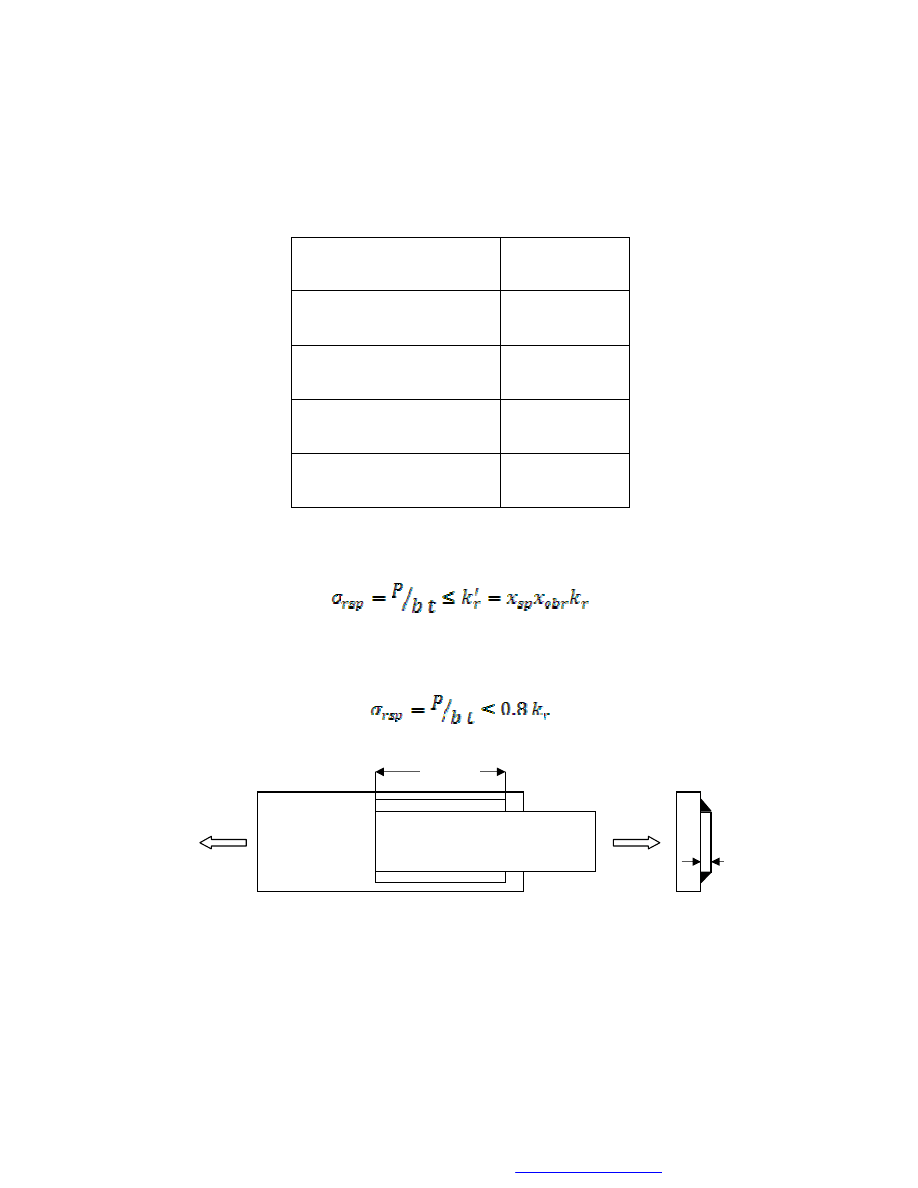
4

naprężeń w grani i na brzegach spoiny, niższymi właściwościami wytrzymałościowymi
materiału spoiwa, tzw. naprężenia spawalniczymi o charakterze skurczowym),
wprowadza się dodatkowo współczynnik x

sp

, zależny od sposobu obciążenia spoiny (tabl.

1).

Tablica 1.

Wartości współczynnika x

sp

W przypadku przewidywanej obróbki spoiny (np. zlicowania brzegu), wprowadza się

do obliczeń współczynnik jakości spoiny x

obr

, a wzór (3) przybiera postać:

Ostatecznie, warunek wytrzymałości rozciąganej, poprzecznej (i skośnej) spoiny

czołowej (nieobrabianej) ma postać:

Rys. 5. Rozciągane połączenie zakładkowe

W przypadku połączenia spawanego wzdłużnego (typu zakładkowego) – rys. 5 –

spoiny pachwinowe o długości l

sp

są ścinane, a warunek wytrzymałości ma postać:

Obciążenie spoiny

x

sp

rozciąganie

0.8

zginanie

0.9

ściskanie

1.0

ścinanie

0.65

(3a)

(4)

P

P

l

sp

t

(5)

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

5

W przypadku, gdy w spoinie pojawiają się naprężenia styczne i normalne, warunek

(1) wymaga obliczenia naprężenia zredukowanego (wg hipotezy energii odkształcenia
postaciowego):

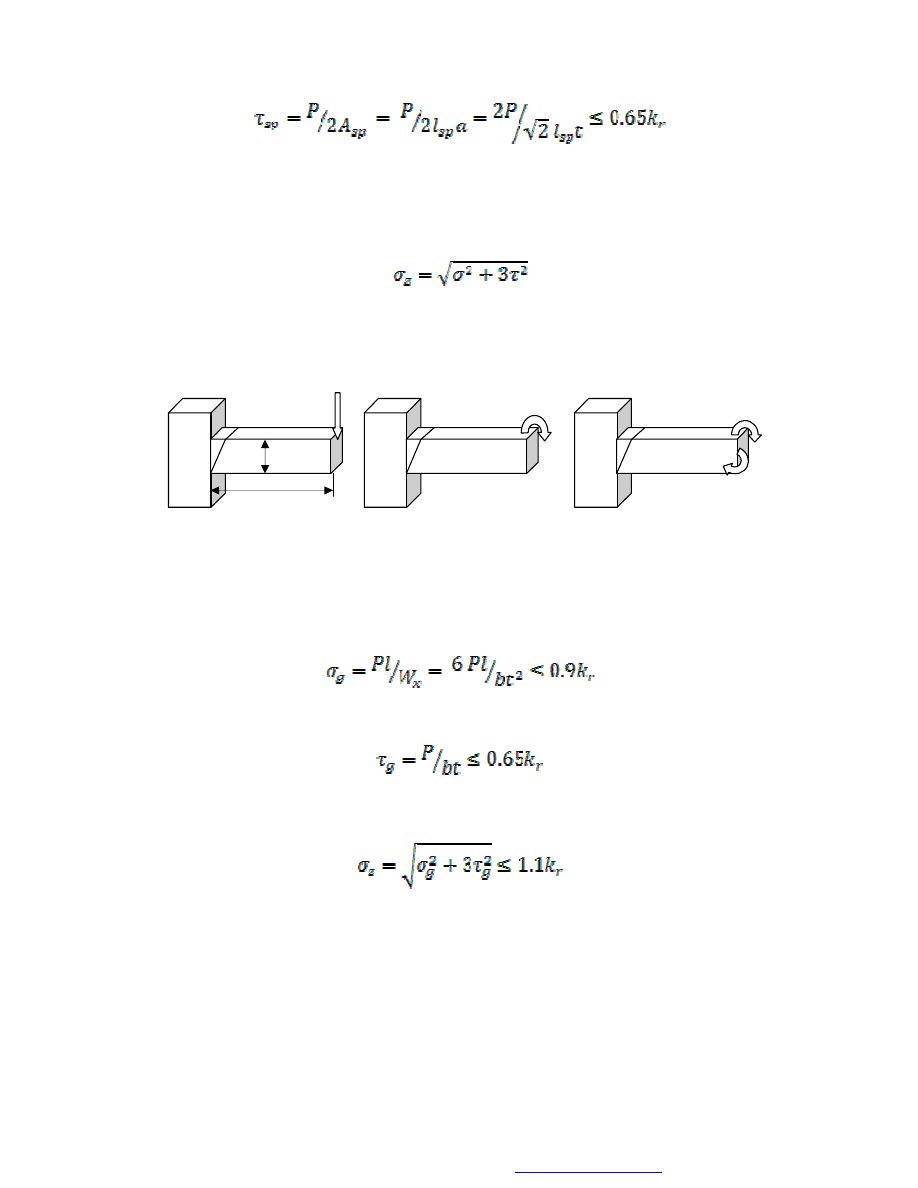
Sytuacja taka może pojawić się np. w przypadku spoiny czołowej pokazanej na rys. 6a.

a)

b) c)

Rys. 6. Spoina czołowa: a) zginana i ścinana, b) zginana w jednej płaszczyźnie,

c) zginana w dwóch płaszczyznach

Dla tego przypadku, warunek wytrzymałościowy na zginanie ma postać:

natomiast warunek na ścinanie określa wzór:

Tzw. warunek wytrzymałości złożonej, uwzględniający wytężenie spoiny określone
wzorem (6), ma postać:

W przypadku spoin pokazanych na rys. 6b i 6c, uwzględnia się jedynie naprężenia
normalne wywołane ich zginaniem. I tak, dla zginania pokazanego na rys. 6b warunek
wytrzymałości spoiny ma postać (7), natomiast w przypadku zginania w dwóch
płaszczyznach (rys. 6c) zakłada się, że wypadkowe naprężenie w spoinie jest (w
przybliżeniu) równe sumie naprężeń pochodzących od momentów M

x

i M

y

:

(6)

P

M

x

M

x

M

y

l

t

(7)

(8)

(9)

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

6

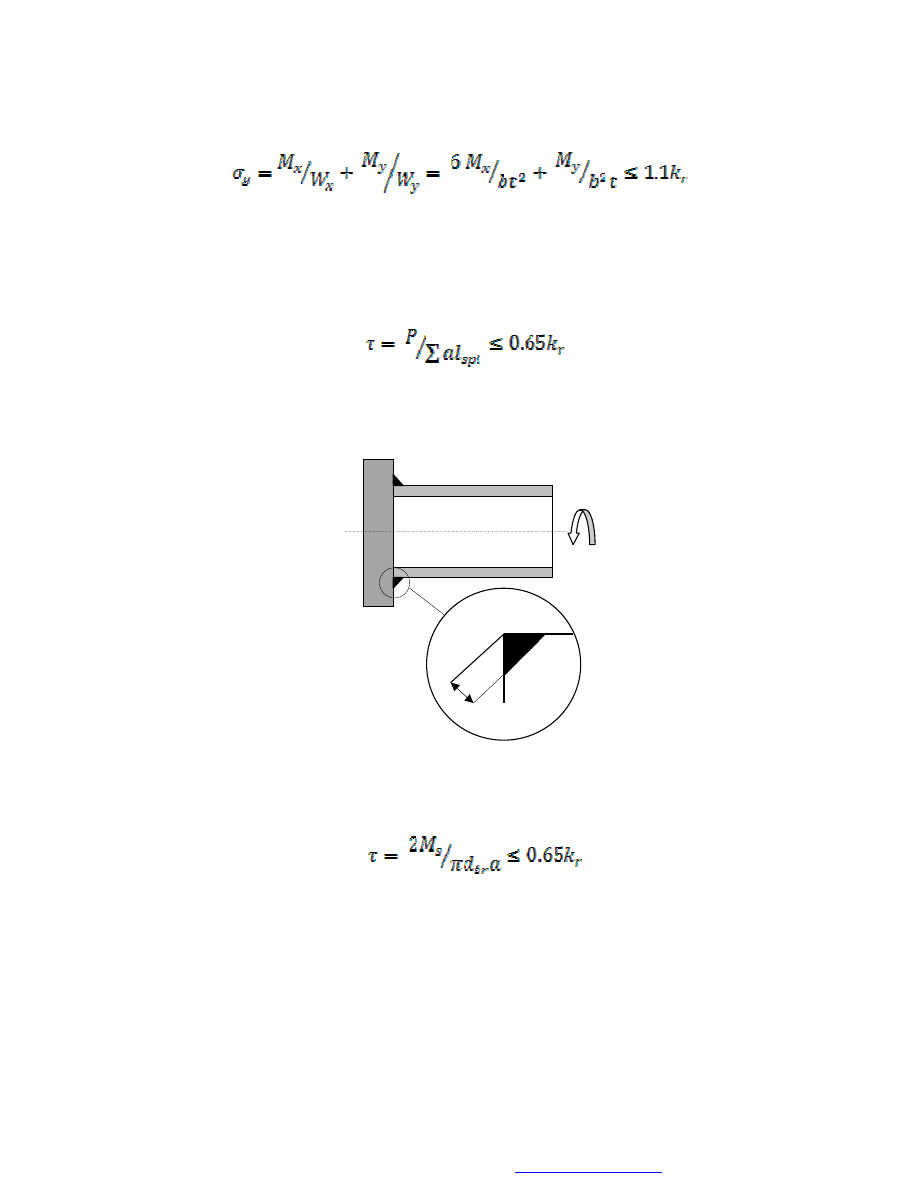
W przypadku spoin pachwinowych i otworowych sprawdzeniu podlega warunek
wytrzymałości na ścinanie, przy czym należy uwzględniać sumę pól powierzchni
przekroju spoin występujących w złączu. Tak więc, warunek wytrzymałościowy ma
postać:

Np. w złączu rury (o średnicy zewnętrznej D i średnicy wewnętrznej d) z tarczą – rys. 7 -
obciążonym momentem skręcającym, do obliczeń należy przyjmować spoinę o grubości
a, i długości l

sp

= πd

śr

( d

śr

= (D+d)/2 )

Rys. 7. Skręcane złącze spawane (spoiny pachwinowe)

Warunek (11) ma więc w tym przypadku postać:

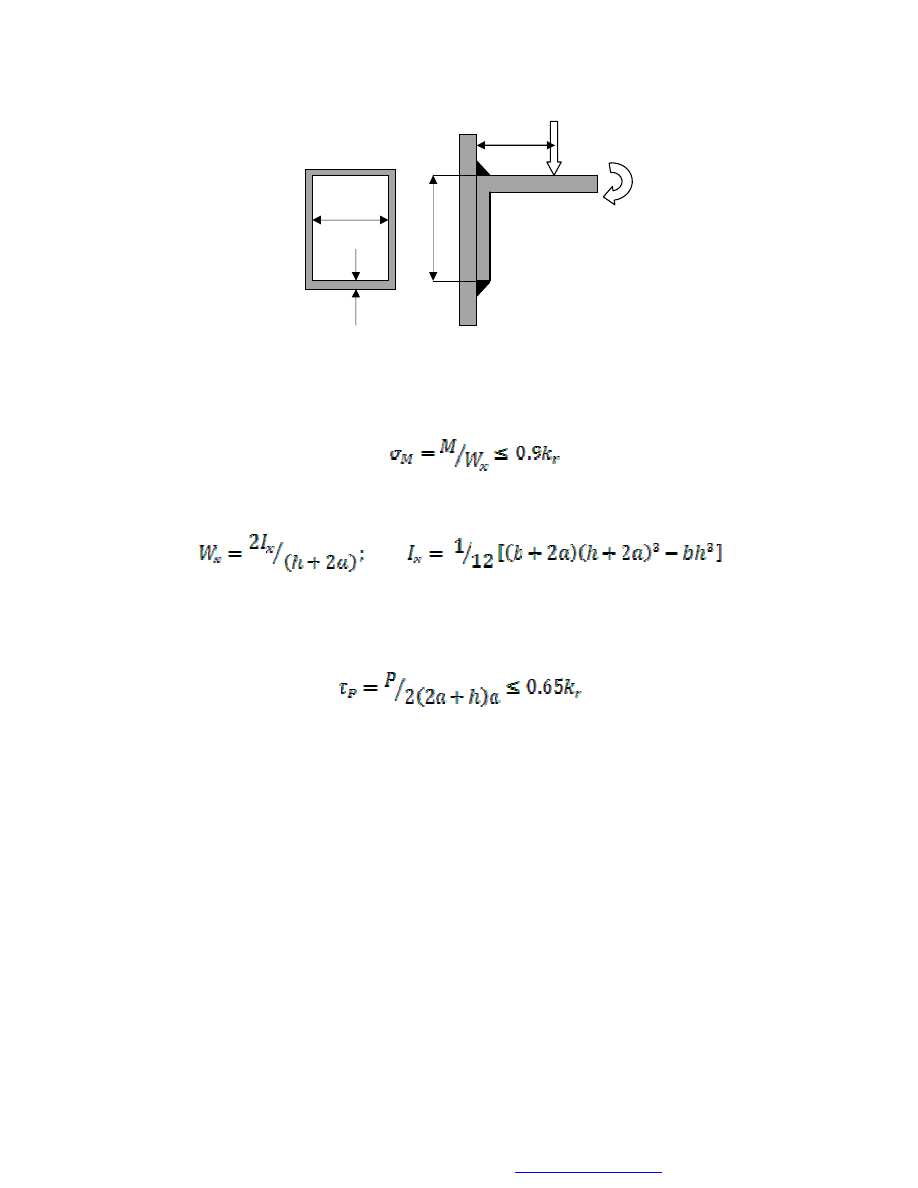
W przypadku obliczania spawanego połączenia wspornika, obciążonego jak na rys. 8,
poza warunkiem na ścinanie dla spoin usytuowanych równolegle do kierunku działania
siły P, należy uwzględnić również zginanie.

(10)

(11)

M

s

a

(12)

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

7

Rys. 8. Zginany wspornik (spoiny pachwinowe)

Tak więc, naprężenia od zginania powinny spełniać warunek:

przy czym:

Natomiast naprężenia styczne, z pominięciem spoin usytuowanych prostopadle do
kierunku działania siły, muszą spełniać warunek:

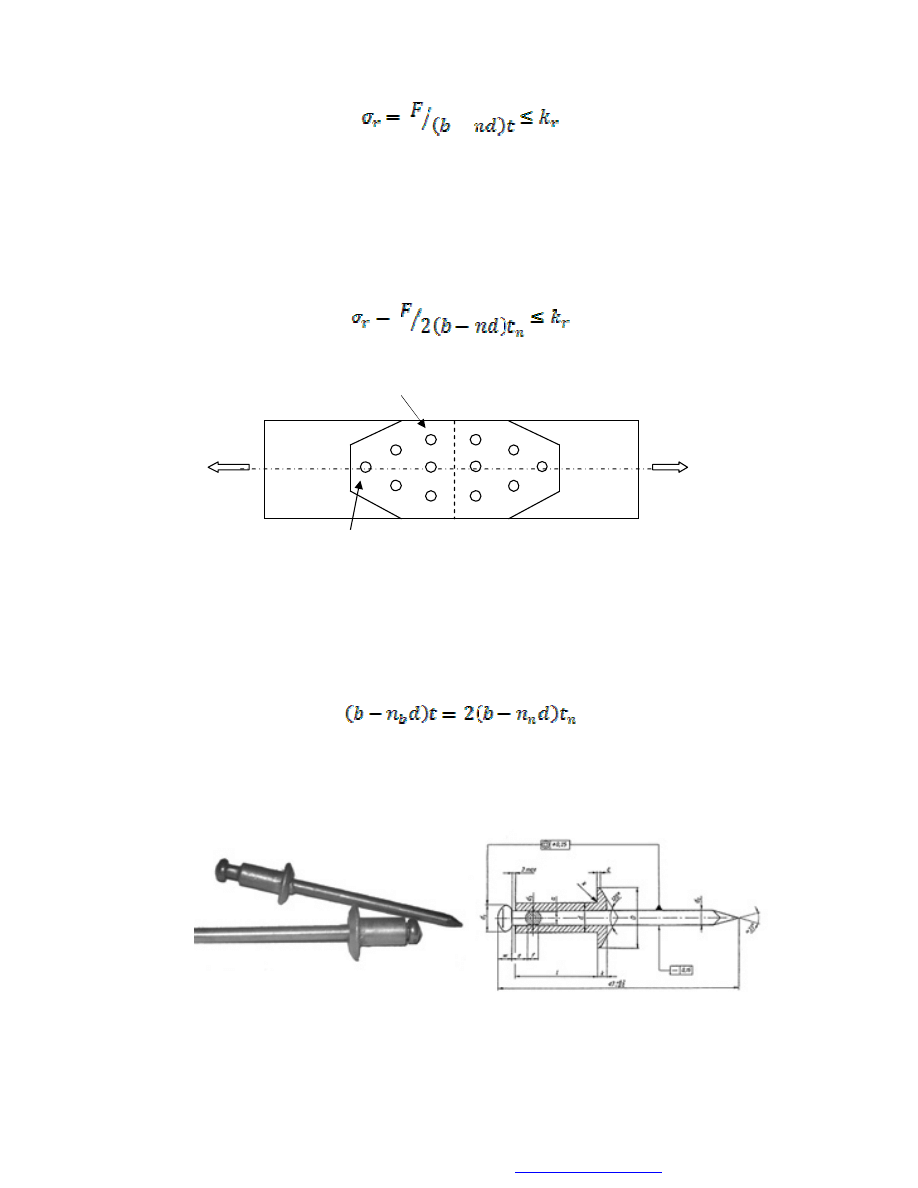
1.2. Obliczanie połączenia nitowego

Połączenia nitowe dzielą się na: mocne – stosowane w konstrukcjach stalowych,
szczelne – stosowane w budowie zbiorników niskociśnieniowych oraz mocno-szczelne –
stosowane w budowie kotłów i zbiorników wysokociśnieniowych. Ze względu na sposób
pracy nitów, w połączeniach mogą wystąpić nity jedno- (połączenia zakładkowe) i
dwucięte (połączenia nakładkowe). Nity mogą być zamykane na zimno lub gorąco
(większe średnice), przy czym są one znormalizowane.

Połączenia nitowe należą do grupy połączeń cierno-kształtowych, jednak w
obliczeniach wytrzymałościowych pomija się tarcie występujące pomiędzy łbami nitów i
łączonymi elementami oraz pomiędzy tymi elementami. Uwzględnia się natomiast
możliwość zniszczenia połączenia nitowego poprzez: ścięcie nitów, nadmierny nacisk
pomiędzy trzonami nitów a ściankami otworu, a także rozerwanie łączonych blach
pomiędzy otworami skrajnego rzędu nitów.

h

P

l

b

a

h

M

(13)

(14)

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

8

Rys. 9. Nity: jednocięte (połączenie zakładkowe)

i dwucięte (połączenie nakładkowe)

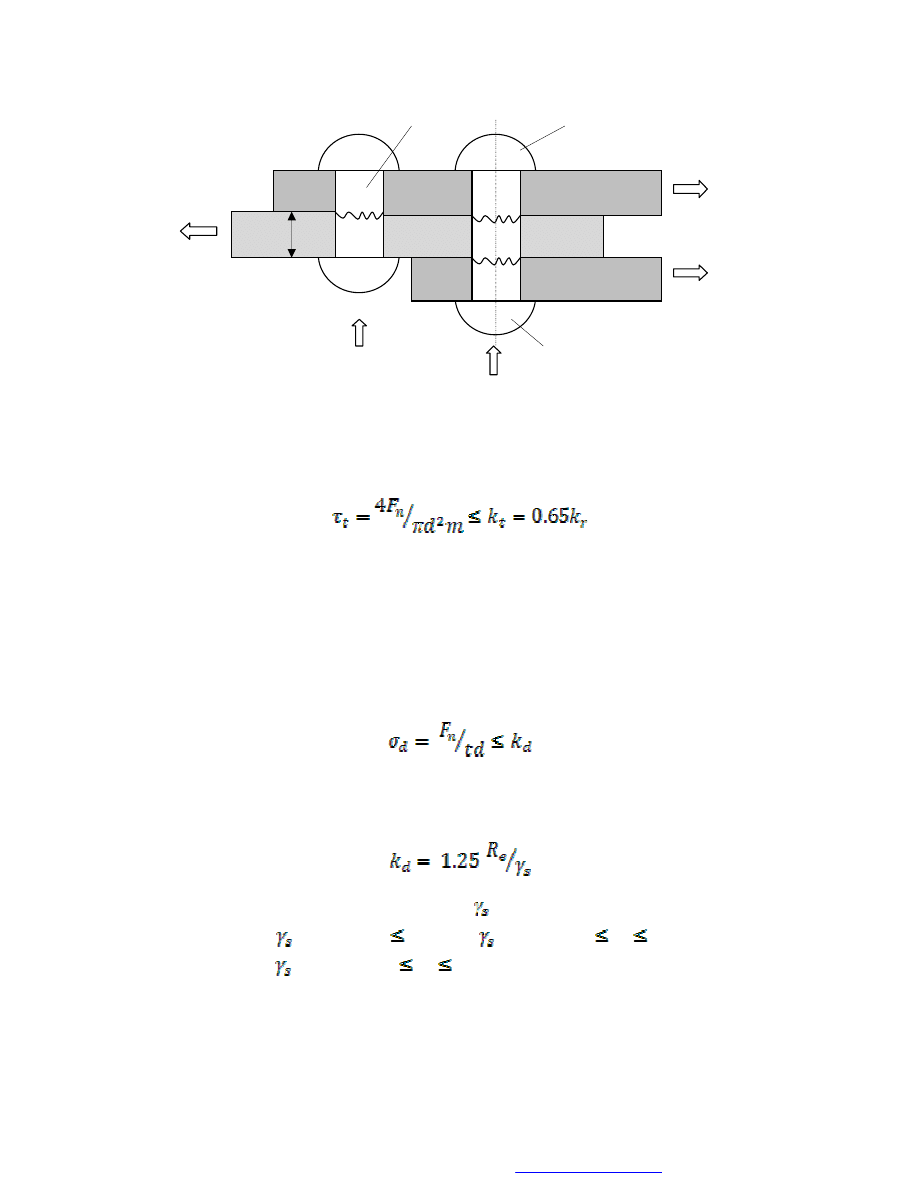
Warunek wytrzymałościowy, ze względu na ścinanie trzonu nitu, ma postać:

przy czym: F

n

– siła działająca na pojedynczy nit, d – średnica trzonu nitu,

m – liczba ścinanych przekrojów (m = 1 dla nitów jednociętych,

m = 2 dla nitów dwuciętych).

Ze względu na nacisk, obliczenia są prowadzone przy założeniu, że siła

dociskająca nit do ścianki otworu, działa na powierzchnię rzutu trzonu na płaszczyznę
prostopadłą do kierunku jej działania. Tak więc, warunek wytrzymałościowy ma
postać:

Należy zauważyć, że w przypadku różnej grubości łączonych elementów (blach)
nacisk należy obliczać dla t

min

. Wartość dopuszczalną nacisku k

d

przyjmuje się ze

wzoru:

w którym: R

e

– granica plastyczności,

- współczynnik zależny od wartości R

e

,

(

= 1.15 dla R

e

360 MPa,

= 1.2 dla 360 R

e

470 MPa,

= 1.25 dla 470 R

e

600 MPa).

Warunek wytrzymałości na rozciąganie łączonych blach w przekroju

osłabionym otworami na nity, w połączeniu zakładkowym, ma postać:

łeb

trzon

zakuwka

Nit jednocięty

Nit dwucięty

F

1

F

2

F

3

(15)

t

(16)

(17)

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

9

gdzie: n – liczba nitów o średnicy d, w skrajnym rzędzie

nitów (przekrój najbardziej narażony na rozerwanie),

F – siła działająca na złącze.

W przypadku złącza nakładkowego dwustronnego (rys. 10), warunek (18)

uwzględnia fakt, że najbardziej obciążonym rzędem nitów jest rząd w nakładce o
grubości t

n

, położony najbliżej środka złącza:

Rys. 10. Dwustronne złącze nakładkowe – niebezpieczny przekrój

Grubość nakładki powinna być tak dobrana, aby nośność łączonych blach była taka
sama jak nakładek, co w praktyce oznacza równość przekrojów blachy i obu nakładek
w przekrojach niebezpiecznych (pokazanych na powyższym rysunku):

Powyższa równość umożliwia wyznaczenie grubości nakładek. Poniżej pokazano
widok tzw. nitów zrywanych, umożliwiających łączenie blach przy dostępie z jednej
strony.

R

y

s

Rys. 11. Widok nitów zrywanych

(18)

(18a)

b

F

F

b

(19)

przekrój niebezpieczny w nakładce - n

n

nitów

przekrój niebezpieczny w blasze – n

b

nitów

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

10

1.3.

Obliczanie połączenia klinowego

Przykładem kształtowego połączenia, stosowanego w budowie maszyn, jest

połączenie klinowe poprzeczne pokazane na rys. 11. Klin o długości l, wysokości b i
szerokości a, umieszczony jest w rowku wykonanym w elementach łączonych, tj. tulei
i wale. Połączenie to umożliwia przekazanie momentu obrotowego M = PR z tulei na
wał. Klin jest ścinany w płaszczyźnie działania siły T, której wartość wynosi:

Pole powierzchni ścinanego przekroju wynosi A = al, a więc warunek
wytrzymałości połączenia określa wzór:

Rys. 12. Połączenie klinowe poprzeczne

1.3.

Obliczanie połączenia sworzniowego

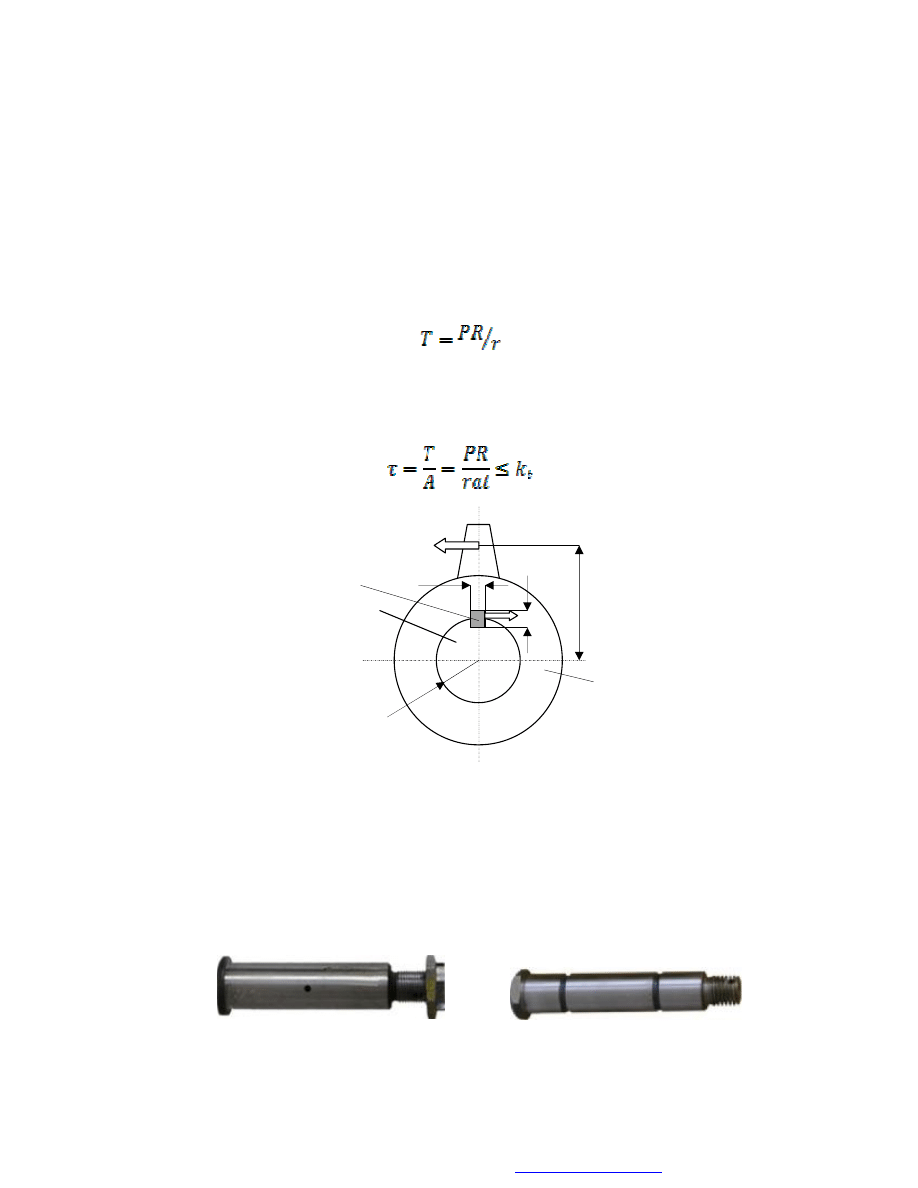
Połączenie sworzniowe jest stosowane wówczas, gdy należy zapewnić możliwość

obrotu łączonych elementów względem siebie – rys. 12. Sworzeń jest z reguły ciasno
osadzany w jednym z tych elementów lub pasowany obrotowo w obu elementach.
Konieczne jest wówczas zabezpieczenie sworznia przed wypadnięciem (np.
zawleczką).

Rys. 13. Widok przykładowych sworzni

(20)

tuleja

P

wał

R

b

a

klin

T

r

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

11

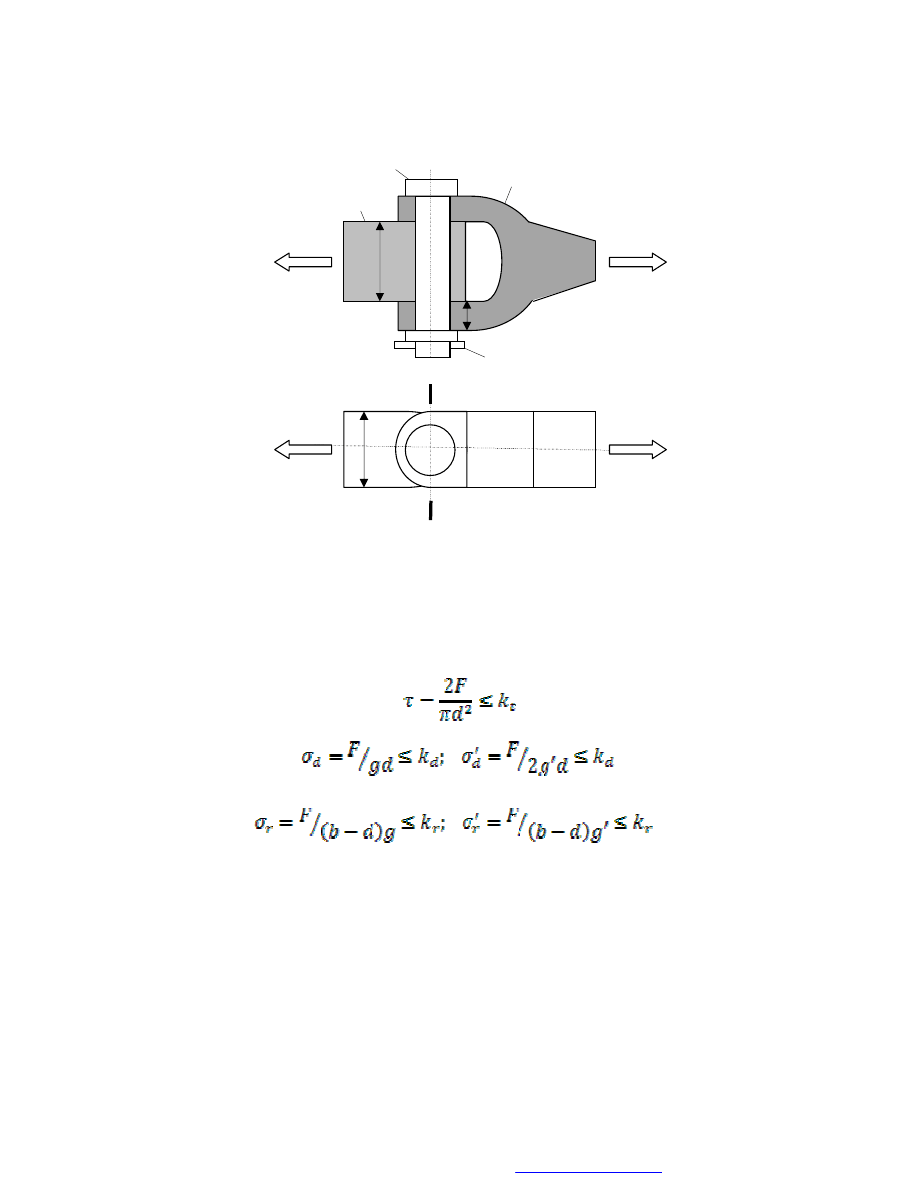
Rys. 14. Połączenie sworzniowe

Obliczenia wytrzymałościowe połączenia sworzniowego są analogiczne do
obliczeń połączenia nitowego. Sworzeń jest ścinany, a jego trzon wywiera nacisk na
ścianki otworów w uchu i wsporniku, ponadto może wystąpić zniszczenia ucha lub
wspornika w przekroju A-A. Tak więc, warunki wytrzymałościowe dla połączenia
pokazanego na rys. 12, mają postać:

Wzory (22) i (23) określają warunki wytrzymałościowe odpowiednio, dla
wspornika i dla ucha przy założeniu, że oba elementy mają tę samą szerokość b.

1.4.

Obliczanie połączeń śrubowych (gwintowych)

Połączenia śrubowe są zaliczane do grupy połączeń kształtowych lub cierno-

kształtowych. Wynika to ze specyfiki łącznika, który dzięki swojej konstrukcji
umożliwia uzyskanie tarcia w połączeniu, Tak więc, nie tylko kształt, ale również siły
tarcia generowane w połączeniu uczestniczą w przenoszeniu obciążeń zewnętrznych.

A

g

g’

b

A

sworzeń

zawleczka

ucho (np. drąga siłownika hydraulicznego)

wspornik

F

F

g

g’

b

(21)

(22)

(23)

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

12

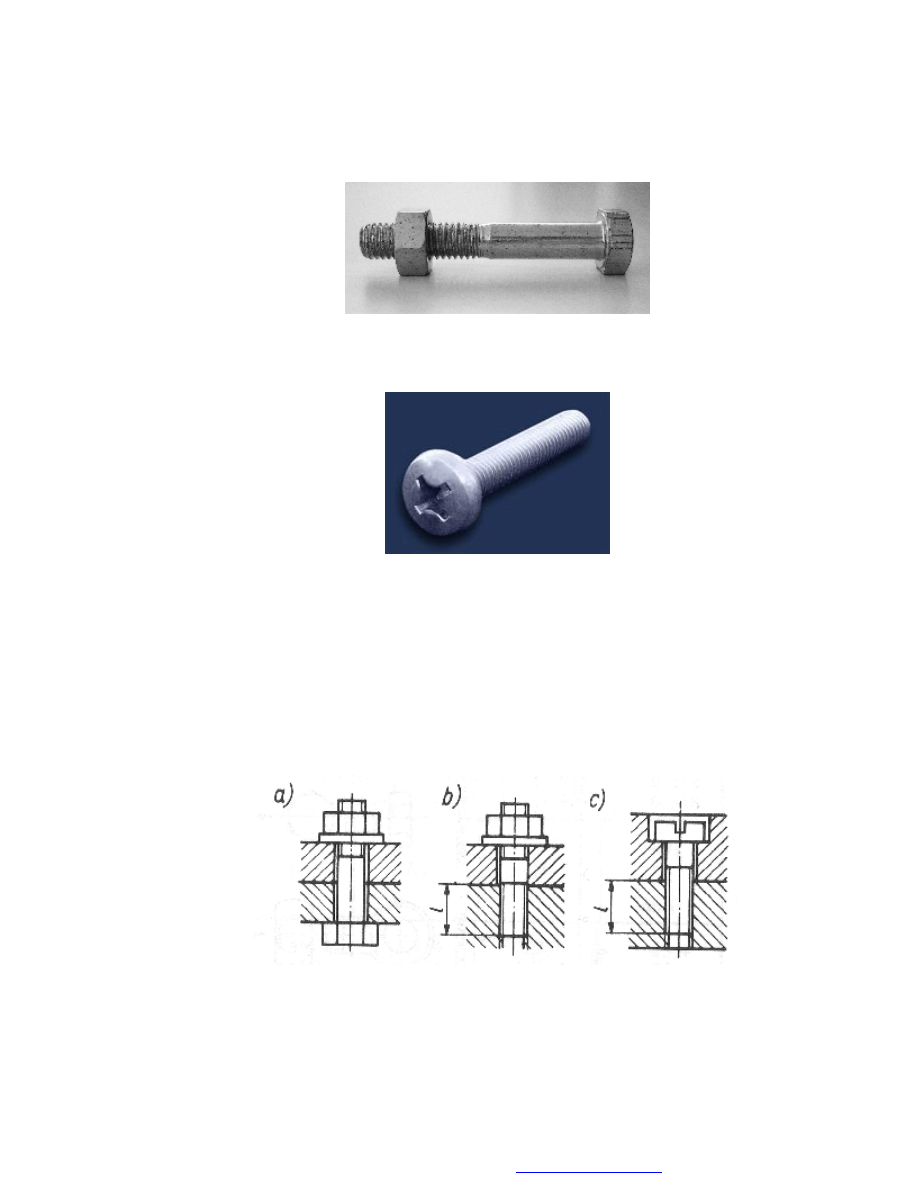
Łącznikami, w takich połączeniach są śruby i nakrętki (rys. 15) lub wkręty (rys. 16).
Elementami pomocniczymi są różnego typu podkładki, np. zabezpieczające przed
odkręcaniem się nakrętki, wyrównujące pochylenie ścianek kształtownika, itp.

Rys. 15. Widok śruby z łbem sześciokątnym i nakrętką

(z gwintem metrycznym)

Rys. 16. Widok wkrętu z łbem walcowym (nacięcie krzyżowe)

Typowe połączenia śrubowe pokazano na rys. 17 – są to: połączenie śrubą i

nakrętką z podkładką (rys. 17a), połączenie śrubą dwustronną (rys. 17) oraz
połączenie wkrętem (rys. 17c). Najczęściej stosowanym rodzajem gwintu jest tzw.
gwint metryczny walcowy, o zarysie trójkąta, o kącie wierzchołkowym wynoszącym
60° - rys. 18a,b. W ruchowych połączeniach śrubowych często stosowane są gwinty o
zarysie trapezowym (rys. 18c), a np. w opakowaniach z tworzyw sztucznych i szkła –
gwint okrągły (rys. 18d).

Rys. 17. Typowe połączenia śrubowe

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

13

Obliczenia wytrzymałościowe śrub (i wkrętów) ściśle wiążą się z obciążeniem

danego połączenia. Z zasady, dąży się do uzyskania osiowego obciążenia śruby oraz
uwzględnia obciążenie momentem skręcającym wywołanym dokręceniem nakrętki. W
przypadku, gdy powierzchnia przylgowa łba śruby lub nakrętki styka się z łączonym
elementem na niewielkiej powierzchni lub wręcz punktowo, należy dodatkowo
uwzględnić zginanie śruby. W praktyce, często w takiej sytuacji stosuje się specjalne
podkładki zapewniające likwidację przyczyny wystąpienia tego rodzaju obciążenia
śruby.

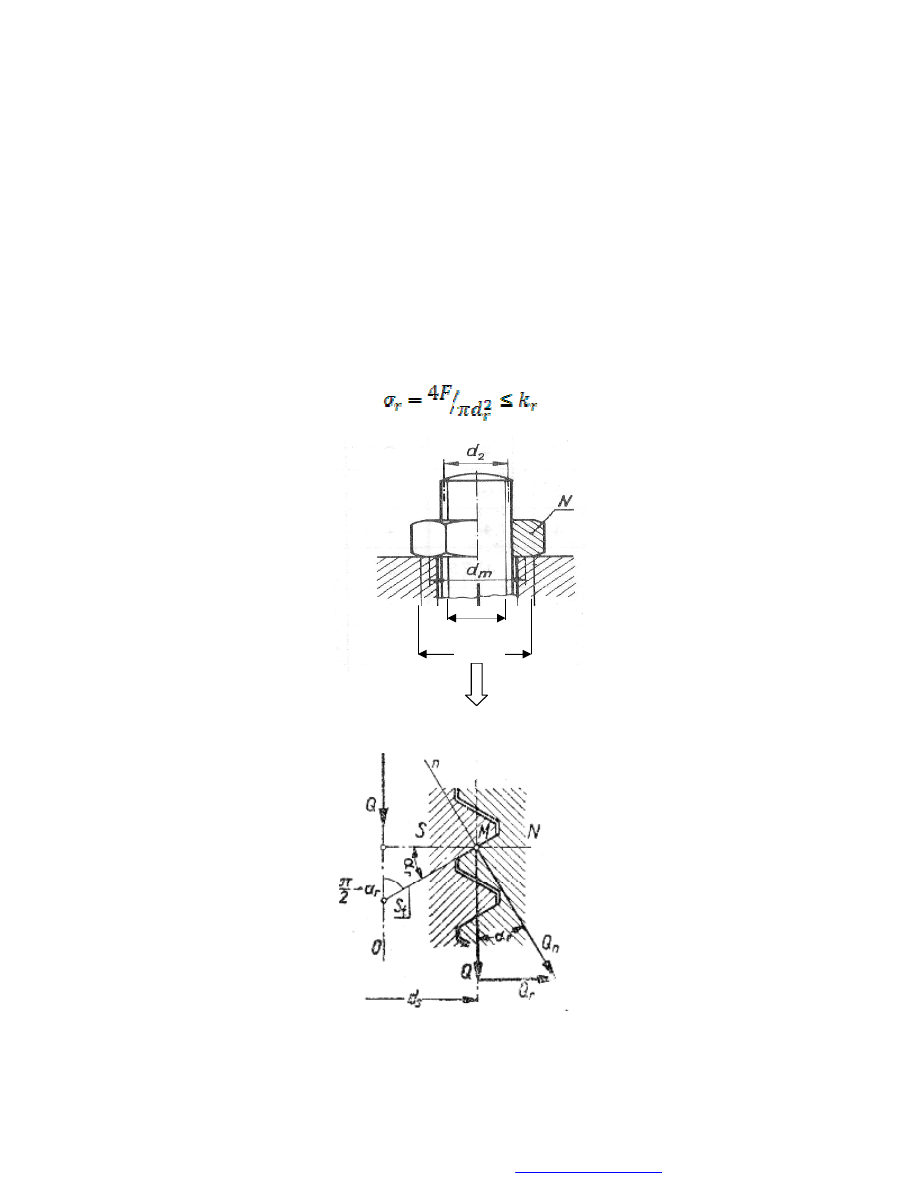
Najprostszym modelem obliczeniowym śruby (o średnicy zewnętrznej d),

obciążonej siłą osiową (np. rozciągającą) Q, pochodzącą od obciążenia zewnętrznego,
jest pręt o średnicy d

r

– rys. 19. Warunek wytrzymałościowy dla obciążenia

statycznego ma wówczas postać:

Rys. 19. Schemat obciążenia śruby siła osiową

Rys. 20. Rozkład sił na powierzchni zwoju gwintu

(24)

Rys.

d

r

Q

d

z

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

14

Uwzględniając kształt zarysu gwintu, zewnętrzne obciążenie śruby Q oddziałuje na

występ gwintu w punkcie określonym przez średnicę podziałową d

s

, siłą Q

n

– rys. 20.

Średnicę podziałową d

s

, w przypadku gwintu metrycznego o zarysie trójkątnym,

określa wzór:

w którym h jest wysokością trójkąta równobocznego o podstawie równoległej do osi
śruby.
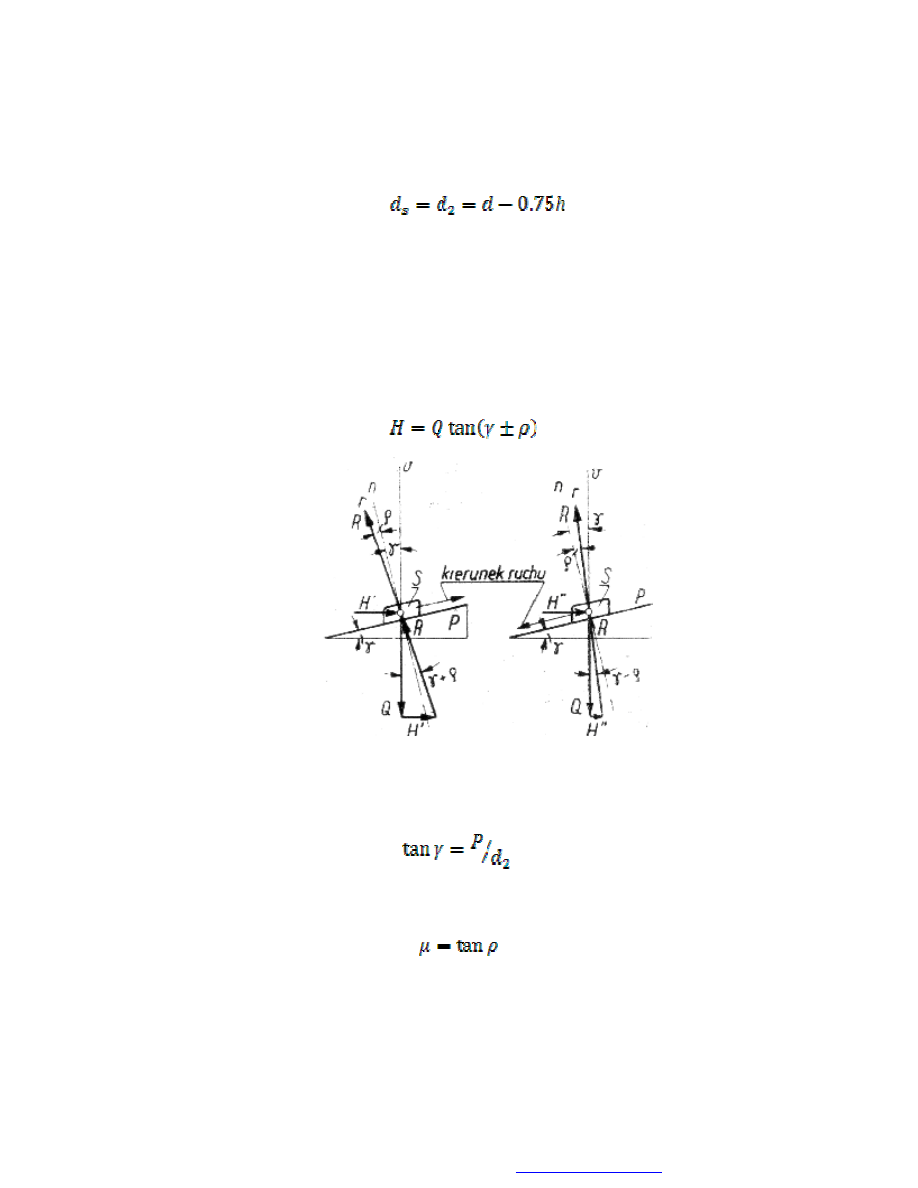
Na skutek tarcia, występującego między powierzchniami zwojów gwintu śruby i
nakrętki, pojawia się moment skręcający. Jeśli przyjąć, że element nakrętki
przemieszcza się względem śruby, jak na rys. 21, tj. po równi pochyłej o wzniosie
odpowiadającym wzniosowi linii śrubowej poprowadzonej przez wierzchołki
występów gwintu, to w zależności od kierunku ruchu, siła H (rys. 22) skręcająca
śrubę jest określona wzorem:

Rys. 22. Rozkład sił z uwzględnieniem tarcia

Kąt wzniosu linii śrubowej jest funkcją skoku gwintu P oraz średnicy podziałowej

d

2

:

natomiast kąt tarcia

ρ

jest funkcją współczynnika tarcia

µ

(przyjmuje się z reguły

µ

=

0.1÷0.2):

(25)

(26)

(27)

(28)

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

15

Ostatecznie, moment skręcający śrubę - wywołany tarciem między zwojami
gwintu śruby i nakrętki - wynosi:

Tak więc, naprężenie styczne wywołane skręcaniem, określa wzór:

Ze względu na złożony stan naprężenia (rozciąganie ze skręcaniem), warunek
wytrzymałościowy uwzględnia naprężenie zredukowane (wg hipotezy H-M-H):

Współczynnik zmienia się w przedziale 0.33÷0.41, dlatego wzór (31) można zapisać

w postaci:

Śruba jest także dodatkowo skręcana na skutek tarcia między nakrętką, a podłożem
(rys. 19). Ten moment skręcający jest wyrażony wzorem:

Tak więc, całkowity moment skręcający śrubę określa wzór:

Znak „+” dotyczy przypadku dokręcania nakrętki.
Współpraca występów gwintu śruby i nakrętki powoduje ich obciążenie o
charakterze powierzchniowym – rys. 23.

Rys. 23. Schemat obciążenia występów gwintu śruby obciążonej osiowo

(29)

(33)

(34)

(30)

(31)

(32)

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

16

Przyjmuje się, że rozkład nacisków jest równomierny i wynosi:

gdzie: n – liczba zwojów przenoszących obciążenie zewnętrzne, D

o

– średnica otworu

nakrętki.
Należy jednak podkreślić, że rzeczywisty rozkład nacisków ma charakter
nierównomierny – rys. 24.

Rys. 24. Charakter rozkładu nacisków: a) na pojedynczym występie,

b) wzdłuż wysokości nakrętki

(35)

a)

b)

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

17

2. Obliczanie sprężyn śrubowych

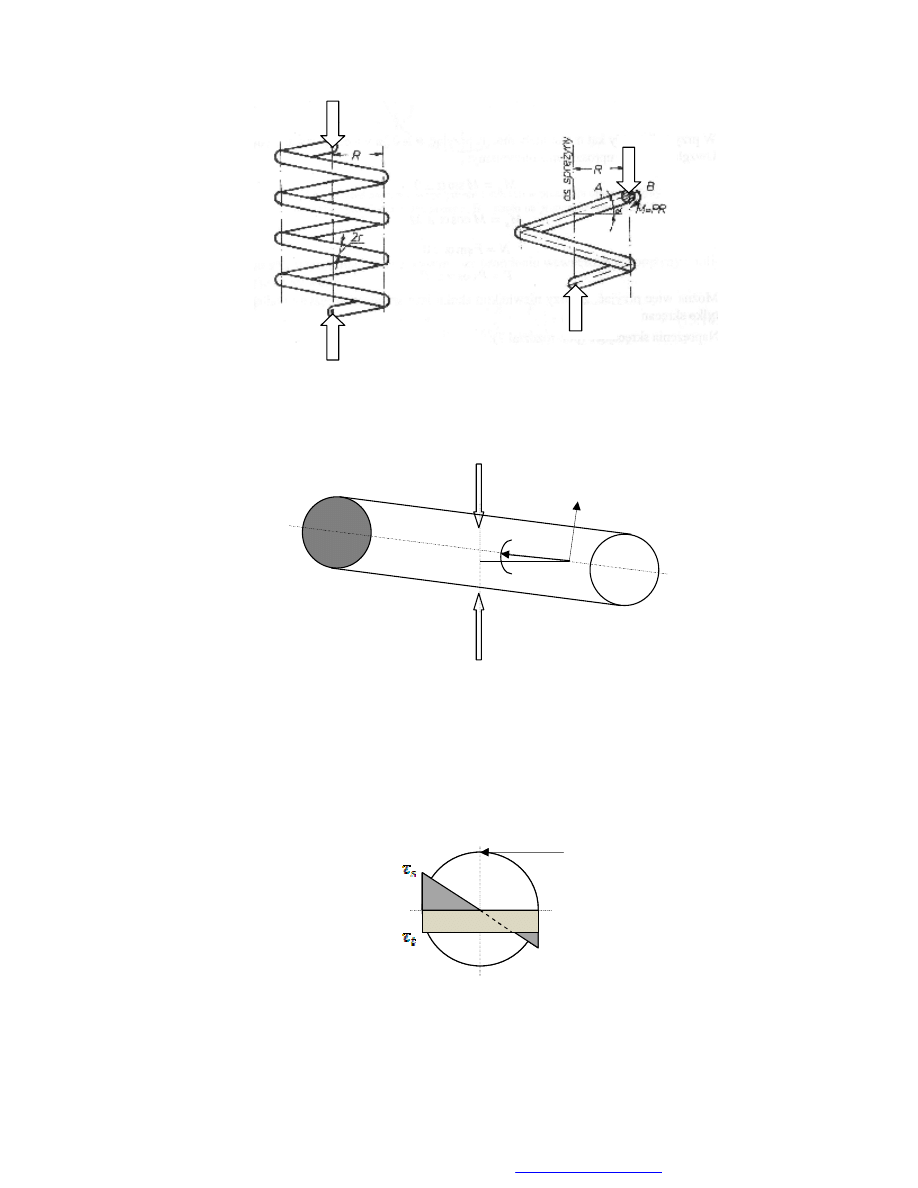
Typowym przykładem sprężyny śrubowej jest sprężyna walcowa zwinięta z drutu
o przekroju kołowym lub pryzmatycznym – rys. 25.

Rys. 25. Widok sprężyn walcowych

Pokazane powyżej sprężyny są tzw. sprężynami naciskowymi, w odróżnieniu od sprężyn

rozciąganych, zwanych naciągowymi – rys. 26.

Rys. 26. Widok sprężyn naciągowych

Z punktu widzenia wytrzymałości materiałów, zwoje sprężyny znajdują się w złożonym

stanie naprężenia. Rozpatrzmy sprężynę naciskową wykonaną z drutu o przekroju kołowym,
o średnicy d – rys. 27. Z zasady, siła obciążająca sprężynę powinna działać w jej osi, aby
zapobiec wyboczeniu.

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

18

Rys. 27. Schemat obciążenia sprężyny o średnicy 2R

W przekroju sprężyny działają następujące obciążenia: siła P oraz moment

wywołany przez tę siłę - M = PR. Ich składowe pokazano na rys. 28.

Rys. 28. Układ współrzędnych do wyznaczania obciążenia przekroju sprężyny

Moment M ma składowe: M

x

= PR sin α = M

g

(wywołujący zginanie) i M

y

=

PR cos α = M

s

(wywołujący skręcanie), natomiast siła P: P

x

= P sin α = N

(wywołująca ściskanie) oraz P

y

= P cos α = T (wywołująca ścinanie). Jeśli pochylenie

zwojów jest małe (α bliskie zeru), to w przekroju dominują naprężenia styczne od
skręcania i ścinania. Ich charakter pokazano na rys. 29.

Rys. 29. Rozkład naprężeń stycznych w przekroju sprężyny

P

P

P

P

P

y

P

x

α

P

2R

2R

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/

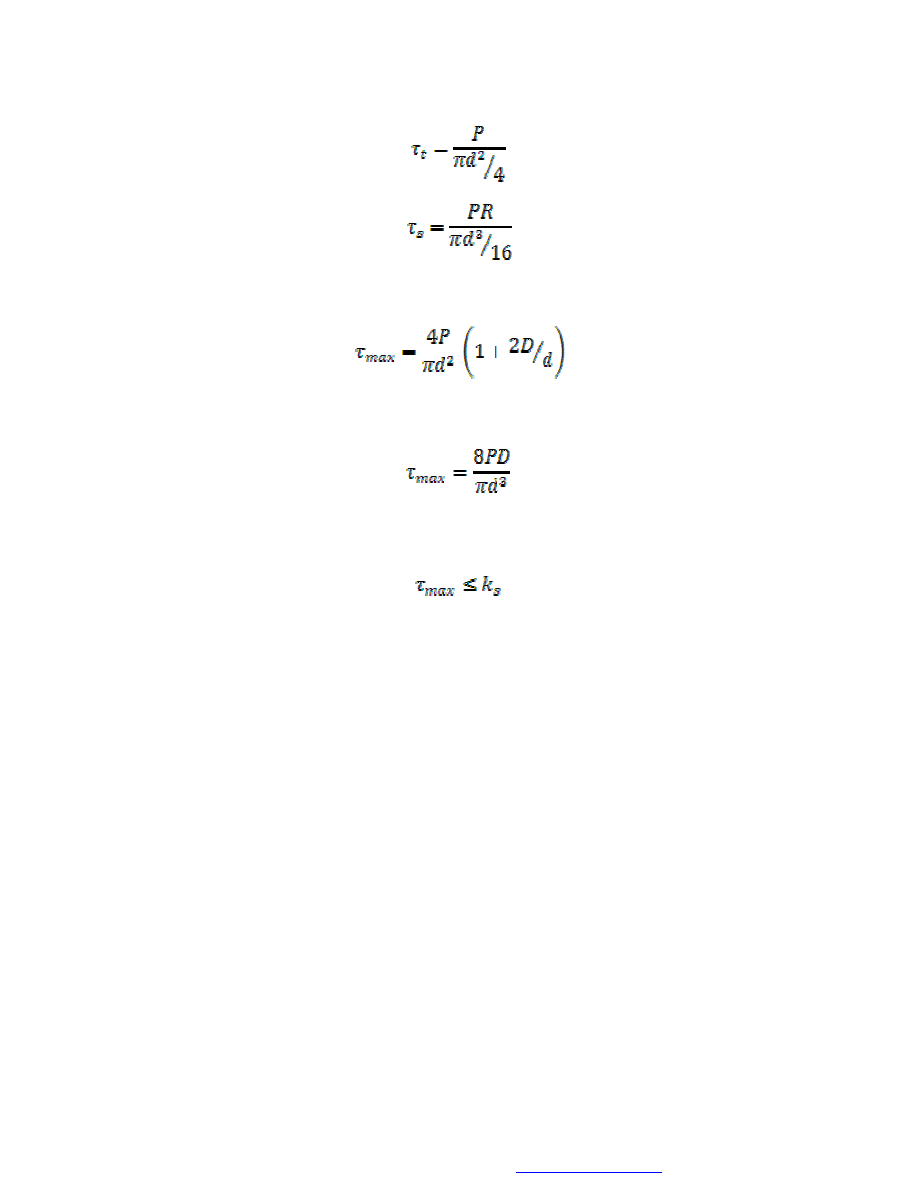
19

Składowe naprężenia styczne wynoszą:

Maksymalne naprężenia styczne występują na wewnętrznym promieniu sprężyny i
wynoszą:

Z kolei, przy D znacznie większym od d maleje wpływ naprężeń tnących, a więc
można je pominąć, a wzór (37) przybiera postać:

Oczywiście, obliczone wartości maksymalnych naprężeń stycznych nie mogą
przekraczać wartości dopuszczalnych k

s

:

Literatura

[1] Żuchowski R., Wytrzymałość materiałów, Oficyna Wydawnicza Politechniki
Wrocławskiej, Wrocław,1996.
[2] Podstawy konstrukcji maszyn, pod red. M.Dietricha, PWN, Warszawa, 1988.
[3] Mały Poradnik Mechanika, WNT, Warszawa, 1985.
[4] Poradnik konstruktora przyrządów precyzyjnych i drobnych, pod red. W.
Trylińskiego, WNT, Warszawa, 1971.
[5] Pyrak S., Szulborski K., Mechanika konstrukcji – przykłady obliczeń, Arkady,
Warszawa, 1998.
[6] Moszyński W., Wykład elementów maszyn, cz.1 Połączenia, Inst. Wyd. SIMP,
Warszawa, 1949.

(36)

(37)

(38)

(39)

PDF stworzony przez wersj

ę demonstracyjną pdfFactory Pro

www.pdffactory.pl/