Komputerowe wspomaganie doboru materiałów

Temat:

Modelowanie zależności między składem chemicznym stali i warunkami obróbki cieplnej

a granicą plastyczności Re (dane do obliczeń w pliku Re.xlsx)

Zadanie 1
Oblicz współczynniki regresji (X

0

, X

1

, X

2

, X

3

)

dla ogólnej postaci równania:

Re=X

0

+X

1

∙C+X

2

∙Mn+X

3

∙To

gdzie: C, Mn

– stężenia masowe odpowiednio: węgla i manganu, To – temperatura

odpuszczania

1. Uaktywnij dodatek Analysis ToolPak (Plik\opcje\dodatki\Analysis ToolPak)
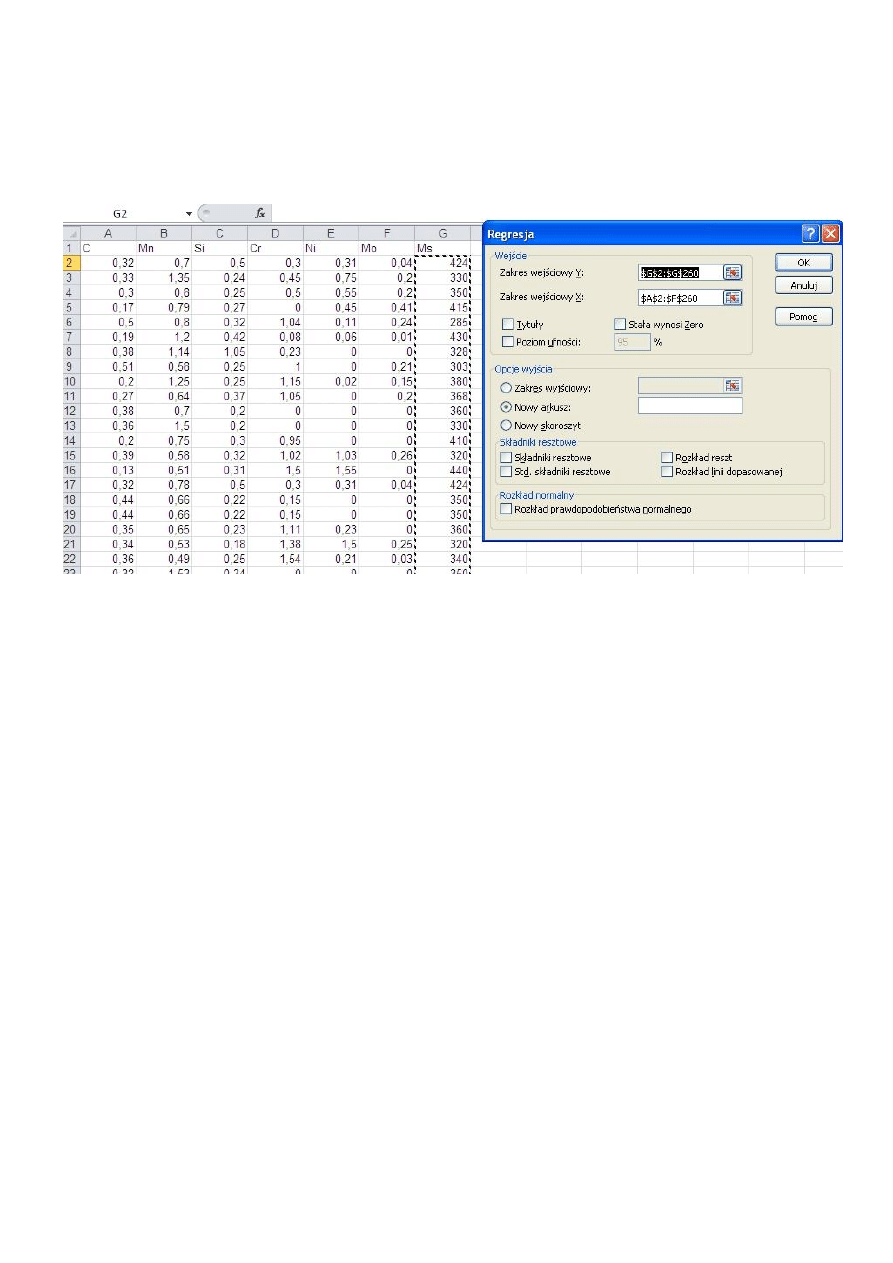
2. Uruchom polecenie Regresja (karta Dane, grupa Analiza, Analiza danych, Regresja)
3. Wybierz zakres danych: zakres wejściowy Y (kolumna Re); zakres wejściowy X (kolumny C,
Mn, To)
uwaga

: jeżeli zakres danych obejmuje wiersz z nazwami zmiennych w oknie Regresja należy

zaznaczyć opcje Tytuły. Obliczone współczynniki (X

0

, X

1

, X

2

, X

3

) zostaną wyświetlone w nowym

arkuszu
4. Oblicz wartość Re dla każdego wiersza danych (wykorzystaj opracowany wzór)
5. Oblicz wartość błędu dla każdego przypadku (wykorzystaj funkcję: moduł liczby() )
6. Oblicz statystyki

: średni błąd bezwzględny, odchylenie standardowe błędu, współczynnik

korelacji

między doświadczalnymi i obliczonymi wartościami Re.

(wykorzystaj funkcje wbudowane arkusza kalkulacyjnego)
7. Określ zakres stosowania opracowanego równania
uwaga:

oblicz wartość minimalną i maksymalną dla każdej zmiennej niezależnej (C, Mn, To)

Zadanie 2
Oblicz współczynniki regresji (X

0

, X

1

, X

2

, X

3

, X

4

) dla ogólnej postaci równania:

Re=X

0

+X

1

∙C+X

2

∙Mn+X

3

∙C∙Mn+X

4

∙To

Obliczenia wykonaj w nowym arkuszu analogicznie jak w zadaniu 1.
uwaga: przed uruchomieniem polecenia R

egresja należy przygotować arkusz danych.

(

wstaw pustą kolumnę między kolumnami Mn i To, a następnie oblicz wartości iloczynu stężeń

węgla i manganu.)

Zadanie 3.
Porównaj równania z zadania 1 i 2. Wybierz równanie, które umożliwia obliczenie wartości Re z
mniejszym błędem. Uzasadnij wybór.

Zadanie 4.
Oblicz

wartość Re:

a) C=0,15%; Mn=1,45%, To=600

°C b) C=0,13%; Mn=0,6%, To=500°C

Zadanie 5.
Oblicz

trzy składy chemiczne stali (stężenia węgla i manganu) oraz temperaturę odpuszczania,

dla

których granica plastyczności Re wynosi 400 MPa

Zadanie 6.
Oblicz składy chemiczne stali i temperaturę odpuszczania, dla których granica plastyczności
przyjmuje wartość maksymalną i minimalną.

Zadanie 7.
Wykonaj wykres prze

dstawiający wpływ węgla na granicę plastyczności Re przy założonych

(stałych) wartościach pozostałych zmiennych.

Uaktywnienie dodatku: Plik\opcje\dodatki\Analysis ToolPak

Uruchamianie dodatku: karta Dane, grupa Analiza, Analiza danych, Regresja

Reszta

– różnica między wartością empiryczną (doświadczalną) zmiennej zależnej

(objaśnianej) a wartością teoretyczną (obliczoną z równania regresji)
Metoda najmniejszy

ch kwadratów poszukiwanie takich wartości współczynników regresji X

0

,

X

1

, X

2

, przy których suma kwadratów reszt osiąga minimum

Statystyki regresji:
Wielokrotność R – współczynnik korelacji
R kwadrat

– współczynnik determinacji r

2

= SSR/SST; informuje, jaka część zmienności

zmiennej objaśnianej została wyjaśniona przez model.
Dopasowany R kwadrat-
Błąd standardowy - standardowy błąd reszt (pierwiastek kwadratowy z MSE)
Obserwacje

– liczba obserwacji w badaniu

Analiza wariancji
df (degree of freedom)

– liczba stopni swobody – liczba niezależnych wyników obserwacji

pomniejszona o liczbę związków, które łączą wyniki ze sobą
SS

– (Sum of Squares) – suma kwadratów - reszt (SSE); regresji (SSR); razem (SST)

MS

– (wartość średnia kwadratów) - reszt (MSE); regresji (MSR)

F

– wartość statystyki F służącej do weryfikacji hipotezy o łącznej istotności zmiennych

objaśniających F=MSR/MSE
Istotność F ( mniejsza od 0,05 – zmienne istotne na poziomie istotności 5%)

Współczynniki – wartości współczynników regresji równania X

0

, X

1

, X

2

…

Błąd standardowy – średni błąd oceny dla współczynnika regresji B

X0

, B

X1

, B

X2

….

tStat

– wartość testu t-Studenta służąca do badania istotności współczynników regresji

t

X1=

X

1

/B

X1

Wartość-p – prawdopodobieństwo zdarzenia, że statystyka t

X

znajdzie się w przedziale ufności

(np. wartość mniejsza od 0,05 informuje, że parametr X jest istotny, a niepewność wynosi 5%)