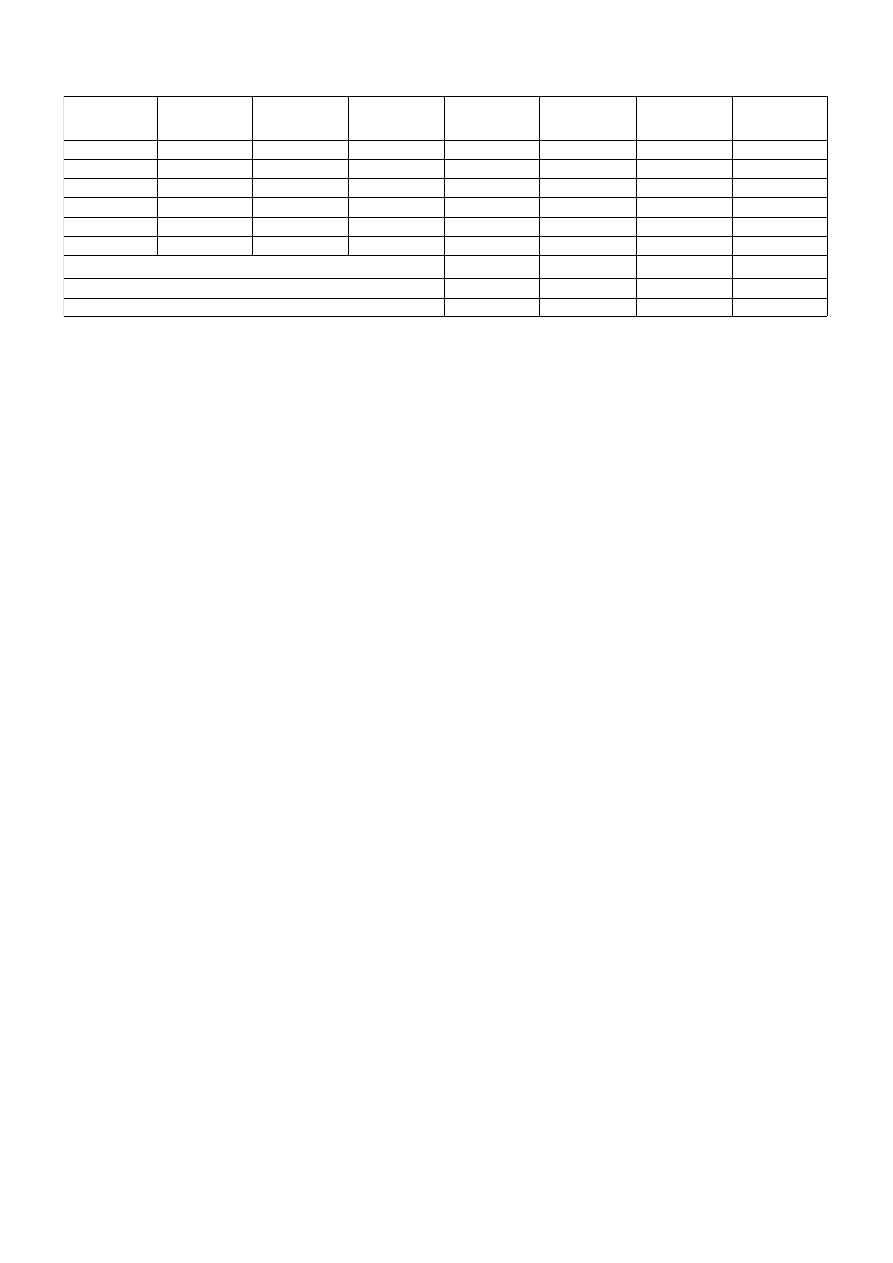
Współczynnika podziału Nernsta K

c 

jest wielkością charakterystyczną dla danego układu dwóch 

cieczy i składnika rozdzielającego się między te ciecze.
Współczynnika podziału Nernsta K

c

 w stałej temperaturze przyjmuję wartość stałą, jest to stosunek 

stężeń substancji rozpuszczonej w obu fazach ciekłych.  W fazie wodnej substancja rozpuszczona 
ulega dysocjacji, w organicznej asocjacji. Wartość współczynnika podziału wskazuję, w jakim 
stopniu dana substancja dzieli się (rozpuszcza się w cieczach) między dwie ciecze. Różnice 
rozpuszczalności wykorzystuję się w ekstrakcji  do rozdziału mieszanin wieloskładnikowych.
Opracowanie wyników:
1. Stężenie kwasu octowego przed podziałem C

i

 i po podziale 



i

C  w warstwie wodnej:

C

i

 =(C

z

*V

z 

)/V

k



i

C  =(C

z

*V

z 

)/V

k

V

k

- objętość roztworu kwasu octowego pobrana do miareczkowania

C

z

 – stężenie zasady sodowej  0,1 mol/dm

3

V

z

- objętość roztworu zasady sodowej zużyta do miareczkowania

2. Stężenie kwasu octowego w warstwie chloroformowej 



i

C :



i

C =C

i

-



i

C

3.  Stopień dysocjacji kwasu octowego

i

  w warstwie wodnej dla poszczególnych stężeń:

i

 =0,003565-0,002812



i

C

4.  Wykres zależności liniowej 
lg[



i

C (1-

i

 )]=f (lg



i

C )wyprowadzony ze zlogarytmowanej postaci równania

lg[



i

C (1-

i

 )]=lgK

c

 +1/n lg



i

C

Wnioski;
Znajomość współczynników podziału substancji pomiędzy nie mieszające się fazy ciekłe ma 
ogromne znaczenie w ekstrakcji.
Celem ćwiczenia było wyznaczenie współczynnika podziału kwasu octowego pomiędzy wodę i 
chloroform K

c

 oraz stałej n. woda dużo lepiej rozpuszcza kwas octowy niż chloroform podczas 

rozdzielania kwasu pomiędzy te dwie ciecze. Stwierdzam także, że kwas octowy występuje w 
warstwie organicznej pod postacią cząsteczek asocjowanych, gdyż n>1 (n = 2,598).

0,34

0,53

-0,189

0,005357

0,9946

0,5259

-0,2791

0,55

0,50

0,048

0,005528

0,9945

0,4947

-0,3056

-1,323

0,66

0,58

0,073

0,005085

0,9949

0,5795

-0,2369

-1,140

0,80

0,69

0,115

0,004629

0,9954

0,6818

-0,1663

-0,939

0,87

0,78

0,085

0,004264

0,9957

0,7767

-0,1098

-1,071

1,09

0,96

0,130

0,003680

0,9963

0,9565

-0,0193

-0,886

Stałe równanie Nernsta

1/n

n

Metoda graficzna

0,3850

2,598

0,1288

1,345

Metoda najmniejszych kwadratów

0,3850

2,598

0,1288

1,345

c

i

 [mol/dm

3

]

C

i

α    

 

[mol/dm

3

]

c

i

β

 [mol/dm

3

]

α

i

1-α

c

i

α

(1-α) 

[mol/dm

3

]

lg[c

i

α

(1-α)]

lgc

i

β 

lgK

c

K

c