L6.1 Systemy liczenia stosowane 

w informatyce

opracowała mgr Anna Śliwińska

Projekt współfinansowany przez

Unię Europejską w ramach

Europejskiego Funduszu Społecznego

Publikacja jest dystrybuowana bezpłatnie

Program Operacyjny Kapitał Ludzki – Priorytet 9 – Działanie 9.1 – Poddziałanie 9.1.2

System pozycyjny 



To sposób zapisywania liczb znany od 
wczesnego średniowiecza polegający na 
używaniu cyfr 

c

n

….c

3

, c

2

, c

1

,c

0 

które zapisane obok siebie interpretuje 
się jako sumę iloczynów tych liczb i potęg 
liczby naturalnej n, nazywanej podstawą 
systemu, o wykładnikach równych 
numerowi pozycji cyfry w ciągu: 

Rodzaje systemów stosowanych

w informatyce

Powszechnie używamy systemu dziesiętnego 

w informatyce zaś stosuje się zamiennie 
systemy:



Dwójkowy (binarny) np.: liczba 1011100



Ósemkowy (oktalny)np.:  567201



Szesnastkowy (heksadecymalny) np.: 115C

Jest to spowodowane tym, iż w komputerach 

łatwo uzyskać dwa różne stany fizyczne (impuls 
lub brak impulsu).

System dziesiętny

System dziesiętny jest systemem pozycyjnym, 

co oznacza, że wartość liczby zależy od 

pozycji na której się ona znajduje np. w 

liczbie 333 każda cyfra oznacza inną wartość 

bowiem:

333= 3*100+3*10+3*1

każdą z cyfr mnożymy przez tzw. wagę pozycji,

która jest kolejną potęgą liczby 10 będącej 

podstawą systemu liczenia co możemy 

zapisać jako:

333

(10)

=3*10

2

+ 3*10

1

+ 3*10

0

Można stworzyć dowolny pozycyjny system 

liczenia o podstawie np. 2, 3, 4, 7, 8, 16.

W technice komputerowej praktyczne 

zastosowanie znalazły systemy:



o podstawie 2  - tzw. system binarny 

(dwójkowy) używany do przechowywania 

i przetwarzania danych przez układy 

elektroniczne komputera



o podstawie 16  - tzw. system 

heksadecymalny  (szesnastkowy), używany 

głównie do prezentacji niektórych 

danych 

m.in. adresów komórek pamięci 

System binarny

Liczbę w systemie binarnym możemy więc 

przedstawić jako:

10111

(2)

= 1*2

4

+0*2

3

+1*2

2

+1*2

1

+1*2

0

Każdą z cyfr mnożymy przez kolejną potęgę liczby 2

będącej podstawą systemu liczenia w 

systemie binarnym  otrzymany wynik jest 

liczbą dziesiętna odpowiadającą podanej.

10111

(2)

= 23

(10)

System szesnastkowy

Analogicznie do systemu dziesiętnego czy binarnego liczbę 

w systemie szesnastkowym (o podstawie 16) możemy  

przedstawić jako:

2541

(16)

=  2*16

3

+  5*16

2

+  4*16

1 

+  1*16

0

natomiast cyframi mogą być liczby:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11,12,13,14,15

A B C  D  E F

aby zapis liczby był jednoznaczny,  tzn. każdej pozycji powinna 

odpowiadać tylko 1 cyfra cyfry od 10 do 15 zastąpiono 

w zapisie literami:  A, B, C, D,  E,  F.

Od systemu do systemu



Posługiwanie się różnymi systemami 

liczenia  wymaga umiejętności nie tylko 

przedstawiania  liczb w różnych 

systemach ale również konwersji  

(zamiany) liczby przedstawionej 

w  jednym systemie na liczbę w innym 

systemie.  



Najwygodniej jest to powierzyć 

komputerowi ale  należy poznać zasady 

takiej zamiany  

Zamiana liczby dziesiętnej

na dwójkową

Podstawowy sposób polega na 

kolejnym dzieleniu liczby dziesiętnej 

przez 2. 

Jeśli nie ma reszty to wpisujemy 0 

a jak jest reszta to 1. 

Liczbę zapisujemy od najstarszego do 

najmłodszego bitu więc:
69

(10)

= 1000101

(2)

Każdą pozycję liczby binarnej nazywamy bitem (binary digit)  
i jest to  najmniejsza jednostka ilości informacji

69

1     najmłodszy

34

0

17

1

8

0

4

0

2

0

1

1

najstarszy

Zamiana liczby binarnej 
na dziesiętną

Przypomnijmy, że aby obliczyć dziesiętną 

wartość liczby binarnej mnożymy cyfrę 
stojącą na każdej pozycji przez jej wagę, 
czyli kolejną potęgę liczby  2 będącej 
podstawą systemu

1000101 

(2)

=1*2

6

+ 0*2

5

+ +0*2

4

+0*2

3 

+ 1*2

2   

+ 0*2

1 

+ 1*2

0 

=

=64+0+0+0+4+0+1=69

Zamiana liczby binarnej 
na heksadecymalną

Liczba dziesiętna 69 to binarnie: 1000101

Algorytm zamiany liczby binarnej na heksadecymalną 

jest następujący:  

dzielimy liczbę binarną na tzw. kęsy 

o długości 4 bity

(licząc od ostatniej pozycji) czyli:

100  0101

Dla każdego kęsa znajdujemy wartość dziesiętną

i zapisujemy ją w postaci heksadecymalnej

binarnie

100  0101

dziesiętnie 

4

5

heksadecymalnie

45

tak więc: 45

(16)

=4*16

1

+ 5*16

0

=64+5= 69

Kod ASCII

Do przechowywania i przetwarzania danych przez układy 

elektroniczne komputera używany jest system binarny. 

Tekst wprowadzany do komputera za pomocą klawiatury należy 

przedstawić jednoznacznie  tzn. przyporządkować  literom 

i innym znakom alfanumerycznym - liczby (numery). 

W 1965 r. powstał w kod 

ASCII

używany przez wszystkich 

użytkowników i twórców oprogramowania.

Jest to kod 7 bitowy, a więc możemy za jego pomocą 

przedstawić 2

7

czyli 128 znaków. 

W 1981 r. IBM wprowadził rozszerzony do 8 bitów kod, 

co pozwala  na przedstawienie 256 znaków

(w tym znaki specjalne,  graficzne,  matematyczne 

i diakrytyczne znaki narodowe)

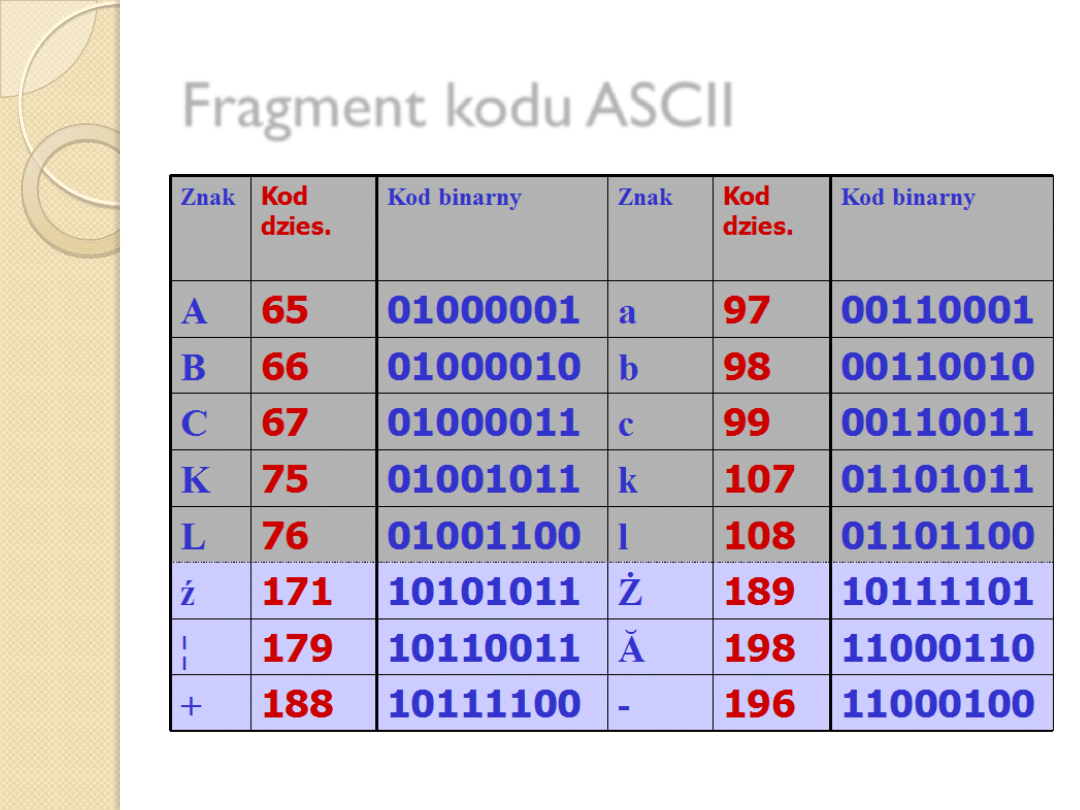
Fragment kodu ASCII

A

l

a

65

108

97

1000001        1101100            1100001

Piszemy Ala w systemie dwójkowym

dziesiętnie

binarnie

Bibliografia



Zdzisław Płoski „Słownik encyklopedyczny 
Informatyka, komputer i Internet”  
Wydanie III Wyd. Europa Wrocław 2002



http://fizar.pu.kielce.pl/fizyka/utk/prezentac
je/systlicz.ppt



http://www.programuj.com/artykuly/rozne
/sysliczb.php