Zespół Szkół Samochodowych im. inż. Tadeusza Tańskiego w Poznaniu
Opracował:	mgr inż. Mirosław Pietrasz
Temat:	Binarny system liczenia, standard TTL

1. Binarny system liczenia

Już nasi praprzodkowie musieli zwrócić uwagę na liczbę dwa: mamy dwie ręce, dwie nogi, dwoje oczu - to mogło być podstawą systemu dwójkowego zwanym też binarnym.

Postęp binarny (kolejne potęgi liczby dwa: 1, 2, 4, 8, 16, ...) znany był w Egipcie, a Egipcjanie wiedzieli, że dwa znaki wystarczą do zapisu dowolnej liczby.

Elementami zbioru znaków systemu binarnego jest para cyfr: 0 i 1. Znak dwójkowy (0 lub 1) nazywany jest bitem. Liczby naturalne w systemie dwójkowym zapisujemy analogicznie jak w systemie dziesiętnym - jedynie zamiast kolejnych potęg liczby dziesięć, stosujemy kolejne potęgi liczby dwa.

Na n bitach można zapisać w naturalnym kodzie binarnym liczby z przedziału: (0, 2n - 1).

2. Standard TTL

Transistor-transistor logic (TTL) to klasa cyfrowych układów scalonych.
Zapoczątkowana przez Texas Instruments w 1961 w rodzinie 7400 TTL była pierwszą techniką masowej produkcji układów scalonych, i nadal jest w szerokim użyciu.
Układy TTL zbudowane są z tranzystorów bipolarnych i zasila się je napięciem stałym 5 V. Działają w logice dodatniej - sygnał TTL jest niski (logiczne "0"), gdy potencjał ma wartość od 0 V do 0,8 V w odniesieniu do masy, wysoki (logiczna "1") przy wartości potencjału między 2 V a 5 V.

Wyróżnia się kilka odmian oznaczonych odpowiednio literami:

• L (Low power) - wersja o małym poborze mocy (10 razy mniejszy niż TTL), ale wolniejsza od standardowej (10 MHz); nigdy nie zyskała popularności, gdyż została niemal natychmiast zastąpiona układami CMOS serii 4000.

• H (High speed) - wersja szybsza od standardowej (58 MHz), ale o większym poborze mocy niż standardowa. Większą szybkość uzyskano przez zastosowanie 2x mniejszych rezystorów, co spowodowało szybsze przełączanie tranzystorów.

• S (Schottky) - odmiana szybka (125 MHz), której tranzystory zawierają dodatkową diodę Schottky'ego włączoną równolegle do złącza kolektor-baza i zabezpieczającą tranzystor przed nasyceniem co powoduje dużo szybsze przechodzenie tranzystora ze stanu przewodzenia do zatkania.

• AS (Advanced Schottky) - ulepszona seria S, charakteryzuje się jeszcze większą szybkością działania.

• LS (Low power Schottky) - wersja S o znacznie niższym poborze prądu (40 MHz), zbliżonym do standardowej bramki; główna seria układów TTL, stosowana w większości zastosowań.

• ALS (Advanced Low power Schottky) - unowocześniona seria LS, z mniejszym poborem mocy.

• F (Fast) - nowoczesna, najszybsza seria TTL (125 MHz).

Ponadto są produkowane układy w technologii CMOS, zgodne końcówkowo z TTL o takich samych oznaczeniach, wyróżniane literami C, AC, HCT, HC itp., np. 74HC00.
Dodatkowo układy CMOS HCT mają takie same poziomy stanów logicznych jak TTL, przez co można je łączyć ze sobą.TTL ma większy pobór prądu niż układy wykonane w technologii CMOS, ale układy tego typu są szybsze.
W technice TTL buduje się - oprócz standardowych układów logicznych - także układy z tzw. otwartym kolektorem na wyjściu (OC). Dzięki temu można realizować "sumę na drucie" (wired OR), obecnie już rzadko stosowany, kiedyś służył do podłączania urządzeń do magistrali albo do podłączania odbiorników większej mocy (np. diod świecących, a nawet żarówek) bezpośrednio do wyjścia bramki.

3. Podstawowe funkcje logiczne

Funkcję, której zmienne lub ona sama przyjmuje wartości ze zbioru {0, 1} nazywamy funkcją boolowską (logiczną, przełączającą). Natomiast układ przetwarzający logiczne sygnały wejściowe na logiczne sygnały wyjściowe nazywa się układem logicznym.

Przy projektowaniu dwustanowych (0 - stan niski, 1 - stan wysoki) układów cyfrowych posługujemy się algebrą Boole'a.

Algebra Boole'a, którą stosujemy w układach, opiera się na trzech zasadniczych funkcjach, którymi są:

• Iloczyn logiczny I (ang. AND), Y = A · B

• Suma logiczna LUB (ang. OR), Y = A + B

• Negacja (inwersja) NIE (ang. NOT),
  

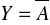
Stosowane są również operatory złożone (pochodne), jak:

• Suma zanegowana:
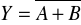
  NOR

• Iloczyn zanegowany:
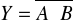
  NAND

• Równoważność:
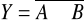
  EX-NOR

• Nierównoważność, zwana sumą modulo 2:
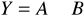
  EOR, XOR

Jedną z postaci algebry Boole'a jest znany rachunek zdań, gdzie zamiast znaków sumy + stosuje się łącznik lub, zamiast znaku iloczynu - łącznik i, a do negacji używamy słowa nie. Algebra Boole'a posługuje się szeregiem praw i tożsamości.

Bibliografia:

1. http://pl.wikipedia.org/wiki/Transistor-transistor_logic

2. http://home.agh.edu.pl/~kca/R4_Uklady_cyfrowe.doc

3. http://www.math.edu.pl/system-binarny

D:\Fronter\EiEWPS\MATERIAŁY DYDAKTYCZNE\Klasa 3 TS\Dział 01 - PODSTAWOWE UKŁADY ELEKTRONICZNE\Materiały\09a_podstawowe funkcje logiczne.doc

1

---