2. Błędy losowe

Definicja gęstości prawdopodobieństwa zmiennej losowej X. Wzory na wyznaczenie wartości

średniej, wariancji i odchylenia standardowego.

1.Gęstość prawdopodobieństwa – nieujemna funkcja p(x) ciągłej zmiennej losowej X taka, że:

( ) 1

p x









oraz prawdopodobieństwo, że zmienna losowa X należy do przedziału

( , )

a b

dane jest

wzorem:

(

)

( )

b

a

P a

X

b

f x dx









2. Wyznaczenie wartości oczekiwanej (średniej) oraz wariancji i odchylenia standardowego

a) dla dyskretnej zmiennej losowej

1

n

i

i

i

x p











,



-wartość średnia ,

i

x

-wartość zmiennej losowej,

i

p

-wartość prawdopodobieństwa

2

2

1

(

)

n

i

i

i

p x













,



-wariancja

2



- odchylenie standardowe – pierwiastek kwadratowy z wariancji

b) dla ciągłej zmiennej losowej

( )

x p x dx













2

2

( ) (

)

p x

x

dx

















2



- odchylenie standardowe – pierwiastek kwadratowy z wariancji

Wyznaczenie średniej wartości dla rozkładu jednostajnego w zadanym przedziale

[ , ]

a b

. Przykład.

( ) 1

p x









1

( )

;

[ , ]

0;

( , )

p x

x

a b

b a

x

a b


















( )

x p x dx













=

1

b

a

x

dx

b a







=

1

b

a

x dx

b a









=

2

1

1

2

b

x

a

b a









2

2

1

2

2

b

a

b a

b a











=>

2

b

a







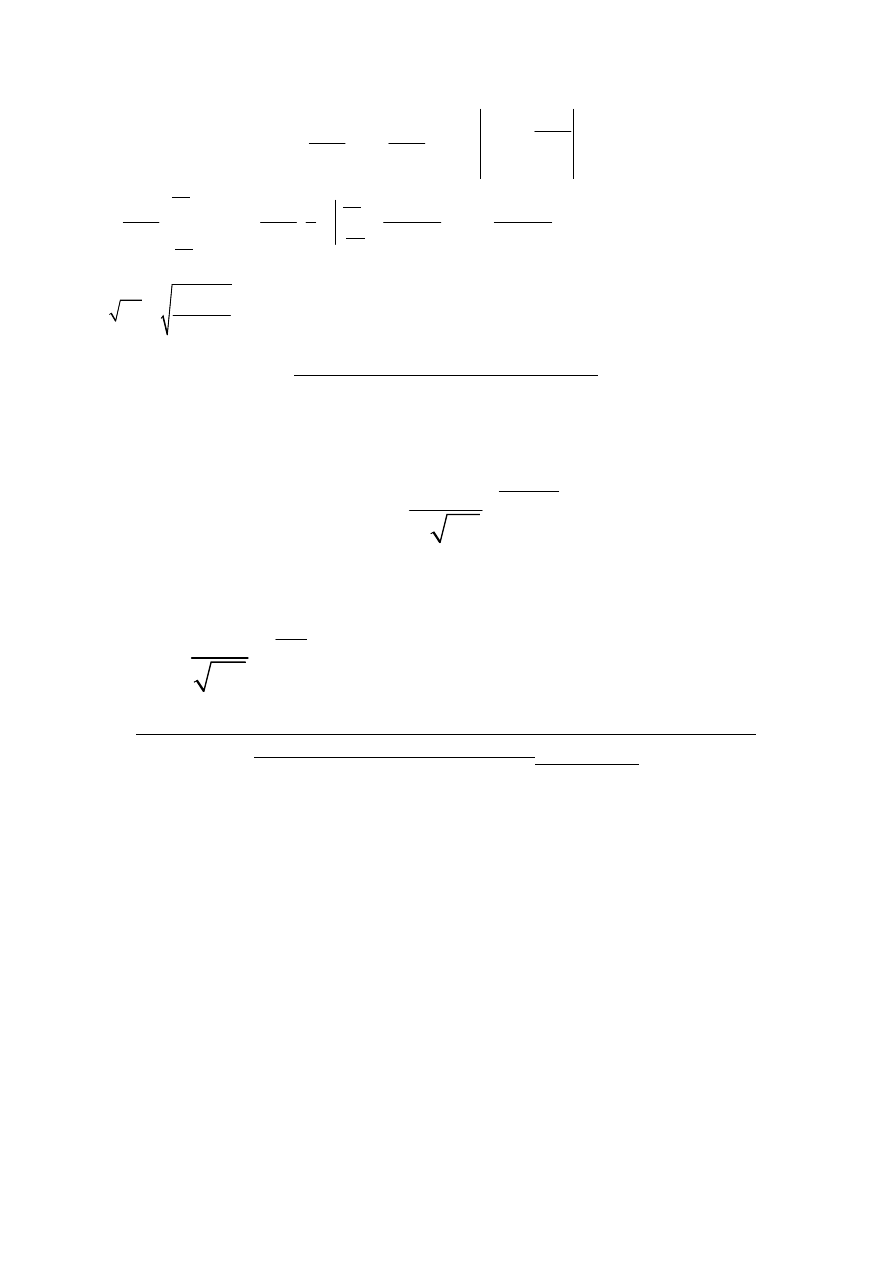
2

2

2

1

( ) (

)

2

2

b

a

b

a

z

x

b a

p x

x

dx

x

dx

b a

dz

dx











 







































 





2

2

2

2

3

2

2

1

1

1

3

12

b a

b a

b a

b a

b a

z dz

z

b a

b a































;





2

2

12

b a











2

2

12

b a







Rozkład normalny i jego postać standardowa.

Funkcja gęstości rozkładu normalnego ze średnią



oraz wariancją

2



, jest przykładem funkcji

Gaussa, dana jest wzorem:

2

2

(

)

2

1

( )

2

x

p x

e















W przypadku, gdy zmienna losowa X ma rozkład z wartością średnia

0





i wariancją

2

1





, to:

2

( )

2

1

( )

2

x

p x

e







jest to postać standardowa rozkładu normalnego.

Definicje: poziom ufności, poziom istotności i przedział ufności. Poziomy ufności dla rozkładu

normalnego odpowiadające przedziałom:

, 2 , 3













Poziom ufności „c” – dla przedziału [-x,x] jest to prawdopodobieństwo, że zmienna losowa X o
rozkładzie normalnym standardowym przyjmuje wartości z tego przedziału.

Poziom istotności „

1 c

  

” – jest to maksymalne dopuszczalne prawdopodobieństwo popełnienia

błędu. Najczęściej przyjmuje się

0.05

 

.

Przedział ufności – jest to zakres , w którym mieście się średnia wartość badanej cechy, która jest
określona na podstawie badanej próby, w populacji. Definiuje on wielkość błędu, o ile uzyskany wynik
może odbiegać od wartości rzeczywistej.

~ 68, 3%

2

2

~ 95%

3

3 ~ 99, 7%

X

X

X

 

 









































Przedziały ufności dla rozkładu normalnego

Wyznaczanie przedziałów ufności dla serii pomiarów w przypadku ich małej (rozkład t-Studenta) i

dużej (rozkład Gaussa) liczby. Zastosowanie wzorów dla konkretnych przypadków.

1. Liczba pomiarów

(

30)

N 

jest duża, wtedy wariancję

2



można zastąpić przez jej

estymator

_

2

2

1

1

(

)

1

N

i

i

S

x

x

N











gdzie

_

x

to estymator wartości średniej



,

_

1

1

N

i

i

x

x

N







,

wtedy:

c

c

S

S

x

z

x

z

N

N











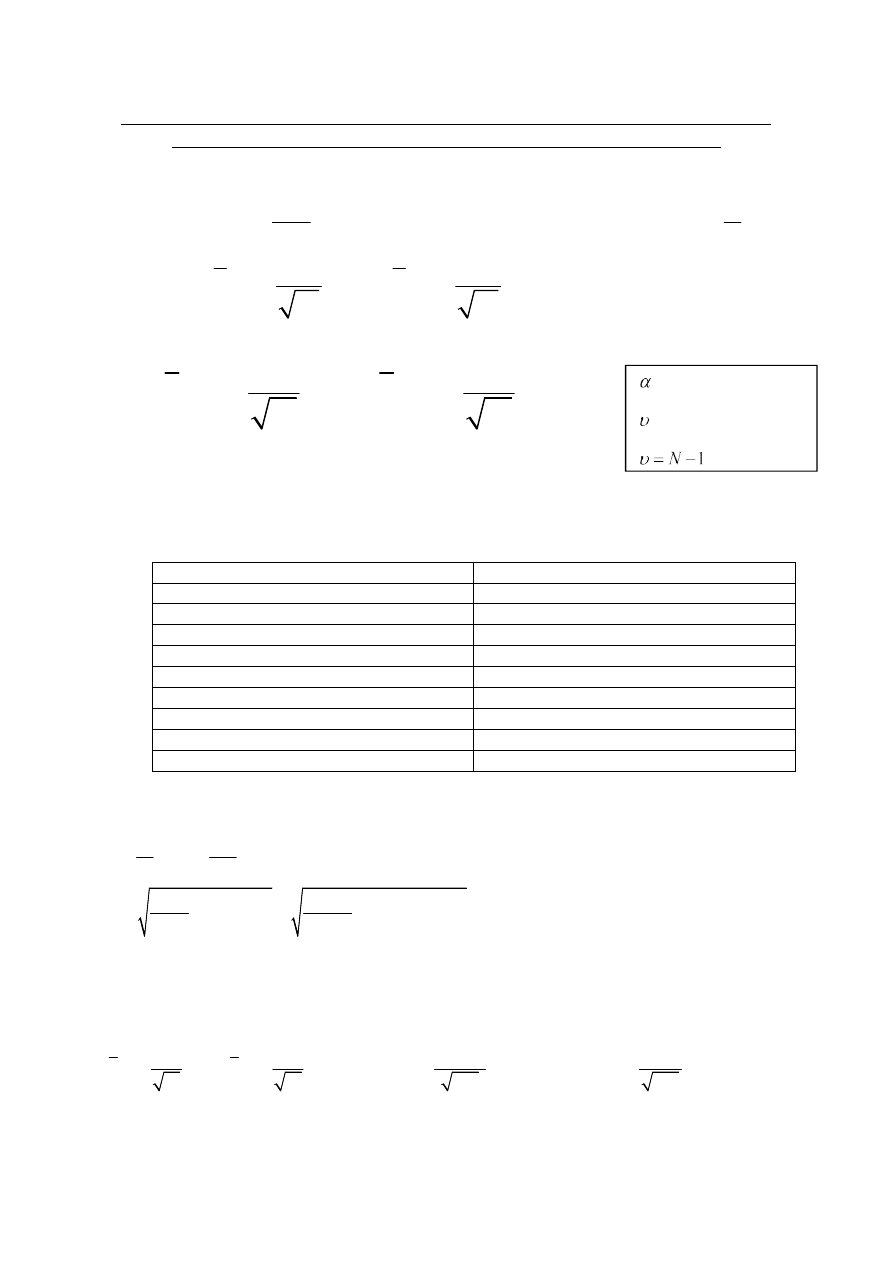
2. Przy małej liczbie pomiarów

(

30)

N 

należy korzystać z rozkładu t-Studenta.

,

,

S

S

x t

x t

N

N

 

 











Przykład: Określić przedział ufności dla 100 pomiarów ciśnienia. Przyjąć poziom ufności c=99%

Ciśnienie [MPa]

Liczba wystąpień

3.970

1

3.980

3

3.990

12

4.000

25

4.010

33

4.020

17

4.030

6

4.040

2

4.050

1





_

1

1

1

3.97 3 3.98 12 3.99 25 4 33 4.01 17 4.02 6 4.03 2 4.04 4.05

4.008

100

N

i

i

x

x

MPa

N







 







 







 

 







100

_

2

2

1

1

1

1

(

)

(

4.008)

0.014

1

100 1

N

i

i

i

i

S

x

x

x

MPa

N























Ze względu na dużą liczbę pomiarów

(

30)

N 

, należy skorzystać z rozkładu Gaussa.

0.99

0.99

2.575

c

z







0.0014

0.014

4.008 2.575

4.008 2.575

4.0044

4.0116

100

100

c

c

S

S

x

z

x

z

N

N











 





















-poziom istotności

-liczba stopni swobody

Przykład: Wyznaczono następujące wartości napięcia:

U[V]

7.5

8.2

7.5

8.6

8.6

8.7

7.4

8.2

7.3

7.8

Określić przedział ufności przy założeniu, że poziom ufności wynosi c=98%.

10

_

1

1

1

1

1

(7.5 8.2 7.5 8.6 8.6 8.7 7.4 8.2 7.3 7.8)

7.98

10

10

N

i

i

i

i

x

x

x

V

N





































10

_

2

2

1

1

1

1

(

)

(

7.89)

0.545

1

9 1

N

i

i

i

i

S

x

x

x

V

N























,

0.02,9

0.98

1

0.02

1 9

2.821

c

c

N

t

t

 







  



 





,

,

S

S

x t

x t

N

N

 

 











0.545

0.545

7.98 2.821

7.98 2.821

7.494

8.446

10

10

















