Logistyka - nauka

Logistyka 6/2013

905

Dr inż. Robert Kostek UTP w Bydgoszczy

Dr inż. Marcin Łukasiewicz UTP w Bydgoszczy

Dr inż. Tomasz Kałaczyński UTP w Bydgoszczy

Optymalizacja tras transportu drogowego w celu minimalizacji emisji CO

2

Streszczenie

W pracy tej przedstawiono zagadnienie optymalizacji drogi transportu pomiędzy

dwoma punktami. Jako kryterium optymalizacji przyjęto minimalizację emisji CO

2

.

Najczęściej przyjmowanym kryterium optymalizacji tras są długość trasy i czas transportu,

natomiast minimalizacja emisji CO

2

nie jest często spotykana. Przyjęcie emisji CO

2

jako

kryterium pociąga za sobą konieczność modelowania ruchu pojazdu, dlatego zastosowano

graf skierowany, w którym wagi krawędzi są funkcjami czasu. Taki model umożliwia

modelowanie zmiennych warunków drogowych w funkcji czasu oraz różnych prędkości

pojazdów w przeciwnych kierunkach jazdy.

1.

Wstęp

W pracy tej przedstawiono zagadnienie modelowania i optymalizacji drogi transportu

pomiędzy dwoma punktami, dla którego jako funkcje kryterialną przyjęto minimalizację

emisji CO

2

. W większości prac z zakresu badań operacyjnych prezentuje się modele

pozwalające na znalezienie najkrótszej lub najszybszej drogi, natomiast zagadnienie emisji

CO

2

nie jest w nich omawiane. Zagadnienie to zamodelowano stosując graf skierowany, w

którym wagi krawędzi są funkcjami czasu. Takie podejście pozwala na odwzorowanie różnej

prędkości ruchu w przeciwnych kierunkach oraz modelowanie zmiennych warunków

drogowych w funkcji czasu, co odnosi się do powstawania zatorów drogowych w godzinach

szczytu. Do rozwiązania takiego zagadnienia należy użyć specjalnych algorytmów, na

przykład genetycznych.

Zagadnienie minimalizacji emisji CO

2

jest ściśle związane z minimalizacją zużycia

paliwa przez pojazd. Ciągnik siodłowy z naczepą o masie całkowitej 40t zużywa około

0,30kg oleju napędowego na kilometr. Roczne jedna ciężarówka pokonuje dystans około

Logistyka - nauka

Logistyka 6/2013

906

120000 [km], co daje roczne zużycie paliwa rzędu 36000 [kg]. To pozwala oszacować emisję

CO

2

dla jednej ciężarówki na 111960 [kg] CO

2

roczne przy założeniu, że spalenie jednego

kilograma oleju napędowego powoduje emisję 3,11 [kg] CO

2

[1]. To pokazuje, że temat

zmniejszenia emisji CO

2

jest wart podjęcia zarówno z uwagi na ekonomikę jak i ekologie

transportu drogowego.

2.

Modelowanie jednostkowego zużycia paliwa

Jednostkowe zużycie paliwa jest funkcją: masy całkowitej pojazdu, prędkości pojazdu,

przełożenia skrzyni biegów, nachylenia drogi, prędkości wiatru, jak i wielu innych

czynników. Do celów praktycznych zależność tę należy wyestymować bazując na wynikach

eksperymentalnych uzyskanych dla danego pojazdu. Jako funkcję estymowaną można przyjąć

wielomian wielu zmiennych, który dobrze opisuje łagodne przebiegi funkcji. Stopień

wielomianu, stałe wielomianu jak i zmienne niezależne określa się na podstawie testów

matematycznych. Testy te pozwalają uchwycić istotne statystycznie wyrazy oraz odrzucić

zmienne nieistotne statystycznie. Przykładowy wielomian opisujący średnie zużycie paliwa w

funkcji masy całkowitej pojazdu przedstawiono poniżej:

g = 0.0002m

2

– 0.0059m + 0.239,

(1)

gdzie:

g – oznacza jednostkowe zużycie paliwa [kg/km], natomiast

m – masę całkowitą pojazdu wyrażoną w [t].

Wzór ten został opracowany dla ciągnika siodłowego z naczepą, których masa brutto znajduje

się w przedziale od 16 do 40 [t]. Podobną zależnością można opisać zużycie paliwa w funkcji

prędkości stosując wielomian stopnia trzeciego. Można także zastosować wielomian

opisujący zużycie paliwa w funkcji dwóch zmiennych, który ma następującą postać:

g = a

0

+a

1

v+a

2

v

2

+a

3

v

3

+a

4

m+a

5

m

2

+a

6

m

3

+a

7

mv+a

8

mv

2

+a

9

m

2

v,

(2)

gdzie:

a

0

... a

9

– oznaczają stałe wielomianu, natomiast

v - reprezentuje prędkość pojazdu.

Logistyka - nauka

Logistyka 6/2013

907

Dla każdego przełożenia skrzyni biegów należy taką funkcje wyestymować. Przy założeniu,

ż

e skrzynia biegów posiada dwanaście przełożeń, należy dwanaście takich funkcji

wyestymować. Dla zadanej masy ładunku, masę całkowitą pojazdu m można w przybliżeniu

potraktować jako stałą. Zakłada się wtedy, że zmiana masy paliwa nie ma istotnego wpływu

na masę całkowitą pojazdu. Pozwala to na znalezienie: prędkości i przełożenia, dla którego

jednostkowe zużycie paliwa będzie najmniejsze; lub przełożenia, dla którego przy zadanej

prędkości pojazdu jednostkowe zużycie paliwa będzie najmniejsze. Innymi słowy, można

zmienić prędkość pojazdu i przełożenie w celu minimalizacji zużycia paliwa. Taka

optymalizacja jest obecnie stosowana w niektórych samochodach ciężarowych, na przykład

firma IVECO stosuje takie rozwiązanie (EcoSwitch, EcoFleet). W rozważanym przypadku,

optymalizacja dotyczy jazdy po płaskim odcinku drogi, pominięto bowiem we wzorze (2) kąt

pochylenia drogi. Zastosowanie trzeciej potęgi we wzorze (2) wynika z nieliniowej

charakterystyki zużycia paliwa.

3.

Modelowanie sieci dróg

Do modelowania sieci dróg można zastosować grafy. Graf składa się z węzłów w

(wierzchołków), które są połączone krawędziami k (łukami). Krawędzie mogą być

skierowane to znaczy, że przebiegają w jednym kierunku lub mogą być nieskierowane to

znaczy, że są dwukierunkowe. Węzłom i krawędzią przyporządkowuje się wartości bądź

funkcje. Matematycy zazwyczaj nie nadają im interpretacji fizycznej, jednak do zastosowań

praktycznych jest ona niezbędna.

Fragment odcinka drogi przedstawiono na rys. 1a. Rozważany odcinek został

podzielony na mniejsze odcinki, to znaczy krawędzie. Każdej krawędzi przyporządkowano

wektor, który zawiera informacje o danej krawędzi. Przykładowe informacje to długość

odcinka drogi, pochylenie, prędkość dopuszczalna, średnia prędkość pojazdów. Takie

podejście pozwala na uwzględnienie różnych warunków jazdy na wybranym odcinku drogi,

natomiast zastosowanie krawędzi skierowanych pozwala na uwzględnienie różnych

warunków jazdy w przeciwnych kierunkach jazdy. Parametr, jakim jest średnia prędkość

pojazdów, podlega dobowym wahaniom wynikającym z przemieszczania się ludzi do i z

pracy oraz oznakowania. Dlatego uwzględnienie wahań prędkości średniej pojazdów pozwala

na modelowanie tworzenia się zatorów drogowych. W kolejnym kroku zablokowane odcinki

drogi mogą być omijane przez pojazdy. Dobowe wahania prędkości średniej pojazdów można

zamodelować stosując ciąg trygonometryczny. Węzły przedstawione na rys.1a nie muszą

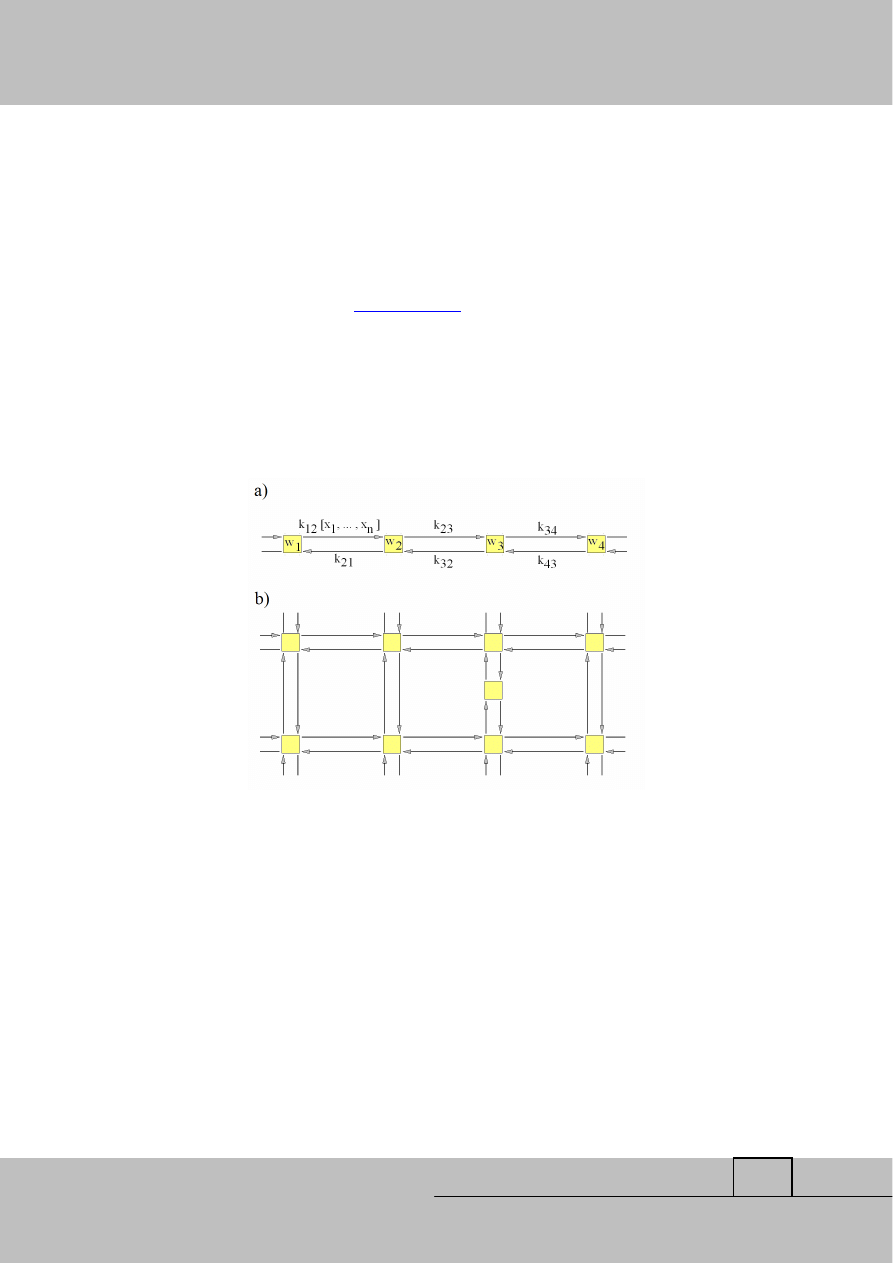
Logistyka - nauka

Logistyka 6/2013

908

mieć interpretacji fizycznej, mogą one oznaczać umowny podział odcinka lub mogą oznaczać

na przykład stacje paliw lub parkingi. W kolejnym kroku można zamodelować sieć dróg (rys.

1b). W przypadku sieci dróg węzły są interpretowane na przykład jako skrzyżowania i

parkingi. Powyższy opis pokazuje jak można zastosować grafy do modelowania

infrastruktury drogowej.

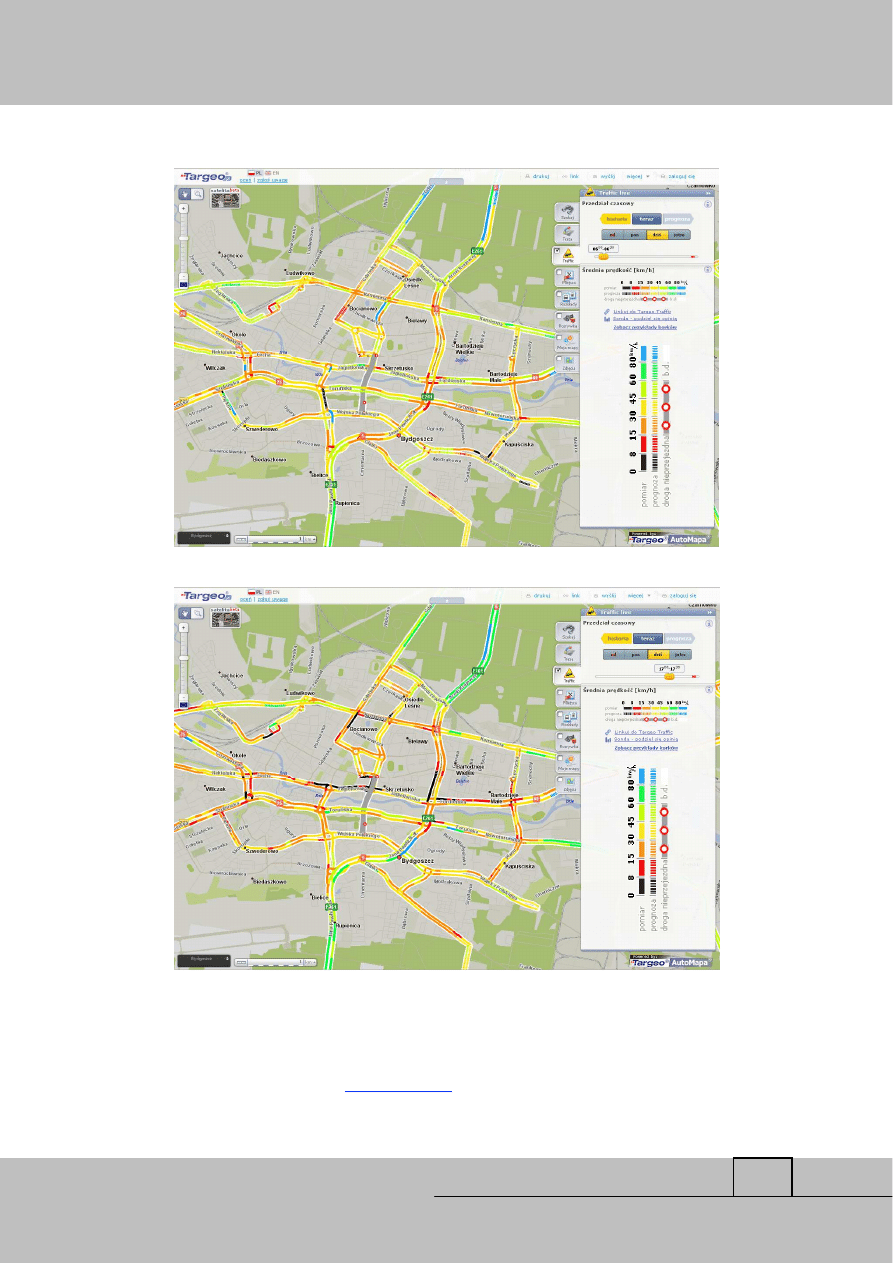
Wizualizacje zmiennych warunków jazdy w trakcje doby można obserwować na

przykład na stronie internetowej

www.targeo.pl

(rys. 2). Przedstawione dane pozwalają na

zlokalizowanie dróg, które powinny być omijane, ponieważ przejazd nimi zabiera najwięcej

czasu. Dane te z kolei są niezbędne do minimalizacji zużycia paliwa i planowania trasy. W

przypadku, gdy wagi krawędzi są funkcją czasu, chwila rozpoczęcia podróży oraz okres

postoju wpływają na uzyskany wynik (zużycie paliwa), stają się więc zmiennymi. To z kolei

dodatkowo komplikuje rozwiązywany problem.

Rys. 1. Modele odcinka drogi a) oraz sieci dróg b) przedstawione formie grafów

Logistyka - nauka

Logistyka 6/2013

909

a)

b)

Rys. 2. Wizualizacje średniej prędkości pojazdów na terenie Bydgoszczy uzyskane

dla godzin 6:00 a) i 17:00 b)

Ź

ródło

www.targeo.pl

(dostęp 23.01.2013)

Logistyka - nauka

Logistyka 6/2013

910

4.

Metody rozwiązania zagadnienia optymalizacyjnego

Rozwiązanie tak sformułowanego zagadnienia optymalizacyjnego staje się trudne,

dlatego w pierwszym przybliżeniu pewne uproszczenie zostanie przyjęte. Czas podróży jest

krótki, dlatego dobowe wahania prędkości średniej pojazdów mogą zostać pominięte. To

założenie można przyjąć dla podróży po mieście. Przyjęcie takiego założenia powoduje, że

krawędzią można przyporządkować wagi G, reprezentujące zużycie paliwa wyrażone w [kg],

które nie są funkcjami czasu. Do rozwiązania tego zagadnienia można zastosować na

przykład algorytmy A*, Dijkstry lub Bellmana-Forda. Istotą tych algorytmów jest porównanie

kosztów ścieżek, które docierają do węzłów [2]. Jeżeli dla jakiegoś fragmentu ścieżki,

zostanie znaleziony objazd, którego suma wag jest mniejsza aniżeli suma wag fragmentu

ś

cieżki, to objazd zostaje włączony do ścieżki. W ten sposób można zmniejszać sumę wag

ś

cieżki. Im bardziej selektywnie algorytm szuka rozwiązania i im niej operacji wykonuje, tym

bardziej jest efektywny. To zagadnienie jest klasyczne i nie wymaga dalszego omawiania.

W kolejnym podejściu można przeanalizować wszystkie możliwe ścieżki w grafie

pomiędzy dwoma wybranymi wierzchołkami. Zakładając, że każdy wierzchołek grafu ma

jedne bezpośrednie połączenie z każdym innym wierzchołkiem grafu (graf pełen), wtedy

liczbę możliwych ścieżek, bez powtórzeń wierzchołków, pomiędzy dwoma wierzchołkami

wyraża się wzorem:

∑

−

=

=













−

=

2

0

!

2

w

N

r

r

w

s

r

r

N

N

,

(3)

gdzie:

N

s

– oznacza liczbę możliwych ścieżek w grafie bez powtórzeń węzłów,

N

w

– reprezentuje liczbę węzłów w grafie,

r – jest liczbą węzłów, przez które przebiega ścieżka.

Jak widać z przedstawionego wzoru N

s

rośnie bardzo szybko wraz ze wzrostem N

w

. Dlatego

dla dużej liczby wierzchołków metoda ta staje się nieefektywna. Jednakże w praktyce węzły

posiadają połączenia bezpośrednie zaledwie z kilkoma innymi węzłami, dlatego wzór (3)

podaje zawyżoną liczbę ścieżek dla typowych przypadków. Podsumowując, przeanalizowanie

każdej możliwej ścieżki daje pewność znalezienia najlepszego rozwiązania, ale jest

czasochłonne.

Logistyka - nauka

Logistyka 6/2013

911

W związku z tym, że przeanalizowanie całego zbioru rozwiązań przy dużej liczbie

węzłów staje się niemożliwe, należy zbiór rozwiązań przeszukać w sposób selektywny. Do

przeszukiwania obszaru rozwiązań można zastosować algorytmy genetyczne [3,4,5,6].

Rozwiązaniami początkowymi mogą być najkrótsze ścieżki oraz najszybsze ścieżki, uzyskane

dla wybranych chwil czasowych. Można do zbioru rozwiązań początkowych przyjąć także

ś

cieżki, które policzono dla różnych chwil zakładając stałą wagę ścieżek G. Wagi te wyrażają

zużycie paliwa w [kg]. Kolejne modyfikacje ścieżek, wykonywane zgodnie z metodą

algorytmów genetycznych, prowadzą do zmniejszenia zużycia paliwa. Modyfikacje te

polegają na budowaniu nowych ścieżek z losowych fragmentów wcześniej przyjętych ścieżek

i losowo wybranych łuków. Jeżeli fragmenty ścieżek nie są połączone, to znaczy zaczynają

się i kończą w różnych węzłach, wtedy należy je połączyć. W ten sposób uzyskuje się nową

populacje ścieżek. Dla nowych ścieżek liczy się sumy wag. Ścieżki dla których suma wag jest

największa, zostają odrzucone i nie biorą udziału w dalszych modyfikacjach. Najlepsze

ś

cieżki z poprzedniej populacji mogą także uczestniczyć w tworzeniu nowej populacji

ś

cieżek. W ten sposób selektywnie przeszukuje się obszar rozwiązań. Wprowadzenie

losowego przeszukiwania pozwala natomiast na wychodzenie z minimów lokalnych.

Kolejna metoda znalezienia lepszej ścieżki to metoda szukania objazdu. Znalezienie

alternatywnej drogi (objazdu) o mniejszym koszcie nie musi oznaczać, że nowa ścieżka w

całości będzie mniej kosztowna, jeśli czasy przejazdu są różne t

1

≠

t

2

. Wagi w pozostałej części

ś

cieżki ulegają zmianie w funkcji czasu, dlatego pozostała część ścieżki powinna zostać

przeliczona powtórnie dla nowych warunków. Problem ten zilustrowano na rys. 3. Liczby

przy krawędziach reprezentują wagi krawędzi (koszty krawędzi), podczas gdy liczby

wewnątrz kwadratów reprezentują koszt dotarcia do poszczególnych węzłów (sumę wag

krawędzi). Algorytm który szuka objazdów wydaje się bardziej selektywny od metody

algorytmów genetycznych, ponadto tylko część ścieżki jest przeliczana ponownie, dlatego

powinien być bardziej efektywny. Podsumowując, algorytmy przeszukiwania i generowania

nowych ścieżek wpływają na czas obliczeń i uzyskane wyniki.

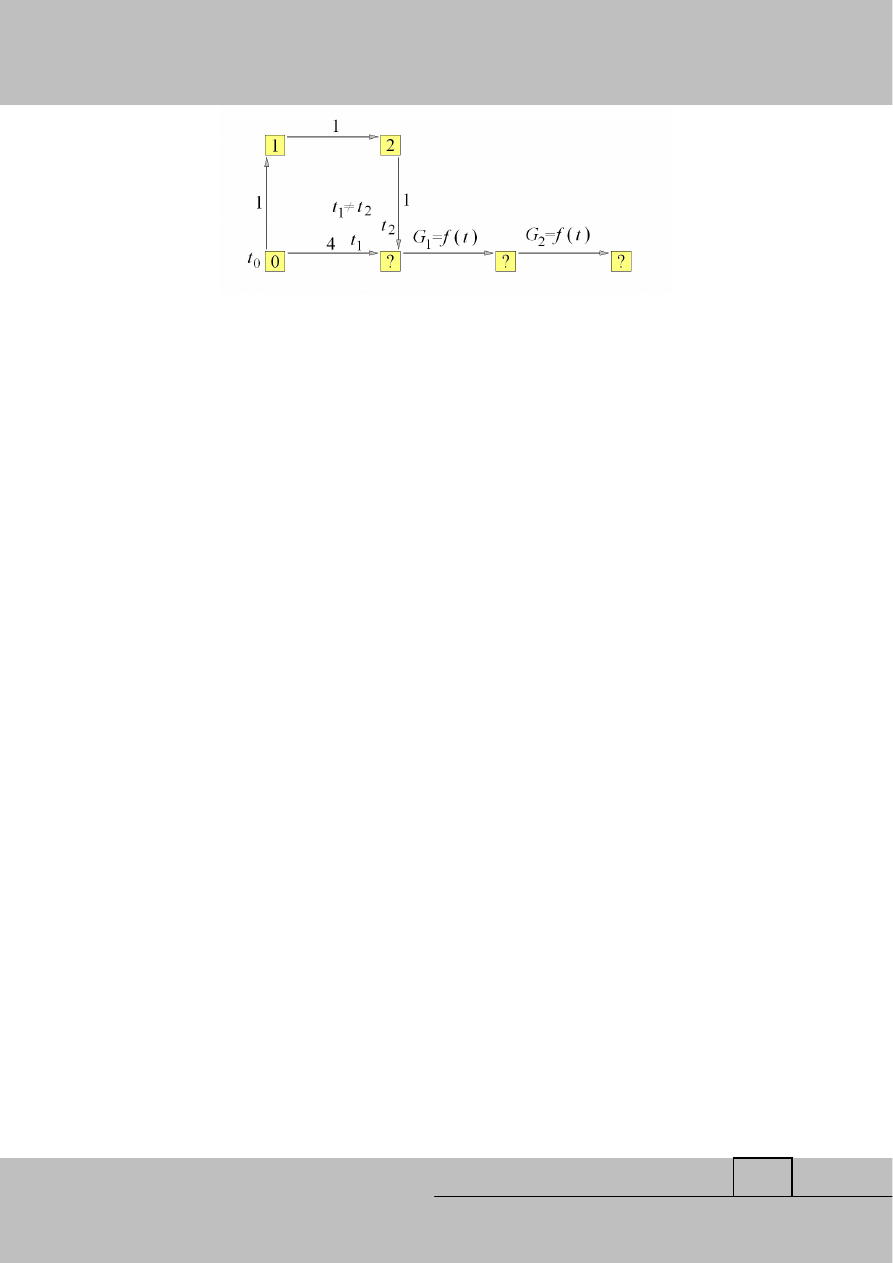
Logistyka - nauka

Logistyka 6/2013

912

Rys. 3. Problem wyboru ścieżki w warunkach zmiennych wag

5.

Podsumowanie

Emisja CO

2

jest istotna z uwagi na negatywne oddziaływanie transportu na

ś

rodowisko. Mapy stosowane do planowania tras przejazdu, jako kryteria przyjmują odległość

lub czas. Są to dwa najczęściej stosowane kryteria, natomiast minimalizacja emisji CO

2

nie

jest spotykana. Nieliczne mapy pozwalają na obliczenie zużycia paliwa i emisji CO

2

, jednak

optymalizacja trasy z uwagi na to kryterium nie jest znana autorom. Dlatego w tej pracy

przedstawiono metody optymalizacji trasy przejazdu, w celu minimalizacji emisji CO

2

.

Zagadnienie omijania korków i minimalizacji zużycia paliwa jest szczególnie istotne

dla firm zajmujących się transportem w miastach. Dotyczy to szczególnie firm rozwożących

przesyłki kurierskie. Zagadnienie to nie jest jednak traktowane w należyty sposób przez

decydentów, nie dostrzegają oni znaczenia właściwego planowania tras. Ponadto niewiele jest

map, które podają aktualne informacje o korkach i utrudnieniach w ruchu.

Kolejnym zagadnieniem, które warto podsumować, jest optymalizacja trasy z

uwzględnieniem zmiennej sytuacji drogowej. Rozwiązanie tego zagadnienia wymaga

zastosowania niestandardowych procedur, co jest interesującym zagadnieniem. Autorom nie

są znane programy komercyjne, które rozwiązują to zagadnienie. W artykule tym

przedstawiono natomiast metody rozwiązania tego zagadnienia.

Redukcja zużycia paliwa ma znaczenie praktyczne z uwagi na ekonomikę transportu,

ponieważ koszt paliwa stanowi około połowę kosztów transportu. Należy jednak podkreślić,

ż

e maksymalizacja zysku w jednostce czasu nie jest tożsama z ograniczeniem kosztów

paliwa.

Logistyka - nauka

Logistyka 6/2013

913

OPTIMISATION OF TRANSPORT ROUTES TO REDUCE CO

2

EMISSION

This article presents optimisation of a transport route between two points. The main aim of

optimisation is reduction of CO

2

emission. Most of handbooks present minimisation of delivery time

or the shortest path; thus reduction of CO

2

emission should be described. The CO

2

emission is

modelled with directed graphs. In the presented model, weights assigned to arcs are functions of time,

which reflects nature of road traffic.

Literatura

[1] Żółtowski A.: Opracowanie poradnika ustalania czynników energetyczno- emisyjnych w

zamówieniach publicznych na zakup pojazdów drogowych, PRACA ITS NR 10483

2011

[2] Sikora W.: Badania operacyjne, Polskie Wydawnictwo Ekonomiczne, 2008

[3] Ahn C., Ramakrishna R.: A genetic algorithm for shortest path routing problem and the

sizing of populations, “IEEE Transactions on Evolutionary Computation” 6, s.566–579,

2002.

[4] Babooa S.S., Narasimhan B.: Genetic algorithm based congestion aware routing

protocol (GA-CARP) for mobile ad hoc networks, “Procedia Technology” 4, s. 177–

181, 2012

[5] Senthilkumarana T., Sankaranarayanan V.: Dynamic congestion detection and control

routing in ad hoc networks, “Journal of King Saud University - Computer and

Information Sciences” 25, s. 25–34, 2013

[6] Shigehiro1 Y., Miyakawa T., Masuda T.: Road traffic control based on genetic

algorithm for reducing traffic congestion, “Electronics and Communications in Japan”

95, s. 11–19, 2012