Seminarium

Seminarium

dyplomowe

dyplomowe

„

„

Komputerowo wspomagana

Komputerowo wspomagana

optymalizacja zadań

optymalizacja zadań

transportowych w rejonach

transportowych w rejonach

obsługi systemu

obsługi systemu

logistycznego”

logistycznego”

Wykonał:

NIEWIEDZIAŁ SEBASTIAN

Specj. Informatyka w inżynierii mechanicznej

Promotor:

dr hab. inż. Edward MICHLOWICZ, prof.
AGH

Celem pracy jest sporządzenie

Celem pracy jest sporządzenie

programu

komputerowego,

wg

programu

komputerowego,

wg

odpowiednich algorytmów, służącego

odpowiednich algorytmów, służącego

do

rozwiązywania

zadań

do

rozwiązywania

zadań

transportowych.

transportowych.

1. Cel i zakres pracy

1. Cel i zakres pracy

2. Wstęp

2. Wstęp

Zadania

transportowe

sprowadzają

się

do

Zadania

transportowe

sprowadzają

się

do

opracowania planu przewozu danego produktu z

opracowania planu przewozu danego produktu z

różnych źródeł zaopatrzenia do punktów, które

różnych źródeł zaopatrzenia do punktów, które

zgłaszają zapotrzebowanie na ten produkt.

zgłaszają zapotrzebowanie na ten produkt.

Kierując się przesłankami dostępności produktów do

Kierując się przesłankami dostępności produktów do

klientów tworzy się infrastrukturę magazynową i sieci

klientów tworzy się infrastrukturę magazynową i sieci

dystrybucji. Ze względu na potrzebę stworzenia

dystrybucji. Ze względu na potrzebę stworzenia

struktury zarządzania i sterowania przepływem

struktury zarządzania i sterowania przepływem

towarów tworzone są rejony obsługi klientów.

towarów tworzone są rejony obsługi klientów.

Analizę logistyczną wyznaczonych rejonów obsługi

Analizę logistyczną wyznaczonych rejonów obsługi

można przeprowadzić, stosując stosunkowo proste

można przeprowadzić, stosując stosunkowo proste

algorytmy,

jeżeli

operujemy

względnie

dobrze

algorytmy,

jeżeli

operujemy

względnie

dobrze

określonymi danymi strukturalnymi i liczbowymi.

określonymi danymi strukturalnymi i liczbowymi.

Przyjmując, że głównym celem jest zapewnienie

Przyjmując, że głównym celem jest zapewnienie

odpowiednich

wielkości

dostaw

do

klientów,

odpowiednich

wielkości

dostaw

do

klientów,

optymalizacja zadania będzie polegała na efektywnej

optymalizacja zadania będzie polegała na efektywnej

obsłudze transportowej przy jak najniższych kosztach

obsłudze transportowej przy jak najniższych kosztach

transportu.

transportu.

a)

a)

Klasyczne zadanie transportowe:

Klasyczne zadanie transportowe:

Znana

jest

lokalizacja

Znana

jest

lokalizacja

m

m

centrów

dystrybucji

centrów

dystrybucji

reprezentowanych przez magazyny

reprezentowanych przez magazyny

L

L

1

1

,...,L

,...,L

m

m

oraz

oraz

lokalizacja

lokalizacja

n

n

klientów

klientów

B

B

1

1

,...,B

,...,B

n

n

,

,

którzy powinni otrzymać

którzy powinni otrzymać

towar z tych magazynów. Znany jest również poziom

towar z tych magazynów. Znany jest również poziom

zapasów każdego magazynu, zapotrzebowanie każdego

zapasów każdego magazynu, zapotrzebowanie każdego

klienta oraz koszty jednostkowe transportu między

klienta oraz koszty jednostkowe transportu między

poszczególnymi dostawcami i odbiorcami. Należy

poszczególnymi dostawcami i odbiorcami. Należy

znaleźć taki plan przewozów aby łączny koszt transportu

znaleźć taki plan przewozów aby łączny koszt transportu

był jak najmniejszy.

był jak najmniejszy.

3. Model matematyczny

3. Model matematyczny

b)

b)

Założenia modelowe:

Założenia modelowe:



każdy z klientów może otrzymać dostawę z dowolnego

każdy z klientów może otrzymać dostawę z dowolnego

magazynu, każdy z magazynów może zaopatrywać wielu

magazynu, każdy z magazynów może zaopatrywać wielu

klientów,

klientów,



podaż i popyt są równe:

podaż i popyt są równe:

gdzie:

gdzie:

a

a

i

i

-

-

poziom zapasu produktu w magazynie

poziom zapasu produktu w magazynie

L

L

i

i

, i = 1,...,m,

, i = 1,...,m,

b

b

j

j

-

-

zamówienie składane przez klienta

zamówienie składane przez klienta

B

B

j

j

, j = 1,...,n,

, j = 1,...,n,



koszt przewiezienia jednej jednostki produktu z magazynu

koszt przewiezienia jednej jednostki produktu z magazynu

L

L

i

i

,

,

do klienta

do klienta

B

B

j

j

wynosi

wynosi

c

c

ij

ij

(gdzie

(gdzie

i = 1,...,m, j = 1,...,n

i = 1,...,m, j = 1,...,n

),

),



zmienną decyzyjną którą należy wyznaczyć jest

zmienną decyzyjną którą należy wyznaczyć jest

wielkość

wielkość

x

x

ij

ij

przewożonej partii z magazynu

przewożonej partii z magazynu

L

L

i

i

,

,

do

do

klienta

klienta

B

B

j

j

(gdzie

(gdzie

i = 1,...,m, j = 1,...,n

i = 1,...,m, j = 1,...,n

),

),



funkcja celu czyli łącznych kosztów transportu

funkcja celu czyli łącznych kosztów transportu

wyraża się wzorem:

wyraża się wzorem:

c)

c)

Zapis matematyczny:

Zapis matematyczny:

Należy znaleźć takie wartosći

Należy znaleźć takie wartosći

x

x

ij

ij

,

,

dla których

dla których

funkcja celu przyjmuje wartość minimalną:

funkcja celu przyjmuje wartość minimalną:

przy warunkach:

przy warunkach:



bilans wydanych produktów z magazynu:

bilans wydanych produktów z magazynu:



bilans produktów otrzymanych przez klienta:

bilans produktów otrzymanych przez klienta:

i = 1,...,m,

i = 1,...,m,

j = 1,...,n.

j = 1,...,n.

d)

d)

Zapis tablicowy:

Zapis tablicowy:

Zadania transportowe mają strukturę liniową. Z funkcji

Zadania transportowe mają strukturę liniową. Z funkcji

celu i warunków ograniczających można utworzyć układ

celu i warunków ograniczających można utworzyć układ

równań liniowych. Rozwiązywanie takiego układu nie

równań liniowych. Rozwiązywanie takiego układu nie

jest jednak zbyt wygodne. Charakterystyczna struktura

jest jednak zbyt wygodne. Charakterystyczna struktura

zadania pozwoliła opracować efektywniejsze algorytmy,

zadania pozwoliła opracować efektywniejsze algorytmy,

w których do zapisu zadania wykorzystuje się tzw. tablice

w których do zapisu zadania wykorzystuje się tzw. tablice

transportowe.

transportowe.

Ograniczenia zapisane są w

Ograniczenia zapisane są w

macierzy transportowej X,

macierzy transportowej X,

do której dostosowana jest

do której dostosowana jest

macierz kosztów C.

macierz kosztów C.

Macierz transportowa

Macierz transportowa

X

X

.

.

Wiersze reprezentują tutaj magazyny, natomiast kolumny

Wiersze reprezentują tutaj magazyny, natomiast kolumny

odbiorców. Każdy wiersz można odczytać jako skrócony

odbiorców. Każdy wiersz można odczytać jako skrócony

zapis warunków wydawania produktów z magazynu.

zapis warunków wydawania produktów z magazynu.

Macierz kosztów

Macierz kosztów

C.

C.

Między

elementami

macierzy

kosztów

Między

elementami

macierzy

kosztów

C

C

i

i

elementami macierzy transportowej

elementami macierzy transportowej

X

X

(bez ostatniego

(bez ostatniego

wiersza i ostatniej kolumny) zachodzi jednoznaczność

wiersza i ostatniej kolumny) zachodzi jednoznaczność

przyporządkowania typu

przyporządkowania typu

c

c

ij

ij

,odpowiada

,odpowiada

x

x

ij

ij

.

.

4. Algorytmy rozwiązania

4. Algorytmy rozwiązania

W postępowaniach prowadzących do wyznaczenia

W postępowaniach prowadzących do wyznaczenia

wielkości dostaw należy wyróżnić dwa etapy:

wielkości dostaw należy wyróżnić dwa etapy:



w

pierwszym

wyznacza

się

wstępny

plan

w

pierwszym

wyznacza

się

wstępny

plan

dopuszczalnego

transportu,

dopuszczalnego

transportu,

pierwsze

bazowe

pierwsze

bazowe

rozwiązanie dopuszczalne

rozwiązanie dopuszczalne

. W tym celu można

. W tym celu można

zastosować jedną z metod:

zastosować jedną z metod:

- kąta północno-zachodniego,

- kąta północno-zachodniego,

- minimalnego elementu macierzy kosztów,

- minimalnego elementu macierzy kosztów,

- aproksymacji Vogel’a,

- aproksymacji Vogel’a,



w drugim etapie na podstawie pierwszego rozwiązania

w drugim etapie na podstawie pierwszego rozwiązania

bazowego wyznacza się

bazowego wyznacza się

rozwiązanie optymalne

rozwiązanie optymalne

.

.

Najczęściej stosowaną metodą jest metoda MODI.

Najczęściej stosowaną metodą jest metoda MODI.

a) Algorytmy wyznaczania rozwiązania bazowego:

a) Algorytmy wyznaczania rozwiązania bazowego:



Sposób postępowania jest we wszystkich wymienionych

Sposób postępowania jest we wszystkich wymienionych

metodach podobny. Należy znaleźć kolejną komórkę

metodach podobny. Należy znaleźć kolejną komórkę

(i, j)

(i, j)

w

w

macierzy transportowej, która nie ma przyporządkowanej

macierzy transportowej, która nie ma przyporządkowanej

wartości

wartości

x

x

ij

ij

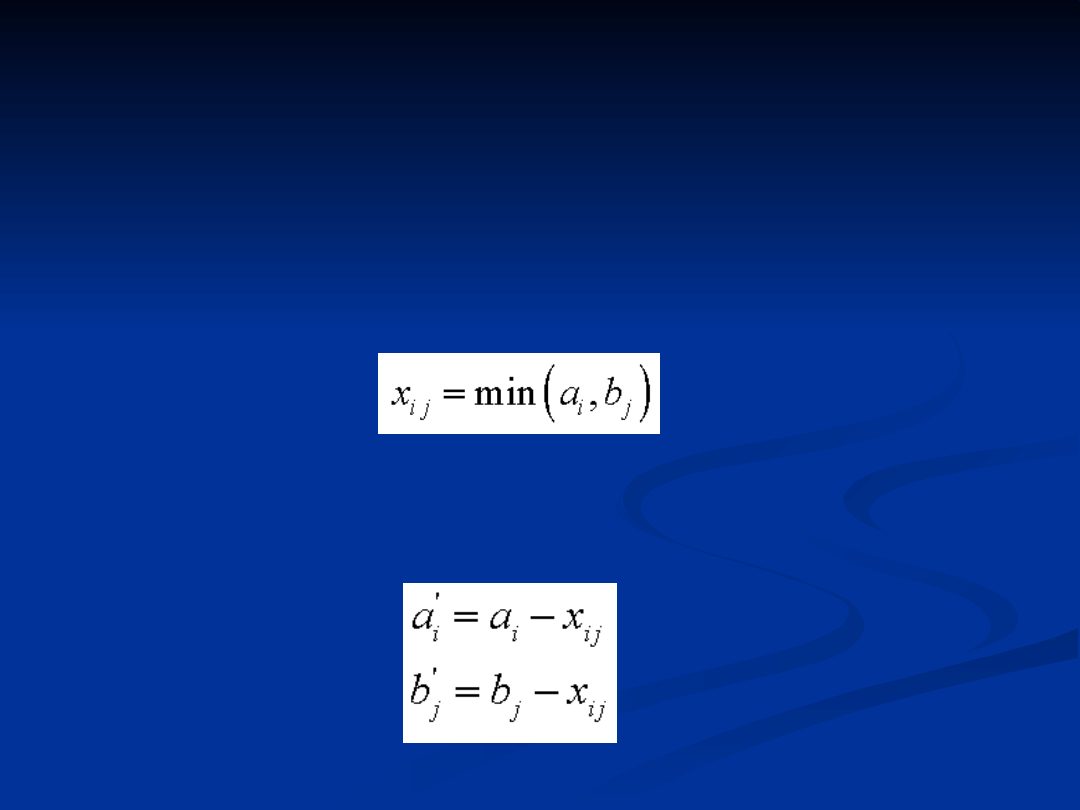
a następnie zaplanować wartość przewozu na

a następnie zaplanować wartość przewozu na

trasie

trasie

(i, j)

(i, j)

na poziomie:

na poziomie:

gdzie

gdzie

a

a

i

i

oraz

oraz

b

b

j

j

oznaczają, odpowiednio, aktualna

oznaczają, odpowiednio, aktualna

podaż i aktualny popyt. Następnie należy

podaż i aktualny popyt. Następnie należy

zmodyfikować wartości

zmodyfikować wartości

a

a

i

i

oraz

oraz

b

b

j

j

, przyjmując:

, przyjmując:

Przynajmniej jedna z tych wartości jest zerem.

Przynajmniej jedna z tych wartości jest zerem.

Jeżeli

Jeżeli

a

a

i

i

' = 0

' = 0

, to pozostałe nierozpatrywane trasy

, to pozostałe nierozpatrywane trasy

od

od

i

i

-tego magazynu należy zaplanować na poziomie

-tego magazynu należy zaplanować na poziomie

zero. Jeżeli

zero. Jeżeli

b

b

i

i

' = 0

' = 0

, to pozostałe nierozpatrywane

, to pozostałe nierozpatrywane

trasy do

trasy do

j

j

-tego klienta należy zaplanować na

-tego klienta należy zaplanować na

poziomie zero.

poziomie zero.

Postępowanie kontynuuje się aż do momentu

Postępowanie kontynuuje się aż do momentu

wypełnienia wszystkich komórek.

wypełnienia wszystkich komórek.



Metoda kąta północno-zachodniego nie uwzględnia

Metoda kąta północno-zachodniego nie uwzględnia

kosztów, może więc generować rozwiązanie dalekie

kosztów, może więc generować rozwiązanie dalekie

od optymalnego. Ze względu na swą prostotę jest

od optymalnego. Ze względu na swą prostotę jest

jednak

powszechnie

wykorzystywana

do

jednak

powszechnie

wykorzystywana

do

wyznaczenia rozwiązania bazowego.

wyznaczenia rozwiązania bazowego.



Znacznie

dokładniejsze

dopuszczalne

rozwiązanie

Znacznie

dokładniejsze

dopuszczalne

rozwiązanie

bazowe, bardziej zbliżone do optymalnego, można

bazowe, bardziej zbliżone do optymalnego, można

uzyskać metodami uwzględniającymi koszty transportu.

uzyskać metodami uwzględniającymi koszty transportu.

Jedną z takich metod jest metoda minimalnego elementu

Jedną z takich metod jest metoda minimalnego elementu

macierzy kosztów w której podstawowym kryterium przy

macierzy kosztów w której podstawowym kryterium przy

wyborze zmiennej

wyborze zmiennej

x

x

ij

ij

jest najtańsza możliwość dostawy.

jest najtańsza możliwość dostawy.

Jest to metoda o prostych zasadach postępowania bardzo

Jest to metoda o prostych zasadach postępowania bardzo

zbliżonych do metody kąta północno-zachodniego.

zbliżonych do metody kąta północno-zachodniego.



Drugą metodą uwzględniającą funkcję kryterium, czyli

Drugą metodą uwzględniającą funkcję kryterium, czyli

koszty transportu jest metoda aproksymacji Vogel’a.

koszty transportu jest metoda aproksymacji Vogel’a.

Należy

ona

do

metod

wyznaczających

jedynie

Należy

ona

do

metod

wyznaczających

jedynie

dopuszczalne rozwiązanie bazowe, ale uzyskiwane

dopuszczalne rozwiązanie bazowe, ale uzyskiwane

wyniki są na ogół tak bliskie optymalnym, że jest

wyniki są na ogół tak bliskie optymalnym, że jest

wykorzystywana powszechnie w dużych zadaniach do

wykorzystywana powszechnie w dużych zadaniach do

szybkiego

wyznaczenia

planów

transportowych.

szybkiego

wyznaczenia

planów

transportowych.

Podstawowym kryterium przy wyborze zmiennej

Podstawowym kryterium przy wyborze zmiennej

x

x

ij

ij

w tej

w tej

metodzie jest różnica między najtańszą a drugą co do

metodzie jest różnica między najtańszą a drugą co do

taniości możliwością dostawy.

taniości możliwością dostawy.

b) Algorytm optymalizacji

b) Algorytm optymalizacji



Po wyznaczeniu bazowego rozwiązania dopuszczalnego,

Po wyznaczeniu bazowego rozwiązania dopuszczalnego,

należy przystąpić do analizy tego rozwiązania. W

należy przystąpić do analizy tego rozwiązania. W

ramach

jednej

iteracji

należy

stwierdzić,

czy

ramach

jednej

iteracji

należy

stwierdzić,

czy

rozpatrywane rozwiązanie (w pierwszej iteracji jest to

rozpatrywane rozwiązanie (w pierwszej iteracji jest to

rozwiązanie bazowe) jest optymalne, jeżeli nie jest,

rozwiązanie bazowe) jest optymalne, jeżeli nie jest,

należy wyznaczyć nowe rozwiązanie. Do tego celu

należy wyznaczyć nowe rozwiązanie. Do tego celu

można zastosować metodę MODI (

można zastosować metodę MODI (

Modified Distribution

Modified Distribution

Methode

Methode

), która wykorzystuje bardzo ważne własności

), która wykorzystuje bardzo ważne własności

zadań dualnych w programowaniu liniowym, a w

zadań dualnych w programowaniu liniowym, a w

szczególności warunków komplementarności.

szczególności warunków komplementarności.



Przedstawione

zadanie

transportowe

należy

Przedstawione

zadanie

transportowe

należy

potraktować jako prymalne zadanie programowania

potraktować jako prymalne zadanie programowania

liniowego, a następnie - zgodnie z ustalonymi regułami -

liniowego, a następnie - zgodnie z ustalonymi regułami -

utworzyć do niego zadanie dualne.

utworzyć do niego zadanie dualne.

Zadanie prymalne

Zadanie prymalne

Zadanie dualne

Zadanie dualne

Funkcja celu:

Funkcja celu:

Ograniczenia:

Ograniczenia:

u

u

i

i

, v

, v

j

j

-

-

zmienne dualne

zmienne dualne



Warunki komplementarności przedstawiające zależności

Warunki komplementarności przedstawiające zależności

między wartościami zmiennych zadania prymalnego a

między wartościami zmiennych zadania prymalnego a

ograniczeniami zadania dualnego mają postać:

ograniczeniami zadania dualnego mają postać:

jeżeli

jeżeli

x

x

ij

ij

> 0,

> 0,

to musi być spełnione równanie:

to musi być spełnione równanie:

u

u

i

i

+ v

+ v

j

j

= c

= c

ij

ij

,

,

jeżeli

jeżeli

u

u

i

i

+ v

+ v

j

j

= c

= c

ij

ij

,

,

to wtedy

to wtedy

x

x

ij

ij

= 0.

= 0.



Wskaźniki optymalności:

Wskaźniki optymalności:



Kryterium

optymalności

-

Kryterium

optymalności

-

jeżeli

wartości

wszystkich wskaźników optymalnosci są dodatnie
lub równe zeru, wtedy rozpatrywane rozwiązanie
jest optymalne. Jeżeli choć jeden ze wskaźników
optymalności jest ujemny, wtedy istnieje możliwość
poprawy tego rozwiązania.

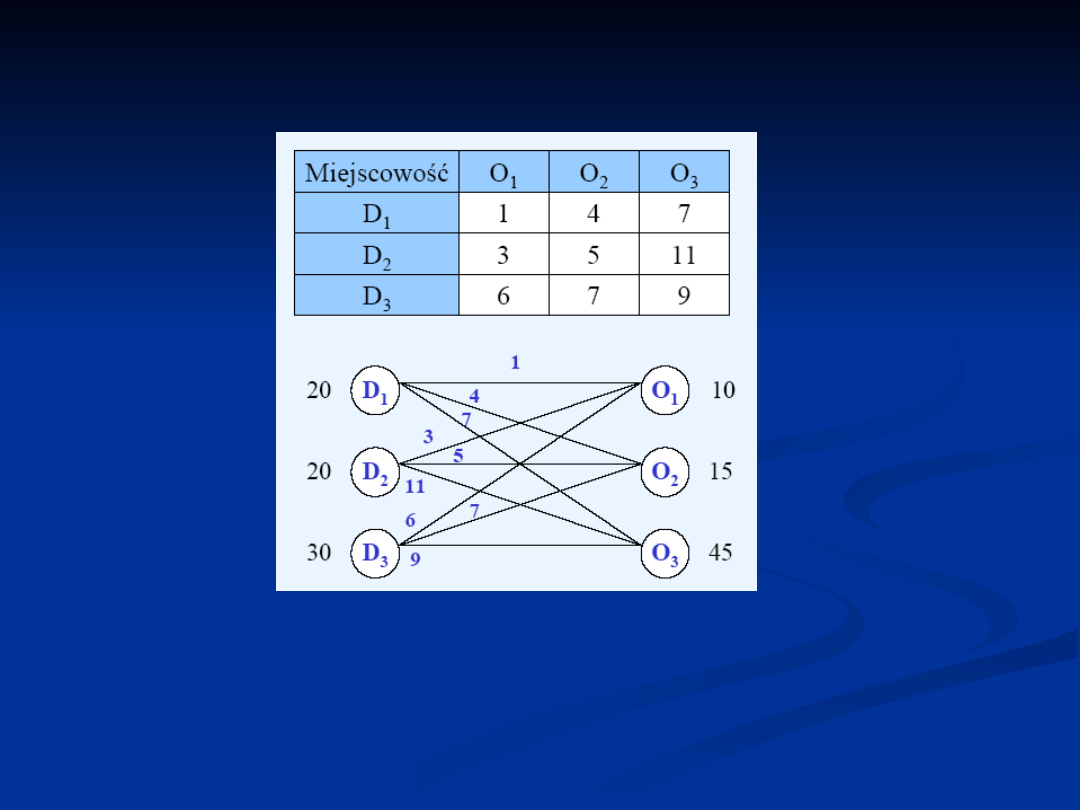
c)

c)

Przykład:

Przykład:



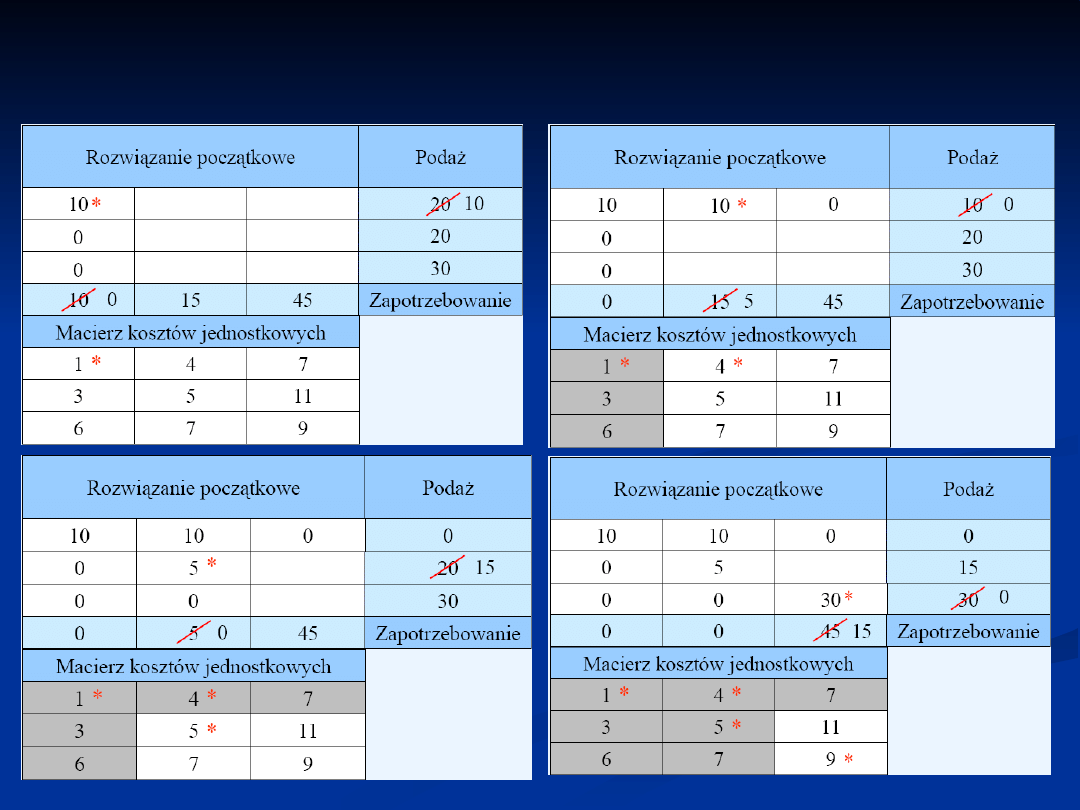
Pierwsze dopuszczalne rozwiązanie bazowe -

Pierwsze dopuszczalne rozwiązanie bazowe -

metoda minimalnego elementu macierzy kosztów:

metoda minimalnego elementu macierzy kosztów:



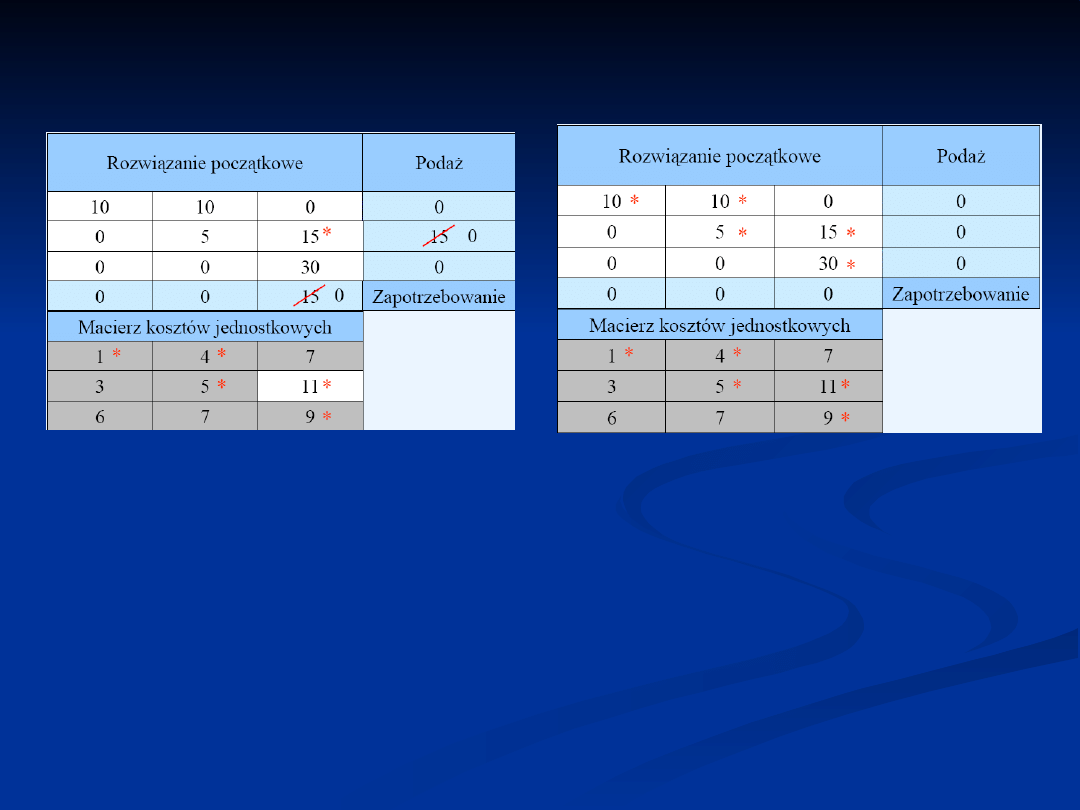
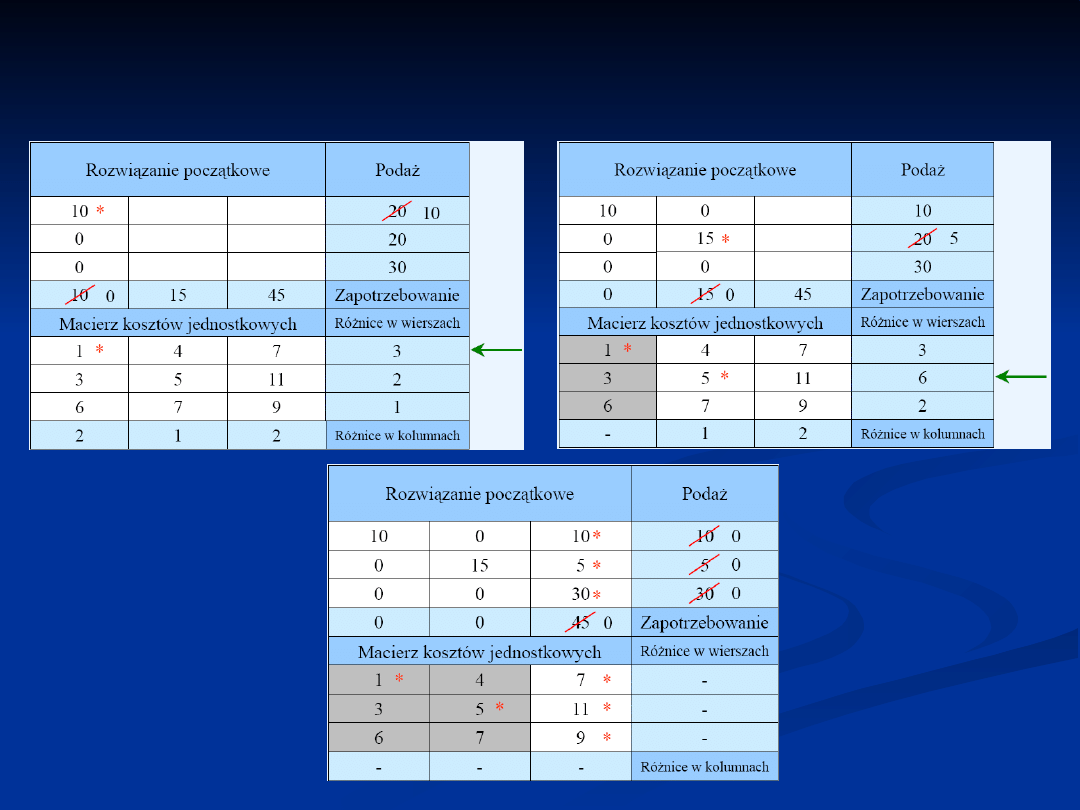
Pierwsze dopuszczalne rozwiązanie bazowe -

Pierwsze dopuszczalne rozwiązanie bazowe -

metoda aproksymacji Vogel’a:

metoda aproksymacji Vogel’a: