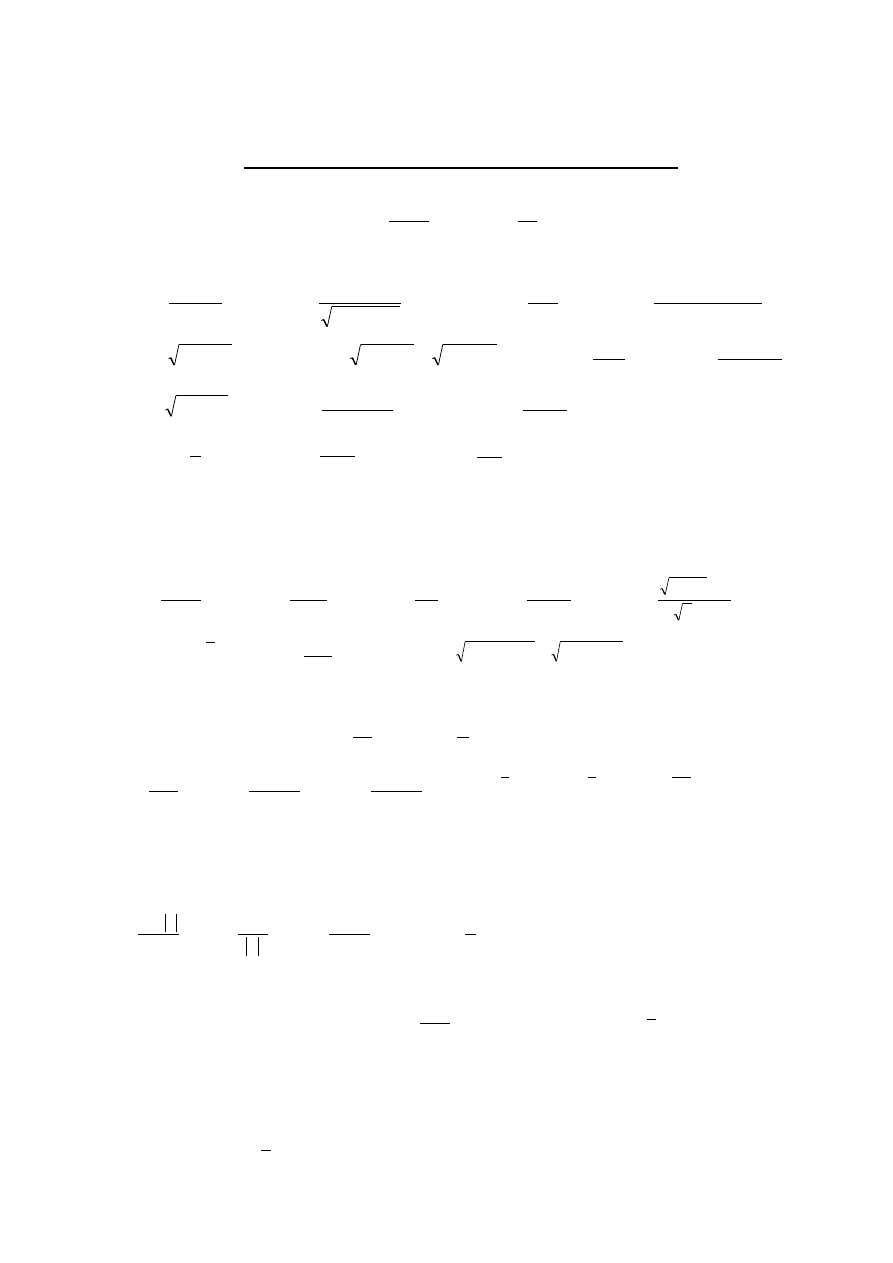
Logistyka, inżynieria bezpieczeństwa
Matematyka II (analiza matematyczna)

2 lista zadań. Granice ciągów i funkcji rzeczywistych. Ciągłość funkcji.

1. Zbadać monotoniczność ciągów:

n!

2

+

n

1

3n

n

3

=

a

b)

,

=

a

a)

n

n



2. Przypomnieć niektóre podstawowe granice ciągów. Wyznaczyć granice danych ciągów:

,

2

n

n

a

k)

,

1

+

3n

4n

+

n

sin

4

3

5

5

2

5

2

n

+

...

+

3

+

2

+

1

2

3n

+

n

2

3

n

5

n

2n

2

n

2

n

n

n

1

+

n

n

n

3

+

n

n

2

2

1)

(

=

=

a

j)

,

+

=

a

i)

,

4

=

a

h)

,

=

a

g)

,

2

5

=

a

f)

,

n

3

=

a

e)

,

=

a

d)

,

+

=

a

c)

,

1

n

+

n

n

=

a

b)

,

=

a

)

a

n

n

n

n

n

2

2

n

2

n

2

n

n

3

n

n



























n

n

n

n

n

n

n

n+

 

 

 

.

=

a

n)

,

=

a

m)

,

=

a

l)

1

2n

n

3n

n

1

n

1

n

2

+

n

n

2

+

1

n

n

n







3. Pojęcie granicy funkcji w punkcie x

0

w sensie definicji Heinego. Twierdzenia o granicy funkcji

złożonych.

4. Wyznaczyć wskazane granice funkcji:

a) lim

b) lim

sin2x

5x

c) lim

tgx

3x

d) lim

e) lim

x 1

4

x 0

x 0

x 0

x 4

x

1

x 1

e

1

e

1

1 2x

3

x

2

3x

x

























,

,

,

,

,

 





)

2

x

-

3

(x

lim

)

i

-

x

lim

h)

,

1

-

x

1

x

3

x

x

lim

g)

,

x)

(1

lim

)

f

x

x

1

0

x

,

1

x

x

1

3x

x

2

2































.

5. Podać wartości granic jednostronnych:

],

[x

lim

[x],

lim

,

2

tg

lim

,

x

1

lim

,

sgn

lim

,

sgn

lim

+

0

x

0

x

1

x

3

0

x

+

0

x

0





















x

x

x

x



.

e

lim

,

2

lim

,

2

lim

,

2

sgn

1

lim

,

2

sgn

1

lim

,

2

3

lim

1

2

1

x

1

+

0

x

1

0

x

0

+

0

x

2





























x

x

x

x

x

x

x

x

x

6. Podać określenie funkcji ciągłej w punkcie x

0

, ciągłej w przedziale otwartym (a; b), ciągłej w

przedziale zamkniętym



a; b



. Co to są punkty nieciągłości pierwszego i drugiego rodzaju ?

7. W jakich punktach dane funkcje nie są ciągłe:

[x]

x

y

[x],

y

,

x

1

arctg

y

,

1

x

x

y

,

x

sinx

y

,

2

y

2



















x

x

x

?

8. Zbadać ciągłość funkcji:



































0

x

dla

0

x

dla

2

=

(x)

0

=

x

dla

1

0

x

dla

x

sinx

=

g(x)

b)

,

0

x

dla

1)

-

(x

0

<

x

dla

1

x

f(x)

a)

1

2

h

c)

,

x

x

.

9. Uzasadnić na podst. twierdzenia Darboux, że równanie ma co najmniej jedno rozwiązanie w podanym
przedziale:

b)

;

;1)

(

1,

2x

x

log

a)

.

x

2

1

(0;1)

3,

x

3

2







