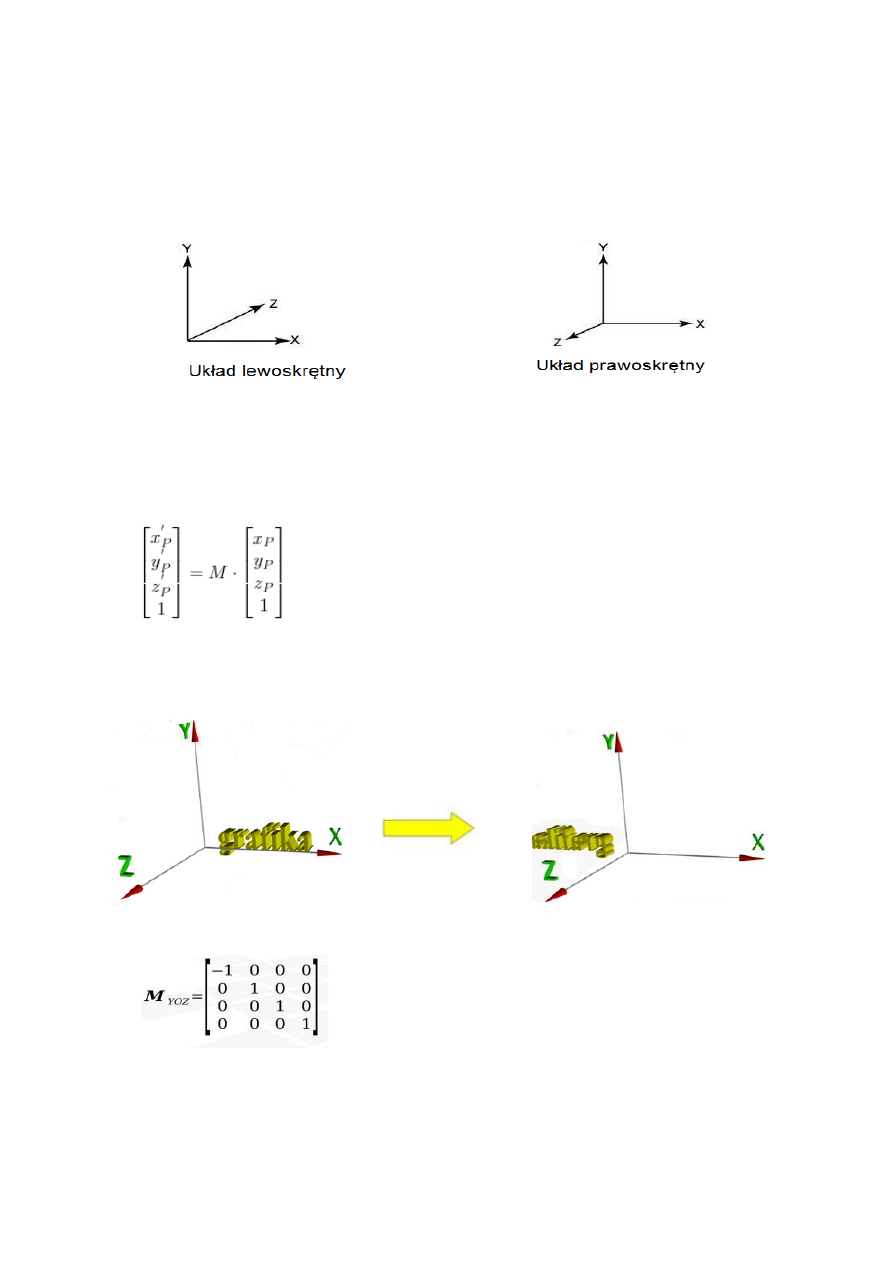
1) Przekształcenia trójwymiarowe

Istnieją dwa typy układów współrzędnych: lewoskrętny i prawoskrętny. Różnią się one
między sobą kierunkiem osi Z. Układ prawoskrętny stosowany jest do opisu położenia
obiektów na scenie. Lewoskrętny natomiast do operacji rzutowania.

Operacje w przestrzeni 3D opisuje macierz 4x4. Jeżeli macierz M opisuje transformacje,
a położenie punktu wektor P ( x

p

, y

p

, z

p

) to:

P' = M * P
czyli

Macierze opisujące symetrie płaszczyznowe względem pozostałych dwóch płaszczyzn
(XOY i YOZ) mają analogiczną postać ze zmienionym znakiem przy 1 w odpowiedniej
kolumnie.
Poniżej jest przedstawiony rysunek symetrii płaszczyznowej względem osi YOZ

Macierz umożliwiająca taką symetrie:

Podobnie macierze opisujące symetrie osiowe względem pozostałych dwóch osi (OY i OZ)
mają analogiczną postać ze zmienionymi znakami.

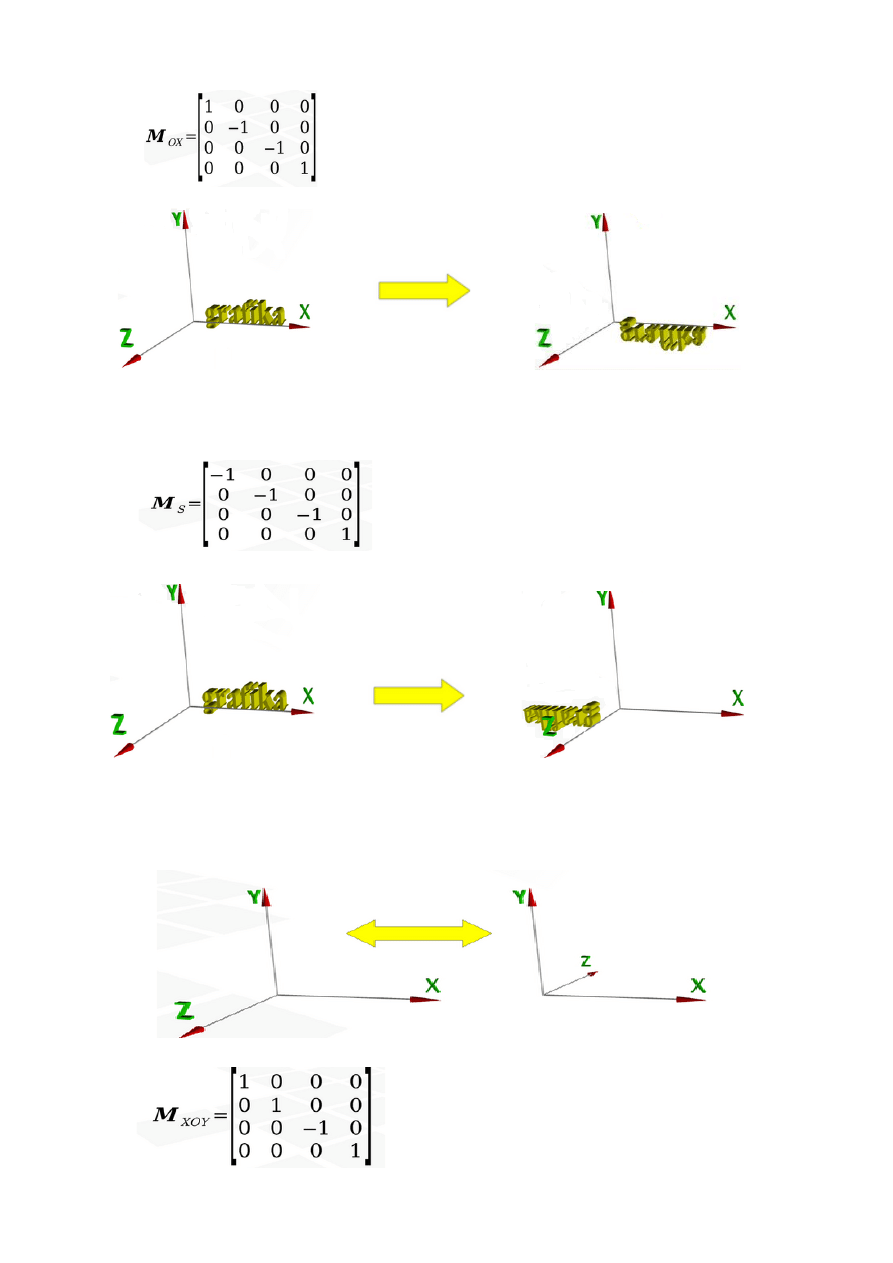
Macierz powyżej jest przedstawiona do obliczeń symetrii osiowej względem osi OX.

Następną symetrią jest symetria środkowa.

Ostatnią z symetrii jest symetria płaszczyznowa względem XOZ. Różni się ona przede
wszystkim od wcześniej przedstawionych tym, że jako jedyna zmienia skrętność układu
współrzędnych.

Jeżeli założyliśmy, że położenie obiektów sceny będzie opisywane w układzie
prawoskrętnym, natomiast rzutowanie będzie rozpatrywane w układzie lewoskrętnym, to
współrzędne tego samego punktu w obu układach będą się różniły znakiem przy
współrzędnej z. Przeliczenie współrzędnych między układami zapewnia macierz symetrii
płaszczyznowej względem XOY.

Jako następne przekształcenie 3D przedstawione zostanie przesunięcie. To przekształcenie
odbywa się analogicznie jak przy przesunięciu na płaszczyźnie. Przesunięcie punktu o
wektor T w postaci macierzowej wygląda następująco.

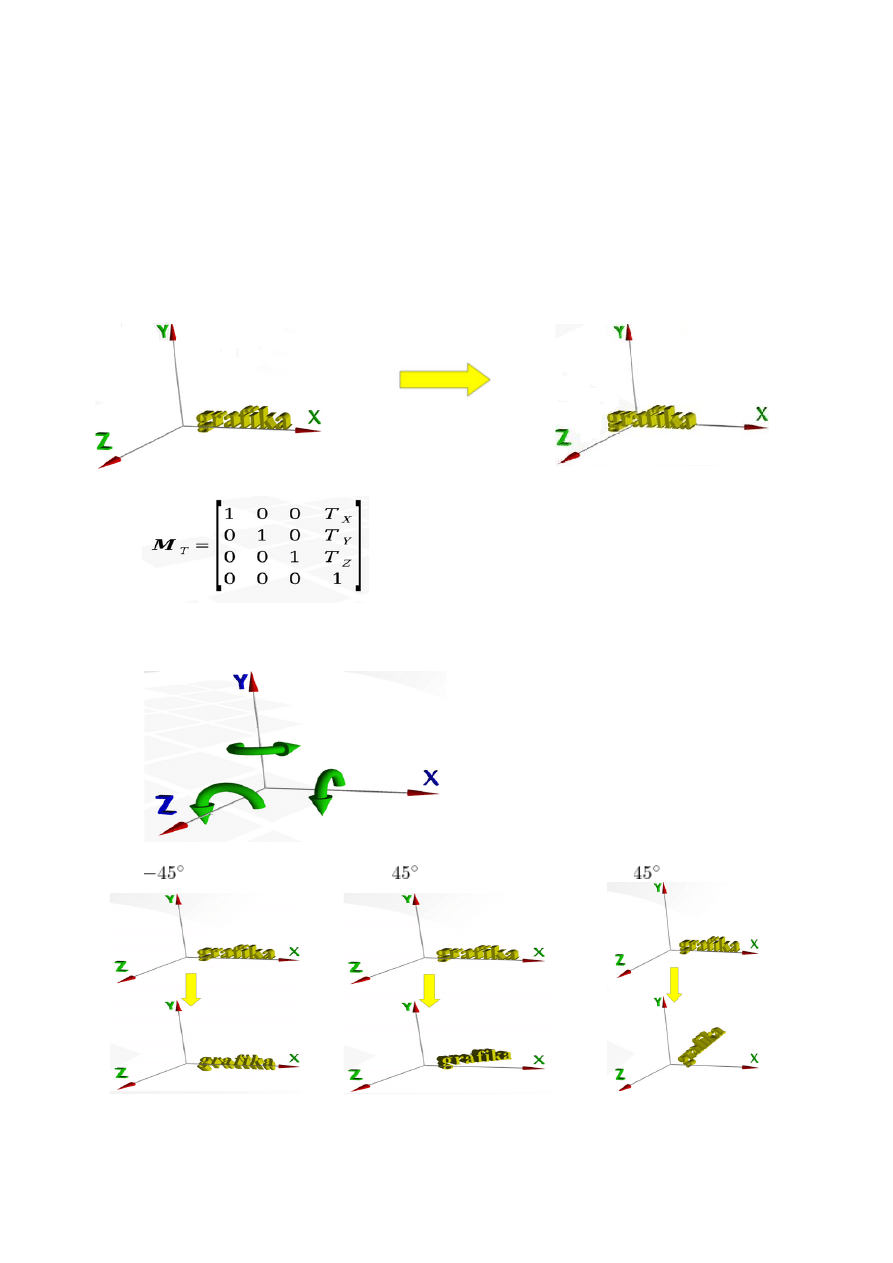
W układzie współrzędnych kartezjańskich trójwymiarowych zdefiniowanie obrotów wokół
osi układu wymaga przyjęcia reguł uznawania obrotów za dodatnie. Najczęściej przyjmuje
się konwencję, według której dodatnie obroty są zdefiniowane zgodnie z rysunkiem.

kat

wokół osi OX

kat

wokół osi OY

kat

wokół osi OZ

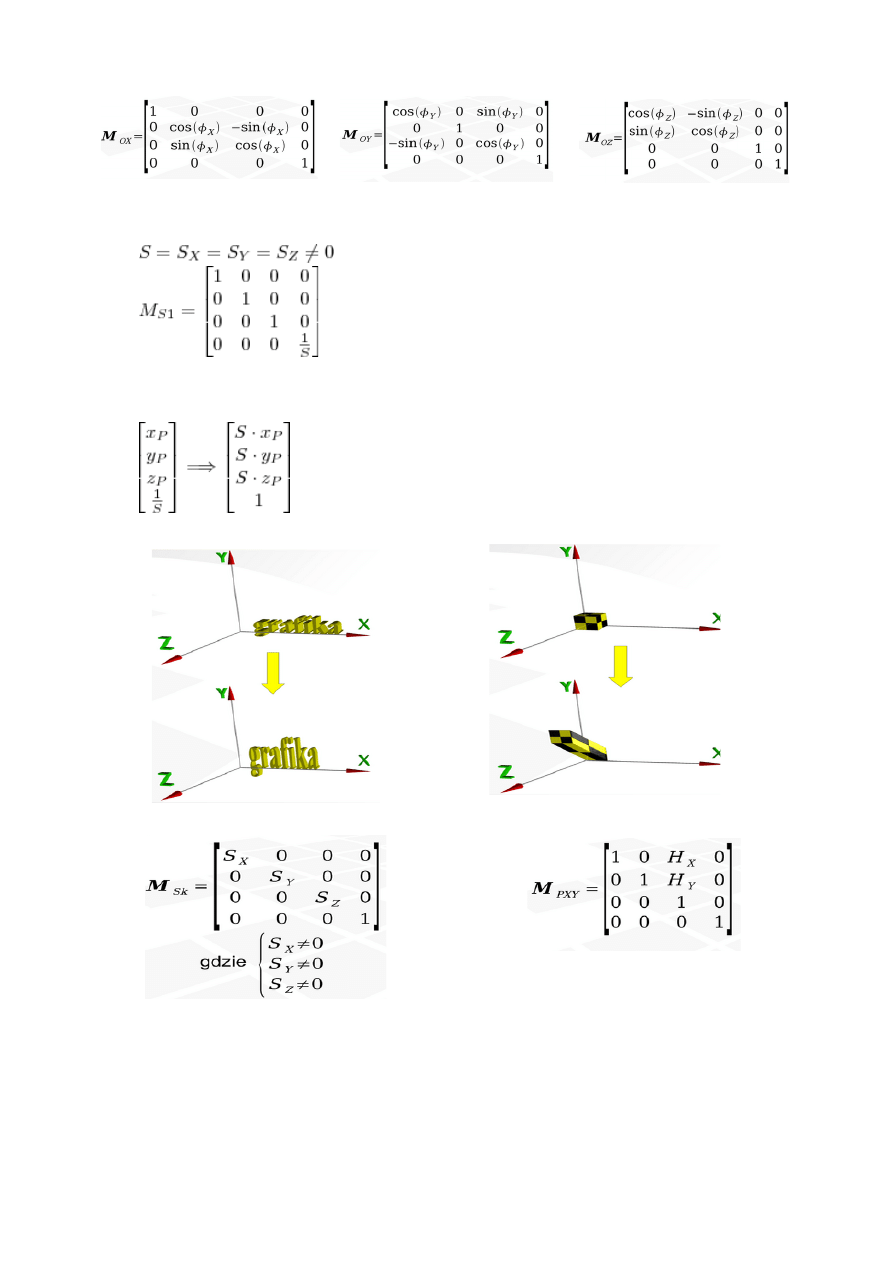
Skalowanie, zresztą tak samo jak pochylenie jest przykładem przekształcenia
nieizometrycznego. Jeżeli chodzi o skalowanie to warto zwrócić uwagę na to, że jeśli

to skalowanie można opisać macierzą:

Ale wynik tej operacji nie jest znormalizowany. Zgodnie z przyjętymi wcześniej zasadami
posługiwania się współrzędnymi jednorodnymi taka operacja jest w tym przypadku
niezbędna.

skalowanie

pochylenie

2) Różnica pomiędzy obcinaniem odcinka od procesu obcinania wieloboku

Obcinanie linii prostej na krawędzi figury geometrycznej wypukłej (jak np. kwadrat czy

prostokąt) zawsze generuje tylko jeden widoczny odcinek tej linii. Oznacza to, że widoczny
odcinek linii można określić przez obliczenie współrzędnych jego punktów końcowych. Ta
prosta właściwość wykorzystana została w liniowym algorytmie obcinania opracowanym
przez D. Cohena i I. Sutherlanda. Pozwala on na szybkie odnajdywanie punktów

końcowych, daje również możliwość bardzo szybkiego odrzucenia linii leżącej całkowicie
poza obszarem widzialnym. Składa się on z dwóch zasadniczych części. W pierwszej
określa się czy badana linia jest całkowicie wewnętrzna czy całkowicie zewnętrzna. W tym
drugim przypadku następuje jej odrzucenie. Jeśli linia nie spełnia żadnego z tych testów to
przechodzi się do drugiej części algorytmu, w której dokonuje się clippingu linii.
Algorytm Cohena-Sutherlanda (1974) służy do obcinania odcinków do prostokątnego okna.
Oznacza to, że należy wybrać odcinki (lub ich fragmenty) do obcięcia na podstawie
położenia ich końców.
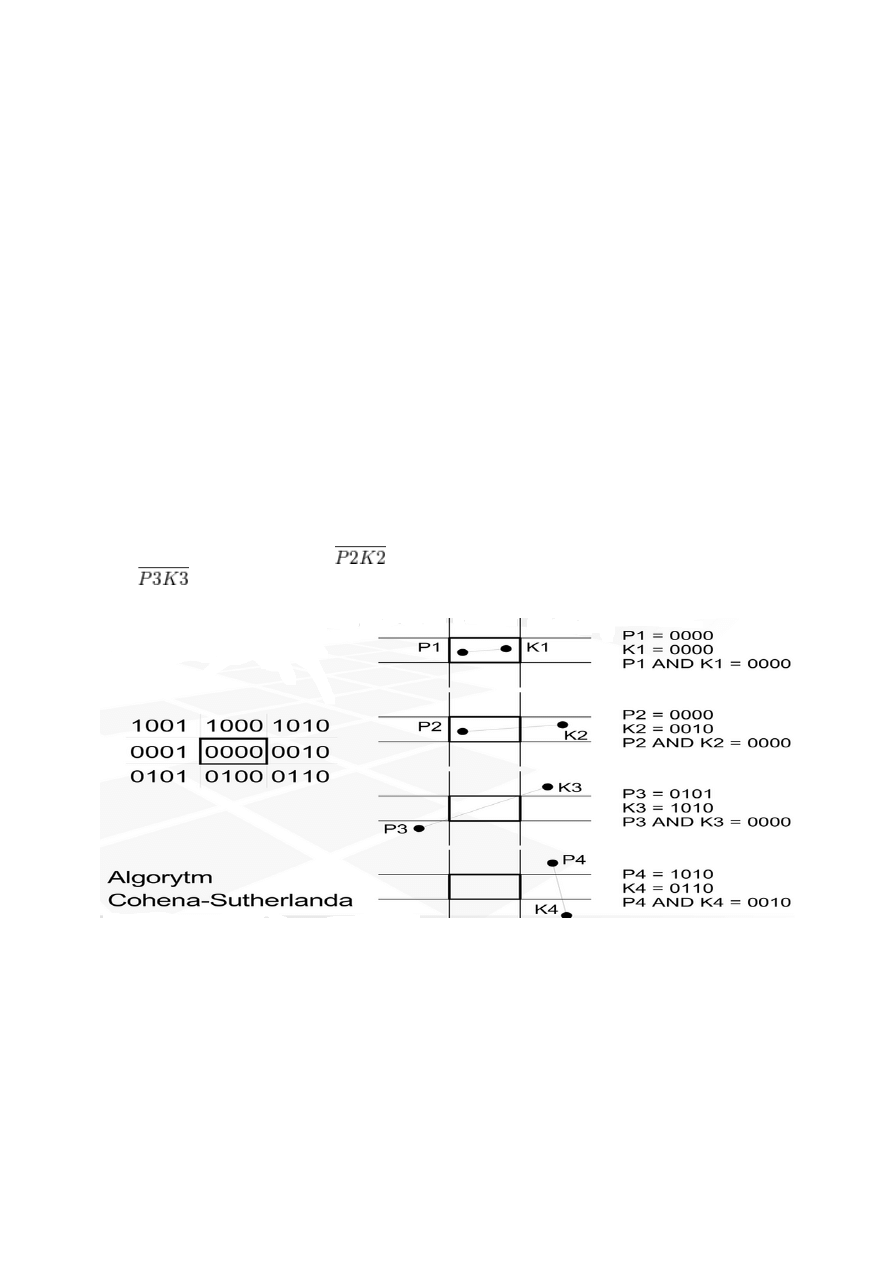
Płaszczyzna została podzielona na 9 obszarów . Prostokąt centralny odpowiada obszarowi
okna. Jednocześnie krawędzie okna wyznaczają cztery proste: prawą, lewą, górna i dolną.
Każdemu obszarowi został przypisany czterobitowy kod. Kolejne bity kodu określają
poziome i pionowe pasy. Operacja AND przeprowadzona na kodach końców odcinka
pozwala odrzucić te odcinki, które na pewno są poza oknem. Spośród pozostałych odcinków
należy wybrać te, które rzeczywiście mają wspólne punkty z oknem oraz przyciąć do jego
rozmiaru. Operacja AND pozwala w tym przypadku wybrać prostą obcinającą.
Jeśli wynik operacji AND jest różny od zera – należy odrzucić odcinek jako nie mający na
pewno punktów wspólnych z oknem.
Jeśli wynik operacji AND jest zerowy – odcinek może przecinać okno. W takiej sytuacji
należy rozważyć przypadek szczególny gdy kody obu końców są zerowe, wtedy cały
rysunek leży wewnątrz okna.
Natomiast jeśli kody końców są niezerowe to określają one którymi prostymi należy
przyciąć odcinek. Odcinek

należy przyciąć prostą prawą (K2=0010). Odcinek

prostymi lewą i dolną (P3=0101) oraz prawą i górną (K3=1010).

Obcinanie innych elementów grafiki takich jak: znaki, łuki kołowe, czy inne krzywe można

zrealizować przez konwersję danego elementu w zbiór liniowych odcinków, który może już
być przetworzony przez algorytm Cohena-Sutherlanda. Często jednak takie dzielenie
elementów grafiki na odcinki jest bardzo niewygodne. Dużo wygodniejszym jest uzyskanie
na wyjściu procesu obcinania elementu obrazu tego samego rodzaju co podawany na
wejściu.
W szczególności odnosi się to do wieloboków rozumianych jako zamknięte kontury
ograniczone prostymi krawędziami.
Z obcinaniem wieloboków wiąże się kilka problemów. Przede wszystkim po obcięciu

wieloboku otrzymuje się kontur, który nie jest już zamknięty. Pociąga to za sobą

konieczność domknięcia konturu poprzez połączenie odpowiednich odcinków krawędzi
obszaru widzialnego. Wyznaczenie prawidłowych odcinków krawędzi do połączenia nie
jest zadaniem łatwym. Po drugie problem stwarza obcinanie wieloboków wklęsłych (tj.
wieloboków posiadających co najmniej jeden kąt > od 180). Cechą charakterystyczną
wklęsłego wieloboku jest uzyskanie po jego obcięciu kilku wieloboków, które należy
połączyć tzw. zdegenerowanymi krawędziami. Z tych względów nie można zastosować
prostego algorytmu liniowego obcinania.
W przypadku obcinania wielokąta, zastosowanie algorytmu obcinania odcinków przynosi
tylko połowiczny sukces. Wielokąt tworzy bowiem zbiór uporządkowanych wierzchołków.
Każdy wierzchołek jest początkiem pewnego boku i jednocześnie jest końcem
poprzedniego boku w danym uporządkowaniu. Potraktowanie boków wielokąta jako zbioru
kładem algorytmu rozwiązującego ten problem jest algorytm Sutherlanda-Hodgmana
obcinania wielokąta.
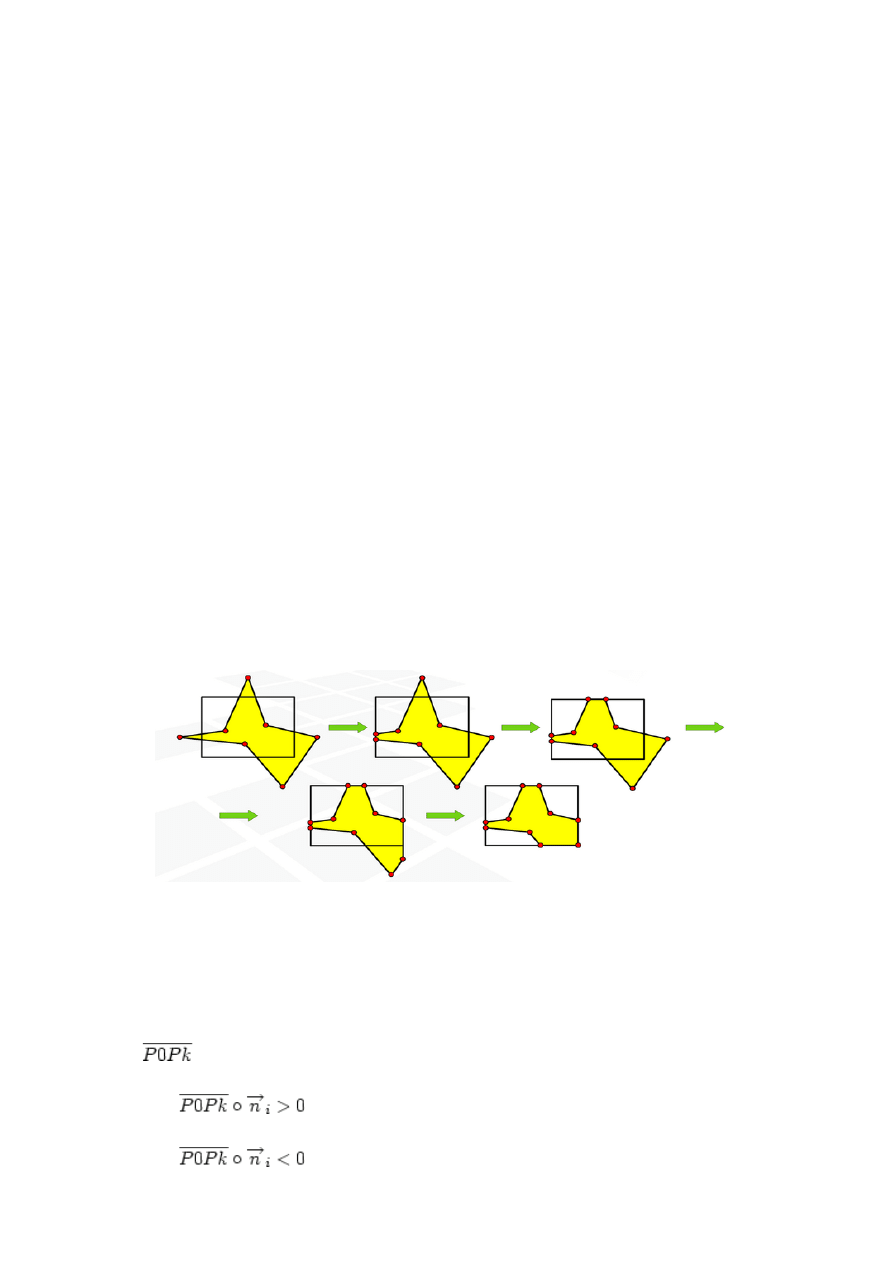
Niech kolejne wierzchołki wielokąta tworzą listę cykliczną
Obcinanie odbywa się kolejno dla prostych zawierających boki okna w ustalonym
porządku. W każdym kroku algorytmu rozpatrywany jest jeden wierzchołek leżący poza
oknem przycinania. Wierzchołek taki jest usuwany z listy ale w jego miejsce wstawiane są
wierzchołki „odpowiadające mu” na brzegu okna. Oczywiście należy wziąć pod uwagę
również i takie przypadki, w których dodany wierzchołek będzie leżał na prostej
zawierającej bok okna ale będzie to wierzchołek, który zostanie również usunięty np. w
następnym kroku. Z drugiej strony możliwy jest także przypadek, kiedy kolejne wierzchołki
wielokąta leżą na zewnątrz okna i wtedy kilka z nich może zostać zastąpionych jednym
punktem na brzegu okna.
odcinków i przycięcie ich powoduje, że tracimy informacje o ich połączeniach.

PrzyAlgorytm Cohena-Sutherlanda bardzo efektywnie klasyfikuje odcinki i jednocześnie
jest bardzo prosty w implementacji. Powoduje to, że jest chyba najczęściej stosowanym
algorytmem przycinania odcinków do prostokątnego okna.

Ma jednak jedną wadę. Często odcinki są przycinane kilka razy (różnymi prostymi) zanim
uzyskają końcową postać. Z punktu widzenia wyznaczania przecięcia nie jest to efektywne.
W 1978 roku Cyrus i Beck zaproponowali całkowicie inne podejście do problemu
obcinania.
Jeśli opiszemy prostą parametrycznie to wzrost parametru określi naturalny zwrot prostej.
Niech punkty P0 i Pk odpowiadają odpowiednio parametrom t=0 i t=tk dla k>0. Wektor

określa zwrot prostej. Można przeanalizować iloczyn skalarny tego wektora i

wektora normalnego (skierowanego na zewnątrz) do boku wielokąta.

Jeśli

to parametr tk określa punkt Pk.który może być „maksymalnym”

punktem przecięcia z wielokątem.

Jeśli

to parametr tk określa punkt Pk.który może być „minimalnym”

punktem przecięcia z wielokątem.
Cyrus i Beck zaproponowali efektywny zestaw operacji parametrycznych do analizy całego
wielokąta. Algorytm ten został w 1984 roku rozszerzony Lianga i Barsky’ego do ogólnego
przypadku 2D obcinania prostymi równoległymi do osi układu współrzędnych oraz 3D
obcinania płaszczyznami prostopadłymi do osi układu współrzędnych.

3) Główne problemy przy wypełnianiu kolorem wieloboku i parametry, które bierzemy pod

uwagę
Pierwszym omawianym algorytmem wypełniania jest wypełnianie przez spójność.

Wypełnianie przez spójność zakłada znajomość punktu startowego (tzw. „ziarna”) wewnątrz
obszaru. Punkt ten jest wypełniany, a następnie startując z niego wypełniamy punkty
sąsiednie (jeśli oczywiście istnieją – jeśli nie są już wypełnione, ani nie są punktami
granicznymi obszaru). Jednocześnie punkty sąsiednie stają się wyjściowymi dla
wypełniania w następnym kroku. Procedura ta jest powtarzana dopóki można wskazać
punkty wyjściowe (niewypełnione) wewnątrz obszaru.

Siatka czterospójna

Siatka ośmiospójna

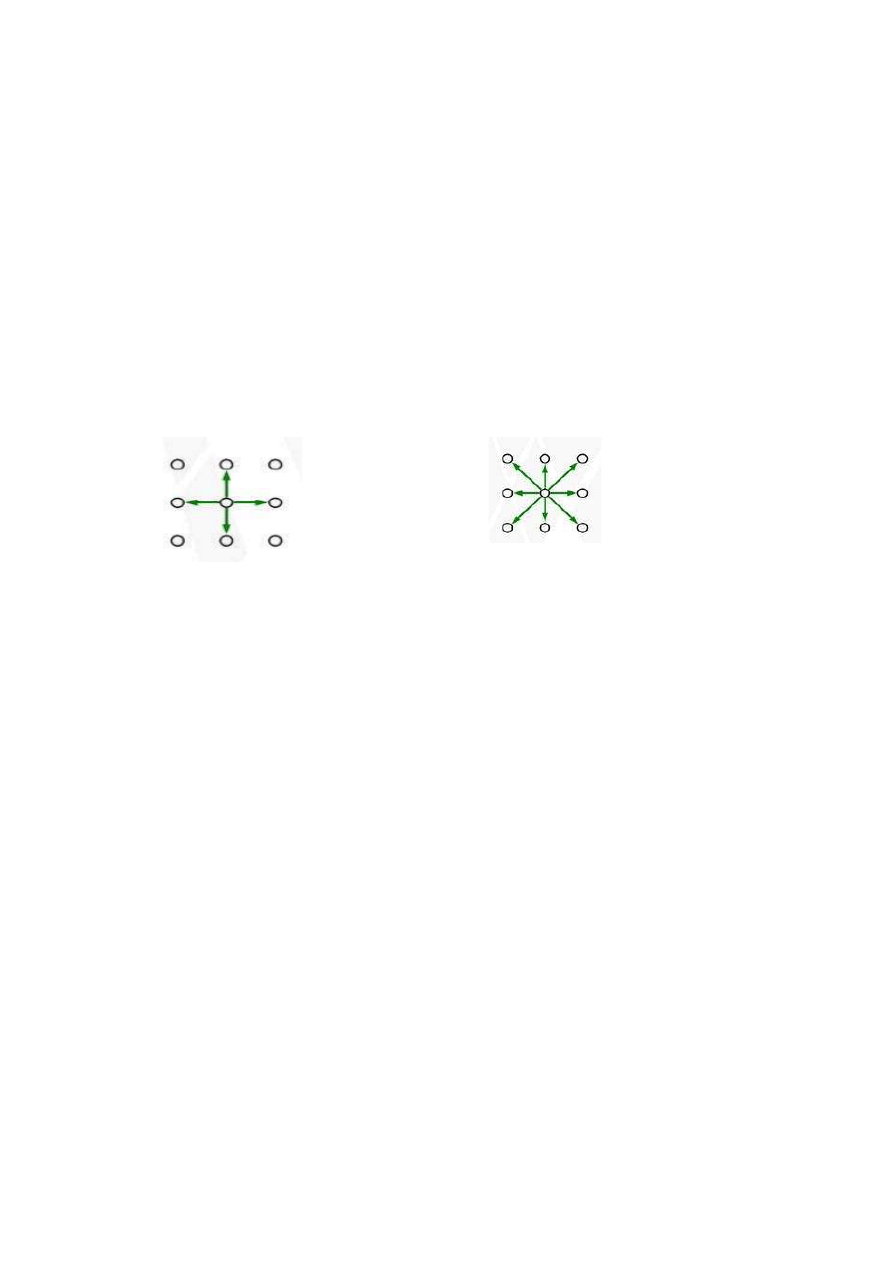
Warto zwrócić tutaj uwagę na problem sąsiedztwa i konieczność dostosowania do niego
kształtu brzegu. Można wyróżnić dwa przypadki. Gdy ruchy po mapie pikseli mogą
odbywać się analogicznie do ruchów wieży po szachownicy – wtedy piksel ma 4 sąsiadów –
siatka jest czterospójna. Gdy dodamy do tego jeszcze ruchy na ukos (odpowiada to
kierunkom ruchów hetmana w szachach), to piksel ma 8 sąsiadów – siatka jest ośmiospójna.
Czytelnik może przeanalizować jak powinien wyglądać rozkład pikseli brzegu dla obu
przypadków aby stanowił on figurę zamkniętą z punktu widzenia możliwości ruchu.
Algorytm stosowany przy takim wypełnieniu siatką czterospójną.
• wybieramy punkt, ktory leży wewnątrz wypełnianego obszaru (tzw. ziarno)
i wypełniamy go (każdy punkt sąsiedni leży wewnątrz tego obszaru lub jest punktem
brzegowym)
• wypełniamy kolejne punkty sąsiednie (jeśli nie są punktami brzegowymi i nie są już
wypełnione)
• punkty sąsiednie stają się kolejnymi punktami startowymi
• procedura jest powtarzana dopóki można znaleźć punkty startowe wewnątrz wypełnianego
obszaru
Wypełnianie przez kontrolę parzystości wykorzystuje pewną właściwość przecięcia brzegu
linią prostą. Jeśli punkty przecięcia ponumerujemy kolejnymi liczbami naturalnymi zgodnie
z orientacją prostej i jeśli będziemy poruszać się po prostej zgodnie z jej orientacją to każde
nieparzyste przecięcie będzie „wejściem” do wnętrza obszaru, natomiast każde parzyste
będzie „wyjściem” na zewnątrz. Zatem, aby wypełnić obszar należy go przecięć prostymi
odpowiadającymi kolejnym rzędom pikseli, a następnie wypełnić odcinkami pomiędzy
każdym nieparzystym przecięciem, a najbliższym parzystym.Oczywiście należy
zmodyfikować to postępowanie dla przypadków szczególnych, gdy punkt przecięcia jest
jednocześnie lokalnym ekstremum brzegu, co zaburza prostą regułę parzystości. Lokalizacja
lokalnego ekstremum możliwa jest na podstawie położenia końców przecinanych odcinków.

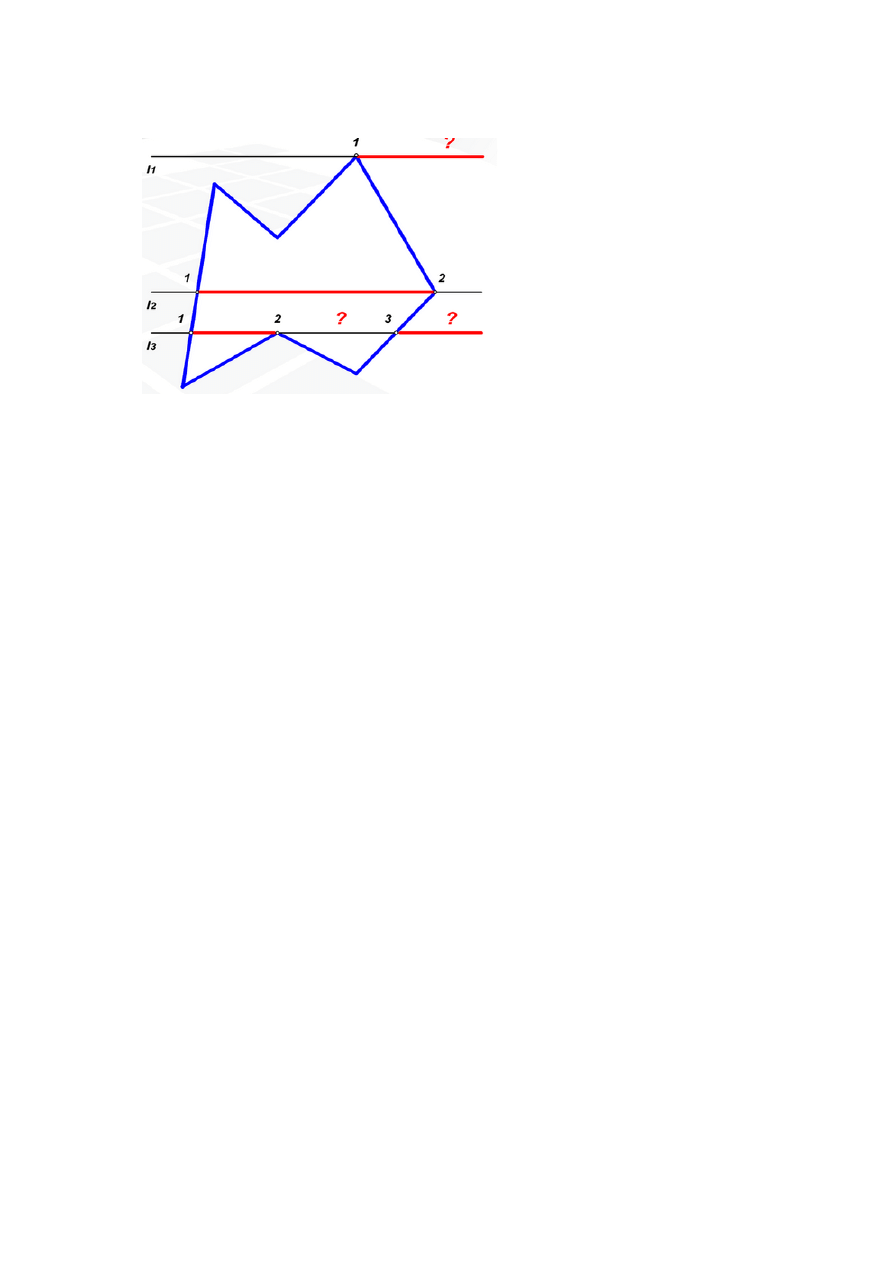
Jeśli są po tej samej stronie prostej wypełniającej – przecinany punkt jest lokalnym
ekstremum i nie należy jego liczyć przy analizie parzystości.

Algorytm stosowany przy tego typu wypełnieniu
• przecinamy wielokąt prostymi równoległymi, odpowiadającymi kolejnym rzędom pikseli
• numerujemy punkty przecięcia prostych z krawędziami wielokąta od lewej do prawej
strony
• każde nieparzyste przecięcie jest „wejściem” do wnętrza wypełnianego obszaru, każde
parzyste
przecięcie jest „wyjściem” na zewnątrz tego obszaru
• wyświetlamy odcinki pomiędzy każdym nieparzystym a najbliższym parzystym
przecięciem

.

W szczególnych przypadkach mogą pojawić się obszary nie dające się wypełnić w sposób
spójny – problem „drzazgi”. Jedynym sposobem rozwiązania tego problemu jest
nadpróbkowanie. Należy spróbkować i wypełnić drzazgę z większą rozdzielczością, a
następnie uśrednić barwę/luminancję wracając do rozdzielczości rastra
Rozwiązanie-nadpróbkowanie

• probkujemy i wypełniamy drzazgę dla większej rozdzielczości
• powracamy do rozdzielczości rastra przez uśrednianie