
RUCH DRGAJACY
Prosty oscylator harmoniczny - równanie ruchu
Ruch harmoniczny prosty
0
2
2
=
+
kx
dt
x
d
m
równanie
)
cos(
δ
ω
+
=
t
A
x
rozwiazanie
m
k
=
2
ω
)
cos(
)
sin(
)
cos(
2
2
2
δ
ω
ω
δ
ω
ω
δ
ω
+
−
=
=
+
−
=
=
+
=
t
A
dt
x
d
a
t
A
dt
dx
v
t
A
x
)
cos(
),
cos(
)
cos(
2
2
δ
ω
ω
δ
ω
δ
ω
ω
+
=
=
+
−
=
+
−
t
A
x
oraz
m
k
a
t
A
m
k
t
A
)
cos(
]
2
cos[
]
)
2
(
cos[
δ
ω
δ
π
ω
δ
ω
π
ω
+
=
+
+
=
+
+
=
t
A
t
A
t
A
x
Okres ruchu
m
k
T
f
i
k
m
T
π
π
ω
π
ω
π
2
1
2
1
2
2
=
=
=
=
=
T
f
π
π
ω
2
2
=
=
,
ω
– czestosc kolowa – jednostka [rad/s], f – czestoscia drgan oscylatora,
A - amplituda ruchu, (
ω
t +
δ
) - faza ruchu,
δ
– stala fazowa (faza poczatkowa).
m
F = 0
F = -kx
F = -kx
x = 0
x
F = ma i F = -kx,
0
lub
2
2
2
2
=
+
=
=
−
kx
dt
x
d
m
dt
x
d
m
ma
kx
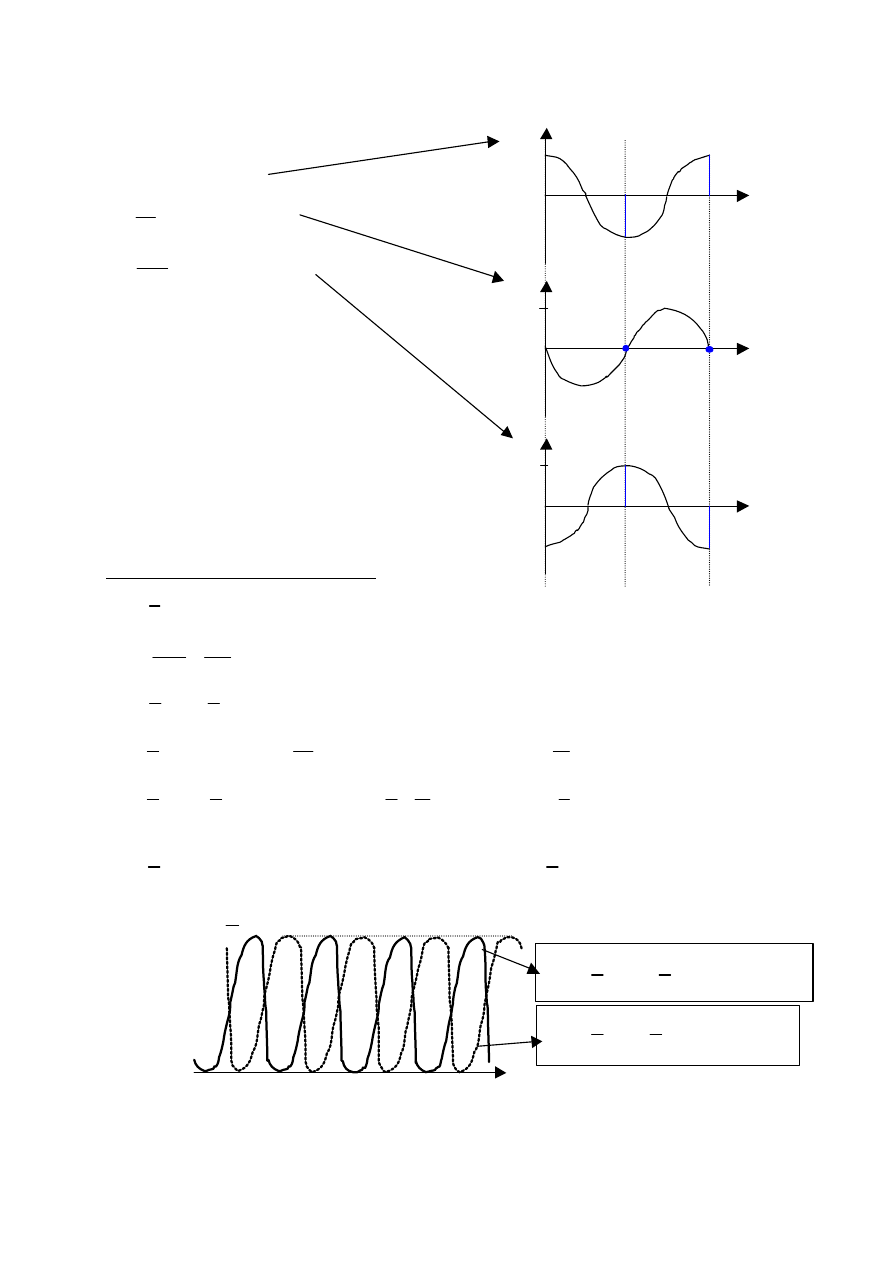
)
cos(
)
sin(
)
cos(
2
2
2
δ
ω
ω
δ
ω
ω
δ
ω
+
−
=
=
+
−
=
=
+
=
t
A
dt
x
d
a
t
A
dt
dx
v
t
A
x
Energia w prostym ruchu harmonicznym
kx
dx
dU
dx
dE
F
t
A
x
i
kx
E
p
p
−
=
=
−
=
+
=
=
)
cos(
2
1
2
δ
ω
)
(
cos
2
1
2
1
2
2
2
δ
ω
+
=
=
t
kA
kx
E
p
)
(
sin
2
1
)
(
sin
2
1
)
(
sin
2
1
2
1
),
sin(
2
1
2
2
2
2
2
2
2
2
2
2
δ
ω
δ
ω
δ
ω
ω
ω
δ
ω
+
=
+
=
+
=
=
=
+
−
=
=
=
t
kA
t
A
m
k
m
t
A
m
mv
E
wtedy
m
k
gdzie
t
A
dt
dx
v
i
mv
E
k
k
)
(
cos
2
1
)
cos(
2
1
2
2
2
δ
ω
δ
ω
+
=
+
=
=
t
kA
E
czyli
t
A
x
ale
kx
E
p
p
a
A
t
x
t
-
ω
2
A
t
v
-
ωA
)
(
sin
2
1
2
1
2
2
2
δ
ω
+
=
=
t
kA
mv
E
k
)
(
cos
2
1
2
1
2
2
2
δ
ω
+
=
=
t
kA
kx
E
p
t
2
2
1
kA
E
E
E
p
k
=
+
=
0
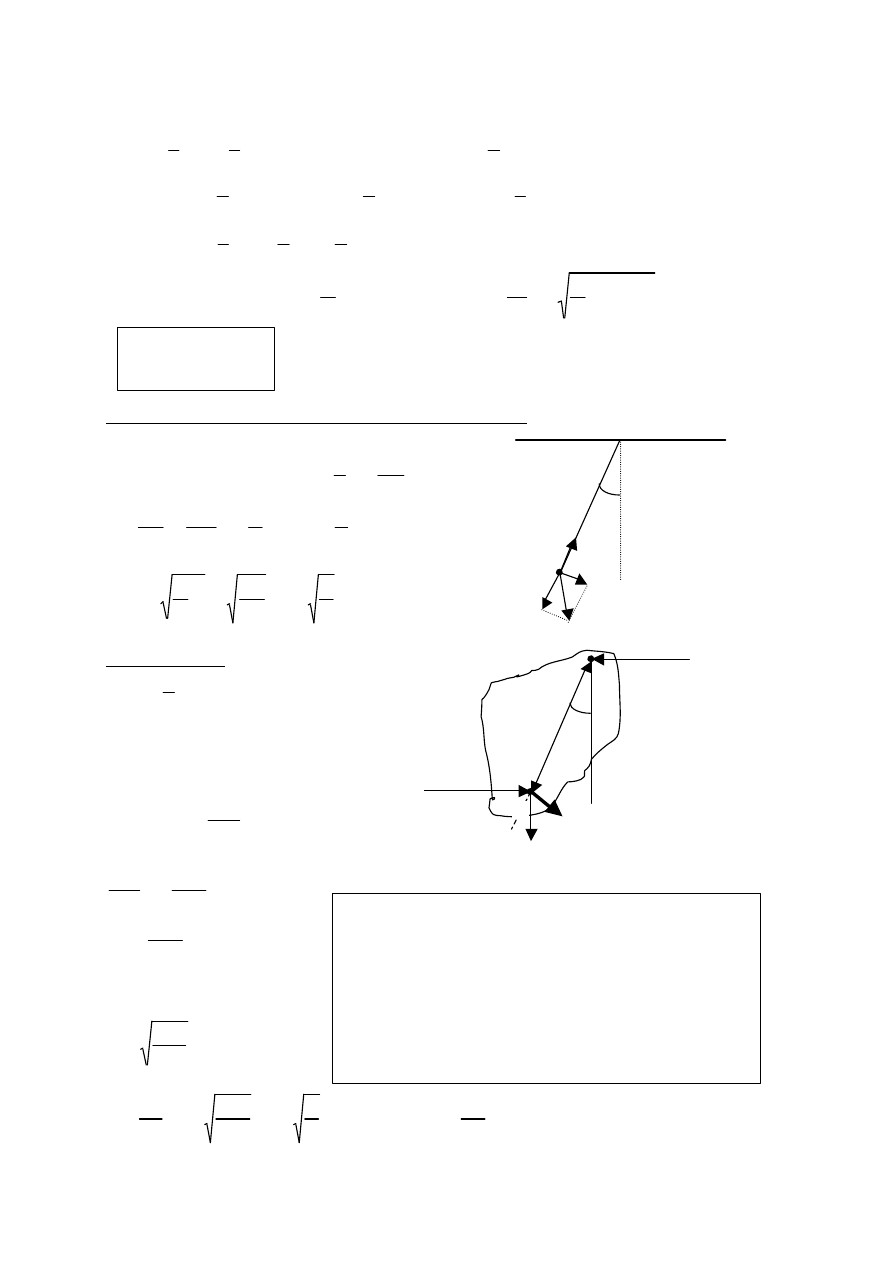
Maksymalna wartosc
2
2
2
max
2
1
2
1
A
m
kA
E
k
ω
=
=
2
max
2
1
kA
E
p
=
2
2
2
2
2
2
1
)
(
cos
2
1
)
(
sin
2
1
kA
t
kA
t
kA
E
E
E
p
k
=
+
+
+
=
+
=
δ
ω
δ
ω
)
(
)
(
)
(
2
1
2
1
2
1
2
2
2
2
2
2
2
2
2
2
2
x
A
m
k
dt
dx
v
i
x
A
m
k
v
x
A
k
mv
czyli
kA
kx
mv
E
E
E
p
k
−
±
=
=
−
=
⇒
−
=
=
+
=
+
=
Wahadlo matematyczne – jako przyklad ruchu harmonicznego
α
sin
mg
F
−
=
sina ~
α
i F~
α.
l
g
x
l
g
dt
x
d
l
mg
k
ma
kx
x
l
mg
l
x
mg
mg
mg
F
=
−
=
=
=
−
=
−
=
−
=
−
≈
−
=
2
2
2
,
,
sin
ω
α
α
Okres drgan w ruchu harmonicznym
g
l
mg
ml
k
m
T
π
π
π
2
2
2
=
=
=
Wahadlo fizyczne
r
mg
M
r
G
M
a
x
a
x
⋅
=
⋅
=
=
⇒
=
ϕ
ϕ
sin
sin
M = - mgasin
ϕ
i M = I
ε
2
2
sin
dt
d
I
mga
ϕ
ϕ
=
sinf ~ f
I
mga
I
mga
dt
d
=
−
=
2
2
2
ω
ϕ
ϕ
I
mga
gdzie
t
=
+
=
ω
α
ω
ϕ
ϕ
)
cos(
0
ma
I
l
gdzie
g
l
mga
I
T
r
r
=
=
=
=
π
π
ω
π
2
2
2
mgcosa
α
mgsina
mg
x = la
l
l
m
R
α
v
max
→
x = 0
v = 0
→
x = A
f
G = mg
a
O
O’
ϕ
Srodek
masy
Punkt
obrotu
m – masa wahadla
a – odleglosc masy od osi obrotu
I – moment bezwladnosci wahadla wzgledem osi obrotu
ϕ
– kat wychylenia z polozenia równowagi
ω
– czestosc kolowa
ϕ
0
– amplituda
α
– stala fazowa
l
r
– dlugosc zredukowana
ϕ
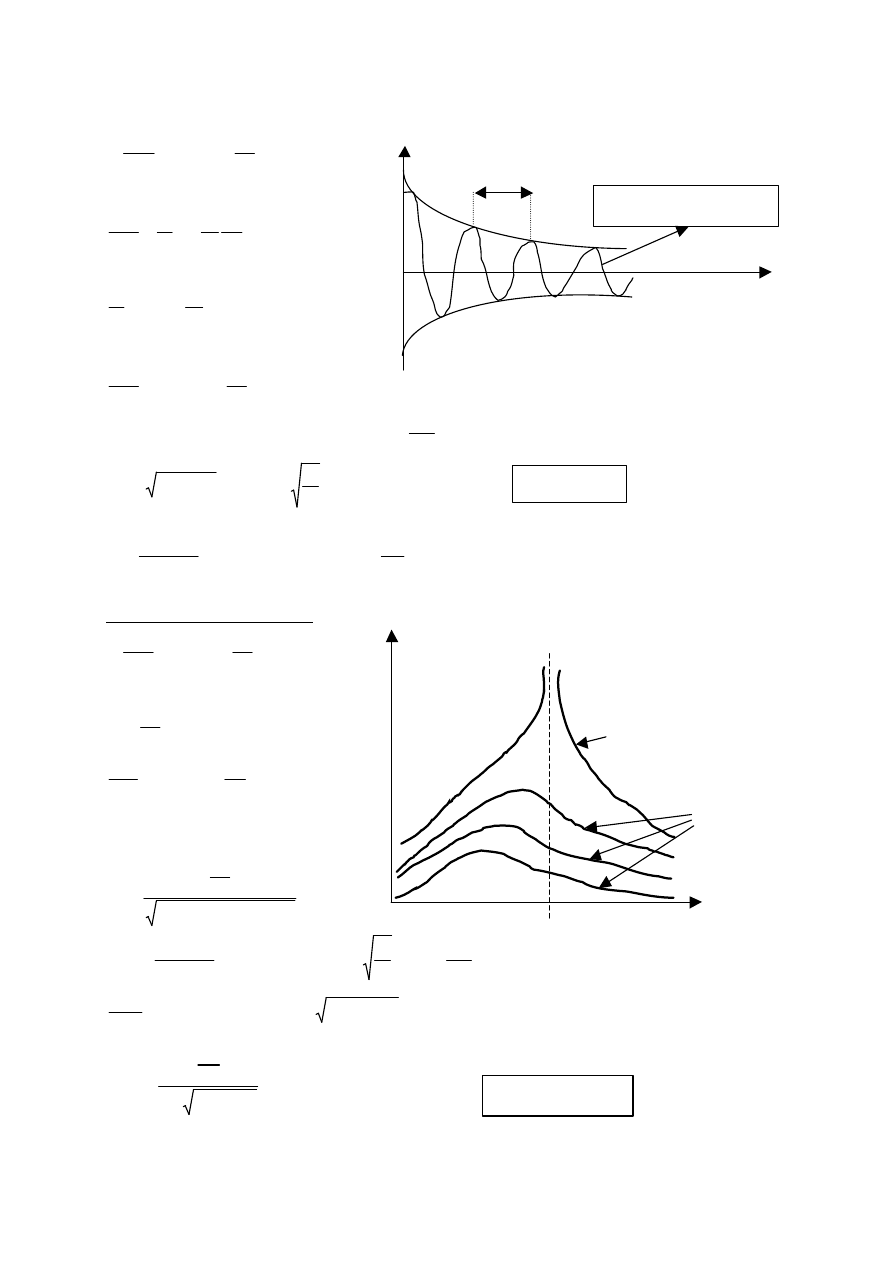
Ruch harmoniczny tlumiony (k
1
- wspólczynnik oporu osrodka)
0
2
2
,
0
0
2
2
1
0
1
2
2
1
2
2
=
+
+
=
=
=
+
+
−
−
=
dt
dx
x
dt
x
d
wtedy
m
k
m
k
i
dt
dx
m
k
x
m
k
dt
x
d
czyli
dt
dx
k
kx
dt
x
d
m
β
ω
β
ω
m
k
m
k
gdzie
t
e
x
x
t
=
−
=
=
+
=
−
0
2
2
0
1
1
1
0
2
)
cos(
ω
β
ω
ω
β
α
ω
β
Tlumienie
λ (T – okres ruchu harmonicznego tlumionego,
δ
– dekrement tlumienia)
T
i
T
gdzie
e
T
t
x
t
x
T
β
λ
δ
ω
π
λ
β
=
=
=
=
+
=
ln
2
)
(
)
(
Ruch harmoniczny wymuszony
t
B
dt
dx
x
dt
x
d
wtedy
m
F
B
dodatkowo
oznaczymy
i
t
F
dt
dx
k
kx
dt
x
d
m
2
2
0
2
2
0
2
0
1
2
2
sin
2
sin
ω
β
ω
ω
=
+
+
=
+
−
−
=
x = x
0
sin(
ω
2
t –
ϕ
)
x
0
,
ϕ
– wielkosci stale
m
k
m
k
gdzie
tg
m
F
x
2
,
2
4
)
(
1
0
2
2
2
0
2
2
2
2
2
2
2
0
0
0
=
=
−
=
+
−
=
β
ω
ω
ω
β
ω
ϕ
ω
β
ω
ω
2
2
0
0
0
2
2
0
2
2
2
0
2
,
2
0
β
ω
β
β
ω
ω
ω
ω
−
=
−
=
=
⇒
=
m
F
x
d
dx
rez
rez
x
0
?
0
ω
2
ß = 0
ß
≠
0 i rosnie
t
x
)
cos(
0
α
ω
β
+
=
−
t
e
x
x
t
T
(
ω
0
2
>
β
2
)
2
2
2
2
0
2
β
ω
ω
+
=
rez
Wyszukiwarka
Podobne podstrony:
Wykł 05 Ruch drgający
Kurs 05 Ruch drgający
05 ruch drgajacy w
Wykł 05 Ruch drgający
2 Ruch drgający i falowy
05 Ruch w ukladach inercjalnych i (2)
ruch drgający, Budownictwo-studia, fizyka
Ruch drgający
Ruch drgający i?lowy
Ruch drgający i?lowy
06 kURS Wykł 06 Ruch drgającyid 6140 ppt
zestaw 11 ruch drgajacy id 5879 Nieznany
Fizyka wykł 7,8 Ruch drgający (M Krasiński)
Egzamin - sciagi, 06. Ruch drgający, 6
10 Ruch drgajacy Bid 11089 Nieznany
13 Ruch drgającyid 14785
więcej podobnych podstron