IEEE TRANSACTIONS ON POWER SYSTEMS , VOL. 21, NO. 2, MAY 2006

997

A New Approach for Substation Expansion Planning

Mohammad Sadegh Sepasian, Hossein Seifi, Senior Member, IEEE, Asghar Akbari Foroud, Seyyed Hadi Hosseini,

and Esmaeil Mohseni Kabir

Abstract—Substation expansion planning (SEP), as a major

module of power system planning modules, is addressed in this
paper. For long-term transmission SEP, a new approach based on a
genetic algorithm (GA) optimization tool is proposed, in which by
defining appropriate objective function and various constraints,
new as well as expansion of existing substation requirements are
determined. The proposed algorithm is successfully tested for the
Iranian Power Grid in 2011.

Index Terms—Genetic algorithm (GA), optimization, power

system planning, substation expansion planning (SEP).

I. I

NTRODUCTION

W

ITH electric power consumption growth, desired new
transmission system elements are needed to overcome

the possible lack of adequacy problems so that with least costs,
various operational constraints are met. In the so-called sub-
station expansion planning (SEP), the problem is to determine
the required expansion capacity of the existing substations as
well as the allocation and size of new substations together with
the required availability times. The existing SEP algorithms are
normally based on several candidate substation buses. The user
should select the candidates, and an optimization algorithm will
choose the best solutions. If the candidates change, the solution
may change.

Over the years, SEP has received attention in the literature.

Reference [1] uses an integer programming approach to solve
the problem, while [2] employs a dynamic programming algo-
rithm. In [3], branch-and-bound dynamic programming is used
in which the optimum solution is found while observing all pos-
sible expansion candidates as well as the cost of active power
losses. In [4], the objective function is the cost of supplying the
loads by multiplying the loads by their respective distances from
the substation. Reference [5] proposes an approach in which
the problem is decomposed into two series problems in which
the first determines the optimal substation capacities, while in
the second, linear programming is employed to determine the
supplying feeders. In [6], mixed integer linear programming is
used, while in [7] and [8], linear programming is employed to
tackle the problem. Reference [9] employs integer programming

Manuscript received August 4, 2005; revised December 5, 2005. Paper no.

TPWRS-00487-2005.

M. S. Sepasian is with Power and Water, Industry University, Tehran, Iran

(e-mail: [e-mail]).

H. Seifi is with Tarbiat-Modares University, Tehran, Iran, and is also with Iran

Power System Engineering Research Center (e-mail: [e-mail]).

A. Akbari Foroud is with Semnan University, Semnan, Iran (e-mail: aak-

[e-mail]).

S. H. Hosseini is with Zanjan University, Zanjan, Iran (e-mail: siedhadi@hot-

mail.com).

E. M. Kabir is with Tavanir Co., Tehran, Iran (e-mail: [e-mail]).
Digital Object Identifier 10.1109/TPWRS.2006.873406

to find the optimal solution while observing the losses to be less
than a prespecified value. Genetic algorithm (GA) is used in [10]
to optimize the problem, while load uncertainties are considered
by a fuzzy-based technique. Reference [11] considers SEP as
a nonlinear optimization problem, while in [12], simulated an-
nealing is employed to find the solution.

While in [2], [4], and [10], the optimum solutions are found

from a list of available candidates, [6] and [9] are able to auto-
matically find the solutions. However, they could not be readily
applied to large-scale problems [13].

In [13], a heuristic algorithm is proposed in which the op-

timum required substation capacities are initially found. There-
after, they are allocated by minimizing a linearized model of
active power losses.

In this paper, a new SEP procedure is proposed in which the

mathematical clustering technique is used to find, initially, a list
of feasible candidates by observing the limitations on substation
capacities, feeder capacities, and voltage regulations. Then, GA
is used to solve an optimization problem in which the alloca-
tions and capacities of new substations as well as the expansion
requirements for the existing ones are determined. The numer-
ical results for the Iranian Power Grid are shown as a large-scale
practical case.

II. P

ROBLEM

F

ORMULATION

While the optimization problem defined for power system

planning may have different objective functions as well as var-
ious constraints [14]–[16], in the SEP problem, the objective is
to determine a mixture of both expansion plans for the existing
substations and the need for new substations so that the loads
are adequately supplied.

The loads to be supplied are widely geographically dis-

tributed. For substation planning, the normal procedure is to
initially determine the distribution substation requirements
and moving upward, to finally determine the transmission
substation requirements. This approach, although accurate and
practical for short and midterm planning, may prove impractical
for long-term studies (say, five years onward) of transmission
substations, as the transmission owner (developer) may wish
to determine the possible allocation and size of the substations
(either new or expansions on existing) without involving in
many details of the downward grids (subtransmission and
distribution). One way to overcome this problem is to propose
an algorithm in which the geographically distributed loads
are somehow assigned to transmission substations. Although
this does not happen in practice, the final transmission alloca-
tions and capacities can prove appropriate, provided various
constraints are properly observed. The assigning procedure
is, however, crucial as an unsuitable procedure can result in

0885-8950/$20.00 © 2006 IEEE

998

IEEE TRANSACTIONS ON POWER SYSTEMS , VOL. 21, NO. 2, MAY 2006

improper solutions. In Section II-A, the system under study is
described. The general optimization problem is presented in
Section II-B. A detailed algorithm is explained in Section III.

A. System Under Study

The existing Iranian Power Grid is made up of 400-, 230-,

132- and, 63-kV transmission and subtransmission elements.
The corresponding grid lengths are roughly 12 000, 23 000,
16 000, and 35 000 km, respectively. The sum of MVA capacity
of the transmission substations (transmission to subtranmis-
sion) is in the order of 90 000 MVA. The summer peak of the
grid in 2004 has roughly been 29 000 MW.

The transmission and subtransmission grids are highly inter-

connected, managed by 16 regional utilities owned by a holder
company (Tavanir). The transmission grid (i.e., 400 and 230 kV)
planning is monitored by Tavanir, while for the subtransmission
grid, the task is performed by regional utilities.

With rapid annual growth of 7%–9% electric consumption,

the grid is confronted by a challenging planning problem for the
years to come. The problem described is this paper addresses
SEP for large-scale transmission systems. It is specifically ap-
plied to 16 utilities of Iranian Power Grid for the summer elec-
tric power peak in 2011 without involving much in the details of
downward systems (subtransmission and distribution). A later
paper will address the corresponding network planning proce-
dure.

B. Optimization Problem

The SEP problem may be defined as an optimization proce-

dure in which all the investment costs as the well as operational
costs have to be minimized while numerous constraints are met.
The final solution should determine

•

expansion capacity of any existing substation (provided
feasible);

•

allocation and size of any new substation;

•

investment costs.

In the following subsections, the objective functions as well

as the constraints are described in detail.

1) Objective Functions: The aim is to supply the loads

through all transmission (transmission to subtransmission)
substations so that

(1)

is minimized.

is the overall plan cost. Other terms are

described below. Note the following.

•

Each load is presented with its value (in MW) and geo-
graphical characteristics (X and Y) in the horizon year.

•

Each load is assumed to be radially supplied by a trans-
mission substation (to ignore the distribution and sub-
transmission effects). Although not accurate in practical
terms, this approach facilitates the planning procedure
with due attention to some practical considerations (see
the following sections).

a)

: A load may be supplied by several nearby

substations. The cost is dependent on the distance between the
load center and the substation as follows:

(2)

in which

cost of all downward grids;
cost of the feeder for supplying the th load by
conductor

(see Section III-B for details);

distance between the th load and the th sub-
station;

S

set of all selected substations;

L(j)

set of all loads connected to the th substa-
tion.

b)

: A major cost is the investment cost for all sub-

stations defined as

(3)

where

fixed cost for the th substation;
variable cost factor for the th substation;
capacity of a new substation ;

S

set of all new substations and all expanded substa-
tions;

SE

set of all expanded substations;
amortizing coefficient for the existing substation ;
capacity of the existing substation .

c)

: Obviously, the closer a substation is to an

existing transmission grid, the more attractive it is, in terms of
general costs. To consider this effect, a term

is in-

cluded in (1), as defined in (4) consisting of two terms, namely,
a fixed cost for the right of way, tower, etc. (dependent on the
voltage level) and a variable cost (dominantly conductor cost)
dependent on the line capacity. Therefore

(4)

where

fixed cost of the upward grid for energizing substa-
tion ;
variable cost factor of the upward grid for ener-
gizing substation ;
upward grid capacity for energizing substation ;
distance between substation to the nearest feeding
point of HV transmission network.

It is evident that

does not show the exact distance for

practical situation. It somehow considers the upward grid in
problem formulation so that substations far from the existing
network are not justified.

SEPASIAN et al.: NEW APPROACH FOR SUBSTATION EXPANSION PLANNING

999

d)

: The losses of the downward grid (as opera-

tional losses) should also be minimized. That is why

is

introduced as

(5)

where

cost of the downward grid losses calculated as in
base year (for 30 years operational period);
conductor resistance of the feeder supplying the

th load (for details, see Section III-B);

change of MVA of the th load with respect to
the base value (current year) (for details, see Sec-
tion III-A);
as before.

e)

: Another term to be considered is the cost of

transformer losses (operational losses), denoted by

and

defined as

(6)

where

fixed cost of the th substation losses;
variable cost factor due to substation losses for full
load conditions;
cost of transformer losses calculated as in base year
(for 30 years operational period);
actual load of the th substation is MVA.

2) Constraints: The following constraints are considered in

the optimization problem:

•

for the downward grid: thermal capacity of the feeder
for supplying the load (Section II-B2a) and with accept-
able voltage drop (Section II-B2b);

•

for the substations: maximum and minimum installation
capacities (Section II-B2c) as well as standard capacities
(Section II-B2d);

•

for the upward grid: thermal capacity of the upward
transmission line (Section II-B2e).

a) Thermal capacity of the downward feeder:

(7)

where

set of loads;
required capacity for supplying the th load.

b) Voltage drop:

(8)

where

actual voltage drop for load ;
acceptable voltage drop;
factor for considering the fact that an already ex-
isting substation has some voltage problems, and

Fig. 1. Normal crossover.

the least amount of extra load should be applied to
this substation.

c) Maximum and minimum installation capacities:

(9)

In (9),

refers to required reserve capacity for the th substa-

tion. For the existing substations,

refers to the maximum

expansion capacity of the substation. For this type of substation,

may be set at a value less than its existing capacity (or even

zero). In that case, the substation may be de-rated (the extra ca-
pacity is considered as a benefit) or even totally removed, pro-
vided the optimization procedure finds it economical.

d) Standard capacities:

(10)

which shows that the substations should be selected from a set
of standard list (available from planning departments).

e) Thermal capacity of the upward lines: Similar to (7),

(11) applies to upward transmission lines

(11)

where

is a set of candidate substations.

C. Solution Algorithm

The following subsections briefly review candidate selection,

GA algorithm, and a refined algorithm.

1) Candidate Selection: To narrow the search space, an ap-

proach is proposed by which a list of suitable candidates is se-
lected for the new substations. The approach is based on the
mathematical clustering concept. For some details, see the Ap-
pendix.

2) GA Algorithm: GA is a metaheuristic approach used for

optimization problems. Some chromosomes are initially gener-
ated. Two operators, namely, crossover and mutation, are there-
after applied, and new chromosomes are then generated.

The decision variables considered in the chromosomes are in

fact the supplying buses as

(12)

where

th chromosome;

feeding bus number for supplying the th load.

Two crossover operators, namely, normal and mathematical,

are applied as shown in Figs. 1 and 2, where

is a random

1000

IEEE TRANSACTIONS ON POWER SYSTEMS , VOL. 21, NO. 2, MAY 2006

Fig. 2. Mathematical crossover.

Fig. 3. Normal mutation.

Fig. 4. Most suitable mutation.

Fig. 5. Dual displacement mutation.

number [0, 1]. Regarding the mutation operator, four options
are proposed to improve the optimization procedure:

•

Normal Mutation as shown in Fig. 3, where

is a

random number in the th variable range.

•

The Most Suitable Mutation as shown in Fig. 4, where

is the most suitable substation for supplying the th

load.

•

Substation Elimination Mutation in which a substation
is randomly selected, and all of its connecting loads are
disconnected and connected to its closest substation.

•

Dual Displacement Mutation as shown in Fig. 5.

In each stage, a fitness value is calculated for each popula-

tion with assigning a penalty factor to the infeasible solutions
(i.e., the ones violating the constraints). To speed up the conver-
gence properties of algorithm and at the same time, to use the

TABLE I

L

OAD

C

ENTERS IN

SEP

FOR

2011

information that may still be useful in rejected chromosomes,
this penalty factor is linearly increased (through iterations) from
zero toward a very high value. The fitness function is in fact the
cost as detailed in (1).

3) A Refined Algorithm: As for a large-scale system, the

search space is quite large (

, where

is the number of load

centers, and

is the number of existing as well as candidate

substations), a two-stage GA is proposed in which, following
the first final run by GA, the evaluated substations are ranked ac-
cording to their number of selection times. Thereafter, a second-
stage GA is run with the candidate buses equal to two times the
number of the first-run results; this time is from the ranked list.
The tests showed that this procedure improves the results.

III. S

PECIFIC

D

ETAILS

The problem formulation was fully discussed in Section II.

Some of detailed descriptions are provided in this section.

A. Load Model

It is assumed that the existing network supplies the base load

of each “load center,” and the new downward grid should be
planned for the load increase. As a result, each load (as denoted
by its magnitude and geographical properties, i.e., X and Y)
is divided into a base value and an increase. For planning the
downward grid, only the increase part is considered, while for
substation loadings and upward grid design, both parts (base and
increase) are considered.

As noted earlier, there are 16 utilities throughout the country.

The number of load centers considered for each region within a
GIS context software is shown in Table I. The load centers are in
the form of small villages or similar, in terms of demand values.

B. Downward Grid

The downward grid of the system under study is in fact the

substransmission level of the Iranian Power Grid. It comprises
63- and 132-kV elements. For cost analysis of the downward
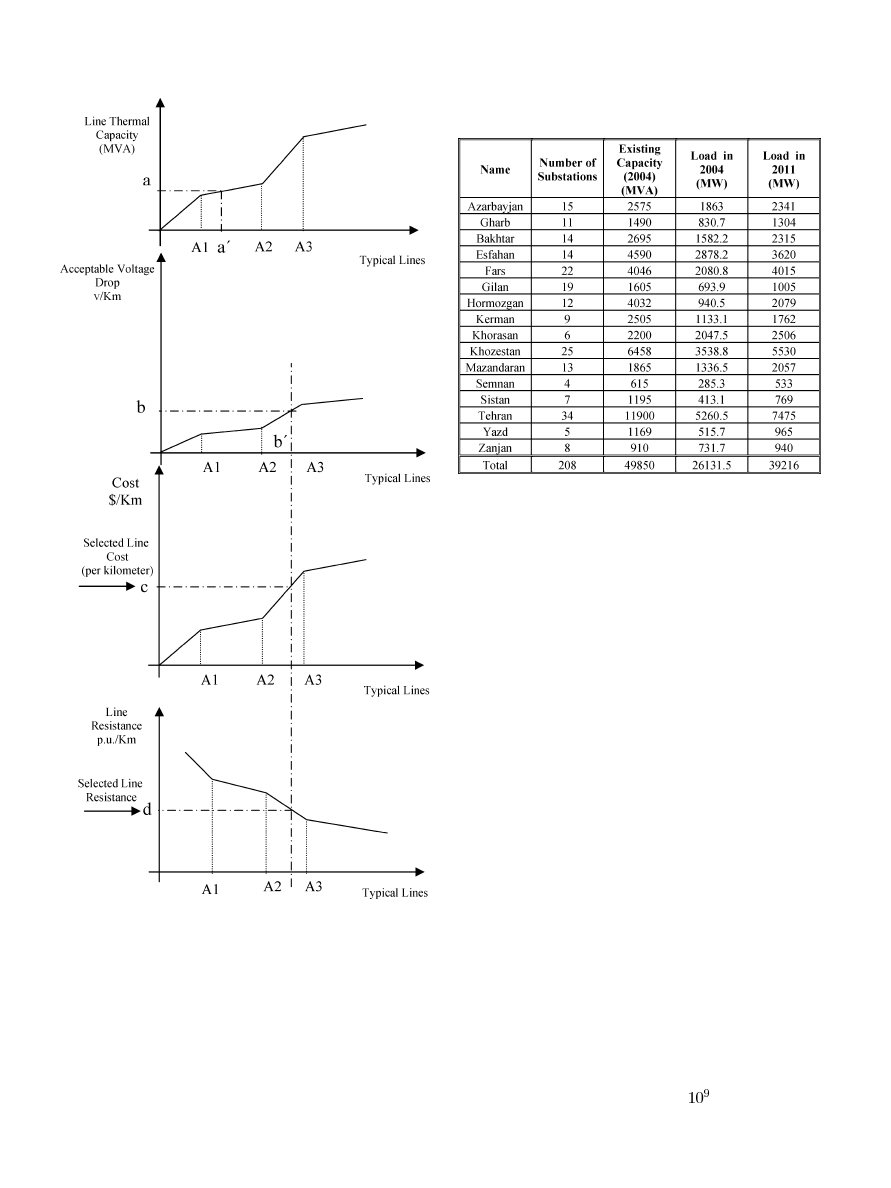
grid, four curves are used as shown in Fig. 6, where the hor-
izontal axis shows the typical standard conductors available,
while the vertical axes are “thermal capacity,” “voltage drop,”
“investment cost,” and “resistance,” respectively. A linear ap-
proximation is assumed between the points, as indicated. The
way these curves are used is as follows. Initially, based on ac-
ceptable voltage drop for the specified load (b), a conductor
size is selected

. Also, based on line thermal capacity (a),

a conductor size is selected, too

.

is selected

as the final choice (for the case demonstrated,

). For the se-

lected conductor, the cost and resistance are then determined
(c,d). Right-of-way sitting difficulties are also observed by a

SEPASIAN et al.: NEW APPROACH FOR SUBSTATION EXPANSION PLANNING

1001

Fig. 6.

Line selection curves.

large number factor in the investment cost. Moreover, advocat-
able loads (to a specific substation) are also considered.

C. Upward Grid

The upward grid of the Iranian Power Grid comprises 400-

and 230-kV elements. The line capacity and the type are de-
termined based on capacity, voltage level, and the type of sup-
plying substation.

TABLE II

U

TILITIES

I

NFORMATION

D. Transmission Substation

The types of transmission substations considered are

400/132-, 400/63-, 230/132-, and 230/63-kV. Various capacities
are available and considered. Alternatives and classifications,
as required for each utility region, are also considered. Within
cities, the reserve is considered as 1/3 of the substation capacity.
For other regions, the reserve is so chosen not to overload the
substation with one transformer, out. As the substation voltage
level is not initially known, both 400- and 230-kV options are
considered. The solution algorithm finds the best solution.

IV. N

UMERICAL

R

ESULTS

A. General

As noted earlier, the proposed algorithm is applied to the Ira-

nian Power Grid involving 16 electric utilities, the details of
which are shown in Table II For each utility, the load is shown
for the last summer peak (2004) as well as for the horizon year
(2011). Within each utility, the load is predicted for each con-
sumption center in the capacity of a small village. Provided the
estimated load is within the capacity of available subtransmis-
sion feeders, the predicted load is considered at its geographical
characteristics (respective X and Y). Otherwise, the load is dis-
cretized so that several loads are considered at the same center.
For large cities, such as the capital (Tehran), the loads are dis-
tributed among existing subtransmission substation geograph-
ical characteristics.

Fig. 7 depicts the load predictions for the consumption centers

of a typical utility (Tehran). Table III shows the characteristics
(capacity and cost) of both subtransmission and transmission
lines employed. The costs are in Iranian

monetary units (R).

The costs of transmission substations (the standard capacities
employed for the Iranian Power Grid) are shown in Table IV.

1002

IEEE TRANSACTIONS ON POWER SYSTEMS , VOL. 21, NO. 2, MAY 2006

Fig. 7.

Load centers in Tehran.

TABLE III

T

YPICAL

L

INES

C

OST AND

T

HERMAL

C

APACITY

TABLE IV

C

APACITY AND

C

OST OF

T

YPICAL

S

UBSTATIONS

: (

A

) 230/63 (KV)

AND

230/132

(KV) S

UBSTATIONS

. (

B

) 400/63 (KV)

AND

400/132 (KV) S

UBSTATIONS

B. Candidate Selection

Within each utility, the algorithm capability is initially as-

sessed by the proposed technique implementation discussed in
Section II-C1. Thereafter, infeasible candidates (infeasible in
terms of either locational, environmental, or similar considera-
tions) are removed, and extra possible candidates (based on, say,
experience) are added. Fig. 8 shows the resulting candidates for
a typical utility (Tehran).

C. Substation Allocation Results

As discussed in Section II-C2, GA is employed for final al-

location of new substations as well as on deciding for the ex-
isting substations expansions. With the GA parameters and tech-
nical/cost parameters shown in Table V, GA is rerun 100 times
for each utility to find the best solution. The final solution is
the best in terms of all costs incurred (see Section II-B1), while

Fig. 8.

Candidate substations in Tehran region.

TABLE V

GA P

ARAMETERS AND

T

ECHNICAL

/C

OST

P

ARAMETERS

TABLE VI

R

ESULT OF

S

UBSTATION

E

XPANSION

P

LANNING FOR

T

EHRAN

E

LECTRIC

U

TILITY

. (

A

) E

XISTING

S

UBSTATIONS

. (

B

) N

EW

S

UBSTATIONS

various constraints are met (see Section II-B2). The details for
a typical region are shown in Table VI. To further assess the
capabilities of the proposed GA in comparison with other GAs,
Table VII shows five typical GA cases (case 1 through case 5), in
which the crossover and mutation operators are set as demon-
strated. The results for the proposed GA are shown as case 6.
The computational time for each case is also shown for 100 GA
rerun on a Pentium IV 3.2-GHz personal computer. As is evi-
dent, although the computational time is increased, the overall
cost is reduced. As the studies conducted are for long-term plan-
ning, the computation burden is quite acceptable. Note that the
results are for Tehran Regional Electric Utility (TREC) as one

SEPASIAN et al.: NEW APPROACH FOR SUBSTATION EXPANSION PLANNING

1003

TABLE VII

R

ESULTS OF

V

ARIOUS

GAs

FOR

T

EHRAN

R

EGIONAL

E

LECTRIC

U

TILITY

TABLE VIII

SEP S

UMMARIES FOR

2011

Fig. 9.

SEP results for 2011.

TABLE IX

C

OMPUTATIONAL

T

IMES FOR

A

LL

U

TILITIES

of the largest in the country. The computational time depends on
the number of load centers (see Table I) and the number of ex-
isting substations (see Table II). While the overall results for the

Iranian Power Grid for the horizon year are shown in Table VIII
and Fig. 9, Table IX demonstrate the computational time for
each utility.

V. C

ONCLUSION

A new approach for the SEP problem was proposed in this

paper. GA was employed as the solution tool of the optimiza-
tion problem. The algorithm does not require the detailed de-
scriptions of the downward as well as upward grids. Therefore,
it can be readily applied to long-term studies. The algorithm
was tested for the Iranian Power Grid in 2011 with quite accept-
able results. The authors are investigating an alternative solution
technique so that the results can be determined more quickly.

A

PPENDIX

The basics of mathematical clustering are described in [17].

Basically we are going to “cluster” the load centers based on
some specific characteristics. In this paper, the load centers are
clustered based on their feeding substations. The algorithm em-
ployed is as follows.

1) Generate two lists for load centers (LL as load list) and all

existing substations (SL as substation list).

2) With due attention to voltage drop constraint, assign each

load to its nearest substation. Remove the assigned loads
from the LL.

3) Choose the most overloaded substation. If no substation

is overloaded, go to step 6.

4) Rank the loads, assigned to the aforementioned substation

(step 3), based on their least distance to the next substa-
tions. From the ranking list, remove the loads (with the
least distance) from the above substation in such a manner
that overloading is removed.

5) Add the unassigned loads to the LL and remove the above

substation from the SL.

6) Provided no load remains in the list, the algorithm ends.

Otherwise, go to step 7.

7) Choose the largest load from the LL and select its nearest

loads so that their overall sum is in the range of the ca-
pacity of a substation. The center of gravity of these loads
is considered as a candidate substation.

8) Add the candidate substation to the SL and repeat the pro-

cedure from step 1.

The above procedure is in fact an engineering-based approach in
which a quite high feasible candidate may be reduced to quite
low and manageable candidate from which the optimum ones
may be chosen by the proposed GA.

R

EFERENCES

[1] U. G. W. Knight, “The logical design of electrical networks using linear

programming methods,” Proc. Inst. Elect. Eng. A, vol. 107, pp. 306–316,
1960.

[2] J. V. Old-eld and M. A. Lang, “Dynamic programming network flow

procedure for distribution system planning,” in Proc. Power Industry
Computer Applications Conf., 1965.

[3] R. N. Adams and M. A. Laughton, “Optimal planning of power net-

works using mixed integer programming,” Proc. IEEE, vol. 121, no. 2,
pp. 139–147, Feb. 1974.

1004

IEEE TRANSACTIONS ON POWER SYSTEMS , VOL. 21, NO. 2, MAY 2006

[4] D. M. Crawford and S. B. Holt, “A mathematical optimization technique

for locating and sizing distribution substations and deriving their optimal
service areas,” IEEE Trans. Power App. Syst., vol. PAS-94, no. 2, pp.
230–235, Apr. 1975.

[5] E. Masud, “An iterative procedure for sizing and timing distribution

substations using optimization techniques,” in Proc. IEEE PES Winter
Meeting, Feb. 1974, pp. 1281–1286.

[6] T. Gönen and B. L. Foote, “Distribution system planning using mixed-

integer programming,” Proc. Inst. Elect. Eng., vol. 128, no. 2, pp. 70–79,
Mar. 1981.

[7] M. J. Carson and G. Corn-eld, “Design of low-voltage distribution net-

works,” Proc. IEEE, vol. 120, no. 5, pp. 585–593, May 1973.

[8]

, “Computer aided design of low-voltage distribution networks,” in

Proc. IEE Computer Aided Design Conf., vol. 86, 1972, pp. 121–124.

[9] T. Belgin, “Distribution system planning using mixed integer program-

ming,” ELEKTR-IK, vol. 6, no. 1, pp. 37–48, 1998.

[10] M. R. Haghifam and M. Shahabi, “Optimal location and sizing of

HV/MV substation in uncertainty load environment using genetic
algorithm,” Elect. Power Syst. Res., vol. 63, pp. 37–50, 2002.

[11] K. Yahav and G. Oron, “Optimal location of electrical substation in re-

gional energy supply systems,” in Proc. IEEE EEIS, Jerusalem, Israel,
Nov. 5–6, 1996, pp. 307–310.

[12] D. E. Bouchard, M. M. A. Salama, and A. Y. Chilchani, “Optimal

feeder routing and optimal substation sizing and placement using
guided evolutionary simulated annealing,” in Proc. IEEE CCECE,
1995, pp. 684–691.

[13] D. Hongwei, Y. Yixin, and H. Chunhua et al., “Optimal planning of dis-

tribution substation locations and sizes—model and algorithm,” Elect.
Power Energy Syst., vol. 18, no. 6, pp. 343–357, 1996.

[14] G. Latorre, R. D. Cruz, J. M. Areiza, and A. Villegas, “Classification

of publications and models on transmission expansion planning,” IEEE
Trans. Power Syst., vol. 18, no. 2, pp. 938–946, May 2003.

[15] I. J. Ramírez-Rosado and J. Antonio Domínguez-Navarro, “Possibilistic

model based on fuzzy sets for the multiobjective optimal planning of
electric power distribution networks,” IEEE Trans. Power Syst., vol. 18,
no. 4, pp. 1801–1810, Nov. 2003.

[16] J. Choi, A. El-Keib, and T. Tran, “A fuzzy branch and bound-based

transmission system expansion planning for the highest satisfaction level
of the decision maker,” IEEE Trans. Power Syst., vol. 20, no. 1, pp.
476–484, Feb. 2005.

[17] W. Li, Adaptive Fuzzy Systems and Control, Design and Stability Anal-

ysis.

Englewood Cliffs, NJ: Prentice-Hall, 2000.

Mohammad Sadegh Sepasian was born in Tehran in 1967. He received the
B.Sc., M.Sc. and Ph.D. degrees from Tabriz University, Tabriz, Iran, Tehran
University, and Tarbiat Modares University, Tehran, in 1990, 1993 and 1999,
respectively.

He is currently with Power and Water University, Tehran (Ministry of Energy)

as an Assistant Professor. His research interests include power system planning
as well as distribution planning issues.

Hossein Seifi (SM’01) was born in Shiraz, Iran, in 1957. He received the B.Sc.
degree from Shiraz University, Shiraz, Iran, in 1980 and the M.Sc. and Ph.D
degrees from the University of Manchester Institute of Science and Technology,
Manchester, U.K., in 1987 and 1989, respectively.

He then joined Tarbiat-modares University, Tehran, Iran, where he is currently

a Full Professor, and at the same time is the Head of the Iran Power System
Engineering Research Center (IPSERC). He was on sabbatical leave in 1995
with ABB Network Partner, Switzerland. His research interests include power
system planning and operational issues.

Dr. Seifi is a Senior Member of the Iran Association of Electrical Engineers.

Asghar Akbari Foroud was born in Hamadan, Iran, in 1972. He received the
B.Sc. and M.Sc. degrees from Tehran University and Tarbiat-modares Univer-
sity, Tehran, Iran, in 1993 and 1996, respectively.

He is now a faculty member with Semnan University, Semnan, Iran. His

research interests include network expansion planning and power system dy-
namics.

Seyyed Hadi Hosseini was born in Saenghaleh, Zanjan, Iran, in 1974. He re-
ceived the B.Sc. degree from Tehran University and the M.Sc. and Ph.D. degrees
from Tarbiat-modares University, Tehran, Iran, in 1996, 1999, and 2005, respec-
tively.

His research interests include power transformer design, high voltage and

insulation, and network expansion planning.

Esmaeil Mohseni Kabir was born in Gilan, Iran, in 1951. He received the B.Sc.
degree from Iran University of Science & Technology, Tehran, Iran, in 1974 and
M.Sc. degrees from Sharif University, Tehran, in 2005.

He is currently a Deputy in planning affairs with Tavanir Co., Tehran. His

research interests include all aspects of power system planning.