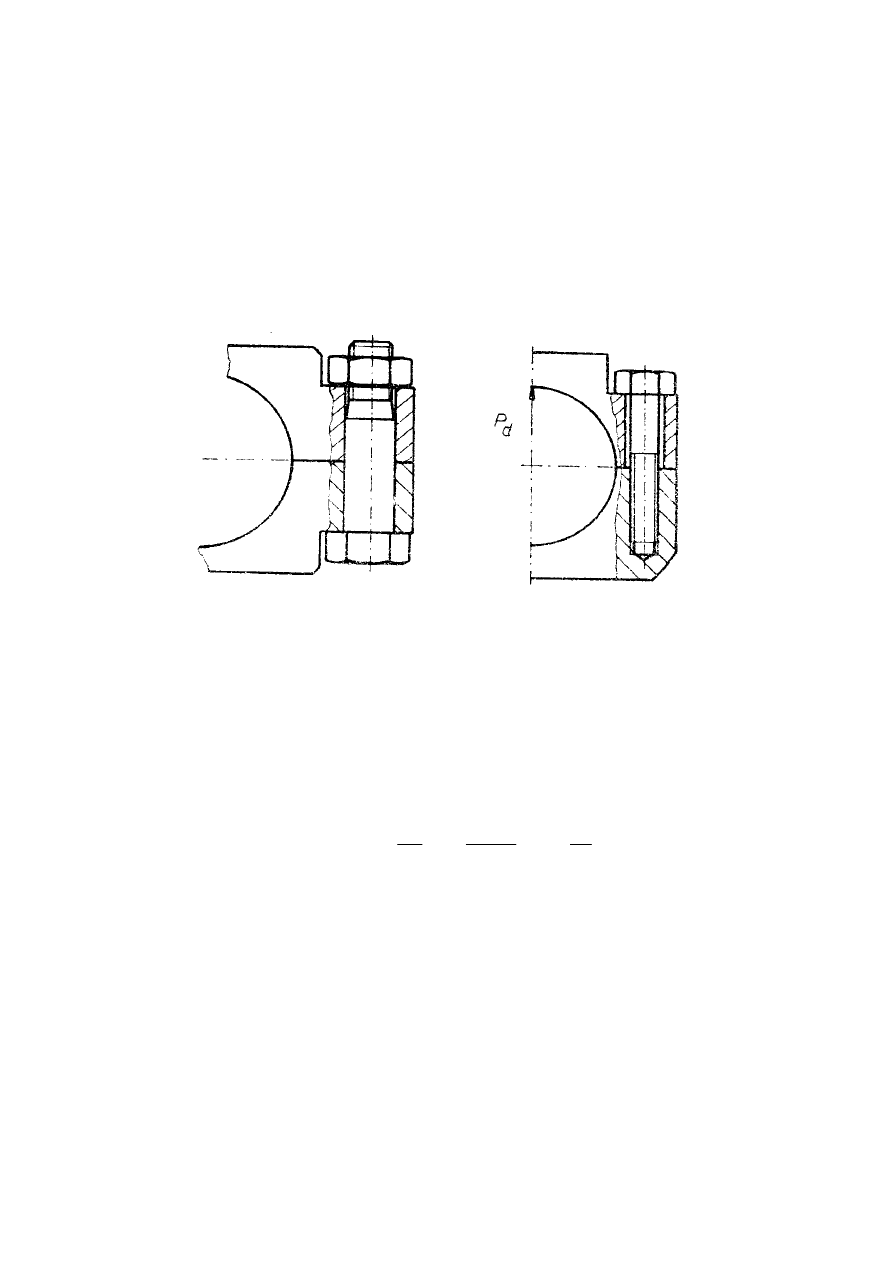
22

Napr

ęż

enia w

ś

rubach ło

ż

yskowych.

W silnikach spalinowych obudowy ło

ż

ysk głównych i korbowodowych s

ą

dzielone.

Elementem ł

ą

cz

ą

cym s

ą

ś

ruby. Wyró

ż

nia si

ę

dwa przypadki zł

ą

cza

ś

rubowego.

Jedno (rys. a ) składa si

ę

z dwóch elementów ł

ą

czonych

ś

rub

ę

i

ś

rub

ę

z nakr

ę

tk

ą

.

Drugie (rys. b) składa si

ę

z jednego elementu ł

ą

czonego, którym jest jednocze

ś

nie

nakr

ę

tk

ą

. W pierwszym przypadku przy skr

ę

conej

ś

rubie ł

ą

czone elementy s

ą

ś

ciskane a

ś

ruba jest rozci

ą

gana. W drugim przypadku elementem

ś

ciskanym jest

dolny element ł

ą

czony, za

ś

ś

ruba jest rozci

ą

gana.

Rodzaje zł

ą

cz

ś

rubowych w ło

ż

yskach głównych.

Elementy zł

ą

cza ulegaj

ą

ce

ś

ciskaniu przyj

ę

to nazywa

ć

kolumienkami lub

kołnierzami. Kolumienka jest cz

ęś

ci

ą

poł

ą

czenia ulegaj

ą

ca

ś

ciskaniu.

W skr

ę

conej

ś

rubie wyst

ę

puj

ą

napr

ęż

enia

σ

r

,którym odpowiada siła rozci

ą

gaj

ą

ca

ś

rub

ę

Q

w

zwana napi

ę

ciem wst

ę

pnym. Pod wpływem napi

ę

cia wst

ę

pnego

ś

ruba

wydłu

ż

a si

ę

o

λ

Cs

Qw

Es

Fs

Is

Qw

Is

s

rs

Is

1

⋅

=

⋅

⋅

=

⋅

Ε

=

⋅

Ε

=

δ

λ

Gdzie:
Es – wydłu

ż

enie wst

ę

pne

ś

ruby

Is – długo

ść

ś

ruby

Es – moduł spr

ęż

ysto

ś

ci wzdłu

ż

nej

ś

ruby

Fs – pole przekroju

ś

ruby

Cs – sztywno

ść

ś

ruby

Równocze

ś

nie elementy

ś

ciskane ulegaj

ą

skróceniu o

∆

w

23

Ck

Qw

Ek

Fk

Ik

Qws

Ik

Ek

k

Lk

k

w

1

=

⋅

⋅

=

⋅

=

⋅

Ε

=

∆

δ

Gdzie:
Ek – skrócenie kolumienki
Lk – długo

ść

kolumienki

Ek – moduł spr

ęż

ysto

ś

ci wzdłu

ż

nej kolumienki

Fk – pole przekroju kolumienki
Ck – sztywno

ść

kolumienki.

Sztywno

ść

C mo

ż

na okre

ś

li

ć

jako sił

ę

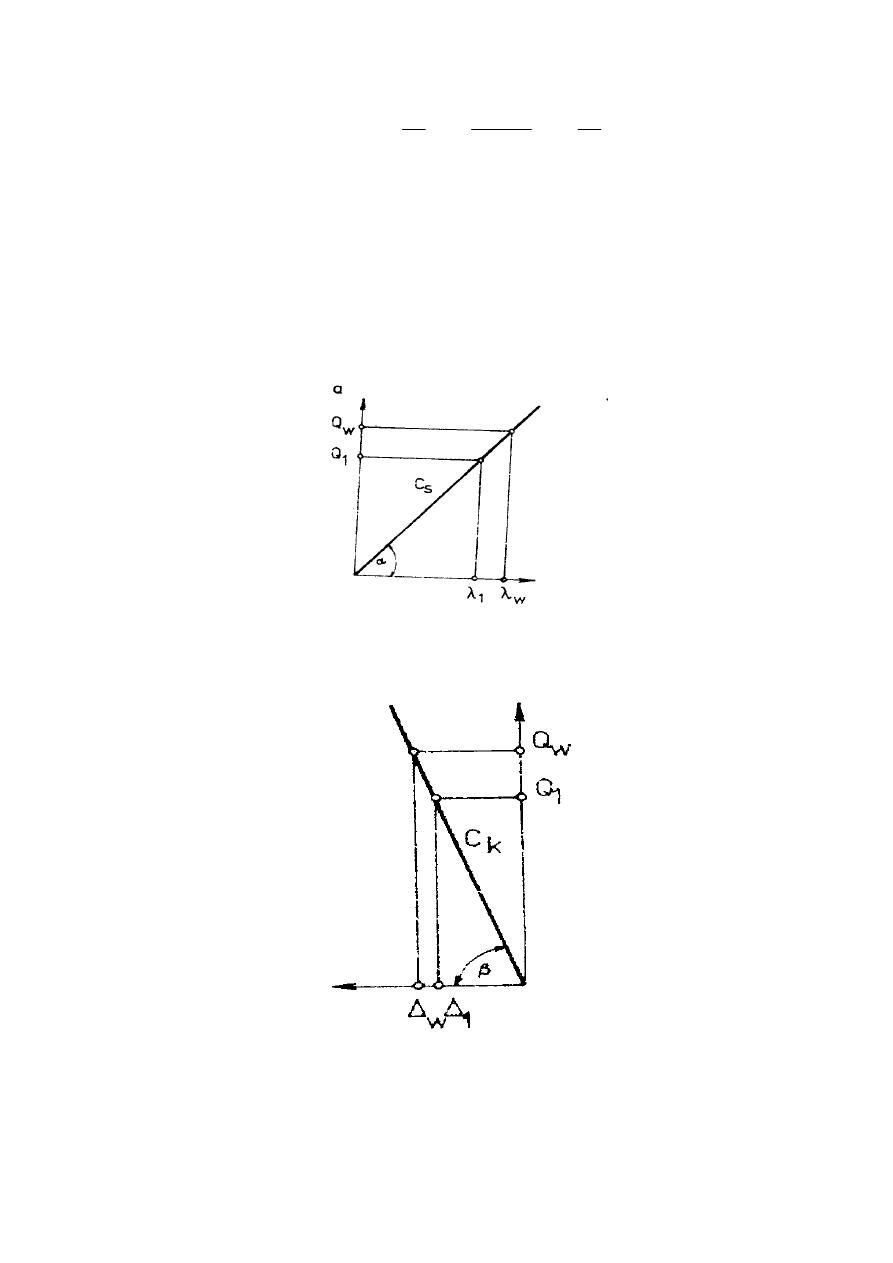
, która wywołuje jednostkowe odkształcenia.

Zale

ż

no

ś

ci te w postaci graficznej przedstawia poni

ż

szy rysunek.

Charakterystyka

ś

ruby.

Charakterystyka kolumienki.

24

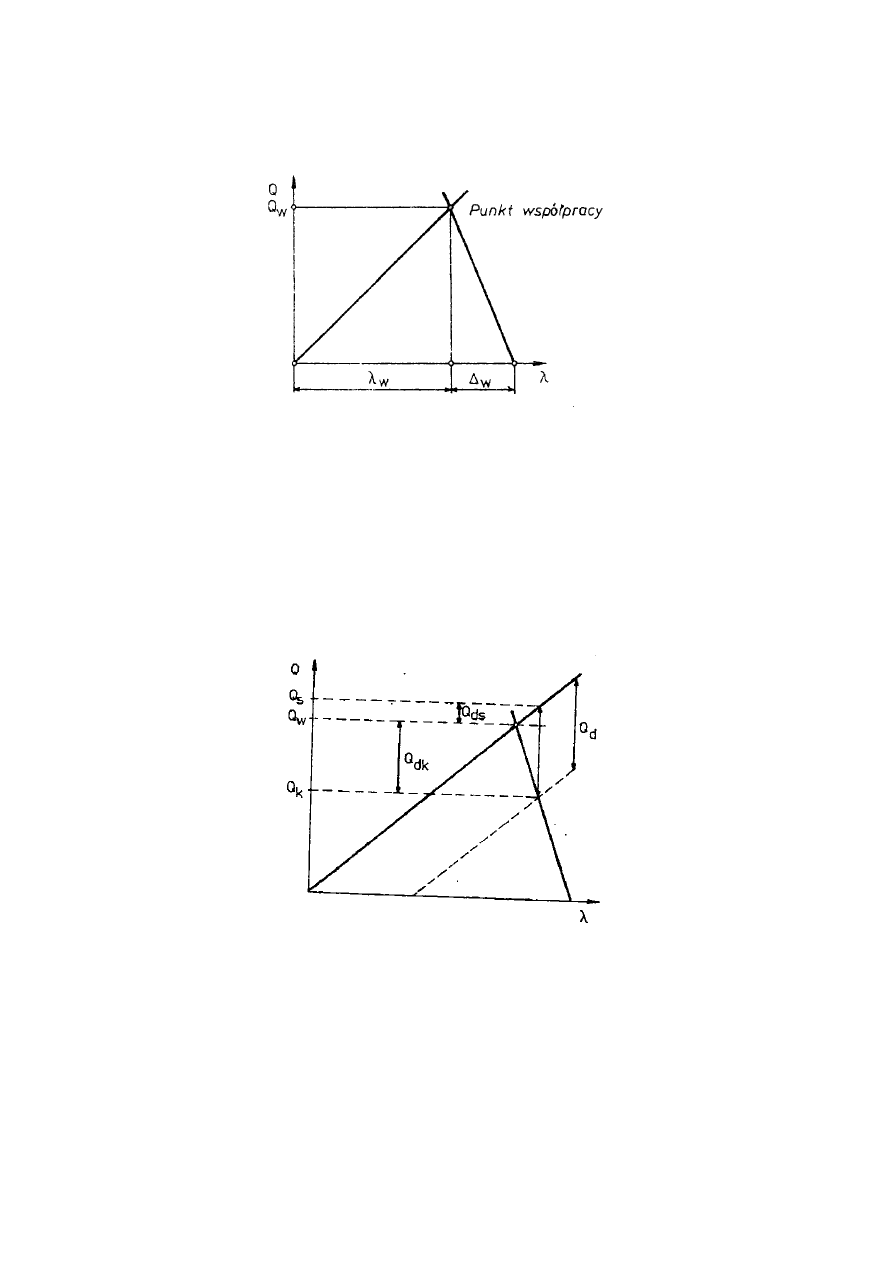
Sprowadzaj

ą

c obie charakterystyki do jednego układu otrzymujemy charakterystyk

ę

zł

ą

cza

ś

rubowego.

Charakterystyka zł

ą

cza

ś

rubowego.

Je

ż

eli w napi

ę

tym wst

ę

pnie zł

ą

czu pojawi si

ę

dodatkowo siła Qd staraj

ą

ca si

ę

oddzieli

ć

od siebie

ś

ciskane elementy, to spowoduje ona dodatkowe obci

ąż

enie

ś

ruby.

Ś

ruba wydłu

ż

y si

ę

o dodatkow

ą

warto

ść

λ

d spowodowan

ą

działaniem siły

Qds. Dodatkowe wydłu

ż

enie

ś

ruby powoduje wydłu

ż

enie kolumienki, czyli

zmniejszenie jej skrócenia równie

ż

o warto

ść

λ

d. W wyniku działania siły dodatkowej

Qd

ś

ruba rozci

ą

gana jest teraz sił

ą

Qd + Qw, a kolumienka

ś

ciskana siła Qw - Qdk

Qds + Qdk = Qd.

Zmiany w zł

ą

czu pod wpływem dodatkowego obci

ąż

enia.

Z powy

ż

szego rysunku wynika,

ż

e wzrost i spadek napr

ęż

e

ń

w elementach zł

ą

cza

nie jest równy dodatkowemu napi

ę

ciu Qd. Ponadto, przyrost napi

ę

cia w

ś

rubie nie

jest równy zmniejszeniu napi

ę

cia w kolumience i zale

ż

y od sztywno

ś

ci

ś

ruby i

kolumienki co przedstawia poni

ż

szy rysunek.

25

Wpływ zmian sztywno

ś

ci

ś

ruby na rozkład sił w zł

ą

czu.

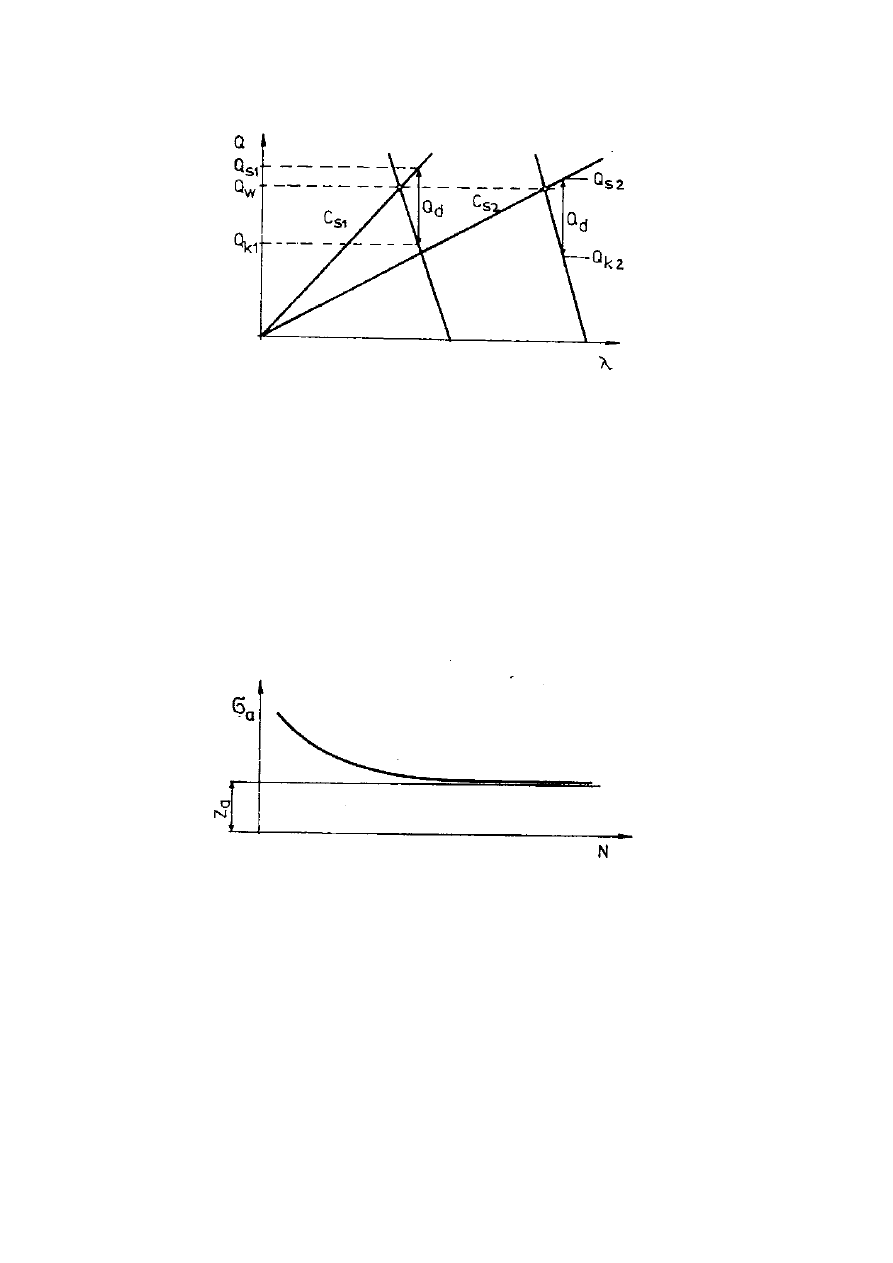
Napr

ęż

enia okresowe charakteryzowane s

ą

przez nast

ę

puj

ą

ce wielko

ś

ci:

-

ś

rednie napr

ęż

enie cyklu

-

amplituda napr

ęż

e

ń

-

współczynnik stało

ś

ci obci

ąż

enia.

Zale

ż

no

ść

mi

ę

dzy amplitud

ą

napr

ęż

e

ń

a liczba cykli zmian obci

ąż

enia, po którym

element obci

ąż

ony ulega zniszczeniu zm

ę

czeniowemu przedstawia tzw. krzywa

Wohlera.

Krzywa Wohlera.

Wykres zm

ę

czeniowy Haigha przedstawia natomiast zale

ż

no

ść

mi

ę

dzy napr

ęż

eniem

ś

rednim a amplitudami granicznymi cykli zm

ę

czeniowych. Przykładowo dla

σ

a1

i

σ

m1

nie nast

ą

pi uszkodzenie

ś

ruby, natomiast dla

σ

a2

i

σ

m2

nale

ż

y spodziewa

ć

si

ę

zm

ę

czeniowego p

ę

kni

ę

cia

ś

ruby.

26

Wykres Haigha.

Pomiar napi

ę

cia wst

ę

pnego.

W praktyce pomiar napi

ę

cia wst

ę

pnego dokonuje si

ę

poprzez:

-

pomiar wydłu

ż

enia

ś

ruby

λ

-

pomiar ci

ś

nienia oleju w specjalnej prasie hydraulicznej do napinania

ś

rub

-

pomiar momentu skr

ę

caj

ą

cego

ś

rub

ę

podczas dokr

ę

cania kluczem dynamo

metrycznym

-

podgrzanie

ś

ruby do okre

ś

lonej temperatury, zmontowanie w stanie gor

ą

cym i

dokr

ę

cenie nakr

ę

tki do pierwszego oporu.

Pomiar wydłu

ż

enia

ś

ruby

λ

s

np. za pomoc

ą

mikrometru, nie jest zawsze mo

ż

liwe. Nie

jest mo

ż

liwe gdy nakr

ę

tka ci

ęż

ko dost

ę

pna lub obudowana ło

ż

yskiem.

Podczas napinania

ś

ruby kluczem dynamo metrycznym, mierzony na kluczu moment

Md słu

ż

y do pokonania momentu skr

ę

caj

ą

cego Ms na gwincie oraz do pokonania

momentu tarcia Mt na oporowej powierzchni nakr

ę

tki lub łba

ś

ruby.

Mt

Ms

Md

+

=

µ

f

Ms

=

o

f

Mt

µ

=

Gdzie:

µ

- współczynnik tarcia na powierzchniach gwintu

µ

o

– współczynnik tarcia na powierzchniach oporowych kolumienki i nakr

ę

tki lub łba

ś

ruby.

27