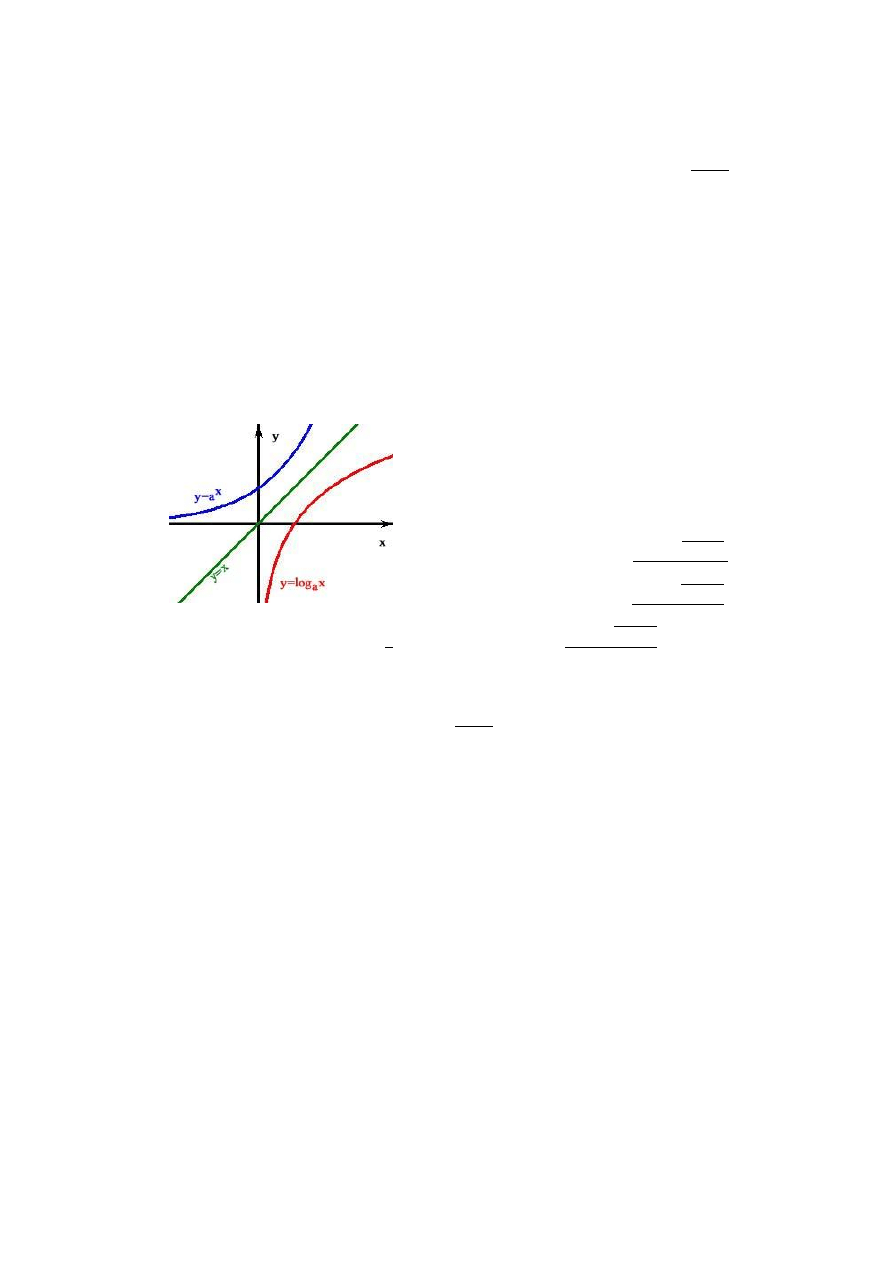
1.  FUNKCJA ODWROTNA 

Twierdzenie 

Niech      

 

   

 

 będzie funkcją klasy  

 

 ,      . Załóżmy, że     

 

   

    

 

 

  

 jest 

rzędu n,         

 

      . Wówczas , w pewnym otoczeniu punkty  

 

     

 

  istnieje 

funkcja         

  

   , odwrotna do f. Jest ona także klasy  

 

. 

 
Własności: 
-  

  

           

-  

 

   

 

     

  

            

  

                   

  

                

  

 

 
 
Tworząc odbicie uzyskujemy funkcję odwrotną:  
 

Przykład 

            

 

                  

 

 

                     

   

   

            

 

           

 

 

                           

 

 

    

 

       

 

   

 

 

    

 

      

 

 

         

 
 

                         

            

 

 

 
Istnienie Funkcji Odwrotnej 

    

 

   

 

      

 

 ,      .     

 

   

    

 

 

  

  ma pełny rząd. Wówcas istnieje funkcja 

odwrotna  

  

          

 

      

 

     

  

            

 

     

 

  

               

        

          

 

    

  

                

  

  to f

-1

 istnieje 

lokalnie. 
 
Przyklad: 
    

 

   

 

     

 

   

 

      

 

    

 

   

 

    

 

    

 

     

    

 

   

 

     

    

 

  

 

    

 

     

 

  

 

    

 

             

 

   

 

     

 

    

 
Ponadto istnienie funkcji odwrotnej definiuje istnienie lokalnego dyfeomorfizmu.