1
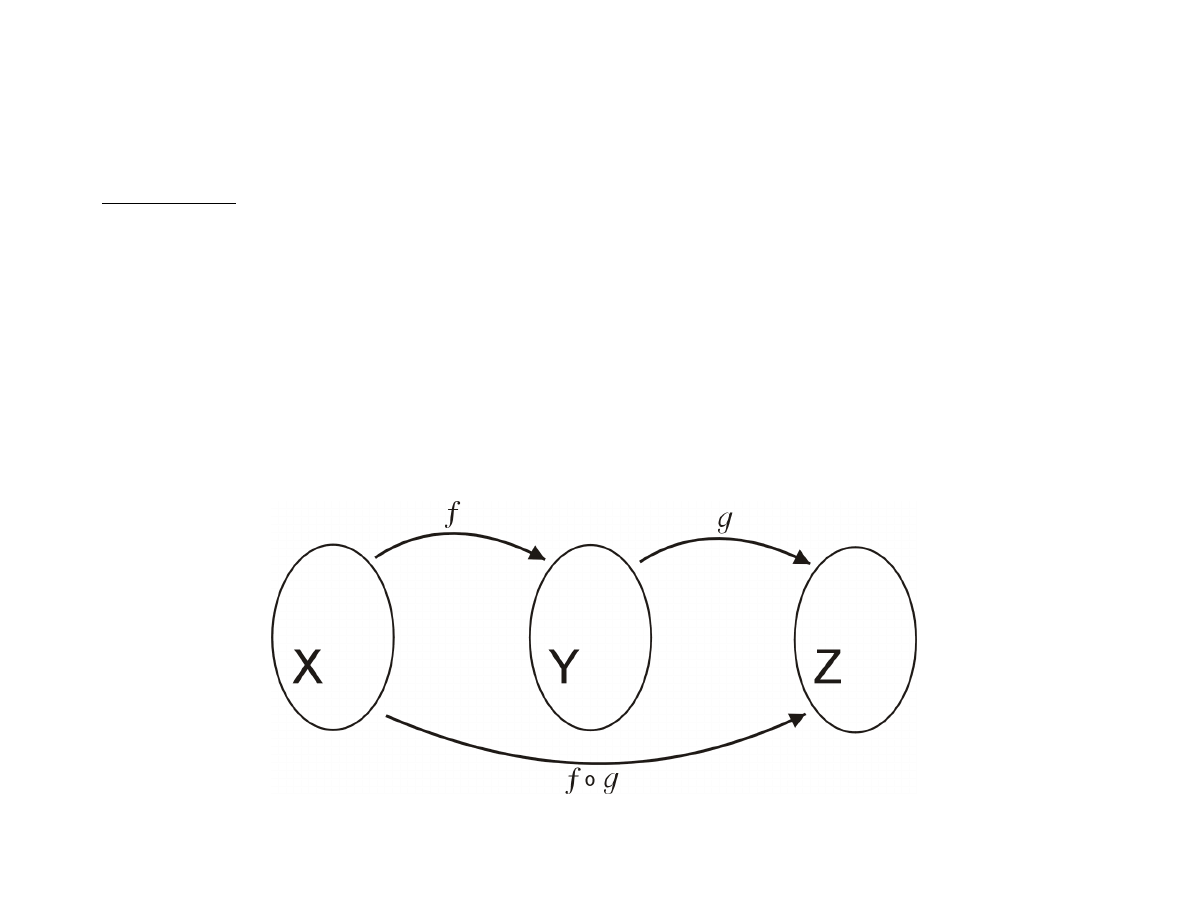
Złożenie funkcji
Definicja
Załóżmy, że
f : X → Y
,
g : Y → Z
są funkcjami.
Złożeniem funkcji
f
i
g
nazywamy funkcję
h : X → Z
daną
wzorem
h(x) = g(f (x))
.
Złożenie
f
i
g
oznaczamy symbolem
f ◦ g
(
h = f ◦ g
),
funkcję
f
nazywamy funkcją wewnętrzną, a funkcję
g
- funkcją
zewnętrzną.
2
Uwaga
•
Złożenie dwóch funkcji rosnących jest funkcją rosnącą.
•
Złożenie dwóch funkcji malejących jest funkcją rosnącą.
• Złożenie funkcji rosnącej i funkcji malejącej jest funkcją malejącą.
Przykład
Określmy funkcje złożone
f ◦ f
,
f ◦ g
,
g ◦ f
,
g ◦ g
, jeżeli
f (x) = x
2 i
g(x) =
√
x
.
3
Funkcja odwrotna
Definicja
Funkcję
f : X → Y
nazywamy funkcją różnowartościową
(injekcją), jeżeli
∀
x
1
,x
2
∈X
( x
1
6= x
2
)
=⇒
f (x
1
) 6= f (x
2
)
!
.
Funkcją różnowartościową będziemy oznaczać:
f : X
1−1
−→ Y
.
Definicja
Funkcję
f : X → Y
nazywamy funkcją ”na”
(surjekcją), jeżeli
W
f
= Y
, tzn.
∀
y∈Y
∃
x∈X
y = f (x).
Funkcją ”na” będziemy oznaczać:
f : X
na
−→ Y
.
4
Definicja
Funkcję, która jest jednocześnie ”1-1” i ”na” nazywamy
funkcją
wzajemnie
jednoznaczną
(bijekcją)
i
oznaczamy
f : X
1−1
−→
na
Y
.
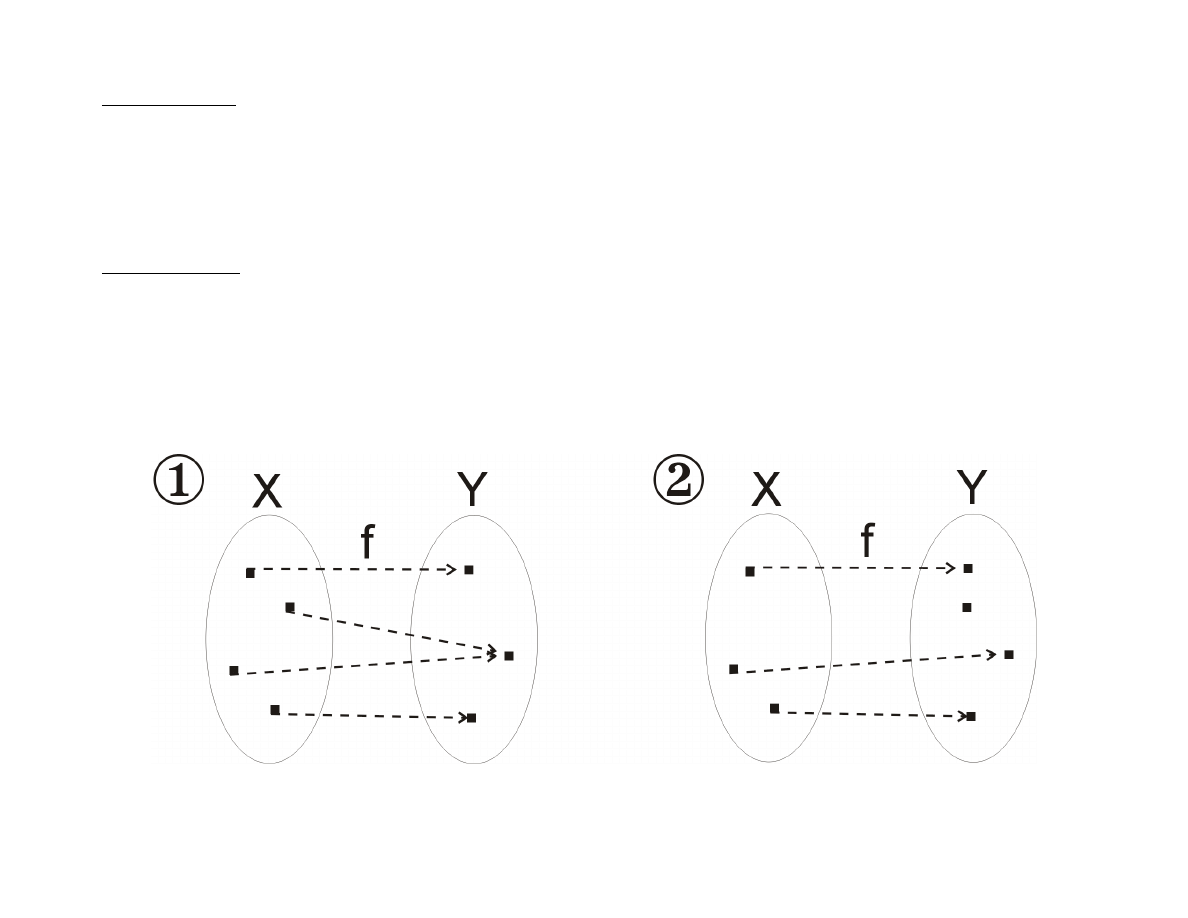
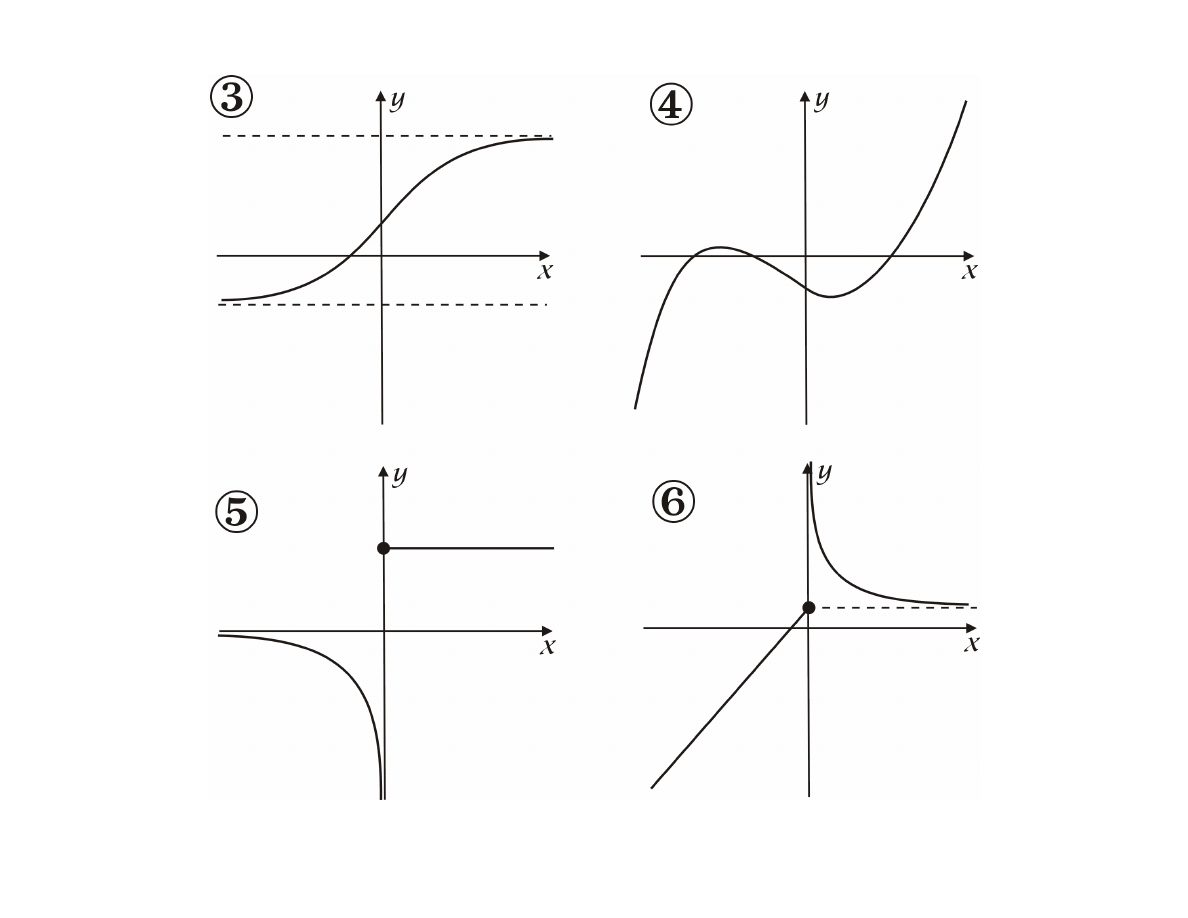
Przykład
Czy funkcje zilustrowane grafami lub wykresami są
różnowartościowe i ”na” ?
5
6
Uwaga
• Złożenie dwóch funkcji różnowartościowych jest funkcją różnowartościową.
•
Funkcja ściśle monotoniczna jest funkcją różnowartościową.
Przykład
Sprawdźmy, czy funkcja
f (x) =
2x − 3
x + 1
jest różnowartościowa w swojej dziedzinie.
7
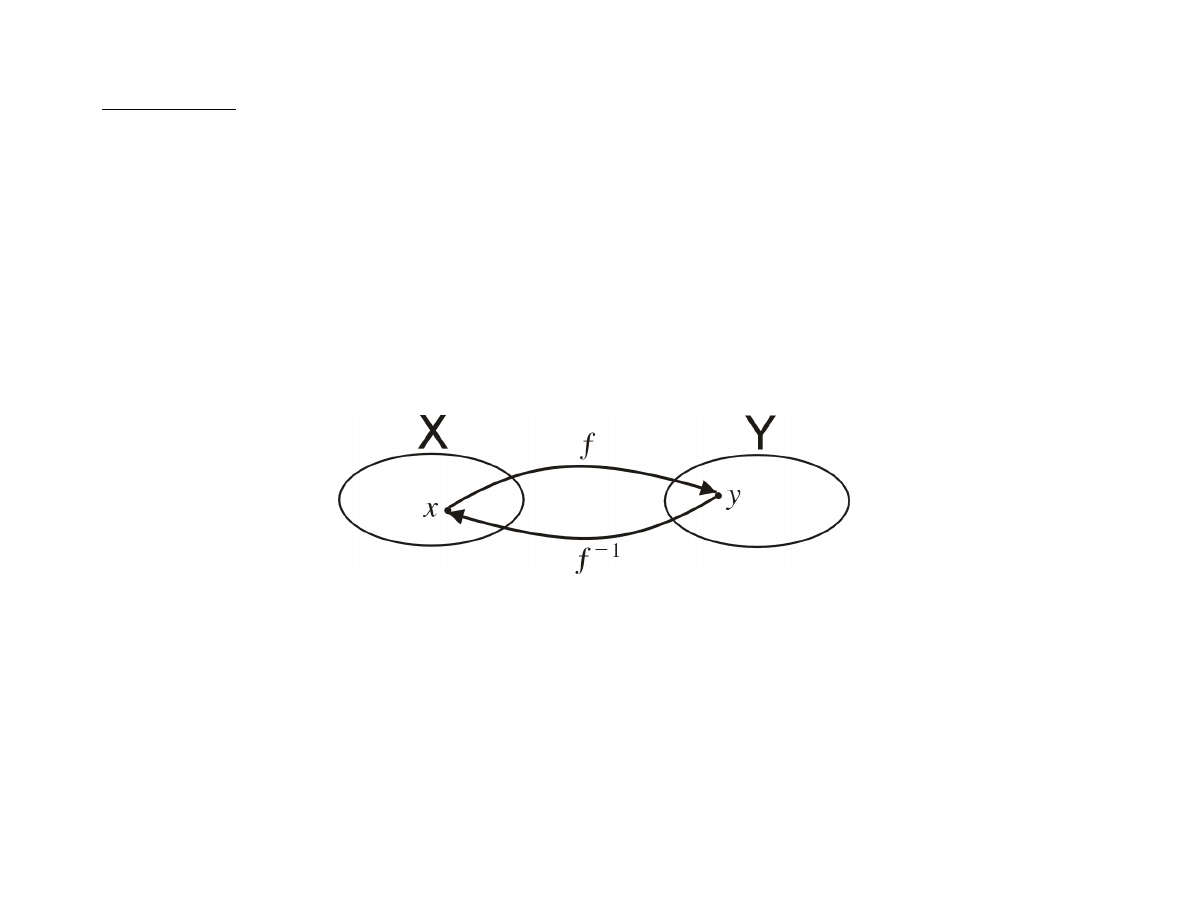
Definicja
Niech
f : X → Y
będzie funkcja wzajemnie jednoznaczną.
Funkcję
f
−1
: Y → X
nazywamy funkcją odwrotną do funkcji
f
,
jeżeli dla każdego
x ∈ X
i
y ∈ Y
f
−1
(y) = x
⇐⇒
y = f (x).
f ◦ f
−1
= Id
X
(f ◦ f
−1
)(x) = f
−1
(f (x)) = f
−1
(y) = x
f
−1
◦ f = Id
Y
(f
−1
◦ f )(y) = f (f
−1
(y)) = f (x) = y
8
Uwaga
Wykres funkcji odwrotnej otrzymujemy z wykresu funkcji
danej, odbijając go symetrycznie względem prostej
y = x
.
Przykład
Wyznaczmy funkcję odwrotną do funkcji:
•
y = x
3
x ∈ R
•
y = x
2
− x
x ∈ [1, +∞)
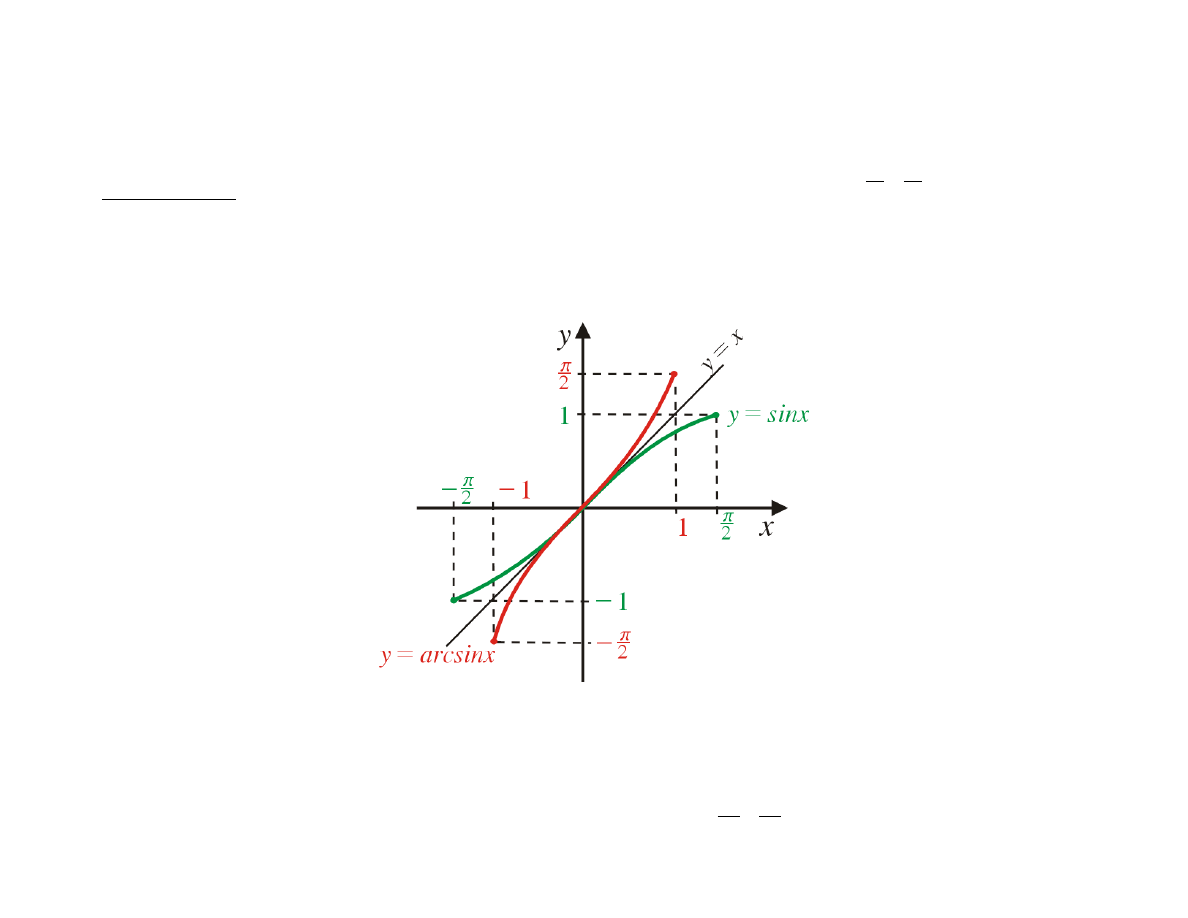
9
Funkcje cyklometryczne
Definicja
Funkcję odwrotną do funkcji
f :
"
−
π
2
,
π
2
#
→ [−1, 1]
danej wzorem
f (x) = sin x
nazywamy funkcją arcsin (czyt. arkus
sinus).
arcsin : [−1, 1] →
−
π
2
,
π
2
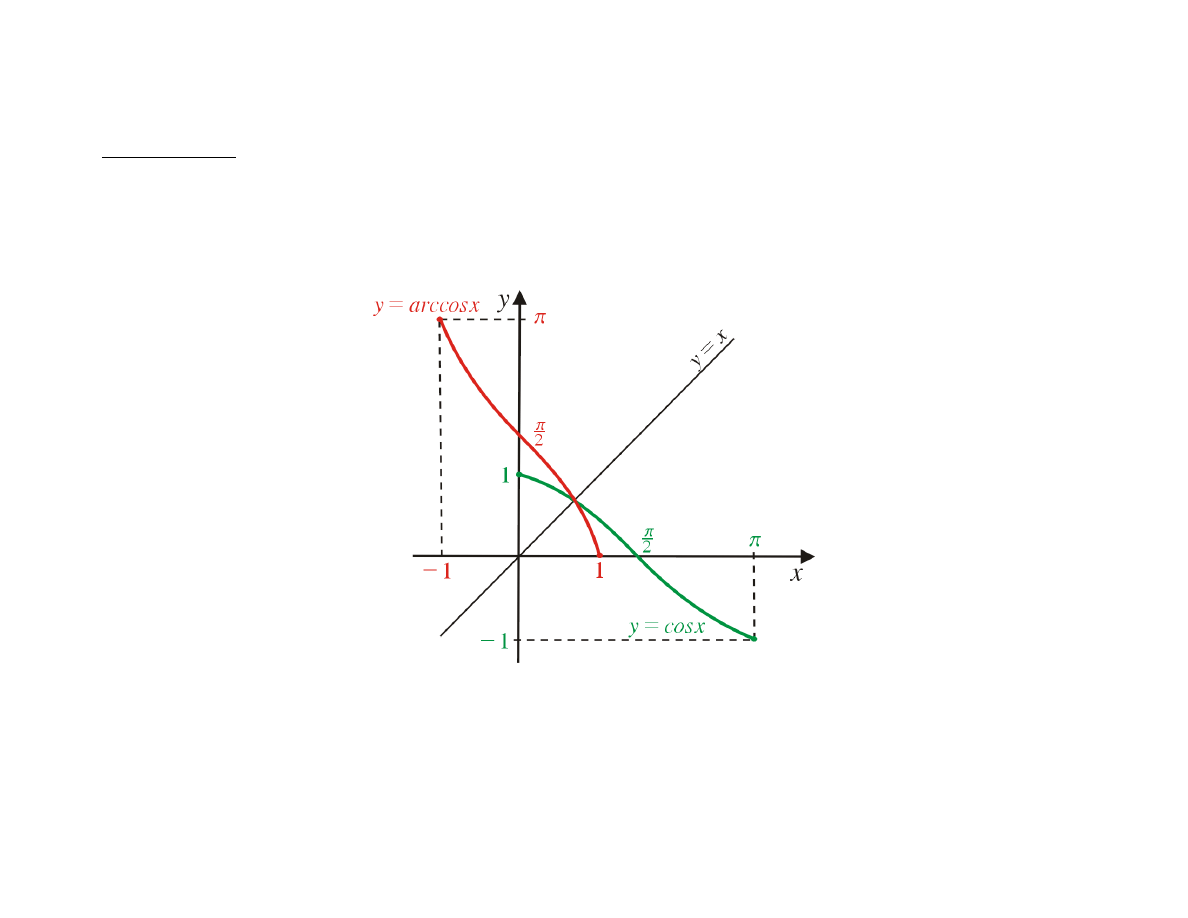
10
Definicja
Funkcję odwrotną do funkcji
f : [0, π] → [−1, 1]
danej wzorem
f (x) = cos x
nazywamy funkcją arccos (czyt. arkus
cosinus).
arccos : [−1, 1] → [0, π]
11
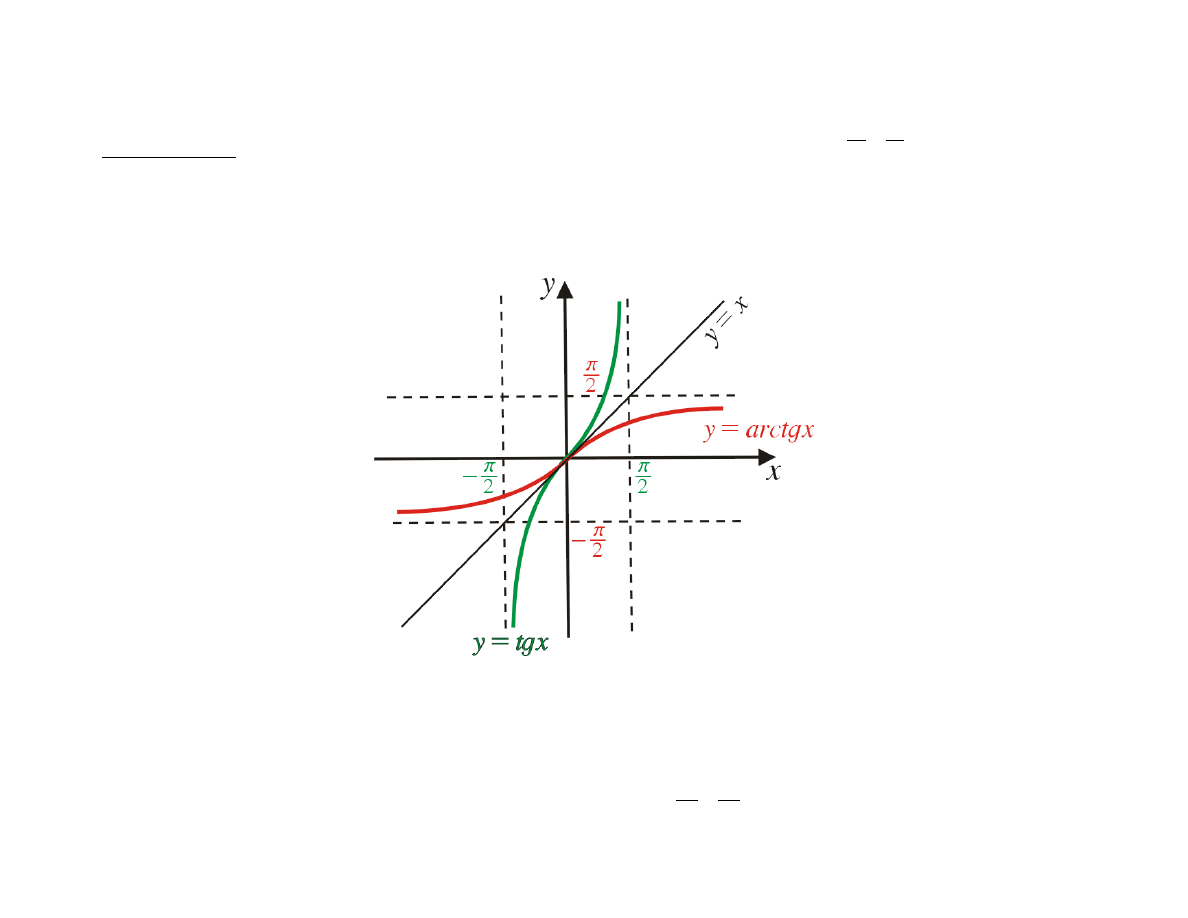
Definicja
Funkcję odwrotną do funkcji
f :
−
π
2
,
π
2
!
→ R
danej
wzorem
f (x) = tg x
nazywamy funkcją arctg (czyt. arkus tangens).
arctg : R →
−
π
2
,
π
2
12
Ćwiczenie
Napisz definicję funkcji arcctg (czyt. arkus kotangens),
jako funkcji odwrotnej do funkcji
f : [0, π] → R
danej wzorem
f (x) = ctg x
.
Przykład
Oblicz:
• arcsin (−
1
2
)
• arccos
√
2
2
• arctg (−
√
3)
13
Podstawowe związki między funkcjami cyklometrycznymi
Dla każdego
x ∈ [−1, 1]
zachodzi:
arcsin x = − arcsin (−x) =
π
2
− arccos x
Dla każdego
x ∈ R
zachodzi:
arctg x = − arctg (−x) =
π
2
− arcctg x
14
Funkcje elementarne
Definicja
Podstawową funkcją elementarną nazywamy funkcję
stałą, potęgową, wykładniczą, logarytmiczną, trygonometryczną lub
cyklometryczną. Funkcję, którą można otrzymać z podstawowych
funkcji elementarnych za pomocą skończonej liczby działań arytmetycznych
oraz operacji złożenia funkcji, nazywamy funkcją elementarną.
Przykład
Następujące funkcje są funkcjami elementarnymi:
• f (x) = a
n
x
n
+ a
n−1
x
n−1
+ . . . + a
2
x
2
+ a
1
x + a
0
• f (x) =
a
n
x
n
+ a
n−1
x
n−1
+ ... + a
2
x
2
+ a
1
x + a
0
b
m
x
m
+ b
m−1
x
m−1
+ ... + b
2
x
2
+ b
1
x + b
0
• f (x) =
3
√
3x
2
+ 1,
f (x) = log
2
(x + 3),
f (x) = sin(arctg x + 1)
• sh x =
e
x
−e
−x
2
,
ch x =
e
x
+e
−x
2
Przykład
Uzasadnić, że funkcja
f : R → [0, +∞]
dana wzorem
15
f (x) = |x|
jest funkcją elementarną.
Przykład
Przykłady funkcji nieelementarnych:
• Funkcja ”signum”:
sgn x =
1
x > 0
0
x = 0
−1
x < 0
• Funkcja ”część całkowita”:
z(x) = k
jeżeli
x ∈ [k, k + 1),
k ∈ Z
• Funkcja Dirichleta:
D(x) =
1
x ∈ Q
0
x ∈ R r Q