Arkusz kalkulacyjny MS EXCEL – ĆWICZENIA 3

Uwaga ! Każde ćwiczenie rozpoczynamy od stworzenia w katalogu „Moje dokumenty”
swojego własnego katalogu roboczego, w którym będziecie Państwo zapisywać swoje
pliki. Po zakończeniu zajęć proszę usunąć swój katalog z dysku twardego (ewentualnie
wcześniej skopiować swoje pliki na własny nośnik lub konto mailowe, itp.)

Do wykonania ćwiczeń należy ściągnąć ze strony plik excel_cw3.xls.

Zadanie 1

Przedstaw na arkuszu schemat spłaty kredytu zgodnie z przyjętymi założeniami:

wielkość kredytu 12 000 zł

okres spłaty 1 rok

oprocentowanie nominalne wynosi 11% rocznie

spłata kredytu w 12 miesięcznych ratach, kapitał + odsetki

Miesiąc

Kapitał do

spłacenia

Rata

kapitałowa

Należne

odsetki

Kwota

spłaty

1

12 000,00 zł

2

3

4

5

6

7

8

9

10

11

12

Razem

x

- zł

- zł

- zł

Oprocentowanie

11%

Objaśnienia:

Ratę kapitałową obliczamy dzieląc kapitał początkowy przez liczbę wszystkich rat.

Kapitał do spłacenia maleje co miesiąc o wartość spłaconej raty. (Kapitał w lutym = Kapitał w

styczniu – rata w styczniu)

Należne odsetki obliczamy mnożąc pozostały do spłacenia kapitał przez oprocentowanie

miesięczne.

Oprocentowanie miesięczne obliczamy dzieląc oprocentowanie nominalne (np. 11%) przez liczbę

dni w roku (rok bankowy = 360 dni) – otrzymujemy oprocentowanie na dzień. Aby otrzymać
oprocentowanie miesięczne mnożymy jeszcze przez długość miesiąca w dniach (miesiąc bankowy =
30 dni): 11% / 360 * 30. Zamiast 11% wpisz adres komórki, w której wpisano oprocentowanie
stosując adresy bezwzględne, np. $A$17.

Kwota spłaty to oczywiście suma raty kapitałowej i odsetek za dany miesiąc.

Zadanie 2

Przedstaw na arkuszu schemat spłaty kredytu jak w Zadaniu 1 zmieniając założenia:

okres spłaty 2 lata

spłata kredytu w 24 miesięcznych ratach, kapitał + odsetki

pozostałe założenia bez zmian

Zadanie 3

Przedstaw na arkuszu schemat spłaty kredytu zgodnie z przyjętymi założeniami:

wielkość kredytu 15 000 zł

okres spłaty 4 lata

oprocentowanie nominalne wynosi 14,5% rocznie

spłata kredytu w 16 kwartalnych ratach, kapitał + odsetki

Miesiąc

Kapitał do spłacenia

Rata

kapitałowa

Należne

odsetki

Kwota

spłaty

3 (kwartał 1)

15 000,00 zł

6 (kwartał 2

itd.)

9

12

15

18

21

24

27

30

33

36

39

42

45

48

Razem

x

- zł

- zł

- zł

oprocentowanie

14,5%

Objaśnienia:

Oprocentowanie kwartalne obliczamy tak jak miesięczne w Zadaniu 1, lecz mnożymy nie przez

długość miesiąca, tylko kwartału – czyli 90 dni.

Zadanie 4 Funkcje PPMT, IPMT, PMT

a) Dla każdego z obliczonych kredytów oblicz odsetki za 1 okres spłaty kredytu wstawiając funkcję
Excela. Wykonuj po kolei polecenia:

Przejdź do menu Wstaw/ Funkcja (fx)

W okienku kategorii wybierz Finansowe/ Nazwa funkcji: „IPMT”/ OK.

(Funkcja ta oblicza wartość spłaconych odsetek w podanym okresie.)

W okienkach formularza wpisuj odpowiednie wartości. Po kliknięciu w polu służącym do

wpisania – czytaj objaśnienia na dole formularza.

b) Dla każdego z obliczonych kredytów oblicz spłatę kapitału za 1 okres spłaty kredytu wstawiając
funkcję Excela. Wykonuj po kolei polecenia:

Przejdź do menu Wstaw/ Funkcja (fx)

W okienku kategorii wybierz Finansowe/ Nazwa funkcji: „PPMT”/ OK.

(Funkcja ta oblicza wartość spłaconych odsetek w podanym okresie.)

W okienkach formularza wpisuj odpowiednie wartości. Po kliknięciu w polu służącym do

wpisania – czytaj objaśnienia na dole formularza.

c) Dla każdego z obliczonych kredytów oblicz spłatę pożyczki za 1 okres spłaty kredytu wstawiając
funkcję Excela. Wykonuj po kolei polecenia:

Przejdź do menu Wstaw/ Funkcja (fx)

W okienku kategorii wybierz Finansowe/ Nazwa funkcji: „PMT”/ OK.

(Funkcja ta oblicza wartość spłaconych odsetek w podanym okresie.)

W okienkach formularza wpisuj odpowiednie wartości. Po kliknięciu w polu służącym do

wpisania – czytaj objaśnienia na dole formularza.

Objaśnienia:

Podaj stopę procentową obliczoną dla danego okresu (miesiąca, kwartału) – czyli oprocentowanie

/ liczbę rat w roku

dla miesiąca wpisz np. 20% / 12

dla kwartału 21% / 4

Okres oznacza kolejny miesiąc lub kwartał spłaty, wpisz 1

Podaj liczbę rat dla całego okresu spłaty kredytu (12, 24, 16)

Wa oznacza wartość początkową kredytu

Wp i Typ można pominąć. Oznaczają one:

WP - wartość końcową – w naszym przypadku 0 (kredyt spłacamy do końca)

Typ = 0 oznacza ratę płatną z dołu, za miniony miesiąc, Typ = 1 oznacza ratę płatną z góry, na

początku miesiąca lub kwartału

OK

Zadanie 5 Funkcja FV

Funkcja FV oblicza przyszłą wartość lokaty przy założeniu stałych płatności (rata – wartość

ujemna), danej wartości początkowej (wa – wartość ujemna) i stałej stopie procentowej
(stopa roczna). =FV(stopa; liczba_rat; rata; wa; typ)

Zadania:

a.

Obliczyć ile będzie pieniędzy na rachunku po 12 miesiącach, jeżeli wkład

początkowy wynosi 1000 zł, co miesiąc wpłacamy 100 zł a oprocentowanie w
stosunku rocznym 6%. Kapitalizacja odsetek następuje co miesiąc.

b.

Bank oferuje następujące usługi:

c. lokatę miesięczną przy oprocentowaniu 28% w stosunku rocznym
d. lokatę kwartalną przy oprocentowaniu 30% w stosunku rocznym

Dysponujemy kwotą 2 000 zł, gdzie korzystniej umieścić te pieniądze na 2 lata ?

Zadanie 6 Funkcja PV

Funkcja PV oblicza wartość bieżącą przyszłych płatności, przy założeniu stałych płatności i

stałej stopie procentowej. Składnia formuły tej funkcji ma następującą postać:

=PV(stopa; liczba_rat; rata; wp; typ)
Stopa – stopa procentowa
Liczba_rat – całkowita liczba płatności i kapitalizacji
Rata – okresowa wpłata nie ulegająca zmianie w czasie (ujemna)
Wp – wartość końcowa
Typ - to cyfra 0 lub 1 wskazująca, kiedy płatność ma miejsce (0 na końcu okresu, 1- na

początku okresu)

a) obliczyć jaką kwotę trzeba zdeponować, aby po 3 latach zgromadzić 20000 zł, jeżeli
kapitalizacja następuje co miesiąc, a oprocentowanie wynosi 8% w skali roku

b) obliczyć jaką kwotę trzeba zdeponować, aby po 2 latach zgromadzić 10000 zł, jeżeli
kapitalizacja następuje co kwartał, a oprocentowanie wynosi 6% w skali roku

c) obliczyć ile należy wpłacić do banku, aby uzyskać po 20 latach 100000
zł.Oprocentowanie wynosi 10% w stosunku rocznym, kapitalizacja co roku.

d) Mamy dwie opcje wynajmu samochodów: miesięczna rata to 500zł kontrakt na 5 lat i
miesięczna rata to 400zł kontrakt na 6 lat. Która opcja jest dla nas bardziej korzystna z
punktu widzenia dzisiejszej wartości przyszłych wpłat przy założeniu, że roczna stopa
procentowa to 4%.

Zadanie 7 Funkcja RATE

RATE(liczba rat; rata; wa; wp; typ; przypuszczenie) – oblicza, jaka powinna być stopa

procentowa, aby lokata początkowa oraz seria płatności osiągnęły przez dany okres
wartość końcową.

a) Bank udziela pożyczki w wysokości 1000 zł na 10 lat, po upływie których otrzymuje

6191,74 zł. Jakie jest oprocentowanie tej pożyczki?

b)Wpłacamy kwotę 1000 zł na konto i zamierzamy wpłacać miesięcznie po 100 zł. Po roku na

koncie jest 2284,16 zł. Jakie jest roczne oprocentowanie konta?

Zadanie 8 Funkcja NPER

NPER(stopa;rata;wa;wp;typ) – oblicza liczbę spłat kredytu przy okresowych stałych wpłatach

i stałej stopie procentowej.

a) Bank udziela pożyczki w wysokości 1000 zł z oprocentowaniem rocznym 10%. Po jakim

czasie wpłacimy do banku 3000 zł, jeżeli co miesiąc będziemy wpłacać 200 zł

b) Przez ile miesięcy trzeba wpłacać do banku po 300 zł, aby zaoszczędzić kwotę 18000 zł,
jeśli wkłady są oprocentowane na 7% w skali roku?

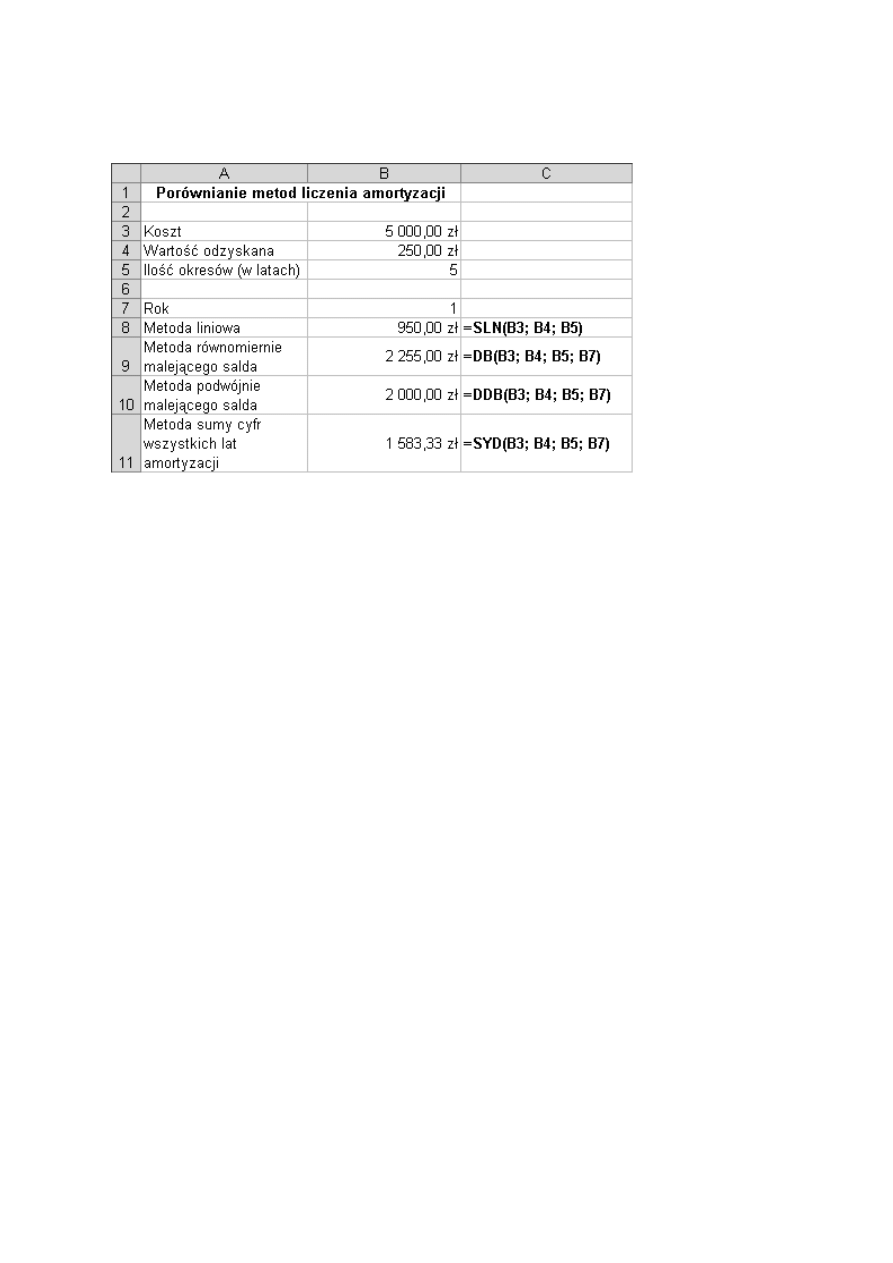
Zadanie 9 Amortyzacja środków trwałych

Amortyzacja

- proces utraty wartości majątku trwałego, wywołany jego zużyciem fizycznym - powstałym w

skutek eksploatacji oraz ekonomicznym (moralnym) - będącym wynikiem postępu technicznego, związanego z
możliwością uzyskania na rynku np. maszyn, urządzeń bardziej wydajnych, tańszych w eksploatacji,
pozwalających uzyskać produkty lepszej jakości. Ta utrata wartości jest przenoszona na wartość produktów
wytworzonych przy wykorzystaniu amortyzowanego majątku trwałego.

Funkcja SLN

Funkcja

SLN

oblicza wartość amortyzacji liniowej środka trwałego dla jednego okresu.

Składnia funkcji jest następująca:

SLN(koszt; odzysk; czas_życia)

gdzie

koszt

to koszt początkowy środka trwałego,

odzysk

to wartość środka trwałego po

zakończeniu okresu amortyzacji (argument ten nazywany jest nieraz wartością odzyskaną
środka trwałego) a

czas_życia

to liczba okresów, w których środek trwały jest amortyzowany

(argument ten nazywany jest nieraz czasem użytkowania środka trwałego). Wszystkie trzy
parametry są wymagane.

Funkcja DB

Funkcja DB oblicza amortyzację środka trwałego w podanym okresie, obliczoną z
wykorzystaniem metody równomiernie malejącego salda. Składnia funkcji jest następująca:

DB(koszt;odzysk;czas_życia;okres;miesiąc)

Pierwsze trzy parametry są identyczne jak w przypadku funkcji

SLN

. Argument

okres

to okres,

dla którego zostanie obliczona amortyzacja. Argument okres musi być wyrażony w tych
samych jednostkach, co argument

czas_życia

. Pierwsze cztery argumenty funkcji są wymagane,

natomiast

miesiąc

(parametr opcjonalny) to liczba miesięcy w pierwszym roku. Jeżeli argument

zostanie pominięty, przyjmowana jest liczba miesięcy równa 12.

Funkcja DDB

Funkcja

DDB

oblicza amortyzację środka trwałego w podanym okresie, obliczoną przy użyciu

metody podwójnie malejącego salda lub innej metody określonej przez użytkownika.
Składnia funkcji jest następująca:

DDB(koszt;odzysk;czas_życia;okres;współczynnik)

Znaczenie pierwszych czterech argumentów jest identyczne jak w przypadku funkcji

DB

;

wszystkie cztery argumenty są wymagane. Ostatni argument,

współczynnik

, to szybkość

zmniejszania się salda. Jeżeli współczynnik ten zostanie pominięty, to zakłada się, że wynosi
2 (metoda podwójnie malejącego salda).

Funkcja SYD

Funkcja

SYD

oblicza amortyzację środka trwałego w podanym okresie metodą sumy cyfr

wszystkich lat amortyzacji. Składnia funkcji jest następująca:

SYD(koszt;odzysk;czas_życia;okres)

Znaczenie argumentów jest identyczne jak w przypadku funkcji

DB

i

DDB

; wszystkie cztery

argumenty są wymagane.

a) Za pomocą metody liniowej obliczyć wartość amortyzacji środka trwałego o koszcie
początkowym 10000 zł, wartości odzyskanej 1000 zł, jeżeli czas użytkowania wynosi 4 lata.

b) Za pomocą metody równomiernie malejącego salda obliczyć wartość amortyzacji maszyny
o koszcie początkowym 55000, wartości odzyskanej 6000 zł, w 2 roku amortyzacji, jeżeli
czas użytkowania wynosi 4 lata przyjmując, że w pierwszym roku maszyna była
wykorzystywana przez 5 miesięcy.

c) Za pomocą metody podwójnie malejącego salda obliczyć amorytzację samochodu o
koszcie 75000 zł, którego wartość odzyskana wynosi 25000 w 3 roku amortyzacji, jeżeli czas
użytkowania wynosi 5 lat. Przeprowadzić też te same obliczenia dla metody ze
współczynnikiem = 1,5.

d) Za pomocą metody sumy cyfr wszystkich lat amortyzacji obliczyć wartość amortyzacji
maszyny o koszcie początkowym 15000, wartości odzyskanej 1000 zł, w 1 roku amortyzacji,
jeżeli czas użytkowania wynosi 4 lata.